Effective Magnetic Field Dependence of the Flux Pinning Energy in FeSe0.5Te0.5 Superconductor
Abstract
:1. Introduction
2. Experimental Details
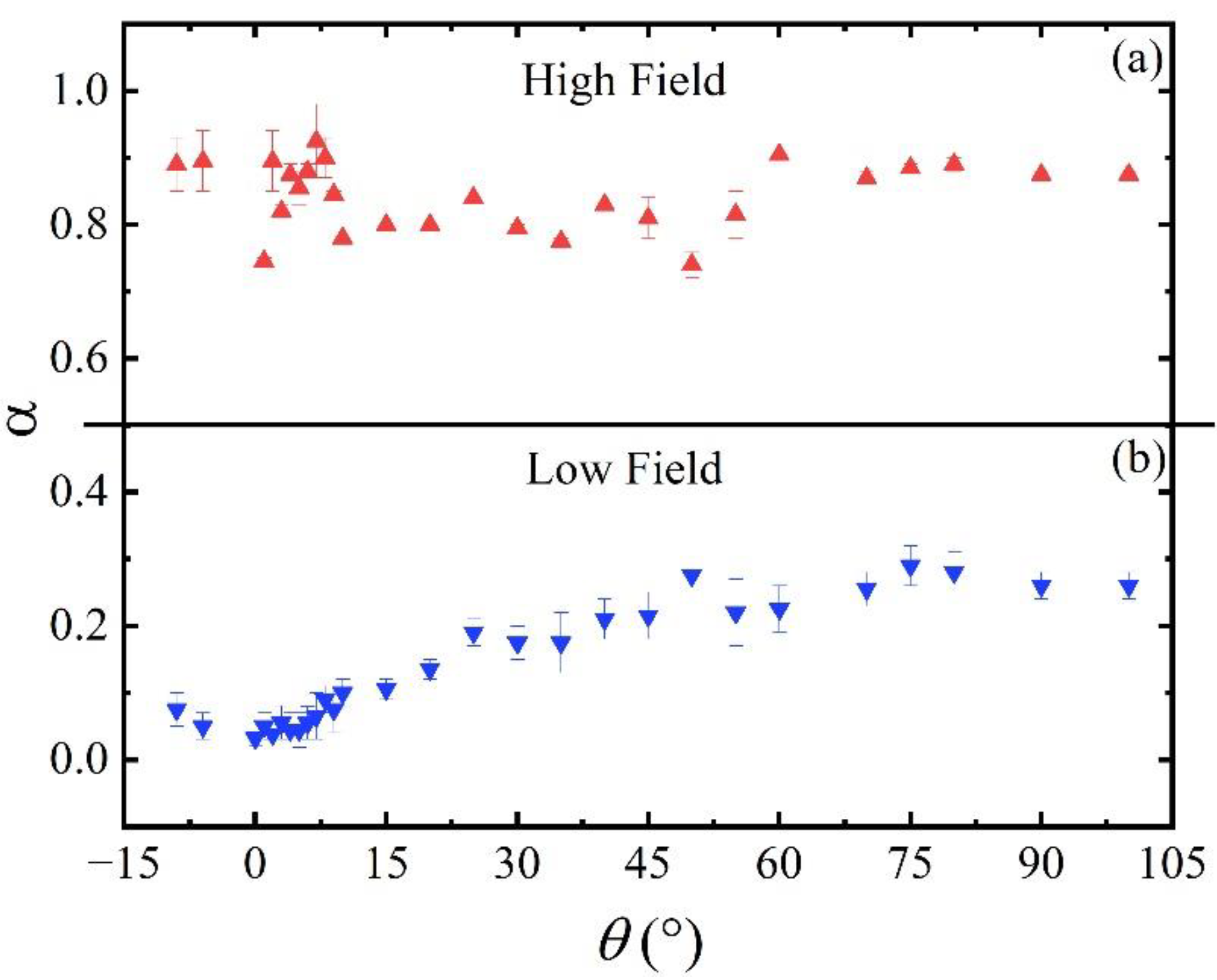
3. Angular Dependence of Flux Pinning Energy
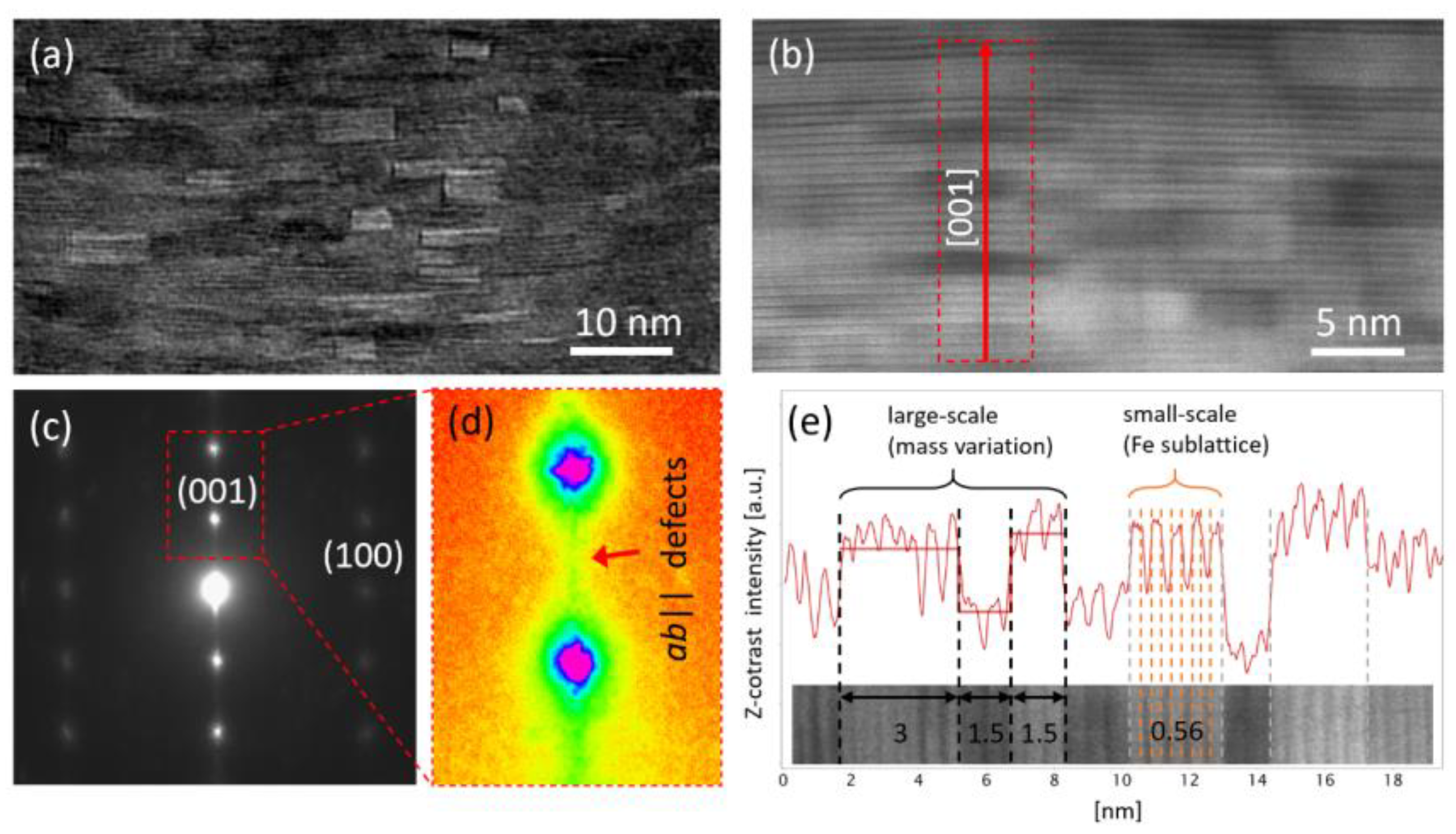
4. Microstructure Analysis of Material Defects
5. Correlation between Nanoscale Defects and Pinning Energy
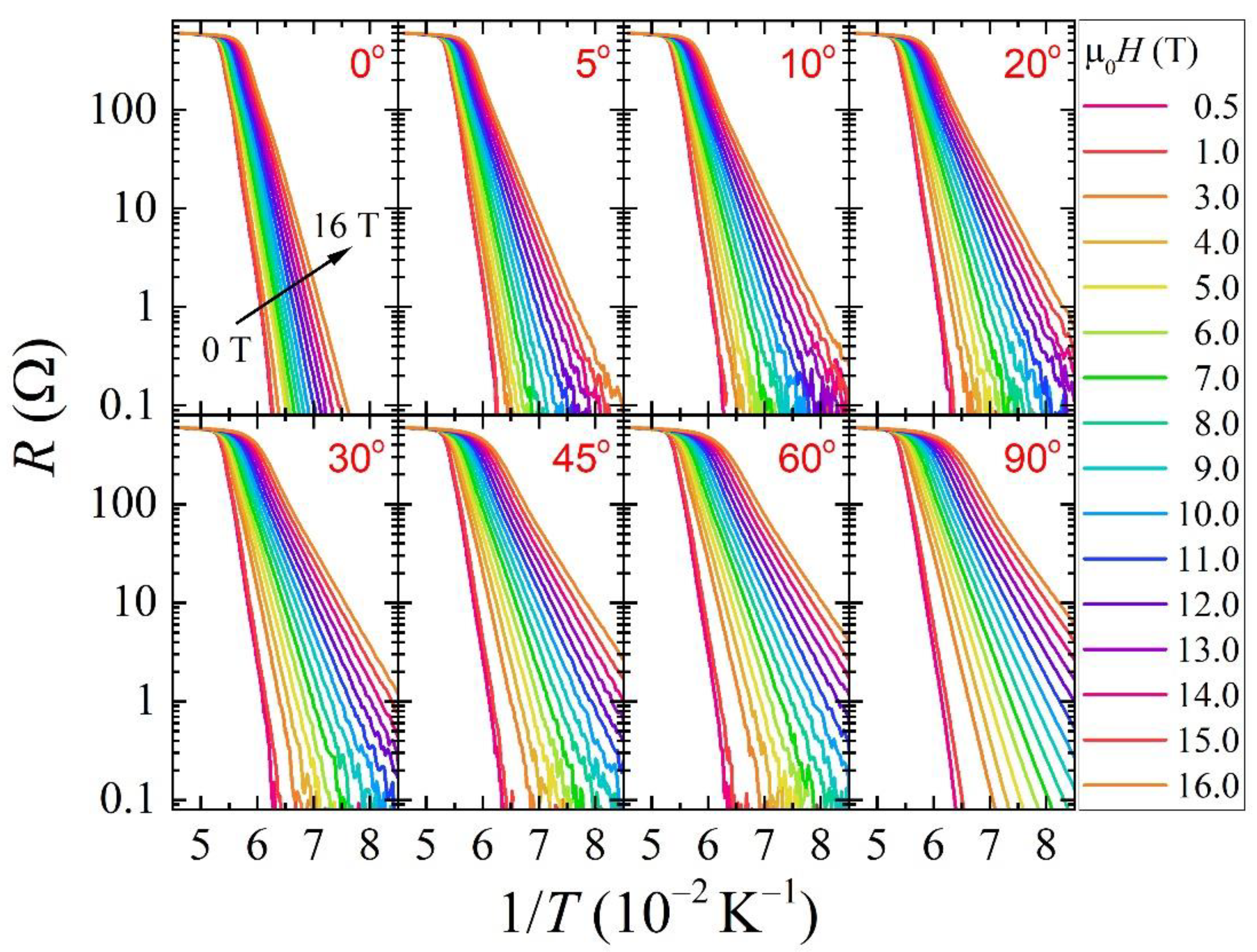
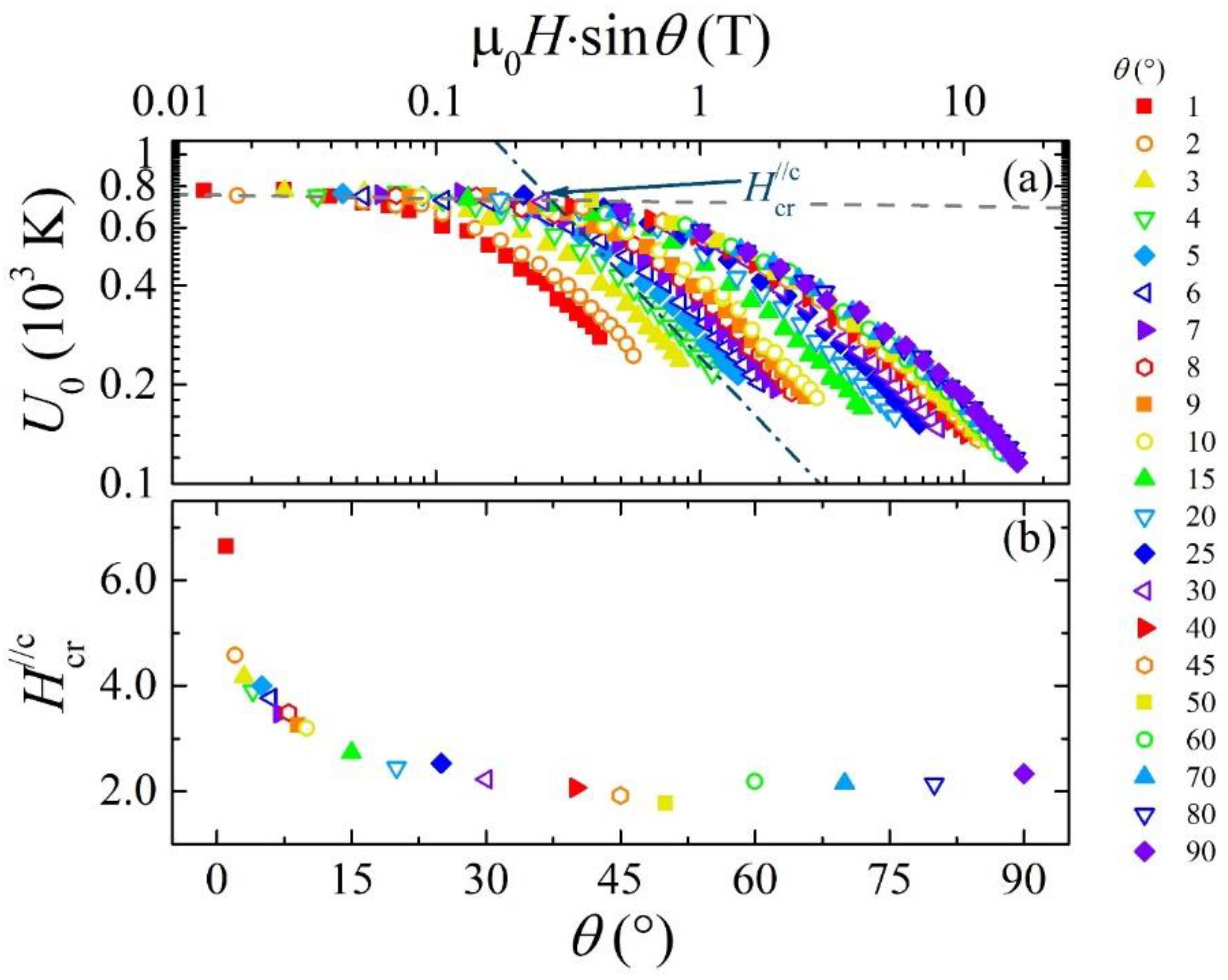
6. Magnetic Field Dependence of Flux Pinning Energy
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blatter, G.; Feigel’Man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Blatter, G.; Geshkenbein, V.; Larkin, A. Low-field phase diagram of layered superconductors: The role of electromagnetic coupling. Phys. Rev. B-Condens. Matter Mater. Phys. 1996, 54, 72–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O1-xFx]FeAs (x= 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
- Hsu, F.C.; Luo, J.Y.; Yeh, K.W.; Chen, T.K.; Huang, T.W.; Wu, P.M.; Lee, Y.C.; Huang, Y.L.; Chu, Y.Y.; Yan, D.C.; et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. USA 2008, 105, 14262–14264. [Google Scholar] [CrossRef] [Green Version]
- Si, W.; Han, S.J.; Shi, X.; Ehrlich, S.N.; Jaroszynski, J.; Goyal, A.; Li, Q. High current superconductivity in FeSe0.5Te0.5-coated conductors at 30 tesla. Nat. Commun. 2013, 4, 1347. [Google Scholar] [CrossRef]
- Iida, K.; Hänisch, J.; Tarantini, C. Fe-based superconducting thin films on metallic substrates: Growth, characteristics, and relevant properties. Appl. Phys. Rev. 2018, 5, 031304. [Google Scholar] [CrossRef]
- Figueras, J.; Puig, T.; Obradors, X. Influence of twin boundaries and randomly oriented correlated dis-order on the liquid vortex plasticity of YBa2Cu3O7. Phys. Rev. B-Condens. Matter Mater. Phys. 2003, 67, 014503. [Google Scholar] [CrossRef]
- Brandt, E.H. The flux-line lattice in superconductors. Rep. Prog. Phys. 1995, 58, 1465–1594. [Google Scholar] [CrossRef] [Green Version]
- Palstra, T.T.M.; Batlogg, B.; van Dover, R.B.; Schneemeyer, L.F.; Waszczak, J.V. Dissipative flux motion in high-temperature super-conductors. Phys. Rev. B 1990, 41, 6621–6632. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, S.; Shi, D.; Wang, Z.; Smith, M.E.; Salem-Sugui, S.; McGinn, P.J. Magnetic relaxation and in-trinsic pinning in a single crystal of Bi2Sr2CaCu2Ox. Phys. Rev. B 1993, 47, 5414–5418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Correa, A.; Mompeán, F.; Guillamón, I.; Herrera, E.; García-Hernández, M.; Yamamoto, T.; Kashiwagi, T.; Kadowaki, K.; Buzdin, A.I.; Suderow, H.; et al. Attractive interaction between superconducting vortices in tilted magnetic fields. Commun. Phys. 2019, 2, 31. [Google Scholar] [CrossRef]
- Buzdin, A.I.; and Simonov, A.Y. Magnetization of anisotropic superconductors in the tilted magnetic field. Phys. C Supercond. Appl. 1991, 175, 143–155. [Google Scholar] [CrossRef]
- Kogan, V.G.; Kirtley, J.R. Determining the vortex tilt relative to a superconductor surface. Phys. Rev. B 2017, 96, 174516. [Google Scholar] [CrossRef] [Green Version]
- Grimaldi, G.; Leo, A.; Martucciello, N.; Braccini, V.; Bellingeri, E.; Ferdeghini, C.; Galluzzi, A.; Polichetti, M.; Nigro, A.; Villégier, J.C.; et al. Weak or Strong Anisotropy in Fe(Se,Te) Superconducting Thin Films Made of Layered Iron-Based Material? IEEE Trans. Appl. Supercond. 2019, 29, 7500104. [Google Scholar] [CrossRef]
- Sylva, G.; Bellingeri, E.; Ferdeghini, C.; Martinelli, A.; Pallecchi, I.; Pellegrino, L.; Putti, M.; Ghigo, G.; Gozzelino, L.; Torsello, D.; et al. Effects of high-energy proton irradiation on the superconducting properties of Fe(Se,Te) thin films. Supercond. Sci. Technol. 2018, 31, 054001. [Google Scholar] [CrossRef] [Green Version]
- Krivanek, O.L.; Chisholm, M.F.; Nicolosi, V.; Pennycook, T.J.; Corbin, G.J.; Dellby, N.; Murfitt, M.F.; Own, C.S.; Szilagyi, Z.S.; Oxley, M.P.; et al. Atom-by-atom structural and chemical analysis by annular dark-field electron micros-copy. Nature 2010, 464, 571–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Treacy, M.M.J. Z Dependence of Electron Scattering by Single Atoms into Annular Dark-Field Detectors. Microsc. Microanal. 2011, 17, 847–858. [Google Scholar] [CrossRef]
- Lei, H.; Hu, R.; Petrovic, C. Critical fields, thermally activated transport, and critical current density of β-FeSe single crystals. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 84, 014520. [Google Scholar] [CrossRef] [Green Version]
- Tinkham, M. Resistive transition of high-temperature superconductors. Phys. Rev. Lett. 1988, 61, 1658–1661. [Google Scholar] [CrossRef]
- Budhani, R.C.; Welch, D.O.; Suenaga, M.; Sabatini, R.L. Field-induced broadening of the resistive transition and two-dimensional nature of flux pinning in Y2Ba4Cu8O16 films. Phys. Rev. Lett. 1990, 64, 1666–1669. [Google Scholar] [CrossRef]
- Shahbazi, M.; Wang, X.L.; Ghorbani, S.R.; Dou, S.X.; Lin, C.T. Thermally activated flux flow in Fe1.06Te0.6Se0.4 single crystal. Phys. C Supercond. Appl. 2015, 519, 60–64. [Google Scholar] [CrossRef]
- Lei, H.; Hu, R.; Choi, E.S.; Petrovic, C. Thermally activated energy and flux-flow Hall effect of Fe1+y(Te1+xSx)z. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 134525. [Google Scholar] [CrossRef] [Green Version]
- Leo, A.; Grimaldi, G.; Guarino, A.; Avitabile, F.; Nigro, A.; Galluzzi, A.; Mancusi, D.; Polichetti, M.; Pace, S.; Buchkov, K.; et al. Vortex pinning properties in Fe-chalcogenides. Supercond. Sci. Technol. 2015, 28, 125001. [Google Scholar] [CrossRef]
- Ahmad, D.; Choi, W.J.; Seo, Y.I.; Seo, S.; Lee, S.; Kwon, Y.S. Thermally activated flux flow in superconducting epitaxial FeSe0.6Te0.4 thin film. Results Phys. 2017, 7, 16–20. [Google Scholar] [CrossRef] [Green Version]
- Scuderi, M.; Pallecchi, I.; Leo, A.; Nigro, A.; Grimaldi, G.; Ferdeghini, C.; Spinella, C.; Guidolin, M.; Trotta, A.; Braccini, V. Nanoscale analysis of superconducting Fe(Se,Te) epitaxial thin films and relationship with pinning properties. Sci. Rep. 2021, in press. [Google Scholar]
- Shahbazi, M.; Wang, X.L.; Ghorbani, S.R.; Dou, S.X.; Choi, K.Y. Angular dependence of pinning potential, upper critical field, and irreversibility field in underdoped BaFe1.9Co0.1As2 single crystal. Appl. Phys. Lett. 2012, 100, 102601. [Google Scholar] [CrossRef] [Green Version]
- Amigó, M.L.; Crivillero, M.V.A.; Franco, D.G.; Badía–Majós, A.; Guimpel, J.; Campo, J.; Damay, F.; Porcher, F.; Condó, A.M.; Nieva, G. Intrinsic pinning by naturally occurring correlated defects in FeSe1-xTex superconductors. Supercond. Sci. Technol. 2017, 30, 085010. [Google Scholar] [CrossRef] [Green Version]
- Teng, M.L.; Yin, Y.W.; Dong, S.N.; Su, T.S.; Zhang, M.J.; Huang, W.C.; Li, X.G. Anisotropic transport property anomaly in K0.8Fe1.65Se2 crys-tal. J. Appl. Phys. 2014, 115, 143905. [Google Scholar] [CrossRef]
- Iida, K.; Hänisch, J.; Reich, E.; Kurth, F.; Hühne, R.; Schultz, L.; Holzapfel, B.; Ichinose, A.; Hanawa, M.; Tsukada, I.; et al. Intrinsic pinning and the critical current scaling of clean epitaxial Fe(Se,Te) thin films. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 87, 104510. [Google Scholar] [CrossRef] [Green Version]
- Leo, A.; Sylva, G.; Braccini, V.; Bellingeri, E.; Martinelli, A.; Pallecchi, I.; Ferdeghini, C.; Pellegrino, L.; Putti, M.; Ghigo, G.; et al. Anisotropic Effect of Proton Irradiation on Pinning Properties of Fe(Se,Te) Thin Films. IEEE Trans. Appl. Supercond. 2019, 29, 7300205. [Google Scholar] [CrossRef]
- Leo, A.; Guarino, A.; Grimaldi, G.; Nigro, A.; Pace, S.; Bellingeri, E.; Kawale, S.; Ferdeghini, C.; Giannini, E. Comparison of the pinning energy in Fe(Se1-xTex) compound be-tween single crystals and thin films. J. Phys. Conf. Ser. 2014, 507, 012029. [Google Scholar] [CrossRef] [Green Version]
- Yeshurun, Y.; Malozemoff, A.P. Giant flux creep and irreversibility in an Y-Ba-Cu-O crystal: An al-ternative to the superconducting-glass model. Phys. Rev. Lett. 1988, 60, 2202–2205. [Google Scholar] [CrossRef]
- Bellingeri, E.; Kawale, S.; Caglieris, F.; Braccini, V.; Lamura, G.; Pellegrino, L.; Sala, A.; Putti, M.; Ferdeghini, C.; Jost, A.; et al. High field vortex phase diagram of Fe(Se,Te) thin films. Supercond. Sci. Technol. 2014, 27, 044007. [Google Scholar] [CrossRef] [Green Version]
- Blatter, G.; Geshkenbein, V.B.; Larkin, A.I. From isotropic to anisotropic superconductors: A scaling approach. Phys. Rev. Lett. 1992, 68, 875. [Google Scholar] [CrossRef]
- Llovo, I.F.; Carballeira, C.; Sóñora, D.; Pereiro, A.; Ponte, J.J.; Salem-Sugui, S.; Sefat, A.S.; Mosqueira, J. Multiband effects on the upper critical field angular dependence of 122-family iron pnictide superconductors. Sci. Rep. 2021, 11, 11526. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.L.; Voss-de Haan, P.; Jakob, G.; Kluge, T.; Haibach, P.; Adrian, H.; Andrei, E.Y. Flux-flow instability and its anisotropy in Bi2Sr2CaCu2O8+δ superconducting films. Phys. Rev. B 1999, 59, 1481. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Nigro, A.; Pace, S.; Braccini, V.; Bellingeri, E.; Ferdeghini, C. Angular dependence of vortex instability in a layered superconductor: The case study of Fe(Se,Te) material. Sci. Rep. 2018, 8, 4150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casaca, A.; Bonfait, G.; Galindo, V.; Sénateur, J.P.; Feinberg, D. Angular Dependence of the Activation Energy in YBCO/PBCO Multilayers. J. Low Temp. Phys. 1999, 117, 1459–1463. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.J.; Ong, C.K. Angular field-dependent dimensional transition in YBa2Cu3O7/PrBa2Cu3O7 superlattice. Phys. C Supercond. Appl. 2000, 329, 279–284. [Google Scholar] [CrossRef]
- Palstra, T.T.M.; Batlogg, B.; Schneemeyer, L.F.; Waszczak, J.V. Thermally Activated Dissipation in Bi2.2Sr2Ca0.8Cu2O8+. Phys. Rev. Lett. 1988, 61, 1662–1665. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.R.; Leo, A.; Nigro, A.; Galluzzi, A.; Polichetti, M.; Braccini, V.; Cialone, M.; Scuderi, M.; Grimaldi, G. Effective Magnetic Field Dependence of the Flux Pinning Energy in FeSe0.5Te0.5 Superconductor. Materials 2021, 14, 5289. https://doi.org/10.3390/ma14185289
Khan MR, Leo A, Nigro A, Galluzzi A, Polichetti M, Braccini V, Cialone M, Scuderi M, Grimaldi G. Effective Magnetic Field Dependence of the Flux Pinning Energy in FeSe0.5Te0.5 Superconductor. Materials. 2021; 14(18):5289. https://doi.org/10.3390/ma14185289
Chicago/Turabian StyleKhan, Masood Rauf, Antonio Leo, Angela Nigro, Armando Galluzzi, Massimiliano Polichetti, Valeria Braccini, Matteo Cialone, Mario Scuderi, and Gaia Grimaldi. 2021. "Effective Magnetic Field Dependence of the Flux Pinning Energy in FeSe0.5Te0.5 Superconductor" Materials 14, no. 18: 5289. https://doi.org/10.3390/ma14185289
APA StyleKhan, M. R., Leo, A., Nigro, A., Galluzzi, A., Polichetti, M., Braccini, V., Cialone, M., Scuderi, M., & Grimaldi, G. (2021). Effective Magnetic Field Dependence of the Flux Pinning Energy in FeSe0.5Te0.5 Superconductor. Materials, 14(18), 5289. https://doi.org/10.3390/ma14185289











