Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk–Blade Assemblies Reinforced by Graphene Nanoplatelets
Abstract
:1. Introduction
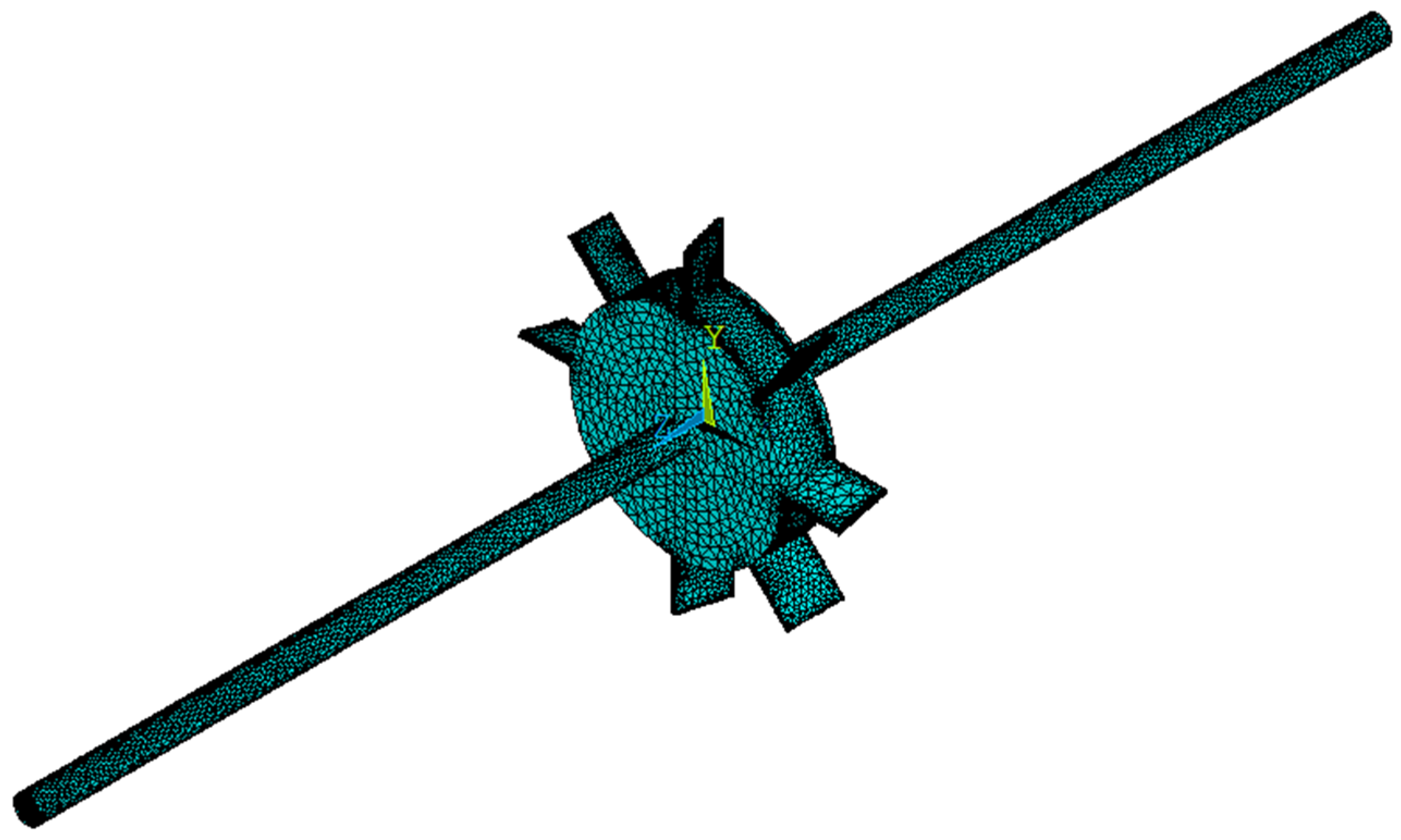
2. Physical Model
3. Finite Element Implementation
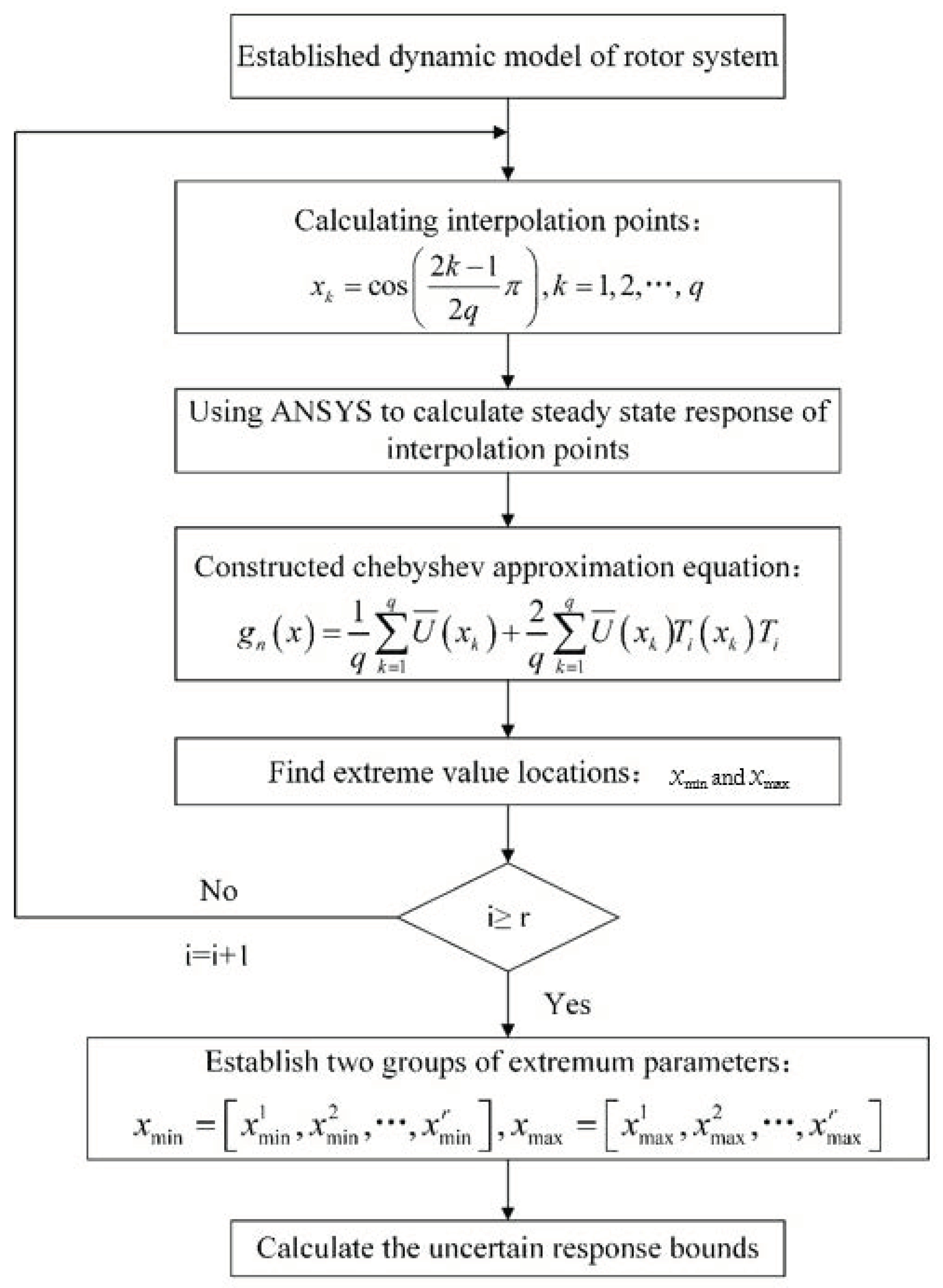
4. Interval Uncertainty Analysis
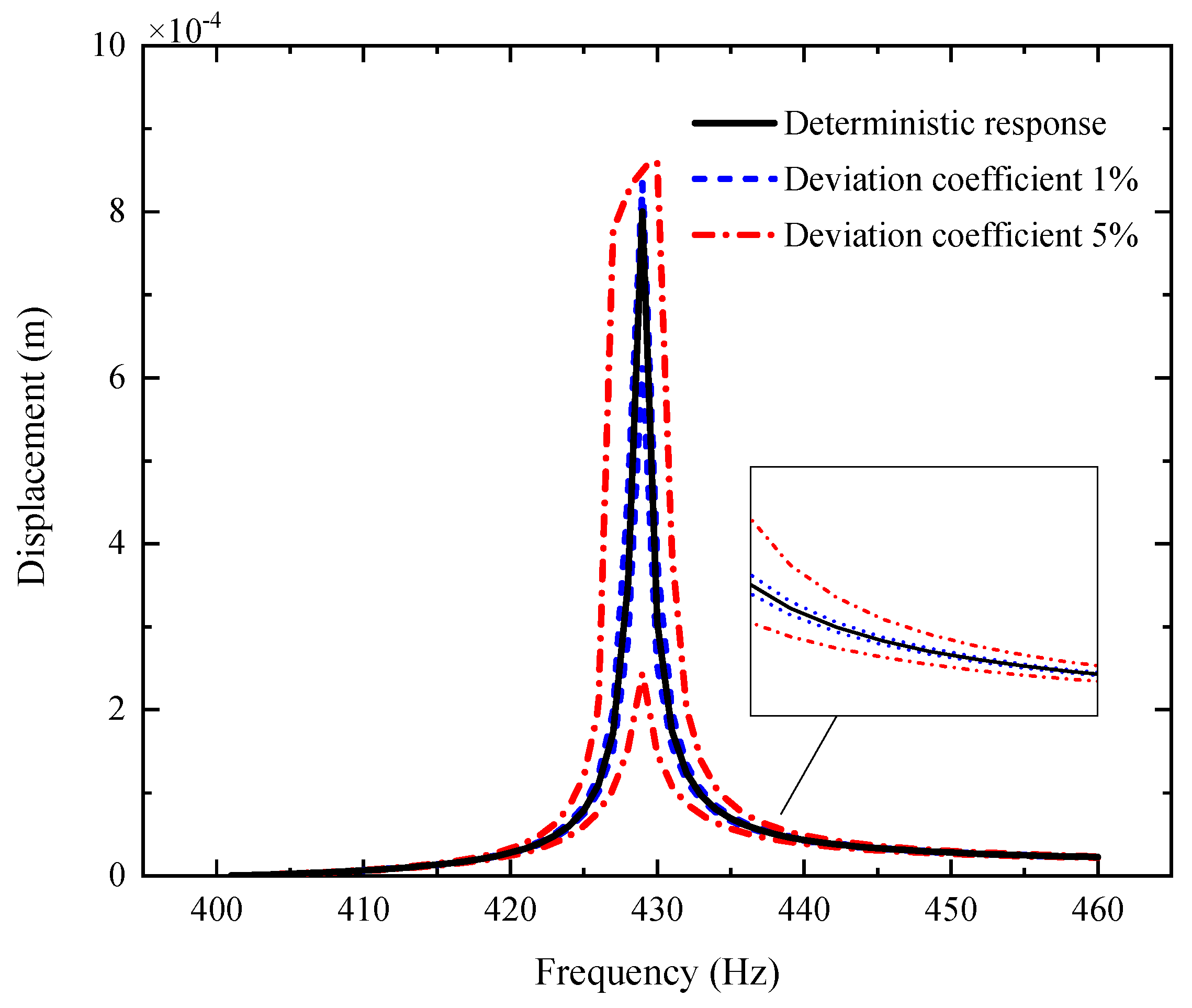
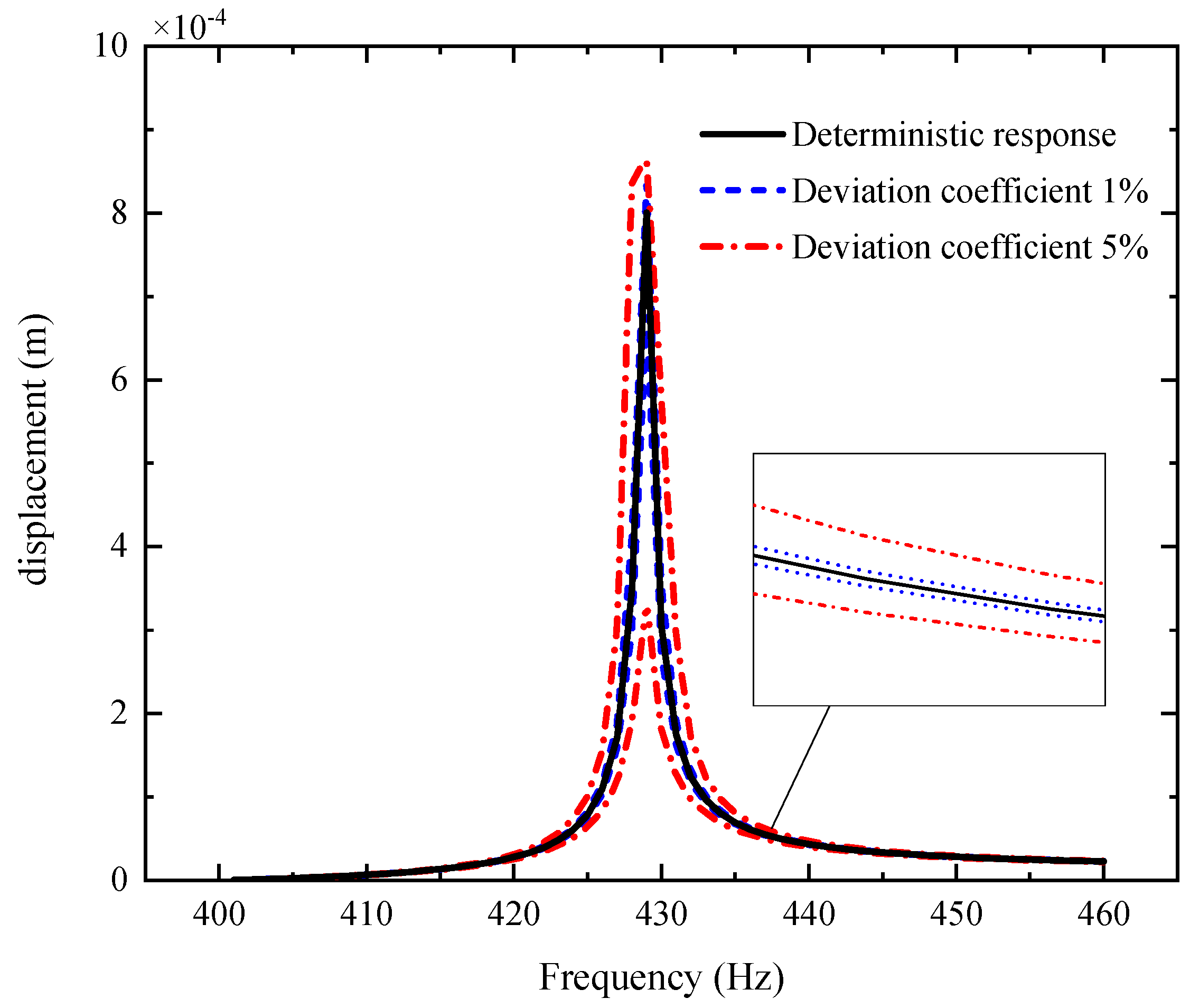
5. Results and Discussions
6. Conclusions
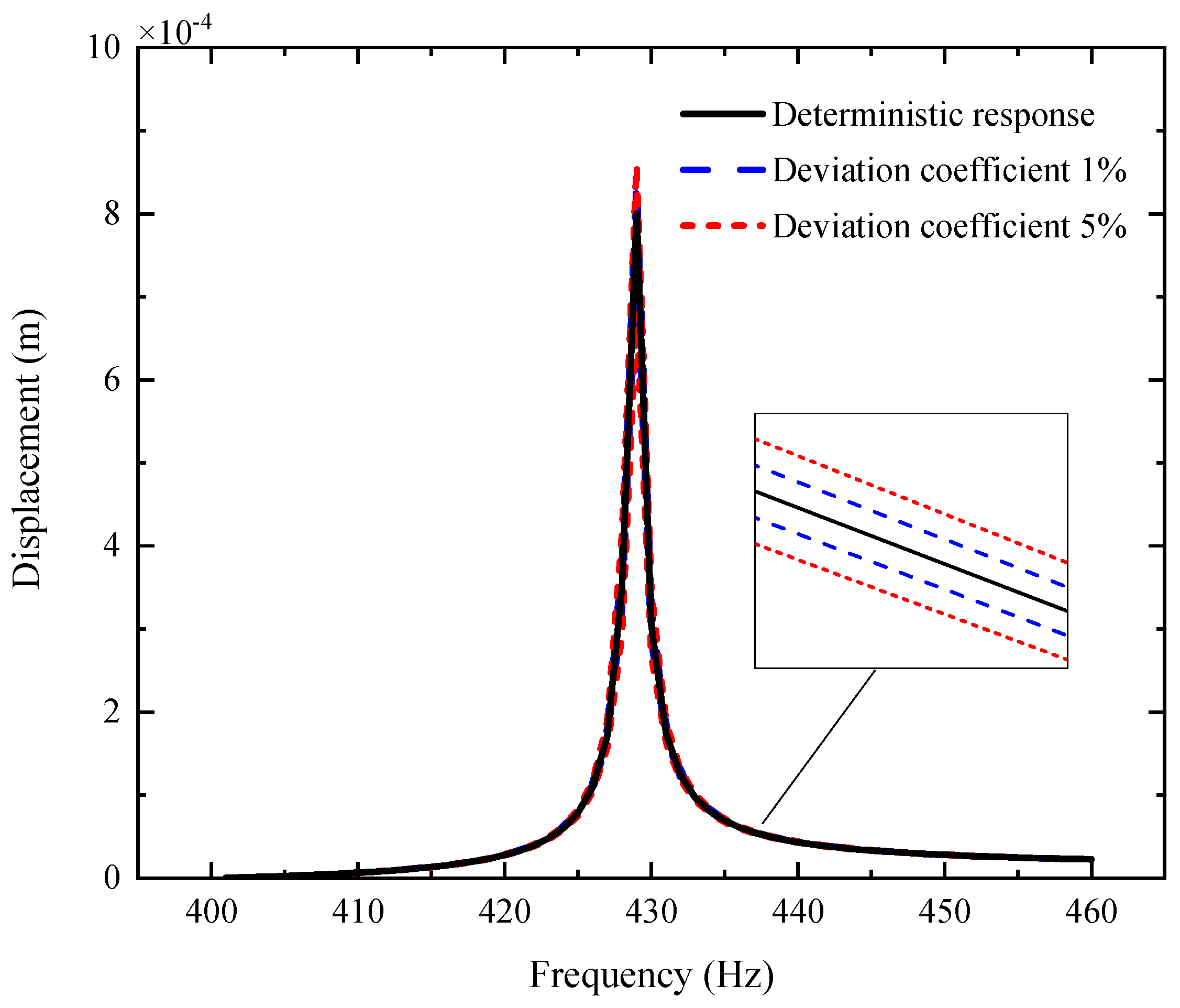
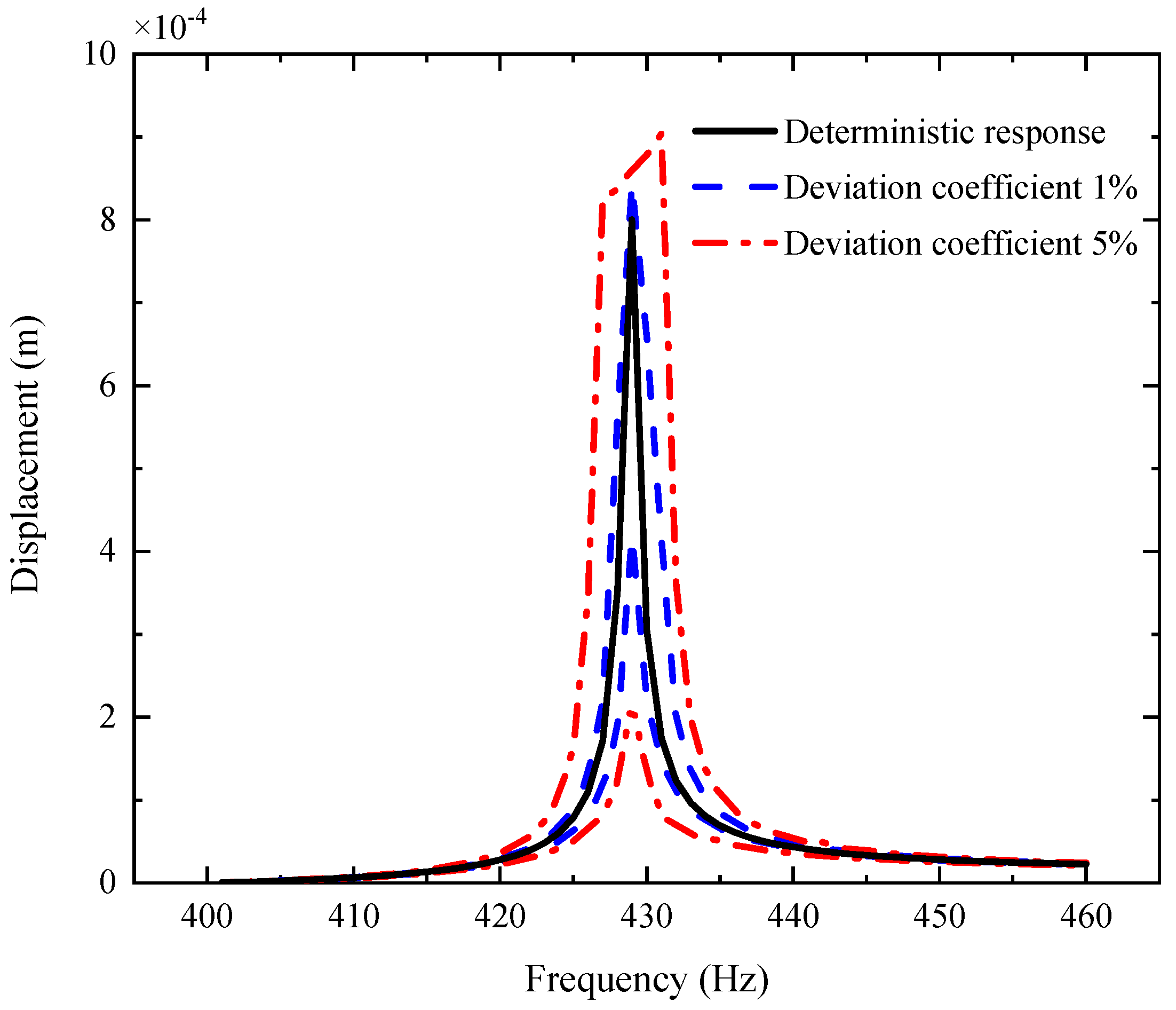
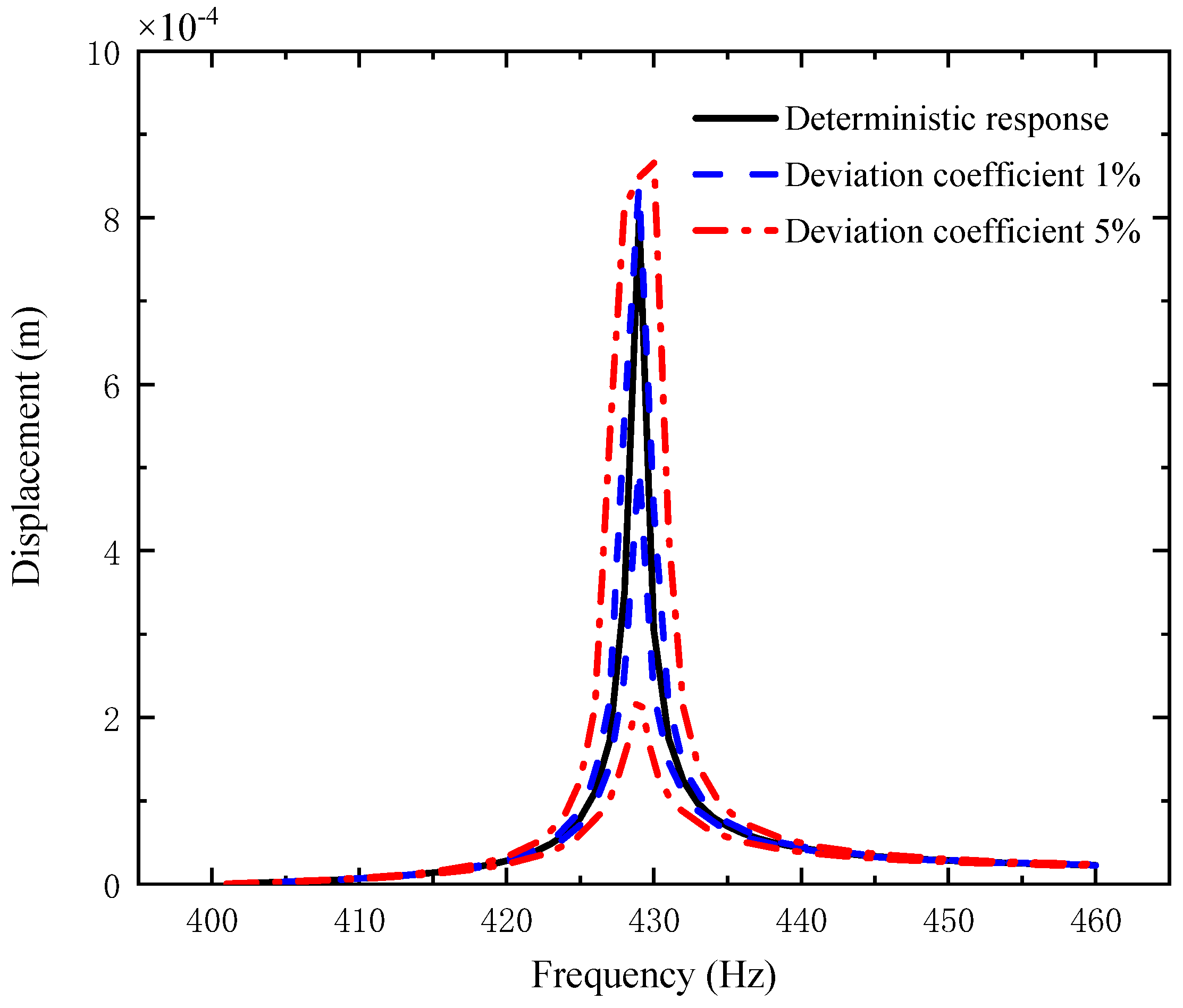
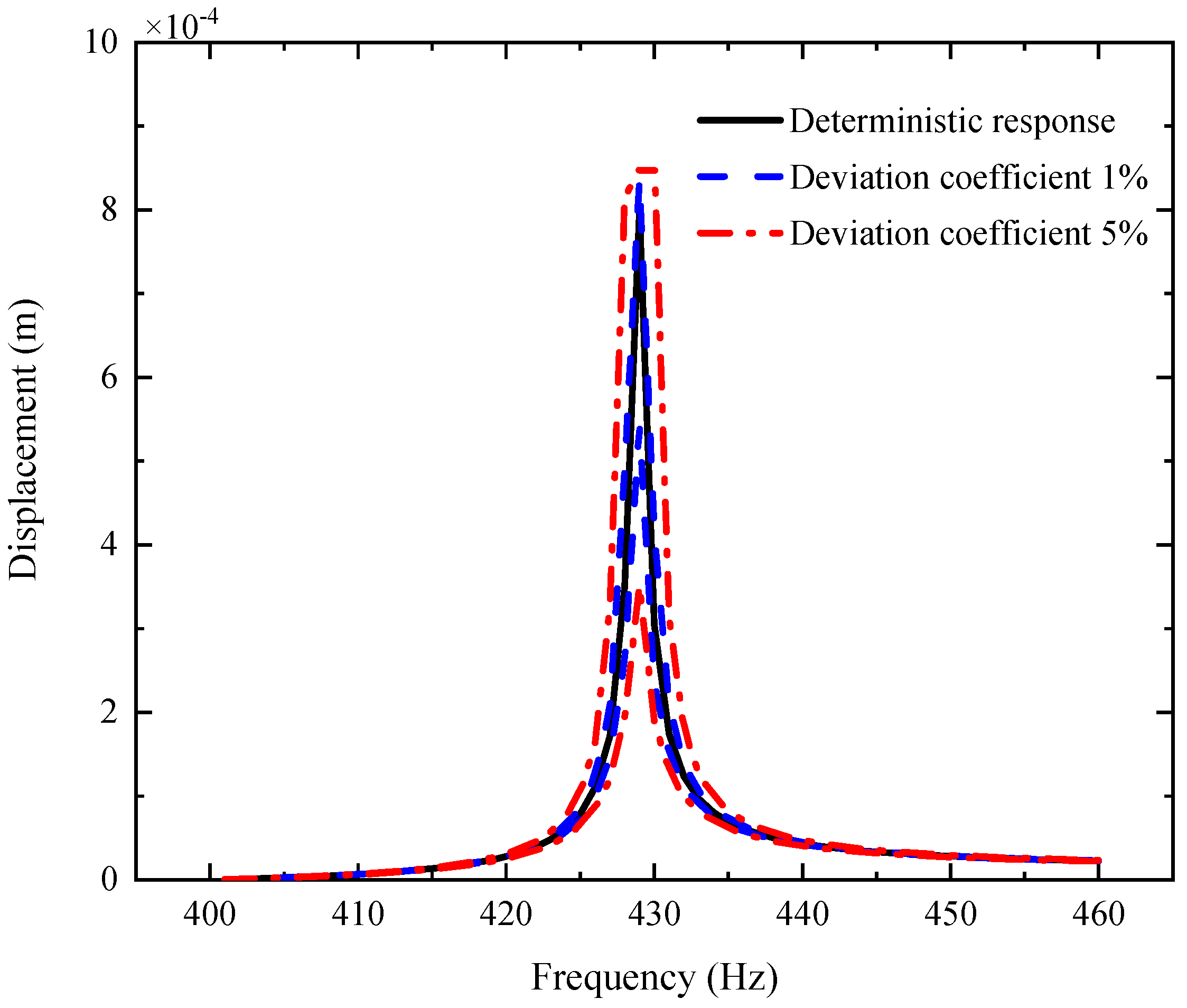
- The uncertain parameters make the fluctuation of the resonance peak larger and the fluctuation of the non-resonance peak smaller.
- The fluctuation coefficient of the GPL length-to-thickness ratio has the greatest influence on the amplitude–frequency response, while that of porosity has the lowest impact.
- The fluctuation of the amplitude–frequency response with double uncertain parameters is much stronger than that with a single uncertain parameter.
- The dimensions of GPLs have greater effects on the vibration behavior of the shaft–disk–blade assembly as thinner GPLs with larger surface areas provide better load transfer capability.
Author Contributions
Funding
Conflicts of Interest
References
- She, H.X.; Li, C.F.; Tang, Q.S.; Wen, B.C. Influence mechanism of disk position and flexibility on natural frequencies and critical speeds of a shaft-disk-blade unit. J. Sound Vib. 2020, 469, 115156. [Google Scholar] [CrossRef]
- Heydari, H.; Khorram, A.; Afzalipour, L. The Influences of Stagger and Pretwist Angles of Blades on Coupling Vibration in Shaft-Disk-Blade Systems. J. Vib. Acoust. 2020, 142, 011007. [Google Scholar] [CrossRef]
- Li, C.F.; She, H.X.; Tang, Q.S.; Wen, B.C. The coupling vibration characteristics of a flexible shaft-disk-blades system with mistuned features. Appl. Math. Model. 2019, 67, 557–572. [Google Scholar] [CrossRef]
- Yadav, H.M.; Nath, N.C.D.; Kim, J.; Shinde, S.K.; Ramesh, S.; Hossain, F.; Ibukun, O.; Lee, J. Nickel-Graphene nanoplatelet deposited on carbon fiber as binder-free electrode for electrochemical supercapacitor application. Polymers 2020, 12, 1666. [Google Scholar] [CrossRef]
- Ding, B.; Fan, Z.; Lin, Q.; Wang, J.; Chang, Z.; Li, T.; Henzie, J.; Kim, J.; Dou, H.; Zhang, X.; et al. Confined Pyrolysis of ZIF-8 Polyhedrons Wrapped with Graphene Oxide Nanosheets to Prepare 3D Porous Carbon Heterostructures. Small Methods 2019, 3, 1900277. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.L.; Wang, Y.Q. Free and forced vibration of beams reinforced by 3D graphene foam. Int. J. Appl. Mech. 2020, 12, 2050056. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, Z.Y.; Zhao, Z.; Xie, L.Y.; Yuan, H.Q. Modeling and free vibration analysis of rotating hub-blade assemblies reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Yang, Y.F.; Pan, H.G. Free vibration analysis of a spinning porous nanocomposite blade reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Song, M.T.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.L.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Twinkle, C.M.; Jeyaraj, P. Free vibration and stability of graphene platelet reinforced porous nano-composite cylindrical panel: Influence of grading, porosity and non-uniform edge loads. Eng. Struct. 2021, 230, 111670. [Google Scholar]
- Mohammad, Y.A.J.; Pedram, B.; Mohammad, H.; Rasool, P. Nonlinear vibration analysis of functionally graded GPL-RC conical panels resting on elastic medium. Thin-Walled Struct. 2021, 160, 107370. [Google Scholar]
- Salehi, M.; Gholami, R.; Ansari, R. Analytical solution approach for nonlinear vibration of shear deformable imperfect FG-GPLR porous nanocomposite cylindrical shells. Mech. Based Des. Struct. Mach. 2021, 49, 430–439. [Google Scholar]
- Nejadi, M.M.; Mohammadimeehr, M.; Mehrabi, M. Free vibration and stability analysis of sandwich pipe by considering porosity and graphene platelet effects on conveying fluid flow. Alexandria Eng. J. 2021, 60, 1945–1954. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, Y.; Zhu, J. On the free vibration and bending analysis of functionally graded nanocomposite spherical shells reinforced with graphene nanoplatelets: Three-Dimensional elasticity solutions. Eng. Struct. 2021, 226, 111376. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Yang, J. Coupled free vibration of spinning functionally graded porous double-bladed disk systems reinforced with graphene nanoplatelets. Materials 2020, 13, 5610. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Pan, H.G.; Yang, J.; Kitipornchai, S. Coupled free vibration of a functionally graded pre-twisted blade-shaft system reinforced with graphene nanoplatelets. Compos. Struct. 2021, 262, 113362. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197, 106335. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Pan, H.G.; Cai, Y. Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Appl. Math. Model. 2021, 93, 578–596. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Wang, Y.Q.; Pan, H.G. Vibration characteristics of graphene nanoplatelet reinforced disk-shaft rotor with eccentric mass. Mech. Adv. Mater. Struct. 2021, 28, 1–21. [Google Scholar]
- Mirmeysam, R.A.; Bekir, B. Free vibration and buckling behavior of functionally graded porous plates reinforced by graphene platelets using spectral Chebyshev approach. Compos. Struct. 2020, 253, 112765. [Google Scholar]
- Wang, Y.Q. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Vibration analysis of circular cylindrical shells made of metal foams under various boundary conditions. Int. J. Mech. Mater. Des. 2019, 15, 333–344. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wu, H.; Yang, F.L.; Wang, Q. An efficient method for vibration and stability analysis of rectangular plates axially moving in fluid. Appl. Math. Mech. 2021, 42, 291–308. [Google Scholar] [CrossRef]
- Siddiq, A.; Arciniega, R.; Sayed, T.E. A variational void coalescence model for ductile metals. Comput. Mech. 2012, 49, 185–195. [Google Scholar] [CrossRef]
- Mir, A.; Luo, X.; Siddiq, A. Smooth particle hydrodynamics study of surface defect machining for diamond turning of silicon. Int. J. Adv. Manuf. Technol. 2017, 88, 2461–2476. [Google Scholar] [CrossRef] [Green Version]
- Baghlani, A.; Najafgholipour, M.A.; Khayat, M. The influence of mechanical uncertainties on the free vibration of functionally graded graphene-reinforced porous nanocomposite shells of revolution. Eng. Struct. 2021, 228, 111356. [Google Scholar] [CrossRef]
- Dong, Y.H.; Li, Y.H.; Chen, D.; Yang, J. Vibration characteristics of functionally graded graphene reinforced porous nanocomposite cylindrical shells with spinning motion. Compos. B Eng. 2018, 145, 1–13. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, C.; Wang, Y.; Yang, J. Bending and vibration analysis of functionally graded trapezoidal nanocomposite plates reinforced with graphene nanoplatelets (GPLs). Compos. Struct. 2017, 180, 799–808. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Liu, Z.F.; Pan, H.G.; Zhang, H.Y.; Yuan, H.Q. Vibration Characteristics of Functionally Graded Porous Nanocomposite Blade-disk-shaft Rotor System Reinforced with Graphene Nanoplatelets. Appl. Compos. Mater. 2021, 28, 717–731. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Liu, Z.-F.; Zhao, T.-Y.; Yang, J. Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk–Blade Assemblies Reinforced by Graphene Nanoplatelets. Materials 2021, 14, 5033. https://doi.org/10.3390/ma14175033
Cai Y, Liu Z-F, Zhao T-Y, Yang J. Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk–Blade Assemblies Reinforced by Graphene Nanoplatelets. Materials. 2021; 14(17):5033. https://doi.org/10.3390/ma14175033
Chicago/Turabian StyleCai, Yi, Zi-Feng Liu, Tian-Yu Zhao, and Jie Yang. 2021. "Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk–Blade Assemblies Reinforced by Graphene Nanoplatelets" Materials 14, no. 17: 5033. https://doi.org/10.3390/ma14175033
APA StyleCai, Y., Liu, Z.-F., Zhao, T.-Y., & Yang, J. (2021). Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk–Blade Assemblies Reinforced by Graphene Nanoplatelets. Materials, 14(17), 5033. https://doi.org/10.3390/ma14175033






