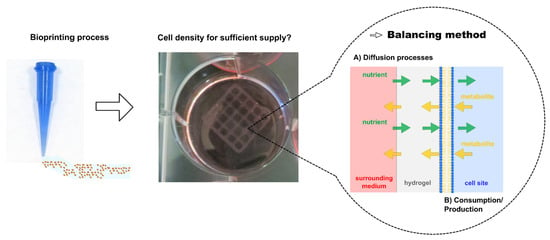
Calculation of Mass Transfer and Cell-Specific Consumption Rates to Improve Cell Viability in Bioink Tissue Constructs
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrogel Preparation
2.2. Analytical Methods
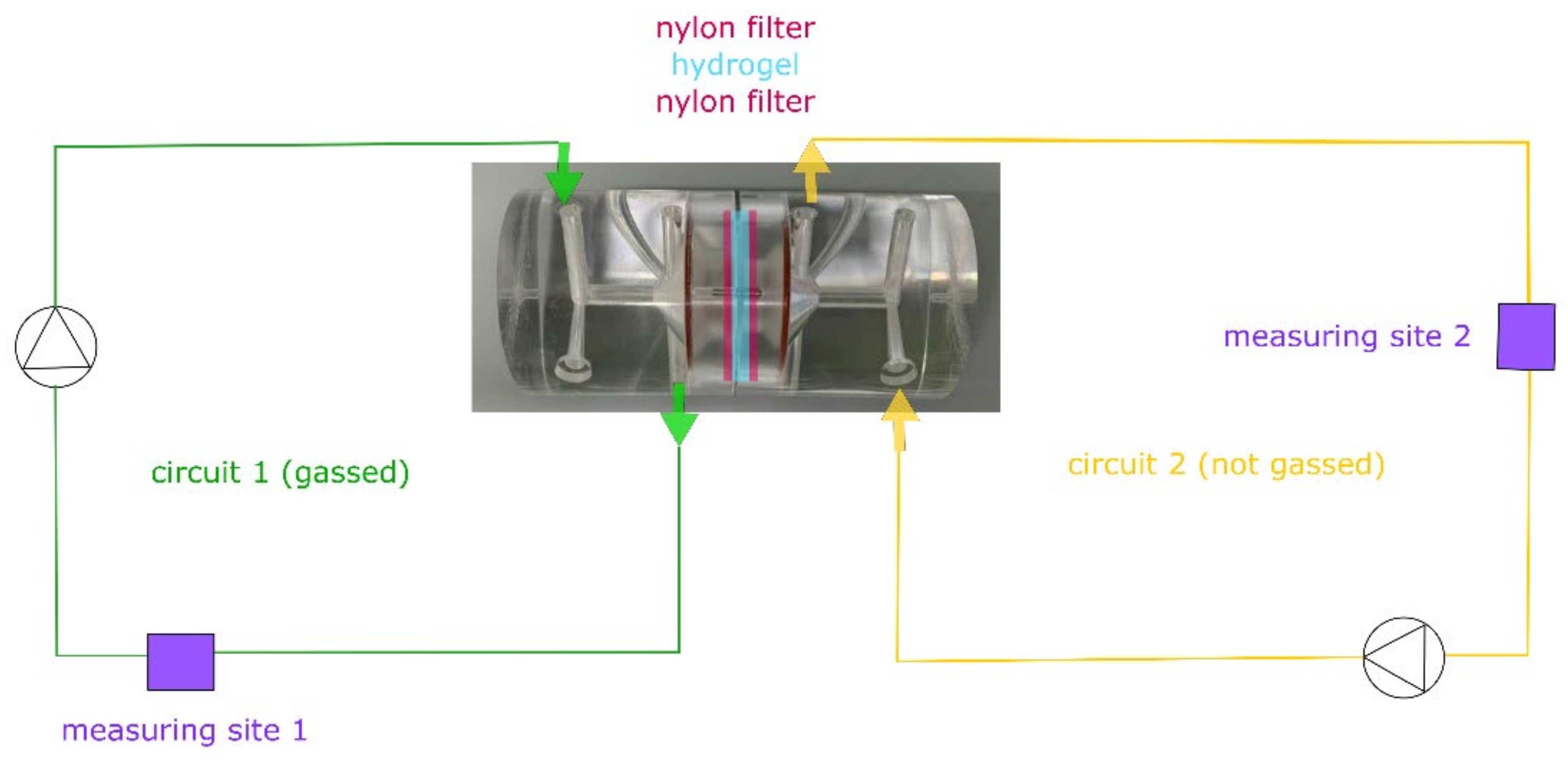
2.3. Diffusion Experiments
2.4. Cell-Specific Parameters
2.4.1. Cultivation of 1.1B4 β-Cells
2.4.2. Cell-Specific Growth and Production/Consumption Rates
2.5. Calculation of Cell Numbers in a Tissue Construct
2.6. Data Analysis
3. Results
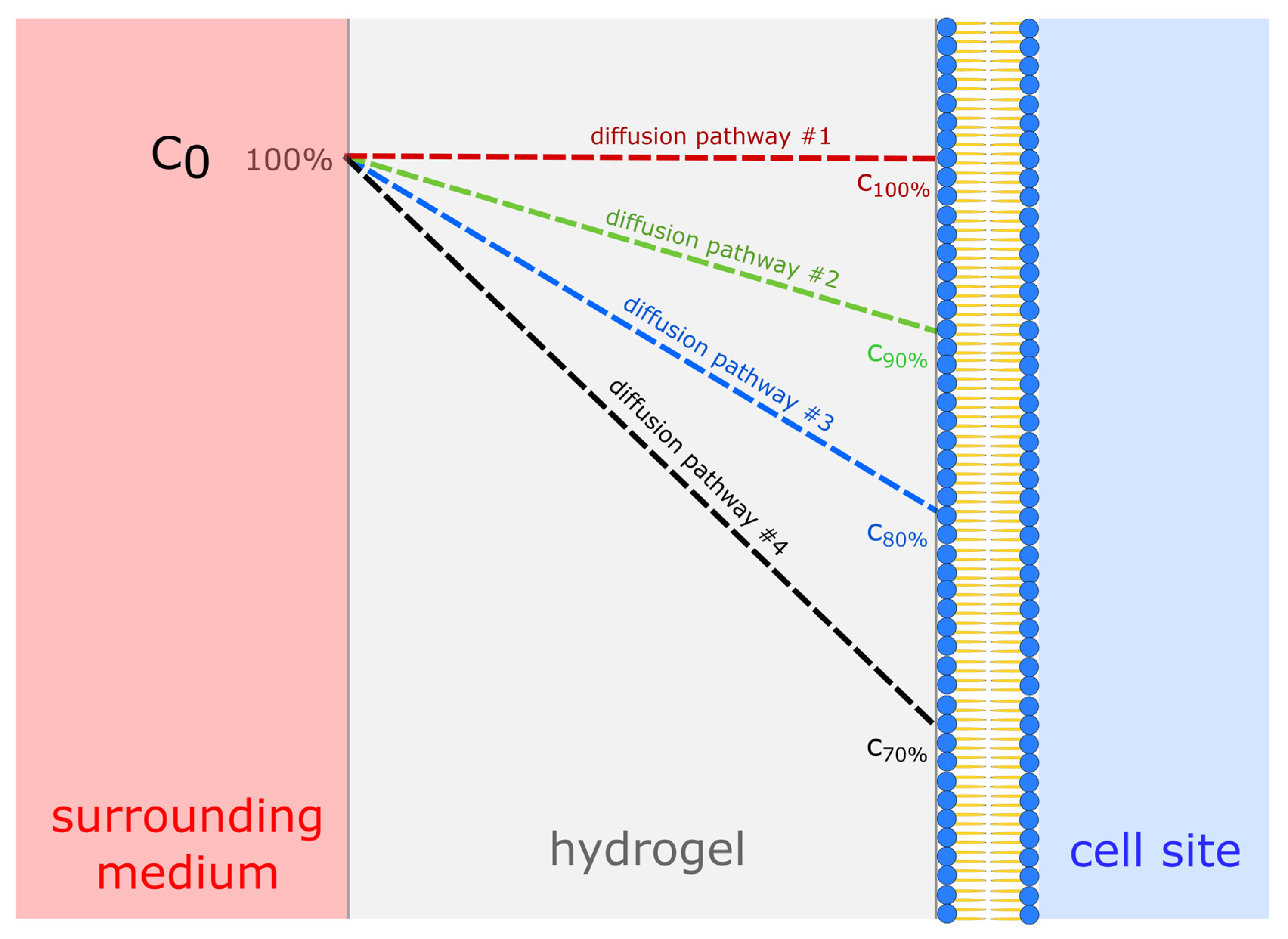
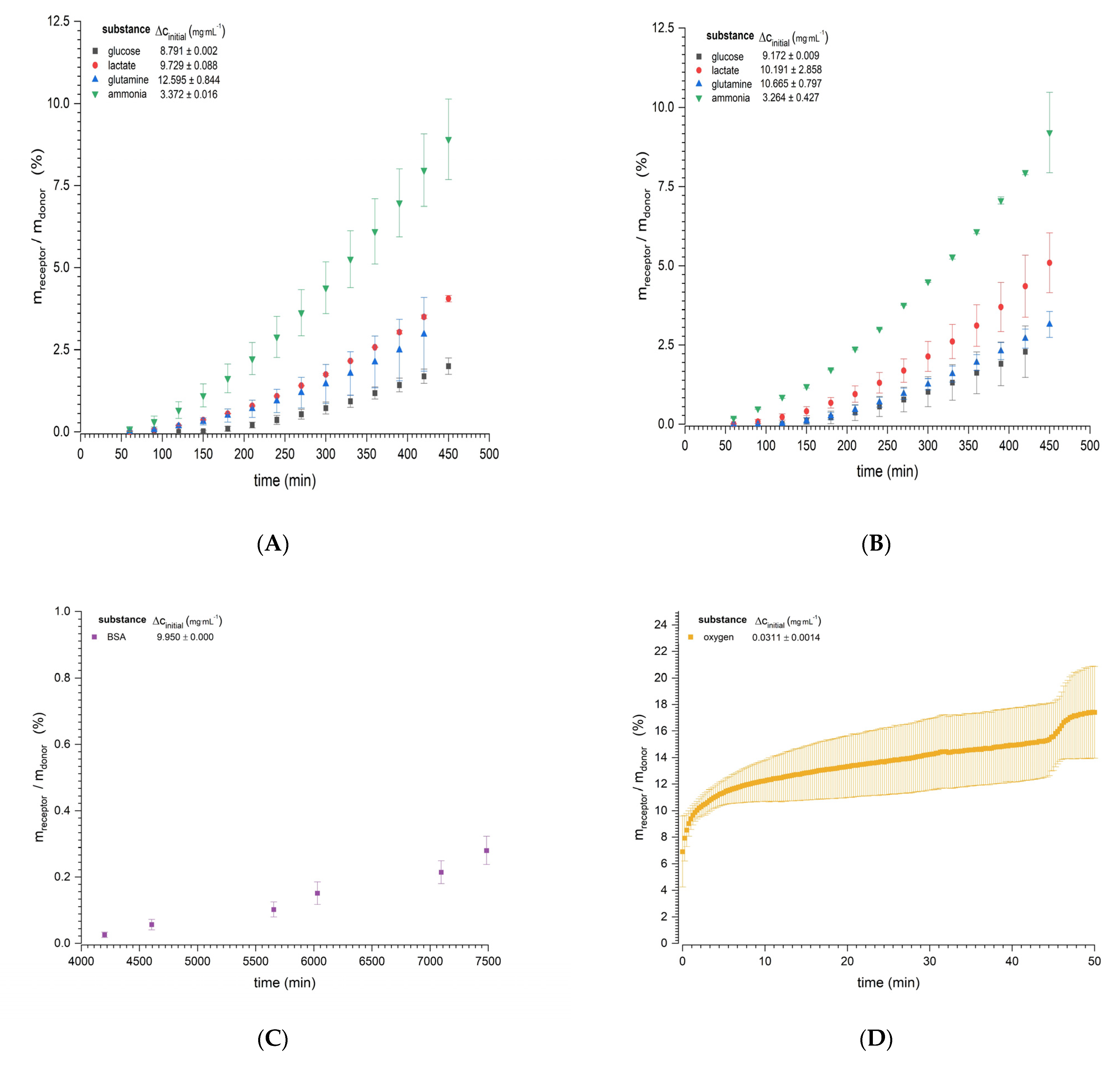
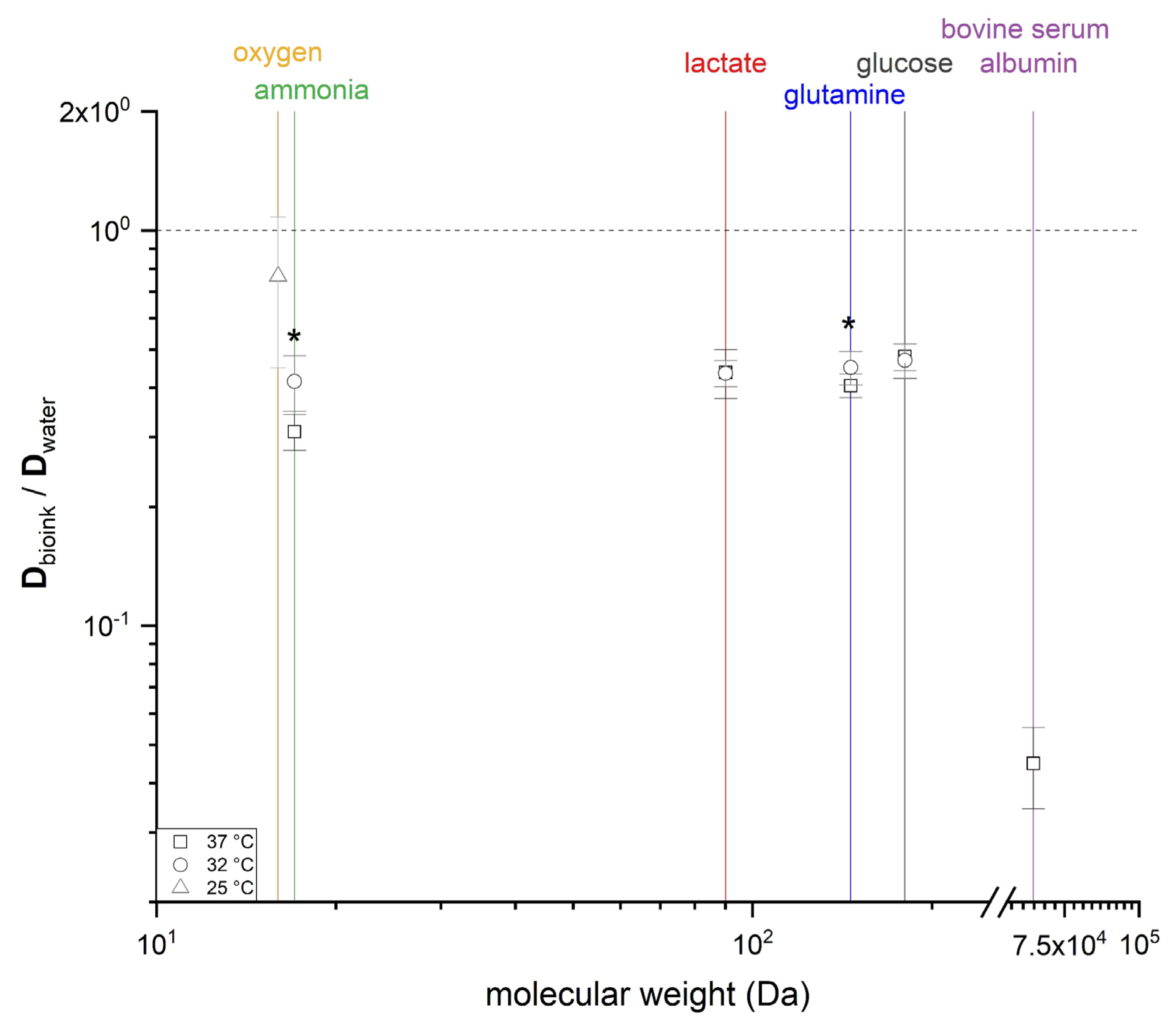
3.1. Diffusion Experiments
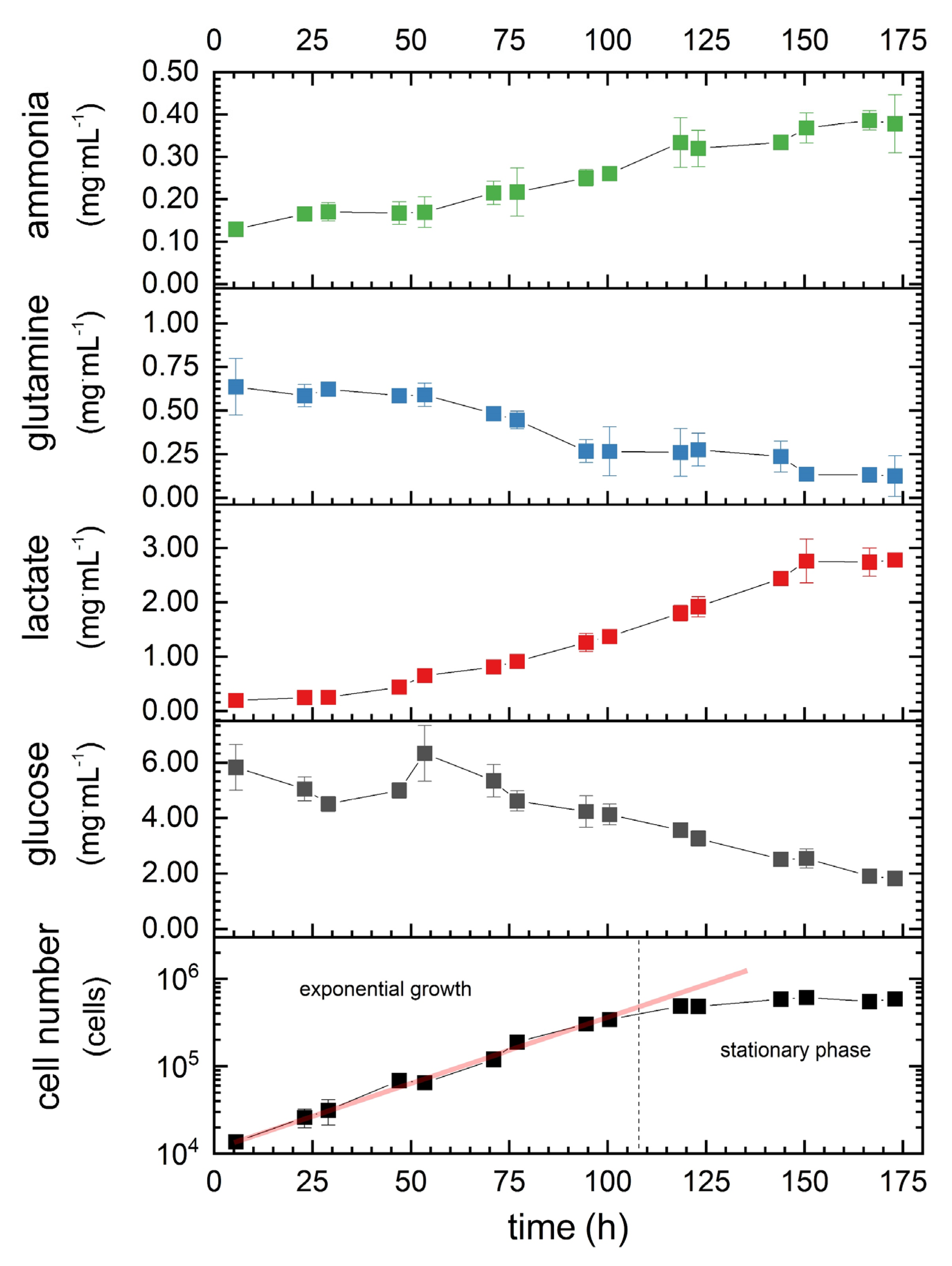
3.2. Cell-Specific Parameters
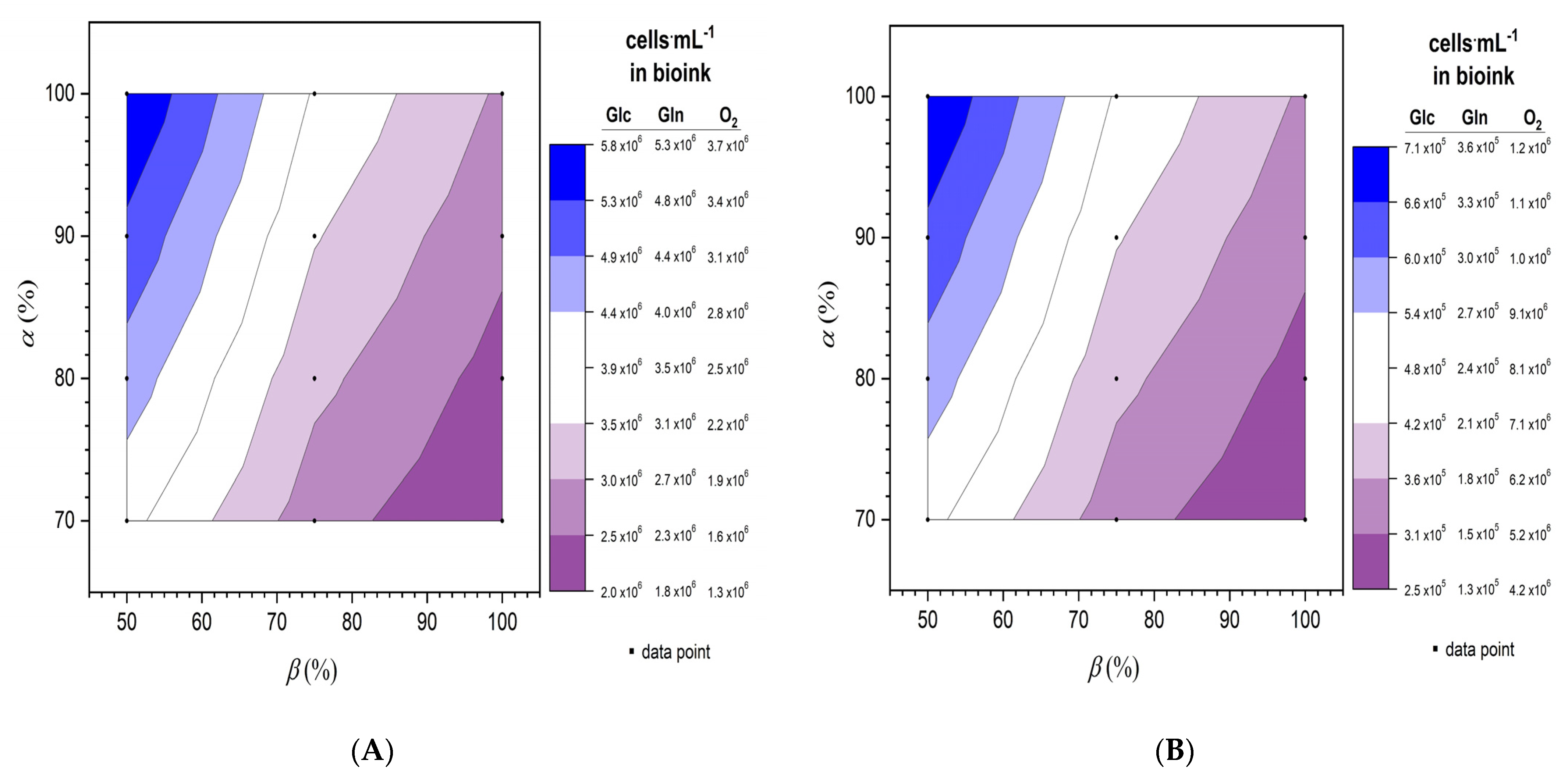
3.3. Calculations of Cell Numbers in a Tissue Construct
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shafiee, A.; Atala, A. Tissue engineering: Toward a new era of medicine. Annu. Rev. Med. 2017, 68, 29–40. [Google Scholar] [CrossRef]
- Moroni, L.; Boland, T.; Burdick, J.A.; de Maria, C.; Derby, B.; Forgacs, G.; Groll, J.; Li, Q.; Malda, J.; Mironov, V.A. Biofabrication: A guide to technology and terminology. Trends Biotechnol. 2018, 36, 384–402. [Google Scholar] [CrossRef]
- Murphy, S.V.; Atala, A. 3D bioprinting of tissues and organs. Nat. Biotechnol. 2014, 32, 773–785. [Google Scholar] [CrossRef]
- Huang, G.; Li, F.; Zhao, X.; Ma, Y.; Li, Y.; Lin, M.; Jin, G.; Lu, T.J.; Genin, G.M.; Xu, F. Functional and biomimetic materials for engineering of the three-dimensional cell microenvironment. Chem. Rev. 2017, 117, 12764–12850. [Google Scholar] [CrossRef]
- Naba, A.; Clauser, K.R.; Ding, H.; Whittaker, C.A.; Carr, S.A.; Hynes, R.O. The extracellular matrix: Tools and insights for the “omics” era. Matrix Biol. 2016, 49, 10–24. [Google Scholar] [CrossRef]
- Barkai, U.; Rotem, A.; de Vos, P. Survival of encapsulated islets: More than a membrane story. World J. Transplant. 2016, 6, 69. [Google Scholar] [CrossRef]
- de Vos, P.; Lazarjani, H.A.; Poncelet, D.; Faas, M.M. Polymers in cell encapsulation from an enveloped cell perspective. Adv. Drug Deliv. Rev. 2014, 67, 15–34. [Google Scholar] [CrossRef]
- Orive, G.; Santos, E.; Poncelet, D.; Hernández, R.M.; Pedraz, J.L.; Wahlberg, L.U.; de Vos, P.; Emerich, D. Cell encapsulation: Technical and clinical advances. Trends Pharmacol. Sci. 2015, 36, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Melchels, F.P.W.; Blokzijl, M.M.; Levato, R.; Peiffer, Q.C.; de Ruijter, M.; Hennink, W.E.; Vermonden, T.; Malda, J. Hydrogel-based reinforcement of 3D bioprinted constructs. Biofabrication 2016, 8, 35004. [Google Scholar] [CrossRef]
- Chaji, S.; Al-Saleh, J.; Gomillion, C.T. Bioprinted three-dimensional cell-laden hydrogels to evaluate adipocyte-breast cancer cell interactions. Gels 2020, 6, 10. [Google Scholar] [CrossRef]
- Ouyang, L.; Yao, R.; Zhao, Y.; Sun, W. Effect of bioink properties on printability and cell viability for 3D bioplotting of embryonic stem cells. Biofabrication 2016, 8, 35020. [Google Scholar] [CrossRef]
- McMurtrey, R.J. Roles of diffusion dynamics in stem cell signaling and three-dimensional tissue development. Stem Cells Dev. 2017, 26, 1293–1303. [Google Scholar] [CrossRef]
- Lipsitz, Y.Y.; Timmins, N.E.; Zandstra, P.W. Quality cell therapy manufacturing by design. Nat. Biotechnol. 2016, 34, 393–400. [Google Scholar] [CrossRef]
- Rathore, A.S.; Winkle, H. Quality by design for biopharmaceuticals. Nat. Biotechnol. 2009, 27, 26–34. [Google Scholar] [CrossRef]
- Øyaas, J.; Storrø, I.; Svendsen, H.; Levine, D.W. The effective diffusion coefficient and the distribution constant for small molecules in calcium-alginate gel beads. Biotechnol. Bioeng. 1995, 47, 492–500. [Google Scholar] [CrossRef]
- Ozturk, S.S.; Riley, M.R.; Palsson, B.O. Effects of ammonia and lactate on hybridoma growth, metabolism, and antibody production. Biotechnol. Bioeng. 1992, 39, 418–431. [Google Scholar] [CrossRef]
- Cruz, H.J.; Ferreira, A.S.; Freitas, C.M.; Moreira, J.L.; Carrondo, M.J. Metabolic responses to different glucose and glutamine levels in baby hamster kidney cell culture. Appl. Microbiol. Biotechnol. 1999, 51, 579–585. [Google Scholar] [CrossRef]
- Altamirano, C.; Paredes, C.; Cairo, J.J.; Godia, F. Improvement of CHO cell culture medium formulation: Simultaneous substitution of glucose and glutamine. Biotechnol. Prog. 2000, 16, 69–75. [Google Scholar] [CrossRef]
- Petry, F.; Weidner, T.; Czermak, P.; Salzig, D. Three-dimensional bioreactor technologies for the cocultivation of human mesenchymal stem/stromal cells and beta cells. Stem Cells Int. 2018, 2018, 2547098. [Google Scholar] [CrossRef]
- Pössl, A.; Hartzke, D.; Schmidts, T.M.; Runkel, F.E.; Schlupp, P. A targeted rheological bioink development guideline and its systematic correlation with printing behavior. Biofabrication 2021, 13, 35021. [Google Scholar] [CrossRef]
- Perkins, T.K.; Johnston, O. A review of diffusion and dispersion in porous media. Soc. Pet. Eng. J. 1963, 3, 70–84. [Google Scholar] [CrossRef]
- Bouchoux, A.; Roux-de Balmann, H.; Lutin, F. Nanofiltration of glucose and sodium lactate solutions: Variations of retention between single-and mixed-solute solutions. J. Membr. Sci. 2005, 258, 123–132. [Google Scholar] [CrossRef]
- Nightingale, E.R., Jr. Phenomenological theory of ion solvation. Effective radii of hydrated ions. J. Phys. Chem. 1959, 63, 1381–1387. [Google Scholar] [CrossRef]
- Li, S.; Li, C.; Liu, Y.; Wang, X.; Cao, Z. Separation of L-glutamine from fermentation broth by nanofiltration. J. Membr. Sci. 2003, 222, 191–201. [Google Scholar] [CrossRef]
- Armstrong, J.K.; Wenby, R.B.; Meiselman, H.J.; Fisher, T.C. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys. J. 2004, 87, 4259–4270. [Google Scholar] [CrossRef]
- Windrem, D.A.; Plachy, W.Z. The diffusion-solubility of oxygen in lipid bilayers. Biochim. Et Biophys. Acta (BBA)-Biomembr. 1980, 600, 655–665. [Google Scholar] [CrossRef]
- Dutta, A.K.; Das, S.; Samanta, S.; Samanta, P.K.; Adhikary, B.; Biswas, P. CuS nanoparticles as a mimic peroxidase for colorimetric estimation of human blood glucose level. Talanta 2013, 107, 361–367. [Google Scholar] [CrossRef] [PubMed]
- Darmaun, D.; Matthews, D.E.; Bier, D.M. Glutamine and glutamate kinetics in humans. Am. J. Physiol. -Endocrinol. Metab. 1986, 251, E117–E126. [Google Scholar] [CrossRef]
- Erecińska, M.; Silver, I.A. Tissue oxygen tension and brain sensitivity to hypoxia. Respir. Physiol. 2001, 128, 263–276. [Google Scholar] [CrossRef]
- Truesdale, G.A.; Downing, A.L.; Lowden, G.F. The solubility of oxygen in pure water and sea-water. J. Appl. Chem. 1955, 5, 53–62. [Google Scholar] [CrossRef]
- Dasarathy, S.; Mookerjee, R.P.; Rackayova, V.; Thrane, V.R.; Vairappan, B.; Ott, P.; Rose, C.F. Ammonia toxicity: From head to toe? Metab. Brain Dis. 2017, 32, 529–538. [Google Scholar] [CrossRef]
- Guarino, R.D.; Dike, L.E.; Haq, T.A.; Rowley, J.A.; Pitner, J.B.; Timmins, M.R. Method for determining oxygen consumption rates of static cultures from microplate measurements of pericellular dissolved oxygen concentration. Biotechnol. Bioeng. 2004, 86, 775–787. [Google Scholar] [CrossRef]
- Flusberg, D.A.; Sorger, P.K. Surviving apoptosis: Life–death signaling in single cells. Trends Cell Biol. 2015, 25, 446–458. [Google Scholar] [CrossRef]
- Li, R.H.; Altreuter, D.H.; Gentile, F.T. Transport characterization of hydrogel matrices for cell encapsulation. Biotechnol. Bioeng. 1996, 50, 365–373. [Google Scholar] [CrossRef]
- Duin, S.; Schütz, K.; Ahlfeld, T.; Lehmann, S.; Lode, A.; Ludwig, B.; Gelinsky, M. 3D Bioprinting of functional islets of langerhans in an alginate/methylcellulose hydrogel blend. Adv. Healthc. Mater. 2019, 8, 1801631. [Google Scholar] [CrossRef]
- Young, M.E.; Carroad, P.A.; Bell, R.L. Estimation of diffusion coefficients of proteins. Biotechnol. Bioeng. 1980, 22, 947–955. [Google Scholar] [CrossRef]
- Devi, C.U.; Chandran, R.B.; Vasu, R.M.; Sood, A.K. Measurement of visco-elastic properties of breast-tissue mimicking materials using diffusing wave spectroscopy. J. Biomed. Opt. 2007, 12, 34035. [Google Scholar] [CrossRef]
- Landry, M.R. Thermoporometry by differential scanning calorimetry: Experimental considerations and applications. Thermochim. Acta 2005, 433, 27–50. [Google Scholar] [CrossRef]
- Sharkawy, A.A.; Klitzman, B.; Truskey, G.A.; Reichert, W.M. Engineering the tissue which encapsulates subcutaneous implants. I. Diffusion properties. J. Biomed. Mater. Res. Off. J. Soc. Biomater. Jpn. Soc. Biomater. 1997, 37, 401–412. [Google Scholar] [CrossRef]
- Wisniewski, N.; Moussy, F.; Reichert, W.M. Characterization of implantable biosensor membrane biofouling. Fresenius’ J. Anal. Chem. 2000, 366, 611–621. [Google Scholar] [CrossRef]
- Hisab, A.S.; Alahmed, J.A.S. The Glycolytic Pathway is the Predominate Path for Glucose Utilization in Human Pancreatic Beta Cells (1.1 B4). Eur. Sci. J. 2018, 14, 41. [Google Scholar] [CrossRef][Green Version]
- Markstedt, K.; Mantas, A.; Tournier, I.; Martínez Ávila, H.; Hagg, D.; Gatenholm, P. 3D bioprinting human chondrocytes with nanocellulose–alginate bioink for cartilage tissue engineering applications. Biomacromolecules 2015, 16, 1489–1496. [Google Scholar] [CrossRef] [PubMed]
- Jedrzejewski, P.M.; Del Val, I.J.; Constantinou, A.; Dell, A.; Haslam, S.M.; Polizzi, K.M.; Kontoravdi, C. Towards controlling the glycoform: A model framework linking extracellular metabolites to antibody glycosylation. Int. J. Mol. Sci. 2014, 15, 4492–4522. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, J.H. The normal weight of the pancreas in the adult human being: A biometric study. Anat. Rec. 1926, 32, 119–132. [Google Scholar] [CrossRef]
- Ionescu-Tirgoviste, C.; Gagniuc, P.A.; Gubceac, E.; Mardare, L.; Popescu, I.; Dima, S.; Militaru, M. A 3D map of the islet routes throughout the healthy human pancreas. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef]
- Park, K.; Jang, J.; Irimia, D.; Sturgis, J.; Lee, J.; Robinson, J.P.; Toner, M.; Bashir, R. ‘Living cantilever arrays’ for characterization of mass of single live cells in fluids. Lab A Chip 2008, 8, 1034–1041. [Google Scholar] [CrossRef]
- Kim, H.-I.; Yu, J.E.; Park, C.-G.; Kim, S.-J. Comparison of four pancreatic islet implantation sites. J. Korean Med Sci. 2010, 25, 203. [Google Scholar] [CrossRef] [PubMed]
- Das, S.K. The size of the human omentum and methods of lengthening it for transplantation. Br. J. Plast. Surg. 1976, 29, 170–174. [Google Scholar] [CrossRef]
- Fotino, N.; Fotino, C.; Pileggi, A. Re-engineering islet cell transplantation. Pharmacol. Res. 2015, 98, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Colton, C.K. Oxygen supply to encapsulated therapeutic cells. Adv. Drug Deliv. Rev. 2014, 67, 93–110. [Google Scholar] [CrossRef]
| Substance | Blood Values | Cell Culture Medium |
|---|---|---|
| Glucose | ~1170 mg·L−1 [27] | 4500 mg·L−1 |
| Glutamine | ~3.73 µg·mL−1 [28] | 27.4 µg·mL−1 |
| Oxygen | ~4.5 mg·L−1 [29] | 6.95 mg·L−1 (36 °C) [30] |
| Substance | Temperature (°C) | Dexperimental × 10−10 (m2·s−1) |
|---|---|---|
| Glucose | 37 | 4.3564 ± 0.3407 |
| 32 | 3.7937 ± 0.3807 | |
| Lactate | 37 | 6.3021 ± 0.8930 |
| 32 | 5.5772 ± 0.4195 | |
| Ammonia | 37 | 8.1957 ± 0.8517 |
| 32 | 9.7921 ± 1.5702 | |
| Glutamine | 37 | 4.7901 ± 0.3353 |
| 32 | 4.7368 ± 0.4589 | |
| BSA | 37 | 0.0423 ± 0.0098 |
| Oxygen | 25 | 17.778 ± 7.325 |
| Parameter | Value |
|---|---|
| µmax | 0.04 h−1 |
| tdouble | 19 h |
| qglucose | −2.6987 × 10−11 mg·s−1·cell−1 |
| qlactate | 1.6082 × 10−11 mg·s−1·cell−1 |
| qglutamine | −0.4261 × 10−11 mg·s−1·cell−1 |
| qammonia | 0.1943 × 10−11 mg·s−1·cell−1 |
| qoxygen [32] | −0.0267 × 10−11 mg·s−1·cell−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pössl, A.; Hartzke, D.; Schlupp, P.; Runkel, F.E. Calculation of Mass Transfer and Cell-Specific Consumption Rates to Improve Cell Viability in Bioink Tissue Constructs. Materials 2021, 14, 4387. https://doi.org/10.3390/ma14164387
Pössl A, Hartzke D, Schlupp P, Runkel FE. Calculation of Mass Transfer and Cell-Specific Consumption Rates to Improve Cell Viability in Bioink Tissue Constructs. Materials. 2021; 14(16):4387. https://doi.org/10.3390/ma14164387
Chicago/Turabian StylePössl, Axel, David Hartzke, Peggy Schlupp, and Frank E. Runkel. 2021. "Calculation of Mass Transfer and Cell-Specific Consumption Rates to Improve Cell Viability in Bioink Tissue Constructs" Materials 14, no. 16: 4387. https://doi.org/10.3390/ma14164387
APA StylePössl, A., Hartzke, D., Schlupp, P., & Runkel, F. E. (2021). Calculation of Mass Transfer and Cell-Specific Consumption Rates to Improve Cell Viability in Bioink Tissue Constructs. Materials, 14(16), 4387. https://doi.org/10.3390/ma14164387