Fatigue Testing of Wearable Sensing Technologies: Issues and Opportunities
Abstract
:1. Introduction
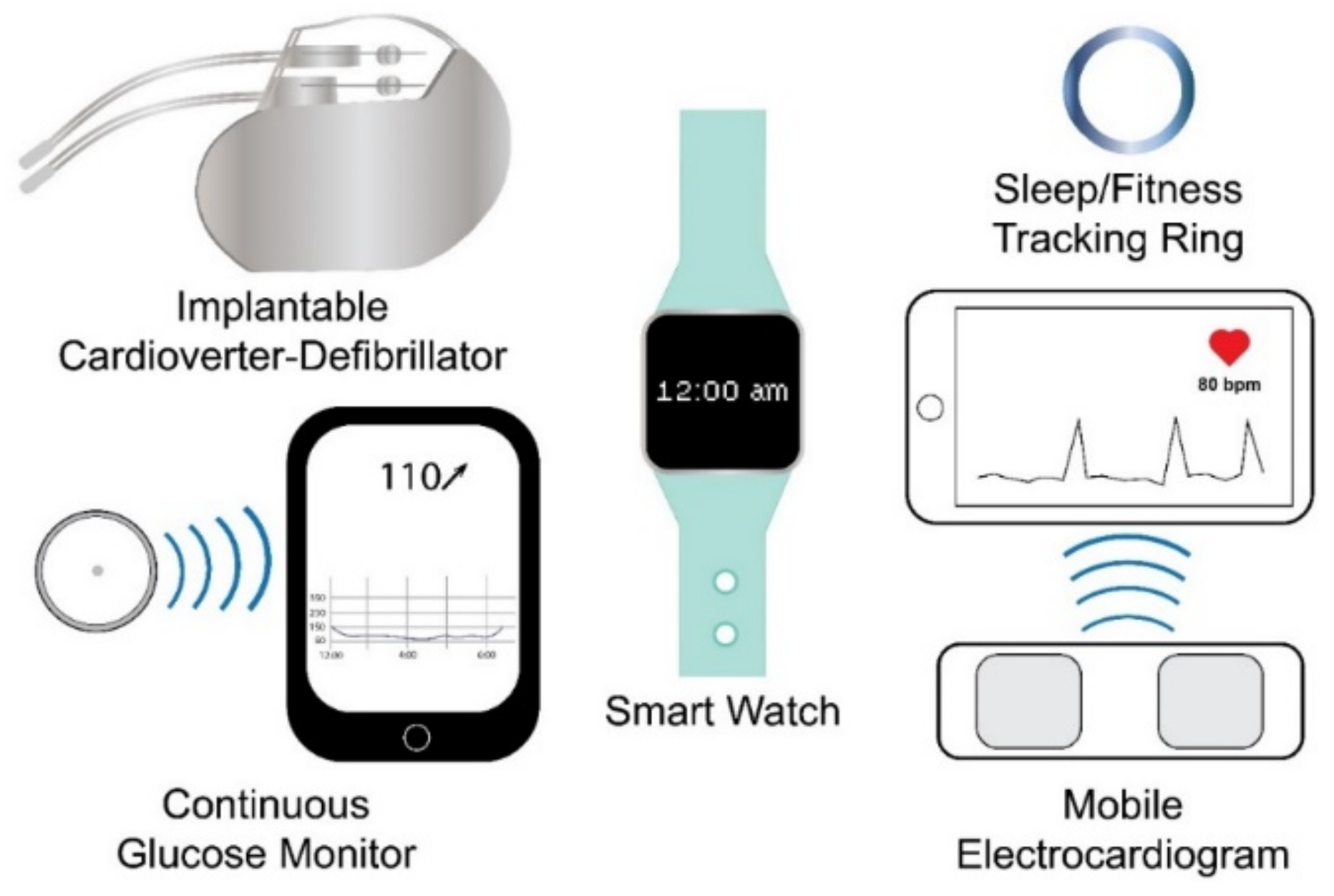
2. Internal Wearable Sensing Technologies
3. External Wearable Sensing Technologies
3.1. Fatigue Properties of Polymeric Stretch Sensors
3.1.1. Polymer Substrates
3.1.2. Polymer Housing
3.1.3. Hydrogels and Ionogels
3.2. Fatigue Properties of Piezoelectric Textiles
3.2.1. Conductive Fibers
3.2.2. Conductively Coated Textiles
3.2.3. Fabric Substrates
3.3. Fatigue Properties of Carbon Nanotube Stretch Sensors and Graphene Stretch Sensors
3.3.1. CNTs with Polymer Substrates
3.3.2. CNTs Incorporated in Piezoelectric Textiles
3.3.3. Additional CNT Sensors
3.3.4. Graphene Sensors
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wang, F.; Liu, S.; Shu, L.; Tao, X.-M. Low-Dimensional Carbon Based Sensors and Sensing Network for Wearable Health and Environmental Monitoring. Carbon 2017, 121, 353–367. [Google Scholar] [CrossRef]
- Yeo, J.C.; Lim, C.T. Emerging Flexible and Wearable Physical Sensing Platforms for Healthcare and Biomedical Applications. Microsyst. Nanoeng. 2016, 2, 1–19. [Google Scholar] [CrossRef]
- Carvalho, H.; Catarino, A.P.; Rocha, A.; Postolache, O. Health Monitoring Using Textile Sensors and Electrodes: An Overview and Integration of Technologies. In Proceedings of the 2014 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Lisbon, Portugal, 11 June 2014; pp. 1–6. [Google Scholar]
- Hehr, A.; Song, Y.; Suberu, B.; Sullivan, J.; Shanov, V.; Schulz, M. Chapter 24—Embedded Carbon Nanotube Sensor Thread for Structural Health Monitoring and Strain Sensing of Composite Materials. In Nanotube Superfiber Materials; Schulz, M.J., Shanov, V.N., Yin, Z., Eds.; William Andrew Publishing: Boston, MA, USA, 2014; pp. 671–712. ISBN 978-1-4557-7863-8. [Google Scholar]
- Li, R.; Nie, B.; Zhai, C.; Cao, J.; Pan, J.; Chi, Y.-W.; Pan, T. Telemedical Wearable Sensing Platform for Management of Chronic Venous Disorder. Ann. Biomed. Eng. 2016, 44, 2282–2291. [Google Scholar] [CrossRef] [PubMed]
- Pegan, J.D.; Zhang, J.; Chu, M.; Nguyen, T.; Park, S.-J.; Paul, A.; Kim, J.; Bachman, M.; Khine, M. Skin-Mountable Stretch Sensor for Wearable Health Monitoring. Nanoscale 2016, 8, 17295–17303. [Google Scholar] [CrossRef]
- Byrom, B.; McCarthy, M.; Schueler, P.; Muehlhausen, W. Brain Monitoring Devices in Neuroscience Clinical Research: The Potential of Remote Monitoring Using Sensors, Wearables, and Mobile Devices. Clin. Pharmacol. Ther. 2018, 104, 59–71. [Google Scholar] [CrossRef] [Green Version]
- Takei, K. Flexible and Stretchable Medical Devices; Wiley-VCH: Weinheim, Germany, 2018. [Google Scholar]
- Bernstein, R.A.; Kamel, H.; Granger, C.B.; Piccini, J.P.; Sethi, P.P.; Katz, J.M.; Vives, C.A.; Ziegler, P.D.; Franco, N.C.; Schwamm, L.H.; et al. Effect of Long-Term Continuous Cardiac Monitoring vs Usual Care on Detection of Atrial Fibrillation in Patients With Stroke Attributed to Large- or Small-Vessel Disease: The STROKE-AF Randomized Clinical Trial. JAMA 2021, 325, 2169. [Google Scholar] [CrossRef]
- Buck, B.H.; Hill, M.D.; Quinn, F.R.; Butcher, K.S.; Menon, B.K.; Gulamhusein, S.; Siddiqui, M.; Coutts, S.B.; Jeerakathil, T.; Smith, E.E.; et al. Effect of Implantable vs Prolonged External Electrocardiographic Monitoring on Atrial Fibrillation Detection in Patients with Ischemic Stroke: The PER DIEM Randomized Clinical Trial. JAMA 2021, 325, 2160. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.; Lee, J.; Yang, D.; Park, B.C.; Ryu, S.; Park, I. A Stretchable Strain Sensor Based on a Metal Nanoparticle Thin Film for Human Motion Detection. Nanoscale 2014, 6, 11932–11939. [Google Scholar] [CrossRef]
- O’Quigley, C.; Sabourin, M.; Coyle, S.; Connolly, J.; Condall, J.; Curran, K.; Corcoran, B.; Diamond, D. Characteristics of a Piezo-Resistive Fabric Stretch Sensor Glove for Home-Monitoring of Rheumatoid Arthritis. In Proceedings of the 2014 11th International Conference on Wearable and Implantable Body Sensor Networks Workshops, Zurich, Sweden, 16–19 June 2014; pp. 23–26. [Google Scholar] [CrossRef]
- Choi, D.Y.; Kim, M.H.; Oh, Y.S.; Jung, S.-H.; Jung, J.H.; Sung, H.J.; Lee, H.W. Highly Stretchable, Hysteresis-Free Ionic Liquid-Based Strain Sensor for Precise Human Motion Monitoring. ACS Appl. Mater. Interfaces 2017, 9, 1770–1780. [Google Scholar] [CrossRef]
- Lorussi, F.; Rocchia, W.; Scilingo, E.P.; Tognetti, A.; De Rossi, D. Wearable, Redundant Fabric-Based Sensor Arrays for Reconstruction of Body Segment Posture. IEEE Sens. J. 2004, 4, 807–818. [Google Scholar] [CrossRef] [Green Version]
- Scilingo, E.P.; Gemignani, A.; Paradiso, R.; Taccini, N.; Ghelarducci, B.; De Rossi, D. Performance Evaluation of Sensing Fabrics for Monitoring Physiological and Biomechanical Variables. IEEE Trans. Inf. Technol. Biomed. 2005, 9, 345–352. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Yang, T.; Li, X.; Zang, X.; Zhu, M.; Wang, K.; Wu, D.; Zhu, H. Wearable and Highly Sensitive Graphene Strain Sensors for Human Motion Monitoring. Adv. Funct. Mater. 2014, 24, 4666–4670. [Google Scholar] [CrossRef]
- Yoon, S.G.; Koo, H.-J.; Chang, S.T. Highly Stretchable and Transparent Microfluidic Strain Sensors for Monitoring Human Body Motions. ACS Appl. Mater. Interfaces 2015, 7, 27562–27570. [Google Scholar] [CrossRef]
- Amjadi, M.; Kyung, K.-U.; Park, I.; Sitti, M. Stretchable, Skin-Mountable, and Wearable Strain Sensors and Their Potential Applications: A Review. Adv. Funct. Mater. 2016, 26, 1678–1698. [Google Scholar] [CrossRef]
- Rose, M.; Curtze, C.; O’Sullivan, J.; El-Gohary, M.; Crawford, D.; Friess, D.; Brady, J.M. Wearable Inertial Sensors Allow for Quantitative Assessment of Shoulder and Elbow Kinematics in a Cadaveric Knee Arthroscopy Model. Arthroscopy 2017, 33, 2110–2116. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jia, Y.; Zhou, Y.; Wang, Y.; Zheng, G.; Dai, K.; Liu, C.; Shen, C. Ultra-Stretchable, Sensitive and Durable Strain Sensors Based on Polydopamine Encapsulated Carbon Nanotubes/Elastic Bands. J. Mater. Chem. C 2018, 6, 8160–8170. [Google Scholar] [CrossRef]
- Xia, S.; Song, S.; Gao, G. Robust and Flexible Strain Sensors Based on Dual Physically Cross-Linked Double Network Hydrogels for Monitoring Human-Motion. Chem. Eng. J. 2018, 354, 817–824. [Google Scholar] [CrossRef]
- Lee, K.Y.; Peters, M.C.; Mooney, D.J. Controlled Drug Delivery from Polymers by Mechanical Signals. Adv. Mater. 2001, 13, 837–839. [Google Scholar] [CrossRef]
- Di, J.; Yao, S.; Ye, Y.; Cui, Z.; Yu, J.; Ghosh, T.K.; Zhu, Y.; Gu, Z. Stretch-Triggered Drug Delivery from Wearable Elastomer Films Containing Therapeutic Depots. ACS Nano 2015, 9, 9407–9415. [Google Scholar] [CrossRef]
- Barton, C.J.; Kappel, S.L.; Ahrendt, P.; Simonsen, O.; Rathleff, M.S. Dynamic Navicular Motion Measured Using a Stretch Sensor Is Different between Walking and Running, and between over-Ground and Treadmill Conditions. J. Foot Ankle Res. 2015, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Luczak, T.; Saucier, D.; Burch, V.R.F.; Ball, J.E.; Chander, H.; Knight, A.; Wei, P.; Iftekhar, T. Closing the Wearable Gap: Mobile Systems for Kinematic Signal Monitoring of the Foot and Ankle. Electronics 2018, 7, 117. [Google Scholar] [CrossRef] [Green Version]
- Saucier, D.; Luczak, T.; Nguyen, P.; Davarzani, S.; Peranich, P.; Ball, J.E.; Burch, R.F.; Smith, B.K.; Chander, H.; Knight, A.; et al. Closing the Wearable Gap—Part II: Sensor Orientation and Placement for Foot and Ankle Joint Kinematic Measurements. Sensors 2019, 19, 3509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chander, H.; Stewart, E.; Saucier, D.; Nguyen, P.; Luczak, T.; Ball, J.E.; Knight, A.C.; Smith, B.K.; Prabhu, R.K. Closing the Wearable Gap—Part III: Use of Stretch Sensors in Detecting Ankle Joint Kinematics During Unexpected and Expected Slip and Trip Perturbations. Electronics 2019, 8, 1083. [Google Scholar] [CrossRef] [Green Version]
- Saucier, D.; Davarzani, S.; Turner, A.; Luczak, T.; Nguyen, P.; Carroll, W.; Burch, V.R.F.; Ball, J.E.; Smith, B.K.; Chander, H.; et al. Closing the Wearable Gap—Part IV: 3D Motion Capture Cameras Versus Soft Robotic Sensors Comparison of Gait Movement Assessment. Electronics 2019, 8, 1382. [Google Scholar] [CrossRef] [Green Version]
- Kumbay Yildiz, S.; Mutlu, R.; Alici, G. Fabrication and Characterisation of Highly Stretchable Elastomeric Strain Sensors for Prosthetic Hand Applications. Sens. Actuators A Phys. 2016, 247, 514–521. [Google Scholar] [CrossRef]
- White, E.L.; Yuen, M.C.; Case, J.C.; Kramer, R.K. Low-Cost, Facile, and Scalable Manufacturing of Capacitive Sensors for Soft Systems. Adv. Mater. Technol. 2017, 2, 1700072. [Google Scholar] [CrossRef]
- Litteken, D. Evaluation of Strain Measurement Devices for Inflatable Structures. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA SciTech Forum, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef] [Green Version]
- Mehrotra, A.; Nimgaonkar, A.; Richman, B. Telemedicine and Medical Licensure—Potential Paths for Reform. N. Engl. J. Med. 2021, 384, 687–690. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.Y.; Mehrotra, A.; Huskamp, H.A.; Uscher-Pines, L.; Ganguli, I.; Barnett, M.L. Trends in Outpatient Care Delivery and Telemedicine During the COVID-19 Pandemic in the US. JAMA Intern. Med. 2021, 181, 388. [Google Scholar] [CrossRef]
- Shachar, C.; Gupta, A.; Katznelson, G. Modernizing Medical Licensure to Facilitate Telemedicine Delivery After the COVID-19 Pandemic. JAMA Health Forum 2021, 2, e210405. [Google Scholar] [CrossRef]
- DeVore, A.D.; Wosik, J.; Hernandez, A.F. The Future of Wearables in Heart Failure Patients. JACC Heart Fail. 2019, 7, 922–932. [Google Scholar] [CrossRef]
- Mohankumar, P.; Ajayan, J.; Mohanraj, T.; Yasodharan, R. Recent Developments in Biosensors for Healthcare and Biomedical Applications: A Review. Measurement 2021, 167, 108293. [Google Scholar] [CrossRef]
- Vailshery, L.S. Global Connected Wearable Devices 2016–2022. Available online: https://www.statista.com/statistics/487291/global-connected-wearable-devices/ (accessed on 29 May 2021).
- Peake, J.M.; Kerr, G.; Sullivan, J.P. A Critical Review of Consumer Wearables, Mobile Applications, and Equipment for Providing Biofeedback, Monitoring Stress, and Sleep in Physically Active Populations. Front. Physiol. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Dunn, J.; Runge, R.; Snyder, M. Wearables and the Medical Revolution. Pers. Med. 2018, 15, 429–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lall, P.; Narangaparambil, J.; Abrol, A.; Leever, B.; Marsh, J. Development of Test Protocols for the Flexible Substrates in Wearable Applications. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May–1 June 2018; pp. 1120–1127. [Google Scholar] [CrossRef]
- Salah, H.; MacIntosh, E.; Rajakulendran, N. Wearable Tech: Leveraging Canadian Innovation to Improve Health; MaRS Discovery District: Toronto, ON, Canada, 2014. [Google Scholar]
- Slade Shantz, J.A.; Veillette, C.J.H. The Application of Wearable Technology in Surgery: Ensuring the Positive Impact of the Wearable Revolution on Surgical Patients. Front. Surg. 2014, 1. [Google Scholar] [CrossRef] [Green Version]
- Kolodzey, L.; Grantcharov, P.D.; Rivas, H.; Schijven, M.P.; Grantcharov, T.P. Wearable Technology in the Operating Room: A Systematic Review. BMJ Innov. 2017, 3. [Google Scholar] [CrossRef] [Green Version]
- Yetisen, A.K.; Martinez-Hurtado, J.L.; Ünal, B.; Khademhosseini, A.; Butt, H. Wearables in Medicine. Adv. Mater. 2018, 30, 1706910. [Google Scholar] [CrossRef]
- Maisel, W.H. Semper Fidelis—Consumer Protection for Patients with Implanted Medical Devices. N. Eng. J. Med. 2008, 358, 985–987. [Google Scholar] [CrossRef] [Green Version]
- Hauser, R.G.; Maisel, W.H.; Friedman, P.A.; Kallinen, L.M.; Mugglin, A.S.; Kumar, K.; Hodge, D.O.; Morrison, T.B.; Hayes, D.L. Longevity of Sprint Fidelis Implantable Cardioverter-Defibrillator Leads and Risk Factors for Failure. Circulation 2011, 123, 358–363. [Google Scholar] [CrossRef] [Green Version]
- Hauser, R.G.; Abdelhadi, R.; McGriff, D.; Retel, L.K. Deaths Caused by the Failure of Riata and Riata ST Implantable Cardioverter-Defibrillator Leads. Heart Rhythm 2012, 9, 1227–1235. [Google Scholar] [CrossRef]
- Rome, B.N.; Kramer, D.B.; Kesselheim, A.S. FDA Approval of Cardiac Implantable Electronic Devices via Original and Supplement Premarket Approval Pathways, 1979–2012. JAMA 2014, 311, 385–391. [Google Scholar] [CrossRef] [Green Version]
- Rome, B.N.; Kramer, D.B.; Kesselheim, A.S. Approval of High-Risk Medical Devices in the US: Implications for Clinical Cardiology. Curr. Cardiol. Rep. 2014, 16, 489. [Google Scholar] [CrossRef] [Green Version]
- Swerdlow, C.D.; Asirvatham, S.J.; Ellenbogen, K.A.; Friedman, P.A. Troubleshooting Implanted Cardioverter Defibrillator Sensing Problems I. Circ. Arrhythmia Electrophysiol. 2014, 7, 1237–1261. [Google Scholar] [CrossRef] [Green Version]
- Cingolani, E.; Goldhaber, J.I.; Marbán, E. Next-Generation Pacemakers: From Small Devices to Biological Pacemakers. Nat. Rev. Cardiol. 2018, 15, 139–150. [Google Scholar] [CrossRef]
- Koneru, J.N.; Jones, P.W.; Hammill, E.F.; Wold, N.; Ellenbogen, K.A. Risk Factors and Temporal Trends of Complications Associated With Transvenous Implantable Cardiac Defibrillator Leads. J. Am. Heart Assoc. 2018, 7, e007691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeForge, W.F. Cardiac Pacemakers: A Basic Review of the History and Current Technology. J. Vet. Cardiol. 2019, 22, 40–50. [Google Scholar] [CrossRef]
- El-Chami, M.F.; Rao, B.; Shah, A.D.; Wood, C.; Sayegh, M.; Zakka, P.; Ginn, K.; Pallotta, L.; Evans, B.; Hoskins, M.H.; et al. Long-Term Performance of a Pacing Lead Family: A Single-Center Experience. Heart Rhythm 2019, 16, 572–578. [Google Scholar] [CrossRef] [PubMed]
- Segan, L.; Samuel, R.; Lim, M.; Ridley, D.; Sen, J.; Perrin, M. Incidence of Premature Lead Failure in 2088 TendrilTM Pacing Leads: A Single Centre Experience. Heart Lung Circ. 2020. [Google Scholar] [CrossRef]
- Sengupta, J.; Storey, K.; Casey, S.; Trager, L.; Buescher, M.; Horning, M.; Gornick, C.; Abdelhadi, R.; Tang, C.; Brill, S.; et al. Outcomes Before and After the Recall of a Heart Failure Pacemaker. JAMA Intern. Med. 2020, 180, 198. [Google Scholar] [CrossRef] [PubMed]
- Adelstein, E.; Zhang, L.; Nazeer, H.; Loka, A.; Steckman, D. Increased Incidence of Electrical Abnormalities in a Pacemaker Lead Family. J. Cardiovasc. Electrophysiol. 2021, 32, 1111–1121. [Google Scholar] [CrossRef] [PubMed]
- Faccioli, S.; Del Favero, S.; Visentin, R.; Bonfanti, R.; Iafusco, D.; Rabbone, I.; Marigliano, M.; Schiaffini, R.; Bruttomesso, D.; Cobelli, C. Accuracy of a CGM Sensor in Pediatric Subjects with Type 1 Diabetes. Comparison of Three Insertion Sites: Arm, Abdomen, and Gluteus. J. Diabetes Sci. Technol. 2017, 11, 1147–1154. [Google Scholar] [CrossRef] [Green Version]
- Klonoff, D.C.; Ahn, D.; Drincic, A. Continuous Glucose Monitoring: A Review of the Technology and Clinical Use. Diabetes Res. Clin. Pract. 2017, 133, 178–192. [Google Scholar] [CrossRef]
- Teoh, S.H. Fatigue of Biomaterials: A Review. Int. J. Fatigue 2000, 22, 825–837. [Google Scholar] [CrossRef]
- Zuckerman, D.M.; Brown, P.; Nissen, S.E. Medical Device Recalls and the FDA Approval Process. Arch. Intern. Med. 2011, 171, 1006–1011. [Google Scholar] [CrossRef] [Green Version]
- Jones, A.-A.D.; Mi, G.; Webster, T.J. A Status Report on FDA Approval of Medical Devices Containing Nanostructured Materials. Trends Biotechnol. 2019, 37, 117–120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- United States Food and Drug Administration. Medical Device Overview. Available online: https://www.fda.gov/industry/regulated-products/medical-device-overview (accessed on 30 May 2021).
- United States Food and Drug Administration. Premarket Approval (PMA). Available online: https://www.fda.gov/medical-devices/premarket-submissions/premarket-approval-pma (accessed on 30 May 2021).
- United States Food and Drug Administration. Premarket Notification 510(k). Available online: https://www.fda.gov/medical-devices/premarket-submissions/premarket-notification-510k (accessed on 30 May 2021).
- Regulation (EU) 2017/745 of the European Parliament and of the Council of 5 April 2017 on Medical Devices, Amending Directive 2001/83/EC, Regulation (EC) No 178/2002 and Regulation (EC) No 1223/2009 and Repealing Council Directives 90/385/EEC and 93/42/EEC (Text with EEA Relevance) Text with EEA RelevanceLex. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A02017R0745-20170505 (accessed on 7 July 2021).
- European Commission, Health Technology and Cosmetics. Guidelines for Medical Devices. In Medical Devices Directives, Clinical Investigation; Clinical Evaluation: A Guide for Manufacturers and Notified Bodies under Directives 93/42/EEC and 90/385/EEC, MEDDEV 2.7/1, Revision 4. 2016. Available online: https://ec.europa.eu/docsroom/documents/17522/attachments/1/translations/en/renditions/native (accessed on 19 July 2021).
- Auricchio, A.; Gropp, M.; Ludgate, S.; Vardas, P.; Brugada, J.; Priori, S.G. Writing Committee for the European Heart Rhythm Association Guidance Document on Cardiac Rhythm Management Product Performance European Heart Rhythm Association Guidance Document on Cardiac Rhythm Management Product Performance. EP Europace 2006, 8, 313–322. [Google Scholar] [CrossRef]
- Swerdlow, C.D.; Kalahasty, G.; Ellenbogen, K.A. Implantable Cardiac Defibrillator Lead Failure and Management. J. Am. Coll. Cardiol. 2016, 67, 1358–1368. [Google Scholar] [CrossRef] [PubMed]
- Mulpuru, S.K.; Madhavan, M.; McLeod, C.J.; Cha, Y.-M.; Friedman, P.A. Cardiac Pacemakers: Function, Troubleshooting, and Management: Part 1 of a 2-Part Series. J. Am. Coll. Cardiol. 2017, 69, 189–210. [Google Scholar] [CrossRef]
- Swerdlow, C.D.; Hayes, D.L.; Zipes, D.P. Pacemakers and Implantable Cardioverter-Defibrillators. In Braunwald’s Heart Disease: A Textbook of Cardiovascular Medicine; Bonow, R.O., Mann, D.L., Zipes, D.P., Libby, P., Braunwald, E., Eds.; Elsevier Saunders: Philadelphia, PA, USA, 2012; pp. 745–768. [Google Scholar]
- Altman, P.A.; Meagher, J.M.; Walsh, D.W.; Hoffmann, D.A. Rotary Bending Fatigue of Coils and Wires Used in Cardiac Lead Design. J. Biomed. Mater. Res. 1998, 43, 21–37. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Yang, W.; Chen, S.J. In Vivo Stress Analysis of a Pacing Lead From an Angiographic Sequence. J. Biomech. Eng. 2011, 133. [Google Scholar] [CrossRef]
- Quinn, T.; Splett, J.; McColskey, J.; Dawson, J.; Smith, D.; Himes, A.; Cooke, D. The Reproducibility of a Proposed Standard Fatigue Test for Cardiac Device Leads. Fourth Symp. Fatigue Fract. Met. Med. Mater. Devices 2019. [Google Scholar] [CrossRef]
- Yamada, T.; Hayamizu, Y.; Yamamoto, Y.; Yomogida, Y.; Izadi-Najafabadi, A.; Futaba, D.N.; Hata, K. A Stretchable Carbon Nanotube Strain Sensor for Human-Motion Detection. Nat. Nanotechnol. 2011, 6, 296–301. [Google Scholar] [CrossRef]
- Atalay, O.; Kennon, W.R.; Husain, M.D. Textile-Based Weft Knitted Strain Sensors: Effect of Fabric Parameters on Sensor Properties. Sensors 2013, 13, 11114–11127. [Google Scholar] [CrossRef]
- Cai, L.; Song, L.; Luan, P.; Zhang, Q.; Zhang, N.; Gao, Q.; Zhao, D.; Zhang, X.; Tu, M.; Yang, F.; et al. Super-Stretchable, Transparent Carbon Nanotube-Based Capacitive Strain Sensors for Human Motion Detection. Sci. Rep. 2013, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Gioberto, G.; Dunne, L.E. Overlock-Stitched Stretch Sensors: Characterization and Effect of Fabric Property. J. Text. Appar. Technol. Manag. 2013, 8, 1–14. Available online: https://ojs.cnr.ncsu.edu/index.php/JTATM/article/view/4417 (accessed on 20 July 2021).
- Zhang, R.; Deng, H.; Valenca, R.; Jin, J.; Fu, Q.; Bilotti, E.; Peijs, T. Strain Sensing Behaviour of Elastomeric Composite Films Containing Carbon Nanotubes under Cyclic Loading. Compos. Sci. Technol. 2013, 74, 1–5. [Google Scholar] [CrossRef]
- Kang, D.; Pikhitsa, P.V.; Choi, Y.W.; Lee, C.; Shin, S.S.; Piao, L.; Park, B.; Suh, K.-Y.; Kim, T.; Choi, M. Ultrasensitive Mechanical Crack-Based Sensor Inspired by the Spider Sensory System. Nature 2014, 516, 222–226. [Google Scholar] [CrossRef] [PubMed]
- Matsuzaki, R.; Tabayashi, K. Highly Stretchable, Global, and Distributed Local Strain Sensing Line Using GaInSn Electrodes for Wearable Electronics. Adv. Funct. Mater. 2015, 25, 3806–3813. [Google Scholar] [CrossRef]
- Borghetti, M.; Serpelloni, M.; Sardini, E.; Pandini, S. Mechanical Behavior of Strain Sensors Based on PEDOT:PSS and Silver Nanoparticles Inks Deposited on Polymer Substrate by Inkjet Printing. Sens. Actuators A Phys. 2016, 243, 71–80. [Google Scholar] [CrossRef]
- Kim, D.-G.; Kim, J.; Jung, S.-B.; Kim, Y.-S.; Kim, J.-W. Electrically and Mechanically Enhanced Ag Nanowires-Colorless Polyimide Composite Electrode for Flexible Capacitive Sensor. Appl. Surface Sci. 2016, 380, 223–228. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Dai, K.; Zheng, G.; Liu, C.; Shen, C.; Yan, X.; Guo, J.; Guo, Z. Electrically Conductive Thermoplastic Elastomer Nanocomposites at Ultralow Graphene Loading Levels for Strain Sensor Applications. J. Mater. Chem. C 2016, 4, 157–166. [Google Scholar] [CrossRef]
- Yang, T.; Li, X.; Jiang, X.; Lin, S.; Lao, J.; Shi, J.; Zhen, Z.; Li, Z.; Zhu, H. Structural Engineering of Gold Thin Films with Channel Cracks for Ultrasensitive Strain Sensing. Mater. Horiz. 2016, 3, 248–255. [Google Scholar] [CrossRef]
- Yokus, M.A.; Foote, R.; Jur, J.S. Printed Stretchable Interconnects for Smart Garments: Design, Fabrication, and Characterization. IEEE Sens. J. 2016, 16, 7967–7976. [Google Scholar] [CrossRef]
- Cao, X.; Wei, X.; Li, G.; Hu, C.; Dai, K.; Guo, J.; Zheng, G.; Liu, C.; Shen, C.; Guo, Z. Strain Sensing Behaviors of Epoxy Nanocomposites with Carbon Nanotubes under Cyclic Deformation. Polymer 2017, 112, 1–9. [Google Scholar] [CrossRef]
- Keulemans, G.; Ceyssens, F.; Puers, R. An Ionic Liquid Based Strain Sensor for Large Displacement Measurement. Biomed. Microdevices 2017, 19, 1. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Y.; Li, Z.; Wang, Y.; Dai, K.; Zheng, G.; Liu, C.; Shen, C. The Effect of Filler Dimensionality on the Electromechanical Performance of Polydimethylsiloxane Based Conductive Nanocomposites for Flexible Strain Sensors. Compos. Sci. Technol. 2017, 139, 64–73. [Google Scholar] [CrossRef]
- Atalay, O. Textile-Based, Interdigital, Capacitive, Soft-Strain Sensor for Wearable Applications. Materials 2018, 11, 768. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Xu, X.; Yu, D.; Xiao, C.; Liu, M.; Huang, J.; Mao, T.; Zheng, C.; Wang, Z.; Wu, X. Highly Stretchable and Fatigue Resistant Hydrogels with Low Young’s Modulus as Transparent and Flexible Strain Sensors. J. Mater. Chem. C 2018, 6, 11193–11201. [Google Scholar] [CrossRef]
- Seyedin, S.; Moradi, S.; Singh, C.; Razal, J.M. Continuous Production of Stretchable Conductive Multifilaments in Kilometer Scale Enables Facile Knitting of Wearable Strain Sensing Textiles. Appl. Mater. Today 2018, 11, 255–263. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, X.; Xin, Y.; Lubineau, G. Coaxial Thermoplastic Elastomer-Wrapped Carbon Nanotube Fibers for Deformable and Wearable Strain Sensors. Adv. Funct. Mater. 2018, 28, 1705591. [Google Scholar] [CrossRef]
- Gao, J.; Li, B.; Huang, X.; Wang, L.; Lin, L.; Wang, H.; Xue, H. Electrically Conductive and Fluorine Free Superhydrophobic Strain Sensors Based on SiO2/Graphene-Decorated Electrospun Nanofibers for Human Motion Monitoring. Chem. Eng. J. 2019, 373, 298–306. [Google Scholar] [CrossRef]
- Isaia, C.; McNally, D.S.; McMaster, S.A.; Branson, D.T. Effect of Mechanical Preconditioning on the Electrical Properties of Knitted Conductive Textiles during Cyclic Loading. Text. Res. J. 2019, 89, 445–460. [Google Scholar] [CrossRef]
- Jia, Y.; Shen, L.; Liu, J.; Zhou, W.; Du, Y.; Xu, J.; Liu, C.; Zhang, G.; Zhang, Z.; Jiang, F. An Efficient PEDOT-Coated Textile for Wearable Thermoelectric Generators and Strain Sensors. J. Mater. Chem. C 2019, 7, 3496–3502. [Google Scholar] [CrossRef]
- Lai, J.; Zhou, H.; Jin, Z.; Li, S.; Liu, H.; Jin, X.; Luo, C.; Ma, A.; Chen, W. Highly Stretchable, Fatigue-Resistant, Electrically Conductive, and Temperature-Tolerant Ionogels for High-Performance Flexible Sensors. ACS Appl. Mater. Interfaces 2019, 11, 26412–26420. [Google Scholar] [CrossRef]
- Liang, A.; Stewart, R.; Bryan-Kinns, N. Analysis of Sensitivity, Linearity, Hysteresis, Responsiveness, and Fatigue of Textile Knit Stretch Sensors. Sensors 2019, 19, 3618. [Google Scholar] [CrossRef] [Green Version]
- Losaria, P.M.; Yim, J.-H. A Highly Stretchable Large Strain Sensor Based on PEDOT—Thermoplastic Polyurethane Hybrid Prepared via in Situ Vapor Phase Polymerization. J. Ind. Eng. Chem. 2019, 74, 108–117. [Google Scholar] [CrossRef]
- Zou, Q.; Zheng, J.; Su, Q.; Wang, W.; Gao, W.; Ma, Z. A Wave-Inspired Ultrastretchable Strain Sensor with Predictable Cracks. Sens. Actuators A Phys. 2019, 300, 111658. [Google Scholar] [CrossRef]
- Melnykowycz, M.; Koll, B.; Scharf, D.; Clemens, F. Comparison of Piezoresistive Monofilament Polymer Sensors. Sensors 2014, 14, 1278–1294. [Google Scholar] [CrossRef] [PubMed]
- Lajimi, S.A.M.; McPhee, J. A Comprehensive Filter to Reduce Drift from Euler Angles, Velocity, and Position Using an IMU. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Jun, S.; Ju, B.-K.; Kim, J.-W. Ultra-Facile Fabrication of Stretchable and Transparent Capacitive Sensor Employing Photo-Assisted Patterning of Silver Nanowire Networks. Adv. Mater. Technol. 2016, 1, 1600062. [Google Scholar] [CrossRef]
- Isaia, C.; McNally, D.; McMaster, S.A.; Branson, D.T. Investigation of Changes in the Electrical Properties of Novel Knitted Conductive Textiles during Cyclic Loading. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6058–6061. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.M.; Cui, X.; Wang, K.L.; Wei, J.Q. Stretchable and Compressible Strain Sensors Based on Carbon Nanotube Meshes. Nanoscale 2016, 8, 19352–19358. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Dong, M.; Huang, W.; Gao, J.; Dai, K.; Guo, J.; Zheng, G.; Liu, C.; Shen, C.; Guo, Z. Lightweight Conductive Graphene/Thermoplastic Polyurethane Foams with Ultrahigh Compressibility for Piezoresistive Sensing. J. Mater. Chem. C 2017, 5, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Manson, S.S. Thermal Stress and Low-Cycle Fatigue; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Bossuyt, F.; Guenther, J.; Löher, T.; Seckel, M.; Sterken, T.; de Vries, J. Cyclic Endurance Reliability of Stretchable Electronic Substrates. Microelectron. Reliab. 2011, 51, 628–635. [Google Scholar] [CrossRef]
- McClay, I.S.; Robinson, J.R.; Andriacchi, T.P.; Frederick, E.C.; Gross, T.; Martin, P.; Valiant, G.; Williams, K.R.; Cavanagh, P.R. A Profile of Ground Reaction Forces in Professional Basketball. J. Appl. Biomech. 1994, 10, 222–236. [Google Scholar] [CrossRef]
- McQuade, M. Effect of Soccer Positions on Steps Taken Per Game. Int. J. Exerc. Sci. Conf. Proc. 2011, 2, 19. [Google Scholar]
- Coffin, L.F. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal. Trans. ASME 1954, 76, 931–950. [Google Scholar]
- Manson, S.S. Behavior of Materials Under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954; pp. 1–34.
- Basquin, O.H. The Exponential Law of Endurance Tests. In Proceedings of the 13th Annual Meeting, Atlantic City, NJ, USA, 28 June–2 July 1910; pp. 625–630. [Google Scholar]
- Persson, B.N.J.; Brener, E.A. Crack Propagation in Viscoelastic Solids. Phys. Rev. E 2005, 71, 036123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, H.J.; Boyce, M.C. Stress–Strain Behavior of Thermoplastic Polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P. A Review on the Mullins Effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef] [Green Version]
- Focatiis, D.S.A.D.; Hull, D.; Sánchez-Valencia, A. Roles of Prestrain and Hysteresis on Piezoresistance in Conductive Elastomers for Strain Sensor Applications. Plast. Rubber Compos. 2012, 41, 301–309. [Google Scholar] [CrossRef] [Green Version]
- McDowell, D.L.; Gall, K.; Horstemeyer, M.F.; Fan, J. Microstructure-Based Fatigue Modeling of Cast A356-T6 Alloy. Eng. Fract. Mech. 2003, 70, 49–80. [Google Scholar] [CrossRef] [Green Version]
- Hughes, J.M.; Lugo, M.; Bouvard, J.L.; McIntyre, T.; Horstemeyer, M.F. Cyclic Behavior and Modeling of Small Fatigue Cracks of a Polycarbonate Polymer. Int. J. Fatigue 2017, 99, 78–86. [Google Scholar] [CrossRef]
- Rabinowitz, S.; Beardmore, P. Cyclic Deformation and Fracture of Polymers. J. Mater. Sci. 1974, 9, 81–99. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical Metallurgy, 3rd ed.; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Niesłony, A.; el Dsoki, C.; Kaufmann, H.; Krug, P. New Method for Evaluation of the Manson–Coffin–Basquin and Ramberg–Osgood Equations with Respect to Compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]
- Terent’ev, V.F. Endurance Limit of Metals and Alloys. Met. Sci. Heat Treat. 2008, 50, 88–96. [Google Scholar] [CrossRef]
- Basan, R.; Rubeša, D.; Franulović, M.; Križan, B. A Novel Approach to the Estimation of Strain Life Fatigue Parameters. Procedia Eng. 2010, 2, 417–426. [Google Scholar] [CrossRef] [Green Version]
- Heckel, T.K.; Christ, H.-J. Isothermal and Thermomechanical Fatigue of Titanium Alloys. Procedia Eng. 2010, 2, 845–854. [Google Scholar] [CrossRef] [Green Version]
- Tehrani, M.; Sarvestani, A. Effect of Chain Length Distribution on Mechanical Behavior of Polymeric Networks. Eur. Polym. J. 2017, 87, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Pastukhov, L.V.; Kanters, M.J.W.; Engels, T.A.P.; Govaert, L.E. Physical Background of the Endurance Limit in Poly(Ether Ether Ketone). J. Polym. Sci. 2020, 58, 716–736. [Google Scholar] [CrossRef]
- Lugo, M.; Fountain, J.E.; Hughes, J.M.; Bouvard, J.-L.; Horstemeyer, M.F. Microstructure-Based Fatigue Modeling of an Acrylonitrile Butadiene Styrene (ABS) Copolymer. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Opp, D.A.; Skinner, D.W.; Wiktorek, R.J. A Model for Polymer Fatigue. Polym. Eng. Sci. 1969, 9, 121–130. [Google Scholar] [CrossRef]
- Wang, G.-T.; Liu, H.-Y.; Saintier, N.; Mai, Y.-W. Cyclic Fatigue of Polymer Nanocomposites. Eng. Fail. Anal. 2009, 16, 2635–2645. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Fatigue Modeling for a Thermoplastic Polymer under Mean Strain and Variable Amplitude Loadings. Int. J. Fatigue 2017, 100, 429–443. [Google Scholar] [CrossRef]
- Andrzejewska, A. Biomechanical Properties of 3D-Printed Bone Models. Biosystems 2019, 176, 52–55. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Load History and Sequence Effects on Cyclic Deformation and Fatigue Behavior of a Thermoplastic Polymer. Polym. Test. 2016, 56, 99–109. [Google Scholar] [CrossRef]
- Hsu, Y.; Dimcic, B.; Gonzalez, M.; Bossuyt, F.; Vanfleteren, J.; Wolf, I.D. Reliability Assessment of Stretchable Interconnects. In Proceedings of the 2010 5th International Microsystems Packaging Assembly and Circuits Technology Conference, Taipei, Taiwan, 20–22 October 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Cataldi, P.; Dussoni, S.; Ceseracciu, L.; Maggiali, M.; Natale, L.; Metta, G.; Athanassiou, A.; Bayer, I.S. Carbon Nanofiber versus Graphene-Based Stretchable Capacitive Touch Sensors for Artificial Electronic Skin. Adv. Sci. 2018, 5, 1700587. [Google Scholar] [CrossRef] [PubMed]
- Maiti, R.; Gerhardt, L.-C.; Lee, Z.S.; Byers, R.A.; Woods, D.; Sanz-Herrera, J.A.; Franklin, S.E.; Lewis, R.; Matcher, S.J.; Carré, M.J. In Vivo Measurement of Skin Surface Strain and Sub-Surface Layer Deformation Induced by Natural Tissue Stretching. J. Mechan. Behav. Biomed. Mater. 2016, 62, 556–569. [Google Scholar] [CrossRef] [Green Version]
- Amjadi, M.; Pichitpajongkit, A.; Lee, S.; Ryu, S.; Park, I. Highly Stretchable and Sensitive Strain Sensor Based on Silver Nanowire–Elastomer Nanocomposite. ACS Nano 2014, 8, 5154–5163. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.-M.; Choi, I.-S.; Kim, B.-J.; Joo, Y.-C. Reliability Issues and Solutions in Flexible Electronics Under Mechanical Fatigue. Electron. Mater. Lett. 2018, 14, 387–404. [Google Scholar] [CrossRef]
- Duan, L.; D’hooge, D.R.; Cardon, L. Recent Progress on Flexible and Stretchable Piezoresistive Strain Sensors: From Design to Application. Prog. Mater. Sci. 2019, 100617. [Google Scholar] [CrossRef]
- Conti, J.C.; Strope, E.R. Radial Compliance of Natural and Mock Arteries: How This Property Defines the Cyclic Loading of Deployed Vascular Stents. Biomed. Sci. Instrum. 2002, 38, 163–172. [Google Scholar]
- Mars, W.V.; Fatemi, A. Observations of the Constitutive Response and Characterization of Filled Natural Rubber Under Monotonic and Cyclic Multiaxial Stress States. J. Eng. Mater. Technol. 2004, 126, 19–28. [Google Scholar] [CrossRef]
- Rajesh, R.; Strope, E.R.; Price, K.S.; Conti, J.C. Frequency Dependent Hysteresis of Silicone and Latex Mock Arteries Used in Stent Testing. Biomed. Sci. Instrum. 2005, 41, 163–168. [Google Scholar] [PubMed]
- Ayoub, G.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.M. Modeling the Low-Cycle Fatigue Behavior of Visco-Hyperelastic Elastomeric Materials Using a New Network Alteration Theory: Application to Styrene-Butadiene Rubber. J. Mech. Phys. Solids 2011, 59, 473–495. [Google Scholar] [CrossRef]
- Narynbek Ulu, K.; Huneau, B.; Verron, E.; Béranger, A.-S.; Heuillet, P. True Stress Controlled Fatigue Life Experiments for Elastomers. Int. J. Fatigue 2017, 104, 171–182. [Google Scholar] [CrossRef]
- Amit, M.; Chukoskie, L.; Skalsky, A.J.; Garudadri, H.; Ng, T.N. Flexible Pressure Sensors for Objective Assessment of Motor Disorders. Adv. Funct. Mater. 2019, 1905241. [Google Scholar] [CrossRef]
- Wang, T.; Ouyang, Z.; Wang, F.; Liu, Y. A Review on Graphene Strain Sensors Based on Fiber Assemblies. SN Appl. Sci. 2020, 2, 862. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Pharr, M. Sideways and Stable Crack Propagation in a Silicone Elastomer. Proc. Natl. Acad. Sci. USA 2019, 116, 9251–9256. [Google Scholar] [CrossRef] [Green Version]
- Winkler, J.R.; Gray, H.B. Long-Range Electron Tunneling. J. Am. Chem. Soc. 2014, 136, 2930–2939. [Google Scholar] [CrossRef] [PubMed]
- Heikenfeld, J.; Jajack, A.; Rogers, J.; Gutruf, P.; Tian, L.; Pan, T.; Li, R.; Khine, M.; Kim, J.; Wang, J.; et al. Wearable Sensors: Modalities, Challenges, and Prospects. Lab Chip 2018, 18, 217–248. [Google Scholar] [CrossRef] [Green Version]
- Koydemir, H.C.; Ozcan, A. Wearable and Implantable Sensors for Biomedical Applications. Annu. Rev. Anal. Chem. 2018, 11, 127–146. [Google Scholar] [CrossRef]
- Wu, W. Stretchable Electronics: Functional Materials, Fabrication Strategies and Applications. Sci. Technol. Adv. Mater. 2019, 20, 187–224. [Google Scholar] [CrossRef] [Green Version]
- Nag, A.; Mukhopadhyay, S.C.; Kosel, J. Wearable Flexible Sensors: A Review. IEEE Sens. J. 2017, 17, 3949–3960. [Google Scholar] [CrossRef] [Green Version]
- Hanson, D.E.; Hawley, M.; Houlton, R.; Chitanvis, K.; Rae, P.; Orler, E.B.; Wrobleski, D.A. Stress Softening Experiments in Silica-Filled Polydimethylsiloxane Provide Insight into a Mechanism for the Mullins Effect. Polymer 2005, 46, 10989–10995. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Zhao, W.; Zhang, M.; Qin, H.; Xie, Y. Flexible, Stretchable Sensors for Wearable Health Monitoring: Sensing Mechanisms, Materials, Fabrication Strategies and Features. Sensors 2018, 18, 645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harito, C.; Utari, L.; Putra, B.R.; Yuliarto, B.; Purwanto, S.; Zaidi, S.Z.J.; Bavykin, D.V.; Marken, F.; Walsh, F.C. Review—The Development of Wearable Polymer-Based Sensors: Perspectives. J. Electrochem. Soc. 2020, 167, 037566. [Google Scholar] [CrossRef]
- Jin, H.; Abu-Raya, Y.S.; Haick, H. Advanced Materials for Health Monitoring with Skin-Based Wearable Devices. Adv. Healthc. Mater. 2017, 6, 1700024. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and Mechanics for Stretchable Electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitesides, G.M. The Origins and the Future of Microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Horowitz, A.I.; Panzer, M.J. Poly(Dimethylsiloxane)-Supported Ionogels with a High Ionic Liquid Loading. Angew. Chem. Int. Ed. 2014, 53, 9780–9783. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts Theory and Application; Springer: Berlin/Heidelberg, Germany, 1967; ISBN 978-3-642-05708-3. [Google Scholar]
- Yoo, S.; Barker, R.L. Comfort Properties of Heat-Resistant Protective Workwear in Varying Conditions of Physical Activity and Environment. Part I: Thermophysical and Sensorial Properties of Fabrics. Text. Res. J. 2005, 75, 523–530. [Google Scholar] [CrossRef]
- Nyoni, A.B.; Brook, D. The Effect of Cyclic Loading on the Wicking Performance of Nylon 6.6 Yarns and Woven Fabrics Used for Outdoor Performance Clothing. Text. Res. J. 2010, 80, 720–725. [Google Scholar] [CrossRef]
- Wang, X.; Kalali, E.N.; Wang, D.-Y. An in Situ Polymerization Approach for Functionalized MoS2/Nylon-6 Nanocomposites with Enhanced Mechanical Properties and Thermal Stability. J. Mater. Chem. A 2015, 3, 24112–24120. [Google Scholar] [CrossRef]
- Jang, K.-I.; Han, S.Y.; Xu, S.; Mathewson, K.E.; Zhang, Y.; Jeong, J.-W.; Kim, G.-T.; Webb, R.C.; Lee, J.W.; Dawidczyk, T.J.; et al. Rugged and Breathable Forms of Stretchable Electronics with Adherent Composite Substrates for Transcutaneous Monitoring. Nat. Commun. 2014, 5, 4779. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Jang, K.-I.; Ma, Y.; Jung, H.N.; Yang, Y.; Cho, M.; Zhang, Y.; Huang, Y.; Rogers, J.A. Fabric-Based Stretchable Electronics with Mechanically Optimized Designs and Prestrained Composite Substrates. Extrem. Mech. Lett. 2014, 1, 120–126. [Google Scholar] [CrossRef] [Green Version]
- Edwards, J.V.; Prevost, N.T.; Condon, B.; French, A.; Wu, Q. Immobilization of Lysozyme-Cellulose Amide-Linked Conjugates on Cellulose I and II Cotton Nanocrystalline Preparations. Cellulose 2012, 19, 495–506. [Google Scholar] [CrossRef]
- Li, Y.-Q.; Huang, P.; Zhu, W.-B.; Fu, S.-Y.; Hu, N.; Liao, K. Flexible Wire-Shaped Strain Sensor from Cotton Thread for Human Health and Motion Detection. Sci. Rep. 2017, 7, 45013. [Google Scholar] [CrossRef]
- Ren, J.; Wang, C.; Zhang, X.; Carey, T.; Chen, K.; Yin, Y.; Torrisi, F. Environmentally-Friendly Conductive Cotton Fabric as Flexible Strain Sensor Based on Hot Press Reduced Graphene Oxide. Carbon 2017, 111, 622–630. [Google Scholar] [CrossRef] [Green Version]
- Raftoyiannis, I.G. Experimental Testing of Composite Panels Reinforced with Cotton Fibers. Open J. Comp. Mater. 2012, 2. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Li, J.; He, Y.; Liu, H.; Cheng, B. A High-Sensitivity and Low-Hysteresis Flexible Pressure Sensor Based on Carbonized Cotton Fabric. Sens. Rep. A Phys. 2019, 294, 45–53. [Google Scholar] [CrossRef]
- Muzaffar, S.; Abbas, M.; Siddiqua, U.H.; Arshad, M.; Tufail, A.; Ahsan, M.; Alissa, S.A.; Abubshait, S.A.; Abubshait, H.A.; Iqbal, M. Enhanced Mechanical, UV Protection and Antimicrobial Properties of Cotton Fabric Employing Nanochitosan and Polyurethane Based Finishing. J. Mater. Res. Technol. 2021, 11, 946–956. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, J.; Yang, X.; Liu, H.; Xu, X.; Ma, L.; Shang, S.; Song, Z. Construction of Antimicrobial and Biocompatible Cotton Textile Based on Quaternary Ammonium Salt from Rosin Acid. Int. J. Biol. Macromol. 2020, 150, 1–8. [Google Scholar] [CrossRef]
- Maghimaa, M.; Alharbi, S.A. Green Synthesis of Silver Nanoparticles from Curcuma Longa, L. and Coating on the Cotton Fabrics for Antimicrobial Applications and Wound Healing Activity. J. Photochem. Photobiol. B Biol. 2020, 204, 111806. [Google Scholar] [CrossRef]
- Gonçalves, J.; Torres, N.; Silva, S.; Gonçalves, F.; Noro, J.; Cavaco-Paulo, A.; Ribeiro, A.; Silva, C. Zein Impart Hydrophobic and Antimicrobial Properties to Cotton Textiles. React. Funct. Polym. 2020, 154, 104664. [Google Scholar] [CrossRef]
- Lumbreras-Aguayo, A.; Meléndez-Ortiz, H.I.; Puente-Urbina, B.; Alvarado-Canché, C.; Ledezma, A.; Romero-García, J.; Betancourt-Galindo, R. Poly(Methacrylic Acid)-Modified Medical Cotton Gauzes with Antimicrobial and Drug Delivery Properties for Their Use as Wound Dressings. Carbohydr. Polym. 2019, 205, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, T.I.; Abd El Aty, A.A. In-Situ Green Myco-Synthesis of Silver Nanoparticles onto Cotton Fabrics for Broad Spectrum Antimicrobial Activity. Int. J. Biol. Macromol. 2018, 118, 2121–2130. [Google Scholar] [CrossRef]
- Rehan, M.; Zaghloul, S.; Mahmoud, F.A.; Montaser, A.S.; Hebeish, A. Design of Multi-Functional Cotton Gauze with Antimicrobial and Drug Delivery Properties. Mater. Sci. Eng. C 2017, 80, 29–37. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, M.; Li, Z.; Liu, Y.; Ren, X.; Huang, T.-S. Preparation of Antimicrobial and Hemostatic Cotton with Modified Mesoporous Particles for Biomedical Applications. Colloids Surf. B Biointerfaces 2018, 165, 199–206. [Google Scholar] [CrossRef]
- Mani, S.; Anbumani, N. Dynamic Elastic Behavior of Cotton and Cotton/Spandex Knitted Fabrics. J. Eng. Fibers Fabr. 2014, 9, 155892501400900100. [Google Scholar] [CrossRef]
- Mattana, G.; Cosseddu, P.; Fraboni, B.; Malliaras, G.G.; Hinestroza, J.P.; Bonfiglio, A. Organic Electronics on Natural Cotton Fibres. Org. Electron. 2011, 12, 2033–2039. [Google Scholar] [CrossRef]
- Lam, C.L.; Rajdi, N.N.Z.M.; Wicaksono, D.H.B. MWCNT/Cotton-Based Flexible Electrode for Electrocardiography. In Proceedings of the 2013 IEEE Sensors, Balitimore, MD, USA, 3–6 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Bin Ahmad, M.A.S.; Harun, F.K.C.; Wicaksono, D.H.B. Hybrid Flexible Circuit on Cotton Fabric for Wearable Electrocardiogram Monitoring. In Proceedings of the 2017 International Electronics Symposium on Engineering Technology and Applications (IES-ETA), Surabaya, Indonesia, 26–27 September 2017; pp. 217–222. [Google Scholar] [CrossRef]
- Yapici, M.K.; Alkhidir, T.E. Intelligent Medical Garments with Graphene-Functionalized Smart-Cloth ECG Sensors. Sensors 2017, 17, 875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ankhili, A.; Tao, X.; Cochrane, C.; Koncar, V.; Coulon, D.; Tarlet, J.-M. Comparative Study on Conductive Knitted Fabric Electrodes for Long-Term Electrocardiography Monitoring: Silver-Plated and PEDOT:PSS Coated Fabrics. Sensors 2018, 18, 3890. [Google Scholar] [CrossRef] [Green Version]
- Saleh, S.M.; Jusob, S.M.; Harun, F.K.C.; Yuliati, L.; Wicaksono, D.H.B. Optimization of Reduced GO-Based Cotton Electrodes for Wearable Electrocardiography. IEEE Sens. J. 2020, 20, 7774–7782. [Google Scholar] [CrossRef]
- Parker, E.; Freeman, C.; Persons, K.; Burch, R.; Ball, J.; Saucier, D.; Middleton, C.; Peranich, P.; Chander, H.; Knight, A.; et al. Deterioration of Textile vs. Electronic Components over Time in Athletic Wearable Devices. In Proceedings of the Smart Biomedical and Physiological Sensor Technology XVIII, Online, 12 April 2021; Volume 11757, p. 1175702. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. Carbon Nanotube Networks: Sensing of Distributed Strain and Damage for Life Prediction and Self Healing. Adv. Mater. 2006, 18, 2837–2841. [Google Scholar] [CrossRef]
- Kobayashi, N.; Izumi, H.; Morimoto, Y. Review of Toxicity Studies of Carbon Nanotubes. J. Occup. Health 2017, 59, 394–407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, L.; Song, B.; Liang, H.; Liu, J.; Feng, X.; Deng, B.; Sun, T.; Shao, L. Toxicity of Graphene-Family Nanoparticles: A General Review of the Origins and Mechanisms. Part. Fibre Toxicol. 2016, 13, 57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Suzuki, R.; Ogata, K.; Nakamura, T.; Dong, A.; Weng, W. Near-Linear Responsive and Wide-Range Pressure and Stretch Sensor Based on Hierarchical Graphene-Based Structures via Solvent-Free Preparation. Polymers 2020, 12, 1814. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Persons, A.K.; Ball, J.E.; Freeman, C.; Macias, D.M.; Simpson, C.L.; Smith, B.K.; Burch V., R.F. Fatigue Testing of Wearable Sensing Technologies: Issues and Opportunities. Materials 2021, 14, 4070. https://doi.org/10.3390/ma14154070
Persons AK, Ball JE, Freeman C, Macias DM, Simpson CL, Smith BK, Burch V. RF. Fatigue Testing of Wearable Sensing Technologies: Issues and Opportunities. Materials. 2021; 14(15):4070. https://doi.org/10.3390/ma14154070
Chicago/Turabian StylePersons, Andrea Karen, John E. Ball, Charles Freeman, David M. Macias, Chartrisa LaShan Simpson, Brian K. Smith, and Reuben F. Burch V. 2021. "Fatigue Testing of Wearable Sensing Technologies: Issues and Opportunities" Materials 14, no. 15: 4070. https://doi.org/10.3390/ma14154070
APA StylePersons, A. K., Ball, J. E., Freeman, C., Macias, D. M., Simpson, C. L., Smith, B. K., & Burch V., R. F. (2021). Fatigue Testing of Wearable Sensing Technologies: Issues and Opportunities. Materials, 14(15), 4070. https://doi.org/10.3390/ma14154070







