The Force Cone Method Applied to Explain Hidden Whirls in Tribology
Abstract
:1. Introduction
2. Materials and Methods
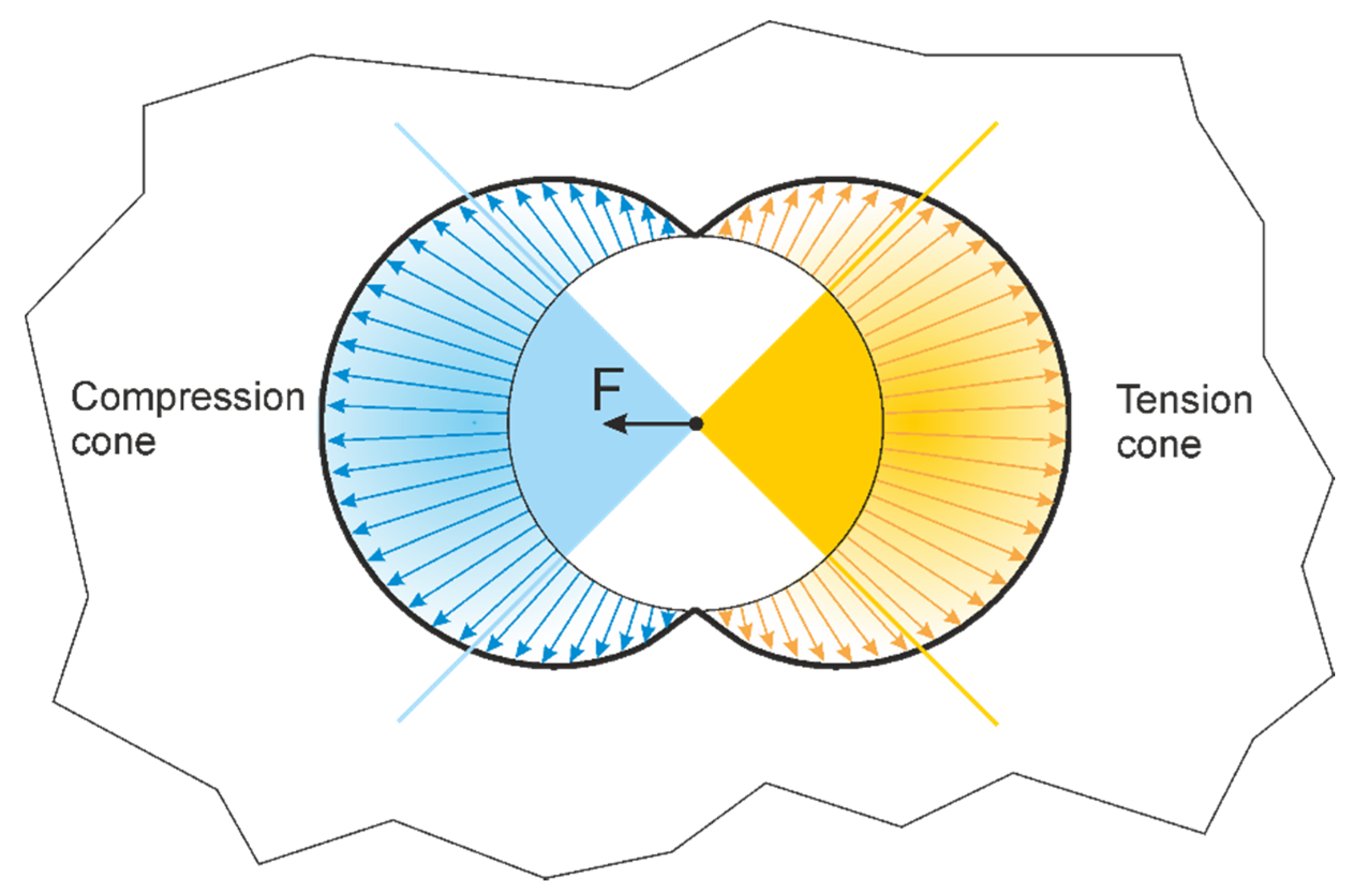
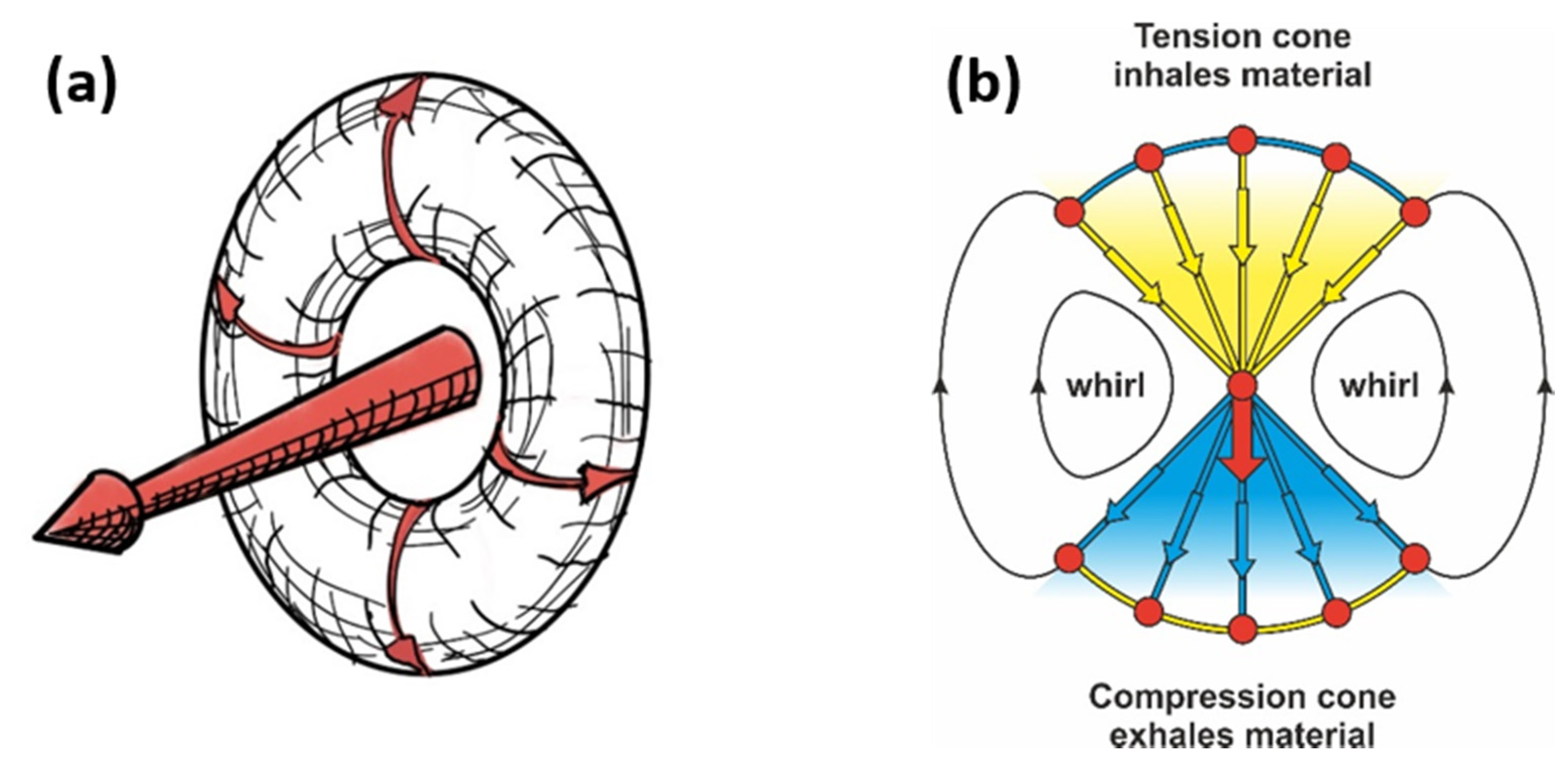
2.1. The Force Cone Method
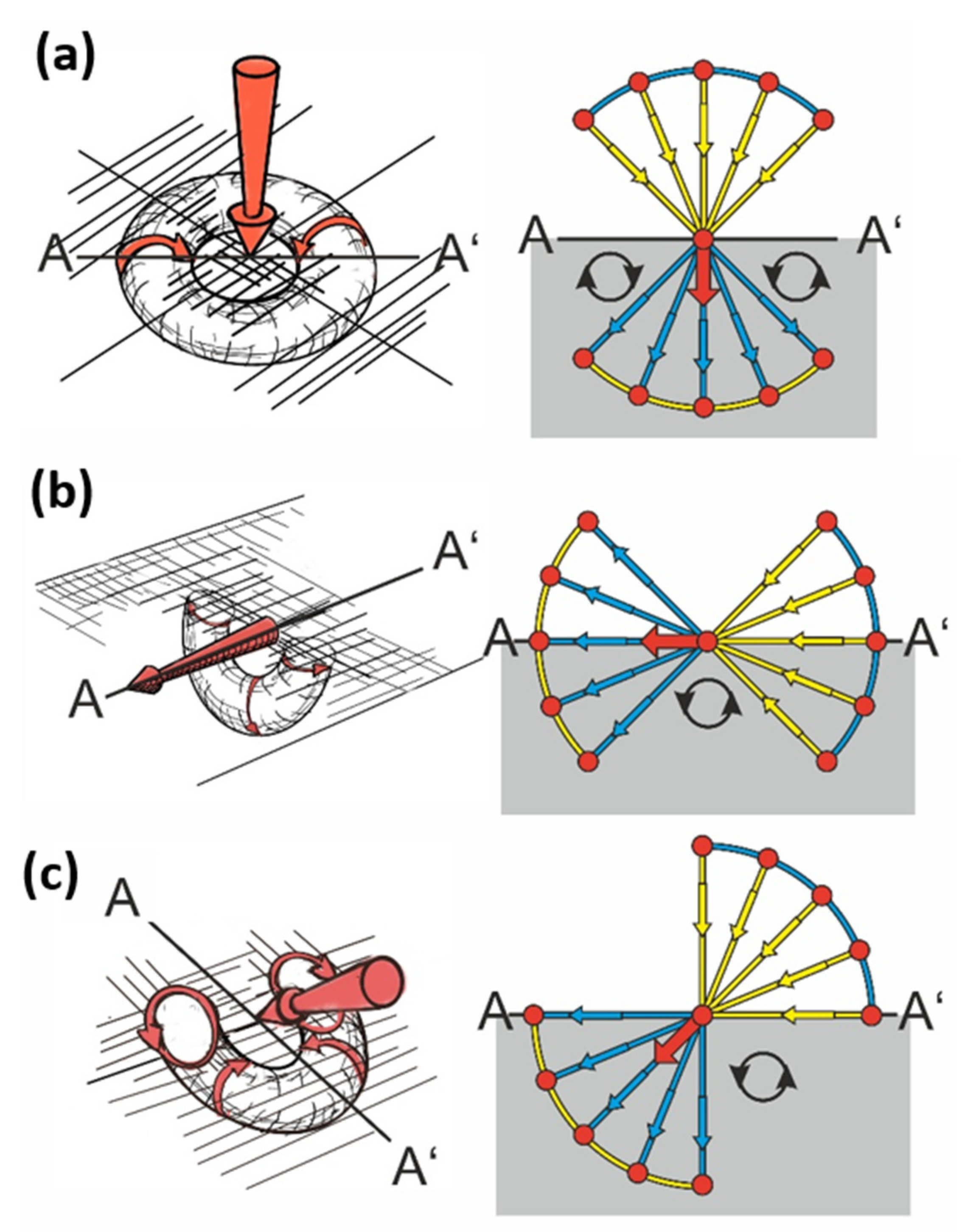
2.2. Application of the Force Cone Method to a Single Point Surface Load
2.3. Finite Element Method
3. Results and Discussion
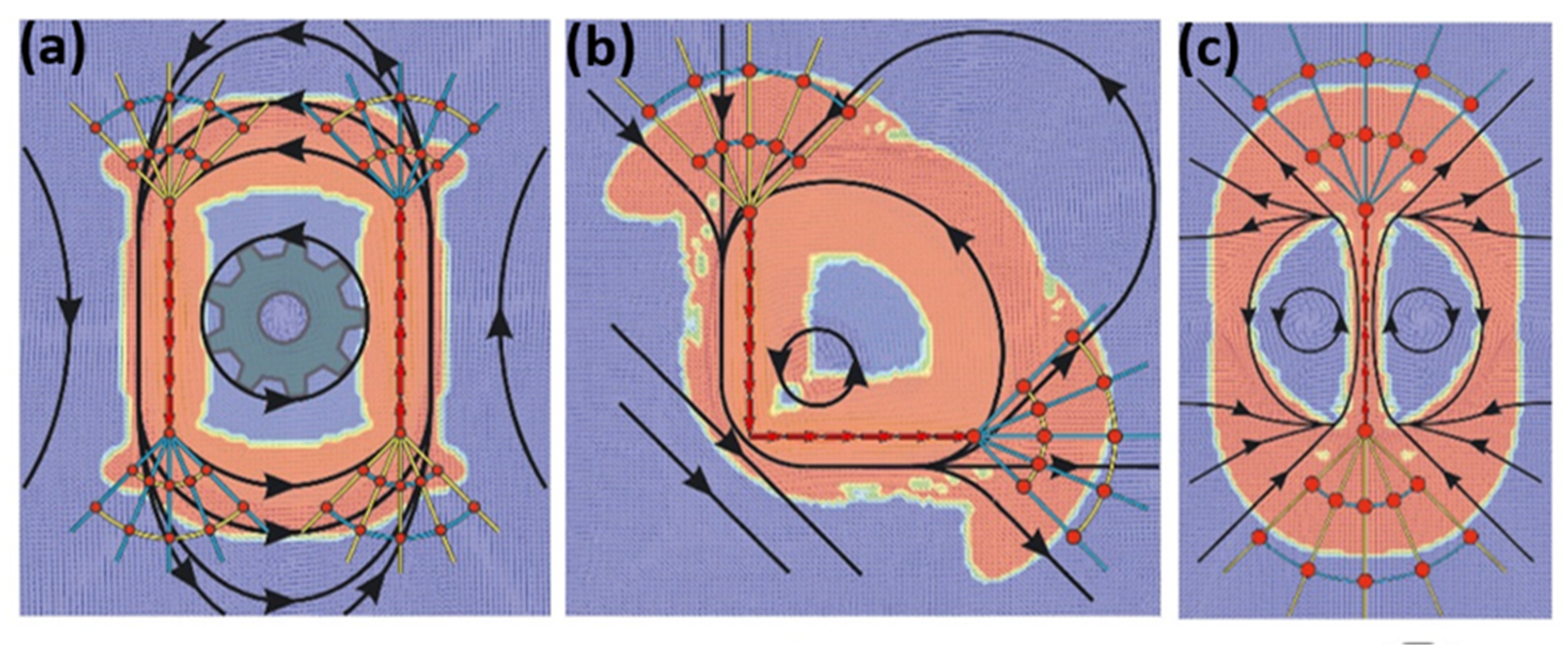
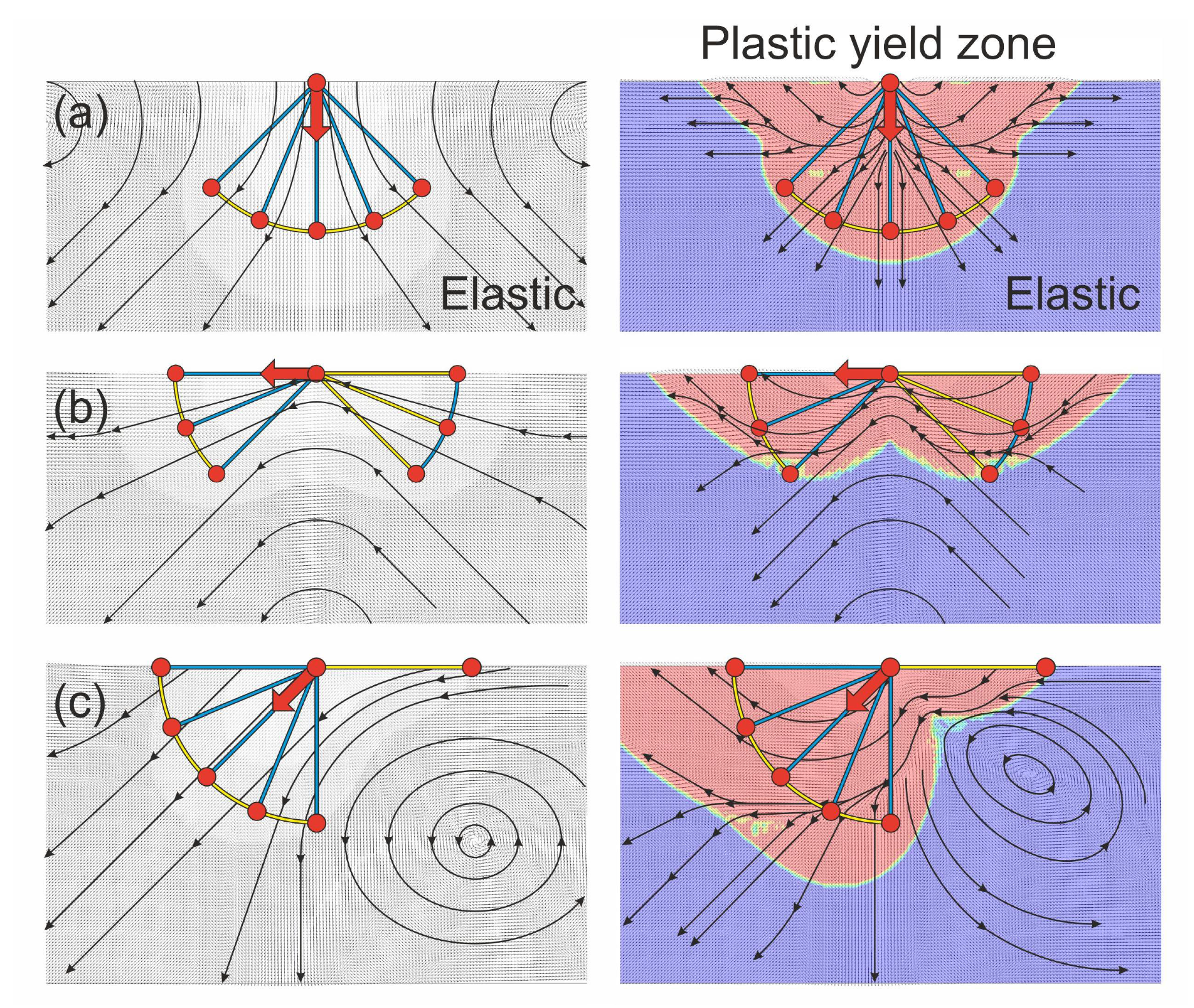
3.1. Finite Element Analysis
3.2. Simplified Model Experiments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Emge, A.; Karthikeyan, S.; Kim, H.J.; Rigney, D.A. The effect of sliding velocity on the tribological behavior of copper. Wear 2007, 263, 614–618. [Google Scholar] [CrossRef]
- Rigney, D.A. Transfer, mixing and associated chemical and mechanical processes during the sliding of ductile materials. Wear 2000, 245, 1–9. [Google Scholar] [CrossRef]
- Hughes, D.A.; Hansen, N. Graded nanostructures produced by sliding and exhibiting universal behavior. Phys. Rev. Lett. 2001, 87, 135503. [Google Scholar] [CrossRef]
- Greiner, C.; Gagel, J.; Gumbsch, P. Solids under Extreme Shear: Friction-Mediated Subsurface Structural Transformations. Adv. Mater. 2019, 31, 1806705. [Google Scholar] [CrossRef] [PubMed]
- Greiner, C.; Liu, Z.; Strassberger, L.; Gumbsch, P. Sequence of stages in the microstructure evolution in copper under mild reciprocating tribological loading. ACS Appl. Mater. Interfaces 2016, 8, 15809–15819. [Google Scholar] [CrossRef] [PubMed]
- Argibay, N.; Chandross, M.; Cheng, S.; Michael, J.R. Linking microstructural evolution and macro-scale friction behavior in metals. J. Mater. Sci. 2016, 52, 2780–2799. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Luo, Z.-P.; Zhang, G.-P.; Schwaiger, R. Microstructural vortex formation during cyclic sliding of Cu/Au multilayers. Scr. Mater. 2015, 107, 67–70. [Google Scholar] [CrossRef] [Green Version]
- Karthikeyan, S.; Kim, H.J.; Rigney, D.A. Velocity and strain-rate profiles in materials subjected to unlubricated sliding. Phys. Rev. Lett. 2005, 95, 106001. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Karthikeyan, S.; Rigney, D. A simulation study of the mixing, atomic flow and velocity profiles of crystalline materials during sliding. Wear 2009, 267, 1130–1136. [Google Scholar] [CrossRef]
- Rigney, D.A.; Karthikeyan, S. The Evolution of Tribomaterial During Sliding: A Brief Introduction. Tribol. Lett. 2010, 39, 3–7. [Google Scholar] [CrossRef]
- Pouryazdan, M.; Kaus, B.J.P.; Rack, A.; Ershov, A.; Hahn, H. Mixing instabilities during shearing of metals. Nat. Commun. 2017, 8, 1611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gola, A.; Schwaiger, R.; Gumbsch, P.; Pastewka, L. Pattern formation during deformation of metallic nanolaminates. Phys. Rev. Mater. 2020, 4, 013603. [Google Scholar] [CrossRef] [Green Version]
- Schmalholz, S.M.; Mancktelow, N.S. Folding and necking across the scales: A review of theoretical and experimental results and their applications. Solid Earth 2016, 7, 1417–1465. [Google Scholar] [CrossRef] [Green Version]
- Eder, S.J.; Rodríguez Ripoll, M.; Cihak-Bayr, U.; Dini, D.; Gachot, C. Unraveling and Mapping the Mechanisms for Near-Surface Microstructure Evolution in CuNi Alloys under Sliding. ACS Appl. Mater. Interfaces 2020, 12, 32197–32208. [Google Scholar] [CrossRef] [PubMed]
- Mattheck, C. Pauli Explain the Form in Nature; KIT Scientif Publishing: Karlsruhe, Germany, 2018. [Google Scholar]
- Mattheck, C. Thinking Tools after Nature; Karlsruher Inst. of Technology-Campus North: Eggenstein-Leopoldshafen, Germany, 2011. [Google Scholar]
- Mattheck, C. Design in Nature: Learning from Trees; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Haller, S. Gestaltfindung: Untersuchungen zur Kraftkegelmethode; KIT Scientific Publishing: Karlsruhe, Germany, 2013; Volume 27. [Google Scholar]
- Kachanov, M.L.; Shafiro, B.; Tsukrov, I. Handbook of Elasticity Solutions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Prandtl, L. Ein Gedankenmodell zur kinetischen Theorie der festen Körper. Z. Angew. Math. Mech. 1928, 8, 85. [Google Scholar] [CrossRef]
- Prandtl, L. Über die Eindringfestigkeit Plastischer Baustoffe und die Festigkeit von Schneiden. Z. Angew. Math. Mech. 1921, 1, 15–20. [Google Scholar] [CrossRef]
- Atkinson, J. An Introduction to the Mechanics of Soils and Foundations: Through Critical State Soil Mechanics; McGraw-Hill Book Company (UK) Ltd.: London, UK, 1993. [Google Scholar]
- Johnson, K.L. Contact Mechanics; University Press: Cambridge, UK, 1987. [Google Scholar]
- Kelvin, L. Note on the integration of the equations of equilibrium of an elastic solid. Camb. Dublin Math. J. 1848, 3, 87–89. [Google Scholar]
- Thompson, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Wolff, K.; Liu, Z.; Braun, D.; Schneider, J.; Greiner, C. Chronology of the microstructure evolution for pearlitic steel under unidirectional tribological loading. Tribol. Int. 2016, 102, 540–545. [Google Scholar] [CrossRef]


| Parameter | Symbol/Description | Value |
|---|---|---|
| Material | ||
| Young’s modulus (MPa) | E | 210,000 |
| Poisson’s ratio | ν | 0.35 |
| Yield strength (MPa) | Re | 20 |
| Plastic tangent modulus (MPa) | ET | 100 |
| Model geometry (2D) | ||
| Width | W | 400 |
| Height | H | 200 |
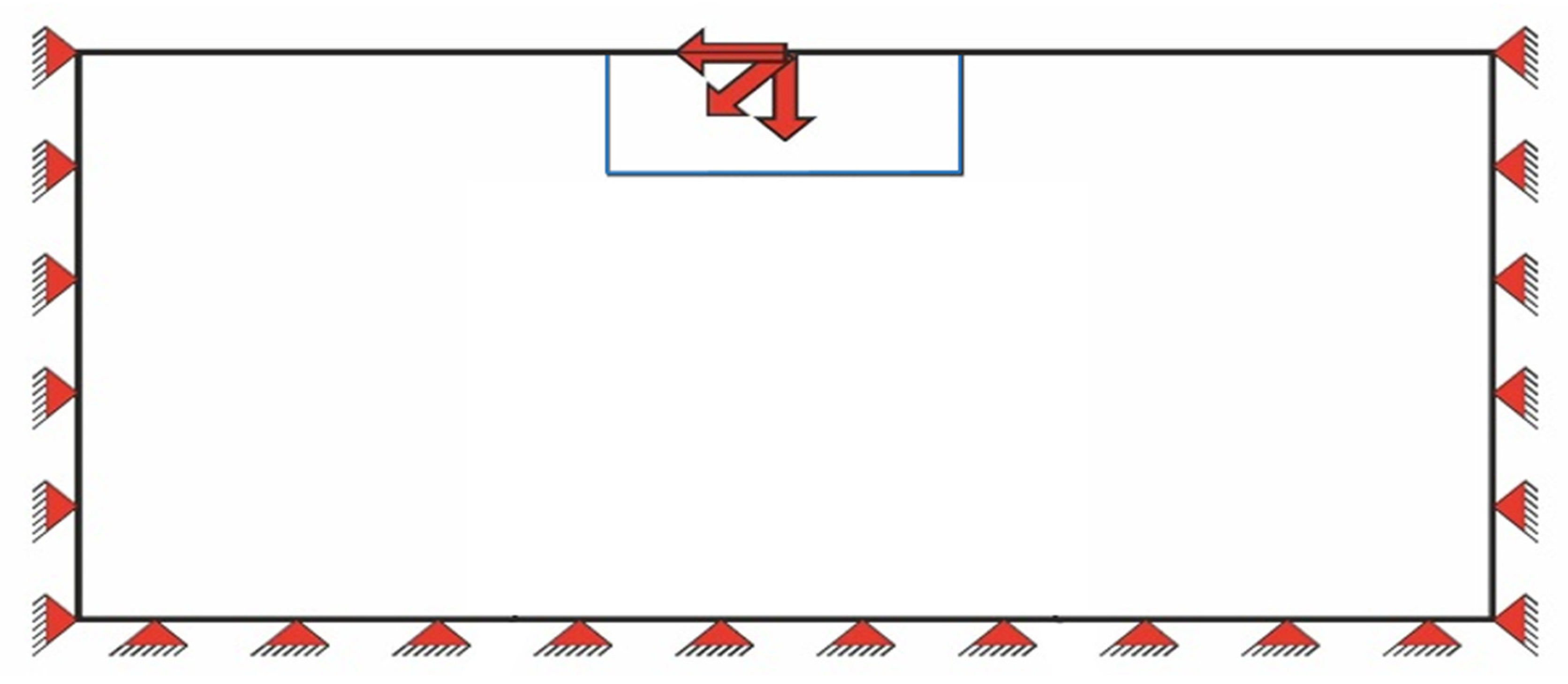
| Boundary conditions | ||
| Number of force loaded nodes | - | 3 |
| Left, right, bottom | - | Clamped |
| Element | ||
| Type | Quad | PLANE 182 1 |
| Size | - | 2 |
| Number | - | 20,000 |
| Stress state | - | Plain strain |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mattheck, C.; Greiner, C.; Bethge, K.; Tesari, I.; Weber, K. The Force Cone Method Applied to Explain Hidden Whirls in Tribology. Materials 2021, 14, 3894. https://doi.org/10.3390/ma14143894
Mattheck C, Greiner C, Bethge K, Tesari I, Weber K. The Force Cone Method Applied to Explain Hidden Whirls in Tribology. Materials. 2021; 14(14):3894. https://doi.org/10.3390/ma14143894
Chicago/Turabian StyleMattheck, Claus, Christian Greiner, Klaus Bethge, Iwiza Tesari, and Karlheinz Weber. 2021. "The Force Cone Method Applied to Explain Hidden Whirls in Tribology" Materials 14, no. 14: 3894. https://doi.org/10.3390/ma14143894
APA StyleMattheck, C., Greiner, C., Bethge, K., Tesari, I., & Weber, K. (2021). The Force Cone Method Applied to Explain Hidden Whirls in Tribology. Materials, 14(14), 3894. https://doi.org/10.3390/ma14143894







