Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions
Abstract
:1. Introduction
2. Material Properties Calculation and Model Establishment
3. Differential Equation of Thin Plate Vibration
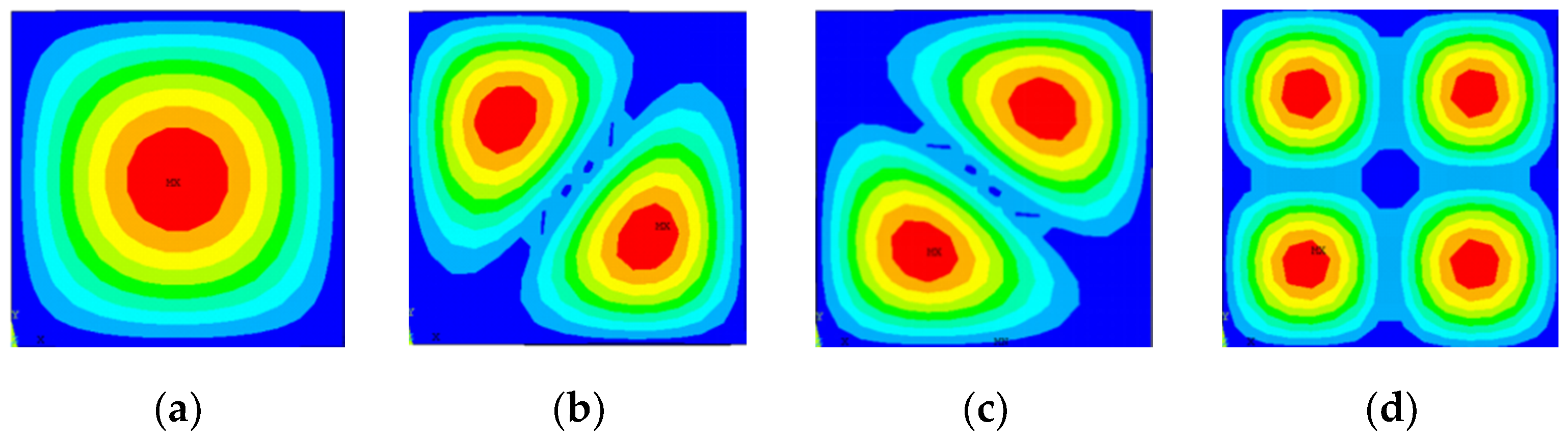
4. Finite Element Analysis
5. Calculation and Discussion
5.1. Analysis of Stratified Convergence of GPL Reinforced Porous Composite Plate and the Influence of Boundary Conditions
5.2. Effect of Porosity Coefficient on Free Vibration Frequency of GPL Reinforced Porous Composite Plate
5.3. Effect of GPL Weight Fraction on Free Vibration Frequency of GPL Reinforced Porous Composite Plate
5.4. Effect of GPL Shape on Free Vibration Frequency of GPL Reinforced Porous Composite Plate
5.5. The Effect of Porous Distribution and GPL Distribution Pattern on the Free Vibration Frequency of GPL Reinforced Porous Composite Plate
6. Conclusions
- The freer the vibration frequency of the GPL reinforced porous composite plate monotonically converged with the increase in the total number of layers, and n = 12 was the most suitable number of layers. With the increase in the fixed edge (C), the vibration frequency of composite plate increased gradually. When the boundary condition was CCCC, the vibration frequency of the porous composite plate at the maximum;
- The freer the vibration frequency of the GPL reinforced porous composite plate decreased with the increase in the porosity coefficient, increased with the increase in the GPL weight fraction, increased with the increase in the LGPL/TGPL, and decreased with the increase in LGPL/WGPL. This can help us better select the size and content of graphene platelets to be applied to practice;
- The maximum free vibration frequency can be obtained by combining the porosity distribution A and with the distribution mode of the GPL pattern X. This combination greatly verifies the properties of the reinforcement materials and the possibility of weight reduction in aircraft design, and can be applied to the aerospace industry, which can play a better role.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Boundary Conditions | Order | e0 = 0.1 | e0 = 0.2 | e0 = 0.3 | e0 = 0.4 | e0 = 0.5 | e0 = 0.6 |
|---|---|---|---|---|---|---|---|
| SSSS | 1 | 102.35 | 99.92 | 97.73 | 95.75 | 94.01 | 92.51 |
| 2 | 255.87 | 249.81 | 244.32 | 239.39 | 235.02 | 231.28 | |
| 3 | 255.87 | 249.81 | 244.32 | 239.39 | 235.02 | 231.28 | |
| 4 | 409.40 | 399.70 | 390.91 | 383.02 | 376.03 | 370.05 | |
| SSCC | 1 | 139.31 | 136.01 | 133.02 | 130.33 | 127.96 | 125.92 |
| 2 | 313.95 | 306.51 | 299.78 | 293.72 | 288.37 | 283.78 | |
| 3 | 313.95 | 306.51 | 299.78 | 293.72 | 288.37 | 283.78 | |
| 4 | 480.47 | 469.09 | 458.78 | 449.51 | 441.32 | 434.29 | |
| SCCC | 1 | 163.01 | 159.15 | 155.65 | 152.50 | 149.72 | 147.34 |
| 2 | 326.93 | 319.19 | 312.17 | 305.87 | 300.29 | 295.51 | |
| 3 | 367.50 | 358.80 | 350.91 | 343.82 | 337.55 | 332.18 | |
| 4 | 520.77 | 508.43 | 497.26 | 487.21 | 478.33 | 470.72 | |
| CCCC | 1 | 182.06 | 177.75 | 173.84 | 170.33 | 167.22 | 164.56 |
| 2 | 377.99 | 369.03 | 360.92 | 353.63 | 347.19 | 341.66 | |
| 3 | 377.99 | 369.03 | 360.92 | 353.63 | 347.19 | 341.66 | |
| 4 | 557.23 | 544.03 | 532.07 | 521.33 | 511.82 | 503.68 |
| Boundary Conditions | Order | wt.% = 0 | wt.% = 0.33 | wt.% = 0.66 | wt.% = 0.88 | wt.% = 1 |
|---|---|---|---|---|---|---|
| SSSS | 1 | 73.33 | 84.15 | 93.61 | 99.37 | 102.35 |
| 2 | 183.31 | 210.37 | 234.03 | 248.41 | 255.87 | |
| 3 | 183.31 | 210.37 | 234.03 | 248.41 | 255.87 | |
| 4 | 293.30 | 336.60 | 374.45 | 397.46 | 409.40 | |
| SSCC | 1 | 99.80 | 114.54 | 127.42 | 135.25 | 139.31 |
| 2 | 224.92 | 258.12 | 287.15 | 304.80 | 313.95 | |
| 3 | 224.92 | 258.12 | 287.15 | 304.80 | 313.95 | |
| 4 | 344.22 | 395.03 | 439.46 | 466.46 | 480.47 | |
| SCCC | 1 | 116.78 | 134.02 | 149.09 | 158.26 | 163.01 |
| 2 | 234.22 | 268.80 | 299.03 | 317.40 | 326.93 | |
| 3 | 263.29 | 302.15 | 336.13 | 356.79 | 367.50 | |
| 4 | 373.09 | 428.17 | 476.32 | 505.59 | 520.77 | |
| CCCC | 1 | 130.43 | 149.69 | 166.52 | 176.75 | 182.06 |
| 2 | 270.80 | 310.77 | 345.72 | 366.97 | 377.99 | |
| 3 | 270.80 | 310.77 | 345.72 | 366.97 | 377.99 | |
| 4 | 399.21 | 458.15 | 509.67 | 540.99 | 557.23 |
| Boundary Conditions | Order | LGPL/TGPL = 10 | LGPL/TGPL = 100 | LGPL/TGPL = 1000 | LGPL/TGPL = 10,000 |
|---|---|---|---|---|---|
| SSSS | 1 | 95.21 | 101.41 | 102.35 | 102.45 |
| 2 | 238.03 | 253.52 | 255.87 | 256.12 | |
| 3 | 238.03 | 253.52 | 255.87 | 256.12 | |
| 4 | 380.85 | 405.63 | 409.40 | 409.79 | |
| SSCC | 1 | 129.59 | 138.03 | 139.31 | 139.44 |
| 2 | 292.06 | 311.06 | 313.95 | 314.26 | |
| 3 | 292.06 | 311.06 | 313.95 | 314.26 | |
| 4 | 446.97 | 476.05 | 480.47 | 480.94 | |
| SCCC | 1 | 151.64 | 161.51 | 163.01 | 163.17 |
| 2 | 304.13 | 323.93 | 326.93 | 327.25 | |
| 3 | 341.88 | 364.12 | 367.50 | 367.86 | |
| 4 | 484.45 | 515.98 | 520.77 | 521.27 | |
| CCCC | 1 | 169.36 | 180.39 | 182.06 | 182.24 |
| 2 | 351.63 | 374.51 | 377.99 | 378.36 | |
| 3 | 351.63 | 374.51 | 377.99 | 378.36 | |
| 4 | 518.38 | 552.11 | 557.23 | 557.77 |
| Boundary Conditions | Order | LGPL/WGPL = 1 | LGPL/WGPL = 2 | LGPL/WGPL = 4 | LGPL/WGPL = 6 | LGPL/WGPL = 8 |
|---|---|---|---|---|---|---|
| SSSS | 1 | 102.39 | 102.35 | 102.27 | 102.18 | 102.10 |
| 2 | 255.98 | 255.87 | 255.66 | 255.46 | 255.25 | |
| 3 | 255.98 | 255.87 | 255.66 | 255.46 | 255.25 | |
| 4 | 409.57 | 409.40 | 409.06 | 408.74 | 408.40 | |
| SSCC | 1 | 139.37 | 139.31 | 139.19 | 139.08 | 138.97 |
| 2 | 314.08 | 313.95 | 313.70 | 313.45 | 313.19 | |
| 3 | 314.08 | 313.95 | 313.70 | 313.45 | 313.19 | |
| 4 | 480.67 | 480.47 | 480.08 | 479.70 | 479.31 | |
| SCCC | 1 | 163.07 | 163.01 | 162.87 | 162.75 | 162.61 |
| 2 | 327.07 | 326.93 | 326.66 | 326.41 | 326.14 | |
| 3 | 367.66 | 367.50 | 367.20 | 366.91 | 366.61 | |
| 4 | 520.98 | 520.77 | 520.34 | 519.93 | 519.51 | |
| CCCC | 1 | 182.14 | 182.06 | 181.91 | 181.77 | 181.62 |
| 2 | 378.14 | 377.99 | 377.68 | 377.38 | 377.07 | |
| 3 | 378.14 | 377.99 | 377.68 | 377.38 | 377.07 | |
| 4 | 557.46 | 557.23 | 556.78 | 556.34 | 555.88 |
References
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.B.T.; Ruoff, R.S. Graphene-based composite materials. J. Nat. 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Rahman, R.; Haque, A. Molecular modeling of crosslinked graphene–epoxy nanocomposites for characterization of elastic constants and interfacial properties. J. Compos. Part B 2013, 54, 353–364. [Google Scholar] [CrossRef]
- Julia, A.; King, D.R.; Klimek, I.; Miskioglu, I.; Odegard, G.M. Mechanical properties of graphene nanoplatelet/epoxy composites. J. Appl. Polym. Sci. 2013, 128, 4217–4223. [Google Scholar]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). J. Compos. Part B 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Alibeigloo, A.; Kari, M.R. Forced vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third order shear deformation theory. J. Thin-Walled Struct. 2008, 47, 653–660. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. J. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Eringen, A. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Polit, O.; Anant, C.; Anirudh, B.; Ganapathi, M. Functionally graded graphene reinforced porous nanocomposite curved beams: Bending and elastic stability using a higher-order model with thickness stretch effect. Compos. Part B Eng. 2019, 166, 310–327. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Liu, D.Y.; Kitipornchai, S.; Chen, W.Q.; Yang, J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos. Struct. 2018, 189, 560–569. [Google Scholar] [CrossRef] [Green Version]
- Reddy, R.M.R.; Karunasena, W.; Lokuge, W. Free vibration of functionally graded-GPL reinforced composite plates with different boundary conditions. Aerosp. Sci. Technol. 2018, 78, 147–156. [Google Scholar] [CrossRef]
- Amirabadi, H.; Farhatnia, F.; Eftekhari, S.A.; Hosseini-Ara, R. Free vibration analysis of rotating functionally graded GPL-reinforced truncated thick conical shells under different boundary conditions. Mech. Based Des. Struct. Mach. 2020, 1–32. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, T.Y.; Zhang, H.Y.; Pan, H.G.; Yuan, H.Q.; Ma, H.; Yin, F.; Tai, X.; Kou, H.; Yuan, H.; et al. Dynamic characteristics of mistuned bladed disk system under rub-impact force. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef]
- Sharma, G.S.; Sarkar, A. Directivity based control of acoustic radiation. J. Appl. Acoust. 2019, 154, 226–235. [Google Scholar] [CrossRef]
- Sharma, G.S.; Sarkar, A. Directivity-Based Passive Barrier for Local Control of Low-Frequency Noise. J. Theor. Comput. Acoust. 2018, 26, 1850012. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Pan, H.G.; Cai, Y. Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Appl. Math. Model. 2021, 93, 578–596. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Pan, H.G.; Yang, J.; Sritawat, K. Coupled free vibration of a functionally graded pre-twisted blade-shaft system reinforced with graphene nanoplatelets. Compos. Struct. 2020, 262, 113362. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Yang, J. Coupled Free Vibration of Spinning Functionally Graded Porous Double-Bladed Disk Systems Reinforced with Graphene Nanoplatelets. Materials 2020, 13, 5610. [Google Scholar] [CrossRef] [PubMed]
- Sharma, G.S.; Faverjon, B.; Dureisseix, D.; Skvortsov, A.; MacGillivray, I.; Audoly, C.; Kessissoglou, N. Acoustic Performance of a Periodically Voided Viscoelastic Medium with Uncertainty in Design Parameters. J. Vib. Acoust. 2020, 142. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197, 106335. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a spinning porous nanocomposite blade reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, Z.Y.; Zhao, Z.; Xie, L.Y.; Yuan, H.Q. Modeling and free vibration analysis of rotating hub-blade assemblies reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Shafiei, N.; Mousavi, A.; Ghadiri, M. On size-dependent nonlinear vibration of porous and imperfect functionally graded tapered microbeams. Int. J. Eng. Sci. 2016, 106, 42–56. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound transmission through a periodically voided soft elastic medium submerged in water. Wave Motion 2017, 70, 101–112. [Google Scholar] [CrossRef]
- Davletshin, A.R.; Ustiuzhanina, S.V.; Kistanov, A.A.; Saadatmand, D.; Dmitriev, S.V.; Zhou, K.; Korznikova, E.A. Electronic structure of graphene– and BN–supported phosphorene. J. Phys. B Phys. Condens. Matter 2018, 534, 63–67. [Google Scholar] [CrossRef]
- Babicheva, R.I.; Dmitriev, S.V.; Korznikova, E.A.; Zhou, K. Mechanical Properties of Two-Dimensional sp 2 -Carbon Nanomaterials. J. Exp. Theor. Phys. 2019, 129. [Google Scholar] [CrossRef]
- Savin, A.; Korznikova, E.; Krivtsov, A.; Dmitriev, S. Longitudinal stiffness and thermal conductivity of twisted carbon nanoribbons. Eur. J. Mech. A 2020, 80. [Google Scholar] [CrossRef]
- Savin, A.V.; Korznikova, E.; Dmitriev, S. Dynamics of surface graphene ripplocations on a flat graphite substrate. Phys. Rev. B 2019, 99, 235411. [Google Scholar] [CrossRef]
- Chen, D.; Kitipornchai, S.; Yang, J. Dynamic response and energy absorption of functionally graded porous structures. Mater. Des. 2018, 140, 473–487. [Google Scholar] [CrossRef] [Green Version]
- Hui-Shen, S.; Feng, L.; Xiang, Y. Nonlinear vibration of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations in thermal environments. J. Nonlinear Dyn. 2017, 90, 899–914. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The Mechanics of Three-Dimensional Cellular Materials. J. Proc. R. Soc. Lond. Ser. A 1982, 382, 43–59. [Google Scholar]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]








| e0 | α | |
|---|---|---|
| 0.1 | 0.1738 | 0.9361 |
| 0.2 | 0.3442 | 0.8716 |
| 0.3 | 0.5103 | 0.8064 |
| 0.4 | 0.6708 | 0.7404 |
| 0.5 | 0.8231 | 0.6733 |
| 0.6 | 0.9612 | 0.6047 |
| Boundary Conditions | Order | MATLAB Calculation Results | ANSYS Analysis Results |
|---|---|---|---|
| SSSS | 1 | 102.35 | 102.22 |
| 2 | 255.87 | 255.77 | |
| 3 | 255.87 | 255.77 | |
| 4 | 409.40 | 406.96 | |
| SSCC | 1 | 139.31 | 140.92 |
| 2 | 313.95 | 314.80 | |
| 3 | 313.95 | 316.02 | |
| 4 | 480.47 | 480.43 | |
| SCCC | 1 | 163.01 | 166.27 |
| 2 | 326.93 | 329.72 | |
| 3 | 367.50 | 370.15 | |
| 4 | 520.77 | 522.59 | |
| CCCC | 1 | 182.06 | 188.34 |
| 2 | 377.99 | 382.58 | |
| 3 | 377.99 | 382.58 | |
| 4 | 557.23 | 561.92 |
| Boundary Conditions\Number of Layers | 2 | 4 | 6 | 8 | 10 | 12 | 100 |
|---|---|---|---|---|---|---|---|
| SSSS | 107.83 | 103.37 | 102.72 | 102.50 | 102.40 | 102.35 | 102.23 |
| SSCC | 146.77 | 140.70 | 139.81 | 139.52 | 139.38 | 139.31 | 139.15 |
| SCCC | 171.74 | 164.64 | 163.60 | 163.25 | 163.09 | 163.01 | 162.82 |
| CCCC | 191.81 | 183.88 | 182.72 | 182.33 | 182.16 | 182.06 | 181.85 |
| Boundary Conditions | Porosity A/GPL X | Porosity A/GPL U | Porosity A/GPL O | Uniform/GPL X | Uniform/GPL U | Uniform/GPL O | Porosity B/GPL X | Porosity B/GPL U | Porosity B/GPL O |
|---|---|---|---|---|---|---|---|---|---|
| SSSS | 102.35 | 93.54 | 86.27 | 100.91 | 92.19 | 85.13 | 98.38 | 89.84 | 83.17 |
| SSCC | 139.31 | 127.32 | 117.43 | 137.35 | 125.48 | 115.87 | 133.91 | 122.28 | 113.20 |
| SCCC | 163.01 | 148.98 | 137.40 | 160.71 | 146.82 | 135.58 | 156.69 | 143.09 | 132.46 |
| CCCC | 182.06 | 166.39 | 153.47 | 179.50 | 163.98 | 151.43 | 175.01 | 159.81 | 147.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.-G.; Wu, Y.-S.; Zhou, J.-N.; Fu, Y.-M.; Liang, X.; Zhao, T.-Y. Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions. Materials 2021, 14, 3879. https://doi.org/10.3390/ma14143879
Pan H-G, Wu Y-S, Zhou J-N, Fu Y-M, Liang X, Zhao T-Y. Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions. Materials. 2021; 14(14):3879. https://doi.org/10.3390/ma14143879
Chicago/Turabian StylePan, Hong-Gang, Yun-Shi Wu, Jian-Nan Zhou, Yan-Ming Fu, Xin Liang, and Tian-Yu Zhao. 2021. "Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions" Materials 14, no. 14: 3879. https://doi.org/10.3390/ma14143879
APA StylePan, H.-G., Wu, Y.-S., Zhou, J.-N., Fu, Y.-M., Liang, X., & Zhao, T.-Y. (2021). Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions. Materials, 14(14), 3879. https://doi.org/10.3390/ma14143879








