Comparative Study and Limits of Different Level-Set Formulations for the Modeling of Anisotropic Grain Growth
Abstract
:1. Introduction
2. The Numerical Framework
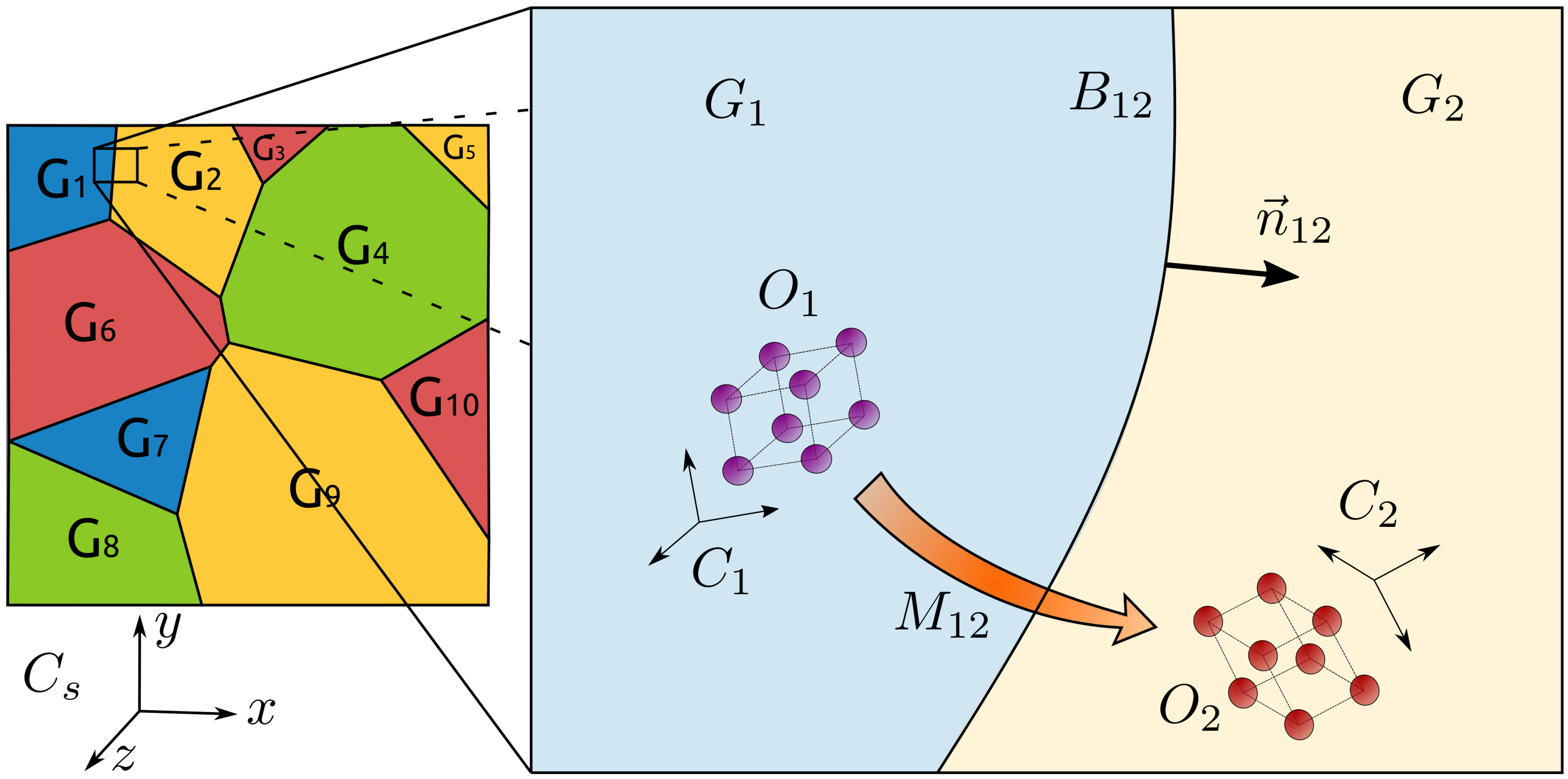
2.1. Crystallographic Definitions
2.2. FE-LS Formulation
3. The Grim Reaper Case
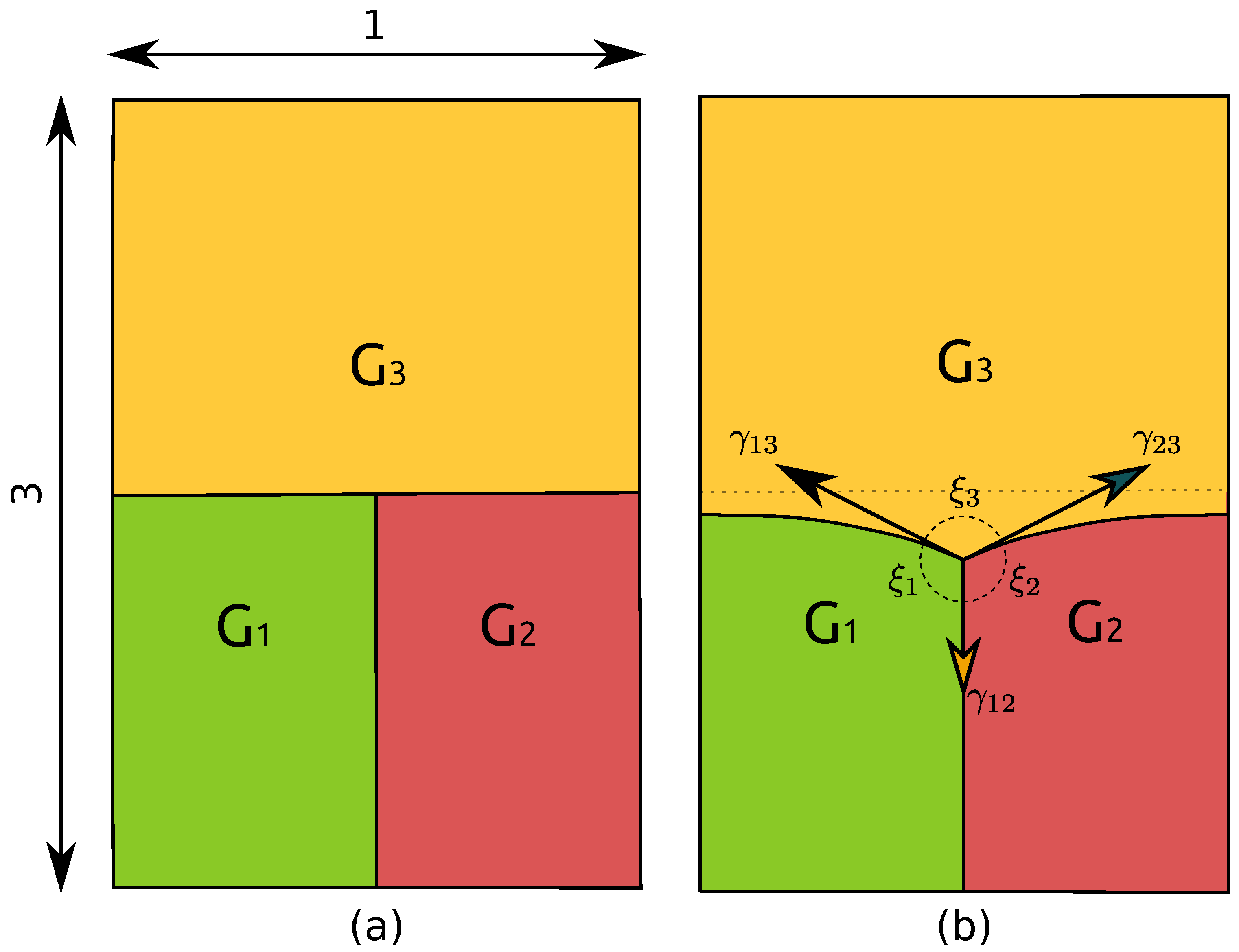
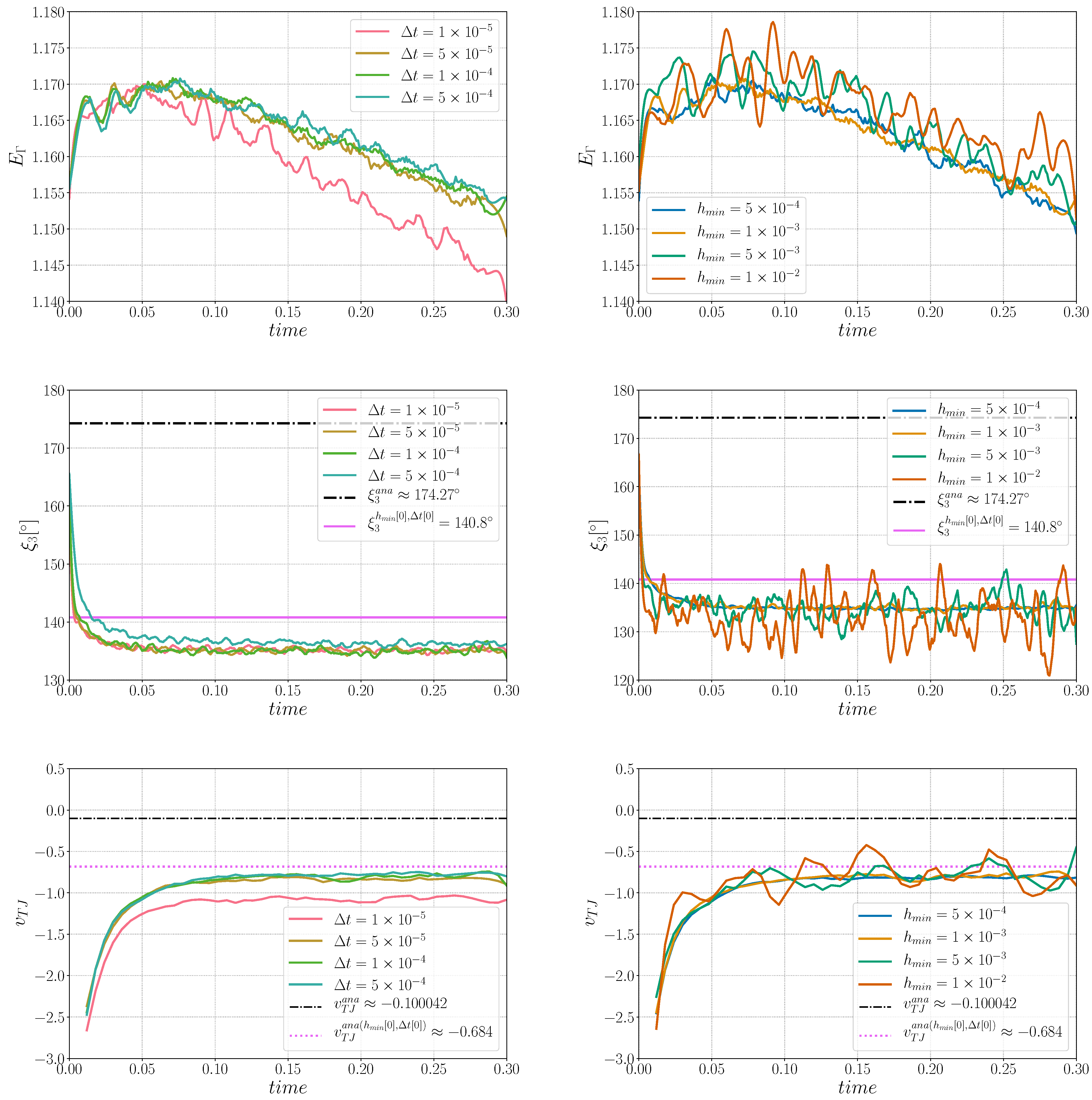
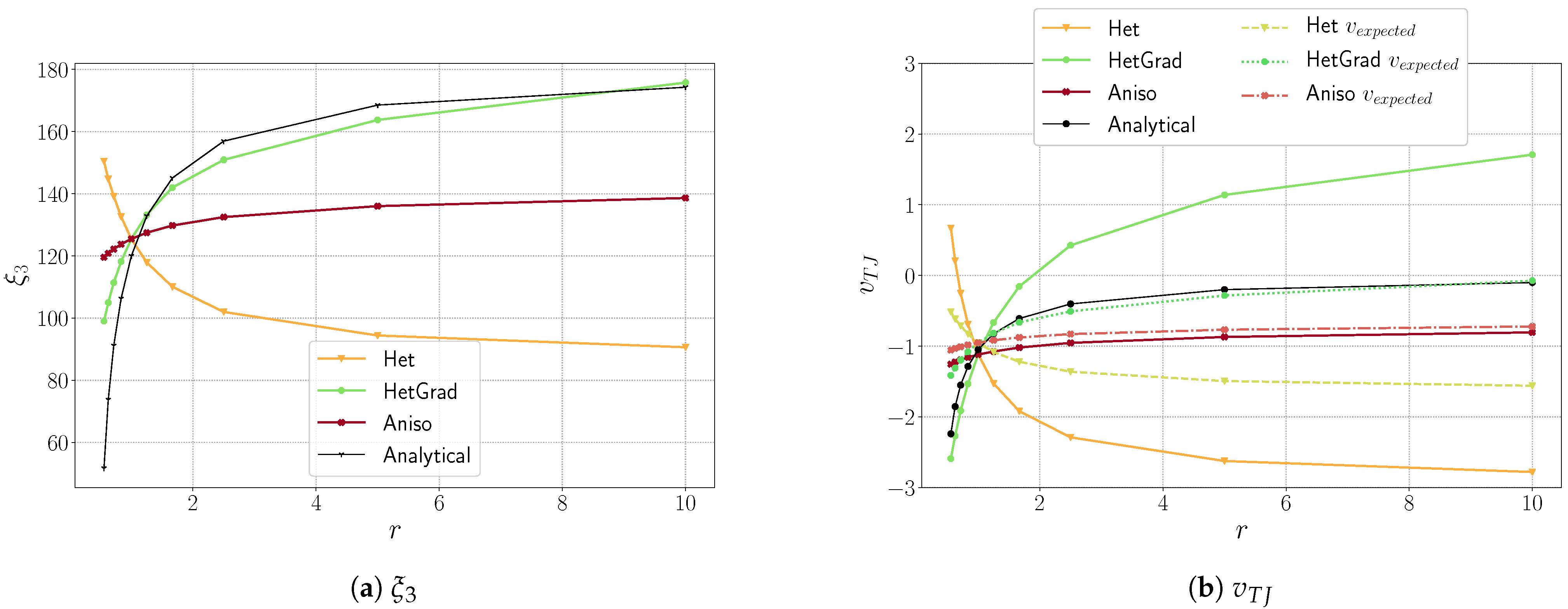
3.1. Description of the Test Case
- The velocity of the triple junction is computed using the relation , where is the y-position of the triple point at time and is the time step.
- The dihedral angles are computed using the methodology presented in [26]: one may define, at each time, a circle of radius with circumference , and divide it into arcs which pass through grain with length . The angle of the arc, , could be approximated thanks to the relation .
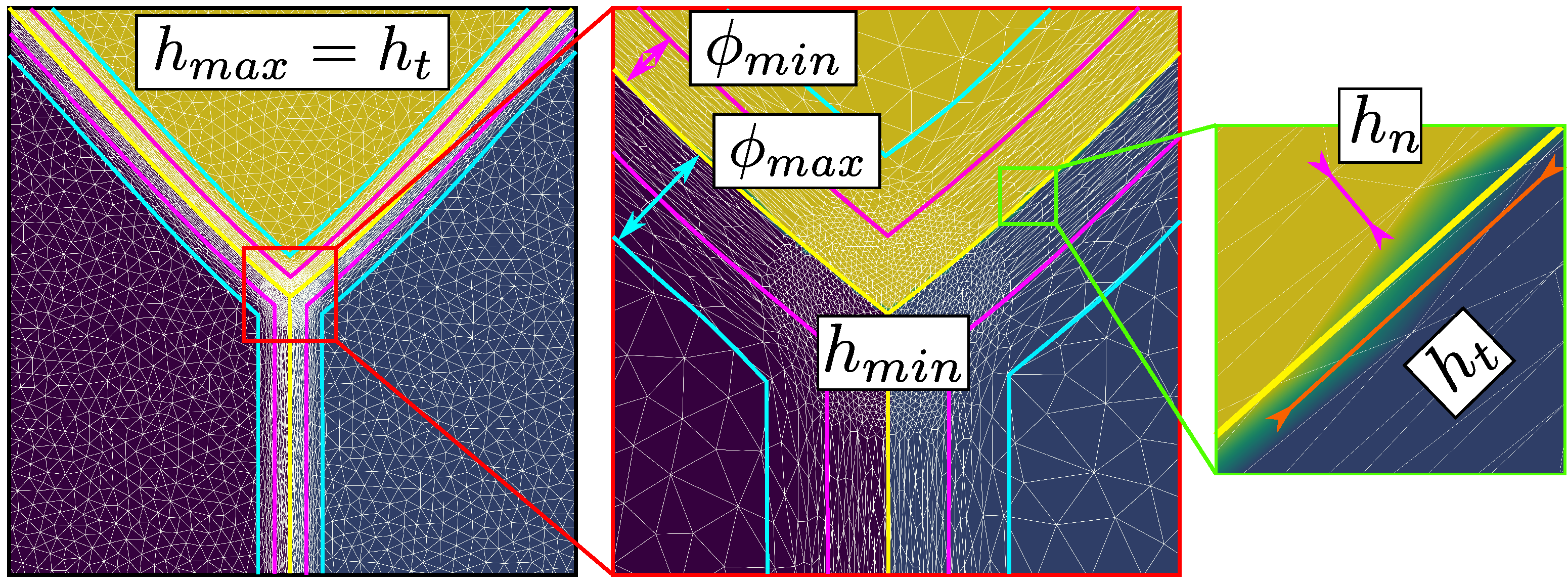
3.2. Numerical Strategy
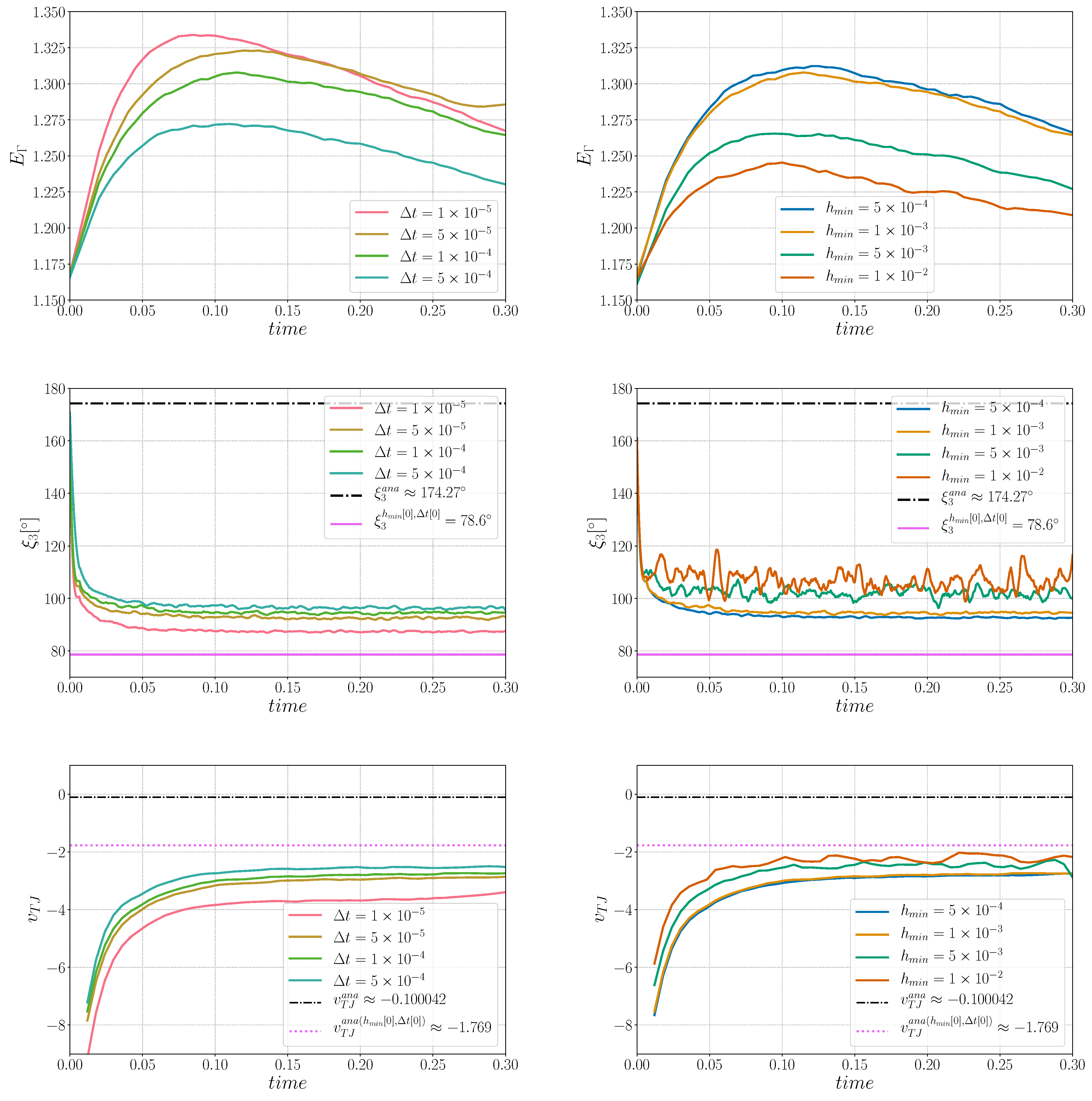
3.3. Results and Analysis
3.4. Conclusions
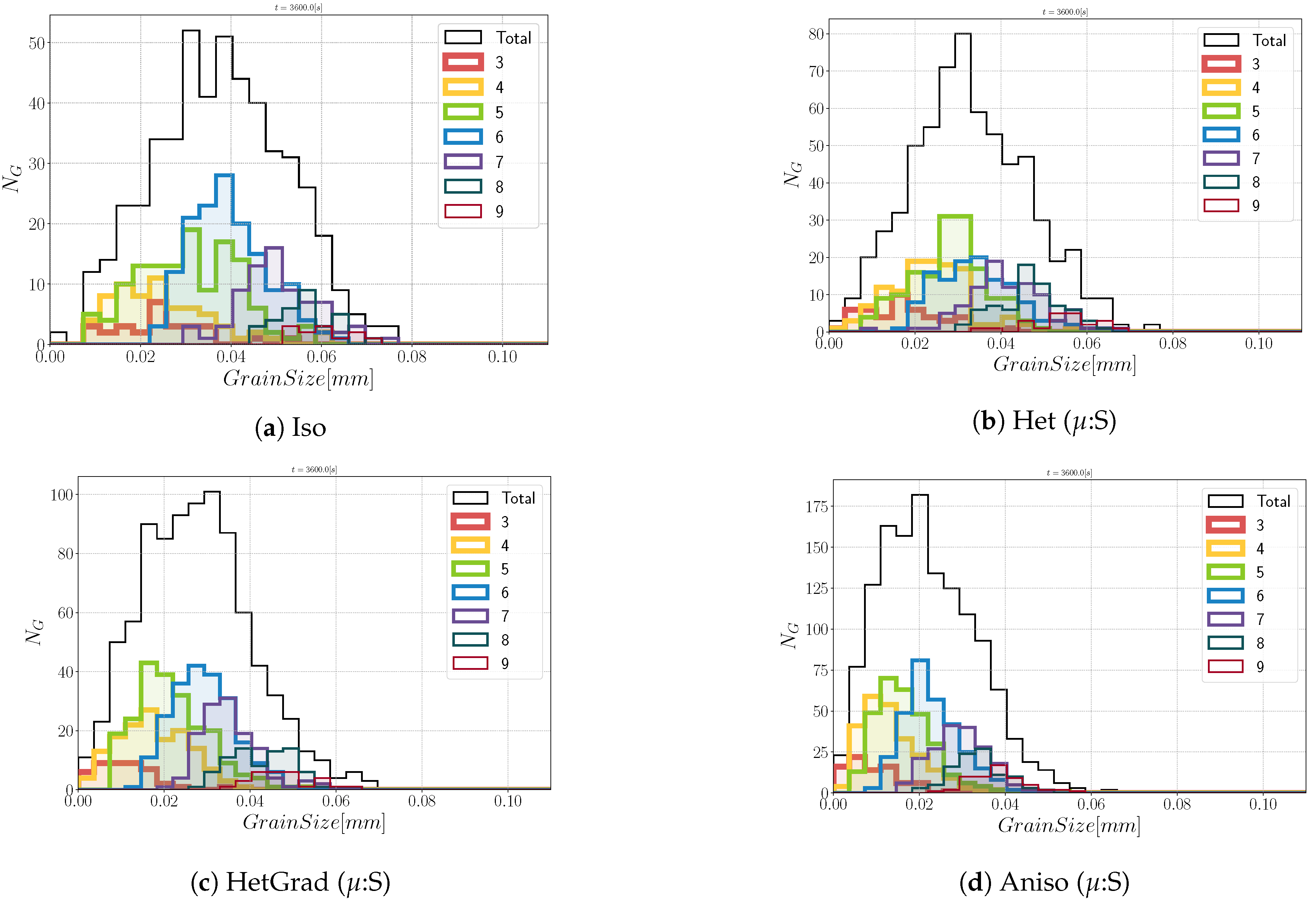
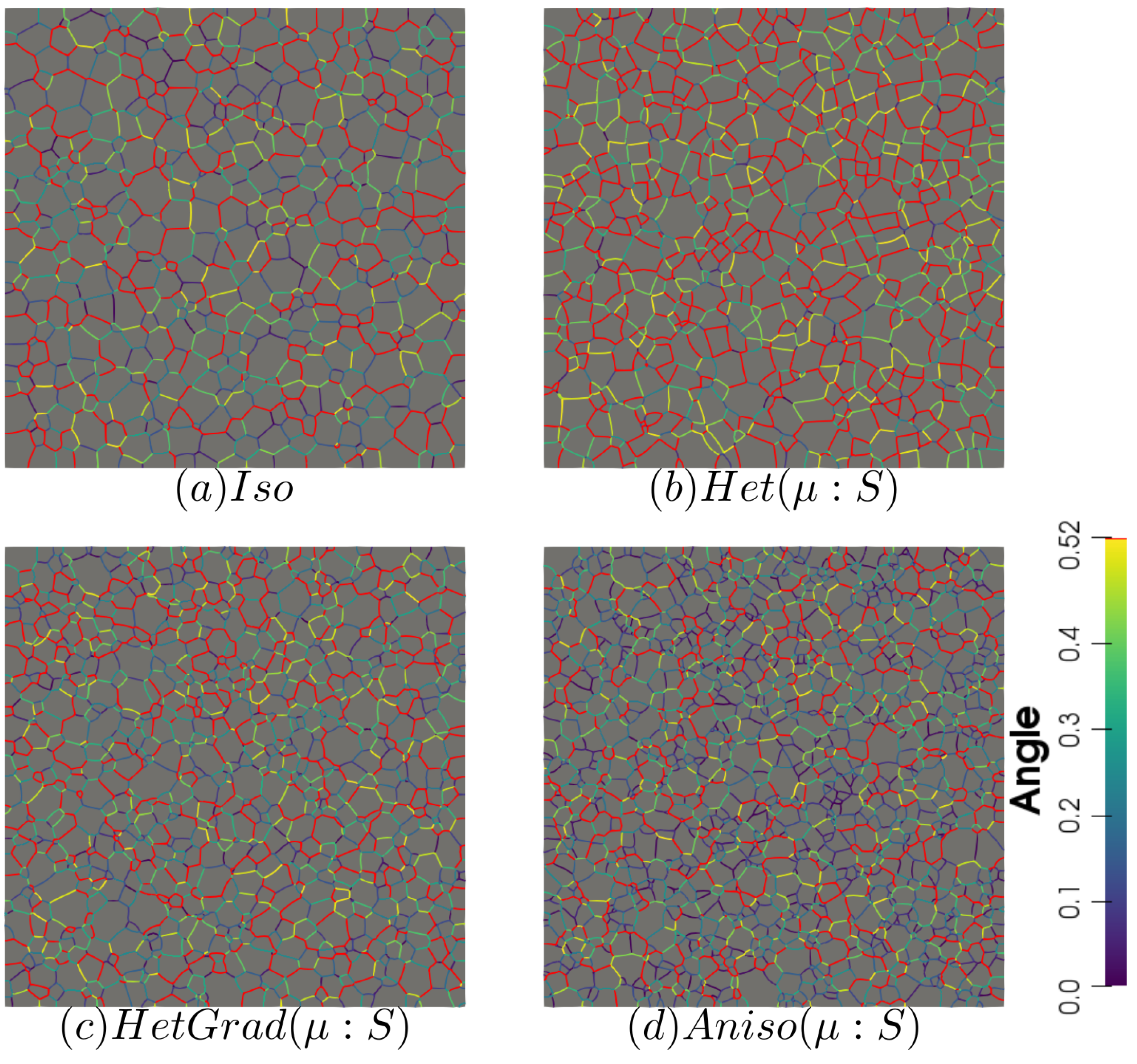
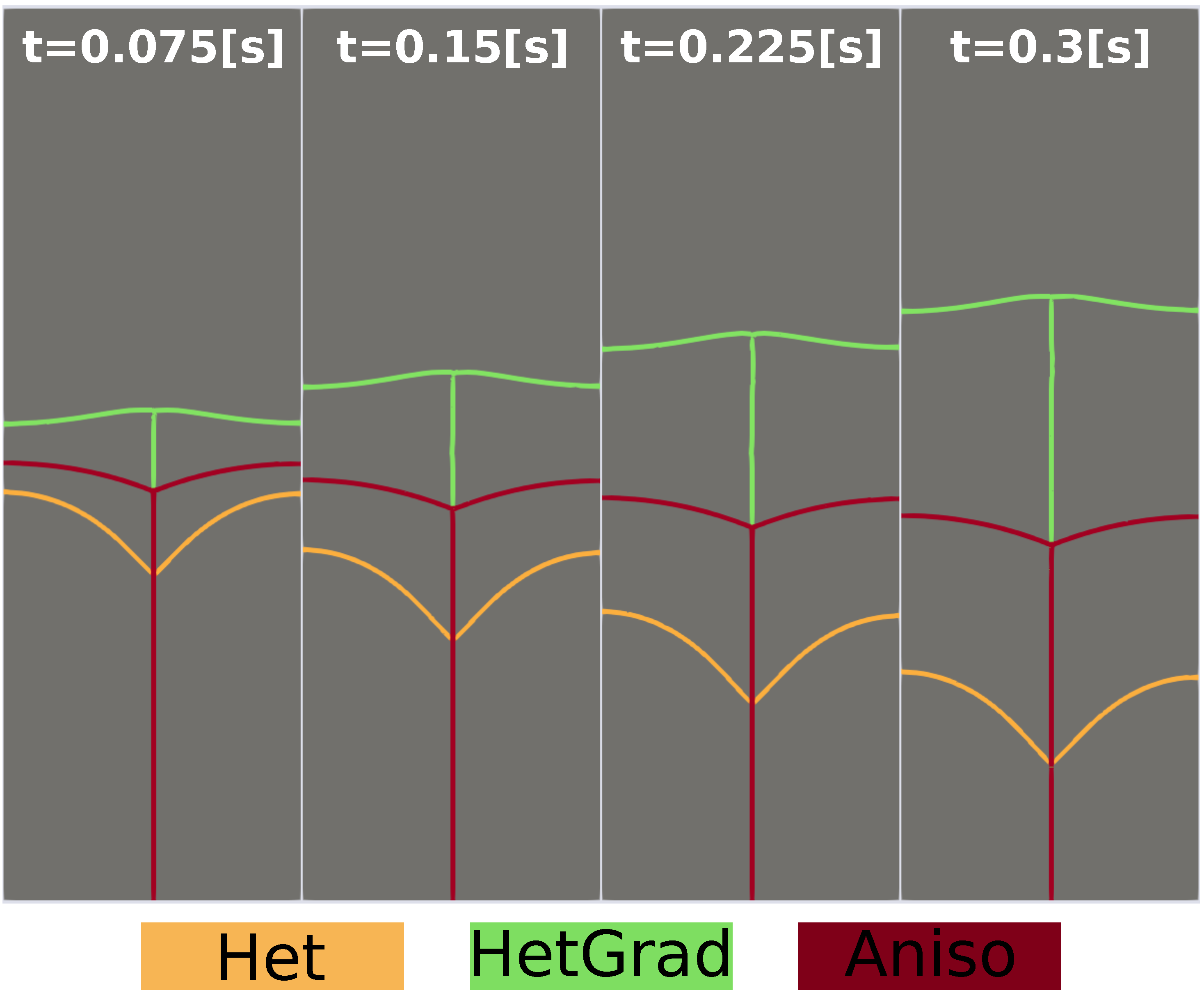
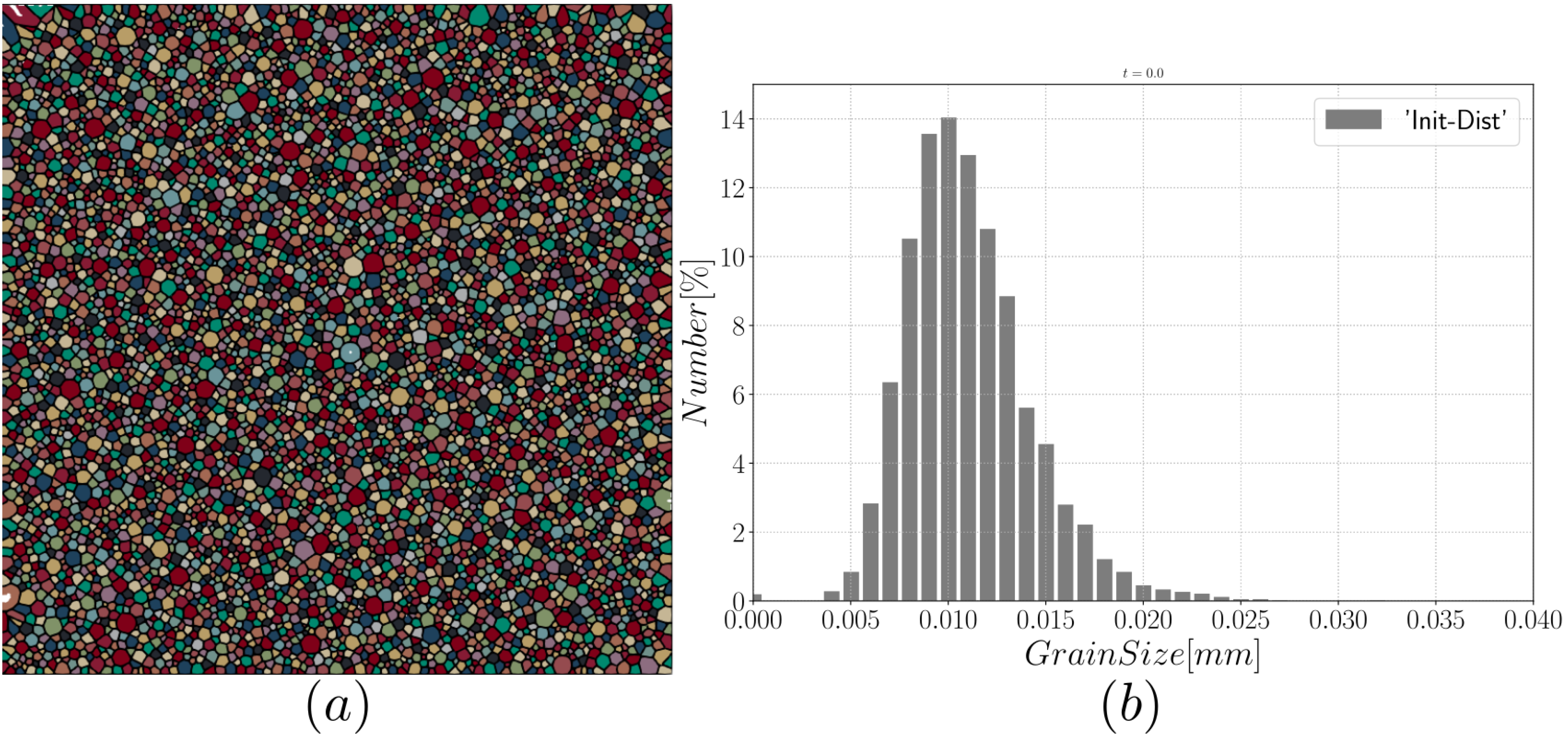
4. Effect of the Texture and Heterogeneous GB Properties during GG Simulations for a Polycrystalline Microstructure
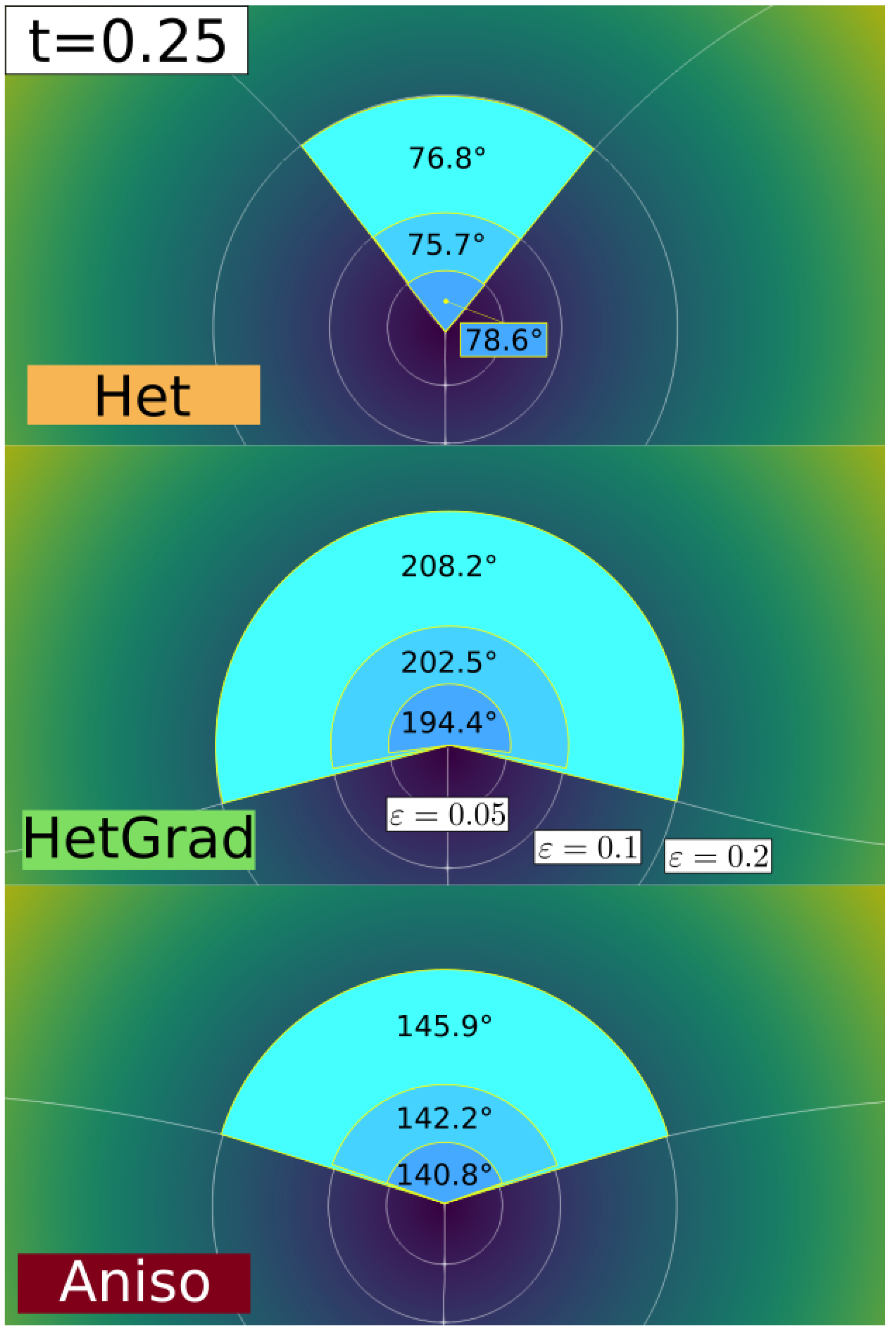
4.1. Effect of the Heterogeneity
4.1.1. Heterogeneous Grain Boundary Energy
4.1.2. Heterogeneous Grain Boundary Energy and Mobility
4.2. CPU Time
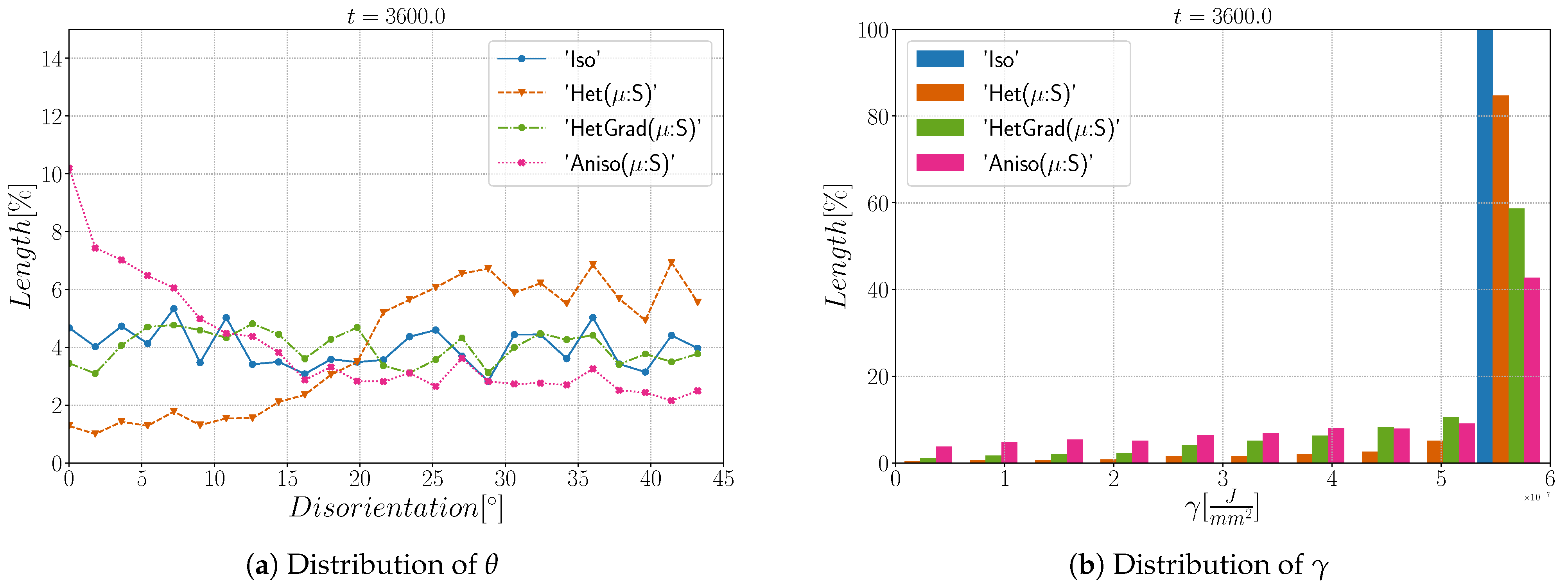
5. Accounting for Mis-Orientation and Inclination Dependence
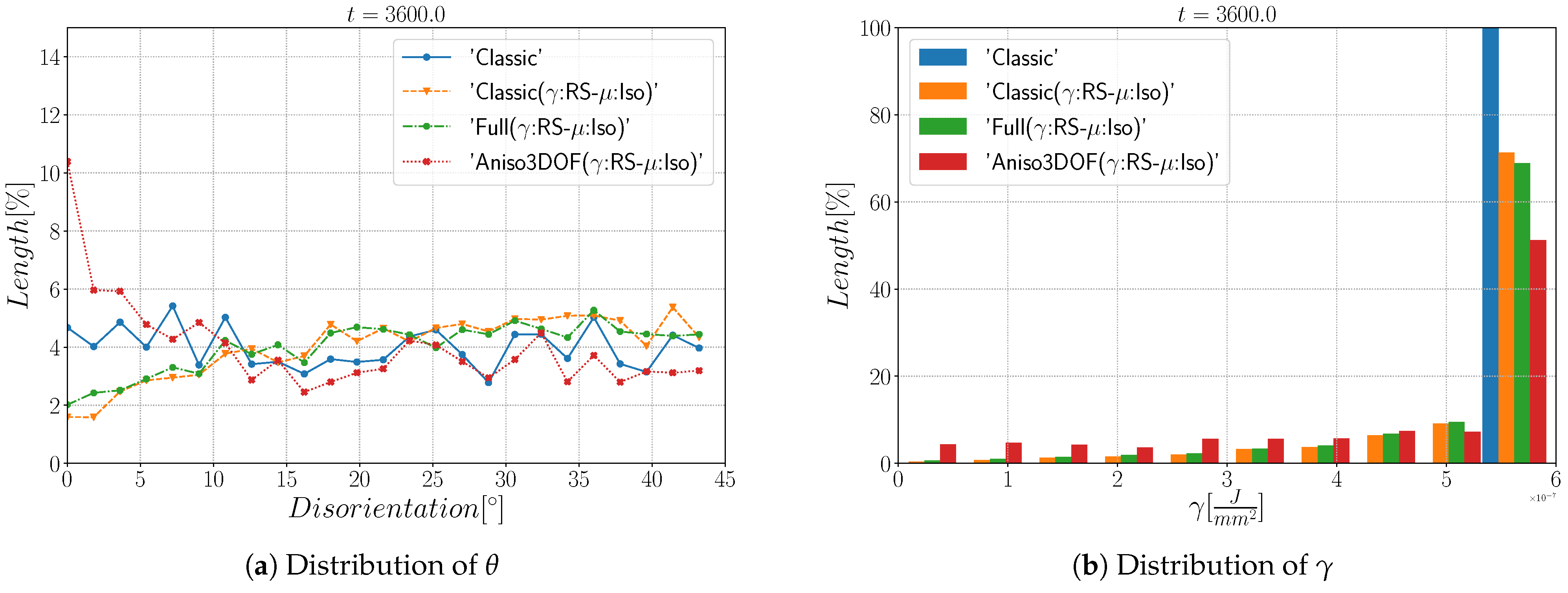
5.1. Triple Junction
5.2. Coherent and Incoherent Twin Boundary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FE | Finite Element |
| GB | Grain Boundary |
| LS | Level Set |
| FE-LS | Finite Element Level-Set |
| DDF | Disorientation Distribution Function |
| GG | Grain Growth |
| Iso | Isotropic formulation |
| Het | Heterogeneous formulation |
| HetGrad | Heterogeneous with Gradient formulation |
| Aniso | Anisotropic formulation |
| SUPG | Streamline Upwind Petrov–Galerkin |
| BC | Boundary Condition |
| RS | Read–Shockley |
| S | Sigmoidal |
| LAGB | Low-Angle Grain Boundary |
| HAGB | High-Angle Grain Boundary |
| GBED | Grain Boundary Energy distribution |
| GB5DOF | Code to compute the GB energy as a function of the mis-orientation |
| and normal orientation [73] | |
| CTB | Coherent Twin Boundary |
| ICB | Incoherent Twin Boundary |
Appendix A. Grim Reaper Case: Effect of the Boundary Conditions



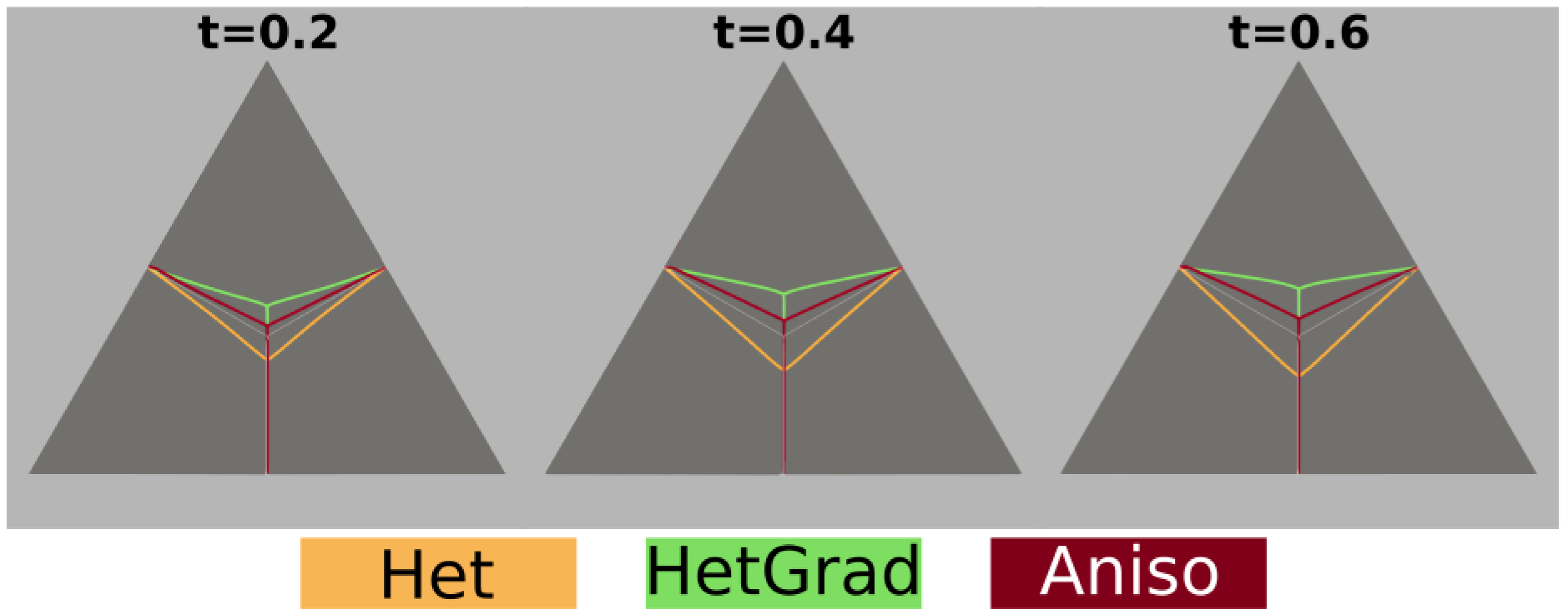
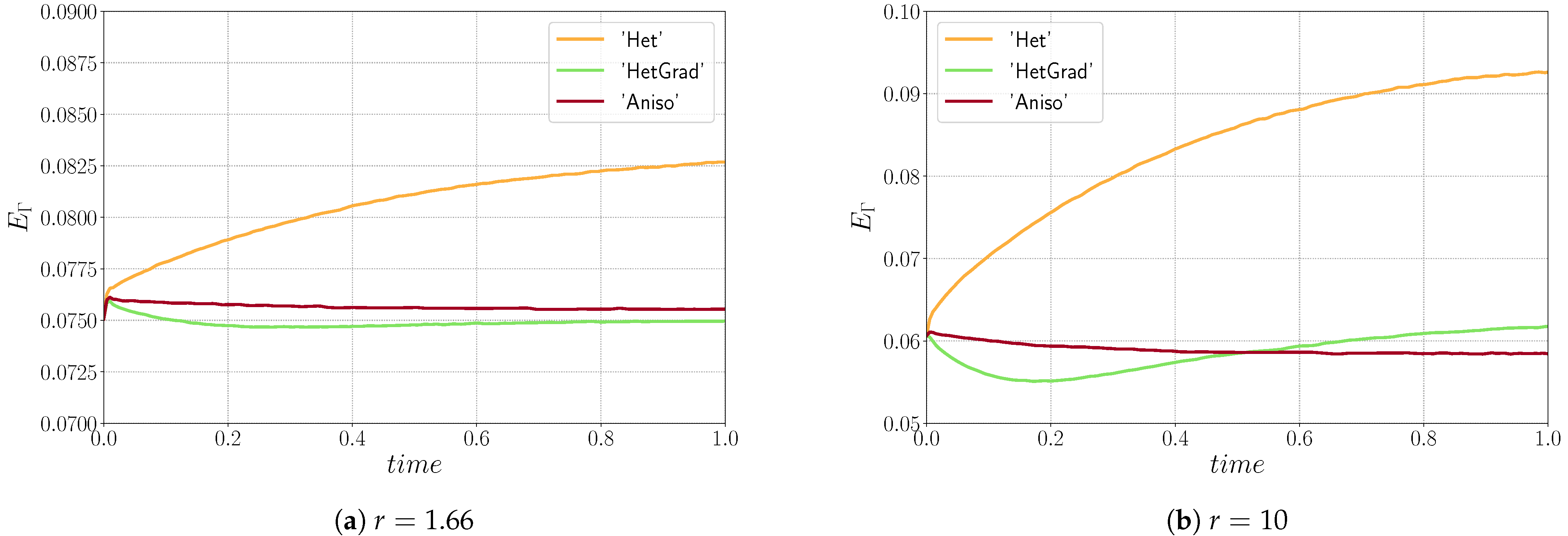
Appendix B. Large-Scale Simulation: Effect of a Strong Texture
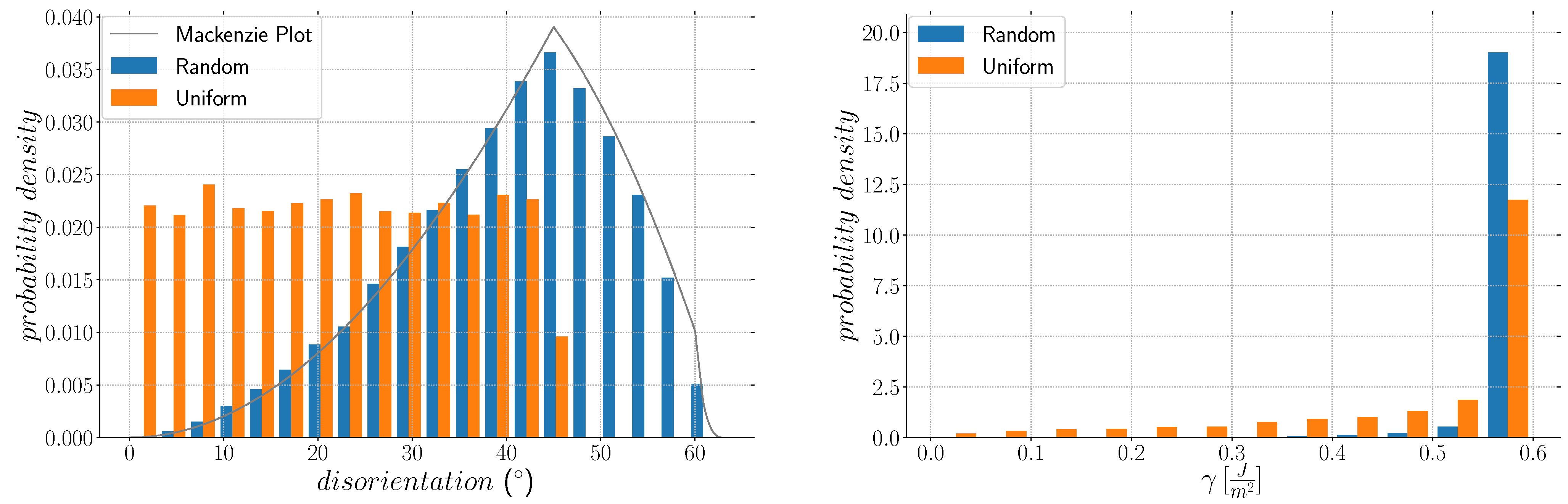
Appendix B.1. Heterogeneous Grain Boundary Energy
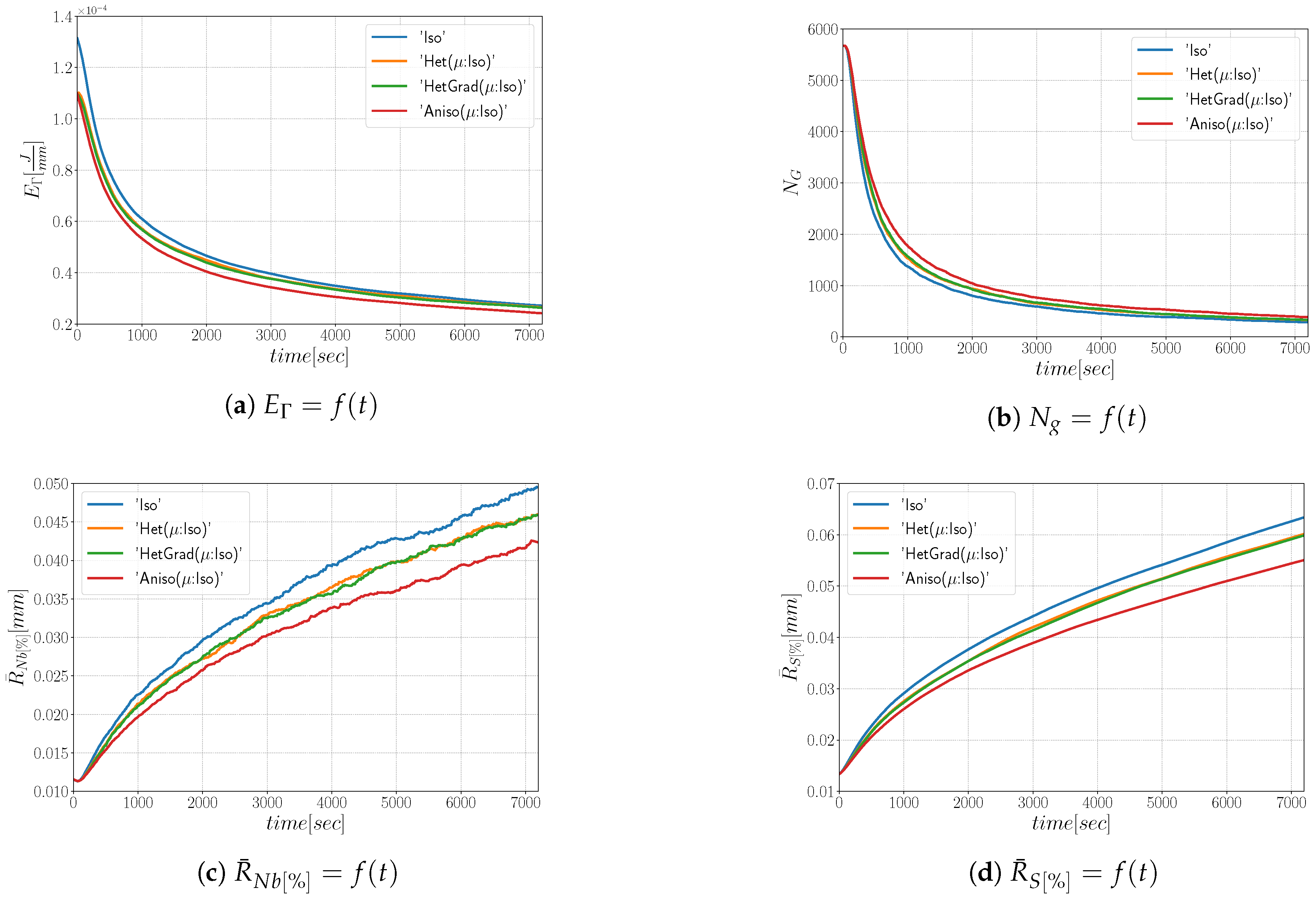
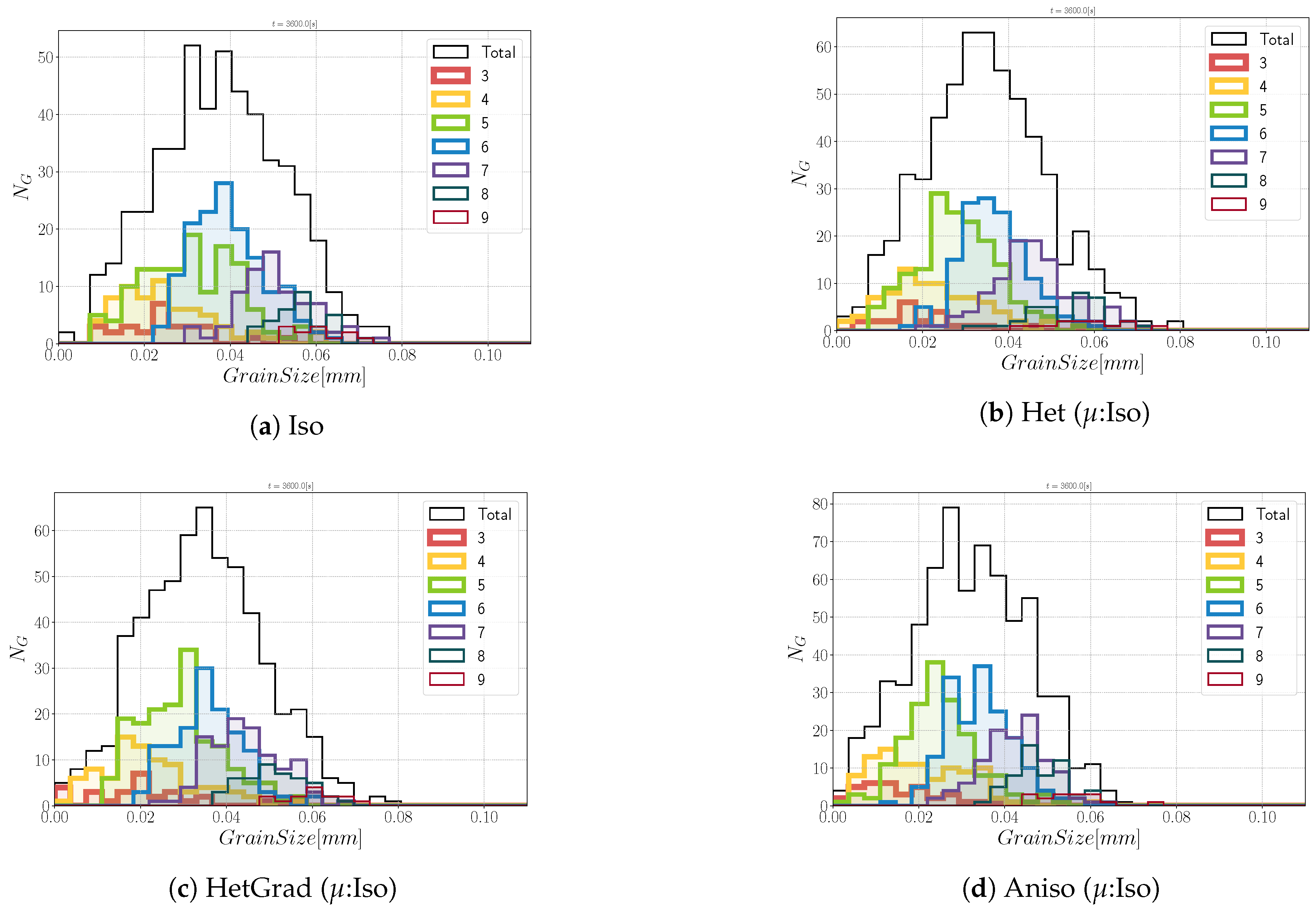
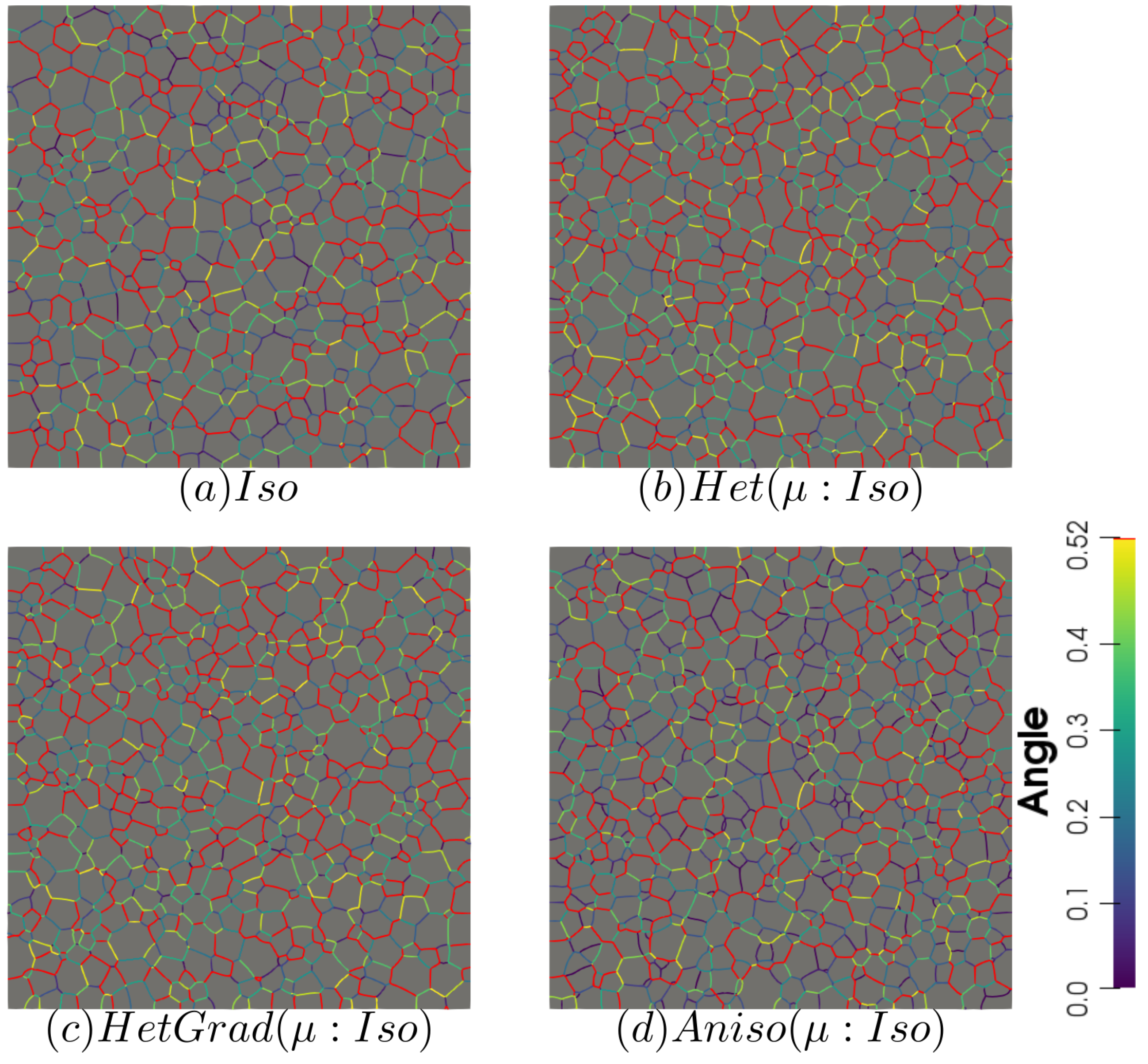

Appendix B.2. Heterogeneous Grain Boundary Energy and Mobility
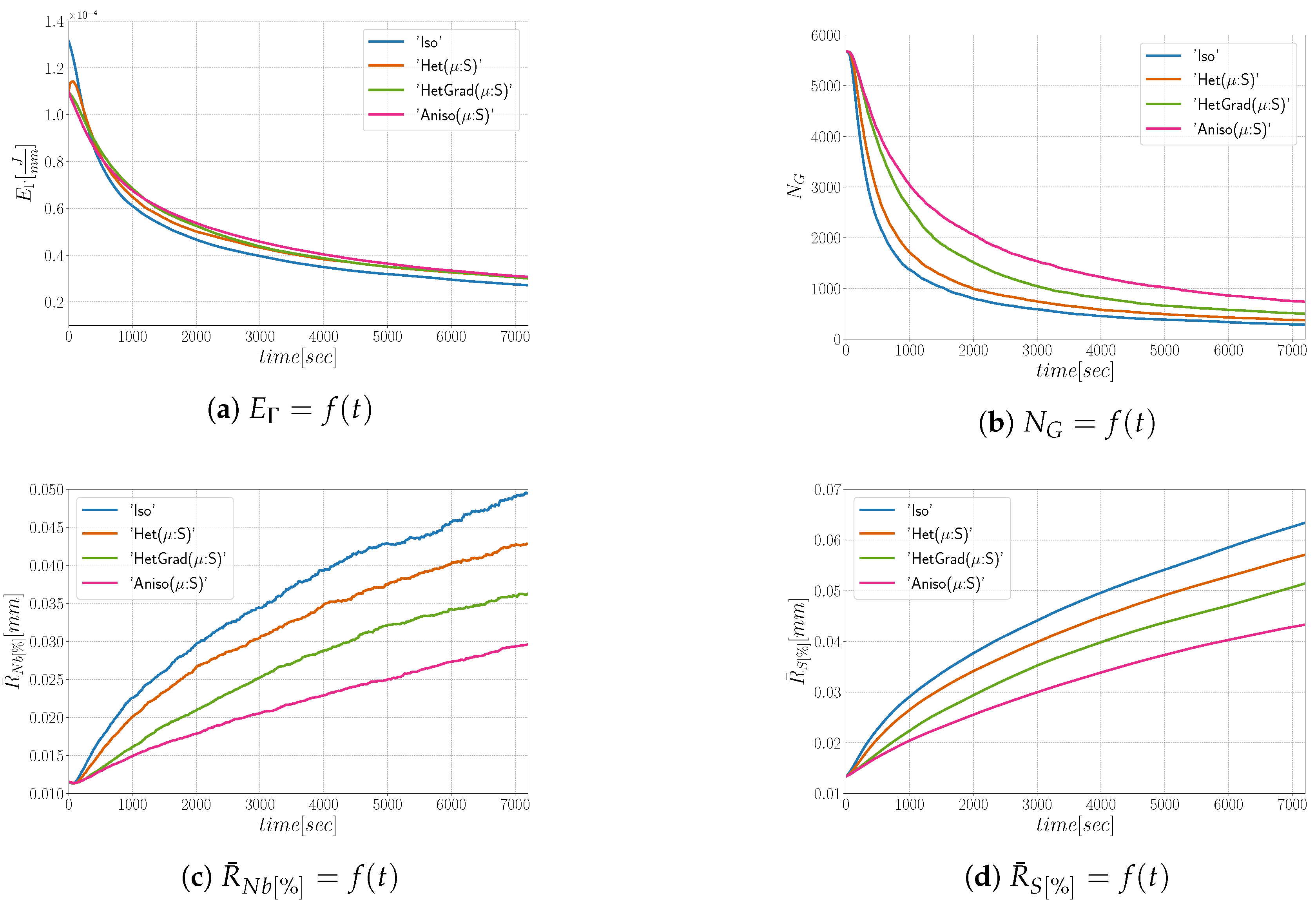
References
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Xiang, Y.; Srolovitz, D.J. Equation of Motion for a Grain Boundary. Phys. Rev. Lett. 2017, 119, 246101. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Cao, G.; Wang, J.; Deng, C.; Li, J.; Zhang, Z.; Mao, S.X. In situ atomistic observation of disconnection-mediated grain boundary migration. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Dake, J.; Schmidt, S.; Molodov, D.; Krill, C., III. Reverse engineering the kinetics of grain growth in Al-based polycrystals by microstructural mapping in 4D. In Proceedings of the 40th Risø International Symposium on Materials Science, Harry Bhadeshia, Denmark, 2–6 September 2019. [Google Scholar]
- Garcke, H.; Nestler, B.; Stoth, B. A multiphase field concept: Numerical simulations of moving phase boundaries and multiple junctions. SIAM J. Appl. Math. 1999, 60, 295–315. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, E.; Takaki, T. Multi-phase-field study of the effects of anisotropic grain-boundary properties on polycrystalline grain growth. J. Cryst. Growth 2017, 474, 160–165. [Google Scholar] [CrossRef]
- Moelans, N.; Wendler, F.; Nestler, B. Comparative study of two phase-field models for grain growth. Comput. Mater. Sci. 2009, 46, 479–490. [Google Scholar] [CrossRef]
- Gao, J.; Thompson, R. Real time-temperature models for Monte Carlo simulations of normal grain growth. Acta Mater. 1996, 44, 4565–4570. [Google Scholar] [CrossRef]
- Upmanyu, M.; Hassold, G.N.; Kazaryan, A.; Holm, E.A.; Wang, Y.; Patton, B.; Srolovitz, D.J. Boundary mobility and energy anisotropy effects on microstructural evolution during grain growth. Interface Sci. 2002, 10, 201–216. [Google Scholar] [CrossRef]
- Hoffrogge, P.W.; Barrales-Mora, L.A. Grain-resolved kinetics and rotation during grain growth of nanocrystalline aluminium by molecular dynamics. Comput. Mater. Sci. 2017, 128, 207–222. [Google Scholar] [CrossRef] [Green Version]
- Sakout, S.; Weisz-Patrault, D.; Ehrlacher, A. Energetic upscaling strategy for grain growth. i: Fast mesoscopic model based on dissipation. Acta Mater. 2020, 196, 261–279. [Google Scholar] [CrossRef]
- Barrales Mora, L.A. 2D vertex modeling for the simulation of grain growth and related phenomena. Math. Comput. Simul. 2010, 80, 1411–1427. [Google Scholar] [CrossRef]
- Wakai, F.; Enomoto, N.; Ogawa, H. Three-dimensional microstructural evolution in ideal grain growth—general statistics. Acta Mater. 2000, 48, 1297–1311. [Google Scholar] [CrossRef]
- Florez, S.; Shakoor, M.; Toulorge, T.; Bernacki, M. A new finite element strategy to simulate microstructural evolutions. Comput. Mater. Sci. 2020, 172, 109335. [Google Scholar] [CrossRef]
- Florez, S.; Alvarado, K.; Muñoz, D.P.; Bernacki, M. A novel highly efficient Lagrangian model for massively multidomain simulation applied to microstructural evolutions. Comput. Methods Appl. Mech. Eng. 2020, 367, 113107. [Google Scholar] [CrossRef]
- Bernacki, M.; Logé, R.E.; Coupez, T. Level set framework for the finite-element modeling of recrystallization and grain growth in polycrystalline materials. Scr. Mater. 2011, 64, 525–528. [Google Scholar] [CrossRef]
- Mießen, C.; Liesenjohann, M.; Barrales-Mora, L.; Shvindlerman, L.; Gottstein, G. An advanced level set approach to grain growth–Accounting for grain boundary anisotropy and finite triple junction mobility. Acta Mater. 2015, 99, 39–48. [Google Scholar] [CrossRef]
- Fausty, J.; Bozzolo, N.; Bernacki, M. A 2D level set finite element grain coarsening study with heterogeneous grain boundary energies. Appl. Math. Model. 2020, 78, 505–518. [Google Scholar] [CrossRef]
- Anderson, M.; Srolovitz, D.; Grest, G.; Sahni, P. Computer simulation of grain growth—I. Kinetics. Acta Metall. 1984, 32, 783–791. [Google Scholar] [CrossRef]
- Lazar, E.A.; Mason, J.K.; MacPherson, R.D.; Srolovitz, D.J. A more accurate three-dimensional grain growth algorithm. Acta Mater. 2011, 59, 6837–6847. [Google Scholar] [CrossRef]
- Smith, C.S. Introduction to Grains, Phases, and Interfaces—An Interpretation of Microstructure. Trans. Am. Inst. Min. Metall. Eng. 1948, 175, 15–51. [Google Scholar]
- Kohara, S.; Parthasarathi, M.N.; Beck, P.A. Anisotropy of boundary mobility. J. Appl. Phys. 1958, 29, 1125–1126. [Google Scholar] [CrossRef]
- Rollett, A.; Srolovitz, D.J.; Anderson, M. Simulation and theory of abnormal grain growth—Anisotropic grain boundary energies and mobilities. Acta Metall. 1989, 37, 1227–1240. [Google Scholar] [CrossRef] [Green Version]
- Hwang, N.M. Simulation of the effect of anisotropic grain boundary mobility and energy on abnormal grain growth. J. Mater. Sci. 1998, 33, 5625–5629. [Google Scholar] [CrossRef]
- Fausty, J.; Bozzolo, N.; Pino Muñoz, D.; Bernacki, M. A novel Level-Set Finite Element formulation for grain growth with heterogeneous grain boundary energies. Mater. Des. 2018, 160, 578–590. [Google Scholar] [CrossRef]
- Zöllner, D.; Zlotnikov, I. Texture Controlled Grain Growth in Thin Films Studied by 3D Potts Model. Adv. Theory Simul. 2019, 2, 1900064. [Google Scholar] [CrossRef]
- Miyoshi, E.; Takaki, T. Validation of a novel higher-order multi-phase-field model for grain-growth simulations using anisotropic grain-boundary properties. Comput. Mater. Sci. 2016, 112, 44–51. [Google Scholar] [CrossRef]
- Chang, K.; Chang, H. Effect of grain boundary energy anisotropy in 2D and 3D grain growth process. Results Phys. 2019, 12, 1262–1268. [Google Scholar] [CrossRef]
- Miyoshi, E.; Takaki, T.; Ohno, M.; Shibuta, Y. Accuracy Evaluation of Phase-field Models for Grain Growth Simulation with Anisotropic Grain Boundary Properties. ISIJ Int. 2019, 60, 160–167. [Google Scholar] [CrossRef] [Green Version]
- Holm, E.A.; Hassold, G.N.; Miodownik, M.A. On misorientation distribution evolution during anisotropic grain growth. Acta Mater. 2001, 49, 2981–2991. [Google Scholar] [CrossRef] [Green Version]
- Kazaryan, A.; Wang, Y.; Dregia, S.; Patton, B. Grain growth in anisotropic systems: Comparison of effects of energy and mobility. Acta Mater. 2002, 50, 2491–2502. [Google Scholar] [CrossRef]
- Fausty, J.; Murgas, B.; Florez, S.; Bozzolo, N.; Bernacki, M. A new analytical test case for anisotropic grain growth problems. Appl. Math. Model. 2021, 93, 28–52. [Google Scholar] [CrossRef]
- Hallberg, H.; Bulatov, V.V. Modeling of grain growth under fully anisotropic grain boundary energy. Model. Simul. Mater. Sci. Eng. 2019, 27, 045002. [Google Scholar] [CrossRef]
- Elsey, M.; Esedoglu, S.; Smereka, P. Simulations of anisotropic grain growth: Efficient algorithms and misorientation distributions. Acta Mater. 2013, 61, 2033–2043. [Google Scholar] [CrossRef] [Green Version]
- Bernacki, M.; Chastel, Y.; Coupez, T.; Logé, R.E. Level set framework for the numerical modelling of primary recrystallization in polycrystalline materials. Scr. Mater. 2008, 58, 1129–1132. [Google Scholar] [CrossRef]
- Bernacki, M.; Resk, H.; Coupez, T.; Logé, R.E. Finite element model of primary recrystallization in polycrystalline aggregates using a level set framework. Model. Simul. Mater. Sci. Eng. 2009, 17. [Google Scholar] [CrossRef] [Green Version]
- Scholtes, B.; Shakoor, M.; Settefrati, A.; Bouchard, P.O.; Bozzolo, N.; Bernacki, M. New finite element developments for the full field modeling of microstructural evolutions using the level-set method. Comput. Mater. Sci. 2015, 109, 388–398. [Google Scholar] [CrossRef]
- Maire, L. Full Field and Mean Field Modeling of Dynamic and Post-Dynamic Recrystallization in 3D—Application to 304L Steel. Ph.D. Thesis, MINES ParisTch. PSL University, Paris, France, 2018. [Google Scholar]
- Osher, S.; Sethian, J.A. Fronts Propagating with Curvature Dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- Merriman, B.; Bence, J.K.; Osher, S.J. Motion of multiple junctions: A level set approach. J. Comput. Phys. 1994, 112, 334–363. [Google Scholar] [CrossRef]
- Zhao, H.; Chan, T.; Merriman, B.; Osher, S. A variational level set approach to multiphase motion. J. Comput. Phys. 1996, 127, 179–195. [Google Scholar] [CrossRef] [Green Version]
- Scholtes, B.; Boulais-Sinou, R.; Settefrati, A.; Pino Muñoz, D.; Poitrault, I.; Montouchet, A.; Bozzolo, N.; Bernacki, M. 3D level set modeling of static recrystallization considering stored energy fields. Comput. Mater. Sci. 2016, 122, 57–71. [Google Scholar] [CrossRef]
- Fausty, J. Towards the Full Field Modeling and Simulation of Annealing Twins Using a Finite Element Level Set Method. Ph.D. Thesis, MINES ParisTch. PSL University, Paris, France, 2020. [Google Scholar]
- Abdeljawad, F.; Foiles, S.M.; Moore, A.P.; Hinkle, A.R.; Barr, C.M.; Heckman, N.M.; Hattar, K.; Boyce, B.L. The role of the interface stiffness tensor on grain boundary dynamics. Acta Mater. 2018, 158, 440–453. [Google Scholar] [CrossRef]
- Du, D.; Zhang, H.; Srolovitz, D.J. Properties and determination of the interface stiffness. Acta Mater. 2007, 55, 467–471. [Google Scholar] [CrossRef]
- Herring, C. Surface tension as a motivation for sintering. In Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids; Springer: New York, NY, USA, 1999; pp. 33–69. [Google Scholar]
- Brooks, A.N.; Hughes, T.J. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Roux, E.; Bernacki, M.; Bouchard, P. A level-set and anisotropic adaptive remeshing strategy for the modeling of void growth under large plastic strain. Comput. Mater. Sci. 2013, 68, 32–46. [Google Scholar] [CrossRef]
- De Micheli, P.; Maire, L.; Cardinaux, D.; Moussa, C.; Bozzolo, N.; Bernacki, M. DIGIMU®: Full field recrystallization simulations for optimization of multi-pass processes. In AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2019; Volume 2113, p. 040014. [Google Scholar]
- Eiken, J. Discussion of the Accuracy of the Multi-Phase-Field Approach to Simulate Grain Growth with Anisotropic Grain Boundary Properties. Isij Int. 2020, 60, 1832–1834. [Google Scholar] [CrossRef]
- Hitti, K.; Laure, P.; Coupez, T.; Silva, L.; Bernacki, M. Precise generation of complex statistical Representative Volume Elements (RVEs) in a finite element context. Comput. Mater. Sci. 2012, 61, 224–238. [Google Scholar] [CrossRef]
- Hitti, K.; Bernacki, M. Optimized Dropping and Rolling (ODR) method for packing of poly-disperse spheres. Appl. Math. Model. 2013, 37, 5715–5722. [Google Scholar] [CrossRef]
- Read, W.T.; Shockley, W. Dislocation models of crystal grain boundaries. Phys. Rev. 1950, 78, 275–289. [Google Scholar] [CrossRef]
- Humphreys, F.J. A unified theory of recovery, recrystallization and grain growth, based on the stability and growth of cellular microstructures—I. The basic model. Acta Mater. 1997, 45, 4231–4240. [Google Scholar] [CrossRef]
- Cruz-Fabiano, A.; Logé, R.; Bernacki, M. Assessment of simplified 2D grain growth models from numerical experiments based on a level set framework. Comput. Mater. Sci. 2014, 92, 305–312. [Google Scholar] [CrossRef]
- Mackenzie, J. Second paper on statistics associated with the random disorientation of cubes. Biometrika 1958, 45, 229–240. [Google Scholar] [CrossRef]
- Chang, K.; Moelans, N. Effect of grain boundary energy anisotropy on highly textured grain structures studied by phase-field simulations. Acta Mater. 2014, 64, 443–454. [Google Scholar] [CrossRef]
- Gruber, J.; Miller, H.; Hoffmann, T.; Rohrer, G.; Rollett, A. Misorientation texture development during grain growth. Part I: Simulation and experiment. Acta Mater. 2009, 57, 6102–6112. [Google Scholar] [CrossRef]
- Cahn, J. Stability, microstructural evolution, grain growth, and coarsening in a two-dimensional two-phase microstructure. Acta Metall. Mater. 1991, 39, 2189–2199. [Google Scholar] [CrossRef]
- Holm, E.; Srolovitz, D.J.; Cahn, J. Microstructural evolution in two-dimensional two-phase polycrystals. Acta Metall. Mater. 1993, 41, 1119–1136. [Google Scholar] [CrossRef] [Green Version]
- Herring, C.; Kingston, W. The Physics of Powder Metallurgy; WE Kingston, Ed.; McGraw Hill: New York, NY, USA, 1951. [Google Scholar]
- Sutton, A.; Banks, E.; Warwick, A. The five-dimensional parameter space of grain boundaries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150442. [Google Scholar] [CrossRef]
- Morawiec, A. Misorientation-angle distribution of randomly oriented symmetric objects. J. Appl. Crystallogr. 1995, 28, 289–293. [Google Scholar] [CrossRef]
- Cahn, J.W.; Taylor, J.E. Metrics, measures, and parametrizations for grain boundaries: A dialog. J. Mater. Sci. 2006, 41, 7669–7674. [Google Scholar] [CrossRef]
- Morawiec, A. Models of uniformity for grain boundary distributions. J. Appl. Crystallogr. 2009, 42, 783–792. [Google Scholar] [CrossRef]
- Patala, S.; Schuh, C.A. Symmetries in the representation of grain boundary-plane distributions. Philos. Mag. 2013, 93, 524–573. [Google Scholar] [CrossRef]
- Homer, E.R.; Patala, S.; Priedeman, J.L. Grain boundary plane orientation fundamental zones and structure-property relationships. Sci. Rep. 2015, 5, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olmsted, D.L. A new class of metrics for the macroscopic crystallographic space of grain boundaries. Acta Mater. 2009, 57, 2793–2799. [Google Scholar] [CrossRef]
- Francis, T.; Chesser, I.; Singh, S.; Holm, E.A.; De Graef, M. A geodesic octonion metric for grain boundaries. Acta Mater. 2019, 166, 135–147. [Google Scholar] [CrossRef]
- Chesser, I.; Francis, T.; De Graef, M.; Holm, E. Learning the grain boundary manifold: Tools for visualizing and fitting grain boundary properties. Acta Mater. 2020, 195, 209–218. [Google Scholar] [CrossRef]
- Olmsted, D.L.; Foiles, S.M.; Holm, E.A. Survey of computed grain boundary properties in face-centered cubic metals: I. Grain boundary energy. Acta Mater. 2009, 57, 3694–3703. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Reed, B.W.; Kumar, M. Grain boundary energy function for fcc metals. Acta Mater. 2014, 65, 161–175. [Google Scholar] [CrossRef]
- Chesser, I.; Holm, E. Understanding the anomalous thermal behavior of Σ3 grain boundaries in a variety of FCC metals. Scr. Mater. 2018, 157, 19–23. [Google Scholar] [CrossRef]
- Garcke, H.; Stoth, B.; Nestler, B. Anisotropy in multi-phase systems: A phase field approach. Interfaces Free. Boundaries 1999, 1, 175–198. [Google Scholar] [CrossRef] [Green Version]
- Brown, J.; Ghoniem, N. Structure and motion of junctions between coherent and incoherent twin boundaries in copper. Acta Mater. 2009, 57, 4454–4462. [Google Scholar] [CrossRef]



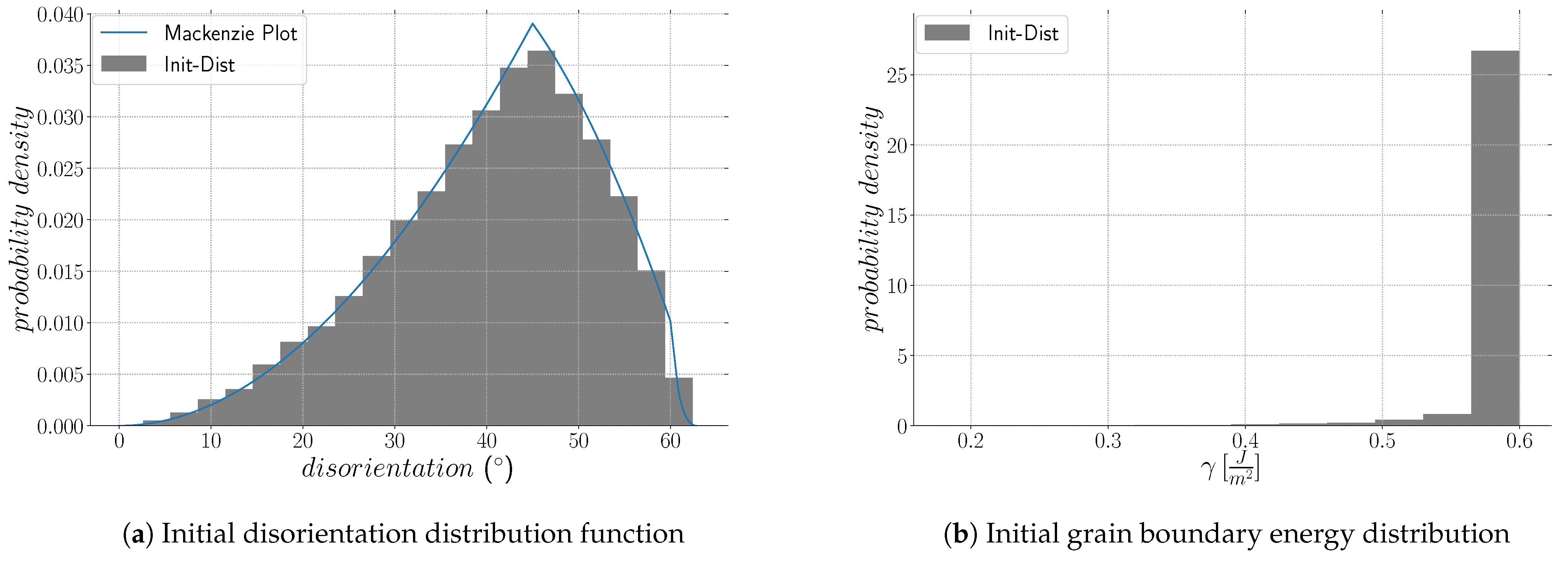
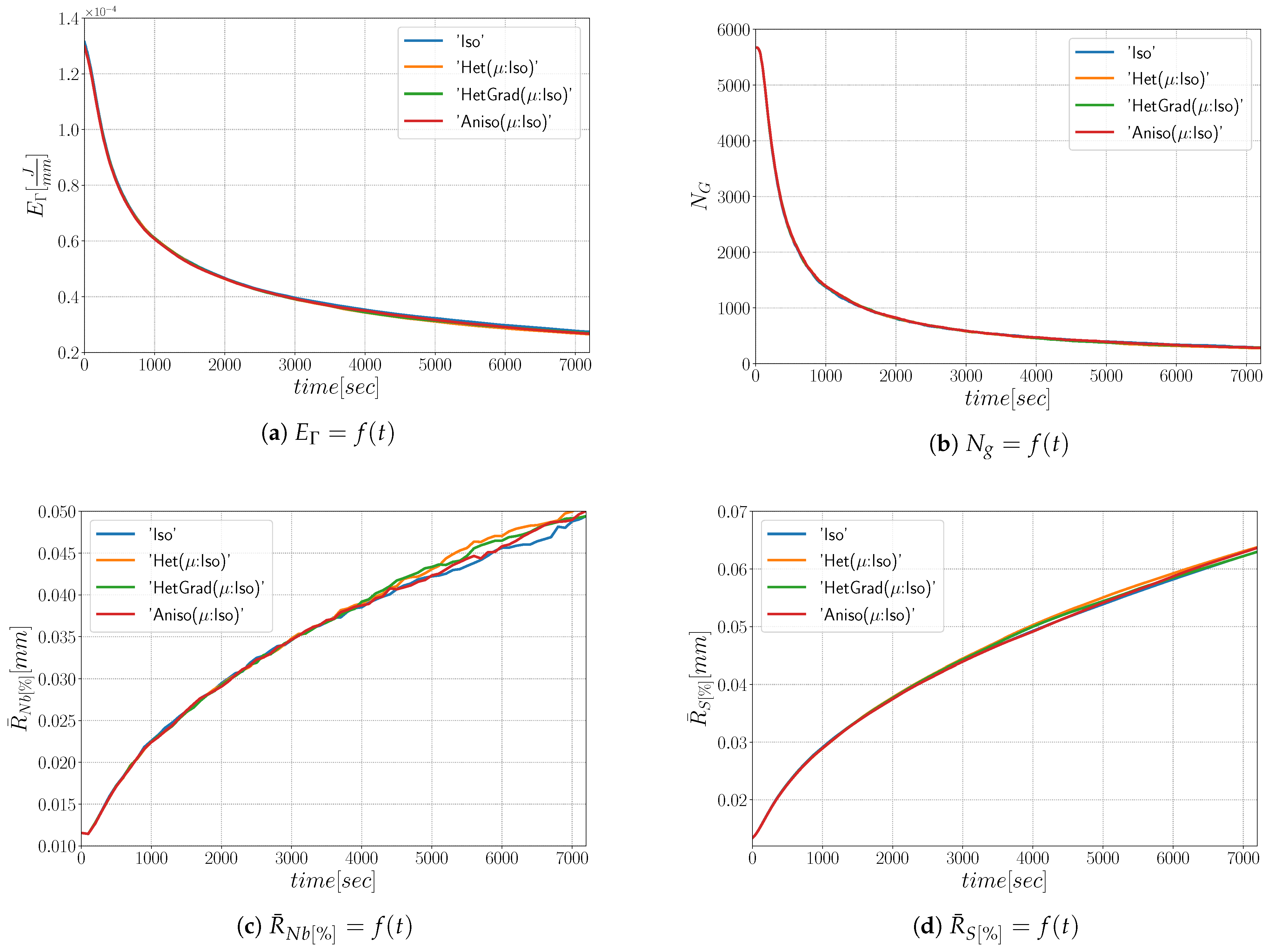
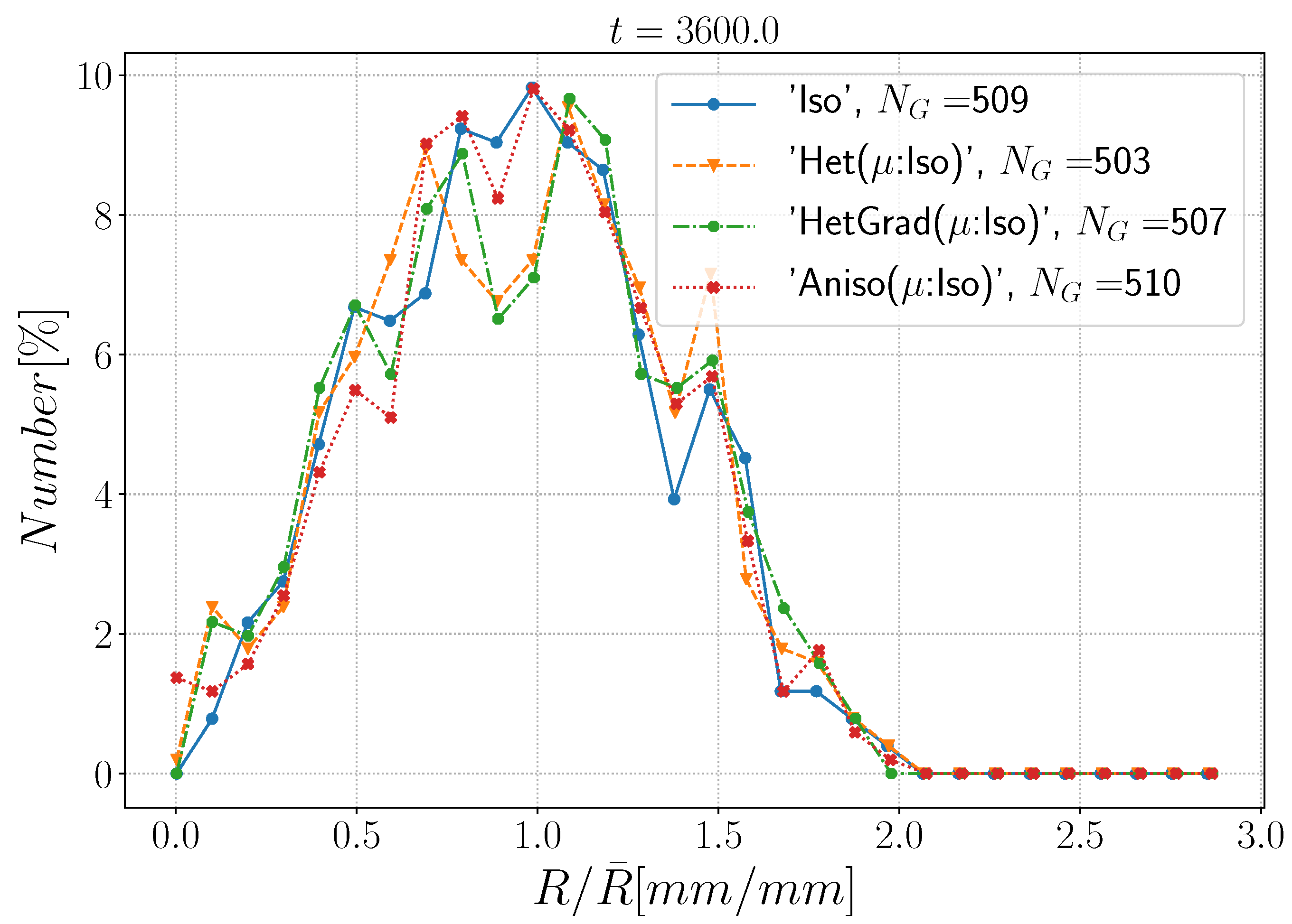
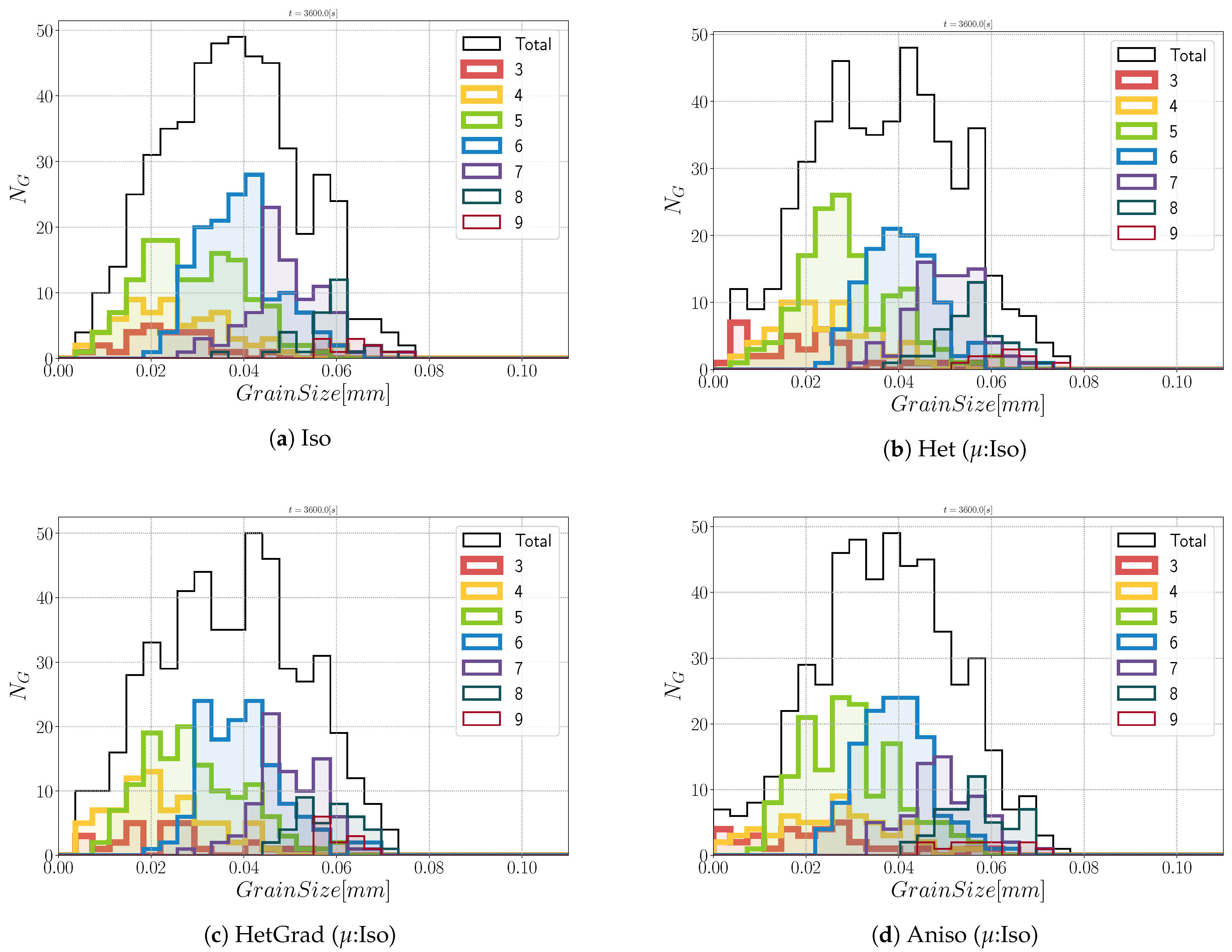
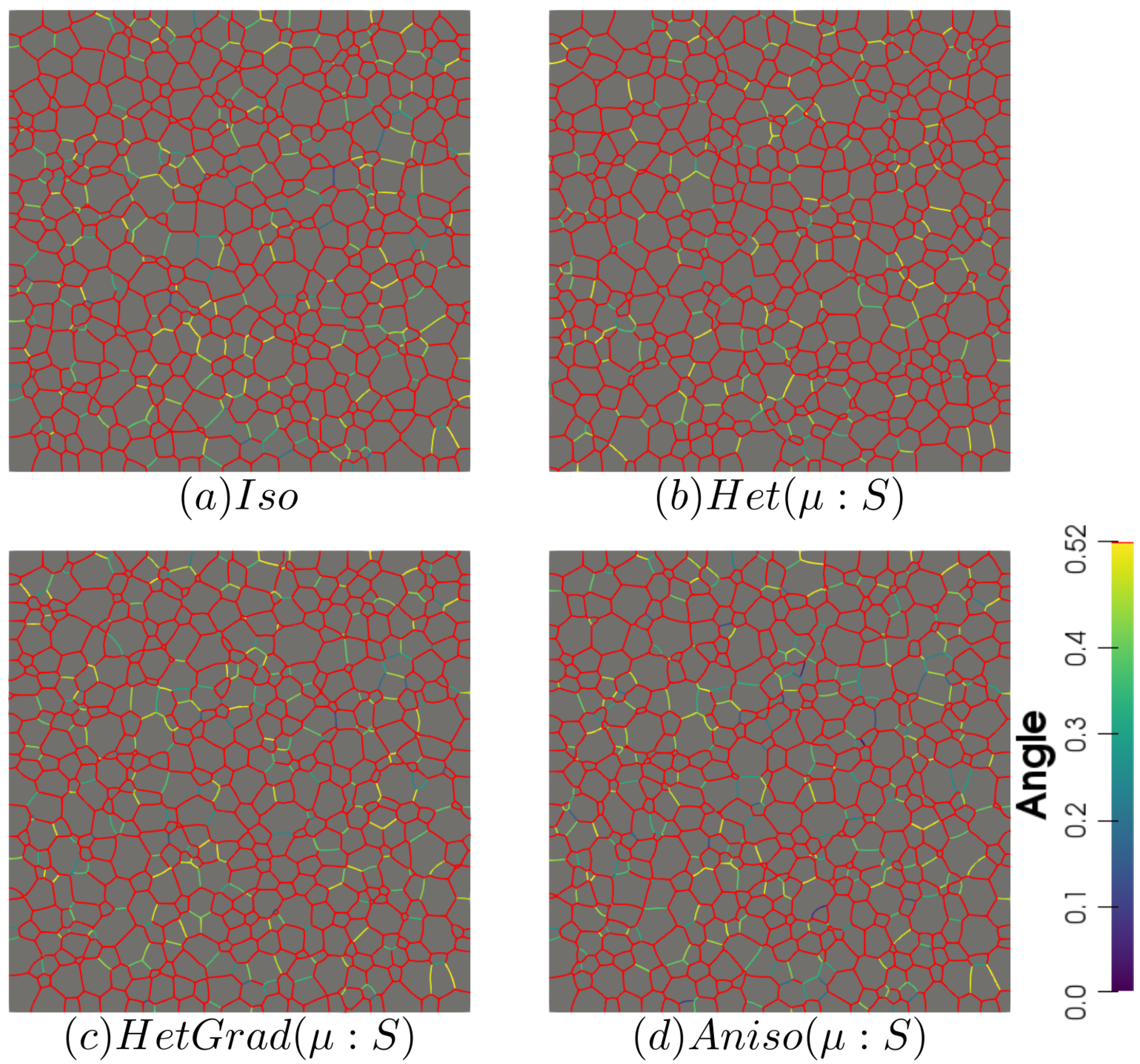

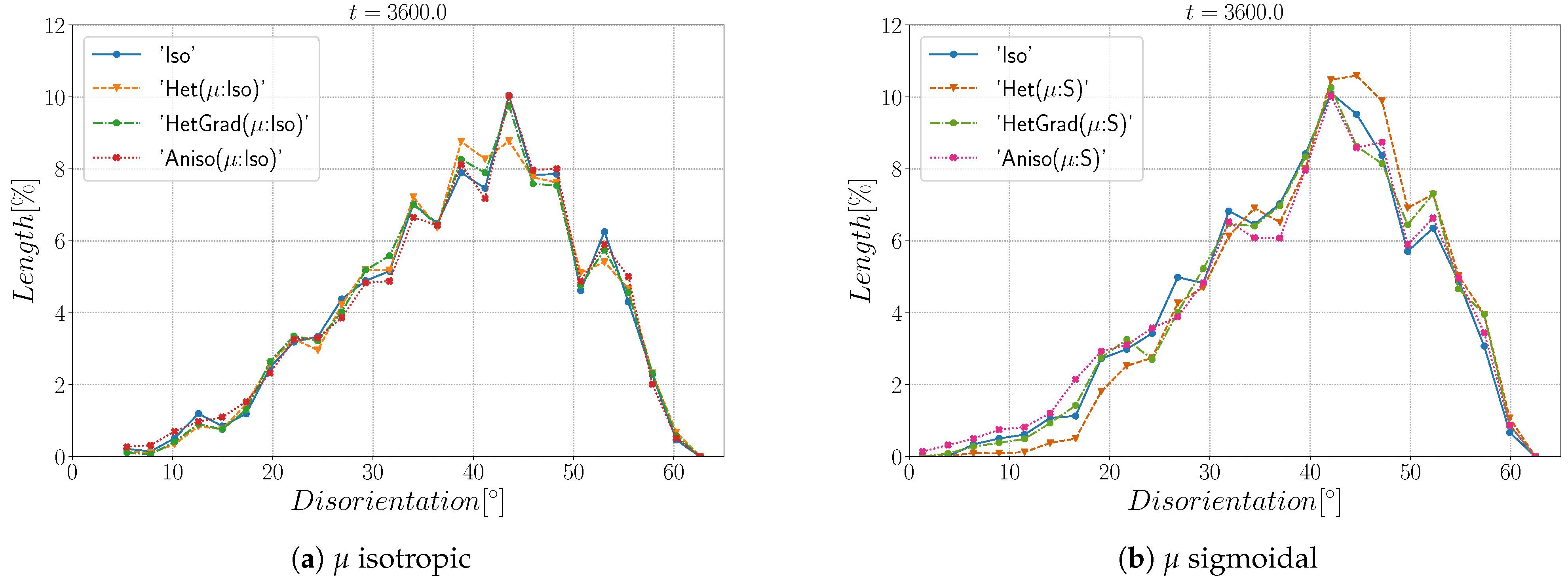
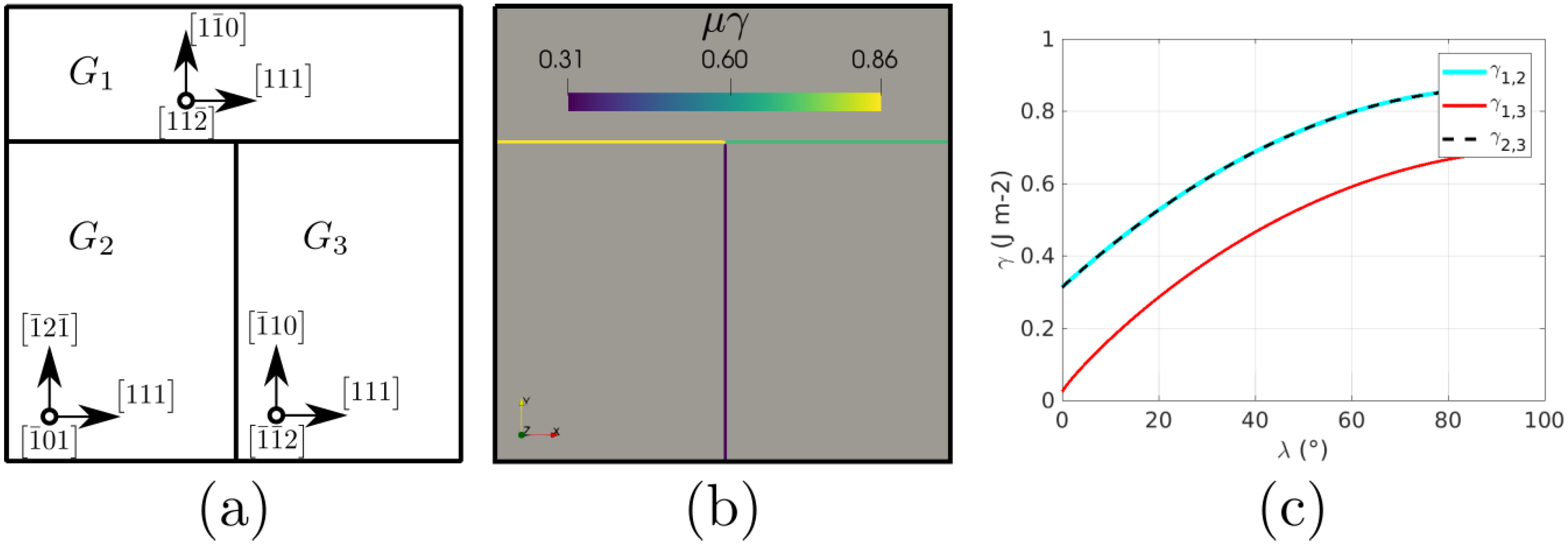
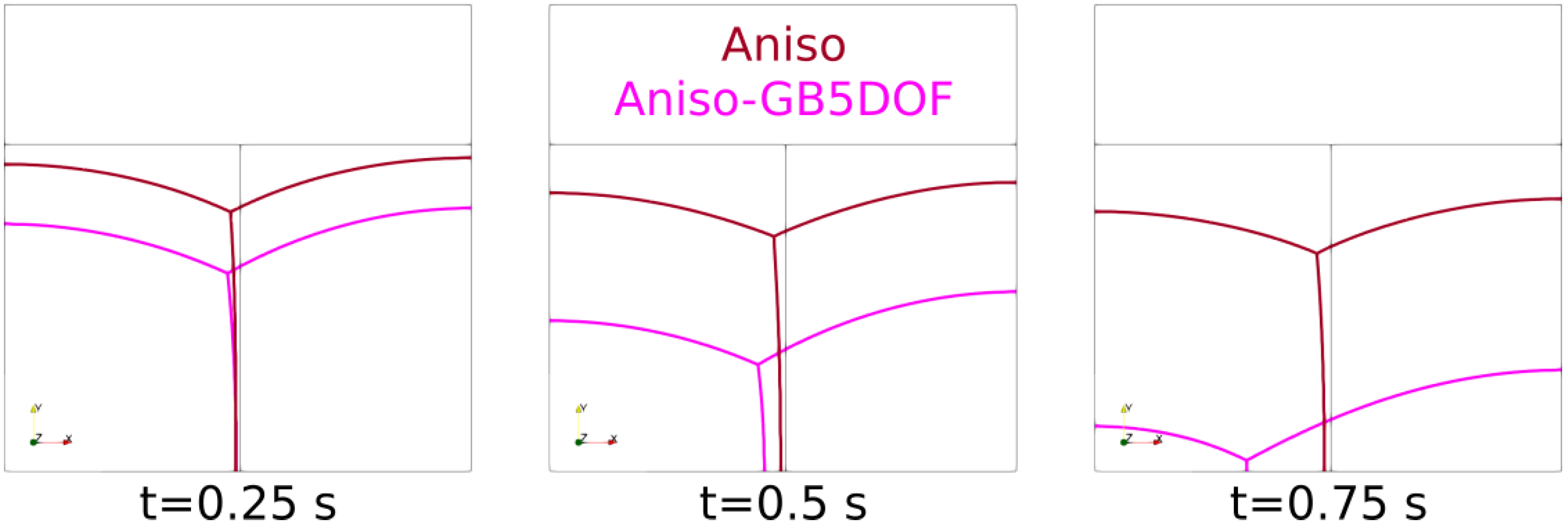
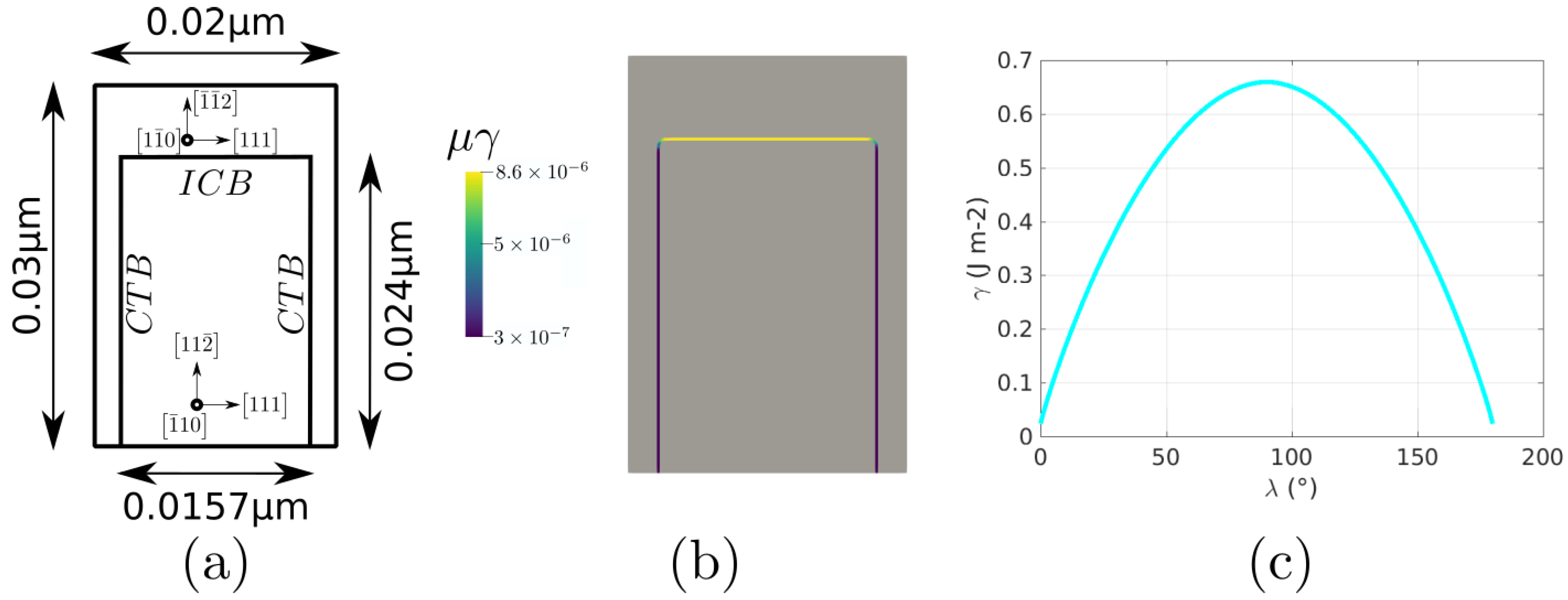
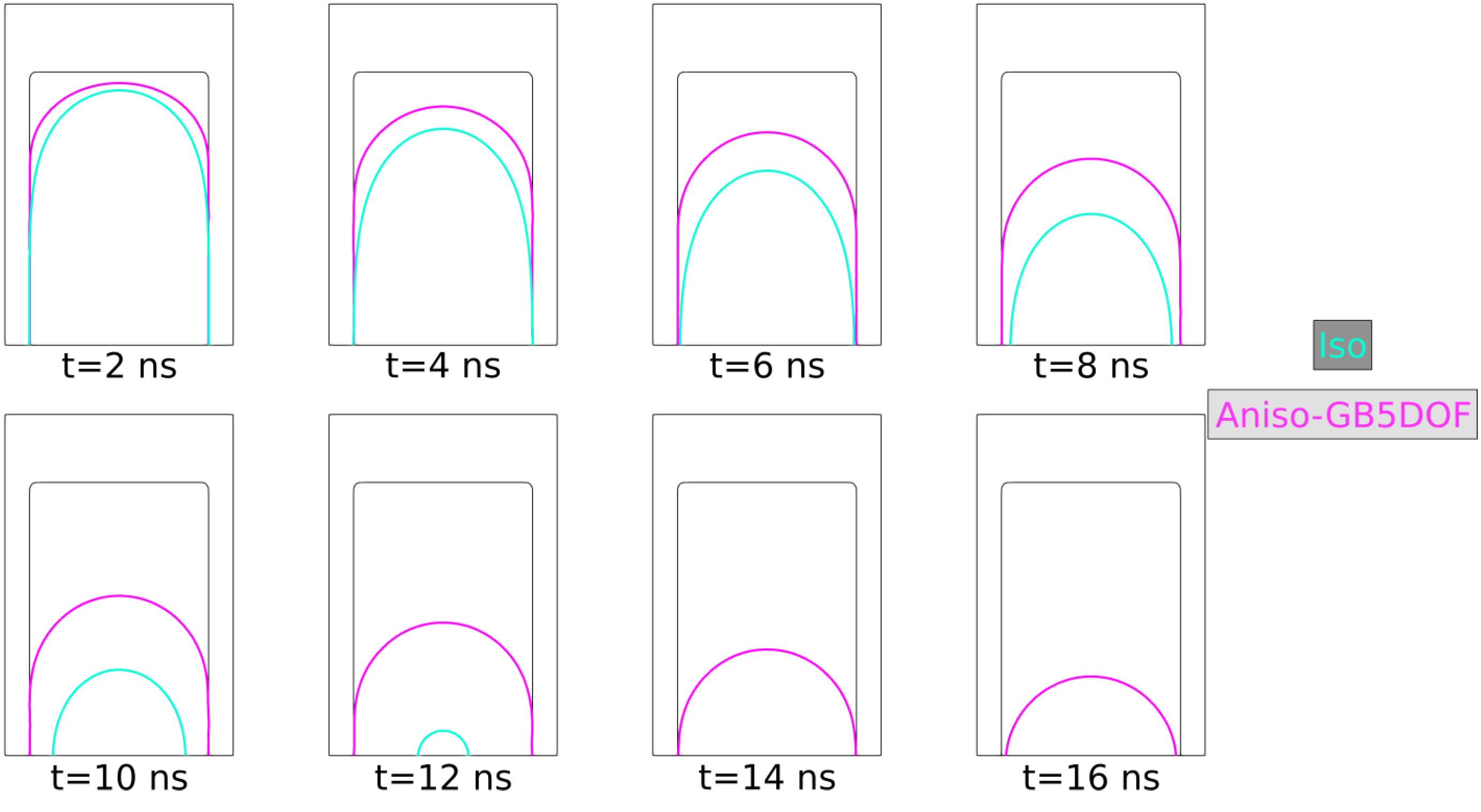
| Case | Iso | Het | HetGrad | Aniso |
|---|---|---|---|---|
| Random | 5.4 | 5.5 | 5.5 | 5.6 |
| Textured | 5.4 | 5.5 | 7.3 | 9.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murgas, B.; Florez, S.; Bozzolo, N.; Fausty, J.; Bernacki, M. Comparative Study and Limits of Different Level-Set Formulations for the Modeling of Anisotropic Grain Growth. Materials 2021, 14, 3883. https://doi.org/10.3390/ma14143883
Murgas B, Florez S, Bozzolo N, Fausty J, Bernacki M. Comparative Study and Limits of Different Level-Set Formulations for the Modeling of Anisotropic Grain Growth. Materials. 2021; 14(14):3883. https://doi.org/10.3390/ma14143883
Chicago/Turabian StyleMurgas, Brayan, Sebastian Florez, Nathalie Bozzolo, Julien Fausty, and Marc Bernacki. 2021. "Comparative Study and Limits of Different Level-Set Formulations for the Modeling of Anisotropic Grain Growth" Materials 14, no. 14: 3883. https://doi.org/10.3390/ma14143883
APA StyleMurgas, B., Florez, S., Bozzolo, N., Fausty, J., & Bernacki, M. (2021). Comparative Study and Limits of Different Level-Set Formulations for the Modeling of Anisotropic Grain Growth. Materials, 14(14), 3883. https://doi.org/10.3390/ma14143883






