Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass
Abstract
:1. Introduction
2. Formulation of the Problem
3. Solution by the Differential Quadrature Method
4. Numerical Examples
4.1. Effect of the Taper Ratio Coefficient on Frequency
4.2. Effect of a Lumped Mass Applied to the Tip
4.3. Effect of the Nonlocal Parameter on Frequency
4.4. Effect of the Dimensionless Rotational Stiffness on Frequency
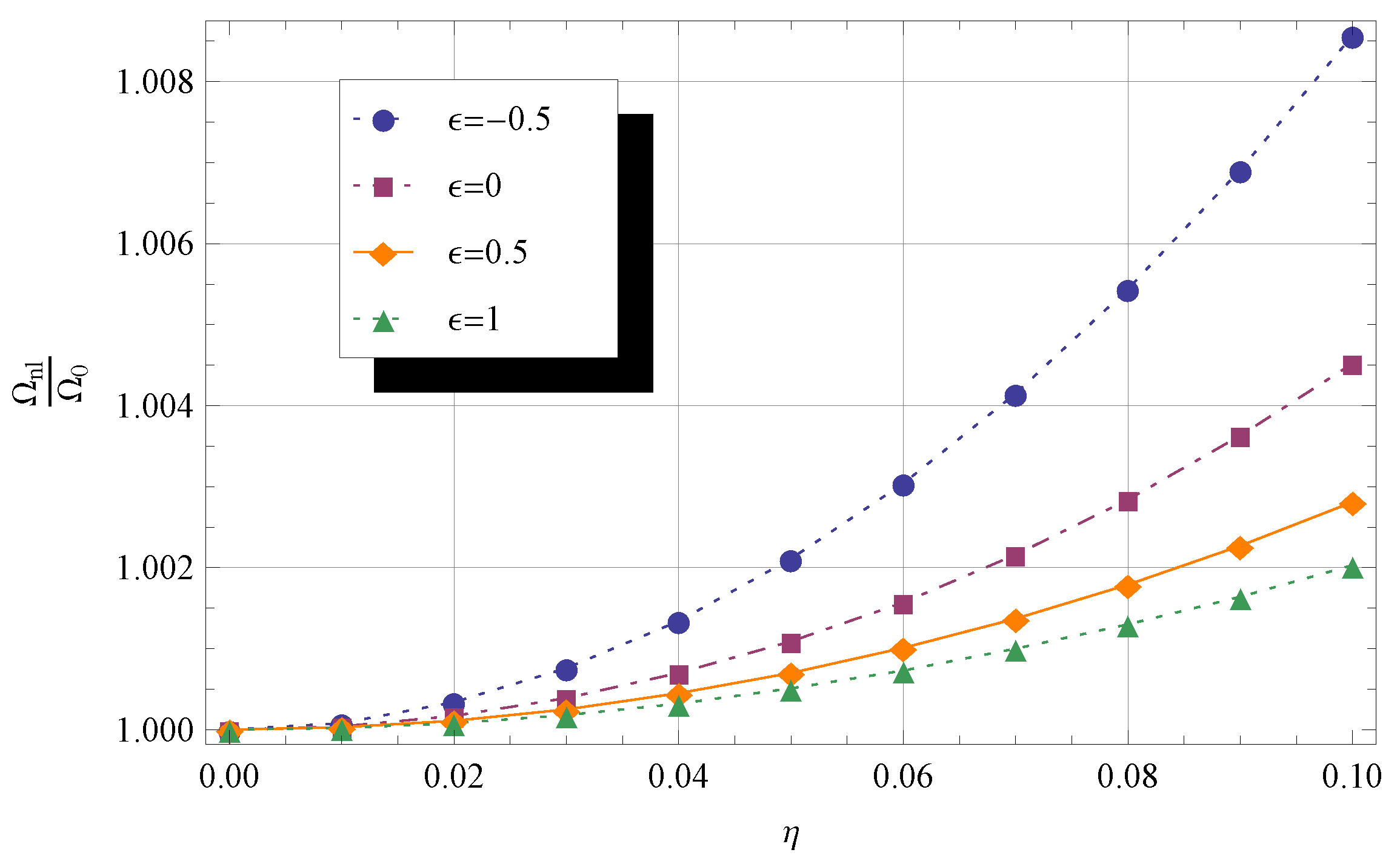
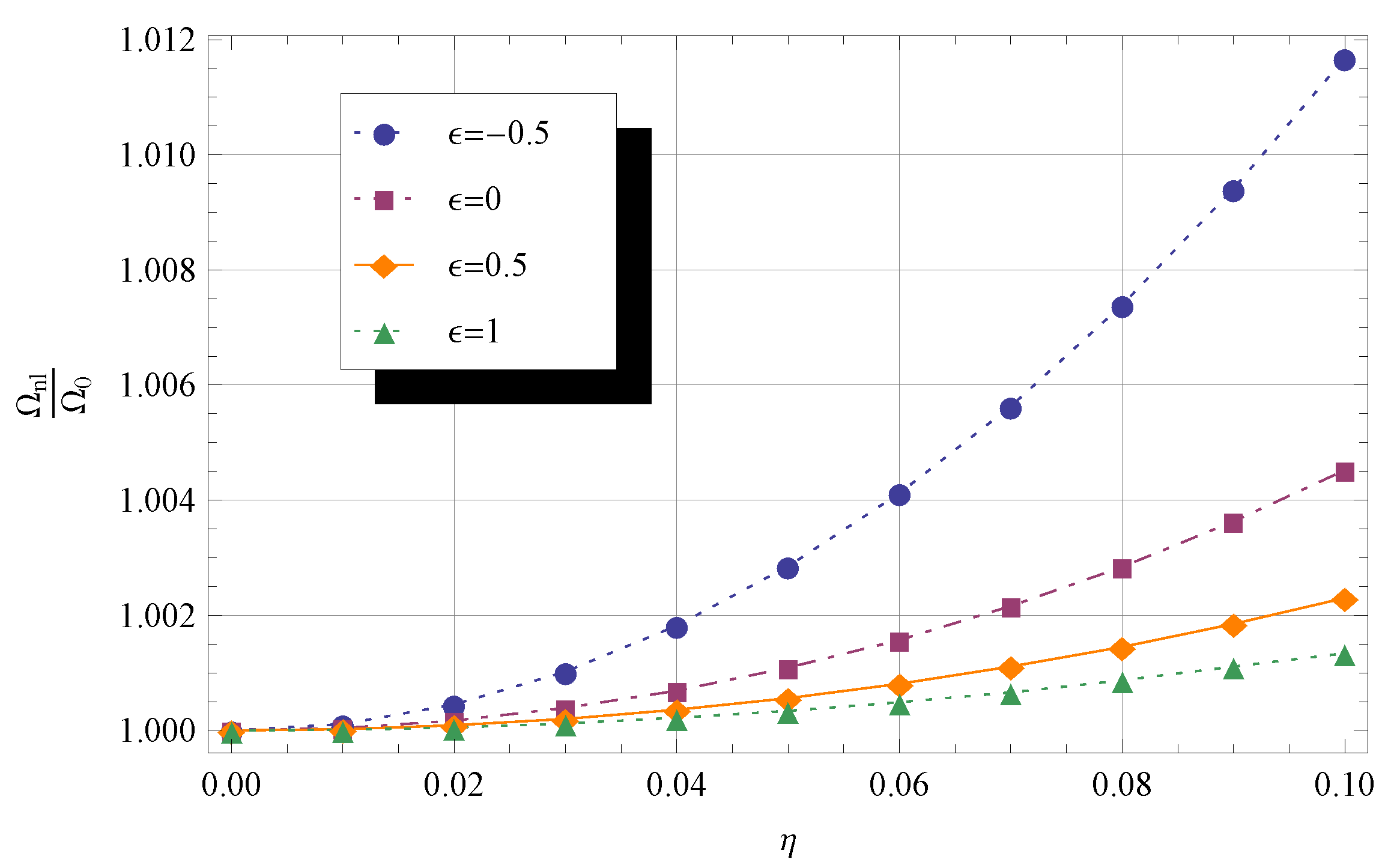
4.5. Effect of the Dimensionless Parameter and Taper Ratio on Frequency Shift
5. Conclusions
- i
- for a fixed value of the frequency shift decreases as the nonlocal parameter and the taper ratio increase;
- ii
- if the rotational stiffness increases, the first three dimensionless frequencies increase and, for , settle at a fixed value;
- iii
- for fixed values of and and increasing the frequency shift increases toward an asymptotic value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Ge, M.; Sattler, K. Observation of fullerene cones. Chem. Phys. Lett. 1994, 220, 192–196. [Google Scholar] [CrossRef]
- Tombler, T.W.; Zhou, C.; Alexseyev, L.; Kong, J.; Dai, H.; Liu, L.; Jayanthi, C.S.; Tang, M.; Wu, S.Y. Reversible electromechanical characteristics of carbon nanotubes underlocal-probe manipulation. Nature 2000, 405, 769–772. [Google Scholar] [CrossRef] [PubMed]
- Ruoff, R.S.; Lorents, D.C. Mechanical and thermal properties of carbon nanotubes. Carbon 1995, 33, 925–930. [Google Scholar] [CrossRef]
- Valipour, P.; Ghasemi, S.E.; Khosravani, M.R.; Ganji, D.D. Theoretical analysis on nonlinear vibration of fluid flow in single-walled carbon nanotube. J. Theor. Appl. Phys. 2016, 10, 211–218. [Google Scholar] [CrossRef] [Green Version]
- Tsukagoshi, K.; Yoneya, N.; Uryu, S.; Aoyagi, Y.; Kanda, A.; Ootuka, Y.; Alphenaar, B. Carbon nanotube devices for nanoelectronics. Phys. B Condens. Matter 2002, 323, 107–114. [Google Scholar] [CrossRef]
- An, K.; Jeong, S.; Hwang, H.; Lee, Y. Enhanced sensitivity of a gas sensor incorporating single-walled carbon nanotube-polypyrrole nanocomposites. Adv. Mater. 2004, 16, 1005–1009. [Google Scholar] [CrossRef]
- Wu, D.H.; Chien, W.T.; Chen, C.S.; Chen, H.H. Resonant frequency analysis of fixed-free single-walled carbon nanotube-based mass sensor. Sens. Actuators Phys. 2006, 126, 117–121. [Google Scholar] [CrossRef]
- Mehdipour, I.; Barari, A.; Domairry, G. Application of a cantilevered SWCNT with mass at the tip as a nanomechanical sensor. Comput. Mater. Sci. 2011, 50, 1830–1833. [Google Scholar] [CrossRef]
- Lavagna, L.; Massella, D.; Pavese, M. Preparation of hierarchical material by chemical grafting of carbon nanotubes onto carbon fibers. Diam. Relat. Mater. 2017, 80, 118–124. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Nasiri Rad, A. Vibrational analysis of carbon nanocones under different boundary conditions: An analytical approach. Mech. Res. Comm. 2014, 56, 130–135. [Google Scholar] [CrossRef]
- Yan, J.; Liew, K.; He, L. Free vibration analysis of single-walled carbon nanotubes using a higher-order gradient theory. J. Sound Vib. 2013, 332, 3740–3755. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2007. [Google Scholar]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Challamel, N.; Wang, C.M. The small length scale effect for a non-local cantilever beam: A paradox solved. Nanotechnology 2008, 19, 345703. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.; Reddy, J. Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Zaera, R.; Serrano, O.; Fernández-Sáez, J. On the consistency of the nonlocal strain gradient elasticity. Int. J. Eng. Sci. 2019, 138, 65–81. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model. Compos. B Eng. 2017, 123, 105–111. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. Variational nonlocal gradient elasticity for nano-beams. Int. J. Eng. Sci. 2019, 143, 73–91. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Ghannadpour, S.; Mohammadi, B.; Fazilati, J. Bending, buckling and vibration problems of nonlocal Euler beams using Ritz method. Compos. Struct. 2013, 96, 584–589. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Nonlocal vibration of carbon nanotubes with attached buckyballs at tip. Mech. Res. Commun. 2011, 38, 62–67. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S. Small scale effect on vibrational response of single-walled carbon nanotubes with different boundary conditions based on nonlocal beam models. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1965–1979. [Google Scholar] [CrossRef]
- Piovan, M.T.; Filipich, C.P. Modeling of non-local beam theories for vibratoryand buckling problems of nano-tubes. In Mecánica Computacional; Bertolino, G., Cantero, M., Storti, M., Teruel, F., Eds.; Asociación Argentina de Mecánica Computacional: Santa Fe, Argentina, 2014; Volume XXXIII, pp. 1601–1614. [Google Scholar]
- Wang, Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics. J. Appl. Phys. 2005, 98, 124301. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wang, C.M. The constitutive relation and small scale parameter of nonlocal continuum mechanics for modelling carbon nanotubes. Nanotechnology 2007, 18, 075702. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Liew, K. Application of nonlocal continuum mechanics to static analysis of micro- and nano-structures. Phys. Lett. A 2007, 363, 236–242. [Google Scholar] [CrossRef]
- Rafiei, M.; Mohebpour, S.R.; Daneshmand, F. Small-scale effect on the vibration of non-uniform carbon nanotubes conveying fluid and embedded in viscoelastic medium. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 44, 1372–1379. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S. Small-scale effect on the vibration of nonuniform nanocantilever based on nonlocal elasticity theory. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 41, 1451–1456. [Google Scholar] [CrossRef]
- Danesh, M.; Farajpour, A.; Mohammadi, M. Axial vibration analysis of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Mech. Res. Commun. 2012, 39, 23–27. [Google Scholar] [CrossRef]
- Sharma, G.S.; Sarkar, A. Directivity-Based Passive Barrier for Local Control of Low-Frequency Noise. J. Theor. Comput. Acoust. 2018, 26, 1850012. [Google Scholar] [CrossRef]
- Sharma, G.S.; Sarkar, A. Directivity based control of acoustic radiation. Appl. Acoust. 2019, 154, 226–235. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Lippiello, M.; Tomasiello, S. Differential quadrature solutions for the nonconservative instability of a class of single-walled carbon nanotubes. Eng. Comput. 2018, 35, 251–267. [Google Scholar] [CrossRef]
- Tang, H.L.; Li, D.K.; Zhou, S.M. Vibration of horn-shaped carbon nanotube with attached mass via nonlocal elasticity theory. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 56, 306–311. [Google Scholar] [CrossRef]
- Van Lier, G.; Van Alsenoy, C.; Van Doren, V.; Geerlings, P. Ab initio study of the elastic properties of single-walled carbon nanotubes and graphene. Chem. Phys. Lett. 2000, 326, 181–185. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of carbon tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef]
- Liew, K.M.; Wong, C.H.; He, X.Q.; Tan, M.J.; Meguid, S.A. Nanomechanics of single and multiwalled carbon nanotubes. Phys. Rev. B 2004, 69, 115429. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Lippiello, M. Hamilton principle for SWCN and a modified approach for nonlocal frequency analysis of nanoscale biosensor. Int. J. Recent Sci. Res. 2015, 6, 2355–2365. [Google Scholar]
- Karličić, D.; Cajić, M.; Adhikari, S. Dynamic stability of a nonlinear multiple-nanobeam system. Nonlinear Dynam. 2018, 93, 1495–1517. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.; Kashef, B.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- De Rosa, M.; Franciosi, C. On natural boundary conditions and DQM. Mech. Res. Commun. 1998, 25, 279–286. [Google Scholar] [CrossRef]
- De Rosa, M.; Lippiello, M. Non-classical boundary conditions and DQM for double-beams. Mech. Res. Commun. 2007, 34, 538–544. [Google Scholar] [CrossRef]
- Chen, W.; Striz, A.G.; Bert, C.W. A new approach to the differential quadrature method for fourth-order equations. Int. J. Numer. Methods Eng. 1997, 40, 1941–1956. [Google Scholar] [CrossRef]
- Tisseur, F.; Meerbergen, K. The quadratic eigenvalue problem. SIAM Rev. 2001, 43, 235–286. [Google Scholar] [CrossRef] [Green Version]
- Mathematica 8; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
- De Rosa, M.; Auciello, N. Free vibrations of tapered beams with flexible ends. Comput. Struct. 1996, 60, 197–202. [Google Scholar] [CrossRef]
- Pryce, J.D. A new measure of relative error for vectors. SIAM J. Numer. Anal. 1984, 21, 202–215. [Google Scholar] [CrossRef]
- Adhikari, S.; Chowdhury, R. The calibration of carbon nanotube based bionanosensors. J. Appl. Phys. 2010, 107, 124322. [Google Scholar] [CrossRef]
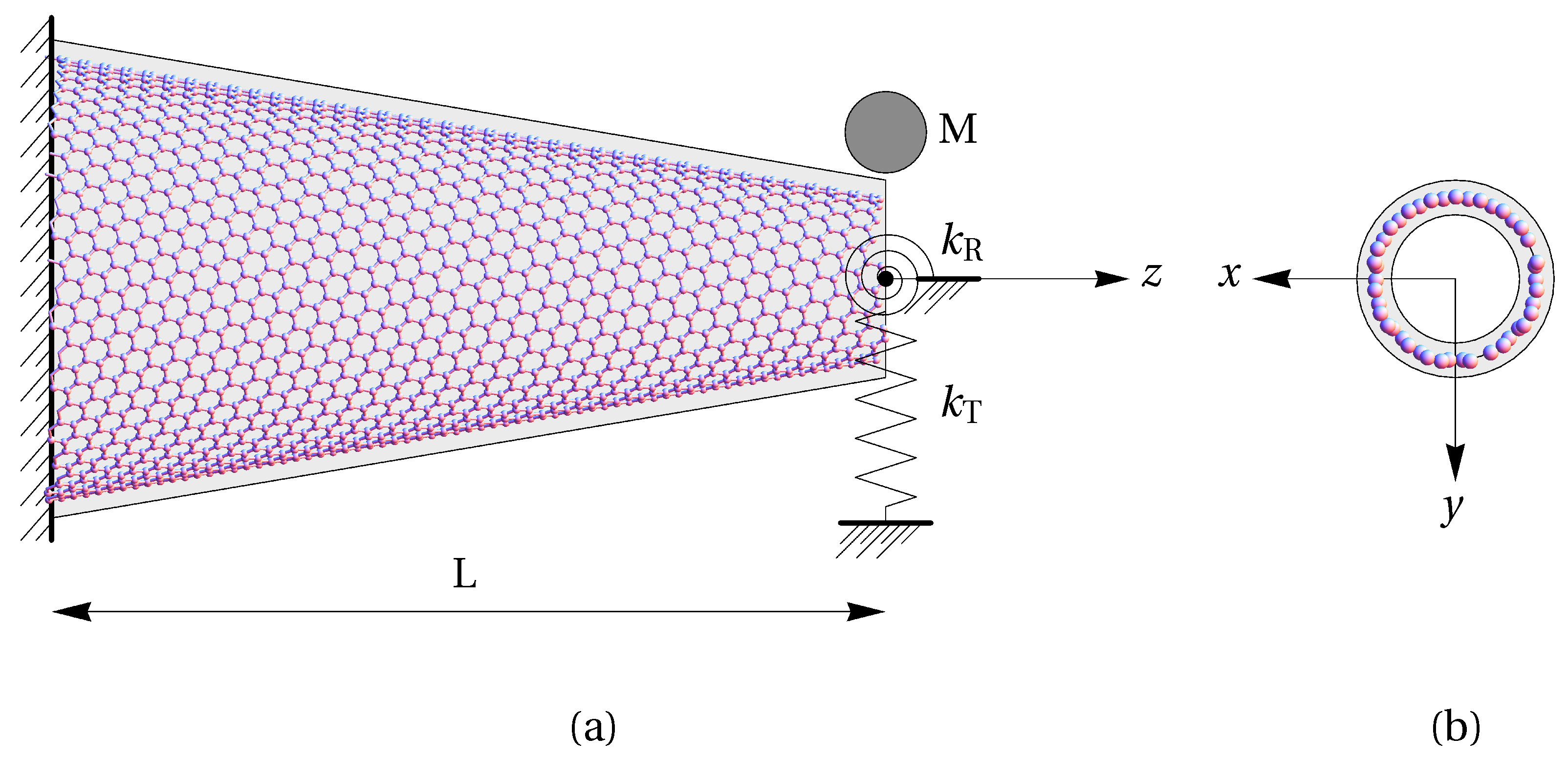
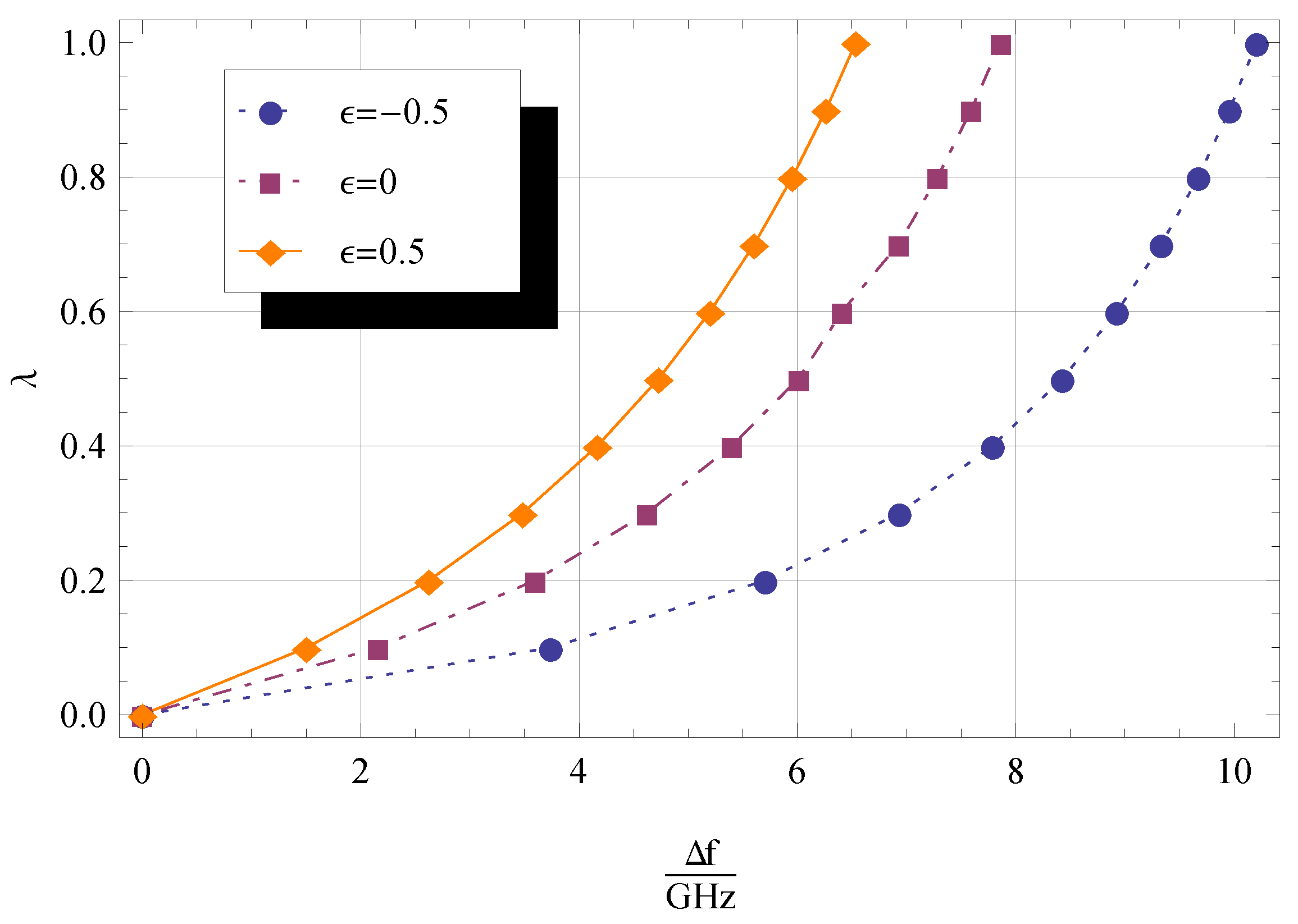
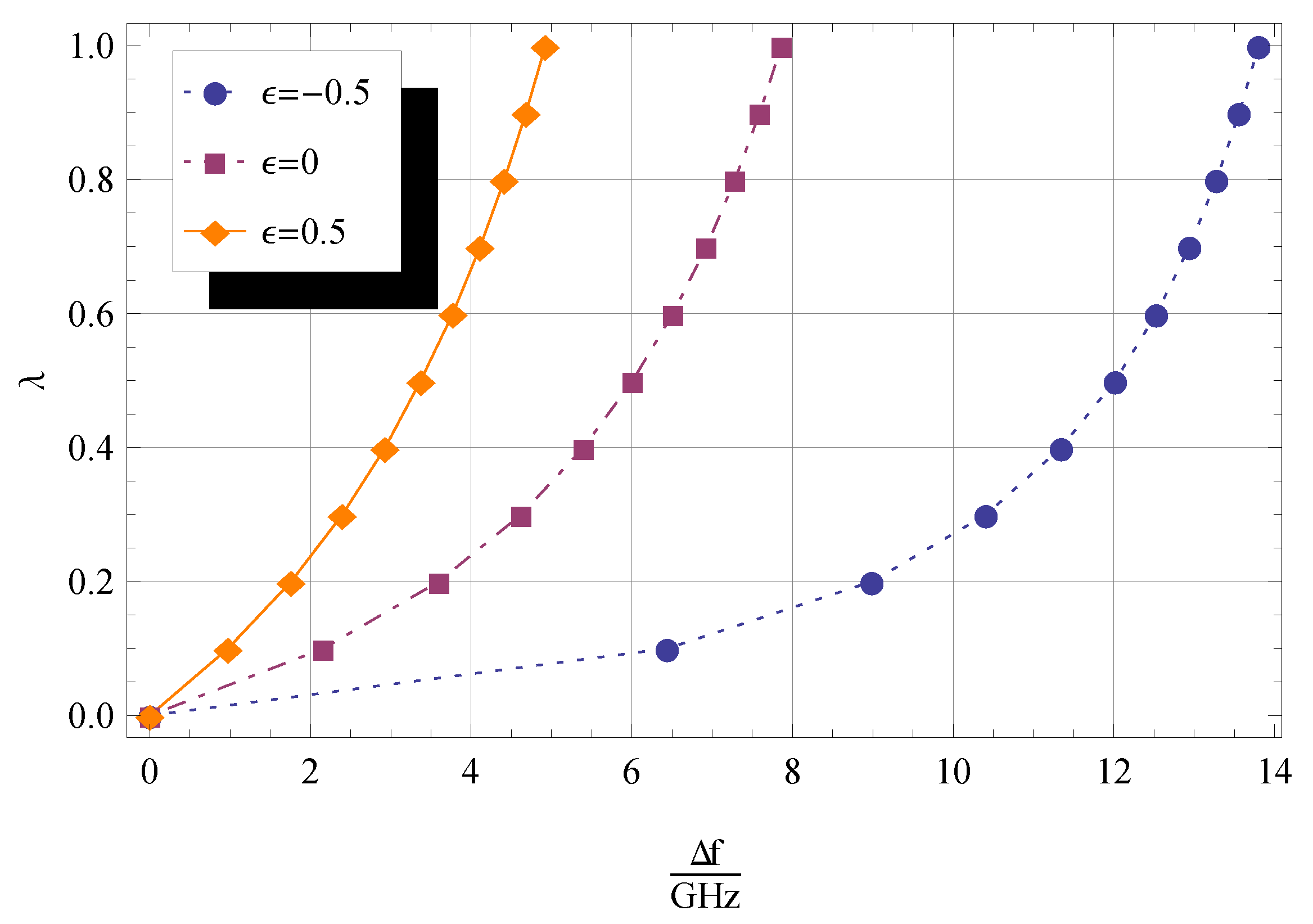
| Properties | Symbol | Value | Unit |
|---|---|---|---|
| Length | L | m | |
| Cross-sectional area | A | 1.70903 | m |
| Second moment of area | 5.71584 | m | |
| Mass density | kg m | ||
| Young’s modulus | E | TPa |
| [49] | |||
|---|---|---|---|
| 1.0 | 1.6113 | 1.6114 | |
| 0.9 | 1.6301 | 1.6302 | |
| 0.8 | 1.6500 | 1.6501 | |
| 0.7 | 1.6712 | 1.6714 | |
| 0.6 | 1.6940 | 1.6940 | 0. |
| 0.5 | 1.7183 | 1.7184 | |
| 0.4 | 1.7445 | 1.7447 | |
| 0.3 | 1.7730 | 1.7730 | 0. |
| 0.2 | 1.8039 | 1.8039 | 0. |
| [49] | |||
|---|---|---|---|
| 1.0 | 1.4421 | 1.4422 | |
| 0.9 | 1.4459 | 1.4459 | 0. |
| 0.8 | 1.4489 | 1.4489 | 0. |
| 0.7 | 1.4511 | 1.4511 | 0. |
| 0.6 | 1.4522 | 1.4522 | 0. |
| 0.5 | 1.4520 | 1.4520 | 0. |
| 0.4 | 1.4503 | 1.4503 | 0. |
| 0.3 | 1.4466 | 1.4466 | 0. |
| 0.2 | 1.4407 | 1.4407 | 0. |
| 0 | 8.4456 | 6.0259 | 4.7428 |
| 0.02 | 8.4449 | 6.0254 | 4.7423 |
| 0.04 | 8.4428 | 6.0236 | 4.7407 |
| 0.06 | 8.4393 | 6.0206 | 4.7382 |
| 0.08 | 8.4344 | 6.0163 | 4.7346 |
| 0.10 | 8.4281 | 6.0109 | 4.7300 |
| 0.12 | 8.4203 | 6.0042 | 4.7244 |
| 0.14 | 8.4110 | 5.9963 | 4.7177 |
| 0.16 | 8.4003 | 5.9871 | 4.7099 |
| 0.18 | 8.3880 | 5.9766 | 4.7011 |
| 0.20 | 8.3740 | 5.9648 | 4.6911 |
| 1.7227 | 2.0201 | 2.1908 | |
| 0 | 12.2826 | 15.9842 | 19.18635 |
| 31.6509 | 43.2472 | 53.5648 | |
| 1.9472 | 2.1502 | 2.2813 | |
| 0.1 | 12.9167 | 16.2385 | 19.3274 |
| 32.6881 | 43.4459 | 53.6609 | |
| 2.4073 | 2.7696 | 2.8486 | |
| 1 | 14.9778 | 17.9400 | 20.4497 |
| 35.1213 | 44.9686 | 54.4768 | |
| 2.5905 | 3.4929 | 4.0616 | |
| 10 | 16.2189 | 21.7424 | 25.2449 |
| 37.4361 | 50.0820 | 59.3719 | |
| 2.6145 | 3.6547 | 4.5134 | |
| 16.4043 | 23.0538 | 28.7191 | |
| 37.8203 | 52.5596 | 65.0277 | |
| 2.6171 | 3.6729 | 4.5717 | |
| 16.4237 | 23.2150 | 29.2433 | |
| 37.8610 | 52.8892 | 66.1246 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Rosa, M.A.; Lippiello, M.; Babilio, E.; Ceraldi, C. Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass. Materials 2021, 14, 3445. https://doi.org/10.3390/ma14133445
De Rosa MA, Lippiello M, Babilio E, Ceraldi C. Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass. Materials. 2021; 14(13):3445. https://doi.org/10.3390/ma14133445
Chicago/Turabian StyleDe Rosa, Maria Anna, Maria Lippiello, Enrico Babilio, and Carla Ceraldi. 2021. "Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass" Materials 14, no. 13: 3445. https://doi.org/10.3390/ma14133445
APA StyleDe Rosa, M. A., Lippiello, M., Babilio, E., & Ceraldi, C. (2021). Nonlocal Vibration Analysis of a Nonuniform Carbon Nanotube with Elastic Constraints and an Attached Mass. Materials, 14(13), 3445. https://doi.org/10.3390/ma14133445









