Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding
Abstract
1. Introduction
1.1. The Issue of the Pounding of Structures due to Seismic Load, and the Existing Solutions
1.2. The Proposition of New Materials as Earthquake Damage Protection
1.3. Contributions of the Present Work
2. Experiments
2.1. Materials
2.2. Samples
2.2.1. Polymeric Reference Samples
2.2.2. Metallic Reference Samples
2.2.3. Composite Type 1 Samples
2.2.4. Composite Type 2 Samples
2.3. Experimental Procedure
3. Results and Discussion
3.1. Quasi-Static Compression
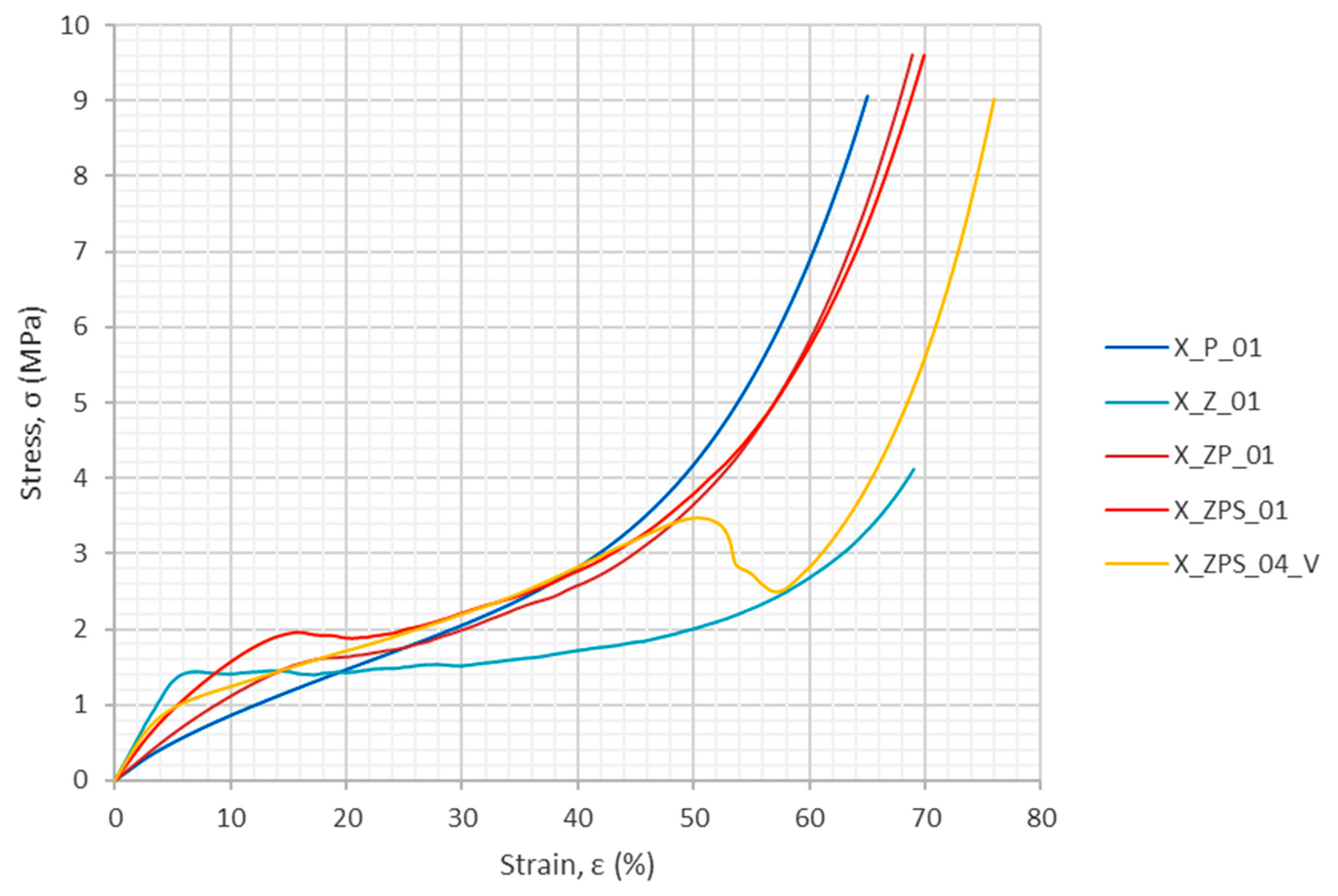
3.1.1. Stress–Strain Results from Quasi-Static Compression
- —the stress which is the first local maximum in the stress–strain graph (the first maximum compressive strength);
- —in the case of no local maximum, one determines the intersection of the extensions of the first two linear sections of the stress–strain graph; the ordinate of the intersection point is the compressive strength.
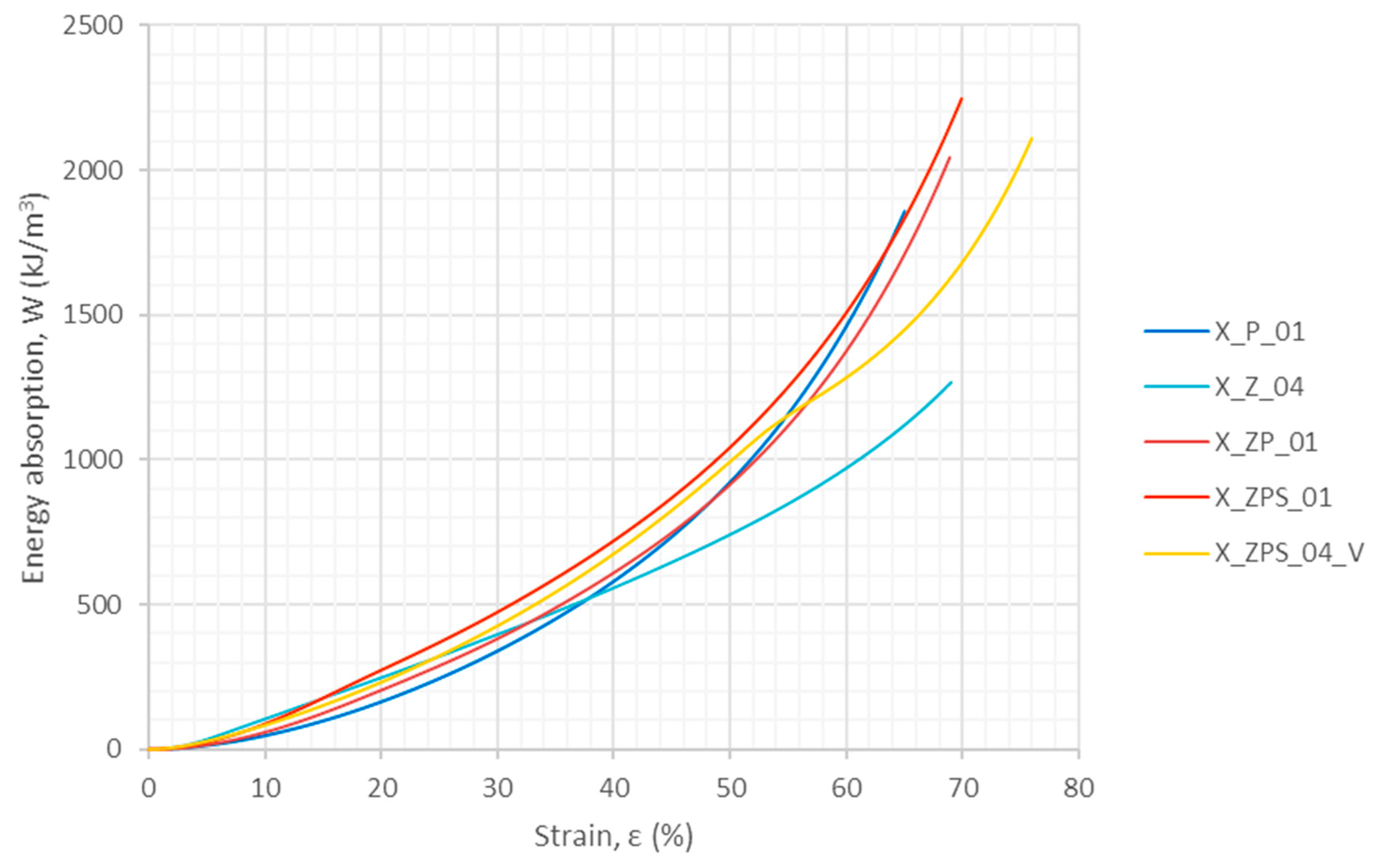
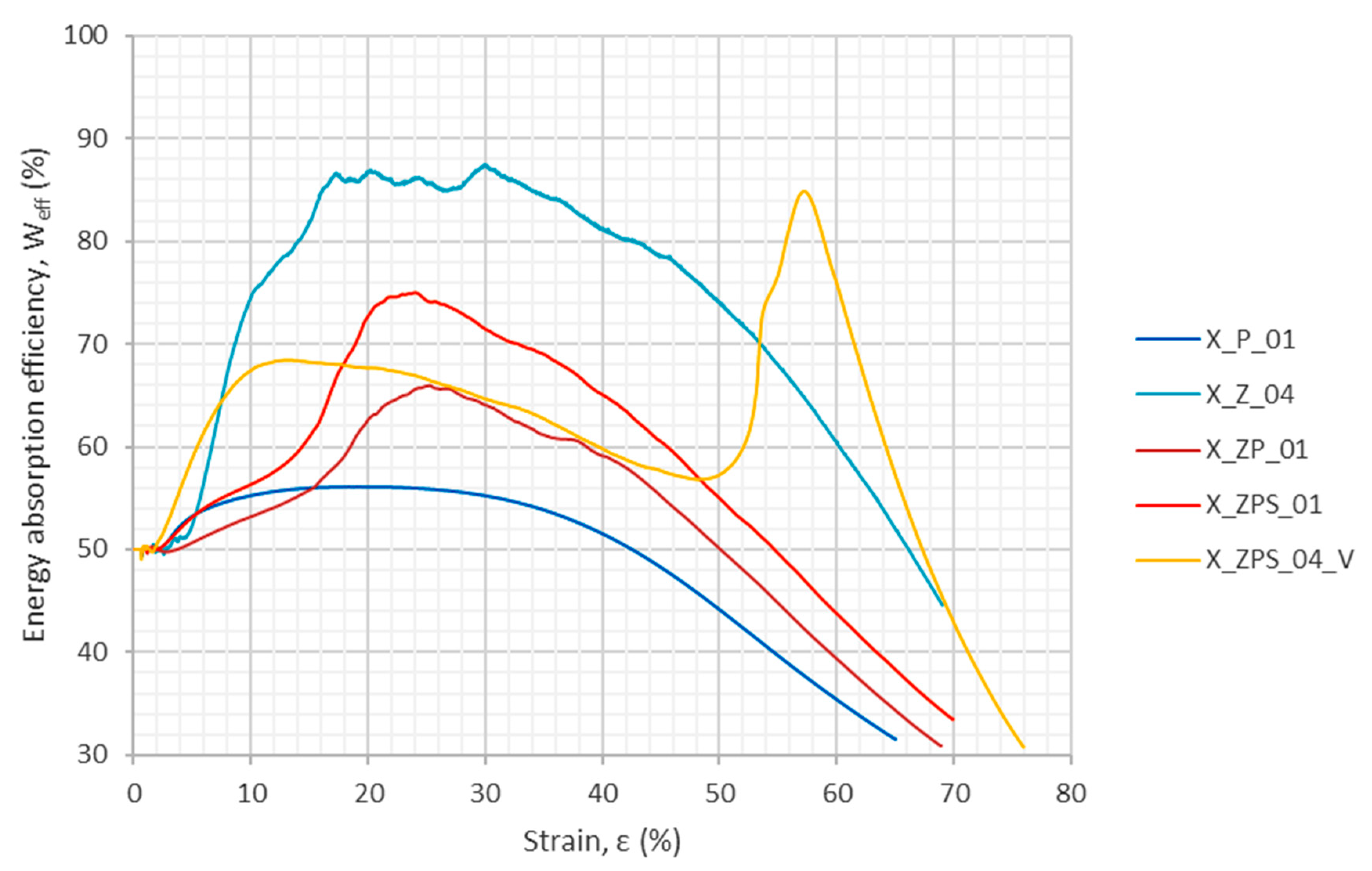
3.1.2. Energy Absorption in Quasi-Static Compression
3.2. Dynamic Uniaxial Compression
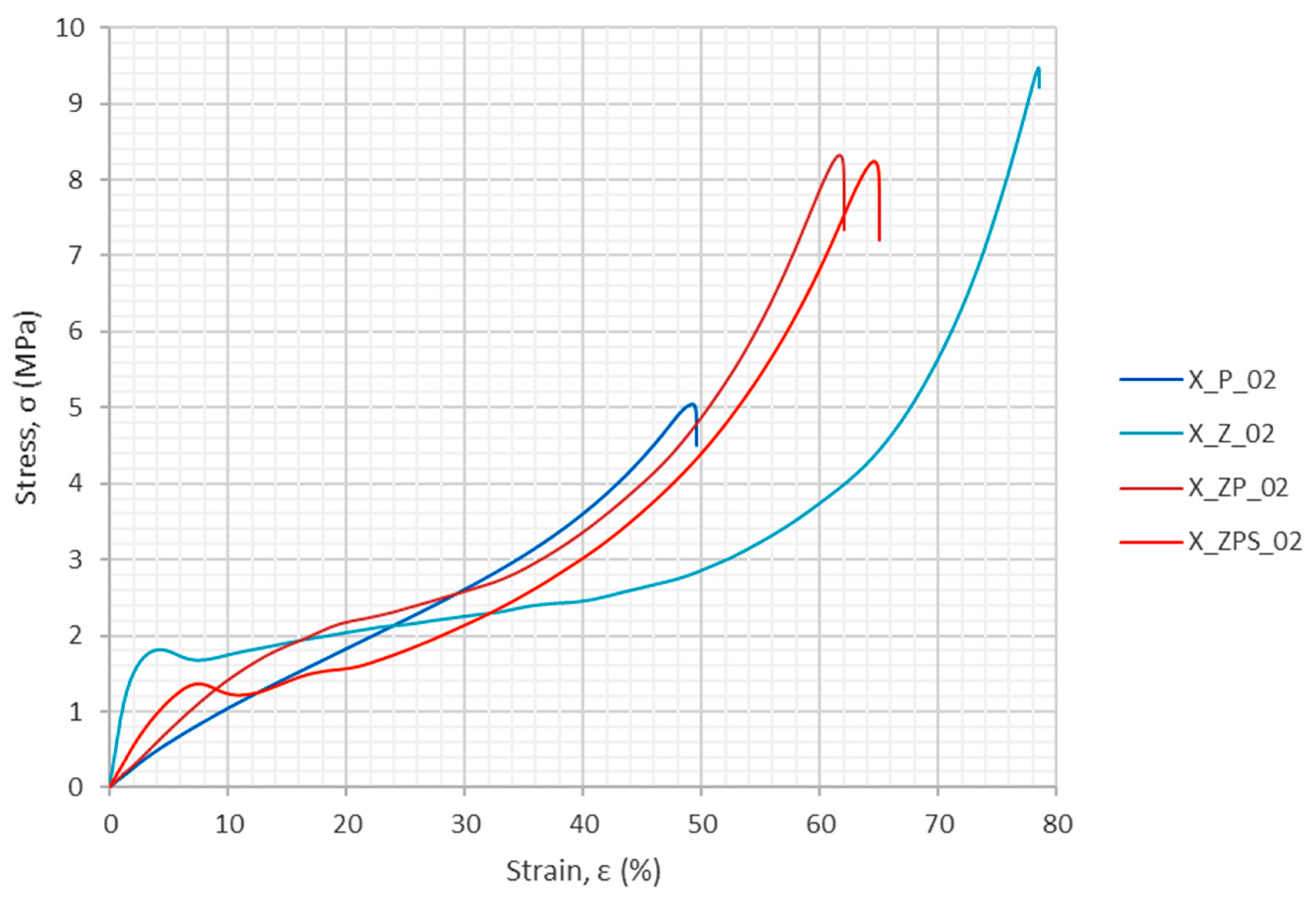
3.2.1. Stress–Strain Results from the Dynamic Uniaxial Compression
- —the stress which is the first local maximum in the stress–strain graph (the first maximum compressive strength in the dynamic experiments);
- —in the case of no local maximum, the ordinate of the intersection of the extensions of the first two linear sections of the stress–strain graph is the compressive strength in the uniaxial dynamic experiments.
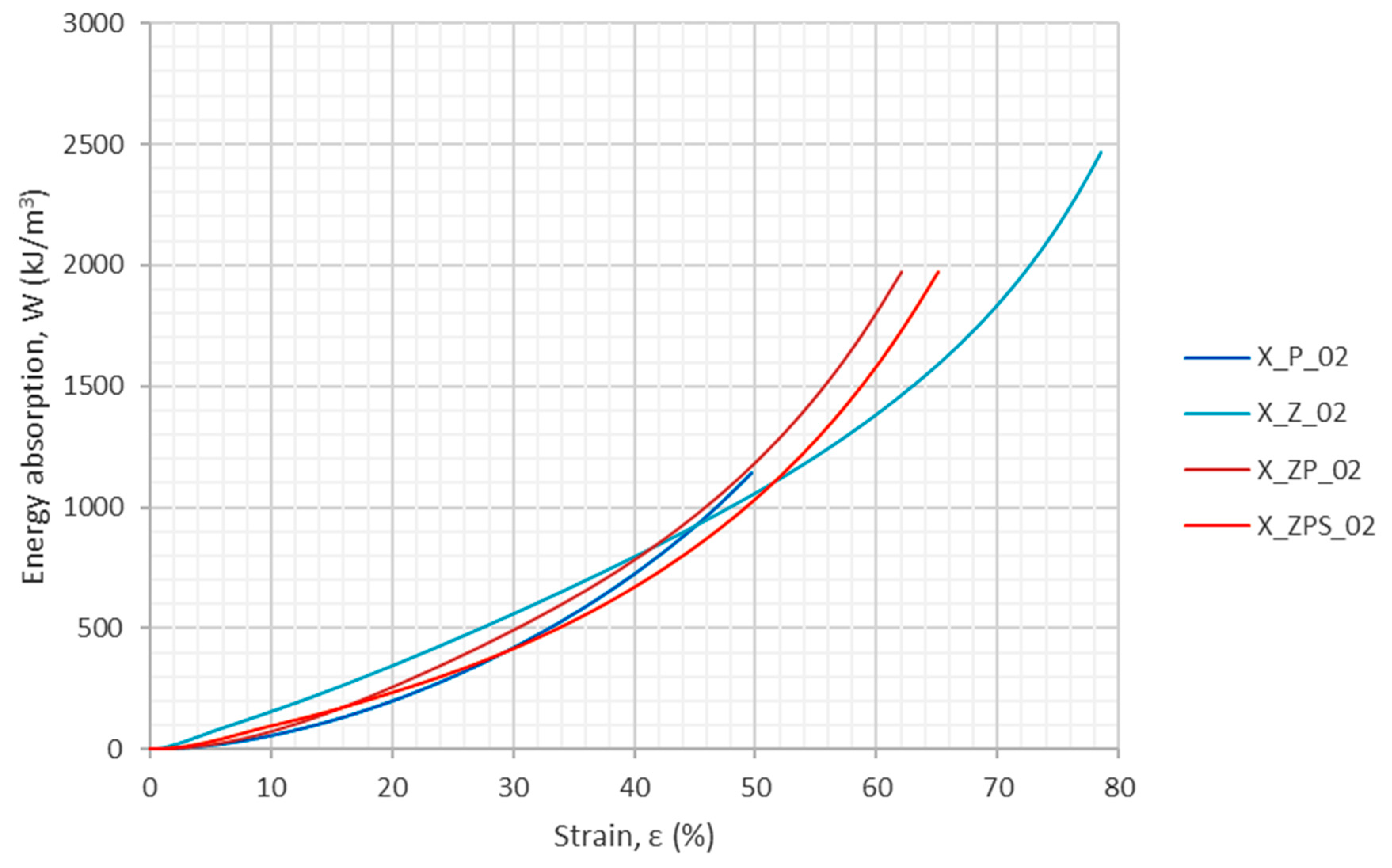
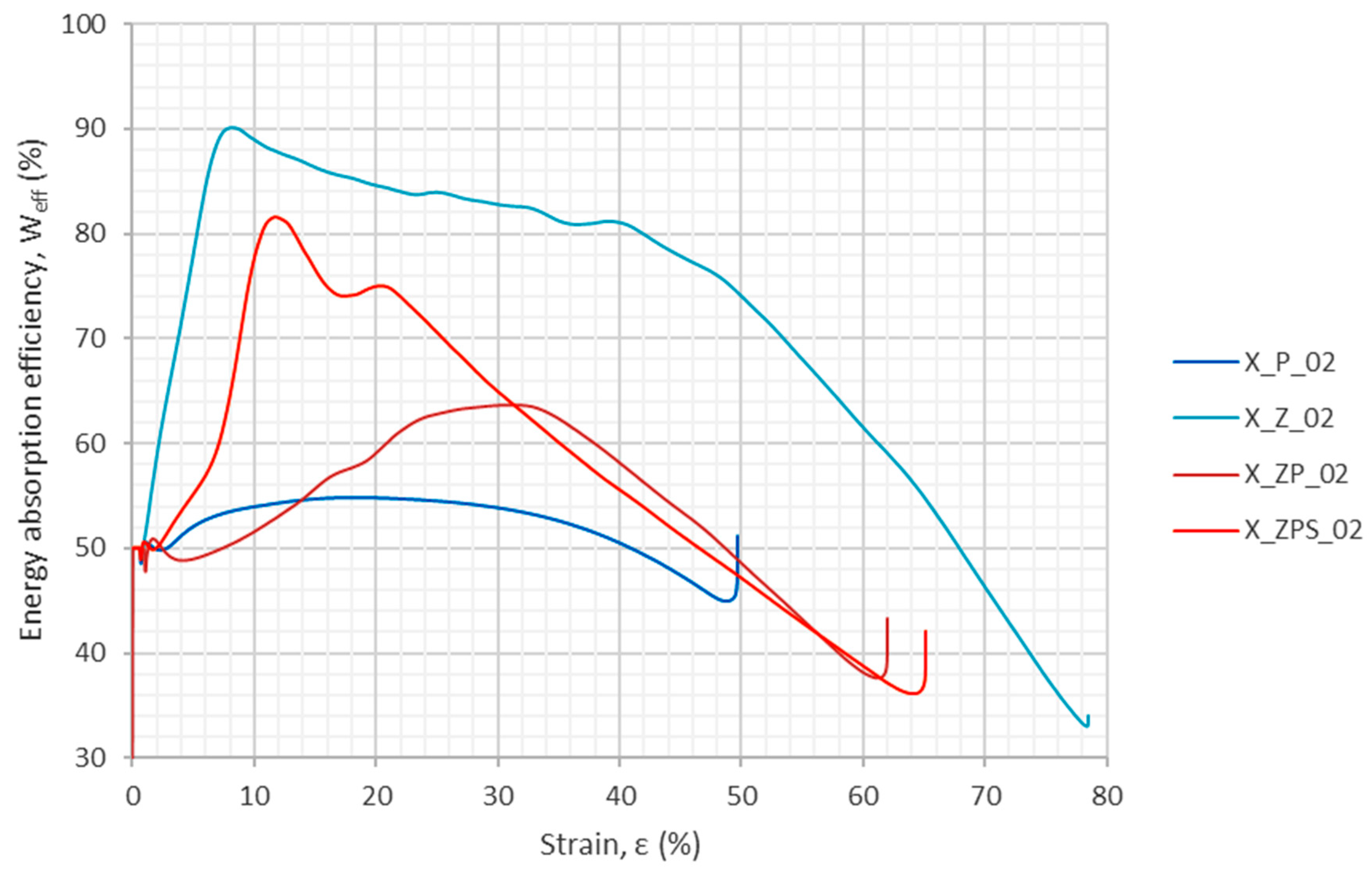
3.2.2. Energy Absorption in Uniaxial Dynamic Compression
3.3. Dynamic Compression with Unloading Loops
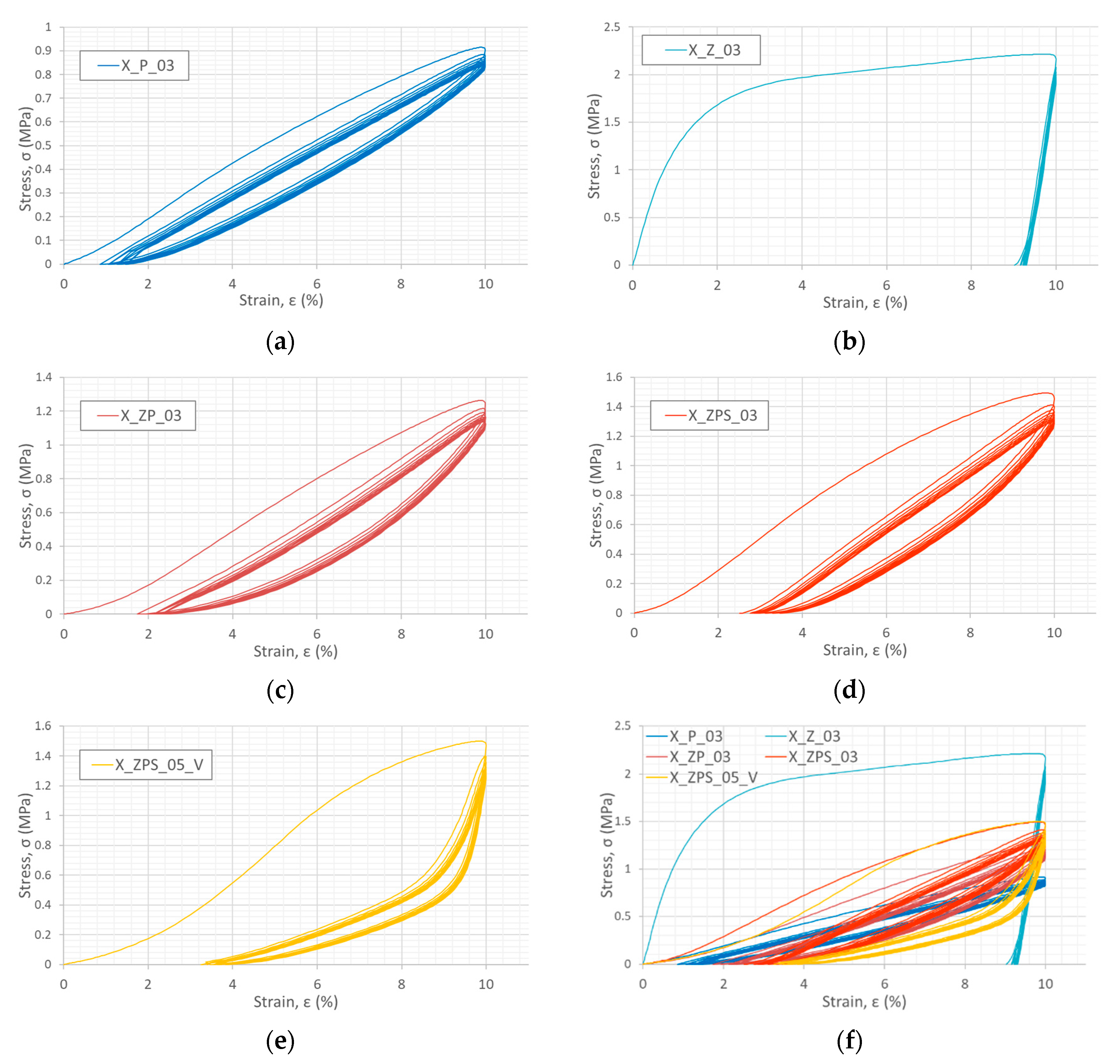
3.3.1. Stress–Strain Results Obtained from Cyclic Dynamic Compression
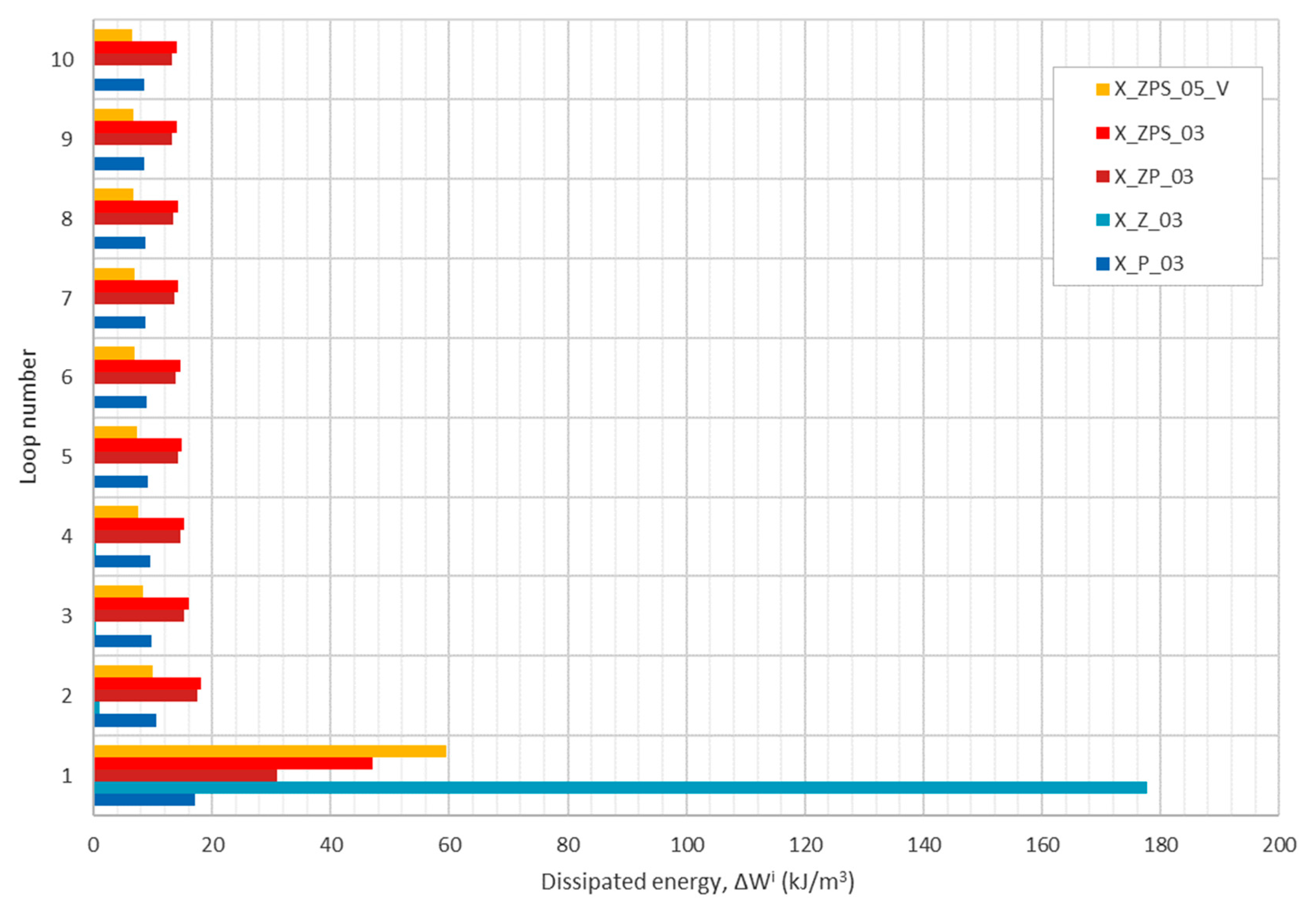
3.3.2. Energy Absorption in Dynamic Cyclic Compression
- the potential elastic strain energy share quotient
- the dissipated energy share quotientwhere is the sum of the energy absorbed in all 10 loops; is the sum of the potential elastic strain energy absorbed in all 10 loops and is the sum of the energy dissipated in all 10 loops.
- the quotient of the accumulated normalized dissipated energywhere is the energy dissipated in the i-th loop, is the energy dissipated in the first loop, and is the loop number; here .
4. Conclusions
- As the primary effect of this research, it has been confirmed that it is possible to combine a special polyurethane material and aluminum foam with a closed-cell structure to produce composite materials of two types, with and without an adhesive layer, and that the composites can work effectively utilizing both the viscoelastic and plastic paths of deformation simultaneously, allowing for singular and repeated collision load bearing in the case of the pounding effect from seismic excitations.
- The experiments were designed as compressions with two strain rates: 10 × 10−3 s−1 (quasi-static) and 0.2 s−1 (dynamic); the dynamic tests were performed as uniaxial compression and compression with 10 loops of unloading at 10% strain. Such conditions were assumed due to the sensitivity of both the polymer and the aluminum foam to the speed of the loading, and in order to mimic the conditions of the seismic collisions of structures, which have a low-cycle repeated pounding character.
- A few measures were proposed to assess the effectiveness of the new composites; among them were the compressive strength, energy absorption efficiency (acc. to Equation (2)), dissipated energy share quotient (acc. to Equation (6)) and quotient of the accumulated normalized dissipated energy (acc. to Equation (7)). The energy absorption efficiency was determined for fixed strain levels, i.e., 10%, 20%, 30% and 40%, and additionally the maximum value was found. In order to appropriately estimate how the studied materials could fit the anti-pounding application, it is necessary to analyze the suggested measures altogether, not separately.
- Such an analysis was performed, and its results confirmed that composite specimens exhibited favorable values of the above indicators. Firstly, in almost all cases, the energy absorption efficiency for the composites was between the values for the uniform polymer and aluminum foam. Especially, the maximum energy absorption efficiency for the new composites in comparison to the uniform polymer specimens was enhanced by 34% and 49%, respectively, in the quasi-static and dynamic experiments. Furthermore, the dissipated energy share quotients showed that the newly proposed materials dissipated from 35% to 44% of the energy absorbed in 10 loading-unloading cycles. For comparison, the cellular metal specimen dissipated 73% and the polymer one dissipated 25% of total absorbed energy. As for the ability of retaining the dissipation capacity for more than just one loading cycle, all of the materials exhibited the trend of keeping an almost constant level of lost energy through loops 2 to 10. The layered materials with the adhesive attained a total capacity of dissipating energy between one and three times more than in the first loop; the aluminum foam only achieved 1.6%, and the polymer and the composite without the bonding achieved above four times more.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef]
- Chen, W.F.; Scawthorn, C. Earthquake Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Miari, M.; Choong, K.K.; Jankowski, R. Seismic pounding between bridge segments: A state-of-the-art review. Arch. Comput. Methods Eng. 2021, 28, 495–504. [Google Scholar] [CrossRef]
- Kazemi, F.; Miari, M.; Jankowski, R. Investigating the effects of structural pounding on the seismic performance of adjacent RC and steel MRFs. Bull. Earthq. Eng. 2021, 19, 317–343. [Google Scholar] [CrossRef]
- Jameel, M.; Islam, A.; Hussain, R.R.; Hasan, S.D.; Khaleel, M. Non-linear FEM analysis of seismic induced pounding between neighboring multi-storey structures. Lat. Am. J. Solids Struct. 2013, 10, 921–939. [Google Scholar] [CrossRef]
- Favvata, M.J. Minimum required separation gap for adjacent RC frames with potential inter-story seismic pounding. Eng. Struct. 2017, 152, 643–659. [Google Scholar] [CrossRef]
- Rezaei, H.; Moayyedi, S.A.; Jankowski, R. Probabilistic seismic assessment of RC box-girder highway bridges with unequal-height piers subjected to earthquake-induced pounding. Bull. Earthq. Eng. 2020, 18, 1547–1578. [Google Scholar] [CrossRef]
- Migda, W.; Szczepański, M.; Lasowicz, N.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Non-linear analysis of inter-story pounding between wood-framed buildings during ground motion. Geosciences 2019, 9, 488. [Google Scholar] [CrossRef]
- Rosenblueth, E.; Meli, R. The 1985 Mexico earthquake. Concr. Int. 1986, 8, 23–34. [Google Scholar]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Bertero, V.V.; Collin, S.R.G. Investigation of the Failures of the Olive View Stairtowers during the San Fernando Earthquake and Their Implications on Seismic Design; EERC Report No. 73-26; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1973. [Google Scholar]
- Anagnostopoulos, S.A. Earthquake induced pounding: State of the art. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; Duma, G., Ed.; Publisher A. A. Balkema: Rotterdam, The Netherlands, 1995; pp. 897–905. [Google Scholar]
- Jeng, V.; Kasai, K.; Maison, B.F. A Spectral difference method to estimate building separations to avoid pounding. Earthq. Spectra 1992, 8, 201–223. [Google Scholar] [CrossRef]
- Elwardany, H.; Seleemah, A.; Jankowski, R.; El-Khoriby, S. Influence of soil-structure interaction on seismic pounding between steel frame buildings considering the effect of infill panels. Bull. Earthq. Eng. 2019, 17, 6165–6202. [Google Scholar] [CrossRef]
- Lopez-Garcia, D. Separation between adjacent non-linear structures for prevention of seismic pounding. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Lopez-Garcia, D.; Soong, T.T. Evaluation of current criteria in predicting the separation necessary to prevent seismic pounding between nonlinear hysteretic structural systems. Eng. Struct. 2009, 31, 1217–1229. [Google Scholar] [CrossRef]
- Kiureghian, A.D. A response spectrum method for random vibration analysis of MDF systems. Earthq. Eng. Struct. Dyn. 1981, 9, 419–435. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Mortezaei, A.; Razavi, S.M.N.; Lasowicz, N.; Jankowski, R. Effective Gap Size Index for Determination of Optimum Separation Distance Preventing Pounding between Buildings during Earthquakes. Appl. Sci. 2021, 11, 2322. [Google Scholar] [CrossRef]
- Sołtysik, B.; Falborski, T.; Jankowski, R. Preventing of earthquake-induced pounding between steel structures by using polymer elements—Experimental study. Procedia Eng. 2017, 199, 278–283. [Google Scholar] [CrossRef]
- Rousakis, T.; Ilki, A.; Kwiecień, A.; Viskovic, A.; Gams, M.; Triller, P.; Ghiassi, B.; Benedetti, A.; Rakicevic, Z.; Colla, C.; et al. Deformable Polyurethane Joints and Fibre Grids for Resilient Seismic Performance of Reinforced Concrete Frames with Orthoblock Brick Infills. Polymers 2020, 12, 2869. [Google Scholar] [CrossRef]
- Rousakis, T.; Papadouli, E.; Sapalidis, A.; Vanian, V.; Ilki, A.; Halici, O.F.; Kwiecień, A.; Zając, B.; Hojdys, Ł.; Krajewski, P.; et al. Flexible joints between RC frames and masonry infill for improved seismic performance—Shake table test. In Brick and Block Masonry—From Historical to Sustainable Masonry; Kubica, J., Kwiecień, A., Bednarz, L., Eds.; Taylor & Francis Group: London, UK, 2020; pp. 499–507. [Google Scholar]
- Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
- Kwiecień, A.; Rakicevic, Z.; Bogdanovic, A.; Manojlovski, F.; Poposka, A.; Shoklarovski, A.; Rousakis, T.; Ilki, A.; Gams, M.; Viskovic, A. PUFJ and FRPU earthquake protection of infills tested in resonance. In Proceedings of the 1st Croatian Conference on Earthquake Engi-684 Neering (1CroCEE), Zagreb, Croatia, 22–24 March 2021. [Google Scholar]
- Lasowicz, N.; Kwiecień, A.; Jankowski, R. Experimental study on the effectiveness of polyurethane flexible adhesive in reduction of structural vibrations. Polymers 2020, 12, 2364. [Google Scholar] [CrossRef]
- Kwiecień, A.; Gams, M.; Rousakis, T.; Viskovic, A.; Korelc, J. Validation of a new hyperviscoelastic model for deformable polymers used for joints between RC frames and masonry infills. Eng. Trans. 2017, 65, 113–121. [Google Scholar]
- Zdanowicz, Ł.; Serega, S.; Tekieli, M.; Kwiecień, A. Polymer flexible joint as a repair method of concrete elements: Flexural 632 testing and numerical analysis. Materials 2020, 13, 5732. [Google Scholar] [CrossRef]
- Kwiecień, A.; Kuboń, P. Dynamic Analysis of Damaged Masonry Building Repaired with the Flexible Joint Method. Arch. Civ. Eng. 2012, 58, 39–55. [Google Scholar] [CrossRef][Green Version]
- Viskovic, A.; Kwiecień, A.; Gams, M.; Zając, B.; Zuccarino, L. Quick seismic protection of weak masonry infilling in filled framed structures using flexible joints. Key Eng. Mater. 2017, 747, 628–637. [Google Scholar] [CrossRef]
- Lee, K.-S.; Sause, R.; Ricles, J.; Ab-Malek, K.; Lu, L.-W. Hysteretic Models for Elastomer Structural Dampers and Application to Non-ductile RC Frame Building. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 1617. [Google Scholar]
- Sikora, W.; Michalczyk, K.; Machniewicz, T. Numerical Modelling of Metal-Elastomer Spring Nonlinear Response for Low-Rate Deformations. Acta Mech. Autom. 2018, 12, 31–37. [Google Scholar] [CrossRef]
- Sikora, W.; Michalczyk, K.; Machniewicz, T. A study of the preload force in metal-elastomer torsion springs. Acta Mech. Autom. 2016, 10, 300–305. [Google Scholar] [CrossRef]
- Kwiecień, A.; Gruszczyński, M.; Zając, B. Tests of Flexible Polymer Joints Repairing of Concrete Pavements and of Polymer Modified Concretes Influenced by High Deformations. Key Eng. Mater. 2011, 466, 225–239. [Google Scholar] [CrossRef]
- Kwiecień, K.; Kwiecień, A.; Stryszewska, T.; Szumera, M.; Dudek, M. Durability of PS-Polyurethane Dedicated for Composite Strengthening Applications in Masonry and Concrete Structures. Polymers 2020, 12, 2830. [Google Scholar] [CrossRef] [PubMed]
- García-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef] [PubMed]
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Rajak, D.K.; Gupta, M. Applications of metallic foams. In An Insight into Metal Based Foams; Advanced Structured Materials; Springer: Singapore, 2020; Volume 145, pp. 21–37. [Google Scholar] [CrossRef]
- Alusion™ by Cymat Technologies Ltd. Available online: http://www.cymat.com/alusion/ (accessed on 23 April 2021).
- Stabilität Vereint Leichtigkeit by Mtalfoam. Available online: http://metalfoam.de/metalfoam/ (accessed on 23 April 2021).
- Kremer, K. Metal Foams for Improved Crash Energy Absorption in Passenger Equipment; Transportation Research Board of the National Academies: Newark, NJ, USA, 2004. [Google Scholar]
- Schäffler, P.; Hanko, G.; Mitterer, H.; Zach, P. Alulight Metal Foam Products. In Proceedings of the Porous Metals and Metallic Foams: Metfoam, Kyoto, Japan, 5–7 September 2007; Lefebvre, L.P., Banhart, J., Dunand, D.C., Eds.; The Japan Institute of Metals: Kyoto, Japan, 2008; pp. 7–10. [Google Scholar]
- Minford, J.D. Handbook of Aluminum Bonding Technology and Data; CRC Press: Boca Raton, FL, USA, 1993; p. 110. [Google Scholar]
- Valdes, B.; Schorr, M.; Zlatev, R.; Carrillo, M.; Stoytcheva, M.; Alvarez, L.; Eliezer, A.; Rosas, N. Corrosion Control in Industry. In Environmental and Industrial Corrosion: Practical and Theoretical Aspects; Valdez, B., Schorr, M., Eds.; InTech: Rijeka, Croatia, 2012; p. 29. [Google Scholar]
- Rossi, S.; Fedel, M.; Da Col, L.; Deflorian, F.; Petrolli, S. Coatings to increase the corrosion behaviour of aluminium foam. Surf. Eng. 2017, 33, 1–6. [Google Scholar] [CrossRef]
- Huebner, S.; Hassler, U.; Duan, Y.; Osman, A.; Maldague, X. Study of the Influence of corrosion on materials properties of Aluminum foams with Computed Tomography and Thermography. In Proceedings of the 4th Symposium for NDT in Aerospace, Augsburg, Germany, 13–14 November 2012. [Google Scholar]
- Pippan, R.; Motz, C.; Kriszt, B.; Zettl, B.; Mayer, H.; Stanzl-Tschegg, S.; Simancik, F.; Kovacik, J. Material properties. In Handbook of Cellular Metals; Degischer, H.-P., Kriszt, B., Eds.; Viley-VCH: Weinheim, Germany, 2002; pp. 179–241. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids, 1st ed.; Pergamon Press: Oxford, UK, 1988. [Google Scholar]
- Banhart, J.; Baumeister, J. Deformation characteristics of metal foam. J. Mater. Sci. 1998, 33, 1431–1440. [Google Scholar] [CrossRef]
- Gawęcki, A. Mechanics of Materials and Structures, 3rd ed.; Wydawnictwo Politechniki Poznańskiej: Poznań, Poland, 1998; Volume 1, pp. 89–105. (In Polish) [Google Scholar]
- Andrews, E.; Sanders, W.; Gibson, L.J. Compressive and tensile behaviour of aluminum foams. Mater. Sci. Eng. A 1999, 270, 113–124. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Linul, E.; Marsavina, L.; Kováčik, J.; Sadowski, T. Dynamic and quasi-static compression tests of closed-cell aluminium alloy foams. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2017, 18, 361–369. [Google Scholar]
- Novak, N.; Vesenjak, M.; Duarte, I.; Tanaka, S.; Hokamoto, K.; Krstulović-Opara, L.; Guo, B.; Chen, P.; Ren, Z. Compressive Behaviour of Closed-Cell Aluminium Foam at Different Strain Rates. Materials 2019, 12, 4108. [Google Scholar] [CrossRef]
- Mukai, T.; Kanahashi, H.; Miyoshi, T.; Mabuchi, M.; Nieh, T.G.; Higashi, K. Experimental study of energy absorption in a close-celled aluminum foam under dynamic loading. Scr. Mater. 1999, 40, 921–927. [Google Scholar] [CrossRef]
- Ruan, D.; Lu, G.; Chen, F.L.; Siores, E. Compressive behaviour of aluminium foams at low and medium strain rates. Compos. Struct. 2002, 57, 331–336. [Google Scholar] [CrossRef]
- Nammi, S.K.; Edwards, G.; Shirvani, H. Effect of cell-size on the energy absorption features of closed-cell aluminium foams. Acta Astronaut. 2016, 128, 243–250. [Google Scholar] [CrossRef]
- Sajek, A. Bonding technology and properties of the adhesive joint of composite aluminum foams. Przegląd Spaw. Weld. Technol. Rev. 2014, 86. (In Polish) [Google Scholar] [CrossRef][Green Version]
- Dudzik, M.; Machniewicz, T.; Stręk, A.M. Modelling of compressive behaviour of closed-cell aluminum with ANN. Materials 2021, in press. [Google Scholar]
- DIN 50134:2008-10 Prüfung von Metallischen Werkstoffen—Druckversuch an Metallischen Zellularen Werkstoffen. Available online: https://www.beuth.de/en/standard/din-50134/108978639 (accessed on 10 June 2021).
- ISO 13314:2011 Mechanical Testing of metals—Ductility Testing—Compression Test for Porous and Cellular Metals. Available online: https://www.iso.org/standard/53669.html (accessed on 10 June 2021).
- Stręk, A.M. Determination of material characteristics in the quasi-static compression test of cellular metal materials. In Wybrane Problem Geotechniki i Wytrzymałości Materiałów dla Potrzeb Nowoczesnego Budownictwa, 1st ed.; Tatara, T., Pilecka, E., Eds.; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2020. (In Polish) [Google Scholar]
- Gregorová, E.; Pabst, W.; Uhlířová, T.; Nečina, V.; Veselý, M.; Sedlářová, I. Processing, microstructure and elastic properties of mullite-based ceramic foams prepared by direct foaming with wheat flour. J. Eur. Ceram. Soc. 2016, 36, 109–120. [Google Scholar] [CrossRef]
- Kováčik, J.; Marsavina, L.; Linul, E. Poisson’s Ratio of Closed-Cell Aluminium Foams. Materials 2018, 11, 1904. [Google Scholar] [CrossRef] [PubMed]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488–489, 347–350. [Google Scholar] [CrossRef]
- Nowak, Z. Constitutive modeling and parameter identification for rubberlike materials. Eng. Trans. 2008, 56, 117–157. [Google Scholar]
- Hopkinson, B.; Williams, G.T. The Elastic Hysteresis of Steel. Proc. R. Soc. 1912, 87, 502–509. [Google Scholar] [CrossRef]
- Dudzik, M.; Stręk, A.M. ANN model of stress-strain relationship for aluminium sponge in uniaxial compression. J. Theor. Appl. Mech. 2020, 58, 385–390. [Google Scholar] [CrossRef]
- Dudzik, M.; Stręk, A.M. ANN Architecture Specifications for Modelling of Open-Cell Aluminum under Compression. Math. Probl. Eng. 2020, 2020, 2834317. [Google Scholar] [CrossRef]
- Finney, R.H. Finite Element Analysis, Engineering with Rubber: How to Design Rubber Components; Gent, A.N., Ed.; Hanser: Munich, Gemany, 2001. [Google Scholar]
- Finney, R.H.; Kumar, A. Development of material constants for nonlinear finite-element analysis. Rubber Chem. Technol. 1988, 61, 879–891. [Google Scholar] [CrossRef]






| Sample ID | a (mm) | b (mm) | h (mm) |
|---|---|---|---|
| X_P_01 | 50.89 | 52.02 | 49.90 |
| X_P_02 | 50.84 | 51.47 | 52.14 |
| X_P_03 | 50.24 | 51.58 | 52.73 |
| X_Z_01 | 50.29 | 50.11 | 50.17 |
| X_Z_02 | 48.80 | 50.00 | 48.00 |
| X_Z_03 | 49.83 | 49.31 | 49.60 |
| X_ZP_01 | 50.21 | 49.73 | 51.20 |
| X_ZP_02 | 49.51 | 50.25 | 52.18 |
| X_ZP_03 | 49.66 | 49.89 | 53.76 |
| X_ZPS_01 | 49.78 | 50.18 | 53.70 |
| X_ZPS_02 | 49.94 | 49.50 | 53.10 |
| X_ZPS_03 | 49.99 | 50.11 | 54.47 |
| X_ZPS_04 | 49.95 | 50.16 | 52.99 |
| X_ZPS_05 | 50.23 | 49.90 | 52.78 |
| Measure | X_P_01 | X_Z_01 | X_ZP_01 | X_ZPS_01 | X_ZPS_04_V |
|---|---|---|---|---|---|
| —compressive strength (first maximum), (MPa) | --- | 1.44 | 1.62 | 1.96 | --- |
| —compressive strength (no first maximum), (MPa) | --- | --- | --- | --- | 0.94 |
| Strain for the compressive strength, (%) | --- | 7.09 | 18.52 | 15.77 | 3.66 |
| Measure | X_P_01 | X_Z_01 | X_ZP_01 | X_ZPS_01 | X_ZPS_04_V |
|---|---|---|---|---|---|
| —energy absorption for 10% strain, (kJ/m3) | 47.54 (1.00) | 104.96 (2.21) | 59.33 (1.25) | 88.30 (1.86) | 83.86 (1.76) |
| —energy absorption efficiency for 10% strain, (%) | 55.25 (1.00) | 74.53 (1.35) | 53.20 (0.96) | 56.34 (1.02) | 67.45 (1.22) |
| —energy absorption for 20% strain, (kJ/m3) | 164.51 (1.00) | 247.58 (1.50) | 204.53 (1.24) | 273.90 (1.66) | 232.05 (1.41) |
| —energy absorption efficiency for 20% strain, (%) | 56.10 (1.00) | 86.75 (1.55) | 62.65 (1.12) | 72.73 (1.30) | 67.68 (1.21) |
| —energy absorption for 30% strain, (kJ/m3) | 340.00 (1.00) | 696.91 (2.05) | 382.35 (1.12) | 474.35 (1.40) | 426.75 (1.26) |
| —energy absorption efficiency for 30% strain, (%) | 55.23 (1.00) | 87.34 (1.58) | 64.06 (1.16) | 71.46 (1.29) | 64.68 (1.17) |
| —energy absorption for 40% strain, (kJ/m3) | 580.58 (1.00) | 557.87 (0.96) | 610.07 (1.05) | 720.90 (1.24) | 675.64 (1.16) |
| —energy absorption efficiency for 40% strain, (%) | 51.54 (1.00) | 81.14 (1.57) | 59.12 (1.15) | 65.08 (1.26) | 59.81 (1.16) |
| —maximum energy absorption efficiency, (%) | 56.11 (1.00) | 87.49 (1.56) | 65.97 (1.18) | 75.01 (1.34) | 68.46 * (1.22) 84.89 (1.51) |
| Strain for the maximum energy absorption efficiency, (%) | 18.36 (1.00) | 29.89 (1.63) | 25.23 (1.37) | 24.02 (1.31) | 13.26 * (0.72) 57.21 (3.12) |
| Measure | X_P_02 | X_Z_02 | X_ZP_02 | X_ZPS_02 |
|---|---|---|---|---|
| —compressive strength (first maximum), (MPa) | --- | 1.81 | --- | 1.36 |
| —compressive strength (no first maximum), (MPa) | --- | --- | 1.78 | --- |
| Strain for the compressive strength, (%) | --- | 4.22 | 12.45 | 7.51 |
| Measure | X_P_02 | X_Z_02 | X_ZP_02 | X_ZPS_02 |
|---|---|---|---|---|
| —energy absorption for 10% strain, (kJ/m3) | 55.88 (1.00) | 154.68 (2.77) | 72.63 (1.30) | 95.61 (1.71) |
| —energy absorption efficiency for 10% strain, (%) | 53.92 (1.00) | 88.99 (1.65) | 51.61 (0.96) | 77.77 (1.44) |
| —energy absorption for 20% strain, (kJ/m3) | 199.39 (1.00) | 344.98 (1.73) | 256.28 (1.29) | 233.56 (1.17) |
| —energy absorption efficiency for 20% strain, (%) | 54.74 (1.00) | 84.60 (1.55) | 59.10 (1.08) | 74.94 (1.37) |
| —energy absorption for 30% strain, (kJ/m3) | 420.02 (1.00) | 558.25 (1.33) | 491.86 (1.17) | 414.63 (0.99) |
| —energy absorption efficiency for 30% strain, (%) | 53.80 (1.00) | 82.79 (1.54) | 63.68 (1.18) | 64.88 (1.21) |
| —energy absorption for 40% strain, (kJ/m3) | 726.63 (1.00) | 793.89 (1.09) | 782.13 (1.08) | 668.77 (0.92) |
| —energy absorption efficiency for 40% strain, (%) | 50.48 (1.00) | 81.06 (1.61) | 58.25 (1.15) | 55.51 (1.10) |
| —maximum energy absorption efficiency, (%) | 54.77 (1.00) | 90.10 (1.65) | 63.72 (1.16) | 81.55 * (1.49) 75.98 (1.39) |
| Strain for the maximum energy absorption efficiency, (%) | 17.95 (1.00) | 8.30 (0.46) | 31.29 (1.74) | 11.63 * (0.65) 20.41 (1.14) |
| Measure | X_P_03 | X_Z_03 | X_ZP_03 | X_ZPS_03 | X_ZPS_05_V |
|---|---|---|---|---|---|
| maximum stress after which the initial unloading started, (MPa) | 0.91 | 2.21 | 1.26 | 1.49 | 1.50 |
| —potential elastic strain energy share quotient after 10 loops, (%) | 75.1 | 27.2 | 64.4 | 64.0 | 56.1 |
| —dissipated energy share quotient after 10 loops, (%) | 24.8 | 72.7 | 35.5 | 35.9 | 43.8 |
| —quotient of accumulated normalized dissipated energy after 10 loops, (%) | 584.4 | 101.6 | 517.2 | 387.0 | 212.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stręk, A.M.; Lasowicz, N.; Kwiecień, A.; Zając, B.; Jankowski, R. Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding. Materials 2021, 14, 3231. https://doi.org/10.3390/ma14123231
Stręk AM, Lasowicz N, Kwiecień A, Zając B, Jankowski R. Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding. Materials. 2021; 14(12):3231. https://doi.org/10.3390/ma14123231
Chicago/Turabian StyleStręk, Anna M., Natalia Lasowicz, Arkadiusz Kwiecień, Bogusław Zając, and Robert Jankowski. 2021. "Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding" Materials 14, no. 12: 3231. https://doi.org/10.3390/ma14123231
APA StyleStręk, A. M., Lasowicz, N., Kwiecień, A., Zając, B., & Jankowski, R. (2021). Highly Dissipative Materials for Damage Protection against Earthquake-Induced Structural Pounding. Materials, 14(12), 3231. https://doi.org/10.3390/ma14123231







