Design of Circular Composite Cylinders for Optimal Natural Frequencies
Abstract
:1. Introduction
2. Materials and Methods
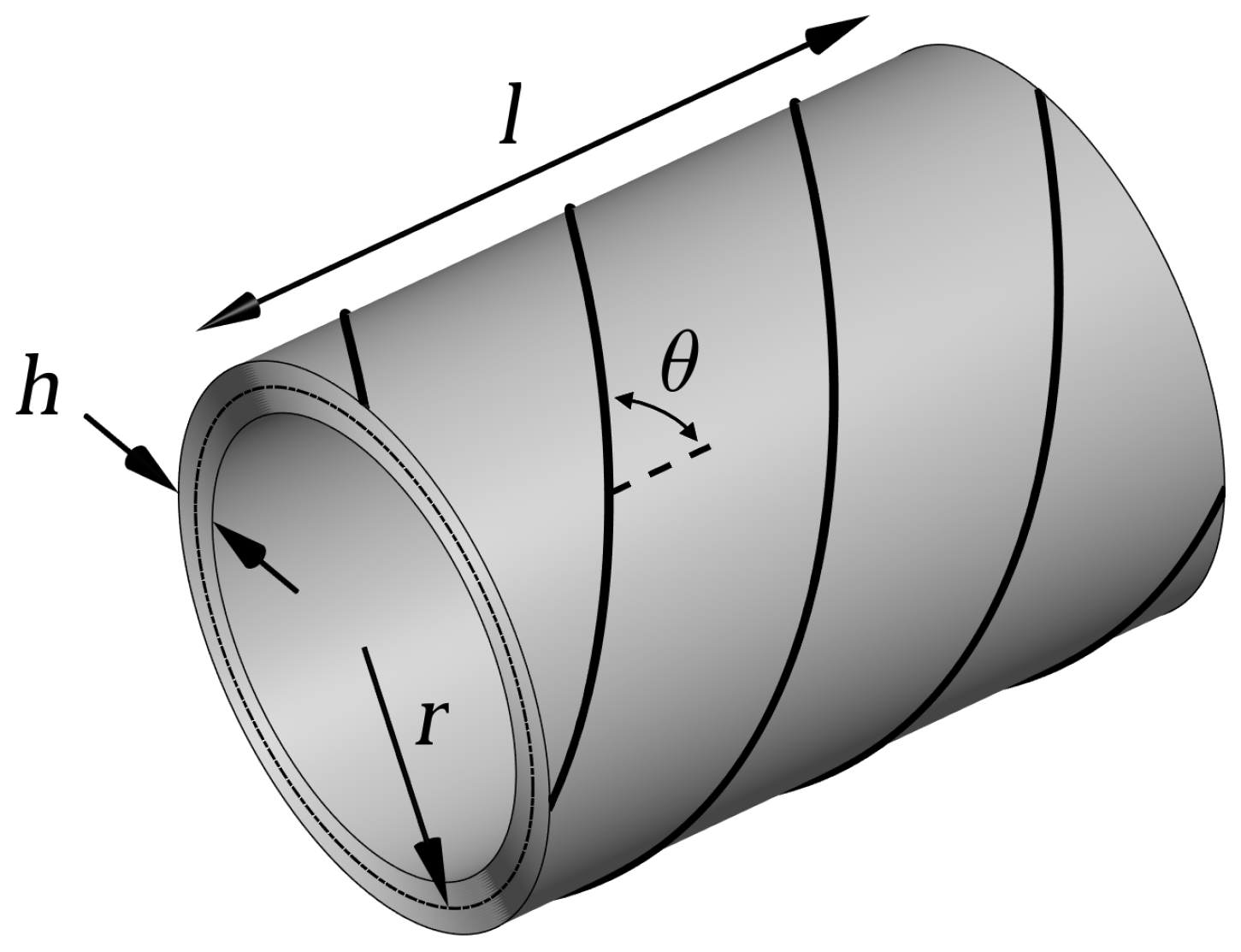
2.1. Laminated Cylindrical Shell
2.2. Stiffness Properties
2.3. Finite Element Analysis
2.4. Optimization
3. Results and Discussion
3.1. Mesh Convergence and Validation
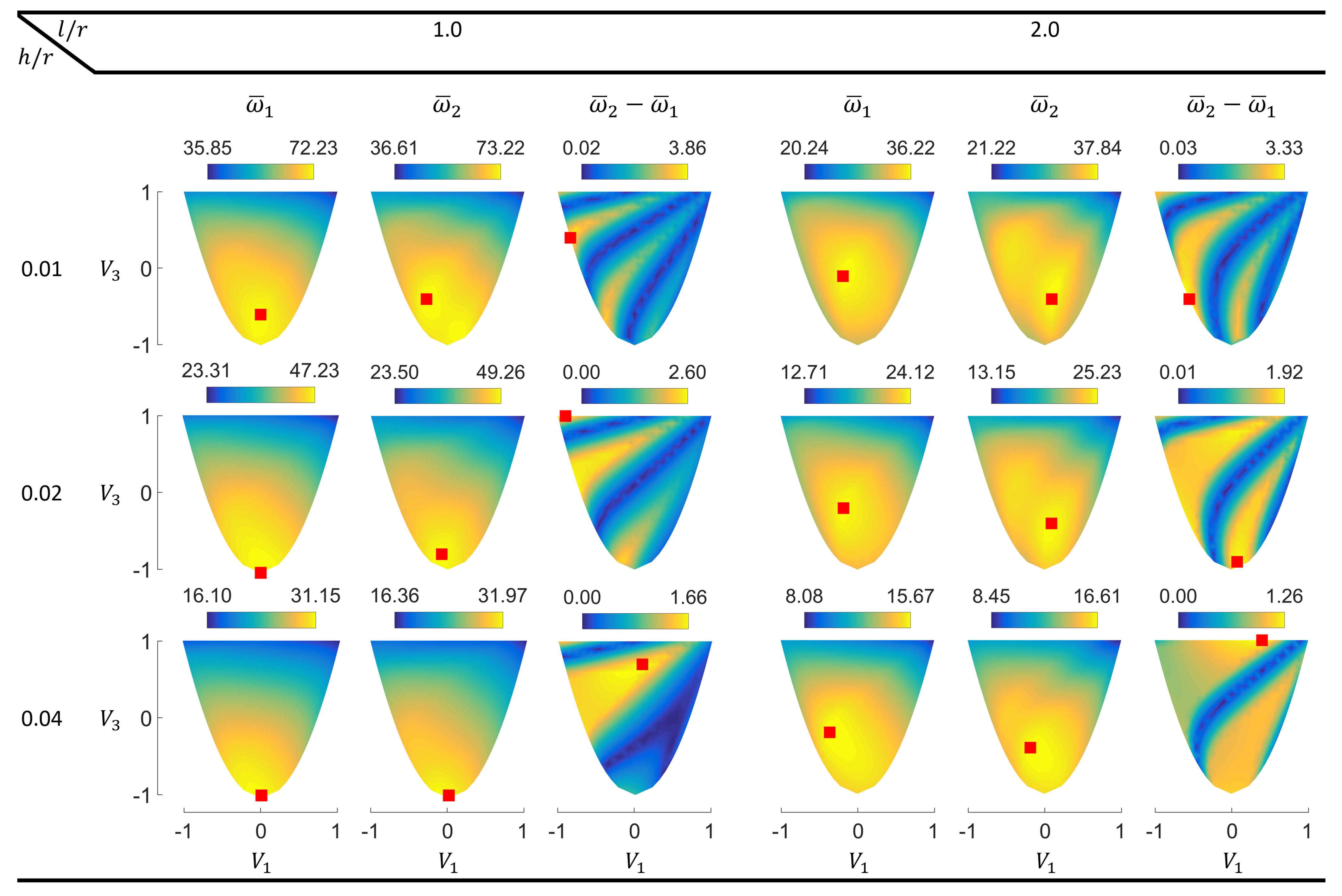
3.2. Eigenfrequency Optimization for Simply Supported Cylinders
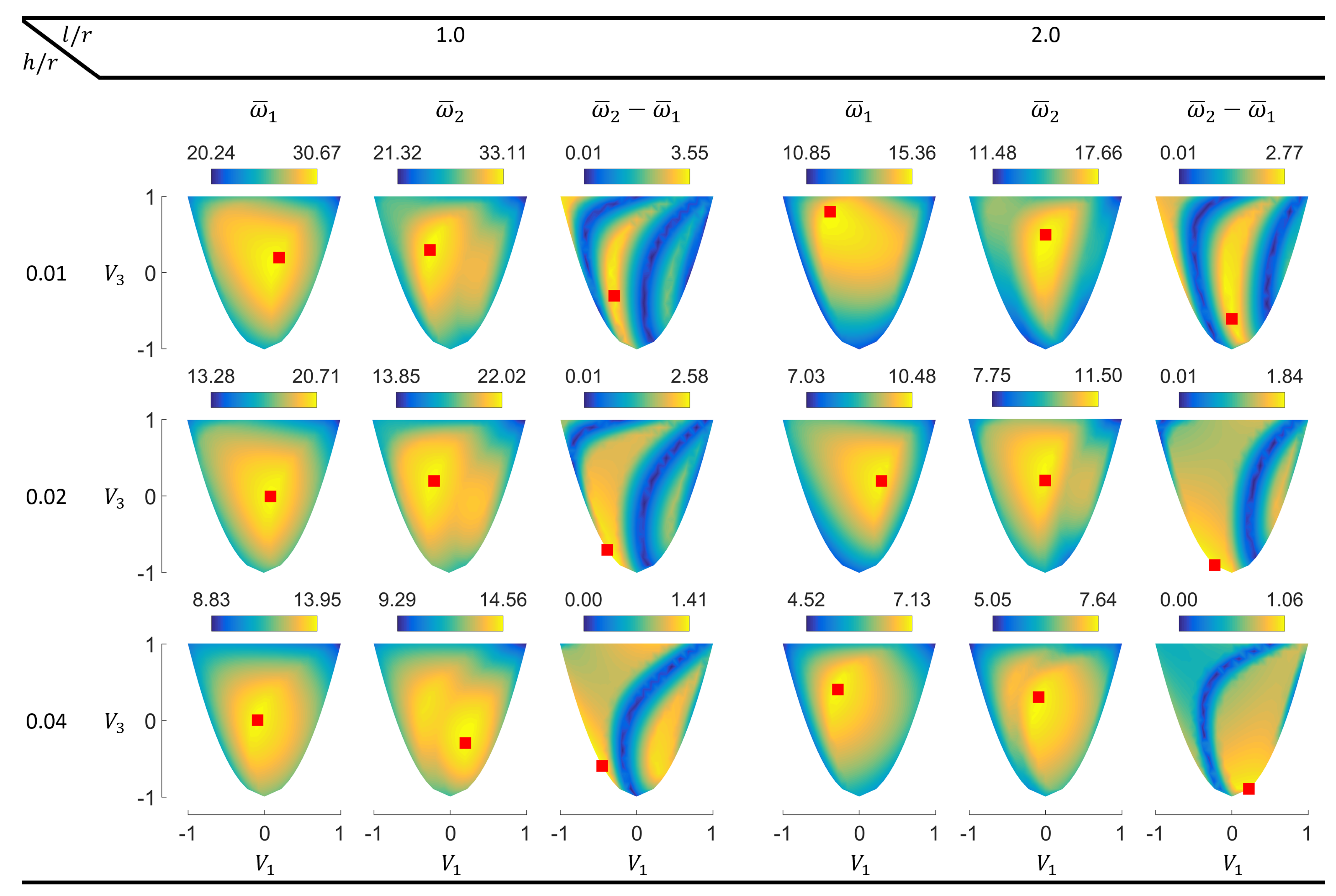
3.3. Eigenfrequency Optimization for Cantilever Cylinders
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nshanian, Y.S.; Pappas, M. Optimal laminated composite shells for buckling and vibration. AIAA J. 1983, 21, 430–437. [Google Scholar] [CrossRef]
- Lam, K.Y.; Loy, C.T. Influence of boundary conditions and fibre orientation on the natural frequencies of thin orthotropic laminated cylindrical shells. Compos. Struct. 1995, 31, 2l–30. [Google Scholar] [CrossRef]
- Shakeri, M.; Yas, M.H.; Gol, M.G. Optimal stacking sequence of laminated cylindrical shells using genetic algorithm. Mech. Adv. Mater. Struct. 2005, 12, 305–312. [Google Scholar] [CrossRef]
- Koide, R.M.; Luersen, M.A. Maximization of fundamental frequency of laminated composite cylindrical shells by ant colony algorithm. J. Aerosp. Technol. Manag. 2013, 5, 75–82. [Google Scholar] [CrossRef] [Green Version]
- Miller, B.; Ziemiański, L. Optimization of dynamic behavior of thin-walled laminated cylindrical shells by genetic algorithms and deep neural networks supported by modal shape identification. Adv. Eng. Softw. 2020, 147, 102830. [Google Scholar] [CrossRef]
- Topal, U. Multiobjective optimization of laminated composite cylindrical shells for maximum frequency and buckling load. Mater. Des. 2009, 30, 2584–2594. [Google Scholar] [CrossRef]
- Miller, B.; Ziemiański, L. Optimization of dynamic and buckling behavior of thin-walled composite cylinder, supported by nature-inspired algorithms. Materials 2020, 13, 5414. [Google Scholar] [CrossRef] [PubMed]
- Adali, S.; Verijenko, V.E. Optimum stacking sequence design of symmetric hybrid laminates undergoing free vibrations. Compos. Struct. 2001, 54, 131–138. [Google Scholar] [CrossRef]
- Farshi, B.; Rabiei, R. Optimum design of composite laminates for frequency constraints. Compos. Struct. 2007, 81, 587–597. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Effect of aspect ratio and boundary conditions on the eigenfrequency optimization of composite panels using lamination parameters. In Proceedings of the 11th ASMO-UK/ISSMO/NOED2016 International Conference on Numerical Optimisation Methods for Engineering Design, Munich, Germany, 18–20 July 2016. [Google Scholar]
- Miller, B.; Ziemiański, L. Maximization of eigenfrequency gaps in composite cylindrical shell using genetic algorithms and neural networks. Appl. Sci. 2019, 9, 2754. [Google Scholar] [CrossRef] [Green Version]
- Albazzan, M.A.; Harik, R.; Tatting, B.F.; Gürdal, Z. Efficient design optimization of nonconventional laminated composites using lamination parameters: A state of the art. Compos. Struct. 2019, 209, 362–374. [Google Scholar] [CrossRef]
- Grenestedt, J.L. Layup optimization and sensitivity analysis of the fundamental eigenfrequency of composite plates. Compos. Struct. 1989, 12, 193–209. [Google Scholar] [CrossRef]
- Serhat, G.; Faria, T.G.; Basdogan, I. Multi-objective optimization of stiffened, fiber-reinforced composite fuselages for mechanical and vibro-acoustic requirements. In Proceedings of the 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Serhat, G.; Basdogan, I. Multi-objective optimization of composite plates using lamination parameters. Mater. Design 2019, 180, 107904. [Google Scholar] [CrossRef]
- Fukunaga, H.; Sekine, H.; Sato, M. Optimal design of symmetric laminated plates for fundamental frequency. J. Sound Vibrat. 1994, 171, 219–229. [Google Scholar] [CrossRef]
- Abdalla, M.M.; Setoodeh, S.; Gürdal, Z. Design of variable stiffness composite panels for maximum fundamental frequency using lamination parameters. Comput. Struct. 2007, 81, 283–291. [Google Scholar] [CrossRef]
- Serhat, G.; Bediz, B.; Basdogan, I. Unifying lamination parameters with spectral-Tchebychev method for variable-stiffness composite plate design. Compos. Struct. 2020, 242C, 112183. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Design of curved composite panels for optimal dynamic response using lamination parameters. Compos. Part B Eng. 2018, 147, 135–146. [Google Scholar] [CrossRef]
- Serhat, G.; Anamagh, M.R.; Bediz, B.; Basdogan, I. Dynamic analysis of doubly curved composite panels using lamination parameters and spectral-Tchebychev method. Comput. Struct. 2020, 239, 106294. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Lamination parameter interpolation method for design of manufacturable variable-stiffness composite panels. AIAA J. 2019, 57, 3052–3065. [Google Scholar] [CrossRef]
- Trias, D.; Maimí, P.; Blanco, N. Maximization of the fundamental frequency of plates and cylinders. Compos. Struct. 2016, 156, 375–384. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Comparison of vibro–acoustic performance metrics in the design and optimization of stiffened composite fuselages. In Proceedings of the 45th International Congress and Exposition on Noise Control Engineering (INTER–NOISE 2016), Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials, 1st ed.; Technomic: Lancaster, UK, 1980; pp. 123–131. [Google Scholar]
- Fukunaga, H.; Vanderplaats, G.N. Stiffness optimization of orthotropic laminated composites using lamination parameters. AIAA J. 1991, 29, 641–646. [Google Scholar] [CrossRef]
- Grenestedt, J.L. Optimization of bent composite cylinders. Compos. Struct. 1995, 30, 103–108. [Google Scholar] [CrossRef]
- Gürdal, Z.; Haftka, R.T.; Hajela, P. Design and Optimization of Laminated Composite Materials, 1st ed.; John Wiley & Sons: New York, NY, USA, 1999; p. 140. [Google Scholar]
- Diaconu, C.G.; Sato, M.; Sekine, H. Layup optimization of symmetrically laminated thick plates for fundamental frequencies using lamination parameters. Struct. Multidisc. Optim. 2002, 24, 302–311. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; p. 135. [Google Scholar]
- Hu, H.-T.; Tzeng, W.-L. Buckling analysis of skew laminate plates subjected to uniaxial inplane loads. Thin Walled Struct. 2000, 38, 53–77. [Google Scholar] [CrossRef]
- Liu, G.R.; Quek, S.S. The Finite Element Method: A Practical Course, 1st ed.; Butterworth-Heinemann: London, UK, 2003; pp. 180–184. [Google Scholar]
- Dutra, T.A.; de Almeida, S.F.M. Composite plate stiffness multicriteria optimization using lamination parameters. Compos. Struct. 2015, 133, 166–177. [Google Scholar] [CrossRef]
- Fedon, N.; Weaver, P.M.; Pirrera, A.; Macquart, T. A method using beam search to design the lay-ups of composite laminates with many plies. Compos. Part C 2021, 4, 100072. [Google Scholar]
- Ntourmas, G.; Glock, F.; Daoud, F.; Schuhmacher, G.; Chronopoulos, D.; Özcan, E. Mixed Integer Linear Programming formulations of the stacking sequence and blending optimisation of composite structures. Compos. Struct. 2021, 264, 113660. [Google Scholar] [CrossRef]
- Serhat, G. Concurrent lamination and tapering optimization of cantilever composite plates under shear. Materials 2021, 14, 2285. [Google Scholar] [CrossRef] [PubMed]
- Langley, R.S. A dynamic stiffness technique for the vibration analysis of stiffened shell structures. J. Sound Vibrat. 1992, 156, 521–540. [Google Scholar] [CrossRef]
- Murphy, A.; Price, M.; Lynch, C.; Gibson, A. The computational post-buckling analysis of fuselage stiffened panels loaded in shear. Thin-Walled Struct. 2005, 43, 1455–1474. [Google Scholar] [CrossRef] [Green Version]
- Autio, M. Determining the real lay-up of a laminate corresponding to optimal lamination parameters by genetic search. Struct. Multidisc. Optim. 2000, 20, 301–310. [Google Scholar] [CrossRef]
- Grenestedt, J.L. Composite plate optimization only requires one parameter. Struct. Optim. 1990, 2, 29–37. [Google Scholar] [CrossRef]
- Kameyama, M.; Fukunaga, H. Optimum design of composite plate wings for aeroelastic characteristics using lamination parameter. Comput. Struct. 2007, 85, 213–224. [Google Scholar] [CrossRef]
- Pellicano, F.; Barbieri, M. Complex dynamics of circular cylindrical shells. Int. J. Nonlinear Mech. 2014, 65, 196–212. [Google Scholar] [CrossRef] [Green Version]
- Foldager, J.; Hansen, J.S.; Olhoff, N. A general approach forcing convexity of ply angle optimization in composite laminates. Struct. Optim. 1998, 16, 201–211. [Google Scholar] [CrossRef]
- Herencia, J.E.; Haftka, R.T.; Weaver, P.M.; Friswell, M.I. Lay-Up optimization of composite stiffened panels using linear approximations in lamination space. AIAA J. 2008, 46, 2387–2391. [Google Scholar] [CrossRef]
- Demir, E.; Yousefi-Louyeh, P.; Yildiz, M. Design of variable stiffness composite structures using lamination parameters with fiber steering constraint. Compos. Part B Eng. 2019, 165, 733–746. [Google Scholar] [CrossRef]
- Alzahabi, B. Non-uniqueness in cylindrical shells optimization. Adv. Eng. Softw. 2005, 36, 584–590. [Google Scholar] [CrossRef]
- Lopatin, A.V.; Morozov, E.V. Fundamental frequency of a cantilever composite cylindrical shell. Compos. Struct. 2015, 119, 638–647. [Google Scholar] [CrossRef]
- Hosokawa, K.; Murayama, M.; Sakata, T. Free vibration analysis of angle-ply laminated circular cylindrical shells with clamped edges. Sci. Eng. Compos. Mater. 2000, 9, 75–82. [Google Scholar] [CrossRef]
| 128 GPa | |
| 11 GPa | |
| 4.48 GPa | |
| 1.53 GPa | |
| 0.25 | |
| 1500 kg/m |
| (,) | Number of Elements | ||||
|---|---|---|---|---|---|
| 168 | 252 | 396 | 572 | 832 | |
| (1.0, 1.0) | 1883.4 | 1850.9, 1.73% | 1820.5, 1.64% | 1805.1, 0.85% | 1795.7, 0.52% |
| (0.0, −1.0) | 3749.4 | 3632.2, 3.13% | 3539.5, 2.55% | 3489.8, 1.40% | 3455.2, 0.99% |
| (−1.0, 1.0) | 2120.0 | 2097.9, 1.04% | 2079.6, 0.87% | 2070.1, 0.46% | 2063.9, 0.30% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serhat, G. Design of Circular Composite Cylinders for Optimal Natural Frequencies. Materials 2021, 14, 3203. https://doi.org/10.3390/ma14123203
Serhat G. Design of Circular Composite Cylinders for Optimal Natural Frequencies. Materials. 2021; 14(12):3203. https://doi.org/10.3390/ma14123203
Chicago/Turabian StyleSerhat, Gokhan. 2021. "Design of Circular Composite Cylinders for Optimal Natural Frequencies" Materials 14, no. 12: 3203. https://doi.org/10.3390/ma14123203
APA StyleSerhat, G. (2021). Design of Circular Composite Cylinders for Optimal Natural Frequencies. Materials, 14(12), 3203. https://doi.org/10.3390/ma14123203






