A Numerical Study on Structural Performance of Railway Sleepers Using Ultra High-Performance Concrete (UHPC)
Abstract
1. Introduction
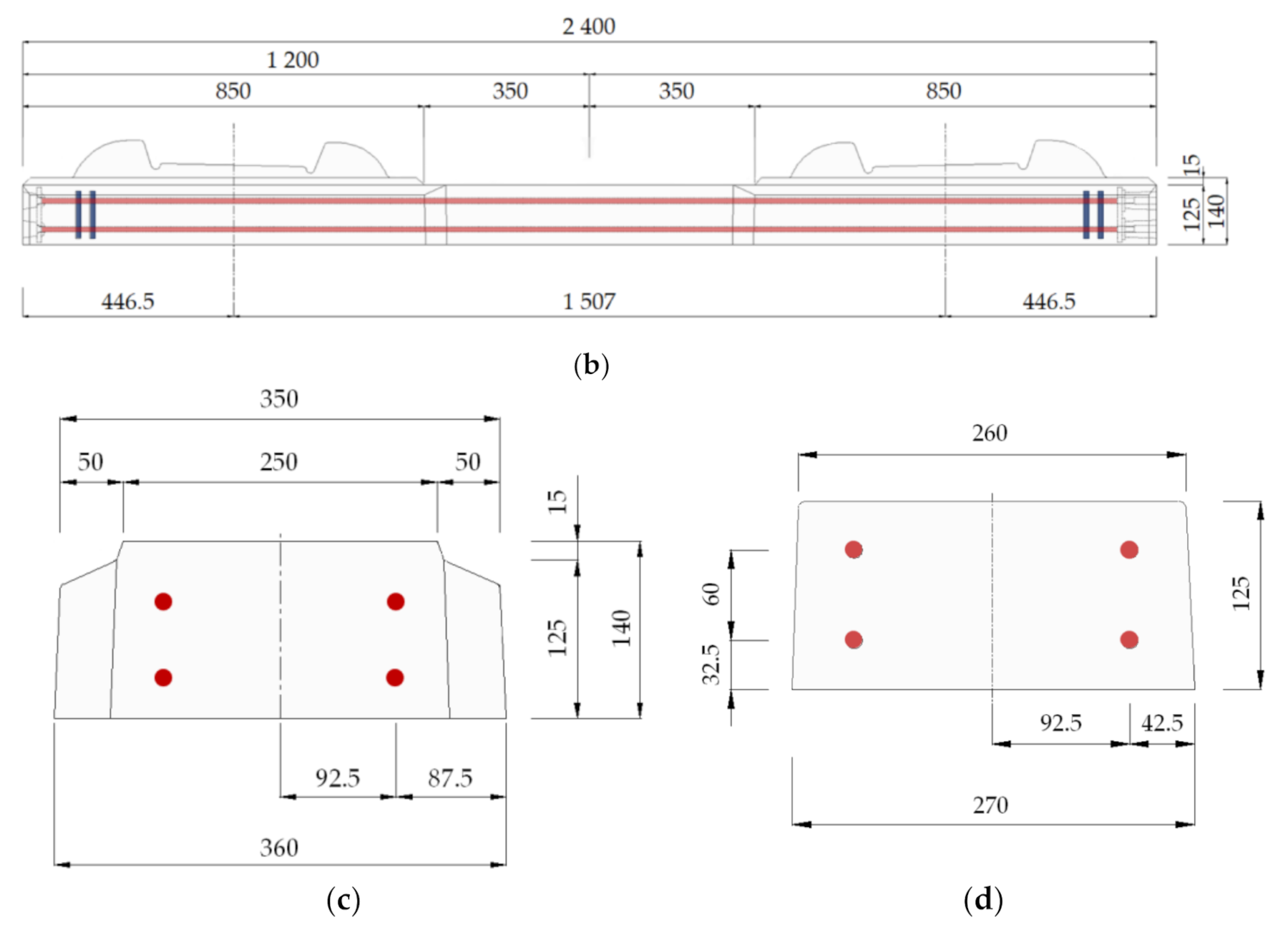
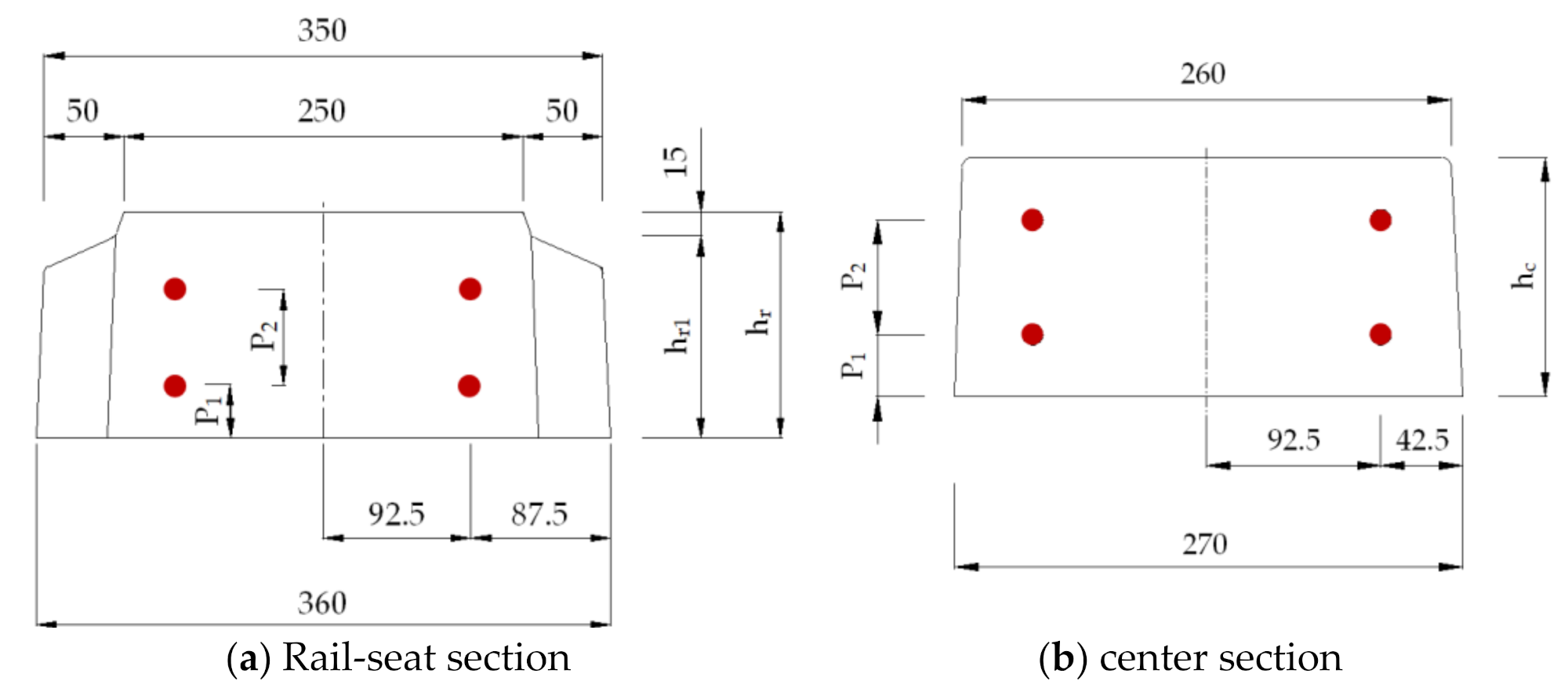
2. Mix Design and Fabrication of UHPC Sleeper
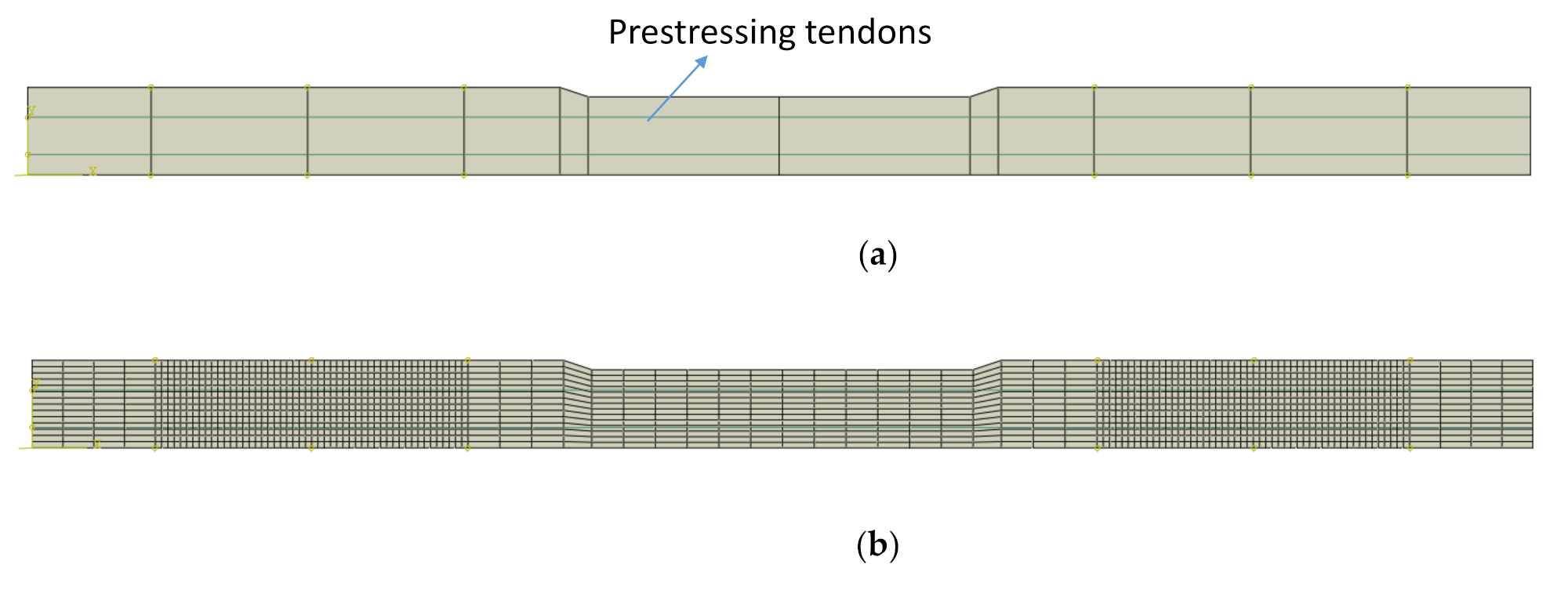
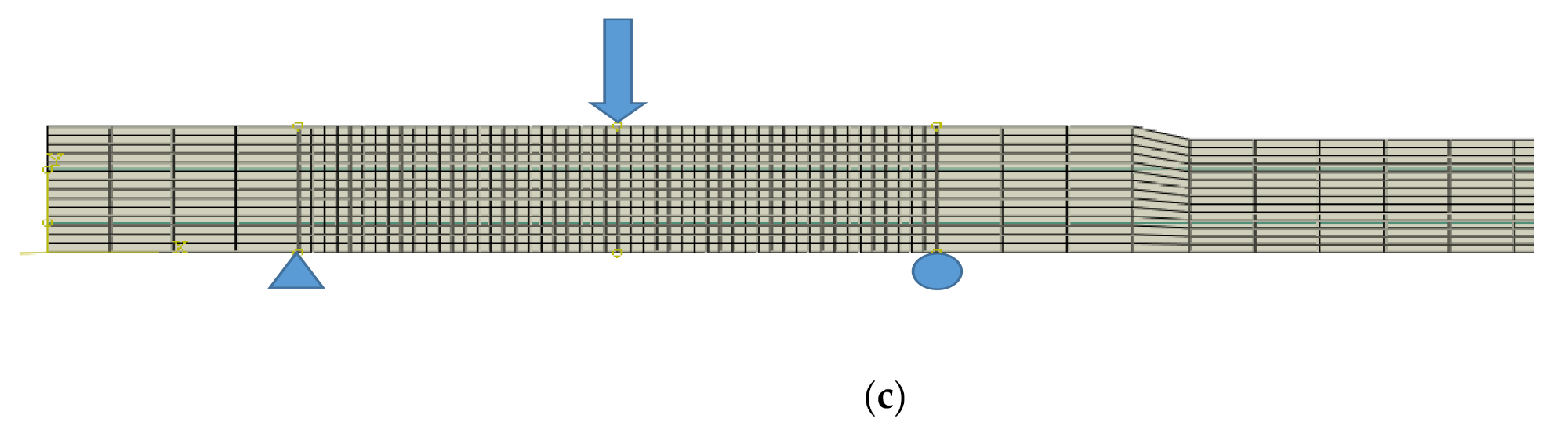
3. Finite Element Modeling
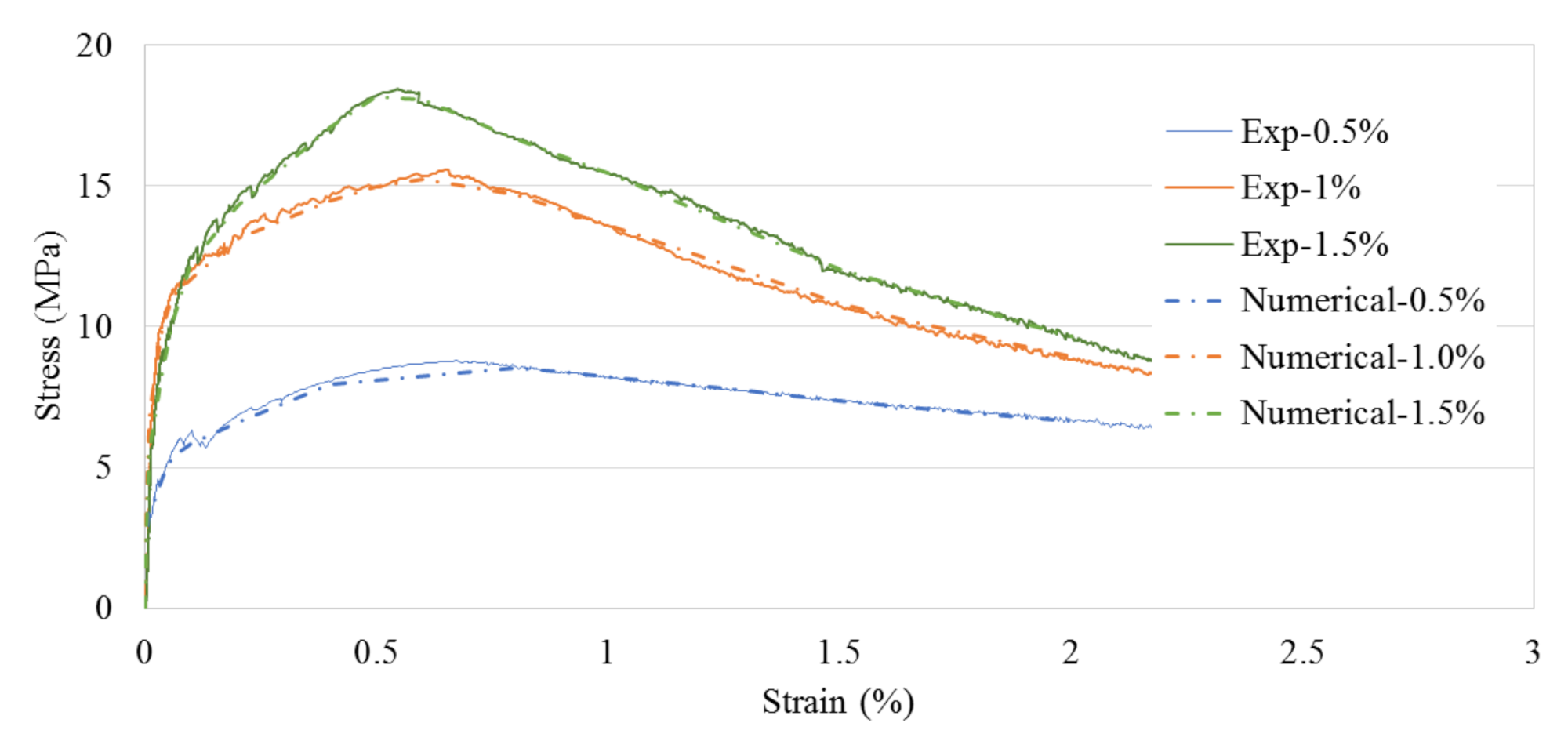
4. Comparisons with Experimental Data
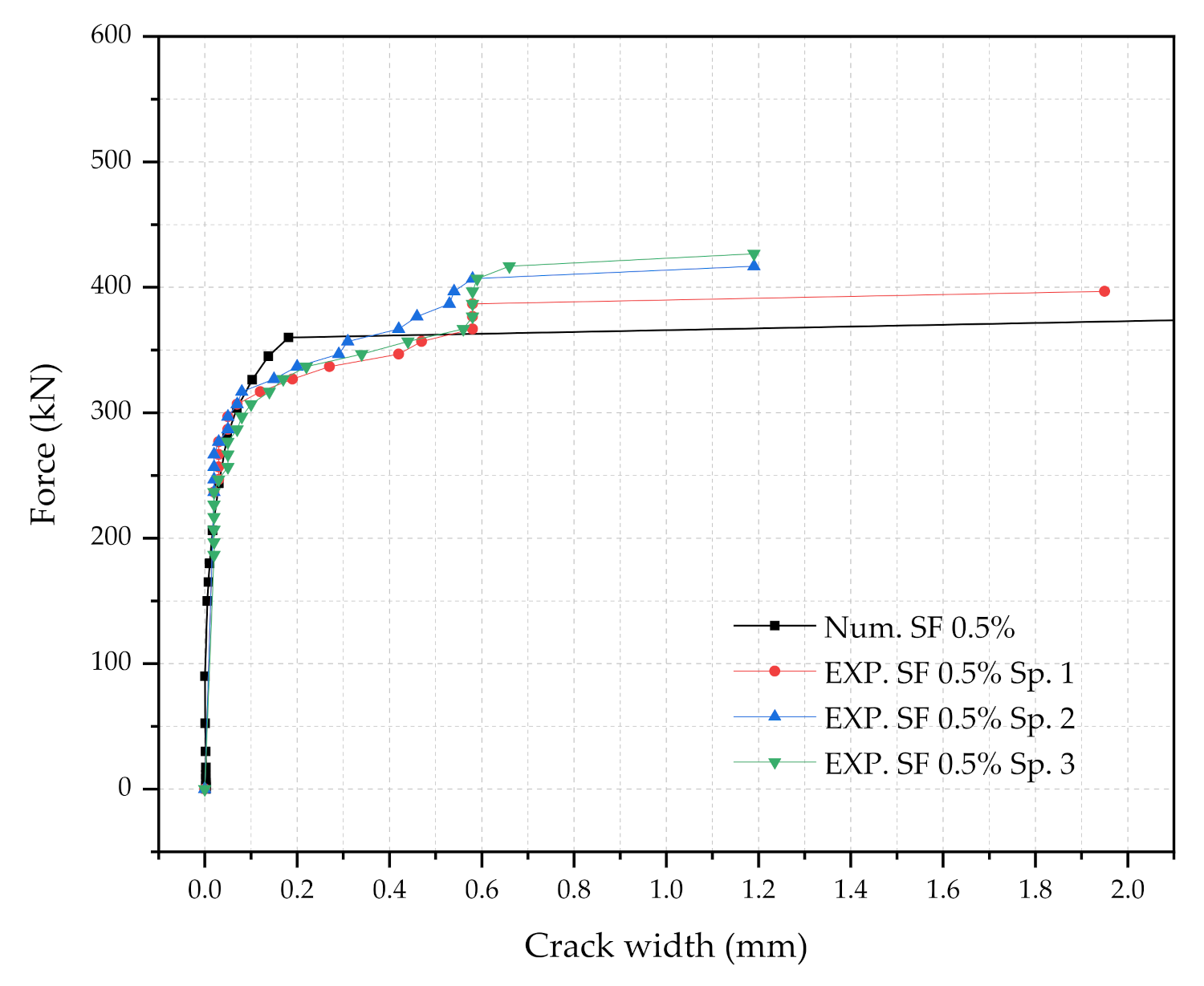
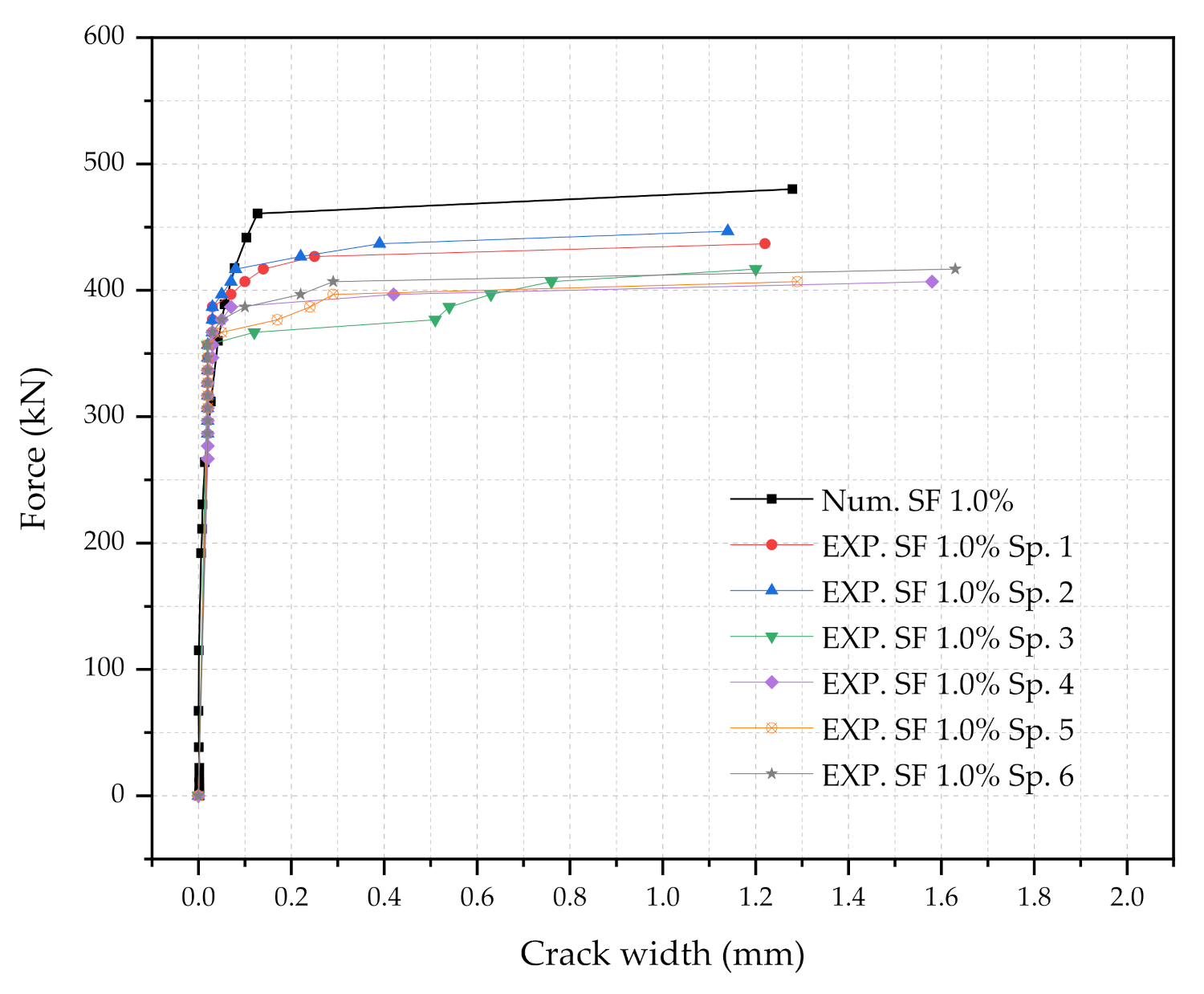
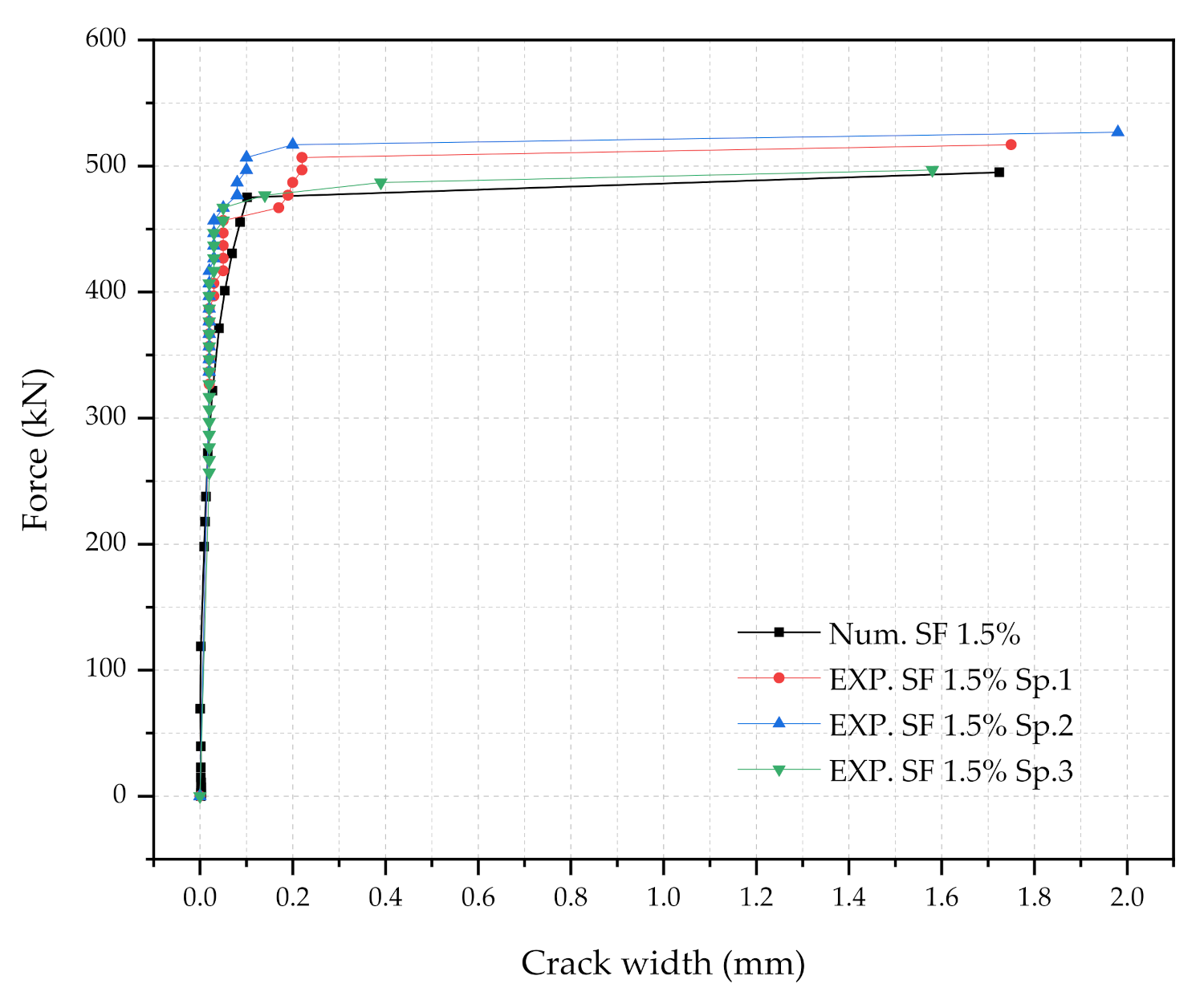
4.1. Summary of the Testing at the Rail-Seat Section
4.2. Validation of the Numerical Sleeper Models
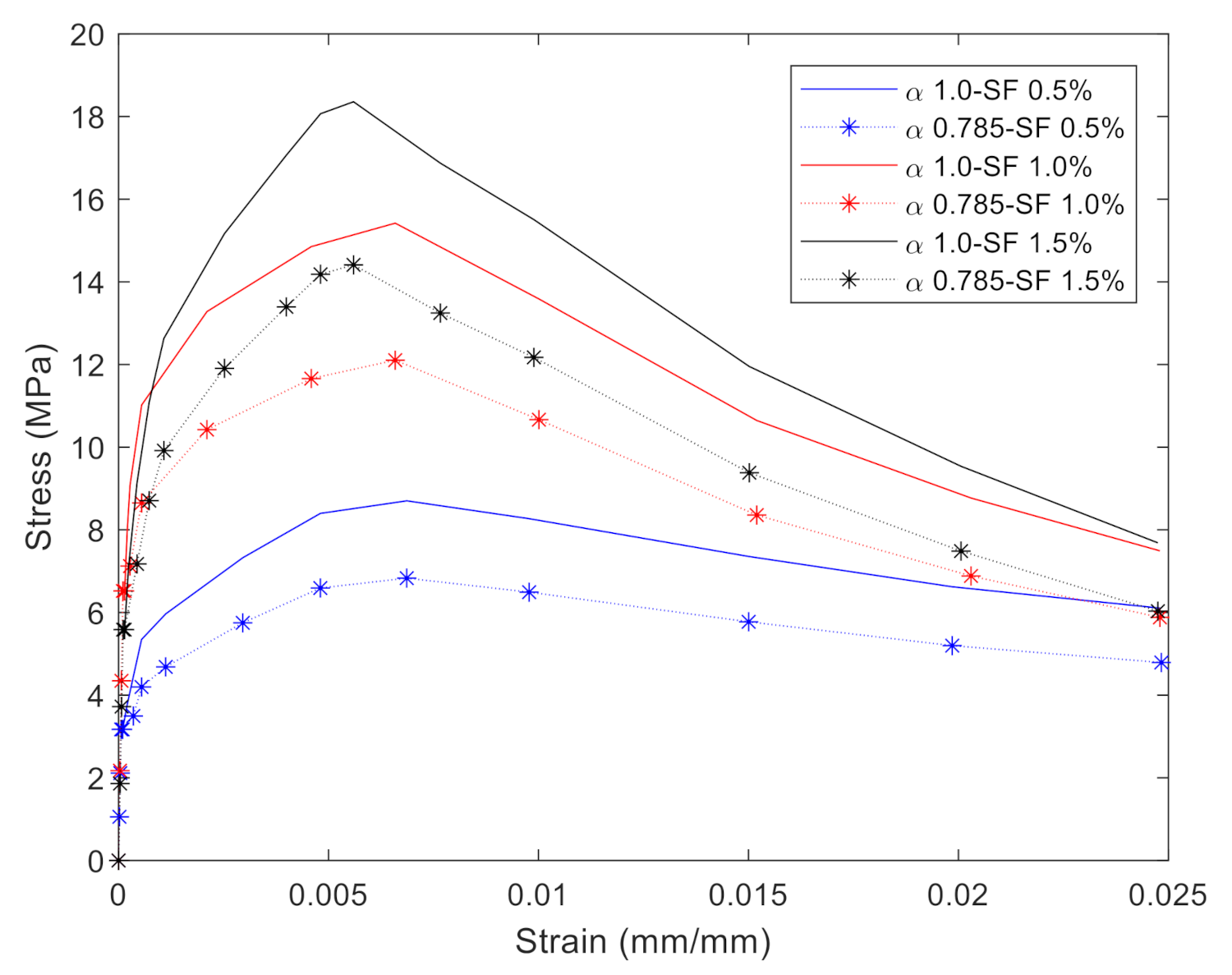
4.2.1. Fiber Orientation Reduction Factor
4.2.2. Validation of the Numerical Models
5. Parametric Study
5.1. Design of Input Parameters
5.2. Analysis Results
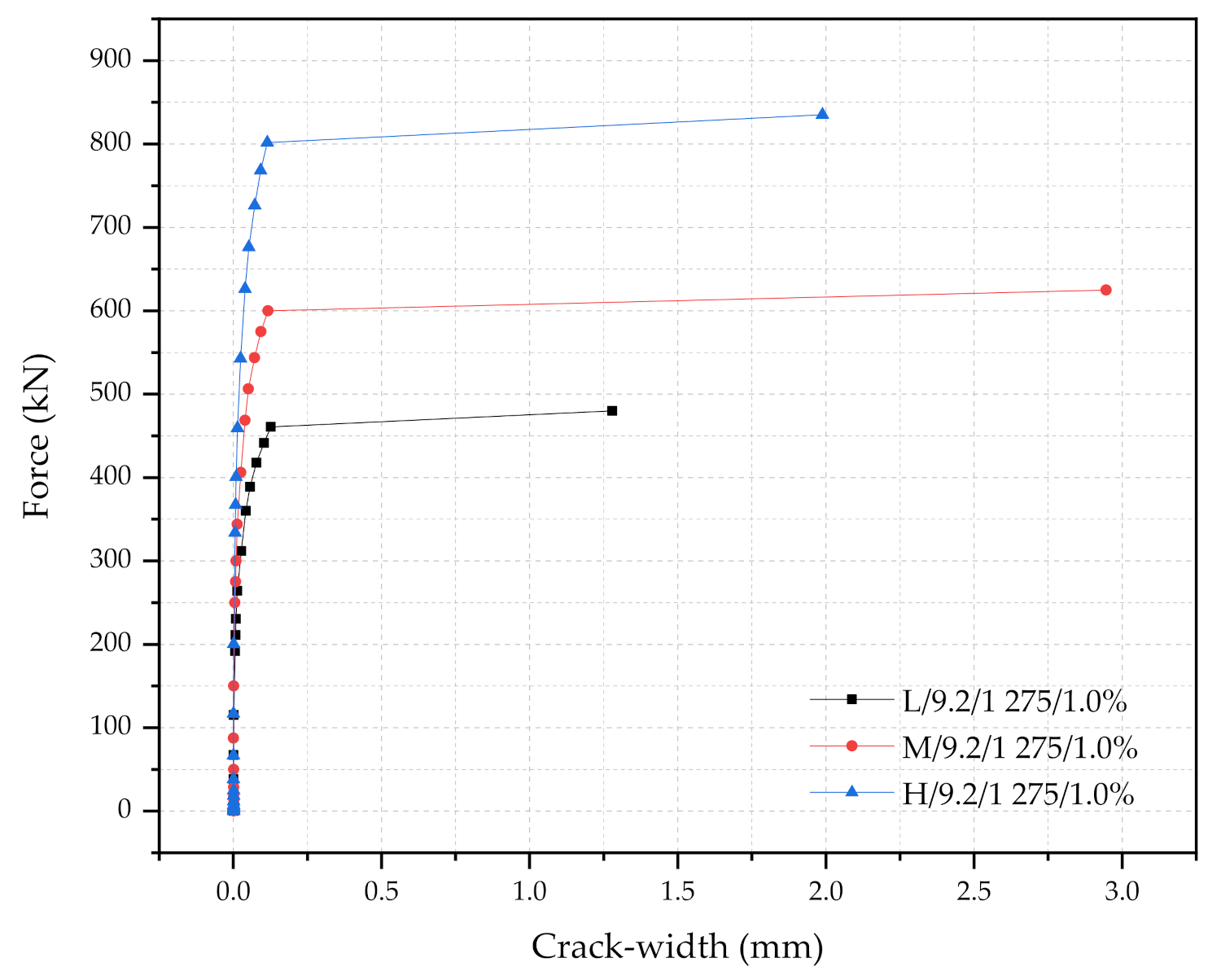
5.2.1. Cross-Sectional Dimensions: L, M and H
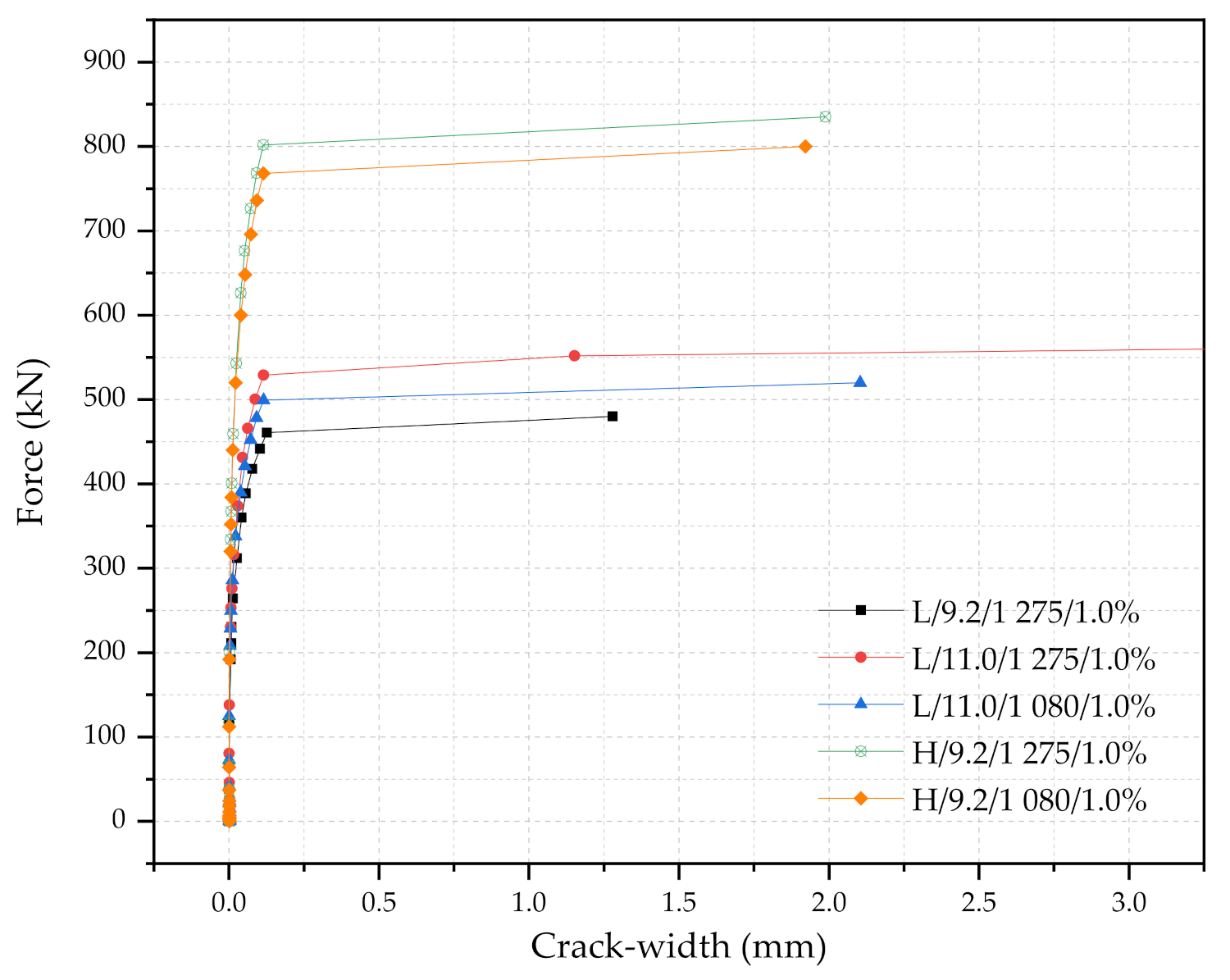
5.2.2. The Diameter and the Yielding Strength of PS Tendons
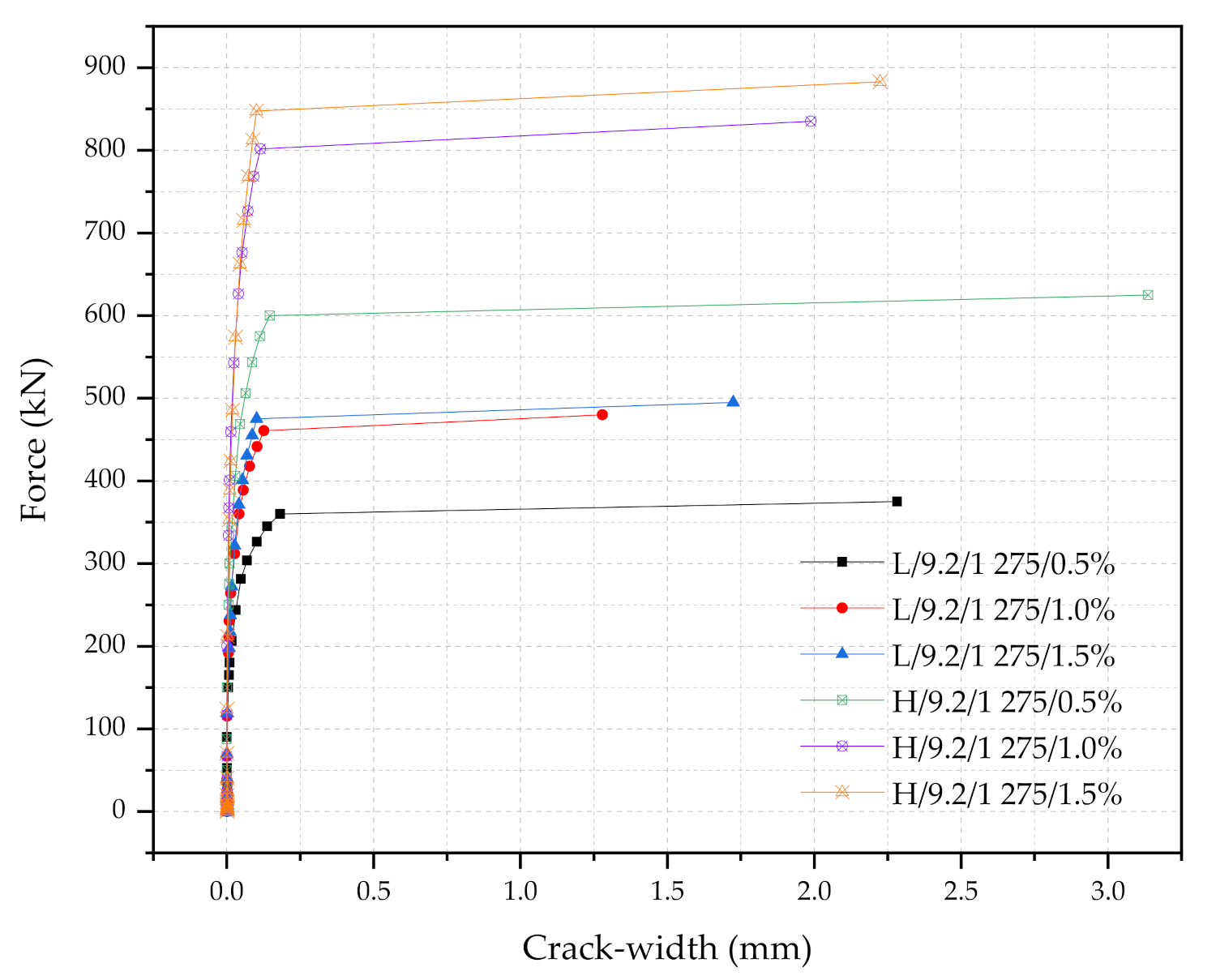
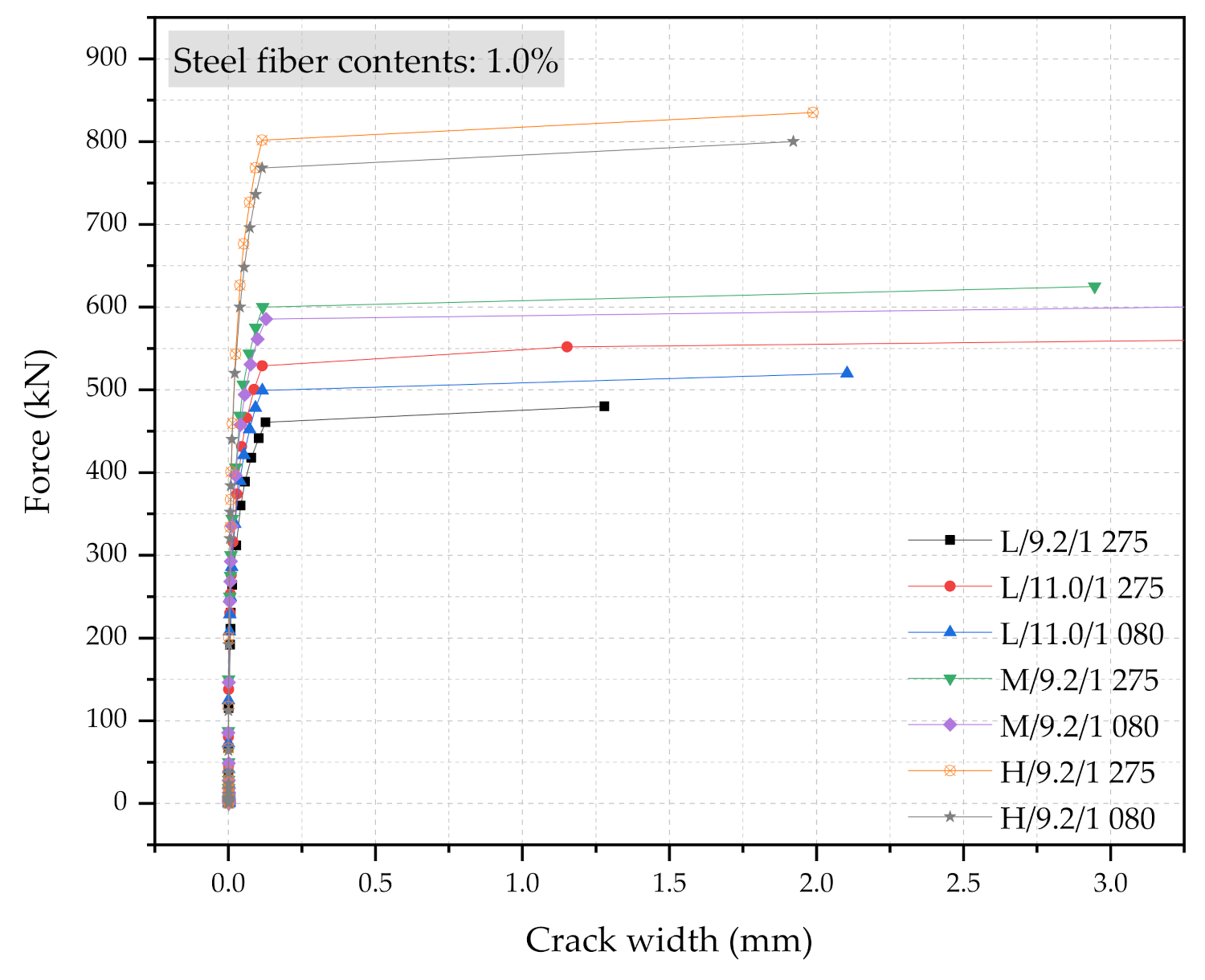
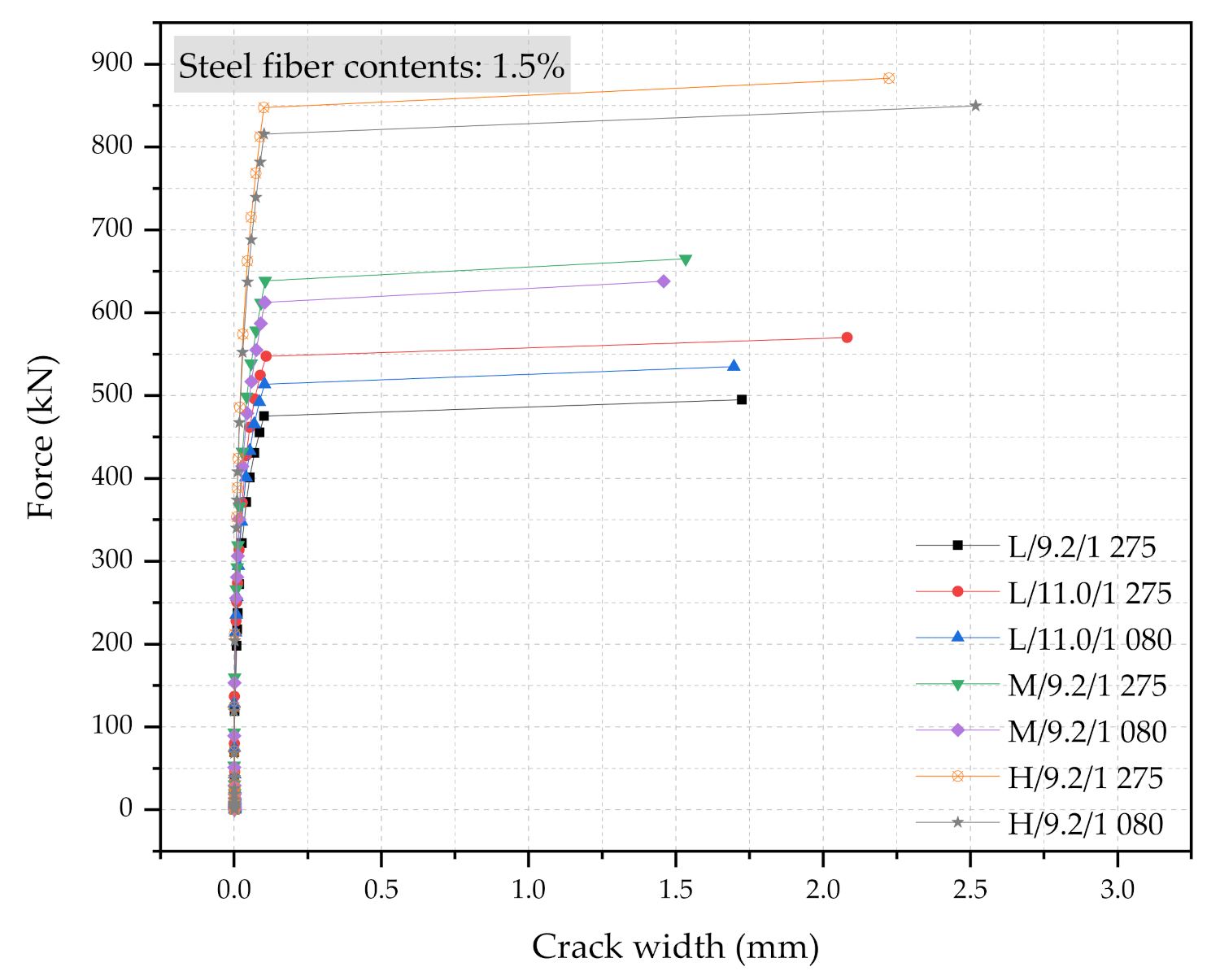
5.2.3. Steel Fiber Contents
6. Discussion
7. Conclusions
- The developed numerical 2D-UHPC sleeper model was capable of representing the force and crack-width relationships. Three UHPC direct tension tests with the 0.5%, 1.0%, and 1.5% steel fiber contents were used for the UHPC tensile constitutive models.
- The fiber orientation factor, , of 0.785 is used to represent the realistic stress-strain behavior of the UHPC in 3D as opposed to the thin coupon test where the fibers are well aligned in a 2D manner.
- The numerical analysis results indicate that the bigger the cross-section is, the higher the load capacities and the safety factor become. However, using a too large cross-section can result in uneconomical design sleepers. The economical design factor, 100FrB/Area is computed to evaluate the economical factor of the UHPC sleeper. When 100FrB/Area is close to 1.0, the UHPC sleeper is economical.
- There are growing interests in using a larger diameter tendon and/or a higher strength tendon. This study recommends using a larger diameter tendon with a lower strength for an economical design.
- A steel fiber content of 0.5% tends to yield to lower strengths UHPC sleepers relative to the 1.0% and 1.5% steel fiber content sleepers.
- Some M-type sleepers with 1.0% steel fiber UHPC show similar performance to H-type sleepers with 0.5% steel fiber UHPC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sadeghi, J.; Kian, A.R.T.; Khabbazi, A.S. Improvement of mechanical properties of railway track concrete sleepers using steel fibers. J. Mater. Civil. Eng. 2016, 28, 04016131. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A. Failures of mainline railway sleepers and suggested remedies–review of current practice. Eng. Fail. Anal. 2014, 44, 17–35. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A. Dynamic properties of railway track and its components: A state-of-the-art review. In New Research on Acoustics; Weiss, B.N., Ed.; Hauppauge, Nova Science: New York, NY, USA, 2008; Volume 28, pp. 197–220. [Google Scholar]
- Pyo, S.; Alkaysi, M.; El-Tawil, S. Crack propagation speed in ultra high performance concrete (UHPC). Constr. Build. Mater. 2016, 114, 109–118. [Google Scholar] [CrossRef]
- Ramezanianpour, A.A.; Esmaeili, M.; Ghahari, S.A.; Najafi, M.H. Laboratory study on the effect of polypropylene fiber on durability, and physical and mechanical characteristic of concrete for application in sleepers. Constr. Build. Mater. 2013, 44, 411–418. [Google Scholar] [CrossRef]
- Shin, H.O.; Yang, J.M.; Yoon, Y.S.; Mitchell, D. Mix design of concrete for prestressed concrete sleepers using blast furnace slag and steel fibers. Cem. Concr. Compos. 2016, 74, 39–53. [Google Scholar] [CrossRef]
- Yang, J.M.; Shin, H.O.; Yoon, Y.S.; Mitchell, D. Benefits of blast furnace slag and steel fibers on the static and fatigue performance of prestressed concrete sleepers. Eng. Struct. 2017, 134, 317–333. [Google Scholar] [CrossRef]
- Bae, Y.; Pyo, S. Effect of steel fiber content on structural and electrical properties of ultra high performance concrete (UHPC) sleepers. Eng. Struct. 2020, 222, 111131. [Google Scholar] [CrossRef]
- EN 13230-2. Railway Applications-Track-Concrete Sleepers and Bearers-Part 2: Prestressed Monoblock Sleepers; European Committee for Standardization (CEN): Brussles, Belgium, 2016. [Google Scholar]
- AS-1085.14. Railway Track Material Part 14: Prestressed Concrete Sleepers; Standard Australia: Sydney, Australia, 2012. [Google Scholar]
- UIC. 713R. Design of Monoblock Concrete Sleepers; UIC Leaflet, International Union of Railways: Paris, France, 2004. [Google Scholar]
- Hashim, D.T.; Hejazi, F.; Lei, V.Y. Simplified Constitutive and Damage Plasticity Models for UHPFRC with Different Types of Fiber. Int. J. Concr. Struct. Mater. 2020, 14, 1–21. [Google Scholar] [CrossRef]
- Pyo, S.; El-Tawil, S.; Naaman, A.E. Direct tensile behavior of ultra high performance fiber reinforced concrete (UHP-FRC) at high strain rates. Cem. Concr. Res. 2016, 88, 144–156. [Google Scholar] [CrossRef]
- Park, S.; Wu, S.; Liu, Z.; Pyo, S. The role of supplementary cementitious materials (SCMs) in ultra high performance concrete (UHPC): A review. Mater. 2021, 14, 1472. [Google Scholar] [CrossRef] [PubMed]
- Pyo, S.; Abate, S.Y.; Kim, H.K. Abrasion resistance of ultra high performance concrete incorporating coarser aggregate. Constr. Build. Mater. 2018, 165, 11–16. [Google Scholar] [CrossRef]
- Pyo, S.; El-Tawil, S. Capturing the strain hardening and softening responses of cementitious composites subjected to impact loading. Constr. Build. Mater. 2015, 81, 276–283. [Google Scholar] [CrossRef]
- Bae, Y.; Pyo, S. Ultra high performance concrete (UHPC) sleeper: Structural design and performances. Eng. Struct. 2020, 210, 110374. [Google Scholar] [CrossRef]
- Auersch, L.; Said, S.; Knothe, E.; Rücker, W. The dynamic behavior of railway tracks with under sleeper pads, finite-element boundary-element model calculations, laboratory tests and field measurements. In Proceedings of the 9th European Conference on Structural Dynamics (EURODYN 2014), Porto, Portugal, 30 June–2 July 2014; pp. 805–812. [Google Scholar]
- Chandra, S.; Shukla, D. Sustainability of Railway Tracks. In Sustainability Issues in Civil Engineering; Springer: Singapore, 2017; pp. 91–104. [Google Scholar]
- Sucharda, O.; Mateckova, P.; Bilek, V. Non-Linear Analysis of an RC Beam Without Shear Reinforcement with a Sensitivity Study of the Material Properties of Concrete. Slovak J. Civ. Eng. 2020, 28, 33–43. [Google Scholar] [CrossRef]
- Valikhani, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Numerical Modeling of Concrete-to-UHPC Bond Strength. Materials 2020, 13, 1379. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.; Yu, H. Numerical Evaluation of Splitting Performance of Prestressed Concrete Prisms With Larger Diameter Prestressing Wires. In Proceedings of the 2019 ASME Joint Rail Conference, Snowbird, UT, USA, 9–12 April 2019. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS Documentation; Dassault Systemes: Providence, RI, USA, 2012. [Google Scholar]
- Pyo, S.; Kim, H.K.; Lee, B.Y. Effects of coarser fine aggregate on tensile properties of ultra high performance concrete. Cem. Concr. Compos. 2017, 84, 28–35. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers (JSCE). Recommendations for Design and Construction of High Performance Fiber Reinforced Cement Composites with Multiple Fine Cracks (HPFRCC); Concrete Engineering Series; Springer: Tokyo, Japan, 2008. [Google Scholar]
- Naaman, A.E. Engineered steel fibers with optimal properties for reinforcement of cement composites. J. Adv. Concr. Technol. 2003, 1, 241–252. [Google Scholar] [CrossRef]
- Pyo, S.; Wille, K.; El-Tawil, S.; Naaman, A.E. Strain rate dependent properties of ultra high performance fiber reinforced concrete (UHP-FRC) under tension. Cem. Concr. Compos. 2015, 56, 15–24. [Google Scholar] [CrossRef]
- Wille, K.; Kim, D.J.; Naaman, A.E. Strain-hardening UHP-FRC with low fiber contents. Mater. Struct. 2011, 44, 583–598. [Google Scholar] [CrossRef]



| Concrete | Young’s modulus | 51.0 GPa |
| Compressive strength | 150 MPa | |
| Poisson’s ratio | 0.2 | |
| Tensile strength (steel fiber 0.5%) | 8.82 MPa | |
| Tensile strength (steel fiber 1.0%) | 15.6 MPa | |
| Tensile strength (steel fiber 1.5%) | 18.4 MPa | |
| Direct stress onset of cracking (steel fiber 0.5%) | 3.17 MPa | |
| Direct stress onset of cracking (steel fiber 0.5%) | 6.52 MPa | |
| Direct stress onset of cracking (steel fiber 0.5%) | 5.58 MPa | |
| Steel tendon | Young’s modulus | 200 GPa |
| Yielding strength | 1275 MPa | |
| Poisson’s ratio | 0.3 |
| Steel fiber contents (%) | 0.5 | 1.0 | 1.5 |
| Yielding stress of prestressing tendon (fy) (MPa) | 1 080 | 1 275 | |
| Diameter of prestressing tendon (φ) (mm) | 9.2 | 11.0 | |
| Cross-sectional parameters | L-Type | M-Type | H-Type |
| Height of the rail-seat section, hr (mm) (hr1, mm) | 140 (125) | 165 (150) | 195 (180) |
| Height of the center section, hc (mm) | 125 | 150 | 180 |
| Location of the prestressing tendon, P1 (mm) | 32.5 | 35 | 50 |
| Location of the prestressing tendon, P2 (mm) | 60 | 75 | 80 |
| Sp. No. | Steel Fiber 0.5% | Sp. No. | Steel Fiber 1.0% | Sp. No. | Steel Fiber 1.5% |
|---|---|---|---|---|---|
| No.1 | L-φ9.2-fy1 275 | No.8 | L-φ9.2-fy1 275 | No.15 | L-φ9.2-fy1 275 |
| No.2 | L-φ11.0-fy1 275 | No9 | L-φ11.0-fy1 275 | No.16 | L-φ11.0-fy1 275 |
| No.3 | L-φ11.0-fy1 080 | No.10 | L-φ11.0-fy1 080 | No.17 | L-φ11.0-fy1 080 |
| No.4 | M-φ09.2-fy1 275 | No.11 | M-φ9.2-fy1 275 | No.18 | M-φ9.2-fy1 275 |
| No.5 | M-φ09.2-fy1 080 | No.12 | M-φ9.2-fy1 080 | No.19 | M-φ9.2-fy1 080 |
| No.6 | H-φ09.2-fy1 275 | No.13 | H-φ9.2-fy1 275 | No.20 | H-φ9.2-fy1 275 |
| No.7 | H-φ09.2-fy1 080 | No.14 | H-φ9.2-fy1 080 | No.21 | H-φ9.2-fy1 080 |
| Simulation Case | Rail-Seat Section Area (mm2) | Force (kN) | Crack Width (mm) | 100FrB/Area | ΔF1 (kN) = (Fr0.05 − Frr) | ΔF2 (kN) = (FrB − Fr0.05) | FrB/2.5Fr0 | |
|---|---|---|---|---|---|---|---|---|
| L/9.2/1 275/1.0% | 47 200 | Frr | 230.4 | 0.008 6 | 1.02 | 158.4 | 91.2 | 1.51 |
| Fr0.05 | 388.8 | 0.056 4 | ||||||
| FrB | 480.0 | 1.28 | ||||||
| M/9.2/1 275/1.0% | 56 075 | Frr | 300.0 | 0.009 | 1.12 | 206.2 | 118.8 | 1.97 |
| Fr0.05 | 506.2 | 0.051 | ||||||
| FrB | 625.0 | 2.94 | ||||||
| H/9.2/1 275/1.0% | 66 725 | Frr | 400.8 | 0.009 4 | 1.25 | 276.5 | 158.7 | 2.63 |
| Fr0.05 | 676.3 | 0.052 8 | ||||||
| FrB | 835.0 | 1.988 | ||||||
| Analysis Case | Rail-Seat Section Area (mm2) | Force (kN) | Crack Width (mm) | 100FrB/Area | ΔF1 (kN) = (Fr0.05 − Frr) | ΔF2 (kN) = (FrB − Fr0.05) | FrB/2.5Fr0 | |
|---|---|---|---|---|---|---|---|---|
| L/9.2/1 275/1.0% | 47 200 | Frr | 230.4 | 0.0086 | 1.02 | 158.4 | 91.2 | 1.51 |
| Fr0.05 | 388.8 | 0.0564 | ||||||
| FrB | 480.0 | 1.28 | ||||||
| L/11.0/1 275/1.0% | 47 200 | Frr | 276.0 | 0.0098 | 1.22 | 155.3 | 142.7 | 1.81 |
| Fr0.05 | 431.3 | 0.0452 | ||||||
| FrB | 575.0 | 7.292 | ||||||
| L/11.0/1 080/1.0% | 47 200 | Frr | 249.6 | 0.0115 | 1.10 | 171.6 | 98.8 | 1.64 |
| Fr0.05 | 421.2 | 0.0532 | ||||||
| FrB | 520.0 | 2.104 | ||||||
| H/9.2/1 275/1.0% | 66 725 | Frr | 400.8 | 0.0094 | 1.25 | 276.5 | 158.7 | 2.63 |
| Fr0.05 | 676.3 | 0.0528 | ||||||
| FrB | 835.0 | 1.988 | ||||||
| H/9.2/1 080/1.0% | 66 725 | Frr | 384.0 | 0.0084 | 1.12 | 264.0 | 152.0 | 2.52 |
| Fr0.05 | 648.0 | 0.0539 | ||||||
| FrB | 800.0 | 1.922 | ||||||
| Analysis Case | Rail-Seat Section Area (mm2) | Force (kN) | Crack Width (mm) | 100FrB/Area | ΔF1 (kN) = (Fr0.05 − Frr) | ΔF2 (kN) = (FrB − Fr0.05) | FrB/2.5Fr0 | |
|---|---|---|---|---|---|---|---|---|
| L/9.2/1 275/0.5% | 47 200 | Frr | 180.0 | 0.0103 | 0.79 | 101.3 | 93.7 | 1.18 |
| Fr0.05 | 281.3 | 0.0487 | ||||||
| FrB | 375.0 | 2.282 | ||||||
| L/9.2/1 275/1.0% | 47 200 | Frr | 230.4 | 0.0086 | 1.02 | 158.4 | 91.2 | 1.51 |
| Fr0.05 | 388.8 | 0.0564 | ||||||
| FrB | 480.0 | 1.28 | ||||||
| L/9.2/1 275/1.5% | 47 200 | Frr | 217.8 | 0.0108 | 1.05 | 183.1 | 94.1 | 1.56 |
| Fr0.05 | 400.9 | 0.0532 | ||||||
| FrB | 495.0 | 1.724 | ||||||
| H/9.2/1 275/0.5% | 66 725 | Frr | 300.0 | 0.0105 | 0.94 | 168.7 | 156.3 | 1.97 |
| Fr0.05 | 468.7 | 0.0454 | ||||||
| FrB | 625.0 | 3.137 | ||||||
| H/9.2/1 275/1.0% | 66 725 | Frr | 400.8 | 0.0094 | 1.25 | 276.5 | 158.7 | 2.63 |
| Fr0.05 | 676.3 | 0.0528 | ||||||
| FrB | 835.0 | 1.988 | ||||||
| H/9.2/1 275/1.5% | 66 725 | Frr | 388.5 | 0.0109 | 1.32 | 273.8 | 220.7 | 2.79 |
| Fr0.05 | 662.3 | 0.0452 | ||||||
| FrB | 883.0 | 2.224 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, M.; Bae, Y.; Pyo, S. A Numerical Study on Structural Performance of Railway Sleepers Using Ultra High-Performance Concrete (UHPC). Materials 2021, 14, 2979. https://doi.org/10.3390/ma14112979
Shin M, Bae Y, Pyo S. A Numerical Study on Structural Performance of Railway Sleepers Using Ultra High-Performance Concrete (UHPC). Materials. 2021; 14(11):2979. https://doi.org/10.3390/ma14112979
Chicago/Turabian StyleShin, Moochul, Younghoon Bae, and Sukhoon Pyo. 2021. "A Numerical Study on Structural Performance of Railway Sleepers Using Ultra High-Performance Concrete (UHPC)" Materials 14, no. 11: 2979. https://doi.org/10.3390/ma14112979
APA StyleShin, M., Bae, Y., & Pyo, S. (2021). A Numerical Study on Structural Performance of Railway Sleepers Using Ultra High-Performance Concrete (UHPC). Materials, 14(11), 2979. https://doi.org/10.3390/ma14112979








