Full-Field Measurements in the Edge Crush Test of a Corrugated Board—Analytical and Numerical Predictive Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Corugated Cardboard
2.2. Measurements
2.3. Optical Measurements of Sample Deformation
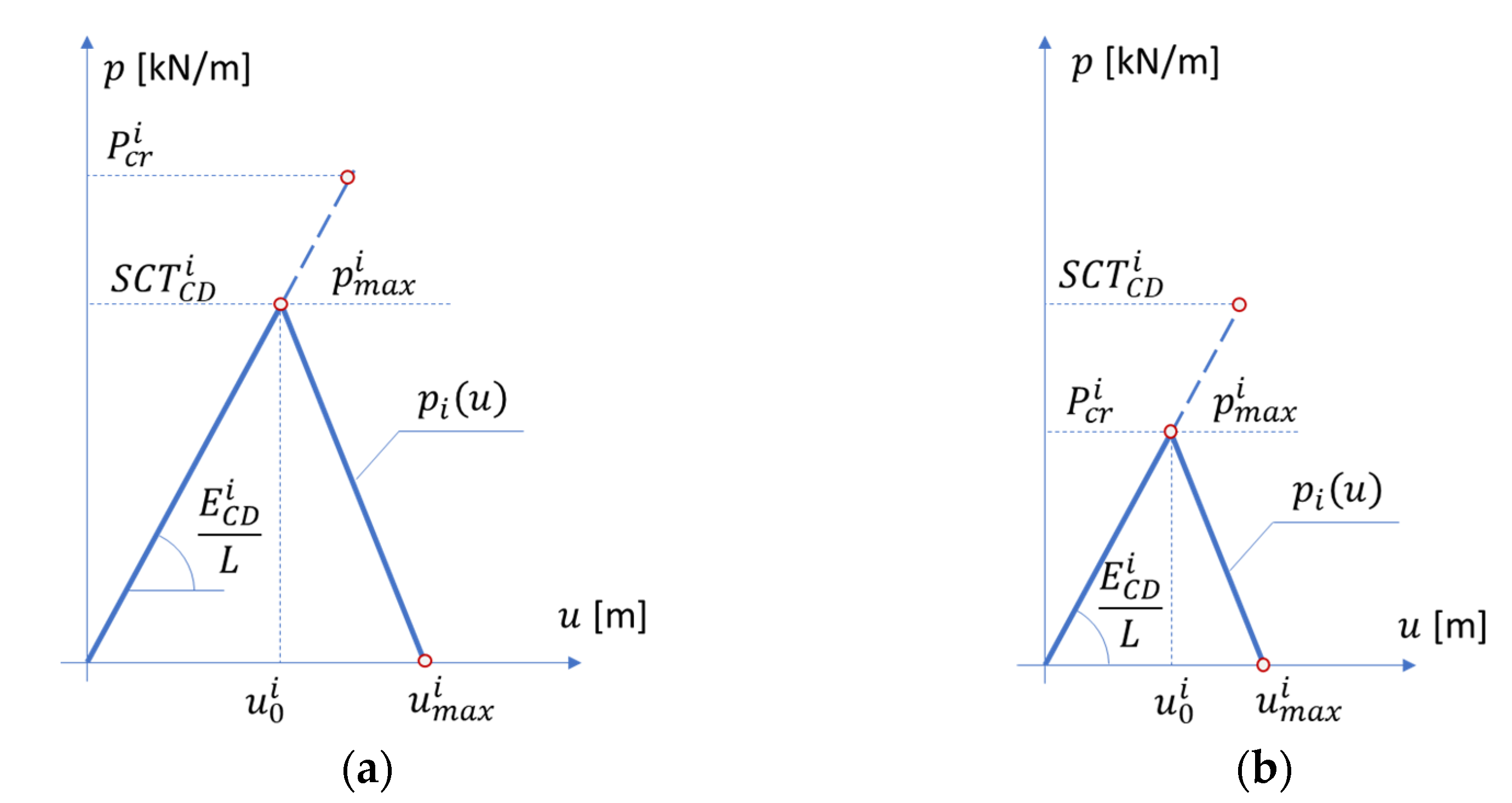
2.4. Predictive Models
3. Results
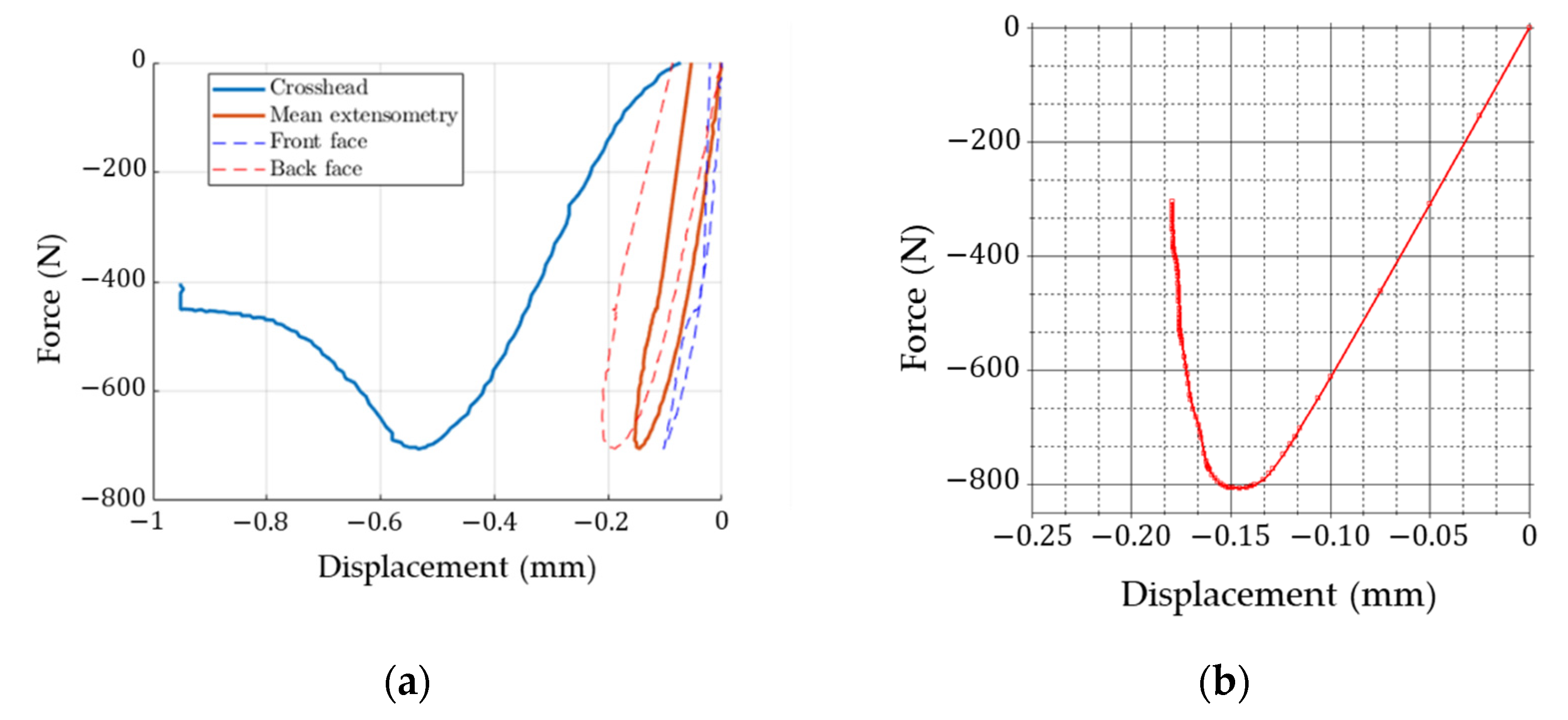
3.1. Edge Crush Test Results
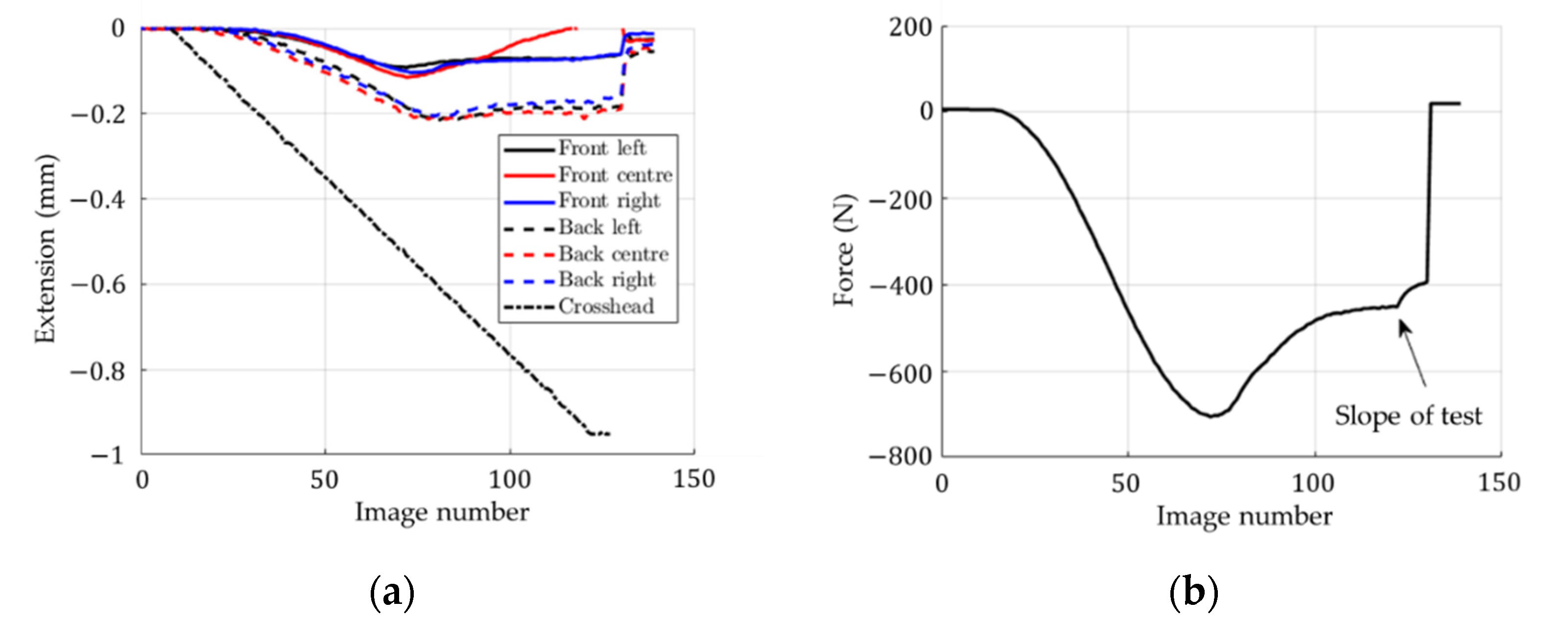
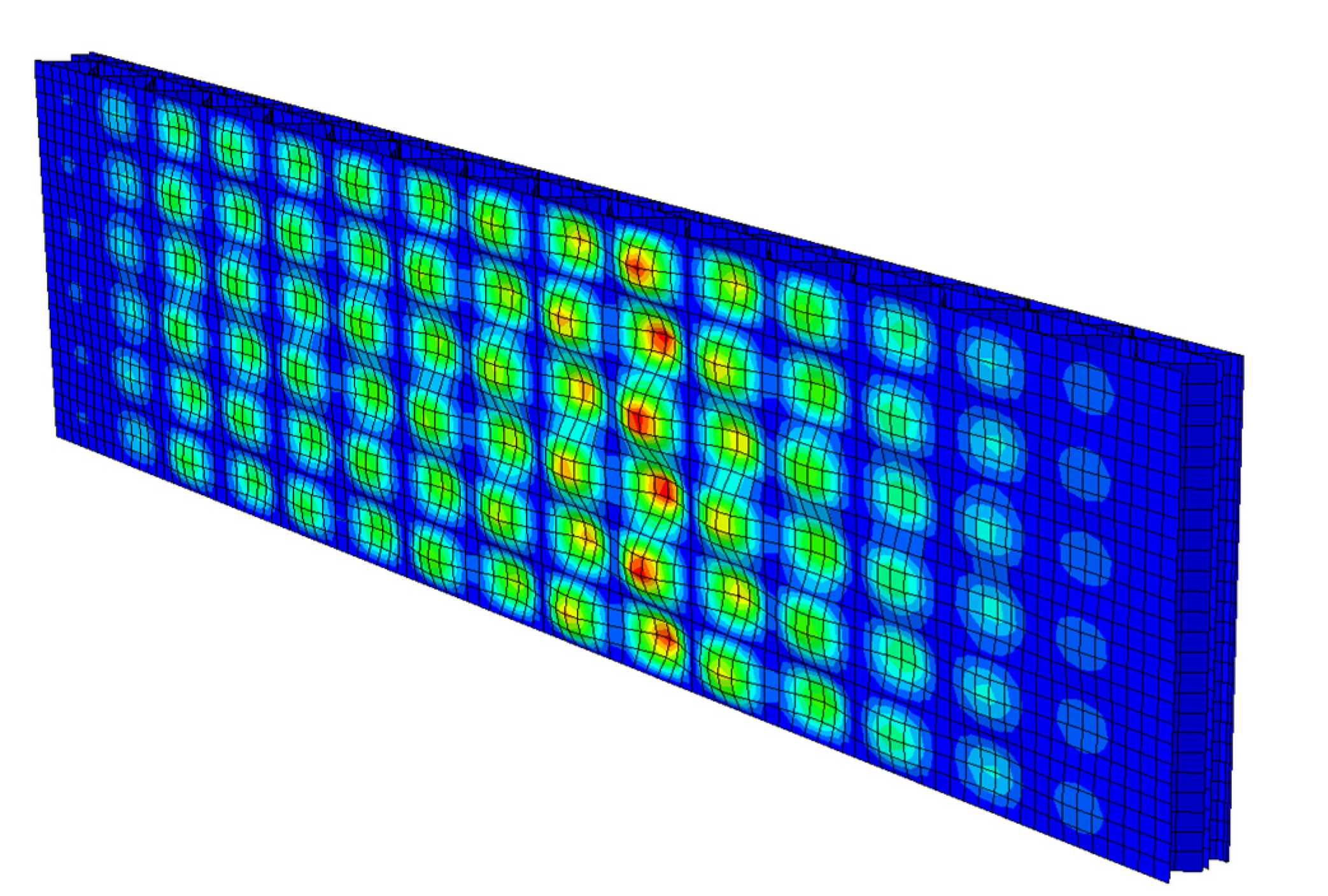
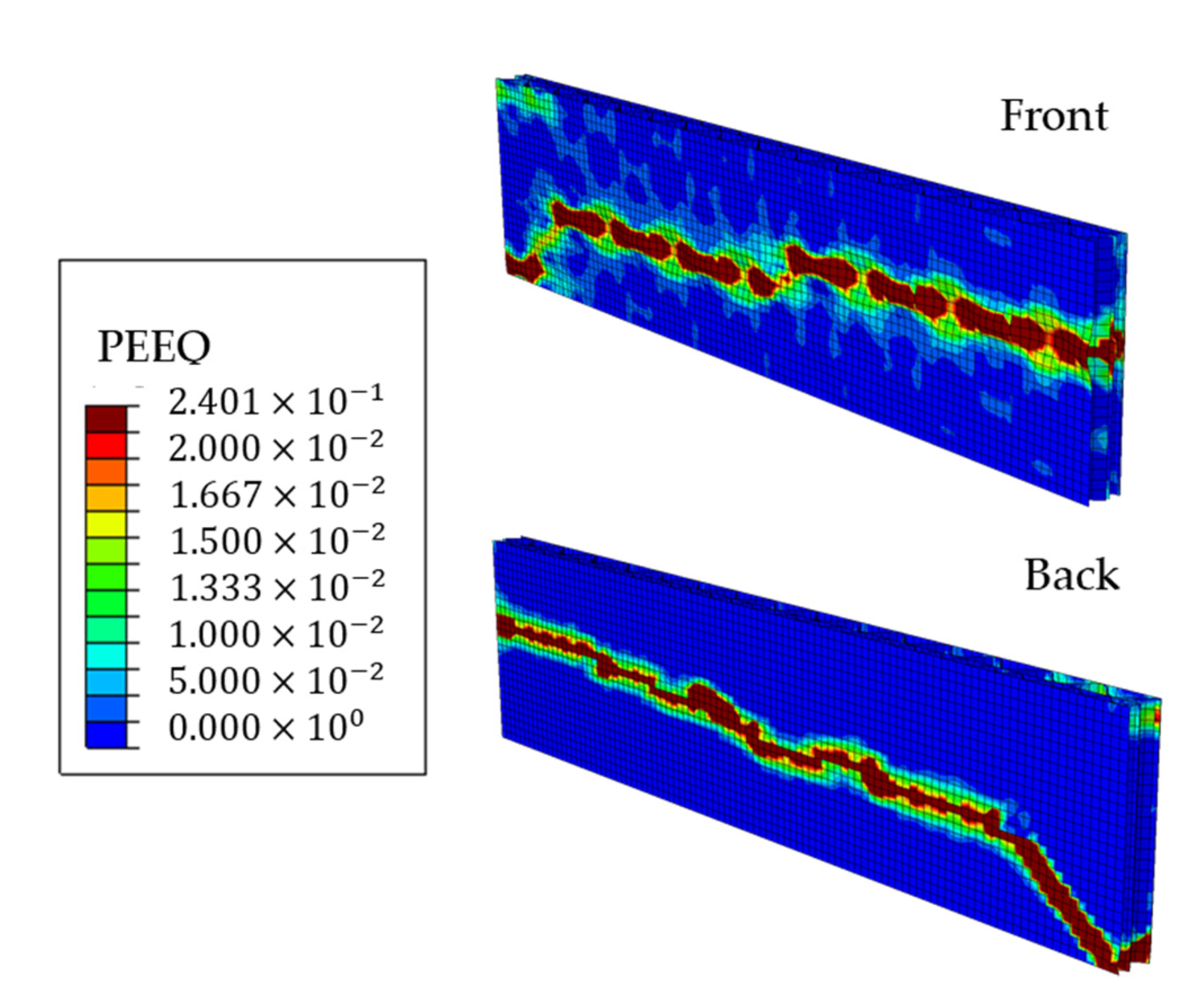
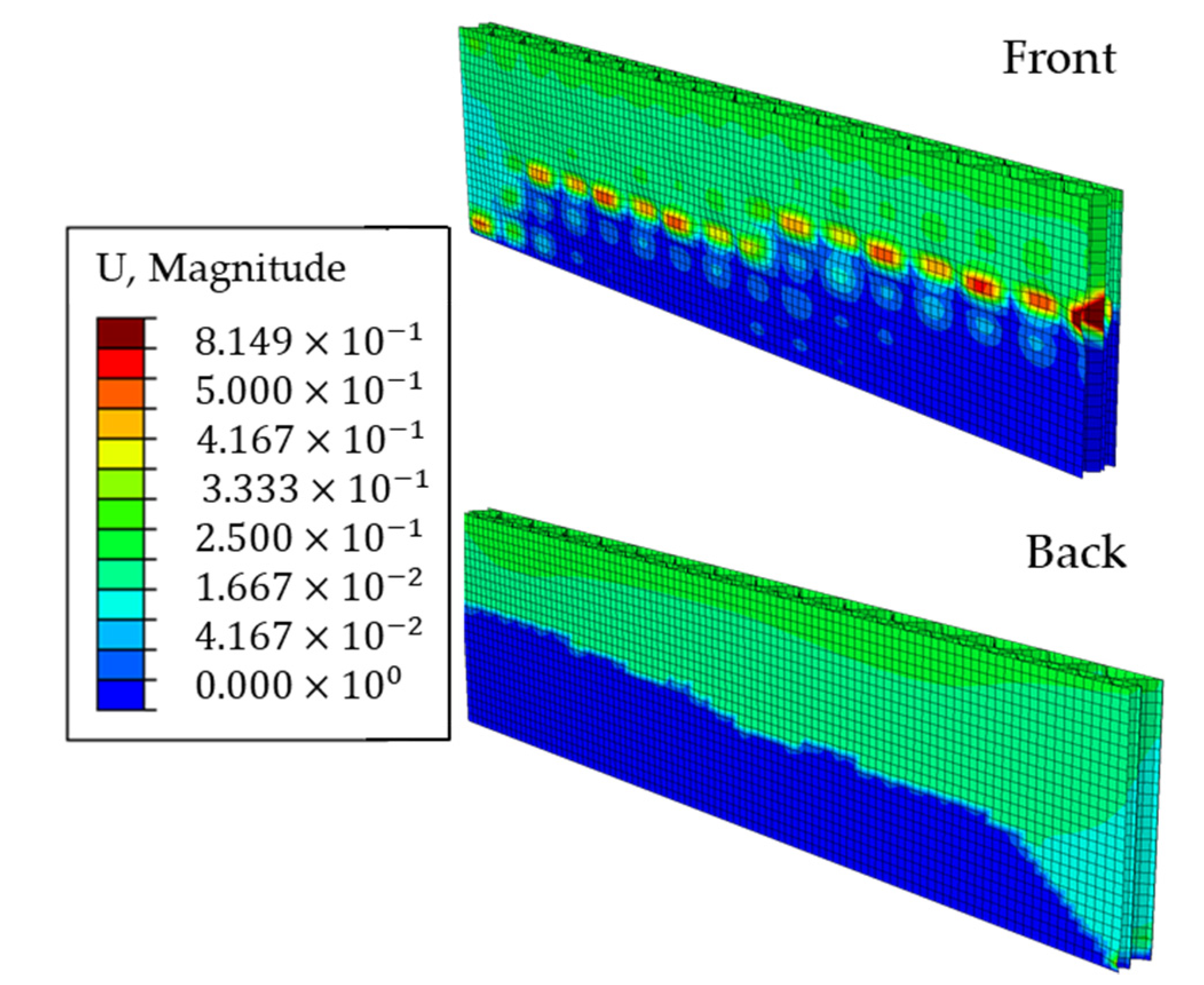
3.2. Optical Measurements Results
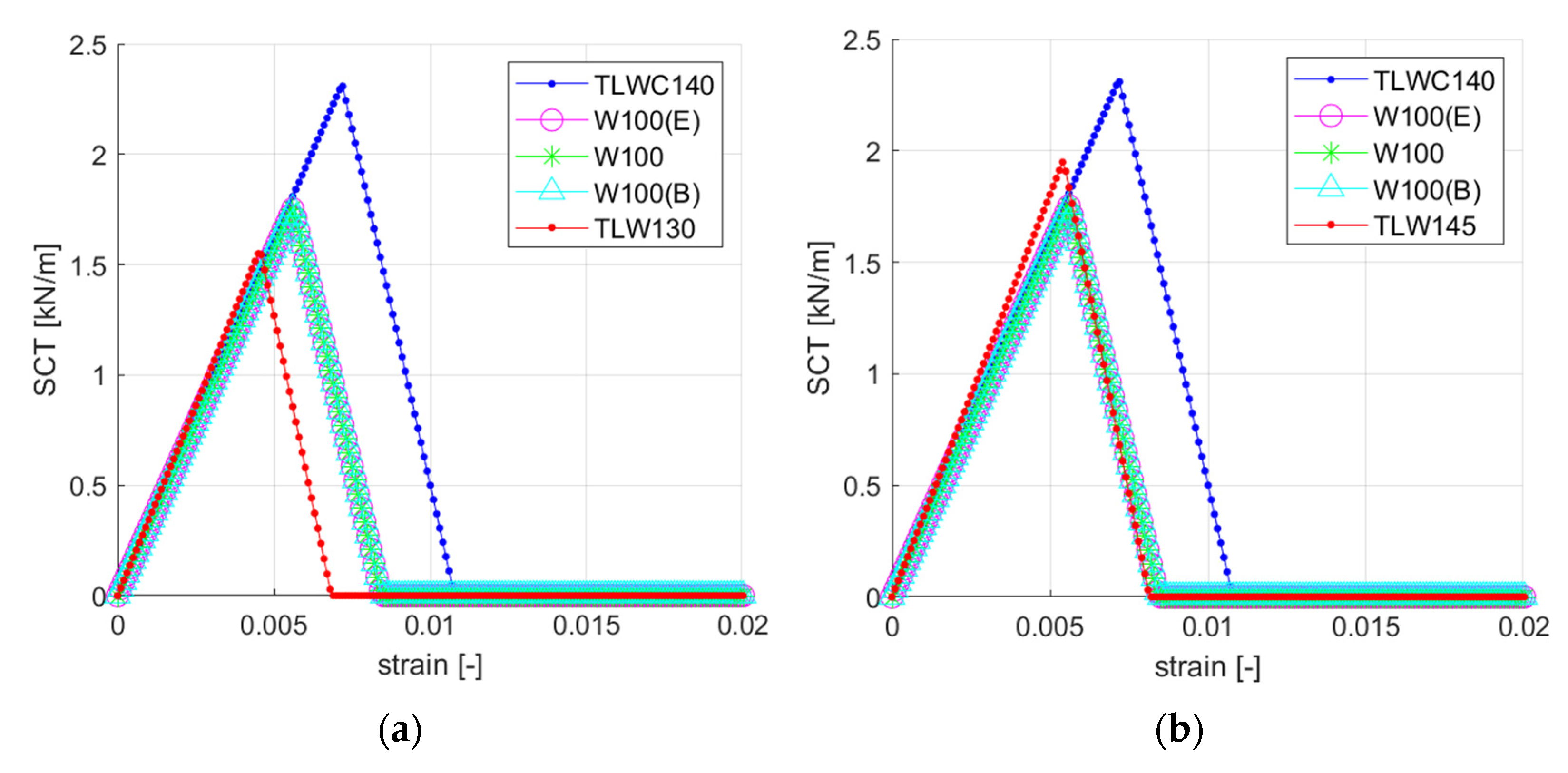
3.3. Predictive Analytical Model
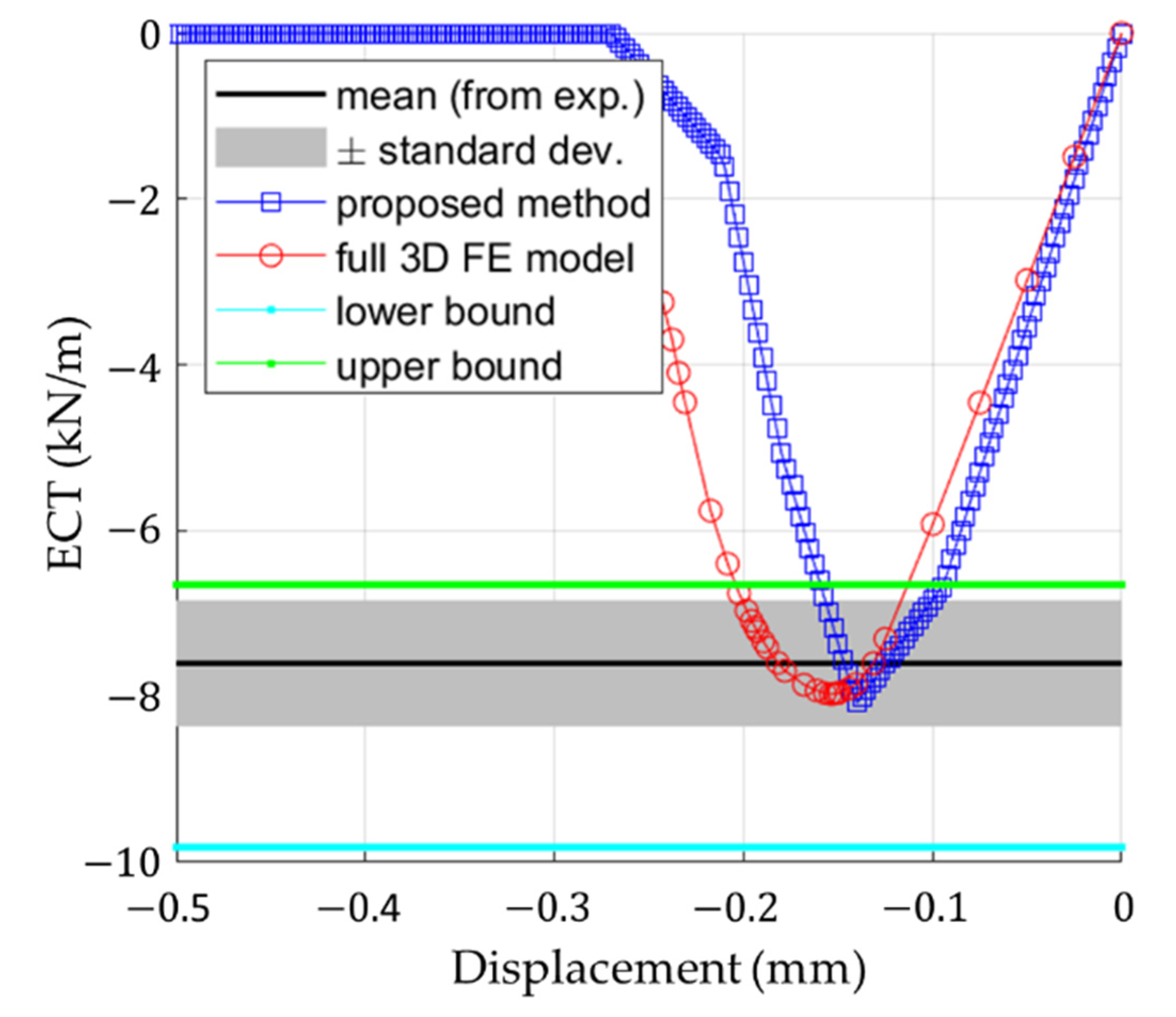
3.4. Predictive Numerical Model
3.5. Compilation of All Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Magnucka-Blandzi, E.; Magnucki, K.; Wittenbeck, L. Mathematical modeling of shearing effect for sandwich beams with sinusoidal corrugated cores. Appl. Math. Model. 2015, 39, 1796–2808. [Google Scholar] [CrossRef]
- Magnucka-Blandzi, E.; Magnucki, K. Transverse shear modulus of elasticity for thin-walled corrugated cores of sandwich beams. Theoretical study. J. Theor. Appl. Mech. 2014, 52, 971–980. [Google Scholar] [CrossRef][Green Version]
- Nordstrand, T.M.; Carlsson, L.A. Evaluation of transverse shear stiffness of structural core sandwich plates. Comp. Struct. 1997, 37, 145–153. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Role of transverse shear modulus in the performance of corrugated materials. Materials 2020, 13, 3791. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and transversal stiffness of orthotropic sandwich panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef] [PubMed]
- Domaneschi, M.; Perego, U.; Borgqvist, E.; Borsari, R. An industry-oriented strategy for the finite element simulation of paperboard creasing and folding. Packag. Tech. Sci. 2017, 30, 269–294. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Kmita-Fudalej, G.; Szewczyk, W.; Kołakowski, Z. Calculation of honeycomb paperboard resistance to edge crush test. Materials 2020, 13, 1706. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Chang, S.; Jung, H.M. Numerical prediction of equivalent mechanical properties of corrugated paperboard by 3D finite element analysis. Appl. Sci. 2020, 10, 7973. [Google Scholar] [CrossRef]
- Wong, J.E.; Mustapha, K.B.; Shimizu, Y.; Kamiya, A.; Arumugasamy, S.K. Development of surrogate predictive models for the nonlinear elasto-plastic response of medium density fibreboard-based sandwich structures. Int. J. Lightweight Mater. Manuf. 2021, 4, 302–314. [Google Scholar]
- FEMat Systems. Available online: http://fematsystems.pl/home_en (accessed on 25 April 2021).
- TAPPI T 839 om-12. Edge Compression Test for Strength of Corrugated Fiberboard Using the Clamp Method (Short Column Test); TAPPI: Peachtree Corners, GA, USA, 2009. [Google Scholar]
- TAPPI T 838 cm-12. Edge Crush Test Using Neckdown; TAPPI: Peachtree Corners, GA, USA, 2009. [Google Scholar]
- FEFCO NO.8. Edgewise Crush Resistance of Corrugated Fiberboard; FEFCO: Brussel, Belgium, 1997. [Google Scholar]
- ISO 3037:2013. Corrugated Fibreboard—Determination of Edgewise Crush Resistance (Unwaxed Edge Method); ISO: Geneva, Switzerland, 2013. [Google Scholar]
- TAPPI T 811 om-11. Edgewise Compressive Strength of Corrugated Fibreboard (Short Column Test); TAPPI: Peachtree Corners, GA, USA, 2009. [Google Scholar]
- ISO 13821:2002. Corrugated Fibreboard—Determination of Edgewise Crush Resistance—Waxed Edge Method; ISO: Geneva, Switzerland, 2002. [Google Scholar]
- Park, J.; Park, M.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packing of agricultural products. Appl. Sci. 2020, 10, 6716. [Google Scholar] [CrossRef]
- Hägglund, R.; Åslund, P.E.; Carlsson, L.A.; Isaksson, P. Measuring thickness changes of edgewise compression loaded corrugated board panels using digital image correlation. J. Sandwich Struct. Mater. 2010, 14, 75–94. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.J.; Vacher, P.; Orgéas, L.; Desloges, I.; Mauret, E. Analysis of the strain and stress field of cardboard box during compression by 3D Digital Image Correlation. Appl. Mech. Mater. 2010, 24–25, 103–108. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.J.; Orgéas, L.; Vacher, P.; Desloges, I.; Mauret, E. Surface stress and strain fields on compressed panels of corrugated board boxes. An experimental analysis by using Digital Image Stereocorrelation. Comp. Struct. 2011, 93, 2861–2873. [Google Scholar] [CrossRef]
- Viguié, J.; Dumont, P.J.J. Analytical post-buckling model of corrugated board panels using digital image correlation measurements. Comp. Struct. 2013, 101, 243–254. [Google Scholar] [CrossRef]
- Borgqvist, E.; Lindström, T.; Tryding, J.; Wallin, M.; Ristinmaa, M. Distortional hardening plasticity model for paperboard. Int. J. Solids Struct. 2014, 51, 2411–2423. [Google Scholar] [CrossRef]
- Cocchetti, G.; Mahini, M.R.; Maier, G. Mechanical characterization of foils with compression in their planes. Mech. Adv. Mater. Struct. 2014, 21, 853–870. [Google Scholar] [CrossRef]
- Garbowski, T.; Maier, G.; Novati, G. On calibration of orthotropic elastic-plastic constitutive models for paper foils by biaxial tests and inverse analyses. Struct. Multidisc. Optim. 2012, 46, 111–128. [Google Scholar] [CrossRef]
- Considine, J.M.; Pierron, F.; Turner, K.T.; Vahey, D.W. General anisotropy identification of paperboard with virtual fields method. Exp. Mech. 2014, 54, 1395–1410. [Google Scholar] [CrossRef]
- Åslund, P.E.; Hägglund, R.; Carlsson, L.A.; Isaksson, P. An analysis of strain localization and formation of face wrinkles in edge-wise loaded corrugated sandwich panels using a continuum damage model. Int. J. Solids Struct. 2015, 56–57, 248–257. [Google Scholar] [CrossRef]
- Zappa, E.; Liu, R.; Bolzon, G.; Shahmardani, M. High resolution non-contact measurement techniques for three-dimensional deformation processes of paperboard laminates. Mater. Today Proc. 2017, 4, 5872–5876. [Google Scholar] [CrossRef]
- Fadiji, T.; Coetzee, C.J.; Opara, U.L. Evaluating the displacement field of paperboard packages subjected to compression loading using digital image correlation (DIC). Food Bioprod. Process. 2020, 123, 60–71. [Google Scholar] [CrossRef]
- FEMat Systems. Available online: http://fematsystems.pl/ect_en (accessed on 25 April 2021).
- Abaqus Unified FEA® Software. Available online: https://www.3ds.com/products-services/simulia/products/abaqus (accessed on 25 April 2021).
- Baum, G.A.; Brennan, D.C.; Habeger, C.C. Orthotropic elastic constants of paper. Tappi 1981, 64, 97–101. [Google Scholar]
- Mann, R.W.; Baum, G.A.; Habeger, C.C. Determination of all nine orthotropic elastic constants for machine-made paper. Tappi 1980, 63, 163–166. [Google Scholar]
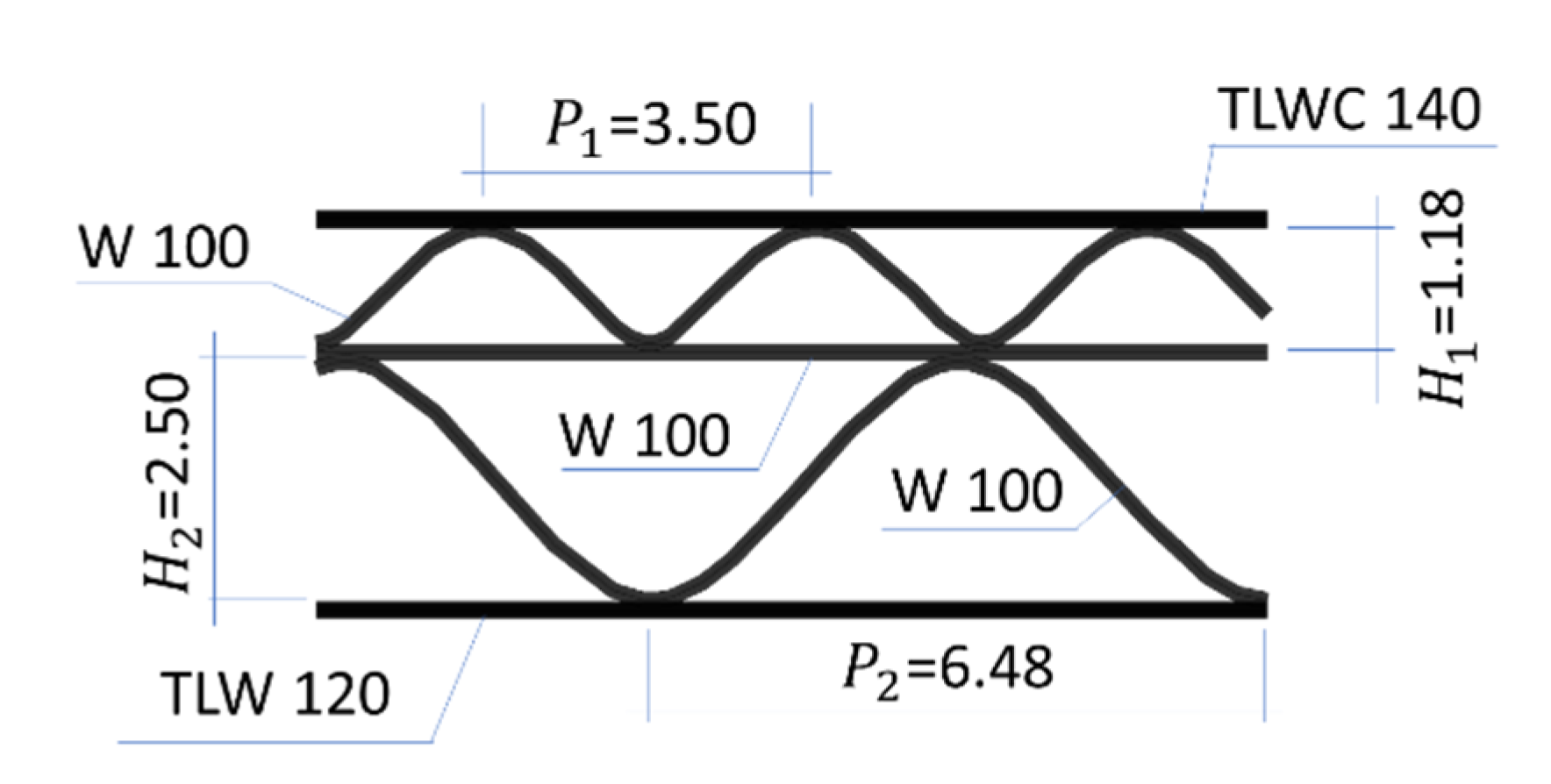


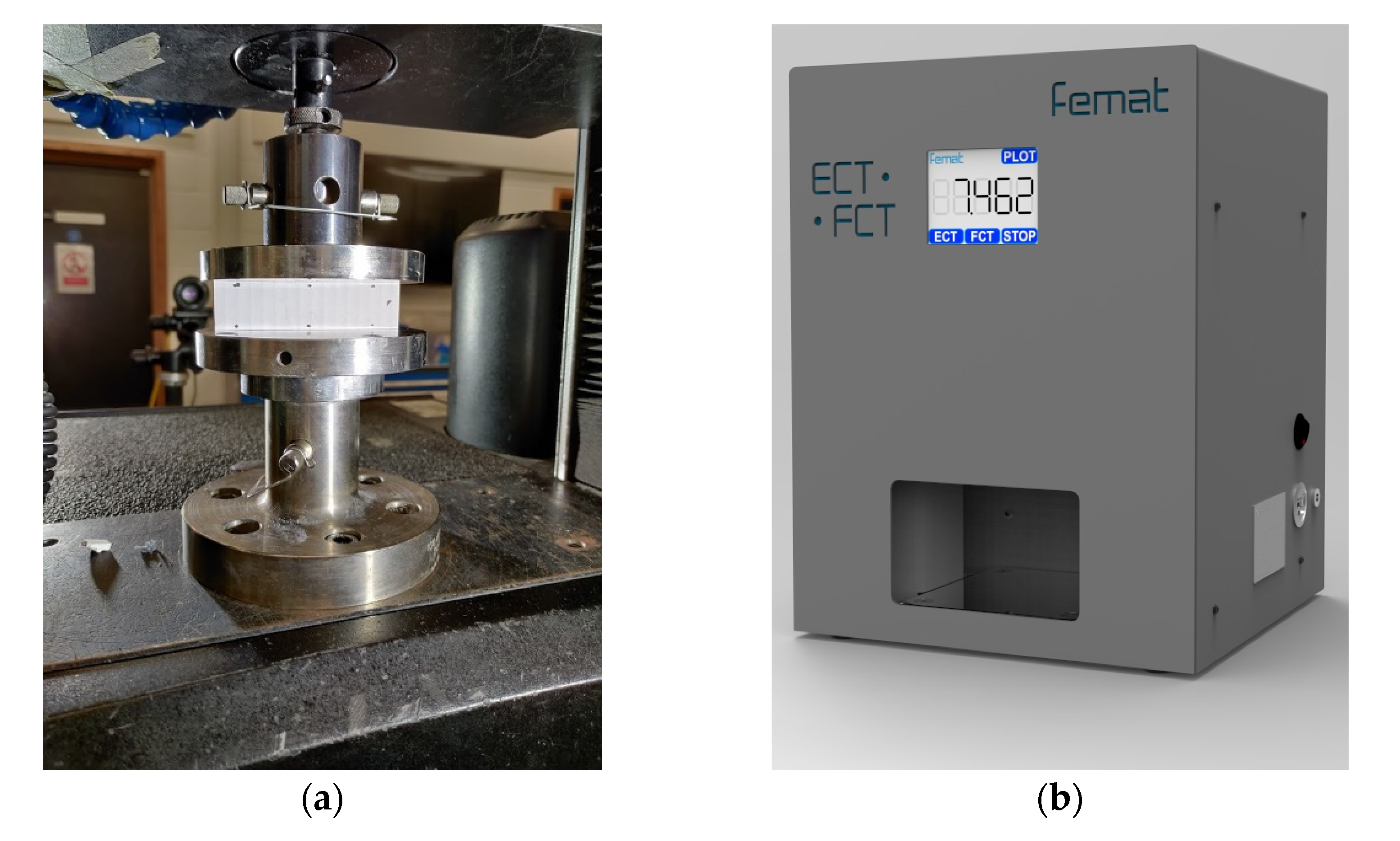





| Wave (Flute) | Pitch [mm] | Height [mm] | Take-Up Ratio [–] |
|---|---|---|---|
| E | 3.50 | 1.18 | 1.242 |
| B | 6.48 | 2.5 | 1.315 |
| Layer Name | Thickness [] | [kN/m] | [kN/m] | [kN/m] |
|---|---|---|---|---|
| TLWC 140 | 180 | 725 | 323 | 2.32 |
| W 100 | 160 | 886 | 328 | 1.76 |
| TLW 120 | 170 | 907 | 313 | 1.81 |
| Layer Name | [MPa] | [MPa] | [–] | [MPa] | [MPa] | [MPa] |
|---|---|---|---|---|---|---|
| TLW 120 | 5669 | 2050 | 0.176 | 1319 | 103 | 59 |
| W 100 | 5537 | 2050 | 0.209 | 1112 | 101 | 59 |
| TLWC 140 | 4028 | 1794 | 0.196 | 1040 | 73 | 51 |
| Layer Name | (mm) | (m) | (kN/m) | (kN/m) |
|---|---|---|---|---|
| TLWC 140 | 3.50 | 25 | 2.32 | 4.212 |
| W 100 (E) | 2.17 | 25 | 1.76 | 9.573 |
| W 100 | - | 25 | 1.76 | - |
| W 100 (B) | 4.26 | 25 | 1.76 | 2.444 |
| TLW 120 | 6.48 | 25 | 1.81 | 1.237 |
| Test/Model | (kN/m) | (kN/m) |
|---|---|---|
| Producer specification | 7.60 | - |
| FEMat—crosshead | 7.51 | 1991 |
| Instron—crosshead | 7.03 | 2142 |
| Instron—opt. extensometry | 7.03 | 6442 |
| Numerical model | 7.94 | 5920 |
| Analytical model | 8.08 | 7063 |
| Reference | Single Layer Improved by 10% | Single Layer Improved by 20% | |||||
|---|---|---|---|---|---|---|---|
| Paperboard Symbol | ECT (kN/m) | Paperboard Symbol | ECT (kN/m) | Diff. (%) | Paperboard Symbol | ECT (kN/m) | Diff. (%) |
| TLWC 140 | 8.08 | TLWC 155 | 8.261 | 2.24 | TLWC 170 | 8.442 | 4.48 |
| W 100 (E) | 8.08 | W 110 (E) | 8.297 | 2.69 | W 120 (E) | 8.515 | 5.38 |
| W 100 | 8.08 | W 110 | 8.255 | 2.17 | W 120 | 8.430 | 4.33 |
| W 100 (B) | 8.08 | W 110 (B) | 8.310 | 2.85 | W 120 (B) | 8.541 | 5.71 |
| TLW 120 | 8.08 | TLW 130 | 8.940 | 10.64 | TLW 145 | 10.046 | 24.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Grabski, J.K.; Marek, A. Full-Field Measurements in the Edge Crush Test of a Corrugated Board—Analytical and Numerical Predictive Models. Materials 2021, 14, 2840. https://doi.org/10.3390/ma14112840
Garbowski T, Grabski JK, Marek A. Full-Field Measurements in the Edge Crush Test of a Corrugated Board—Analytical and Numerical Predictive Models. Materials. 2021; 14(11):2840. https://doi.org/10.3390/ma14112840
Chicago/Turabian StyleGarbowski, Tomasz, Jakub Krzysztof Grabski, and Aleksander Marek. 2021. "Full-Field Measurements in the Edge Crush Test of a Corrugated Board—Analytical and Numerical Predictive Models" Materials 14, no. 11: 2840. https://doi.org/10.3390/ma14112840
APA StyleGarbowski, T., Grabski, J. K., & Marek, A. (2021). Full-Field Measurements in the Edge Crush Test of a Corrugated Board—Analytical and Numerical Predictive Models. Materials, 14(11), 2840. https://doi.org/10.3390/ma14112840








