Anomalous Properties of the Dislocation-Free Interface between Si(111) Substrate and 3C-SiC(111) Epitaxial Layer
Abstract
1. Introduction
2. Experimental Technique and Ellipsometric Analysis
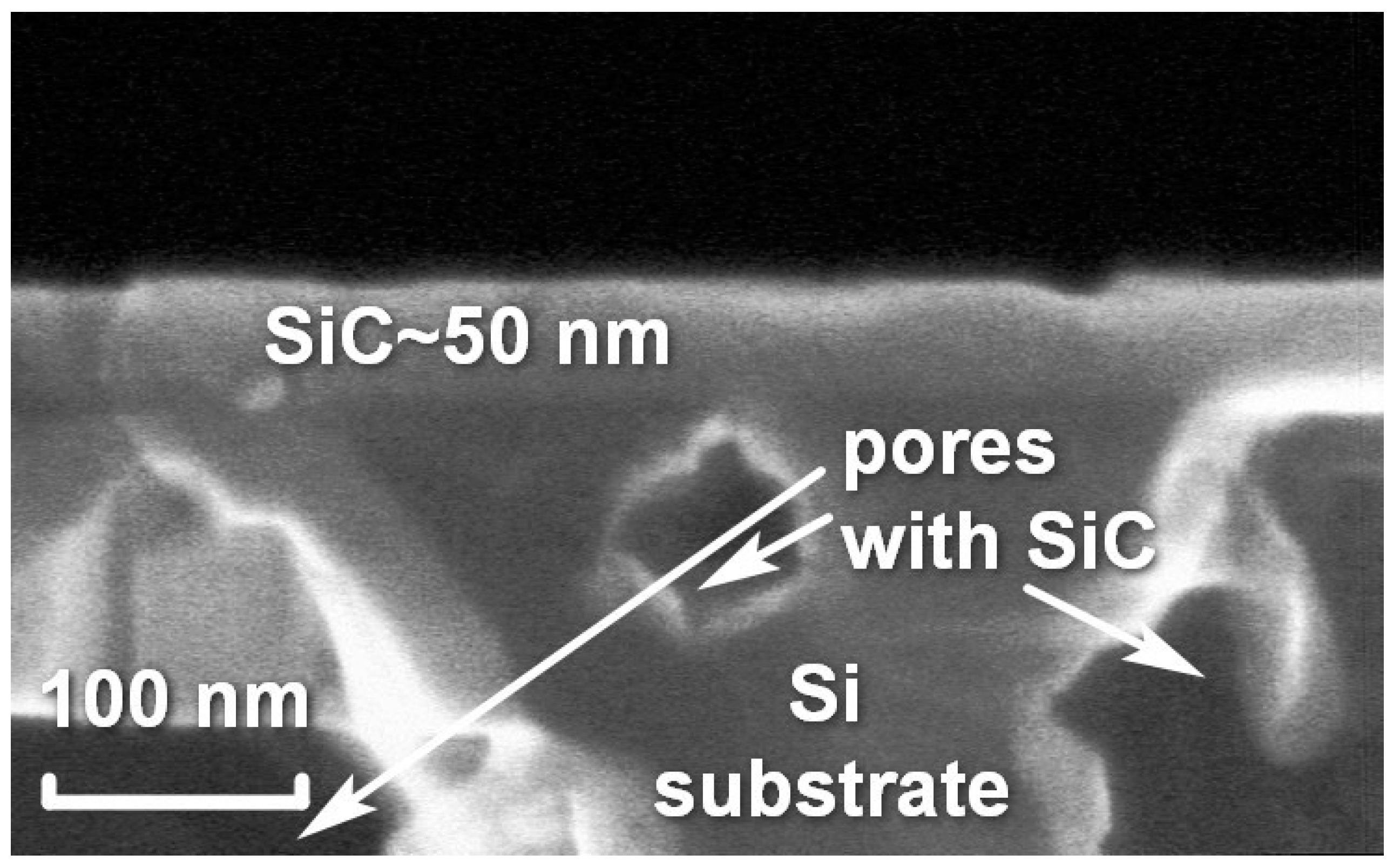
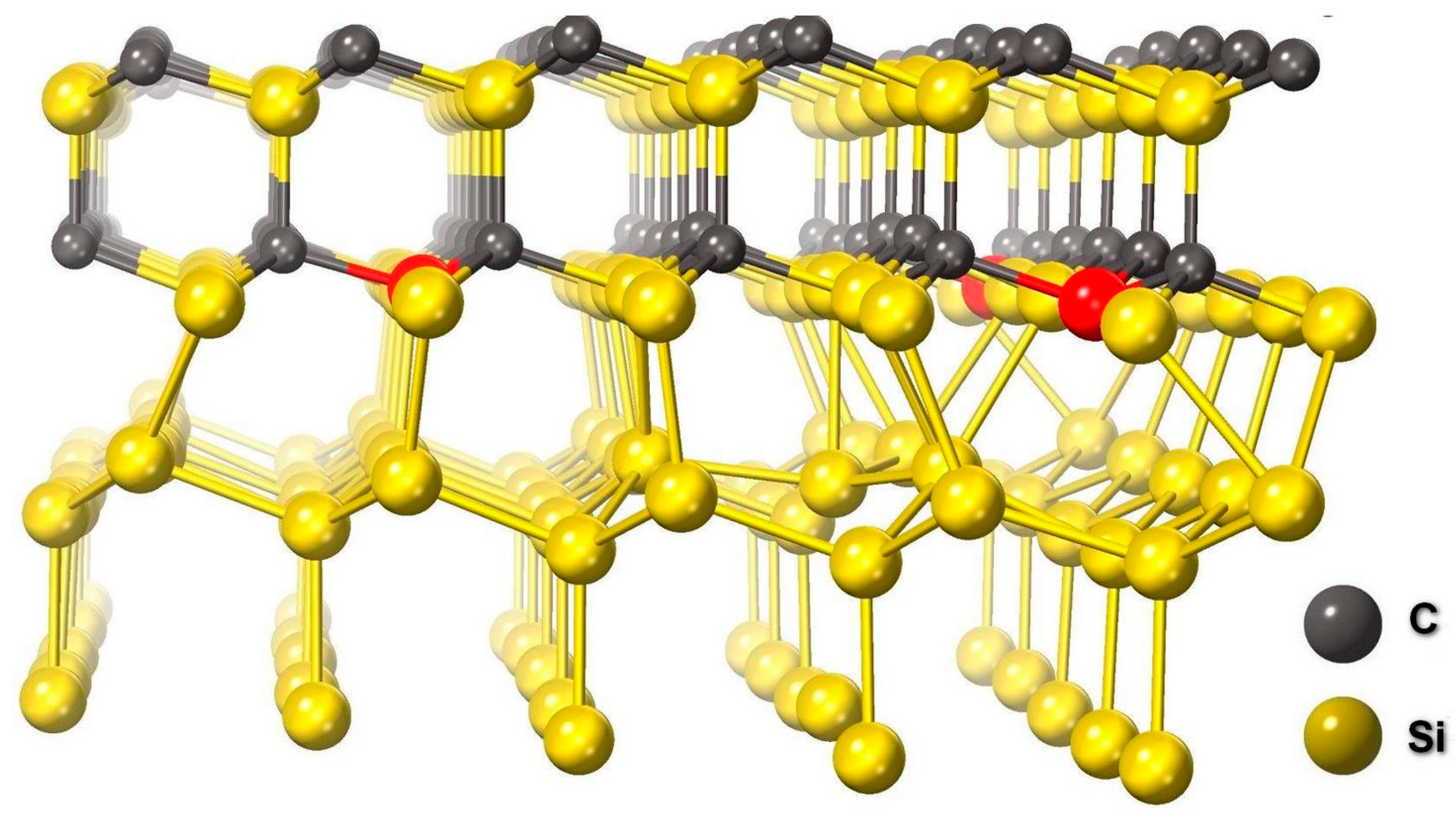
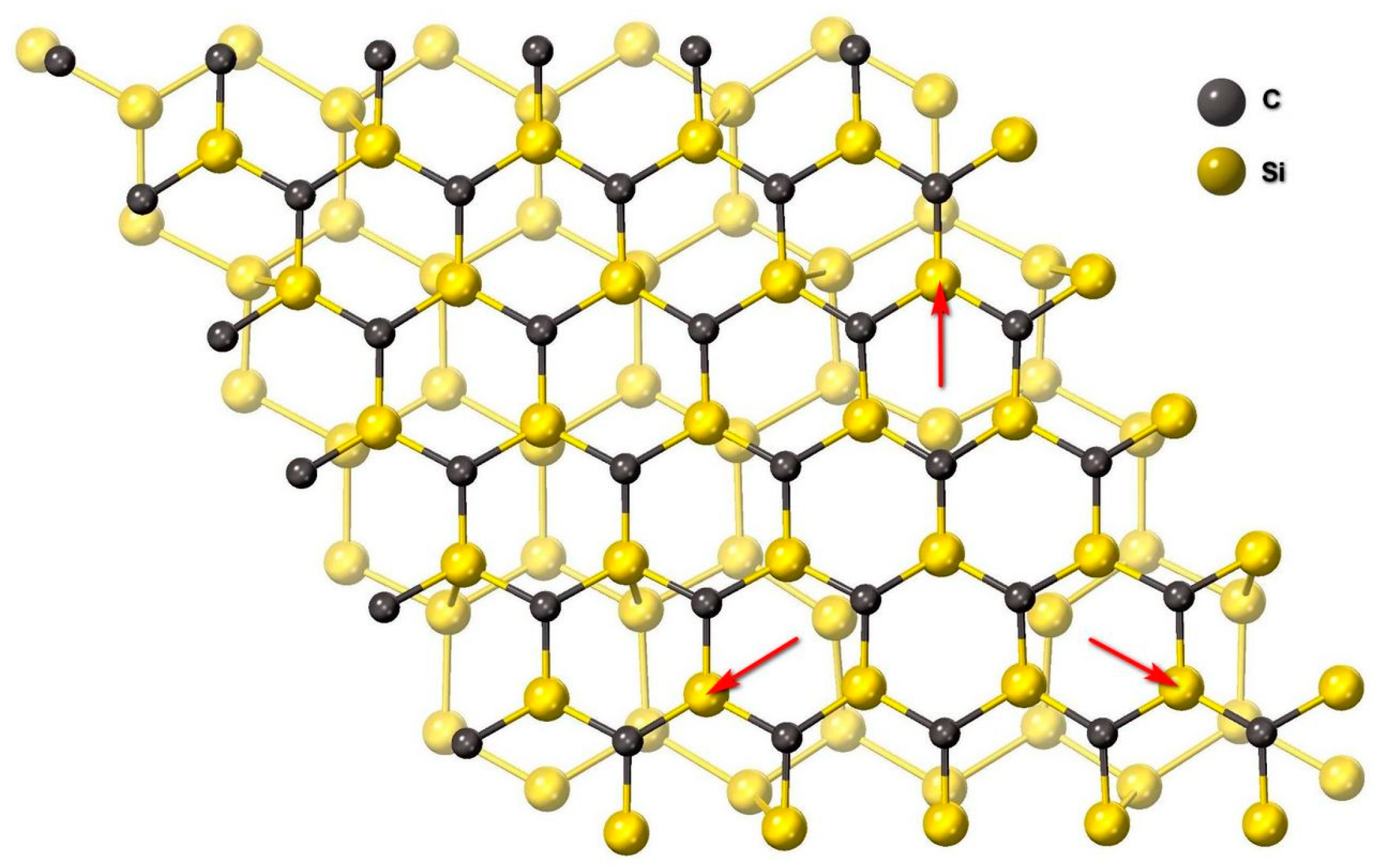
3. Analysis of a 3C-SiC(111)/Si(111) Interface Obtained by the Epitaxial Method of Coordinated Substitution of Atoms
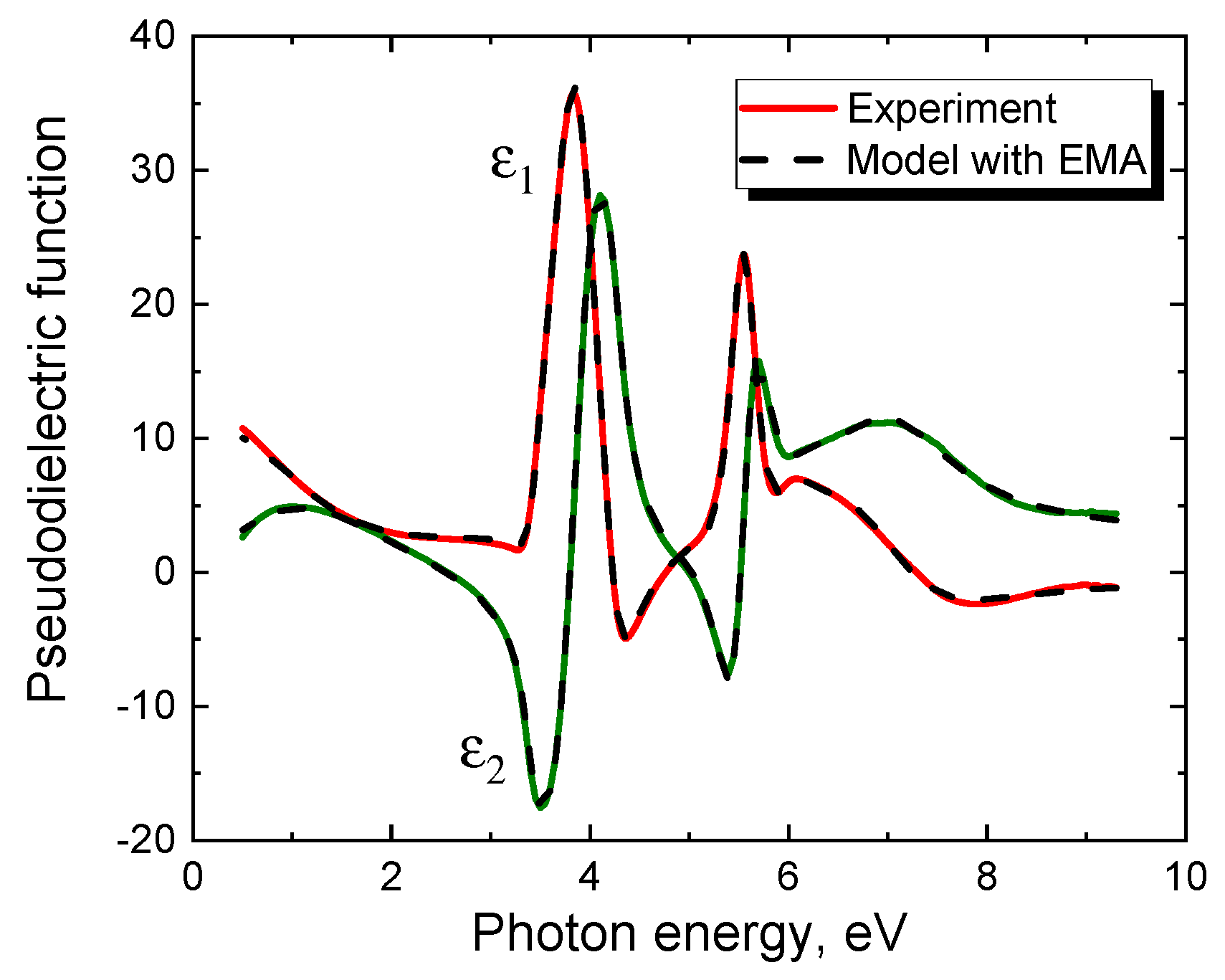
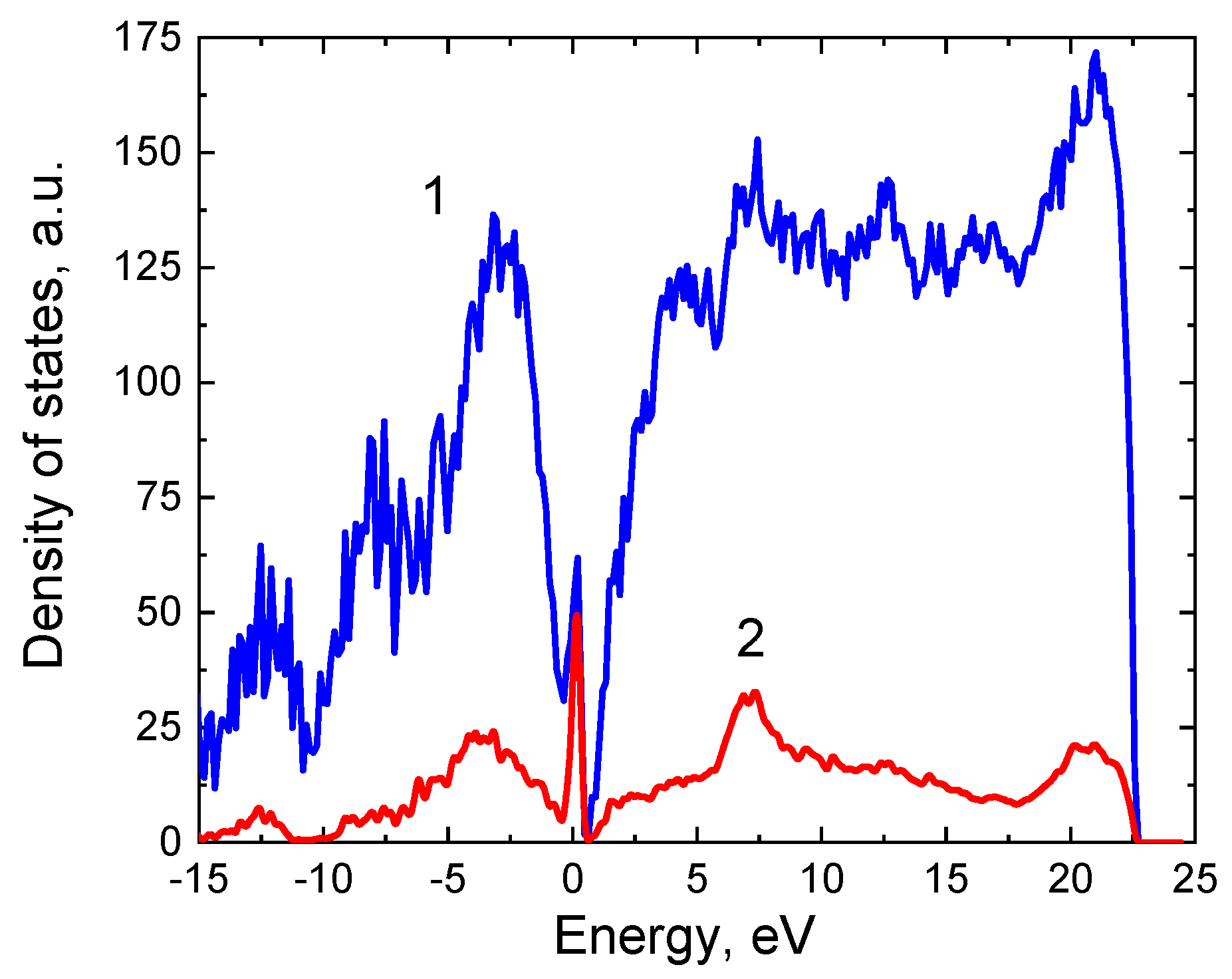
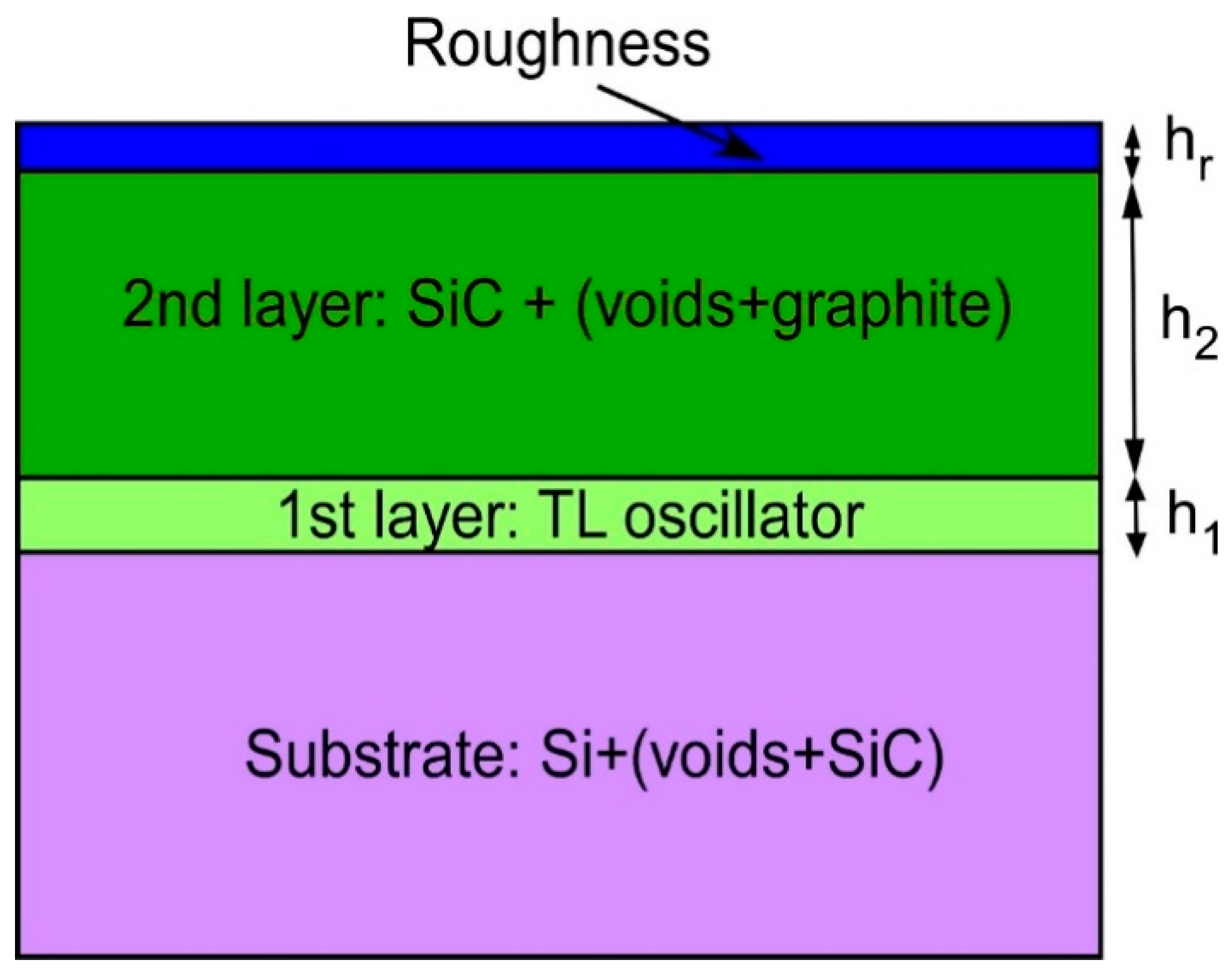
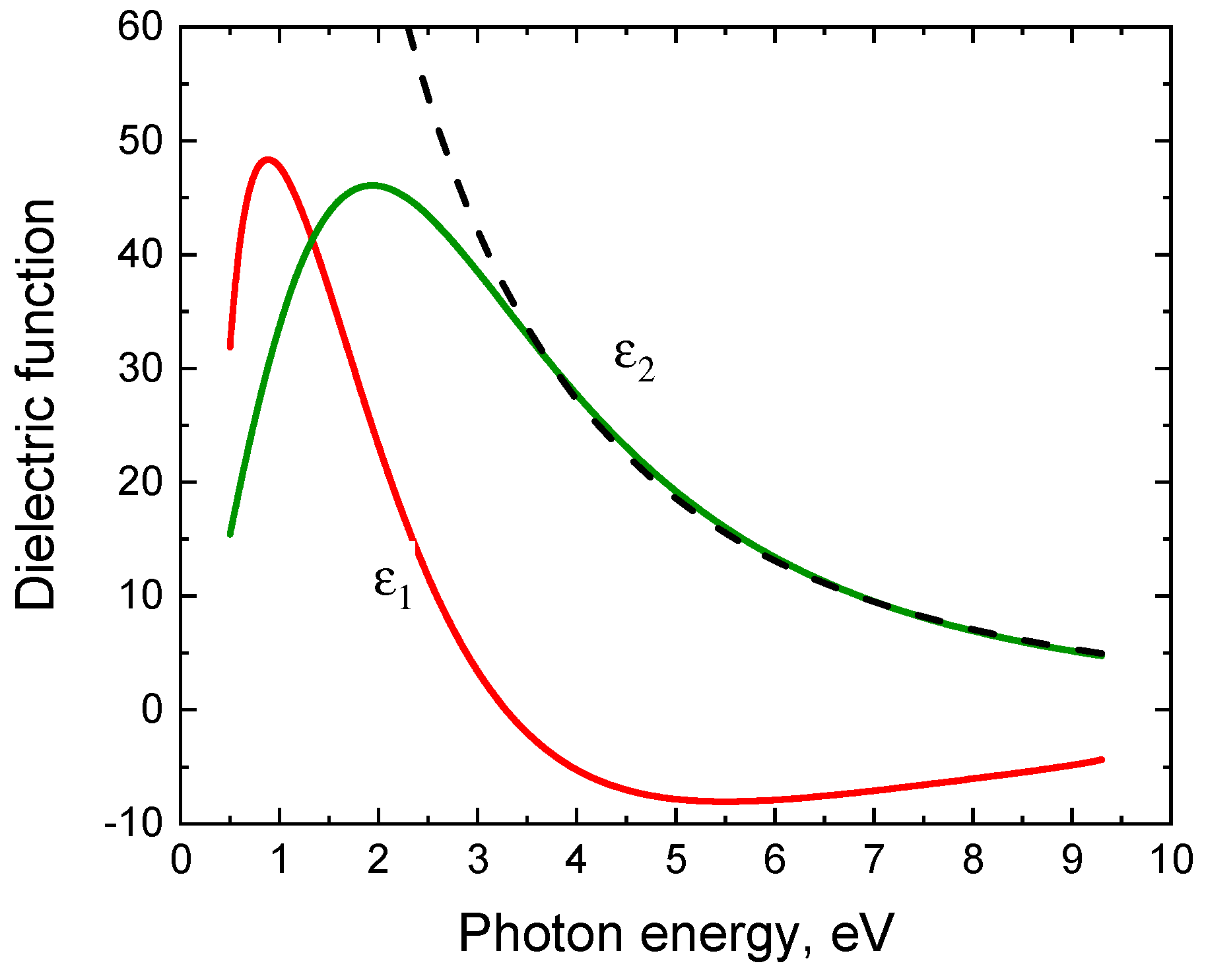
4. Ellipsometric Analysis of the 3C-SiC(111)/Si(111) Samples with an Account of the Semimetal Layer at the Interface
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kimoto, T.; Cooper, J.A. Fundamentals of Silicon Carbide Technology: Growth, Characterization, Devices and Applications; Wiley-IEEE Press: Singapore, 2014; p. 400. [Google Scholar]
- Kukushkin, S.A.; Osipov, A.V. Theory and practice of SiC growth on Si and its applications to wide-gap semiconductor films. J. Phys. D Appl. Phys. 2014, 47, 313001. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Quantum mechanical theory of epitaxial transformation of silicon to silicon carbide. J. Phys. D Appl. Phys. 2017, 50, 464006. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V.; Feoktistov, N.A. Synthesis of epitaxial silicon carbide films through the substitution of atoms in the silicon crystal lattice: A review. Phys. Solid State 2014, 56, 1507–1535. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Drift mechanism of mass transfer on heterogeneous reaction in crystalline silicon substrate. Phys. B Condens. Matter 2017, 512, 26–31. [Google Scholar] [CrossRef]
- Fujiwara, H.; Collins, R.W. Spectroscopic Ellipsometry for Photovoltaics V.1. Fundamental Principles and Solar Cell Characterization; Springer: Cham, Switzerland, 2018; p. 594. [Google Scholar]
- Jellison, G.E.; Modine, F.A. Parameterization of the optical functions of amorphous materials in the interband region. Appl. Phys. Lett. 1996, 69, 371–373. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Phase Equilibrium in the Formation of Silicon Carbide by Topochemical Conversion of Silicon. Phys. Solid State 2016, 58, 747–751. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. The Optical Properties, Energy Band Structure, and Interfacial Conductance of a 3C-SiC(111)/Si(111) Heterostructure Grown by the Method of Atomic Substitution. Tech. Phys. Lett. 2020, 46, 1103–1106. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. A Quantum-Mechanical Model of Dilatation Dipoles in Topochemical Synthesis of Silicon Carbide from Silicon. Phys. Solid State 2017, 59, 1238–1241. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. The Gorsky Effect in the Synthesis of Silicon-Carbide Films from Silicon by Topochemical Substitution of Atoms. Tech. Phys. Lett. 2017, 43, 631–634. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V.; Soshnikov, I.P. Growth of epitaxial SiC layer on Si (100) surface of n- and p- type of conductivity by the atoms substitution method. Rev. Adv. Mater. 2017, 52, 29–42. [Google Scholar]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Abavare EK, K.; Iwata, J.I.; Yaya, A.; Oshiyama, A. Surface energy of Si(110)- and 3C-SiC(111)-terminated surfaces. Phys. Status Solidi B 2014, 251, 1408–1415. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Adachi, S. The Handbook of Optical Constants of Metals; World Scientific: Singapore, 2012; p. 671. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kukushkin, S.A.; Osipov, A.V. Anomalous Properties of the Dislocation-Free Interface between Si(111) Substrate and 3C-SiC(111) Epitaxial Layer. Materials 2021, 14, 78. https://doi.org/10.3390/ma14010078
Kukushkin SA, Osipov AV. Anomalous Properties of the Dislocation-Free Interface between Si(111) Substrate and 3C-SiC(111) Epitaxial Layer. Materials. 2021; 14(1):78. https://doi.org/10.3390/ma14010078
Chicago/Turabian StyleKukushkin, Sergey A., and Andrey V. Osipov. 2021. "Anomalous Properties of the Dislocation-Free Interface between Si(111) Substrate and 3C-SiC(111) Epitaxial Layer" Materials 14, no. 1: 78. https://doi.org/10.3390/ma14010078
APA StyleKukushkin, S. A., & Osipov, A. V. (2021). Anomalous Properties of the Dislocation-Free Interface between Si(111) Substrate and 3C-SiC(111) Epitaxial Layer. Materials, 14(1), 78. https://doi.org/10.3390/ma14010078





