DFT Study of MAX Phase Surfaces for Electrocatalyst Support Materials in Hydrogen Fuel Cells
Abstract
1. Introduction
2. Theoretical Method
3. Results and Discussion
3.1. Bulk Properties
3.2. Electronic Properties
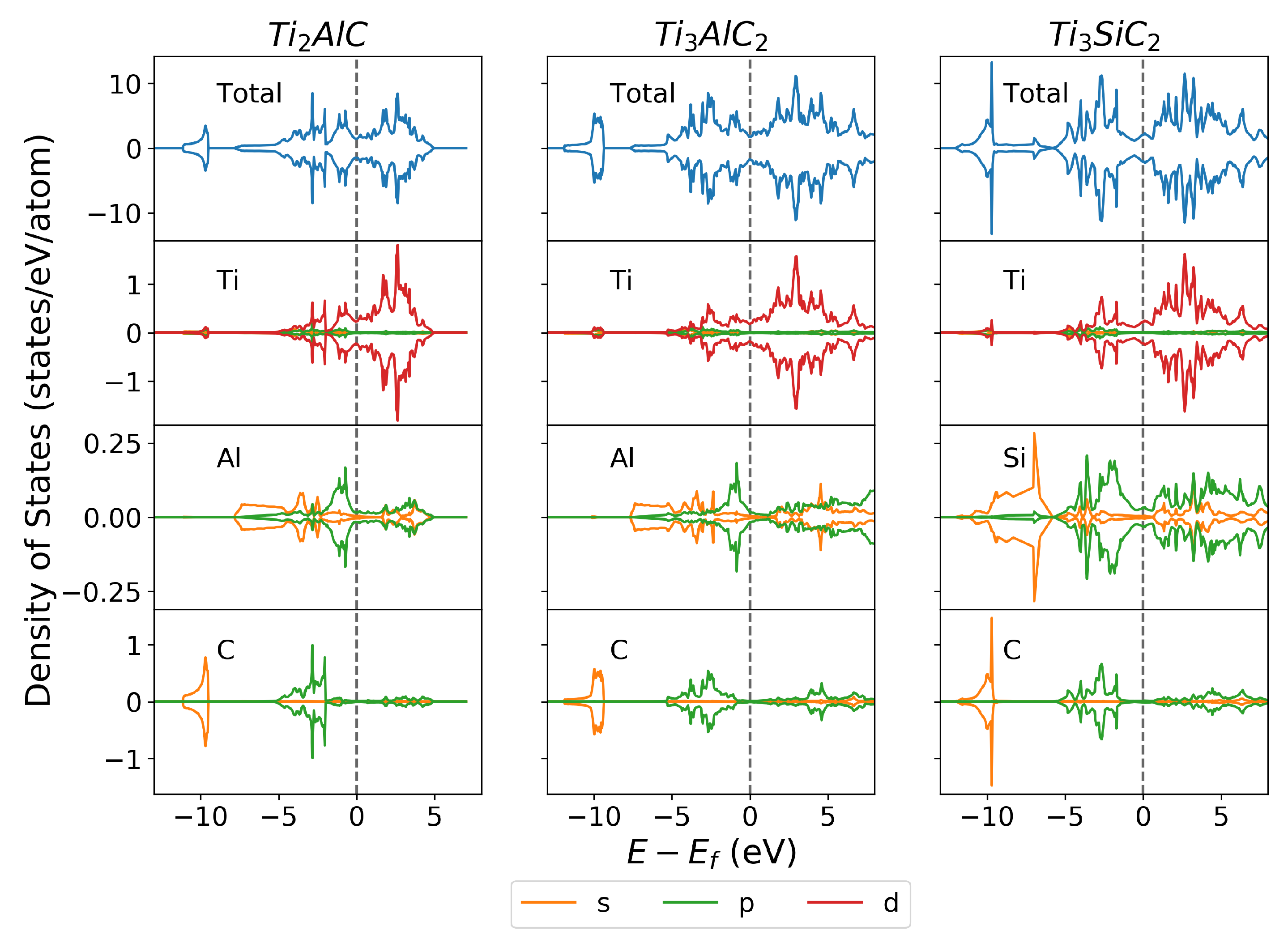
3.2.1. Density of States
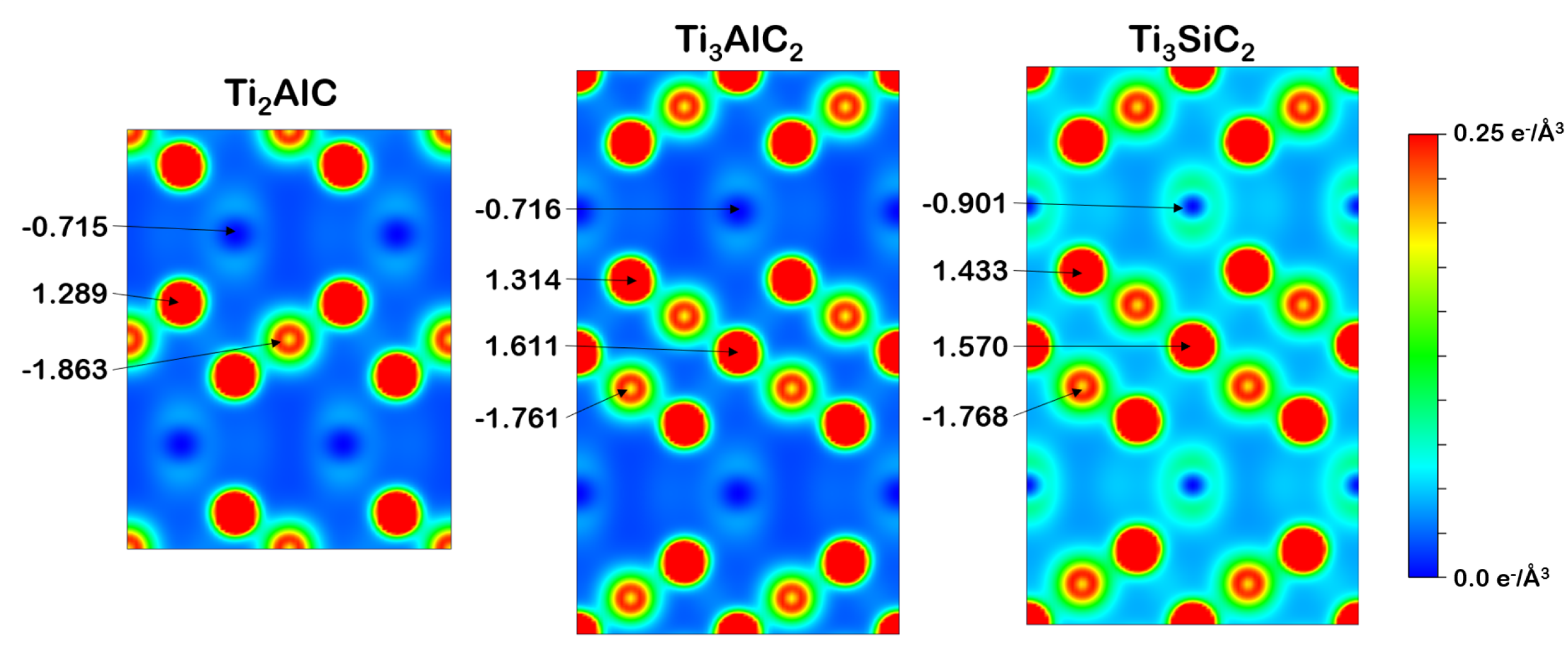
3.2.2. Charge Density and Bader Charge Analysis
3.2.3. Vacancy Formation Energy
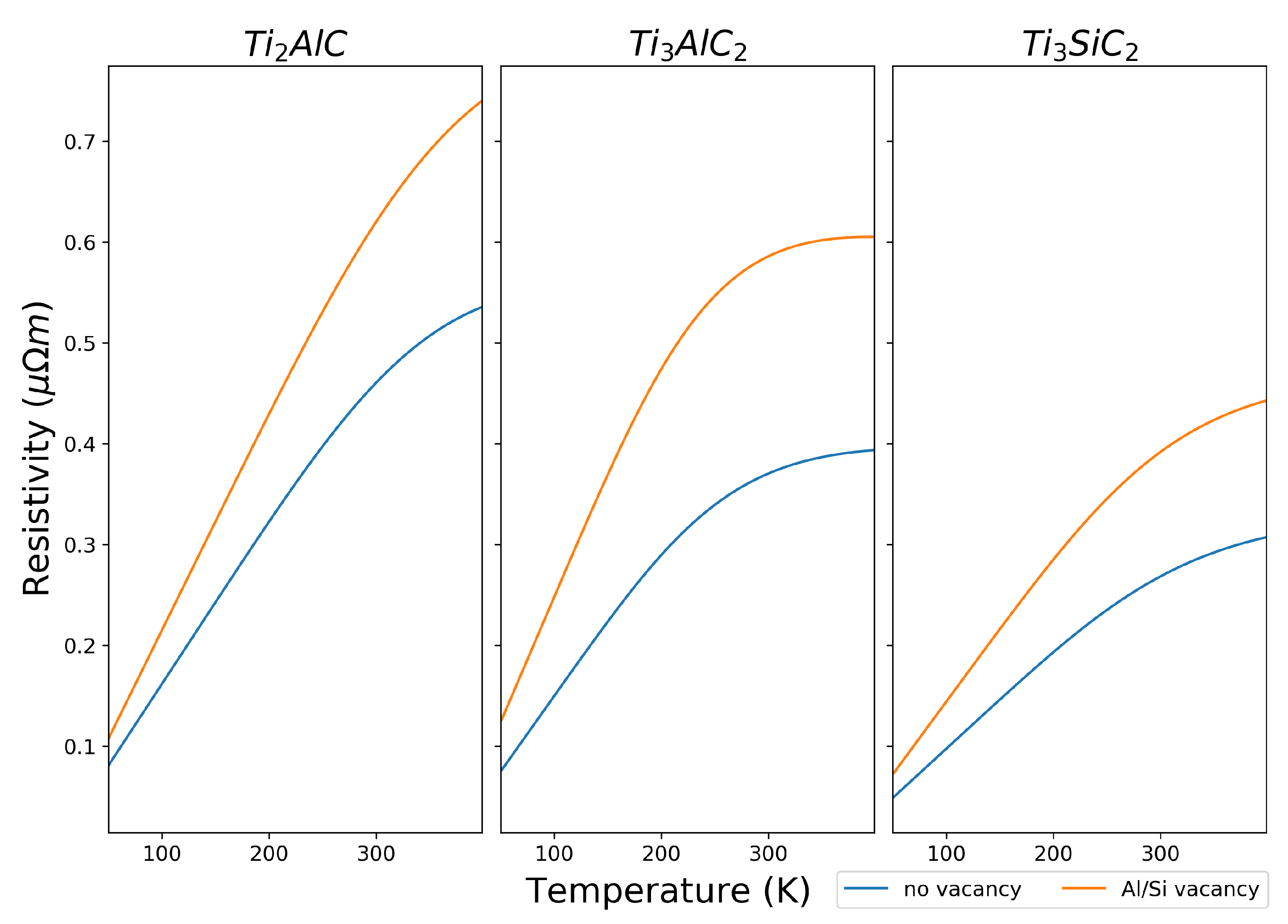
3.2.4. Electrical Conductivity
3.3. Cleavage Energies
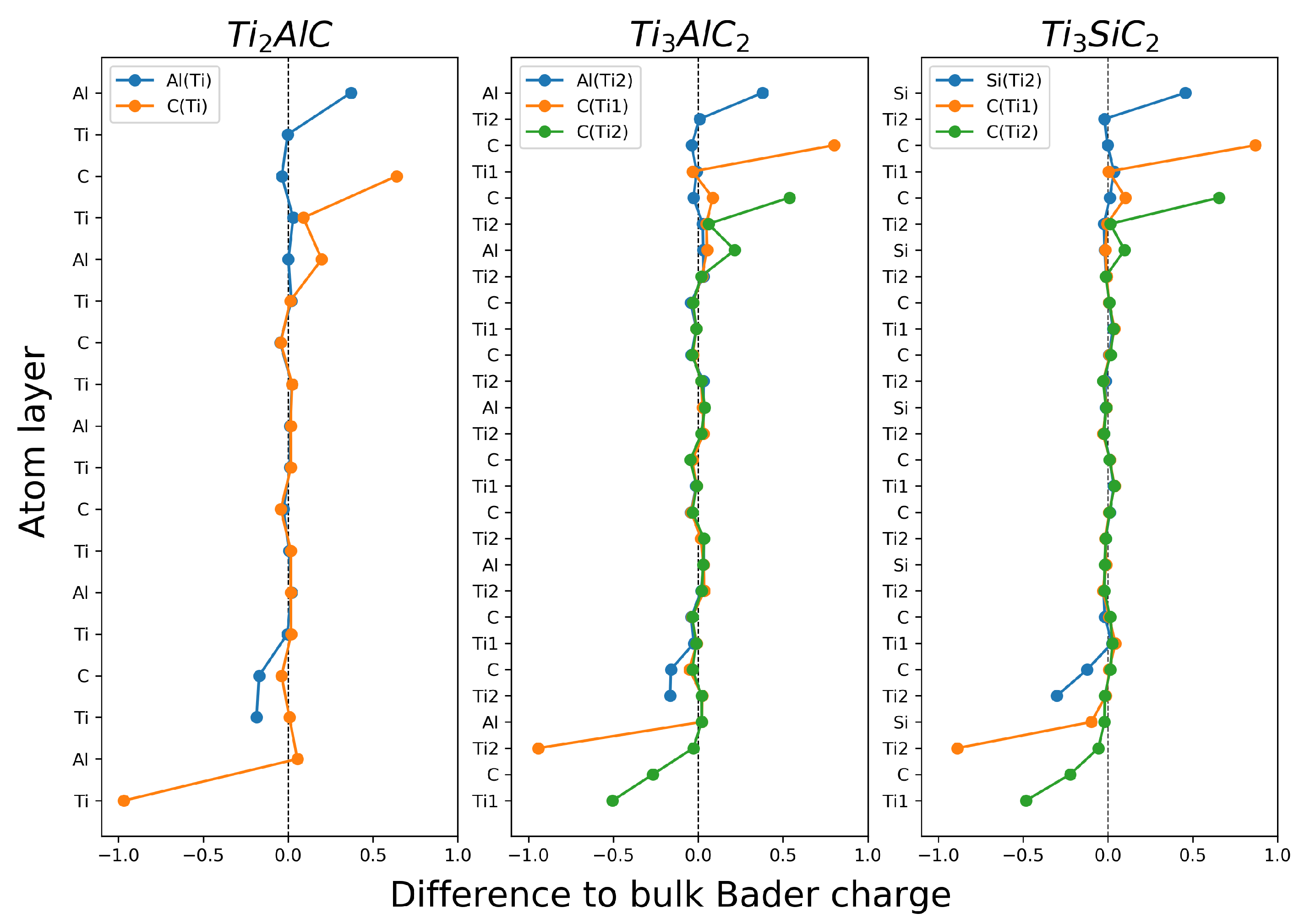
Surface Bader Charge Difference
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barsoum, M.W. MAX Phases, 1st ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013. [Google Scholar]
- Barsoum, M.W.; Radovic, M. Elastic and Mechanical Properties of the MAX Phases. Annu. Rev. Mater. Res. 2011, 41, 195–227. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Layered Machinable and Electrically Conductive Ti2AlC and Ti3AlC2 Ceramics: A Review. J. Mater. Sci. Technol. 2010, 26, 385–416. [Google Scholar] [CrossRef]
- Jeitschko, W.; Nowotny, H. Die Kristallstruktur von Ti3SiC2—Ein neuer Komplexcarbid-Typ. Monatshefte für Chemie Chemical Monthly 1967, 98, 329–337. [Google Scholar] [CrossRef]
- Nowotny, V.H. Strukturchemie einiger verbindungen der übergangsmetalle mit den elementen C, Si, Ge, Sn. Prog. Solid State Chem. 1971, 5, 27–70. [Google Scholar] [CrossRef]
- Wolfsgruber, H.; Nowotny, H.; Benesovsky, F. Die Kristallstruktur von Ti3GeC2. Monatshefte für Chemie und Verwandte Teile Anderer Wissenschaften 1967, 98, 2403–2405. [Google Scholar] [CrossRef]
- Pietzka, M.A.; Schuster, J.C. Summary of constitutional data on the aluminum-carbon-titanium system. J. Phase Equilibria 1994, 15, 392–400. [Google Scholar] [CrossRef]
- Pietzka, M.A.; Schuster, J.C. Phase Equilibria in the Quaternary System Ti-Al-C-N. J. Am. Ceram. Soc. 1996, 79, 2321–2330. [Google Scholar] [CrossRef]
- Barsoum, M.W.; El-Raghy, T. Synthesis and Characterization of a Remarkable Ceramic: Ti3SiC2. J. Am. Ceram. Soc. 1996, 79, 1953–1956. [Google Scholar] [CrossRef]
- Barsoum, M.W. Physical Properties of the MAX Phases. Encycl. Mater. Sci. Technol. 2006, 1, 1–6. [Google Scholar] [CrossRef]
- Sharma, S.; Pollet, B.G. Support materials for PEMFC and DMFC electrocatalysts—A review. J. Power Sources 2012, 208, 96–119. [Google Scholar] [CrossRef]
- Sun, Z.; Ahuja, R. Ab initio study of the Cr2AlC (0001) surface. Appl. Phys. Lett. 2006, 88, 161913. [Google Scholar] [CrossRef]
- Music, D.; Sun, Z.; Ahuja, R.; Schneider, J.M. Electronic structure of M2AlC (0001) surfaces (M = Ti, V, Cr). J. Phys. Condens. Matter 2006, 18, 8877–8881. [Google Scholar] [CrossRef]
- Music, D.; Sun, Z.; Ahuja, R.; Schneider, J.M. Surface energy of M2AC (0001) determined by density functional theory (M = Ti, V, Cr; A = Al, Ga, Ge). Surf. Sci. 2007, 601, 896–899. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.Y.; Zhou, Y.C. Stable M2AlC (0001) surfaces (M = Ti, V and Cr) by first-principles investigation. J. Phys. Condens. Matter 2008, 20. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Wang, S.Q. First-principles study of Ti3AC2 (A = Si, Al) (001) surfaces. Acta Mater. 2007, 55, 4645–4655. [Google Scholar] [CrossRef]
- Orellana, W.; Gutiérrez, G. First-principles calculations of the thermal stability of Ti3SiC2 (0001) surfaces. Surf. Sci. 2011, 605, 2087–2091. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhou, Y.C.; Liao, T.; Zhang, J.; Lin, Z. A first-principles investigation of the phase stability of Ti2AlC with Al vacancies. Scr. Mater. 2008, 58, 227–230. [Google Scholar] [CrossRef]
- Liao, T.; Wang, J.Y.; Zhou, Y.C. Ab initio modeling of the formation and migration of monovacancies in Ti2AlC. Scr. Mater. 2008, 59, 854–857. [Google Scholar] [CrossRef]
- Liao, T.; Wang, J.Y.; Zhou, Y.C. First-principles investigation of intrinsic defects and (N, O) impurity atom stimulated Al vacancy in Ti2AlC. Appl. Phys. Lett. 2008, 93, 261911. [Google Scholar] [CrossRef]
- Tan, J.; Han, H.; Wickramaratne, D.; Liu, W.; Zhao, M.; Huai, P. A comparative first-principles study of the electronic, mechanical, defect and acoustic properties of Ti2AlC and Ti3AlC. J. Phys. D Appl. Phys. 2014, 47, 215301. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B.; Wang, J.Y.; Zhou, Y.C. Theoretical investigation of thermodynamic stability and mobility of the intrinsic point defects in Ti3AC2 (A = Si, Al). Phys. Chem. Chem. Phys. 2015, 17, 8927–8934. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Han, H.; Yin, G.; Wang, C.Y.; Hou, Y.Y.; Tang, J.; Dai, J.X.; Ren, C.L.; Zhang, W.; Huai, P. First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2. Materials 2017, 10, 103. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Xue, J.; Wang, Y.; Huang, Q. Ab initio study of irradiation tolerance for different Mn+1AXn phases: Ti3SiC2 and Ti3AlC2. J. Appl. Phys. 2014, 115, 023503. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Wang, J.Y.; Zhou, Y.C.; Peng, S.; Long, X. Role of Nanolaminated Crystal Structure on the Radiation Damage Tolerance of Ti3SiC2: Theoretical Investigation of Native Point Defects. J. Nanomater. 2013, 2013, 831590. [Google Scholar] [CrossRef]
- Middleburgh, S.C.; Lumpkin, G.R.; Riley, D. Accommodation, Accumulation, and Migration of Defects in Ti3SiC2 and Ti3AlC2 MAX Phases. J. Am. Ceram. Soc. 2013, 96, 3196–3201. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Oxidation behavior of Ti3AlC2 powders in flowing air. J. Mater. Chem. 2002, 12, 2781–2785. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Oxidation behavior of Ti3AlC2 at 1000–1400 °C in air. Corros. Sci. 2003, 45, 891–907. [Google Scholar] [CrossRef]
- Barsoum, M.W.; El-Raghy, T.; Ogbuji, L.U.J.T. Oxidation Of Ti3SiC2 in Air. J. Electrochem. Soc. 1997, 144, 2508. [Google Scholar] [CrossRef]
- Sun, Z.; Zhou, Y.; Li, M. High temperature oxidation behavior of Ti3SiC2-based material in air. Acta Mater. 2001, 49, 4347–4353. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.; Vosko, S.; Jackson, K.; Pederson, M.; Singh, D.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. Condens. Matter Mater. Phys. 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Chadi, D.J.; Cohen, M.L. Special Points in the Brillouin Zone. Phys. Rev. B 1973, 8, 5747–5753. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Barsoum, M.W. The MN+1AXN phases: A new class of solids. Prog. Solid State Chem. 2000, 28, 201–281. [Google Scholar] [CrossRef]
- Hettinger, J.D.; Lofland, S.E.; Finkel, P.; Meehan, T.; Palma, J.; Harrell, K.; Gupta, S.; Ganguly, A.; El-Raghy, T.; Barsoum, M.W. Electrical transport, thermal transport, and elastic properties of M2AlC (M = Ti, Cr, Nb, and V). Phys. Rev. B 2005, 72, 115120. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.H.; Huang, M.; Cuma, M.; Liu, F. Relative stability of Si surfaces: A first-principles study. Surf. Sci. 2005, 588, 61–70. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Madsen, G.K.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]
- Lane, N.J.; Naguib, M.; Lu, J.; Hultman, L.; Barsoum, M.W. Structure of a new bulk Ti5Al2C3 MAX phase produced by the topotactic transformation of Ti2AlC. J. Eur. Ceram. Soc. 2012, 32, 3485–3491. [Google Scholar] [CrossRef]
- Schuster, J.C.; Nowotny, H.; Vaccaro, C. The ternary systems: CrAlC, VAlC, and TiAlC and the behavior of H-phases (M2AlC). J. Solid State Chem. 1980, 32, 213–219. [Google Scholar] [CrossRef]
- Son, W.; Duong, T.; Talapatra, A.; Gao, H.; Arróyave, R.; Radovic, M. Ab-initio investigation of the finite-temperatures structural, elastic, and thermodynamic properties of Ti3AlC2 and Ti3SiC2. Comput. Mater. Sci. 2016, 124, 420–427. [Google Scholar] [CrossRef]
- Jeitschko, W.; Nowotny, H.; Benesovsky, F. Carbides of formula T2MC. J. Less Common Met. 1964, 7, 133–138. [Google Scholar] [CrossRef]
- Mattsson, A.E.; Schultz, P.A.; Desjarlais, M.P.; Mattsson, T.R.; Leung, K. Designing meaningful density functional theory calculations in materials science—A primer. Model. Simul. Mater. Sci. Eng. 2005, 13. [Google Scholar] [CrossRef]
- Magnuson, M.; Mattesini, M. Chemical bonding and electronic-structure in MAX phases as viewed by X-ray spectroscopy and density functional theory. Thin Solid Films 2017, 621, 108–130. [Google Scholar] [CrossRef]
- Scabarozi, T.; Ganguly, A.; Hettinger, J.D.; Lofland, S.E.; Amini, S.; Finkel, P.; El-Raghy, T.; Barsoum, M.W. Electronic and thermal properties of Ti3Al(C0.5,N0.5)2, Ti2Al(C0.5,N0.5) and Ti2AlN. J. Appl. Phys. 2008, 104, 073713. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Microstructure and properties of Ti3AlC2 prepared by the solid–liquid reaction synthesis and simultaneous in-situ hot pressing process. Acta Mater. 2002, 50, 3143–3151. [Google Scholar] [CrossRef]
- Pantea, D.; Darmstadt, H.; Kaliaguine, S.; Sümmchen, L.; Roy, C. Electrical conductivity of thermal carbon blacks: Influence of surface chemistry. Carbon 2001, 39, 1147–1158. [Google Scholar] [CrossRef]
- Pawbake, A.; Waykar, R.; Jadhavar, A.; Kulkarni, R.; Waman, V.; Date, A.; Late, D.; Pathan, H.; Jadkar, S. Wide band gap and conducting tungsten carbide (WC) thin films prepared by hot wire chemical vapor deposition (HW-CVD) method. Mater. Lett. 2016, 183, 315–317. [Google Scholar] [CrossRef]
| MAX Phase | a | c | Bulk Modulus | Type | Source |
|---|---|---|---|---|---|
| Ti2AlC | 3.070 | 13.762 | 138.4 | DFT | this work |
| 3.067 | 13.75 | 136 | DFT | [56] | |
| 3.052 | 13.64 | - | Experimental | [57] | |
| - | - | 144 | Experimental | [45] | |
| 3.04 | 13.6 | - | Experimental | [3] | |
| Ti3AlC2 | 3.075 | 18.678 | 158.3 | DFT | this work |
| 3.083 | 18.66 | 156 | DFT | [56] | |
| 3.075 | 18.58 | - | Experimental | [7] | |
| 3.075 | 18.58 | 165 | Experimental | [3] | |
| 3.075 | 18.578 | 165 | Experimental | [44] | |
| Ti3SiC2 | 3.0665 | 17.865 | 193.8 | DFT | this work |
| 3.077 | 17.715 | 192.61 | DFT | [58] | |
| 3.068 | 17.67 | - | Experimental | [59] | |
| 3.0665 | 17.671 | 185 | Experimental | [44] | |
| 3.066 | 17.671 | - | Experimental | [4] |
| MAX Phase | Vacancy Formation Energy |
|---|---|
| Ti2AlC | 2.882 |
| Ti3AlC2 | 2.812 |
| Ti3SiC2 | 2.167 |
| MAX Phase | Surface | Mirror Surface | Cleavage Energy |
|---|---|---|---|
| Ti2AlC | Al(Ti) | Ti(C) | 1.924 |
| C(Ti) | Ti(Al) | 5.254 | |
| Ti3AlC2 | Al(Ti2) | Ti2(C) | 1.909 |
| C(Ti1) | Ti2(Al) | 6.480 | |
| C(Ti2) | Ti1(C) | 4.639 | |
| Ti3SiC2 | Si(Ti2) | Ti2(C) | 2.802 |
| C(Ti1) | Ti2(Si) | 6.479 | |
| C(Ti2) | Ti1(C) | 5.143 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gertzen, J.; Levecque, P.; Rampai, T.; van Heerden, T. DFT Study of MAX Phase Surfaces for Electrocatalyst Support Materials in Hydrogen Fuel Cells. Materials 2021, 14, 77. https://doi.org/10.3390/ma14010077
Gertzen J, Levecque P, Rampai T, van Heerden T. DFT Study of MAX Phase Surfaces for Electrocatalyst Support Materials in Hydrogen Fuel Cells. Materials. 2021; 14(1):77. https://doi.org/10.3390/ma14010077
Chicago/Turabian StyleGertzen, Jonathan, Pieter Levecque, Tokoloho Rampai, and Tracey van Heerden. 2021. "DFT Study of MAX Phase Surfaces for Electrocatalyst Support Materials in Hydrogen Fuel Cells" Materials 14, no. 1: 77. https://doi.org/10.3390/ma14010077
APA StyleGertzen, J., Levecque, P., Rampai, T., & van Heerden, T. (2021). DFT Study of MAX Phase Surfaces for Electrocatalyst Support Materials in Hydrogen Fuel Cells. Materials, 14(1), 77. https://doi.org/10.3390/ma14010077





