Constitutive Models for Dynamic Strain Aging in Metals: Strain Rate and Temperature Dependences on the Flow Stress †
Abstract
1. Introduction
2. Constitutive Models
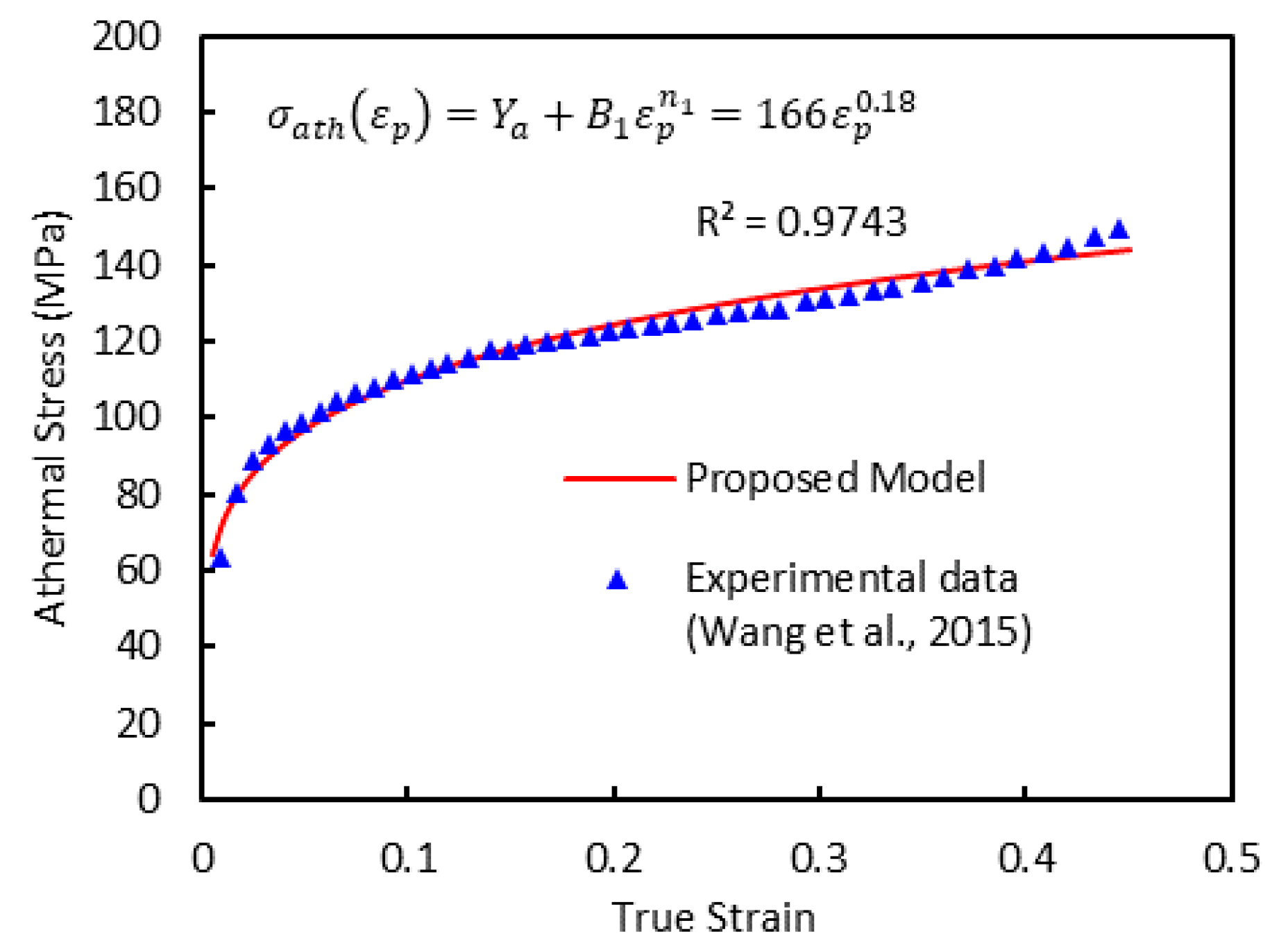
2.1. Athermal and Thermal Stresses
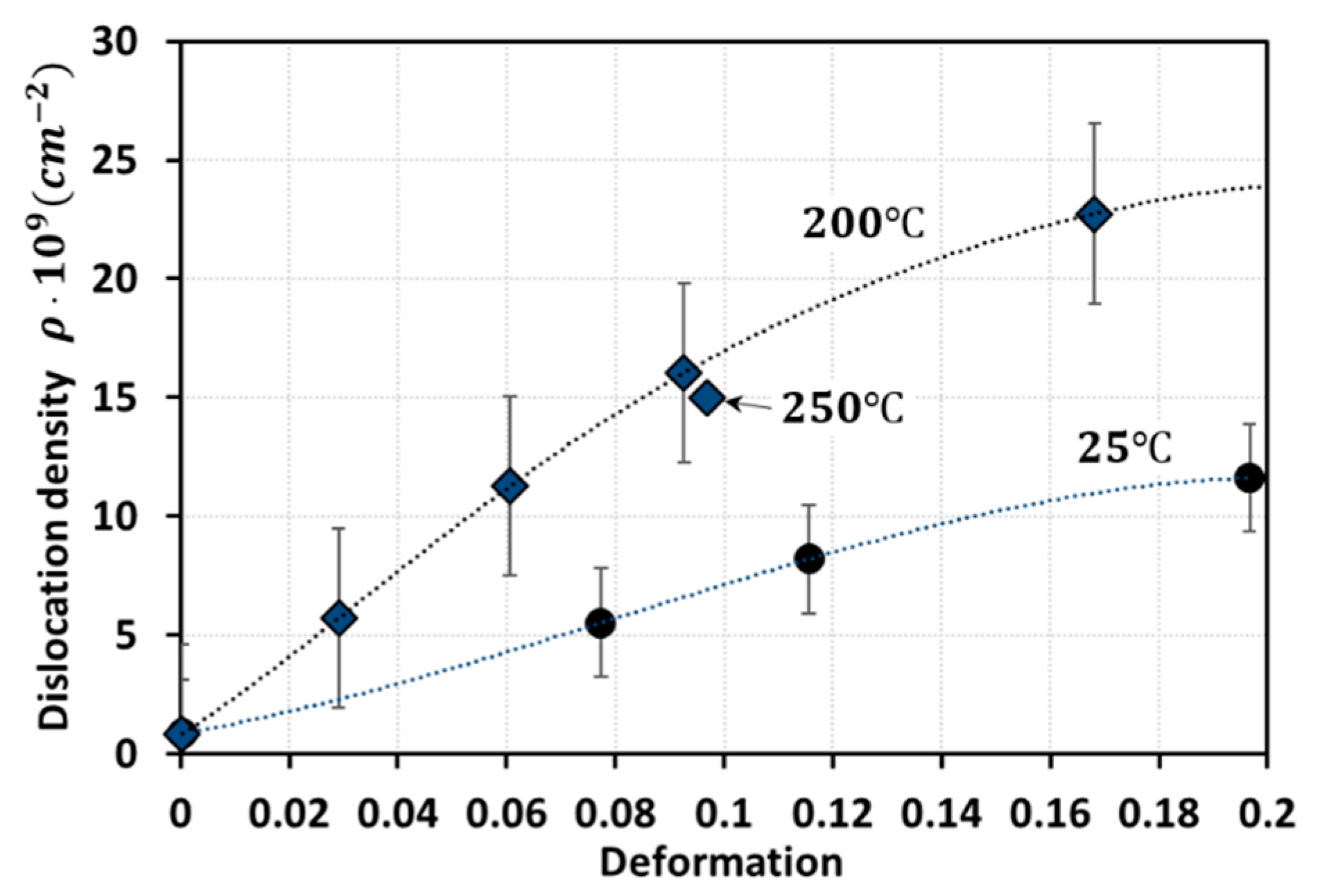
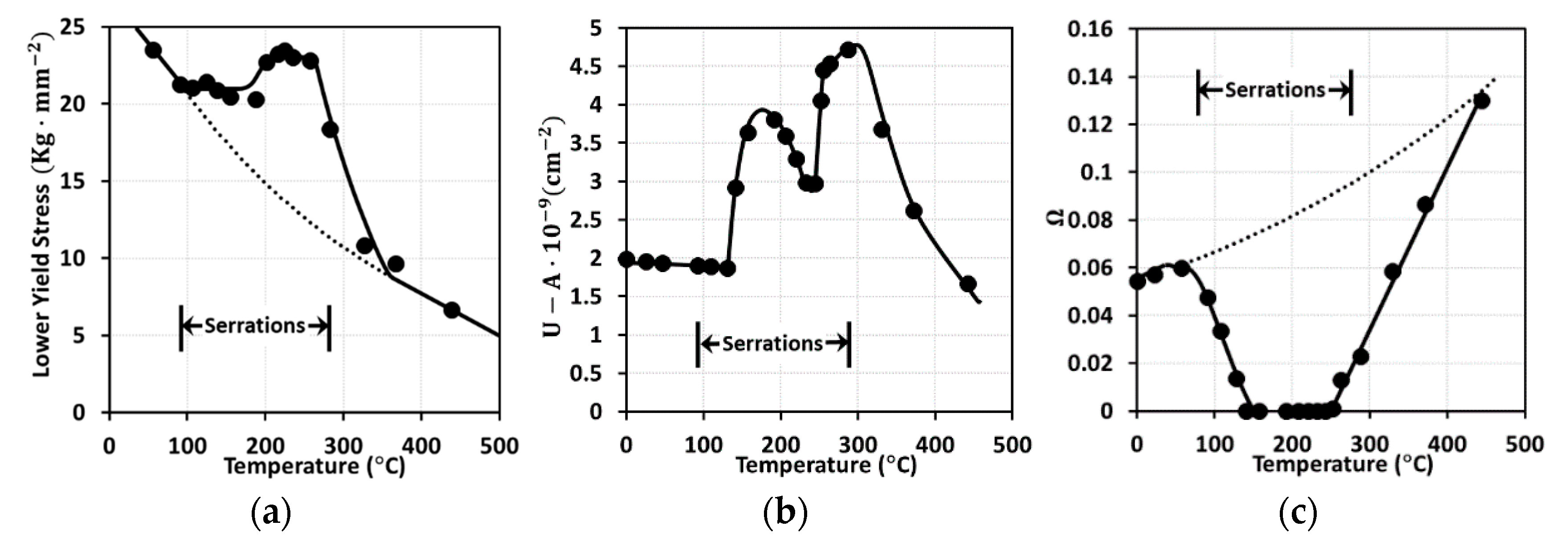
2.2. DSA-Induced Stress
2.2.1. Proposed Model I (PM I)
2.2.2. Proposed Model II (PM II)
3. Model Validation and Calibration
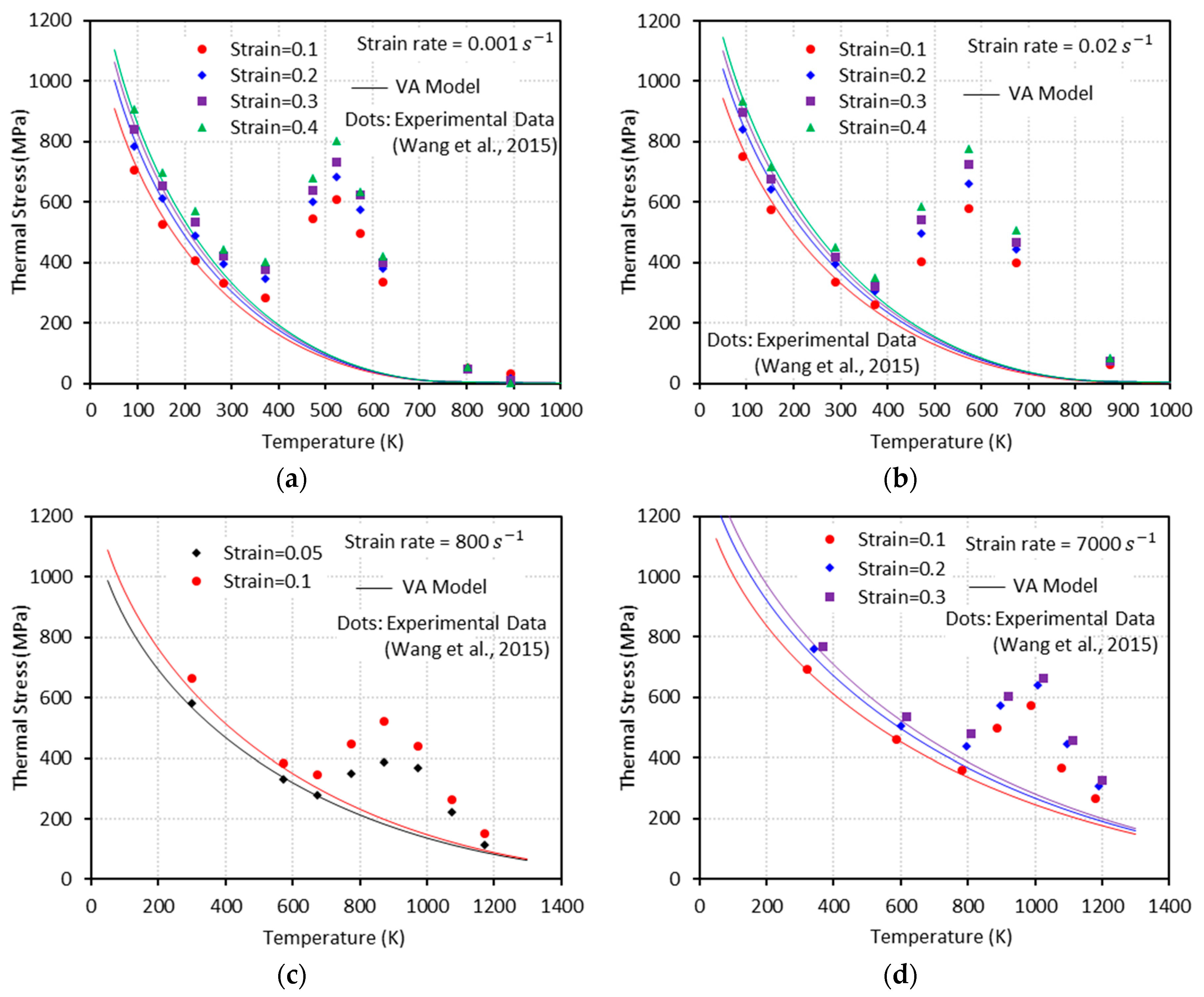
3.1. Athermal and Thermal Stressesl
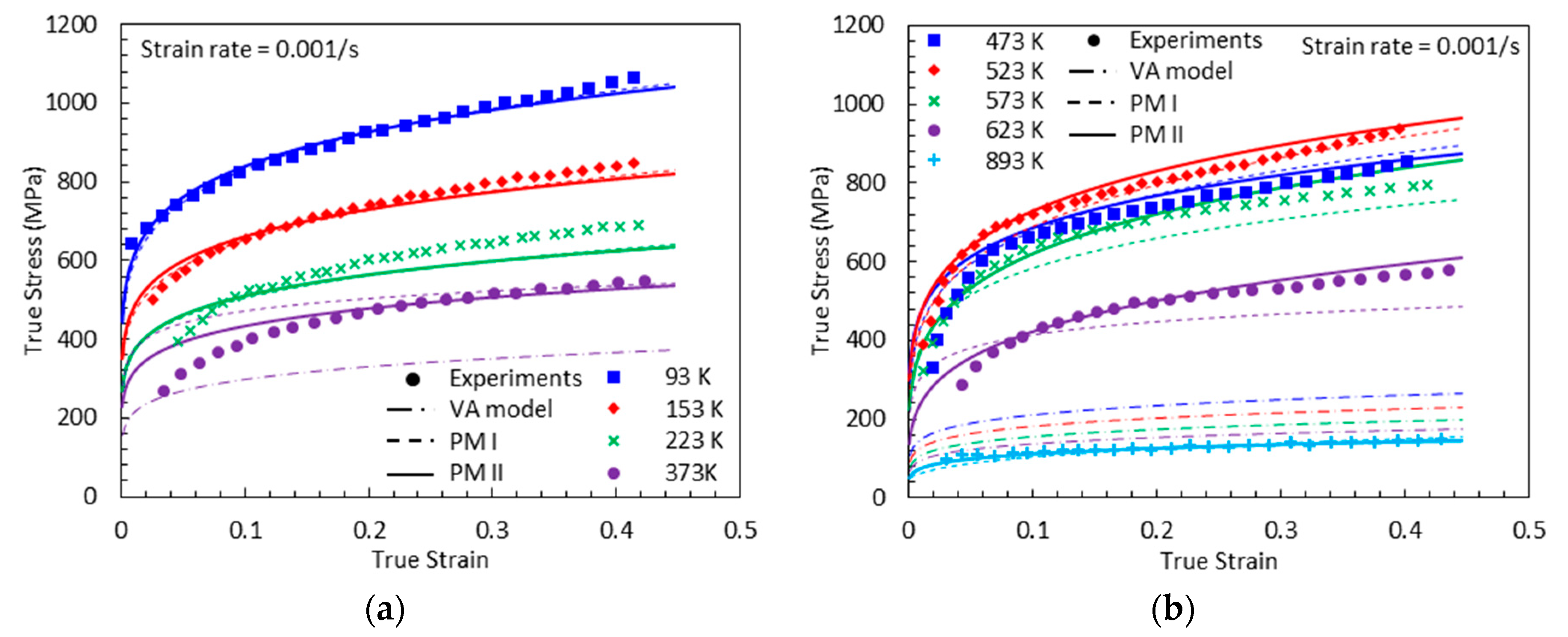
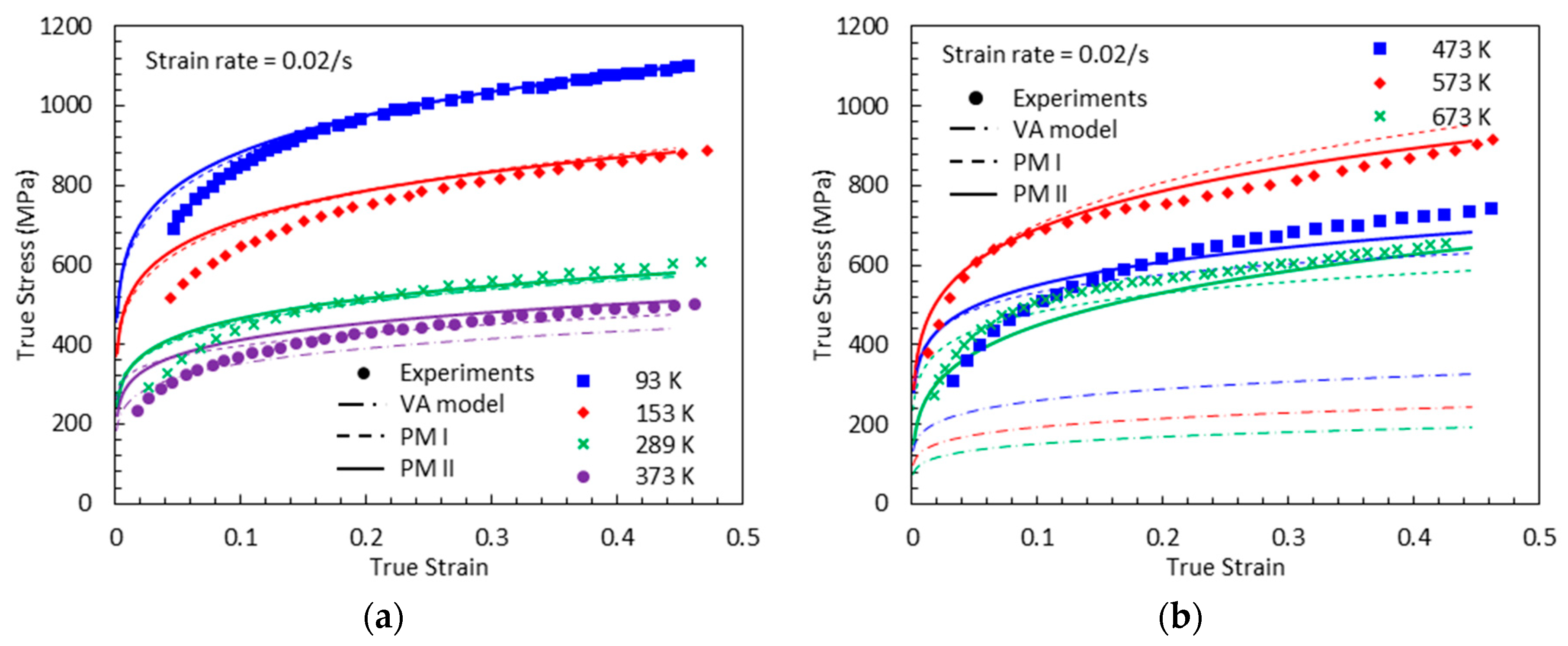
3.2. DSA-Induced Stress
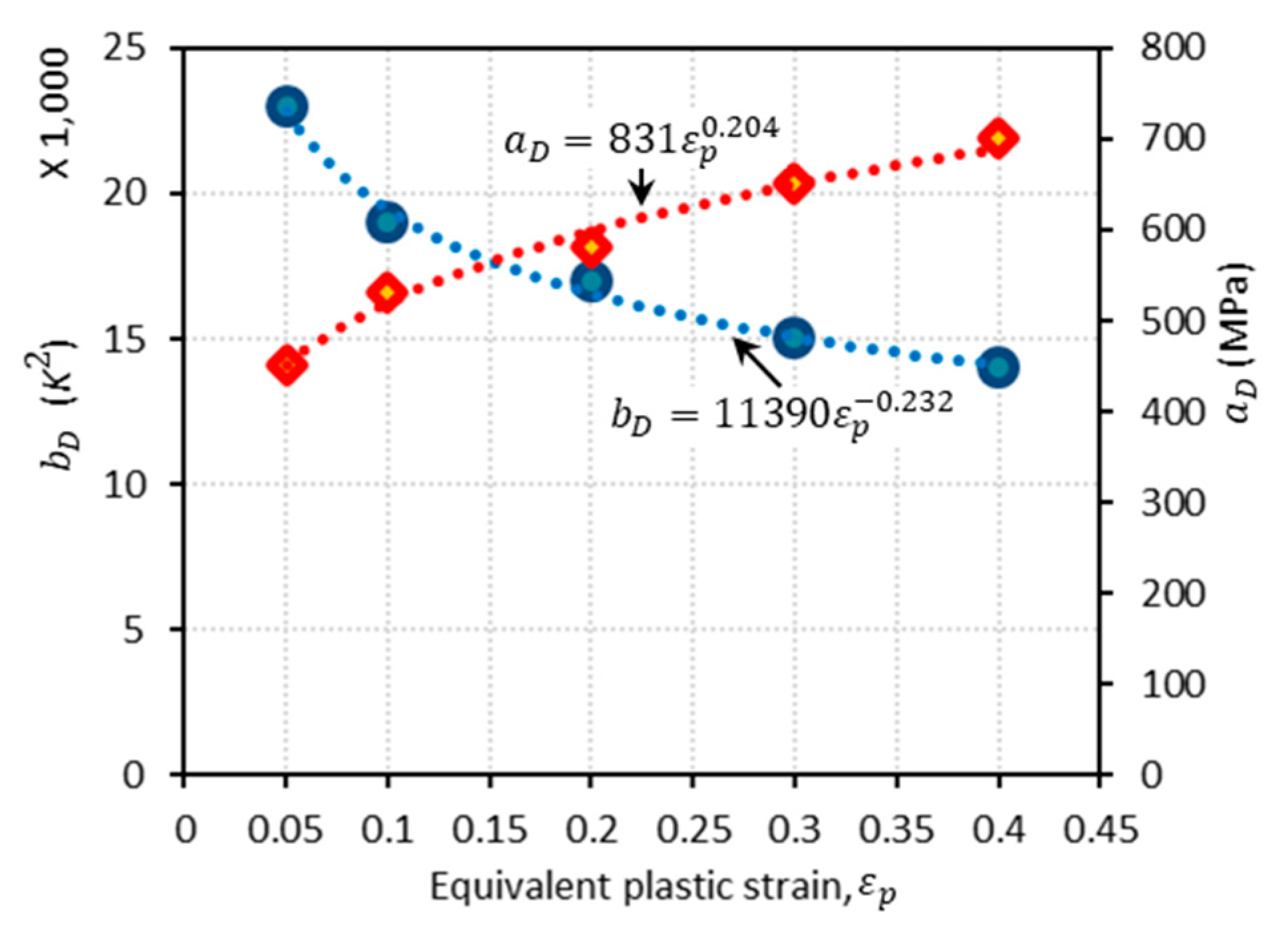
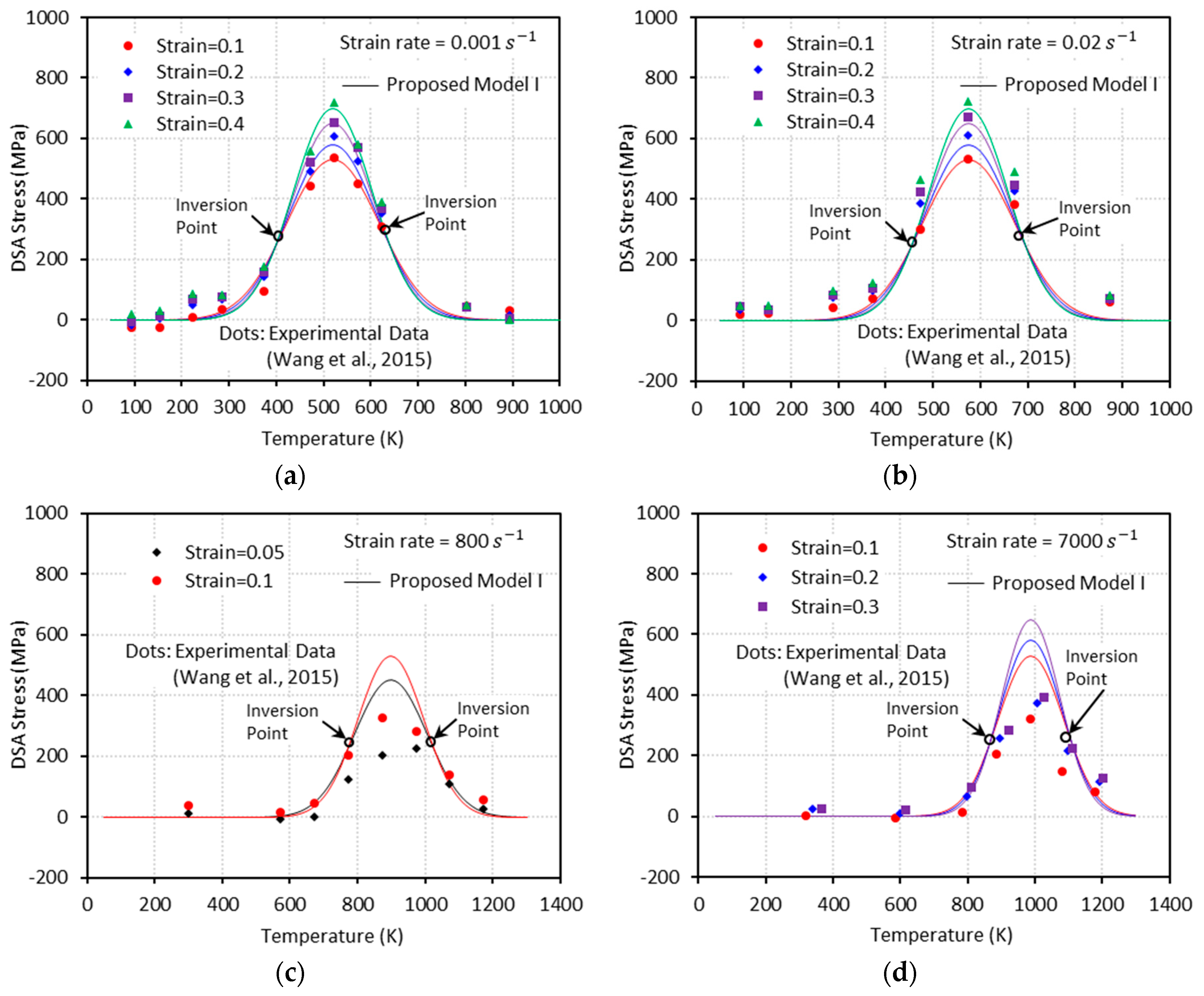
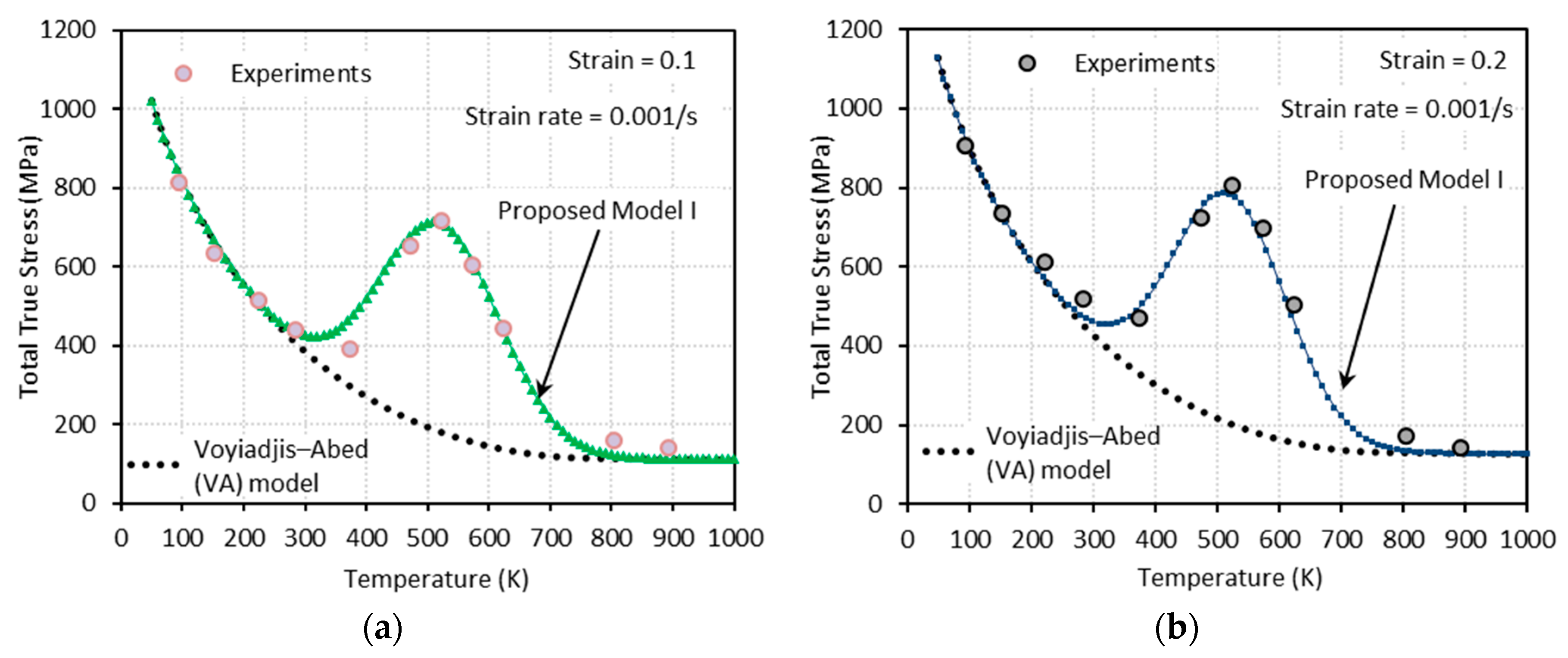
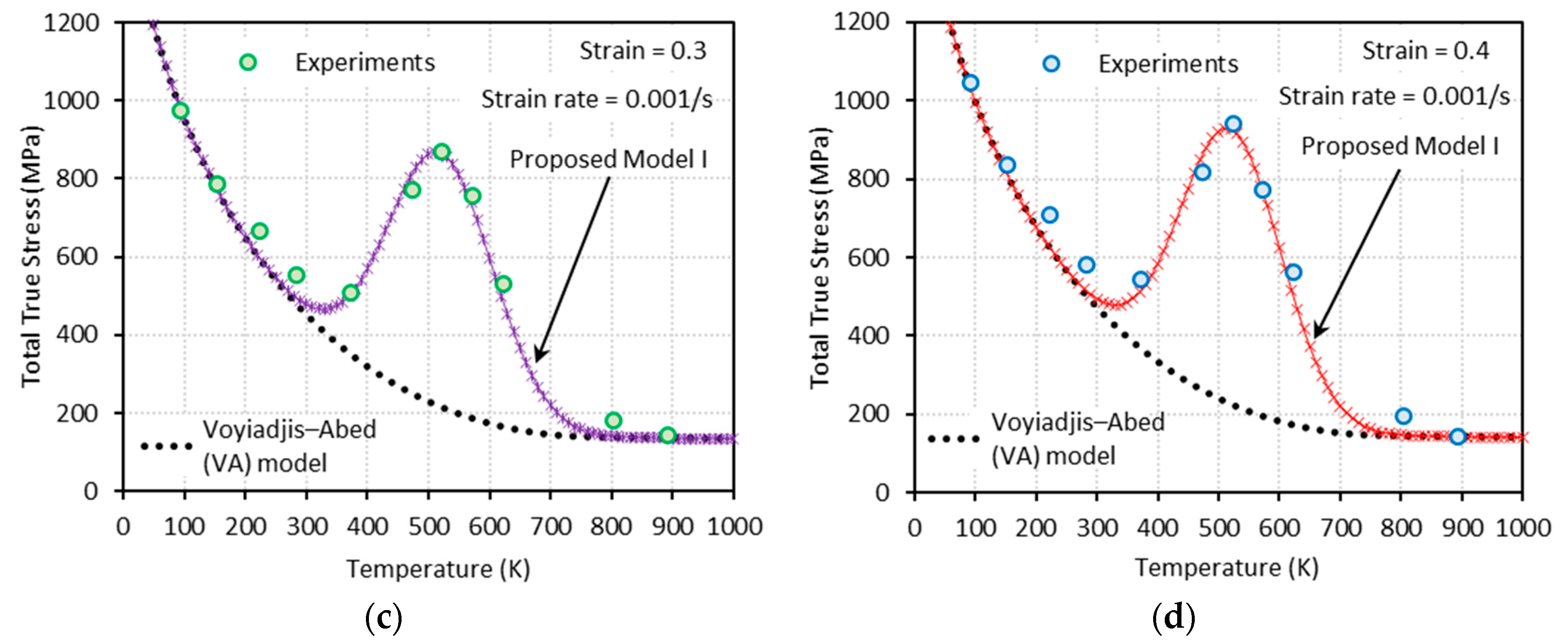
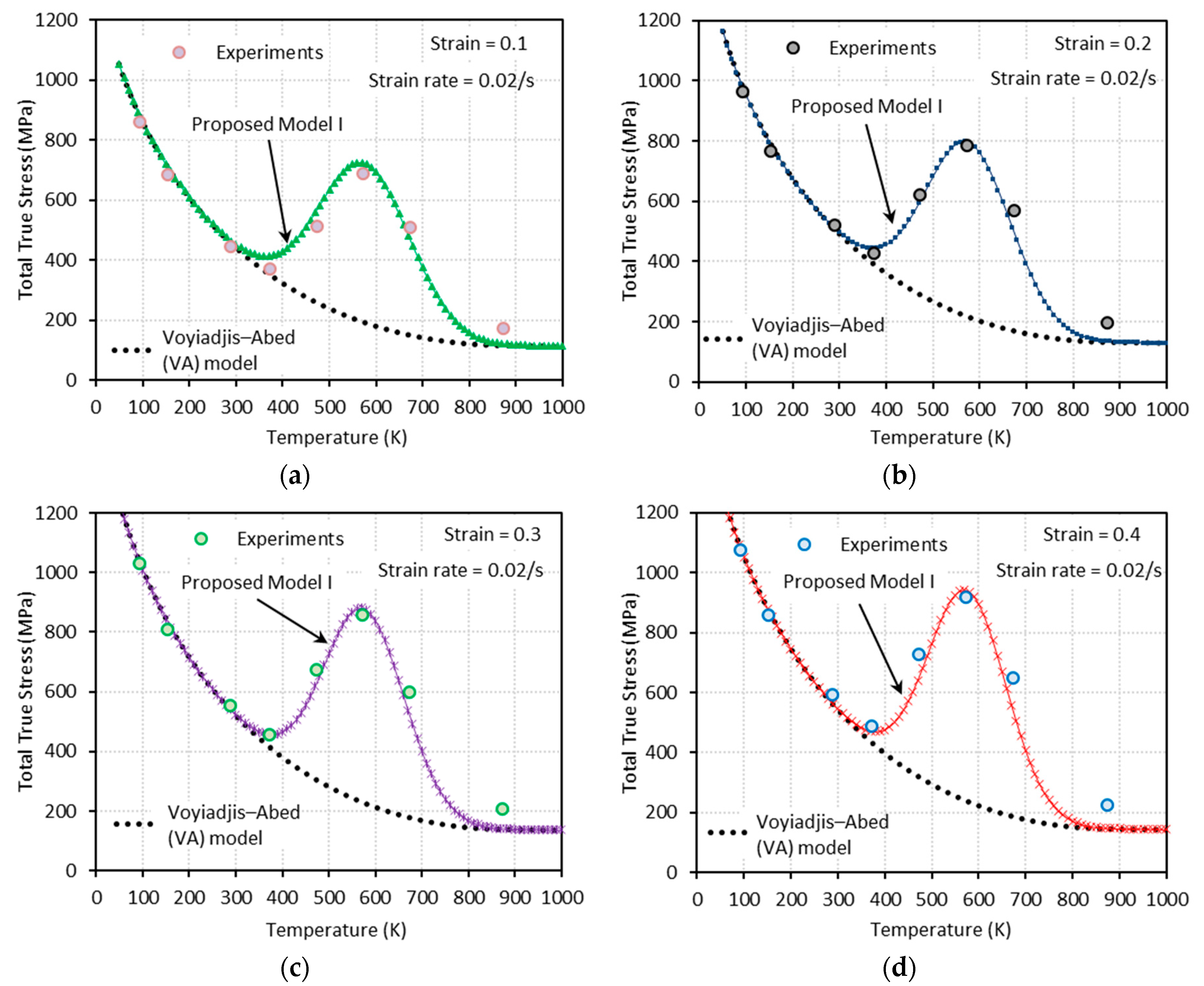
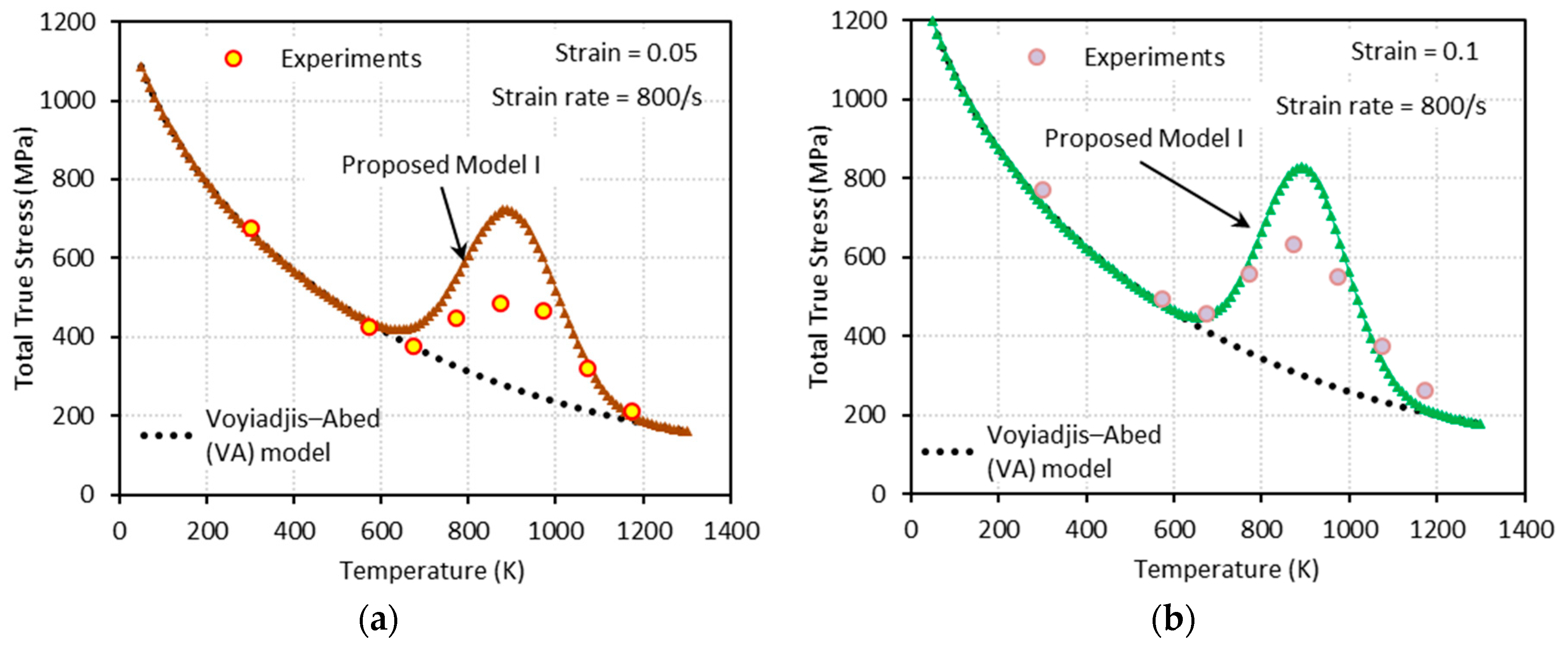
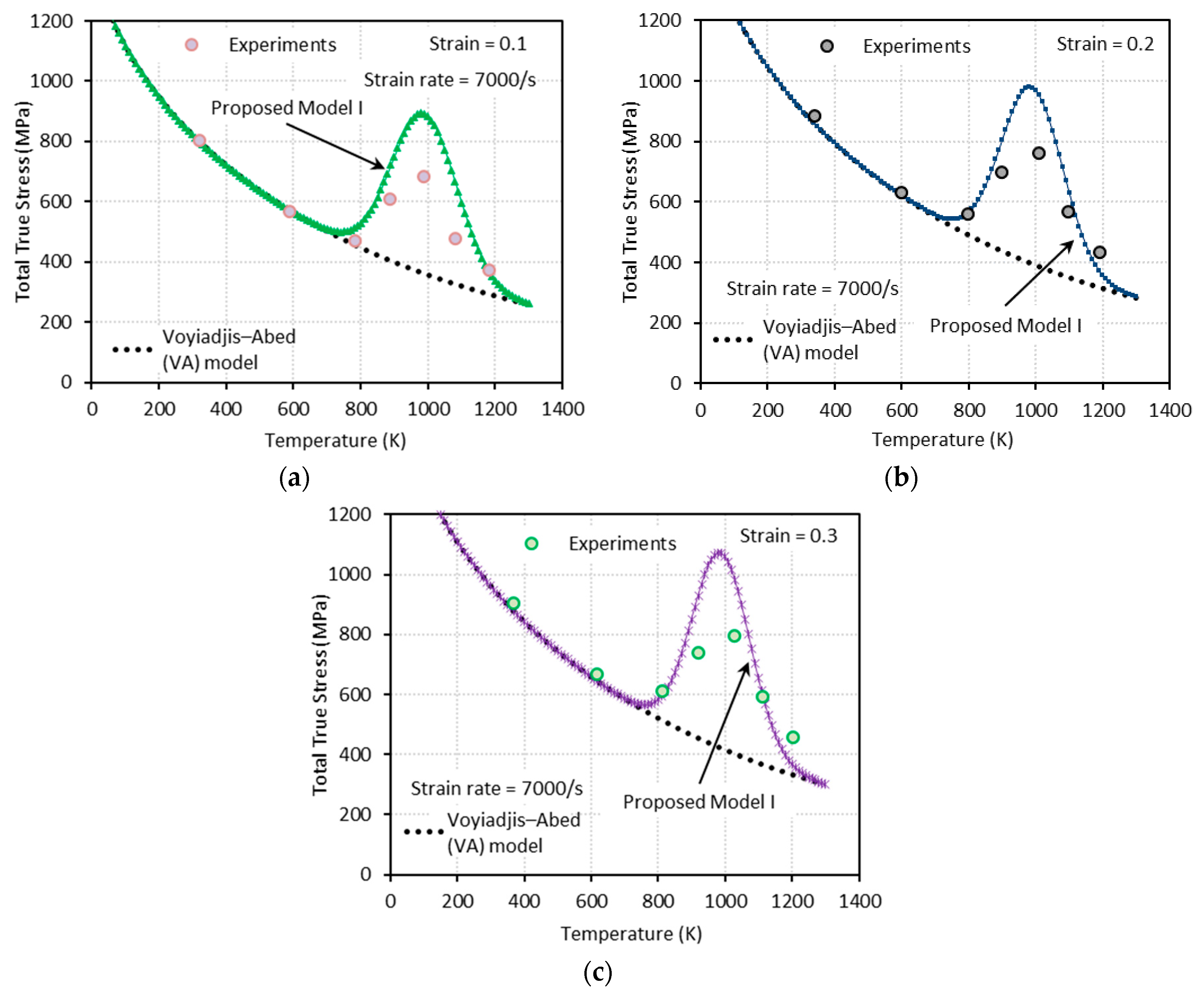
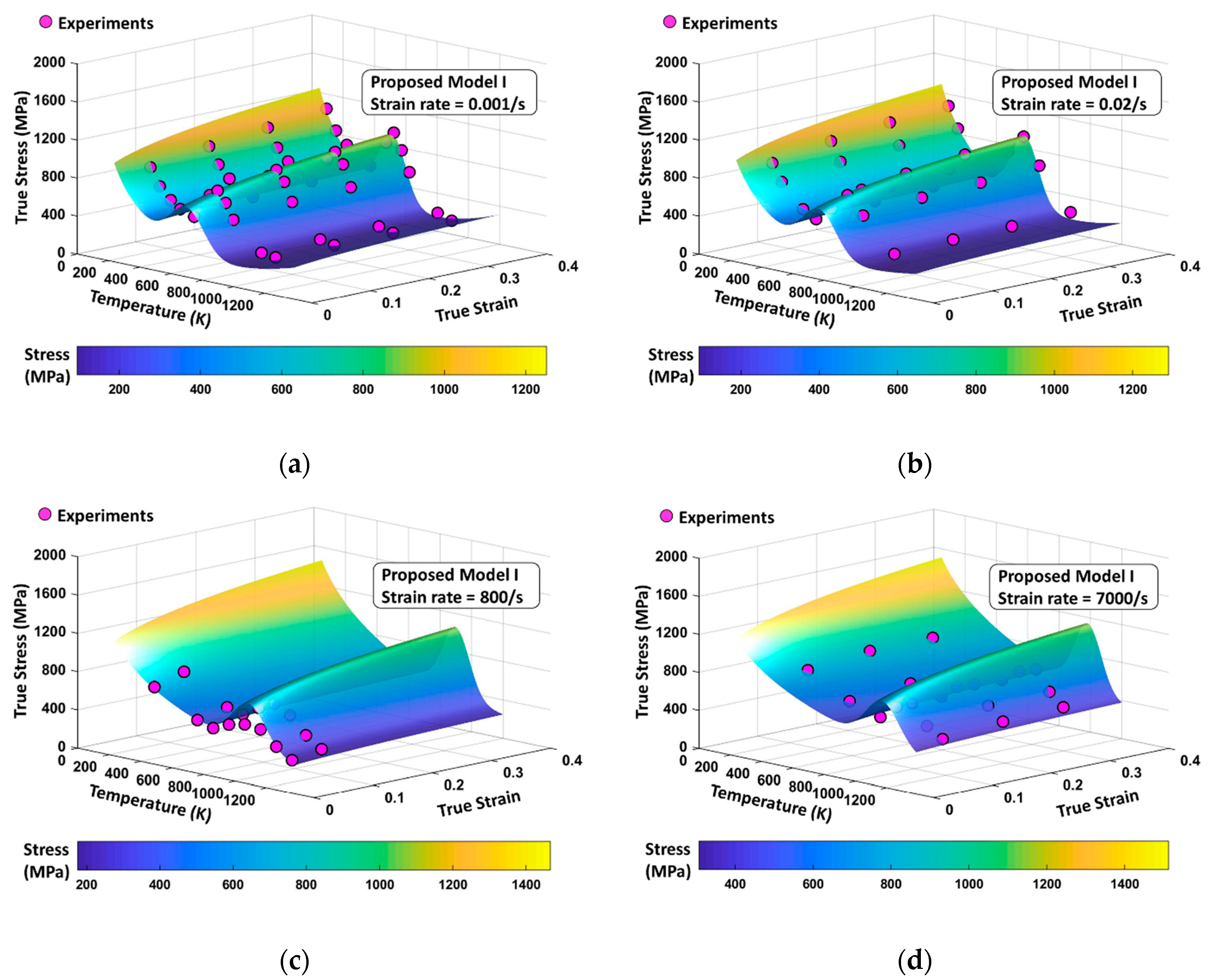
3.2.1. Proposed Model I (PM I)
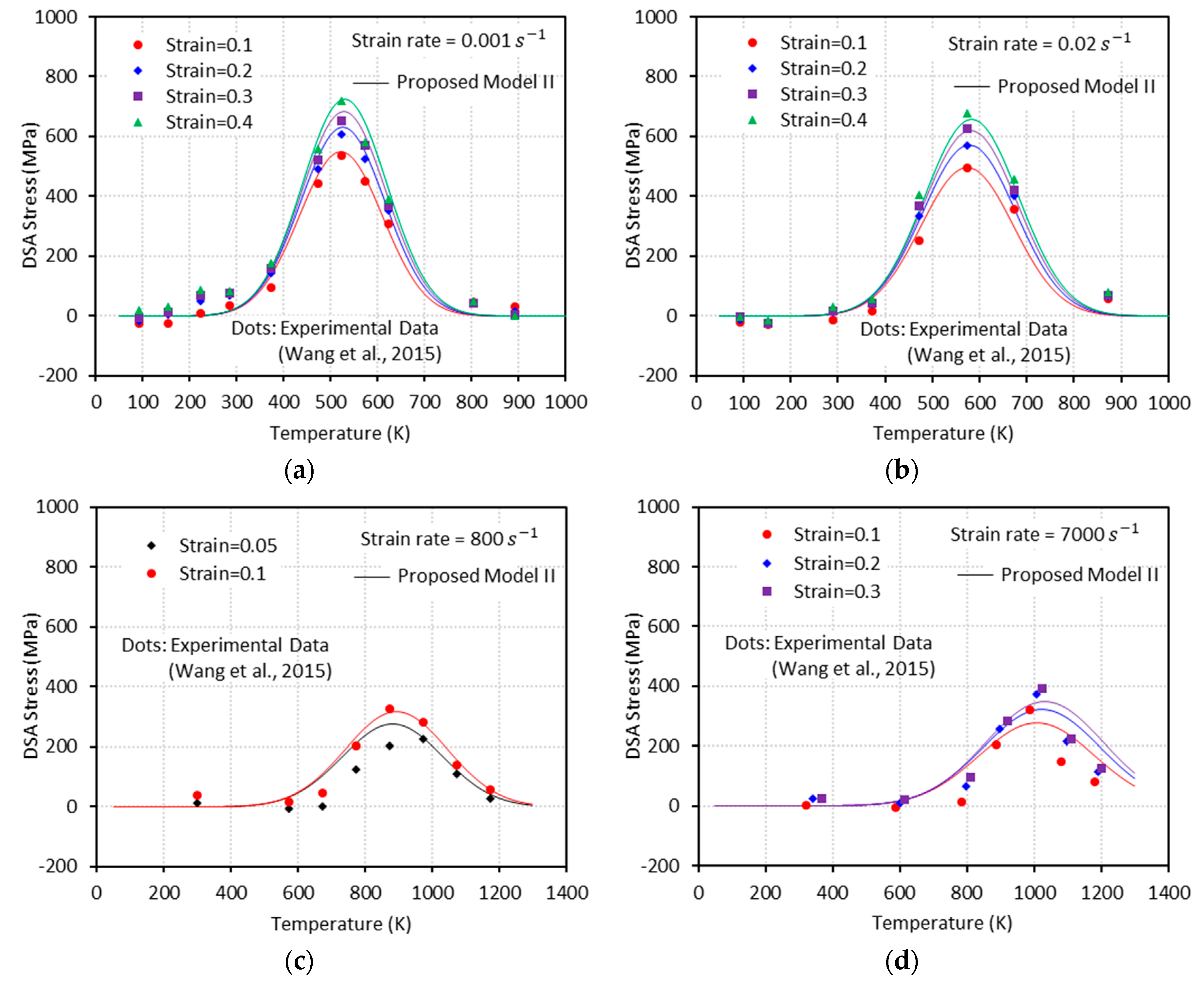
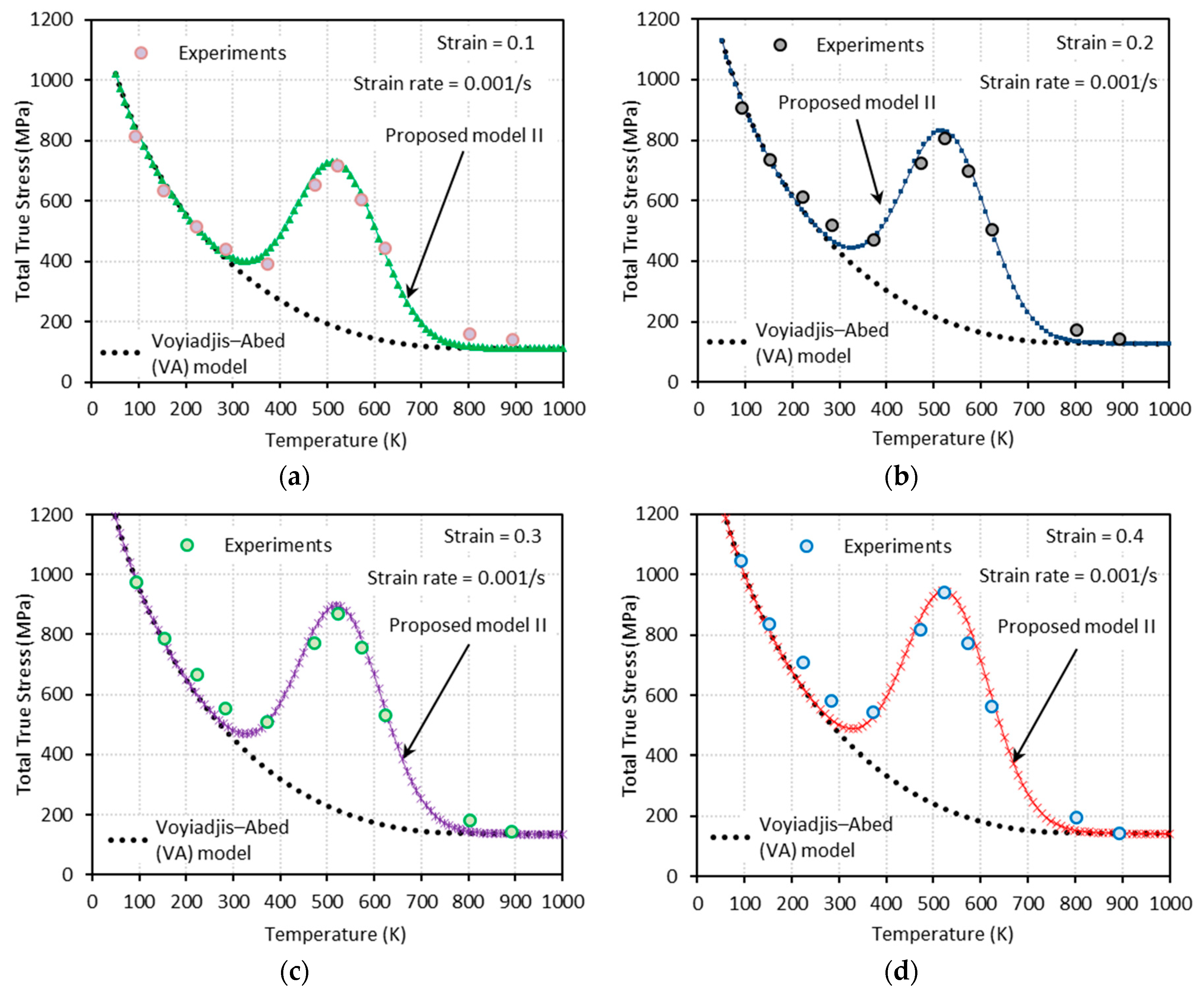
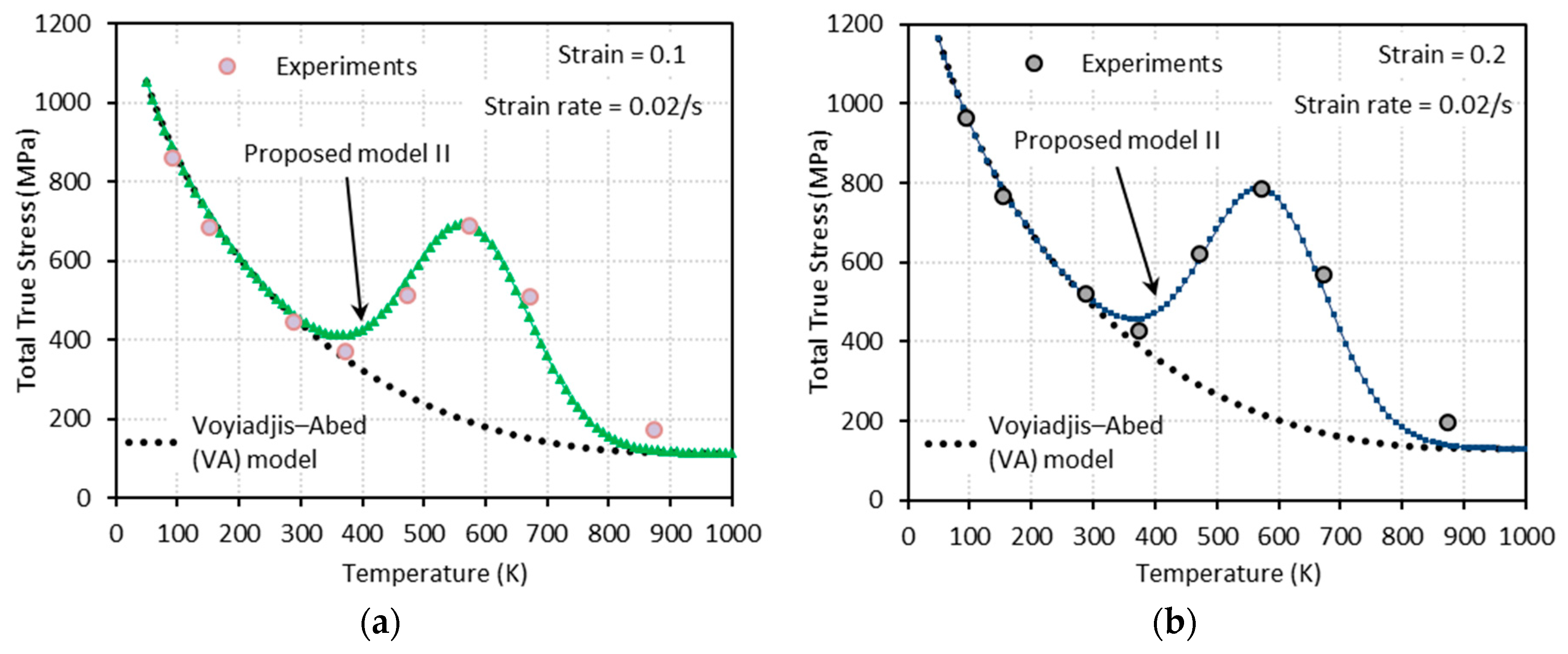
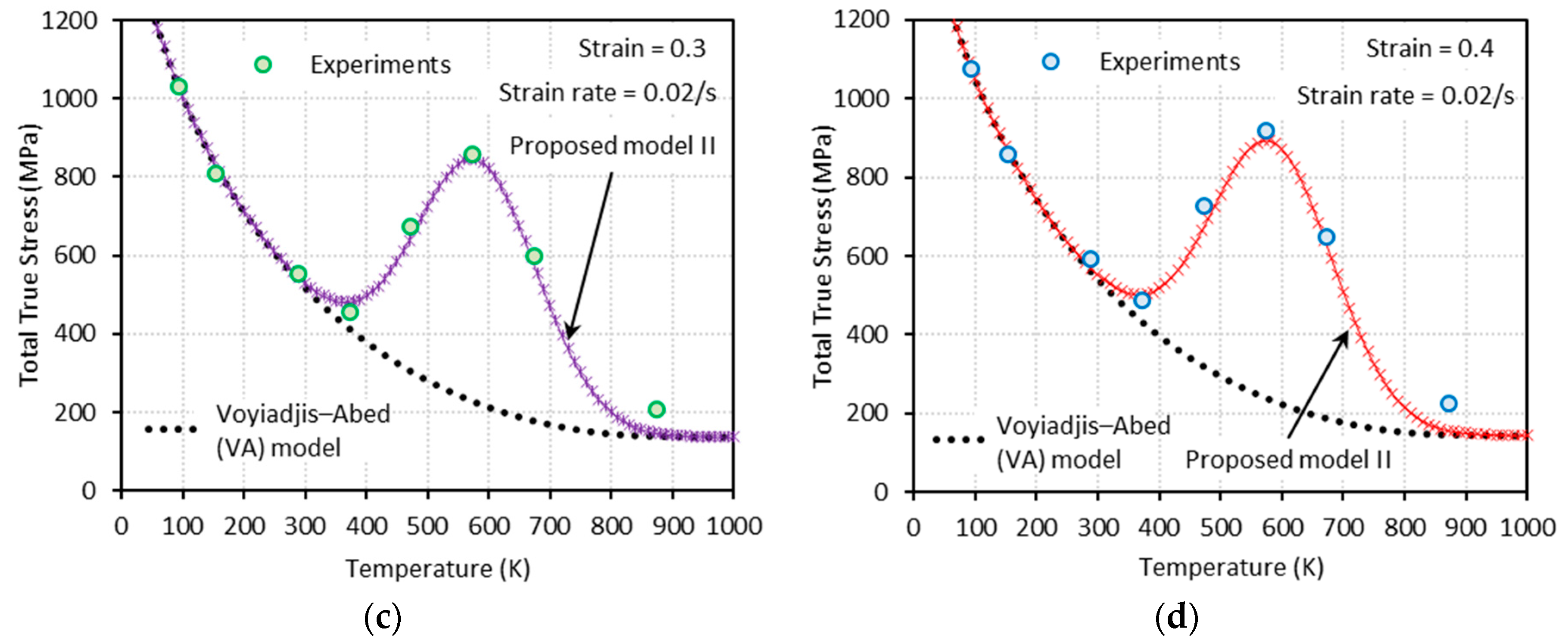
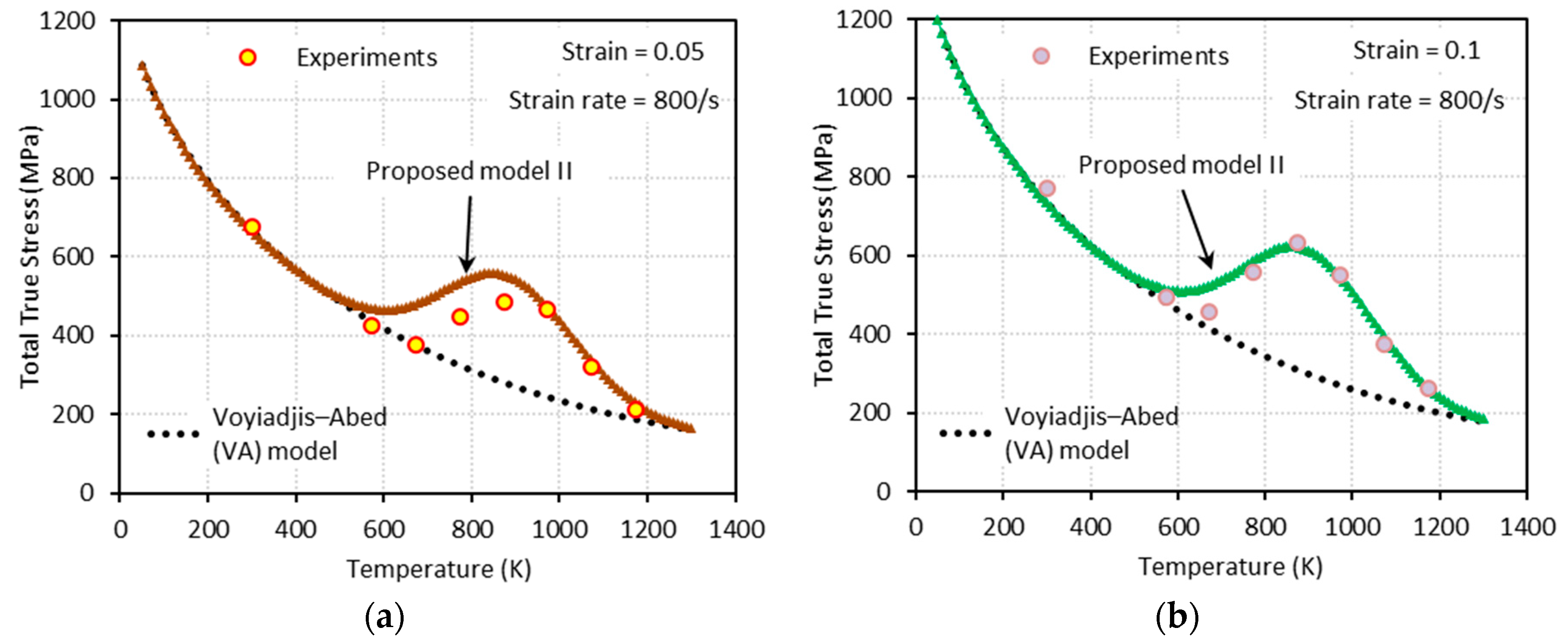
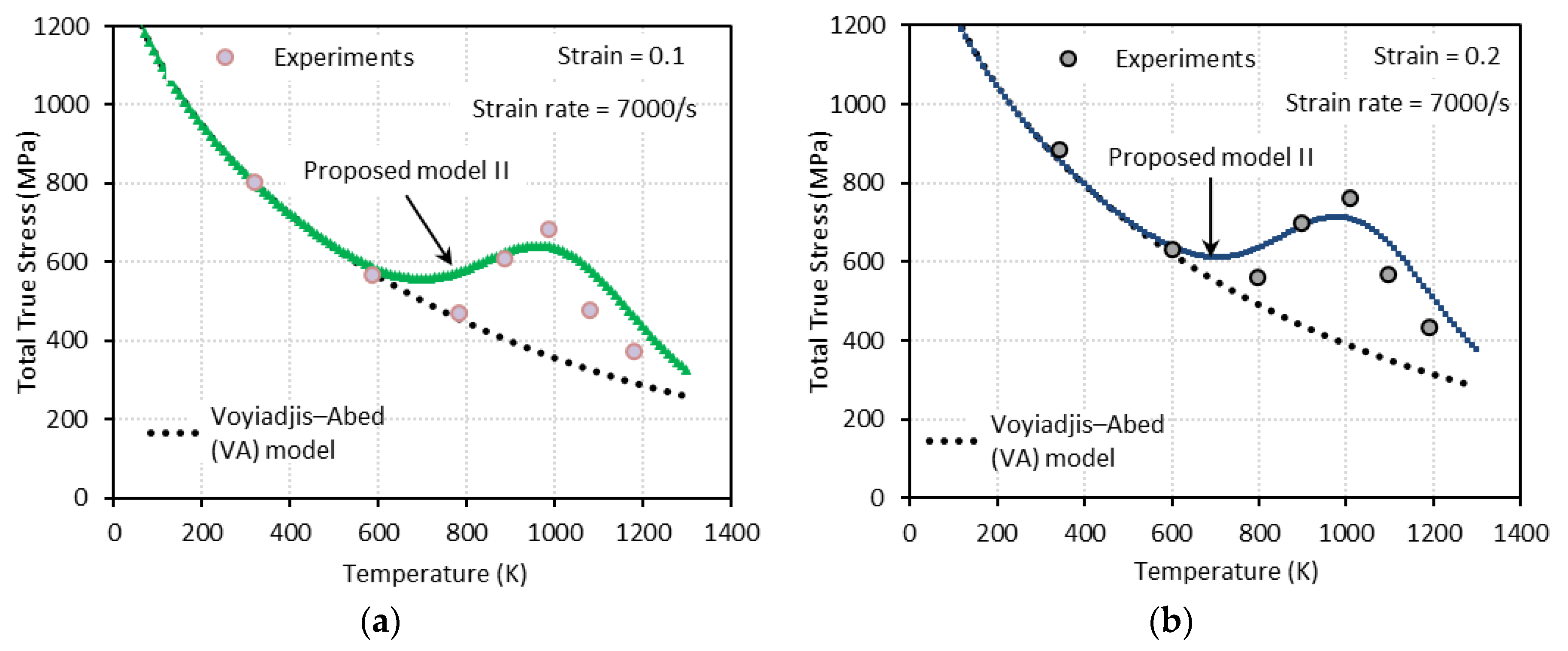
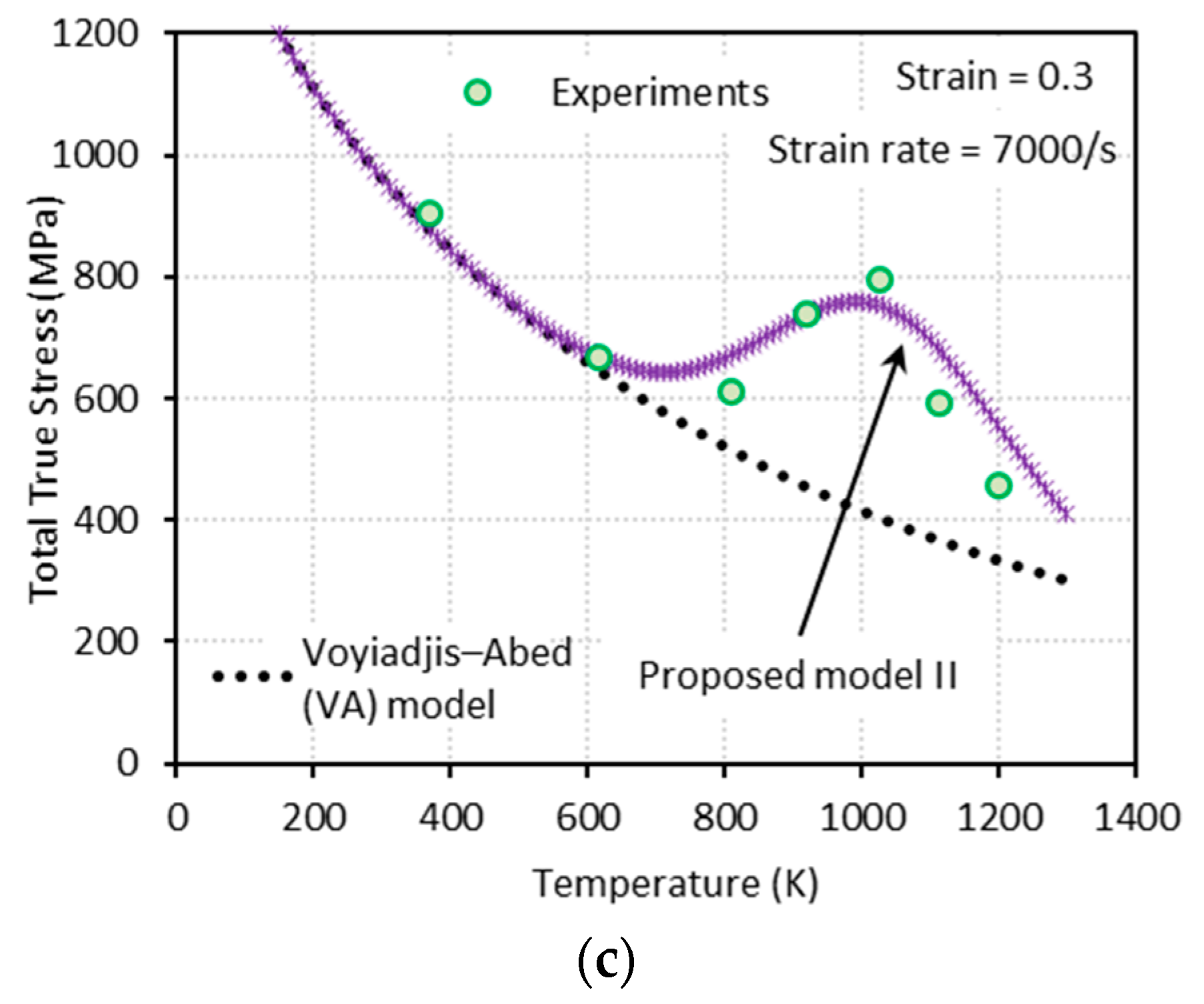
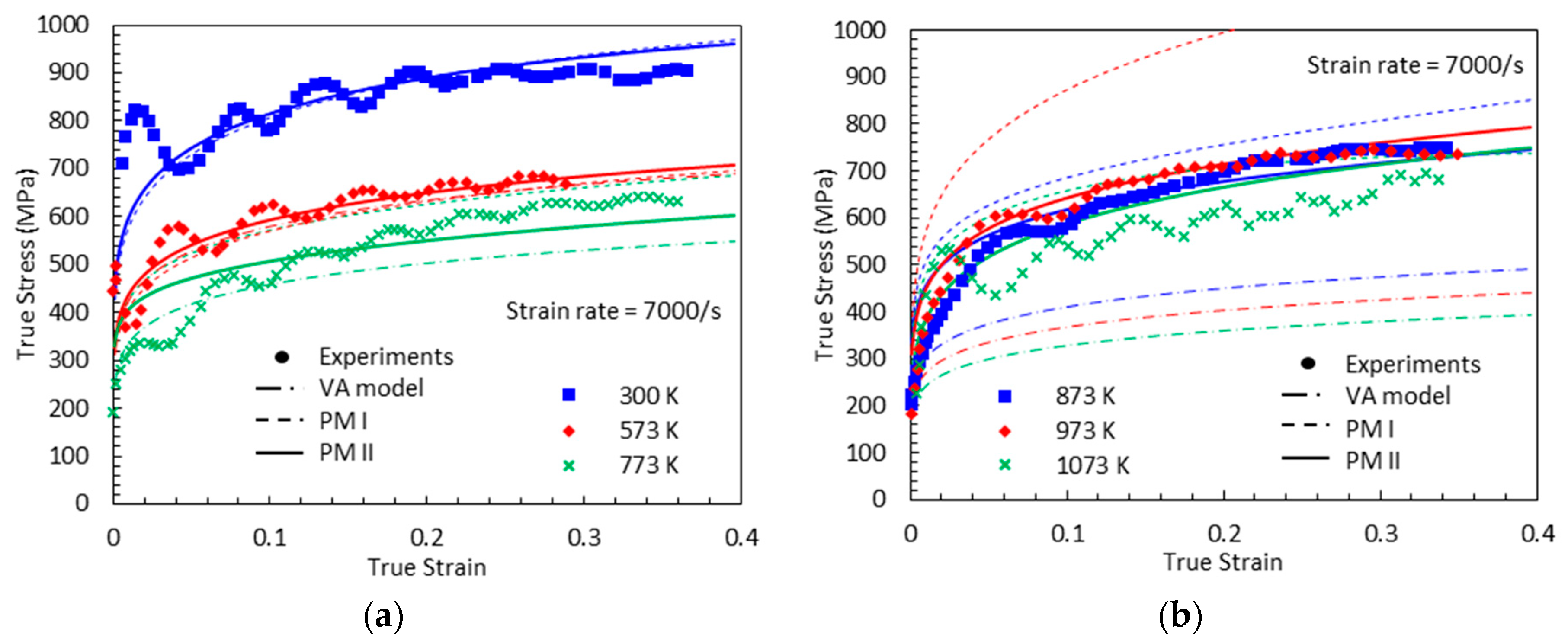
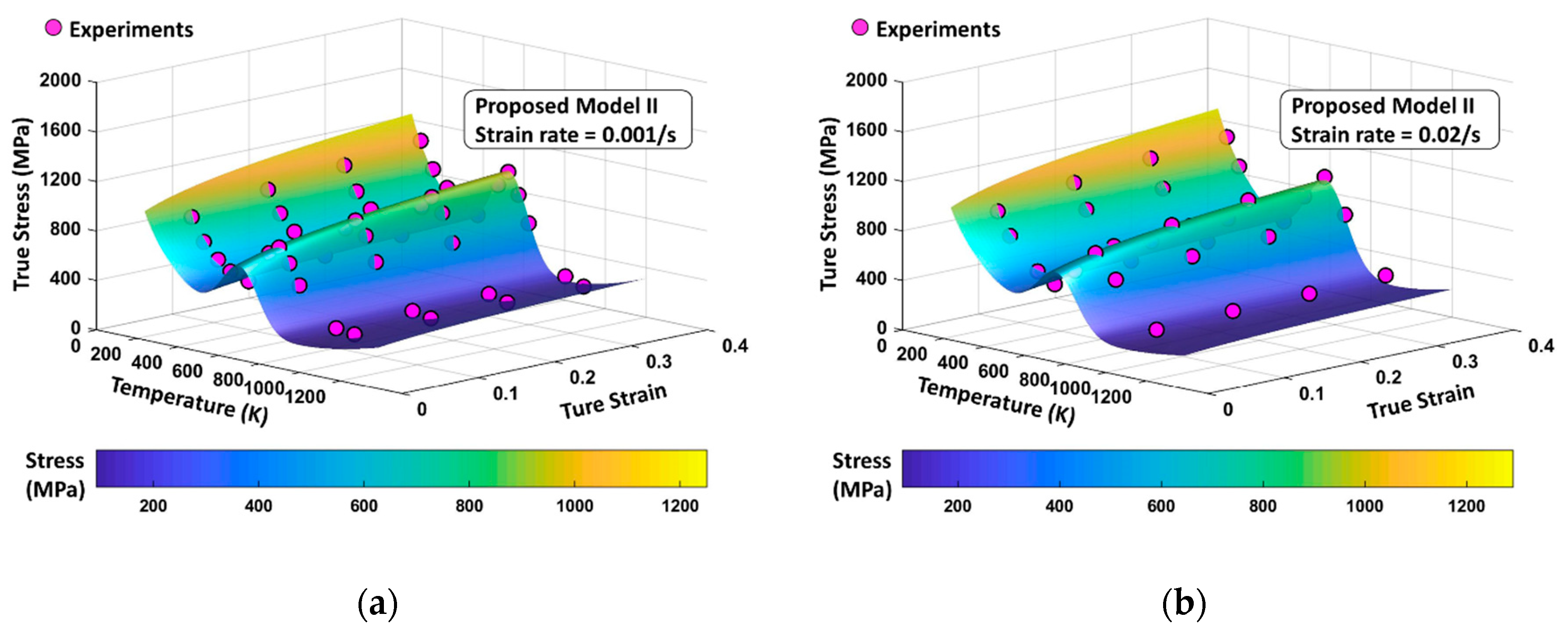
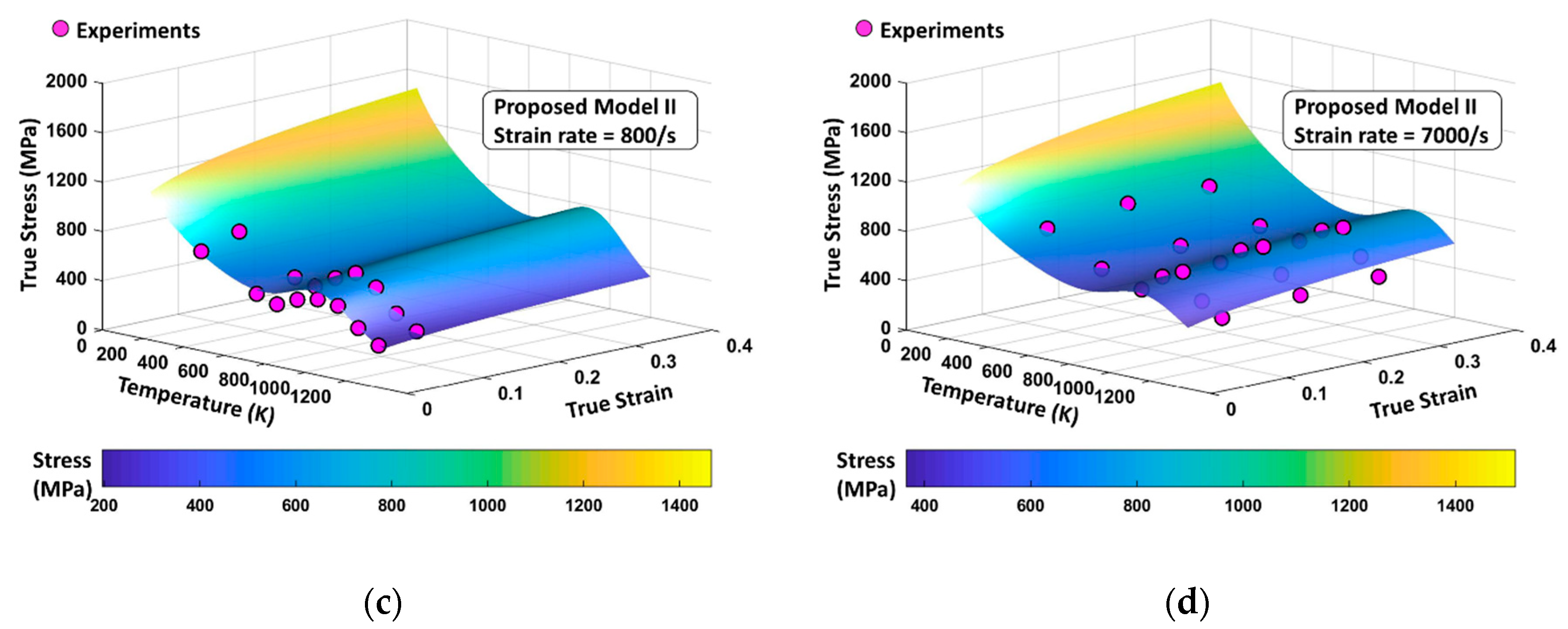
3.2.2. Proposed Model II (PM II)
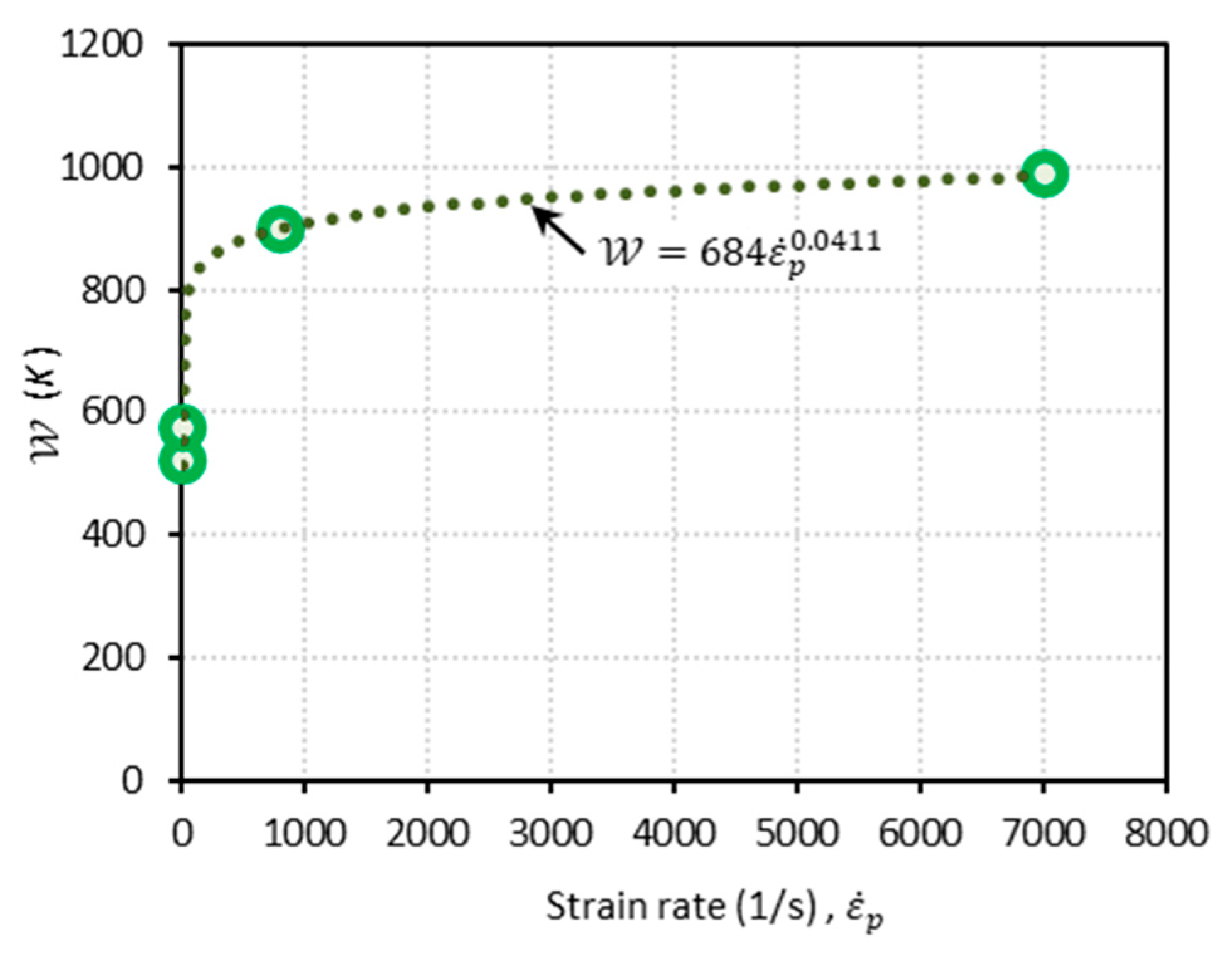
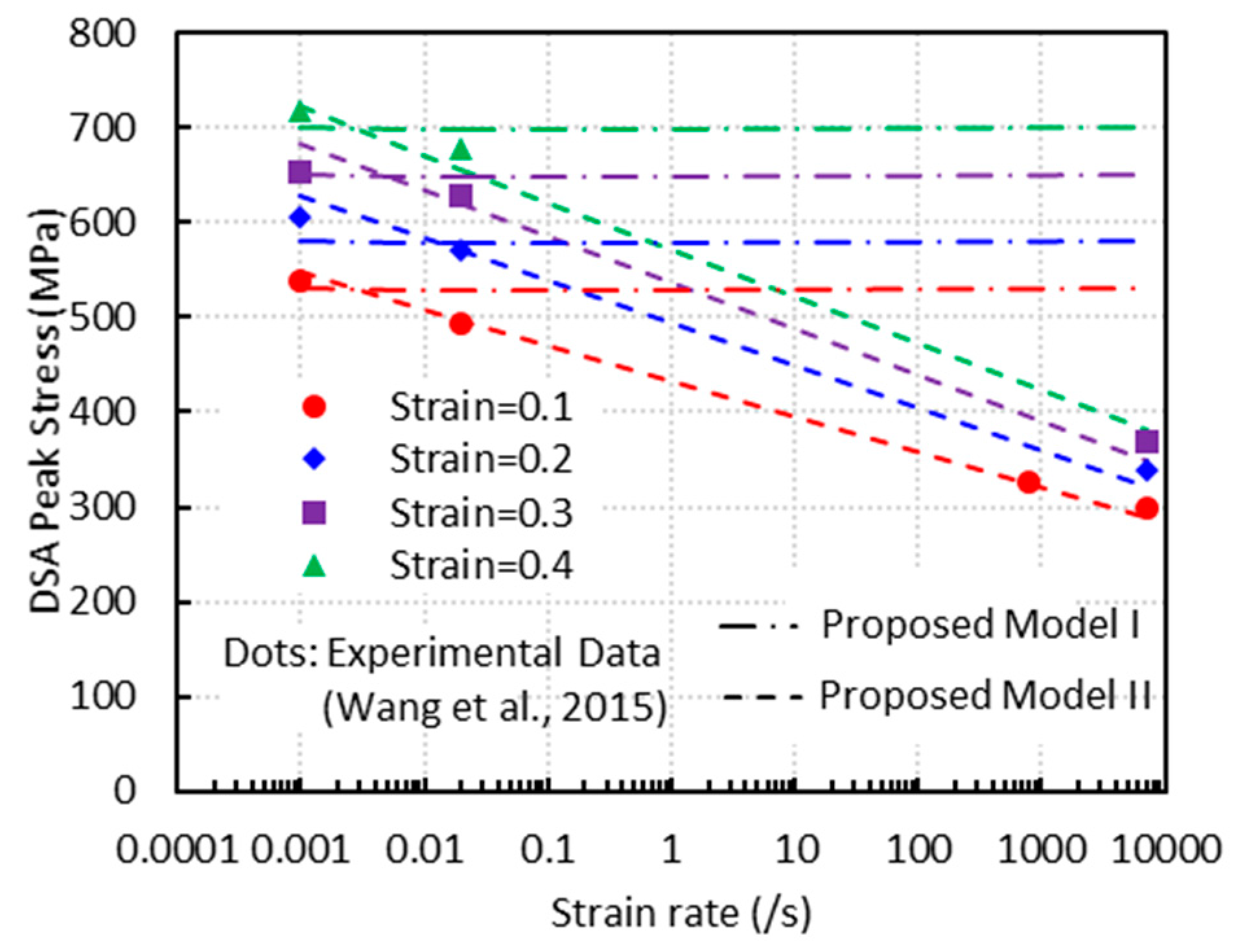
3.2.3. Strain Rate Effect on the DSA Stress
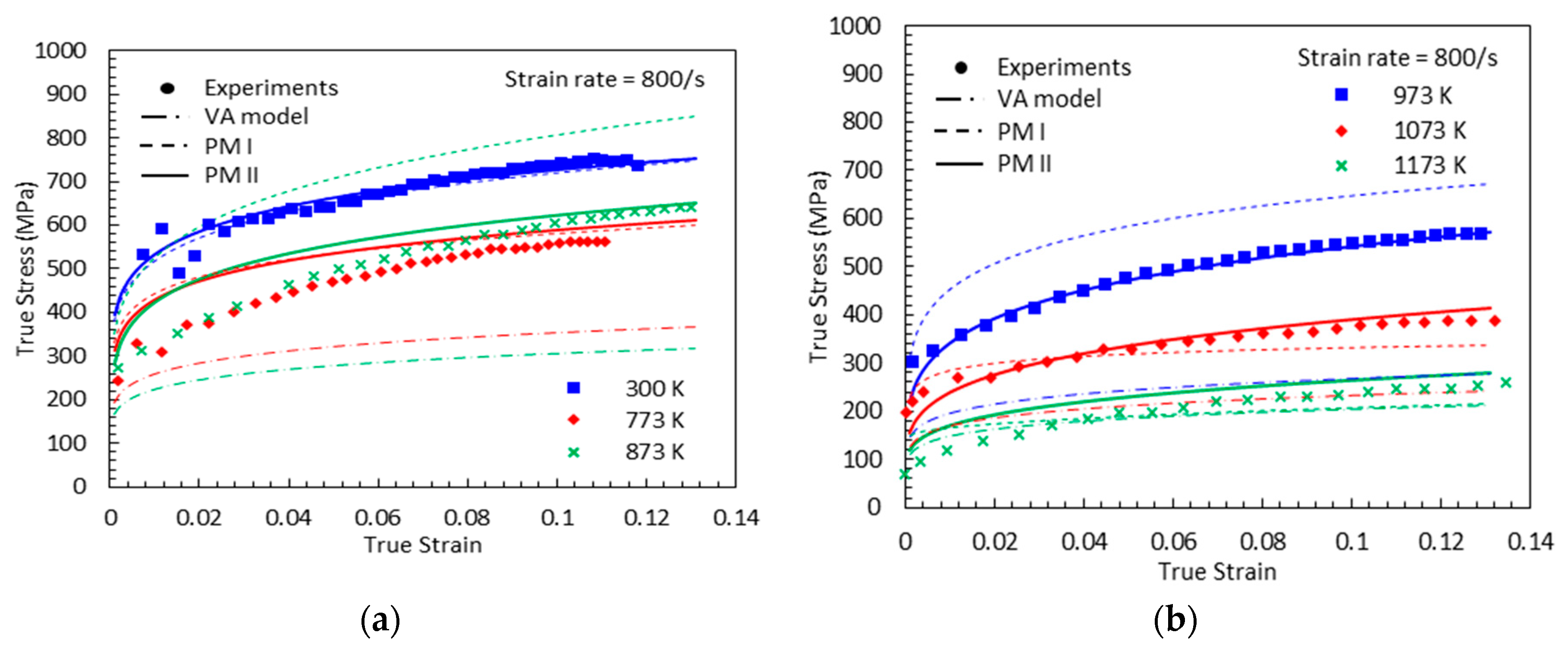
4. Comparison between the Model Predictions (VA Model, Proposed Model I, and Proposed Model II) and the Experimental Measurements
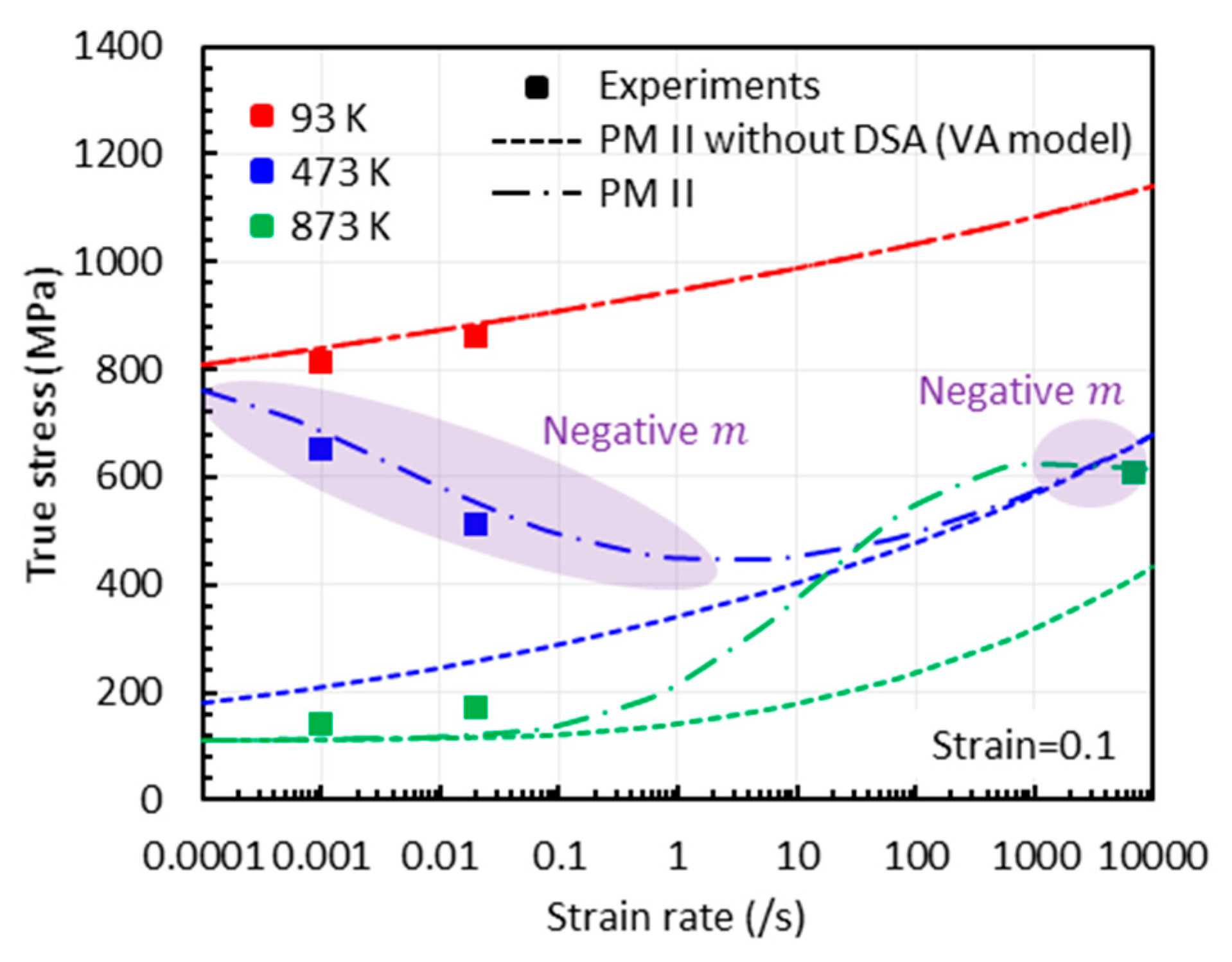
5. Strain Rate Sensitivity
6. Conclusions
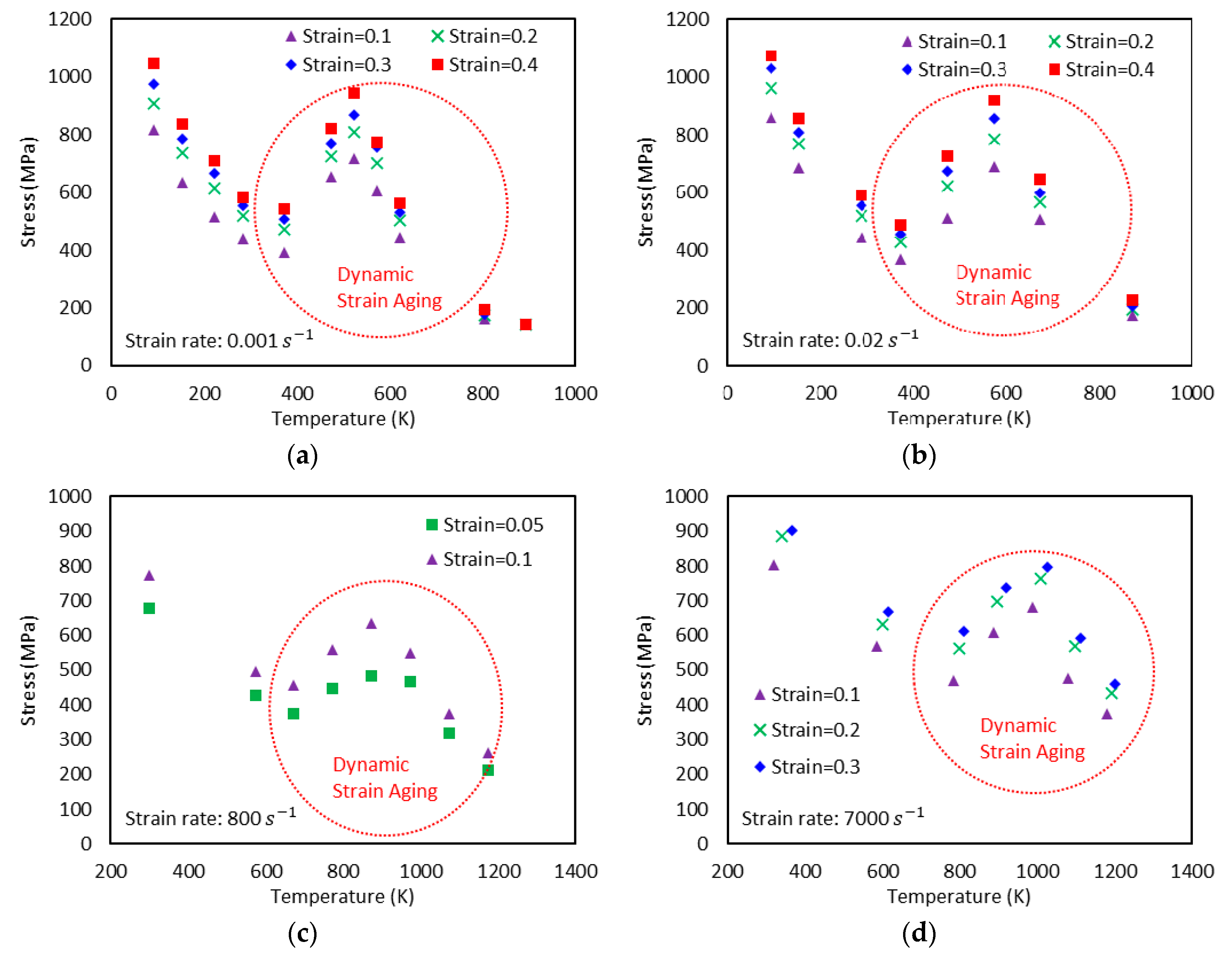
- Dynamic strain aging, which is characterized by the bell-shaped hardening in stress-temperature curves, appears under both quasi-static and dynamic loadings. As the strain rate increases, this bell-shaped hardening moves to elevated temperature region and the magnitude of hardening reduces.
- The VA model is not able to predict the bell-shaped hardening.
- The proposed model II shows an excellent agreement with the experimental results at both low and high strain rates, whereas the proposed model I fails to capture them at high strain rates.
- The negative strain rate sensitivity due to DSA is well captured by the proposed model II unlike the VA model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Guo, W.-G.; Gao, X.; Su, J. The third-type of strain aging and the constitutive modeling of a Q235B steel over a wide range of temperatures and strain rates. Int. J. Plast. 2015, 65, 85–107. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.; Cheng, J. Mechanical properties and deformation mechanisms of a commercially pure titanium. Acta Mater. 1999, 47, 3705–3720. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Li, Y. Flow stress of f.c.c. polycrystals with application to OFHC Cu. Acta Mater. 1998, 46, 565–577. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W. High strain-rate response of commercially pure vanadium. Mech. Mater. 2000, 32, 243–260. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W. Flow stress of commercially pure niobium over a broad range of temperatures and strain rates. Mater. Sci. Eng. A 2000, 284, 202–210. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Isaacs, J. Direct measurement of isothermal flow stress of metals at elevated temperatures and high strain rates with application to Ta and TaW alloys. Acta Mater. 1997, 45, 907–919. [Google Scholar] [CrossRef]
- Abed, F.; Saffarini, M.H.; Abdul-Latif, A.; Voyiadjis, G.Z. Flow Stress and Damage Behavior of C45 Steel Over a Range of Temperatures and Loading Rates. J. Eng. Mater. Technol. 2017, 139, 021012. [Google Scholar] [CrossRef]
- Guo, W.-G.; Gao, X. On the constitutive modeling of a structural steel over a range of strain rates and temperatures. Mater. Sci. Eng. A 2013, 561, 468–476. [Google Scholar] [CrossRef]
- Yuan, K.; Guo, W.; Li, P.; Wang, J.; Su, Y.; Lin, X.; Li, Y. Influence of process parameters and heat treatments on the microstructures and dynamic mechanical behaviors of Inconel 718 superalloy manufactured by laser metal deposition. Mater. Sci. Eng. A 2018, 721, 215–225. [Google Scholar] [CrossRef]
- Cottrell, A. LXXXVI. A note on the Portevin-Le Chatelier effect. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1953, 44, 829–832. [Google Scholar] [CrossRef]
- McCormick, P. Theory of flow localisation due to dynamic strain ageing. Acta Met. 1988, 36, 3061–3067. [Google Scholar] [CrossRef]
- Li, M.; Gao, C.; Xu, J. Discrete dislocation dynamics simulations in a cylinder. IOP Conf. Ser. Mater. Sci. Eng. 2015, 74, 012009. [Google Scholar] [CrossRef]
- Bergström, Y.; Roberts, W. A dislocation model for dynamical strain ageing of α-iron in the jerky-flow region. Acta Met. 1971, 19, 1243–1251. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J.R. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Abed, F.; Voyiadjis, G.Z. Plastic deformation modeling of AL-6XN stainless steel at low and high strain rates and temperatures using a combination of bcc and fcc mechanisms of metals. Int. J. Plast. 2005, 21, 1618–1639. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y.; Rusinek, A.; Rusinek, Y.S.A. Constitutive model for metals with dynamic strain aging. Mech. Mater. 2019, 129, 352–360. [Google Scholar] [CrossRef]
- Klepaczko, J. Physical-state variables—The key to constitutive modeling in dynamic plasticity? Nucl. Eng. Des. 1991, 127, 103–115. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y. A physically based constitutive model for dynamic strain aging in Inconel 718 alloy at a wide range of temperatures and strain rates. Acta Mech. 2019, 231, 19–34. [Google Scholar] [CrossRef]
- Rusinek, A.; Zaera, R.; Klepaczko, J. Constitutive relations in 3-D for a wide range of strain rates and temperatures—Application to mild steels. Int. J. Solids Struct. 2007, 44, 5611–5634. [Google Scholar] [CrossRef]
- Bammann, D.J.; Aifantis, E.C. On a proposal for a continuum with microstructure. Acta Mech. 1982, 45, 91–121. [Google Scholar] [CrossRef]
- Klepaczko, J.R. Modelling of structural evolution at medium and high strain rates, FCC and BCC metals. Const. Relat. Their Phys. Basis 1987, 387–395. [Google Scholar]
- Arrhenius, S. Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Zeitschrift für Phys. Chem. 1889, 4, 96–116. [Google Scholar]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodynamics and Kinetics of Slip. Prog. Mater. Sci. 1975, 19, 1–281. [Google Scholar]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Rittel, D.; Zhang, L.; Osovski, S. The dependence of the Taylor–Quinney coefficient on the dynamic loading mode. J. Mech. Phys. Solids 2017, 107, 96–114. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Nandy, T.; Feng, Q.; Pollock, T. Elevated temperature deformation and dynamic strain aging in polycrystalline RuAl alloys. Intermetallics 2003, 11, 1029–1038. [Google Scholar] [CrossRef]
- Peng, K.; Qian, K.; Chen, W. Effect of dynamic strain aging on high temperature properties of austenitic stainless steel. Mater. Sci. Eng. A 2004, 379, 372–377. [Google Scholar] [CrossRef]
- Fressengeas, C.; Molinari, A. Instability and localization of plastic flow in shear at high strain rates. J. Mech. Phys. Solids 1987, 35, 185–211. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y. Strain gradient continuum plasticity theories: Theoretical, numerical and experimental investigations. Int. J. Plast. 2019, 121, 21–75. [Google Scholar] [CrossRef]
- Song, Y.; Voyiadjis, G.Z. Small scale volume formulation based on coupled thermo-mechanical gradient enhanced plasticity theory. Int. J. Solids Struct. 2018, 134, 195–215. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y. Effect of passivation on higher order gradient plasticity models for non-proportional loading: Energetic and dissipative gradient components. Philos. Mag. 2016, 97, 1–28. [Google Scholar] [CrossRef]
- Song, Y.; Voyiadjis, G.Z. Strain gradient finite element model for finite deformation theory: Size effects and shear bands. Comput. Mech. 2020, 1–28. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y.; Park, T. Higher-Order Thermomechanical Gradient Plasticity Model with Energetic and Dissipative Components. J. Eng. Mater. Technol. 2017, 139, 021006. [Google Scholar] [CrossRef]
- Song, Y.; Voyiadjis, G.Z. A two-dimensional finite element model of the grain boundary based on thermo-mechanical strain gradient plasticity. J. Theor. Appl. Mech. 2018, 56, 377–391. [Google Scholar] [CrossRef]
- Zhang, B.; Song, Y.; Voyiadjis, G.Z.; Meng, W.J. Assessing texture development and mechanical response in microscale reverse extrusion of copper. J. Mater. Res. 2018, 33, 978–988. [Google Scholar] [CrossRef]
- Song, Y. Finite-Element Implementation of Piezoelectric Energy Harvesting System from Vibrations of Railway Bridge. J. Energy Eng. 2019, 145, 04018076. [Google Scholar] [CrossRef]
| () | () | () | () | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Garcia-Gonzalez, D.; Rusinek, A. Constitutive Models for Dynamic Strain Aging in Metals: Strain Rate and Temperature Dependences on the Flow Stress. Materials 2020, 13, 1794. https://doi.org/10.3390/ma13071794
Song Y, Garcia-Gonzalez D, Rusinek A. Constitutive Models for Dynamic Strain Aging in Metals: Strain Rate and Temperature Dependences on the Flow Stress. Materials. 2020; 13(7):1794. https://doi.org/10.3390/ma13071794
Chicago/Turabian StyleSong, Yooseob, Daniel Garcia-Gonzalez, and Alexis Rusinek. 2020. "Constitutive Models for Dynamic Strain Aging in Metals: Strain Rate and Temperature Dependences on the Flow Stress" Materials 13, no. 7: 1794. https://doi.org/10.3390/ma13071794
APA StyleSong, Y., Garcia-Gonzalez, D., & Rusinek, A. (2020). Constitutive Models for Dynamic Strain Aging in Metals: Strain Rate and Temperature Dependences on the Flow Stress. Materials, 13(7), 1794. https://doi.org/10.3390/ma13071794







