L-Box Form Filling of Thixotropic Cementitious Paste and Mortar
Abstract
1. Introduction
2. Rheological Background
2.1. Rheological Parameters Due to Colloidal Particle Structuration
2.2. Rheological Measurements
2.3. Empirical Stoppage Tests as Rheological Measuring Tool
3. Materials and Methods
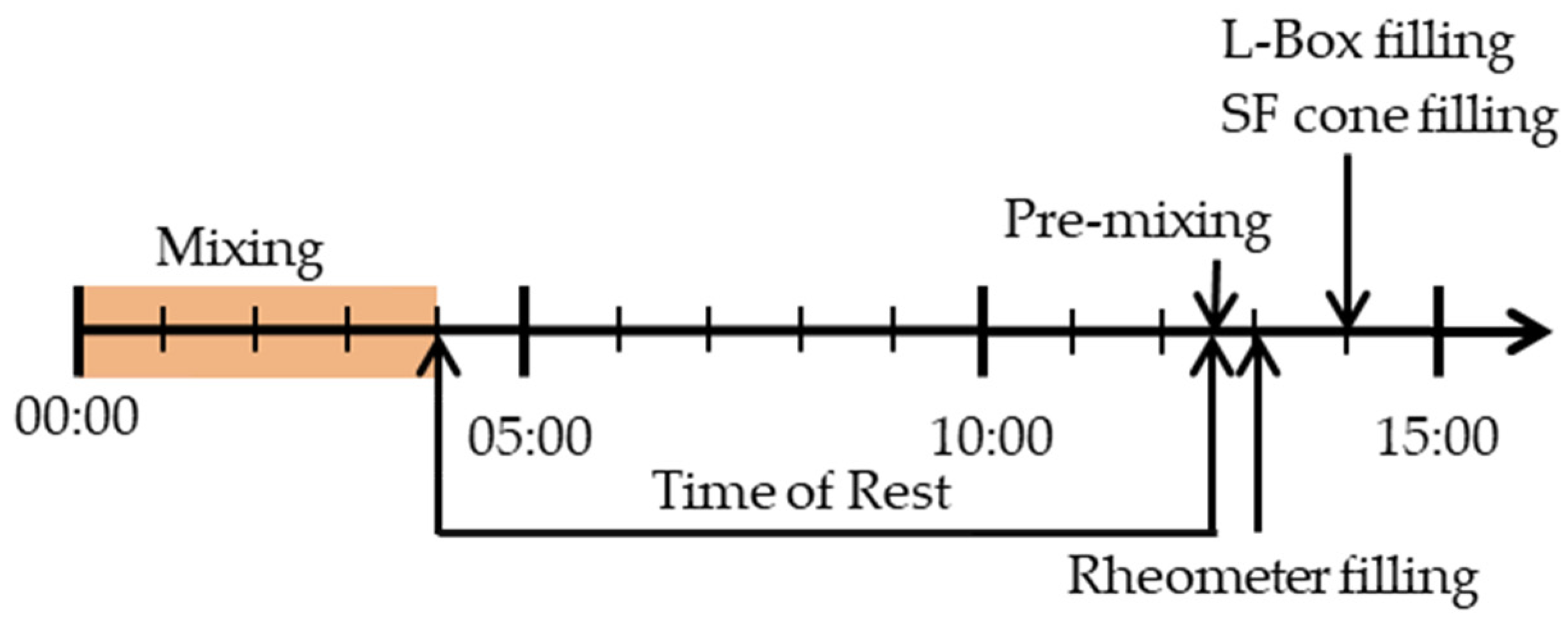
3.1. Concept of Investigation
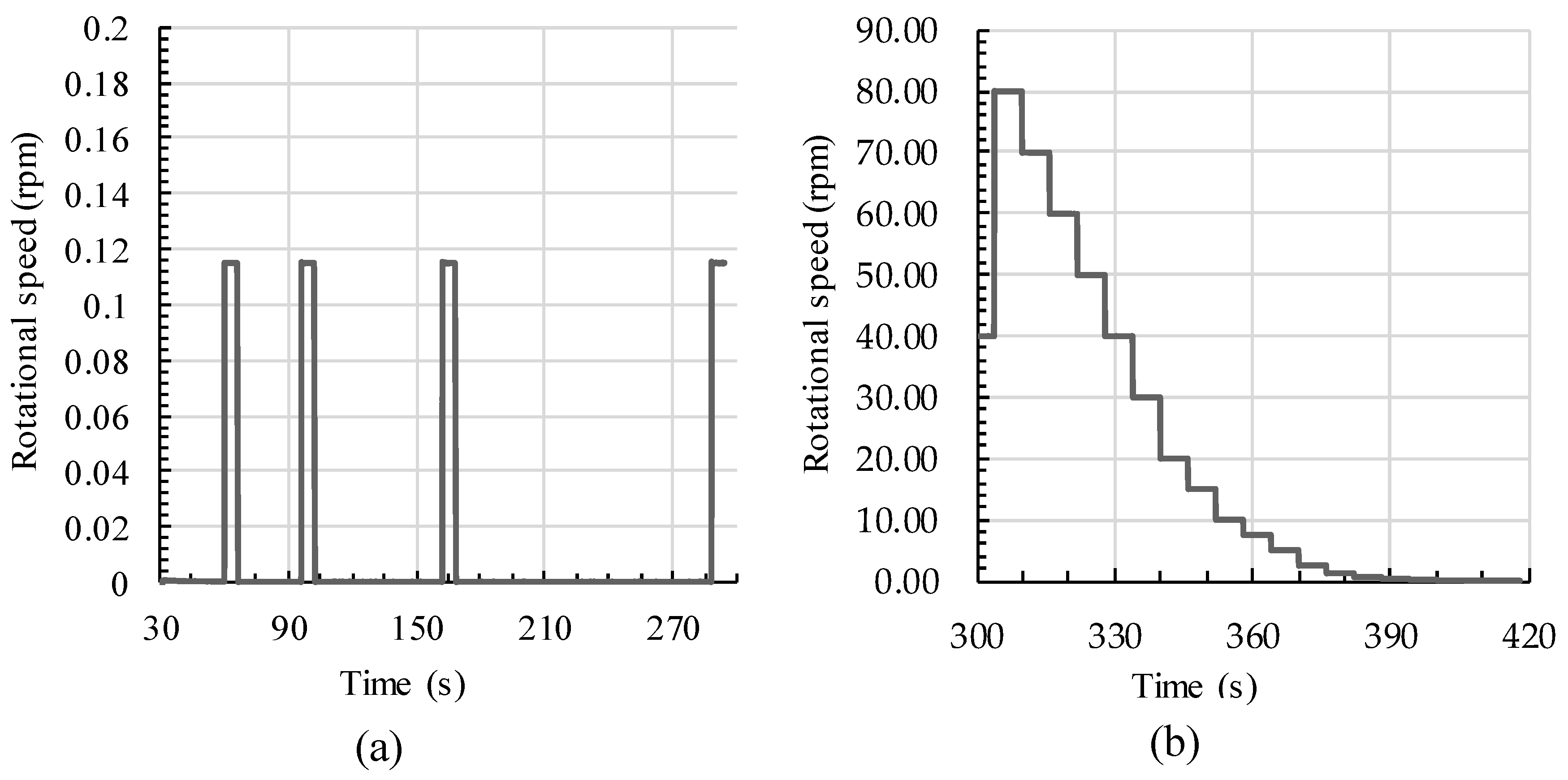
3.2. Rheological Measurements
3.3. Empirical Stoppage Tests
4. Results and Discussion
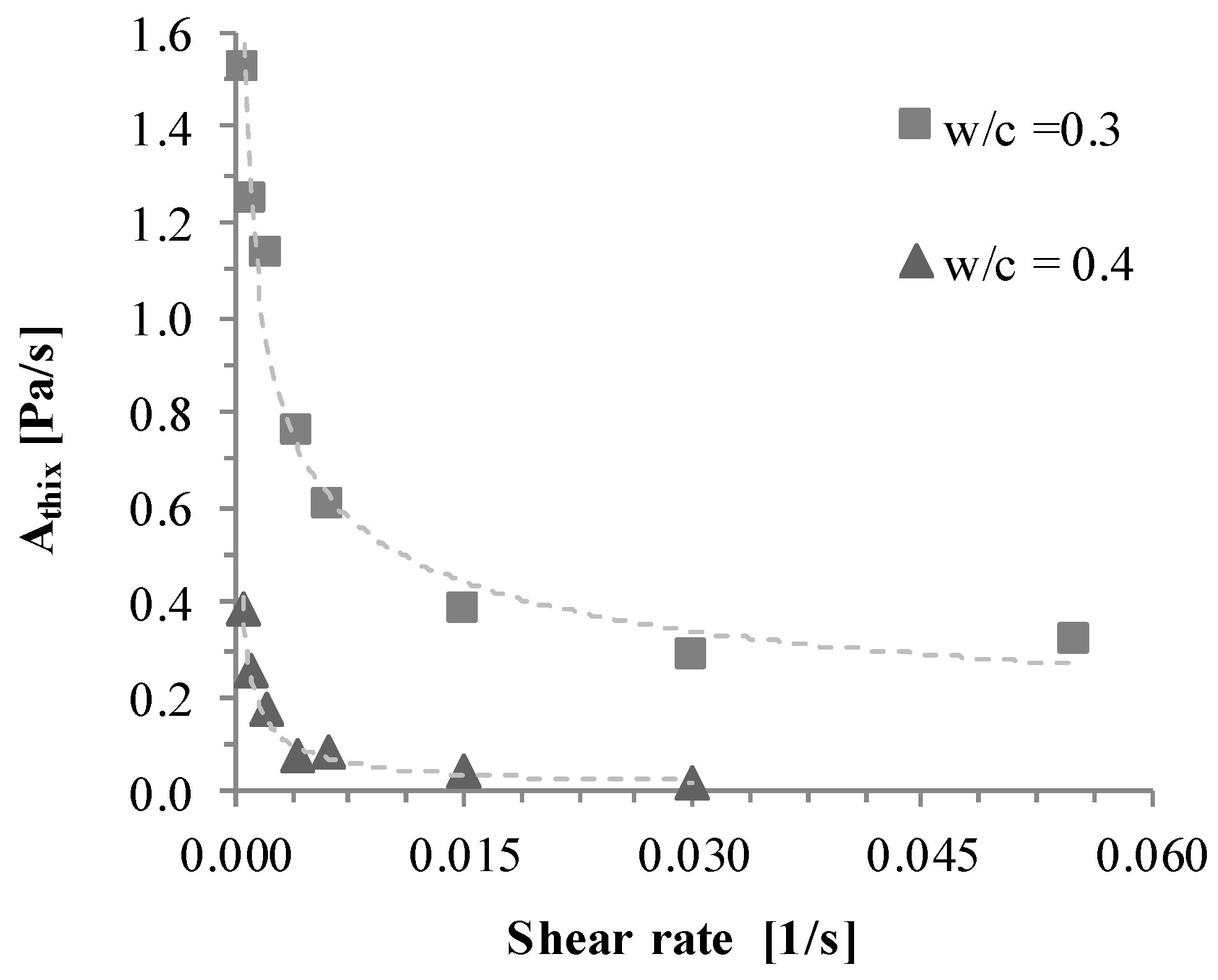
4.1. Rheological Parameters
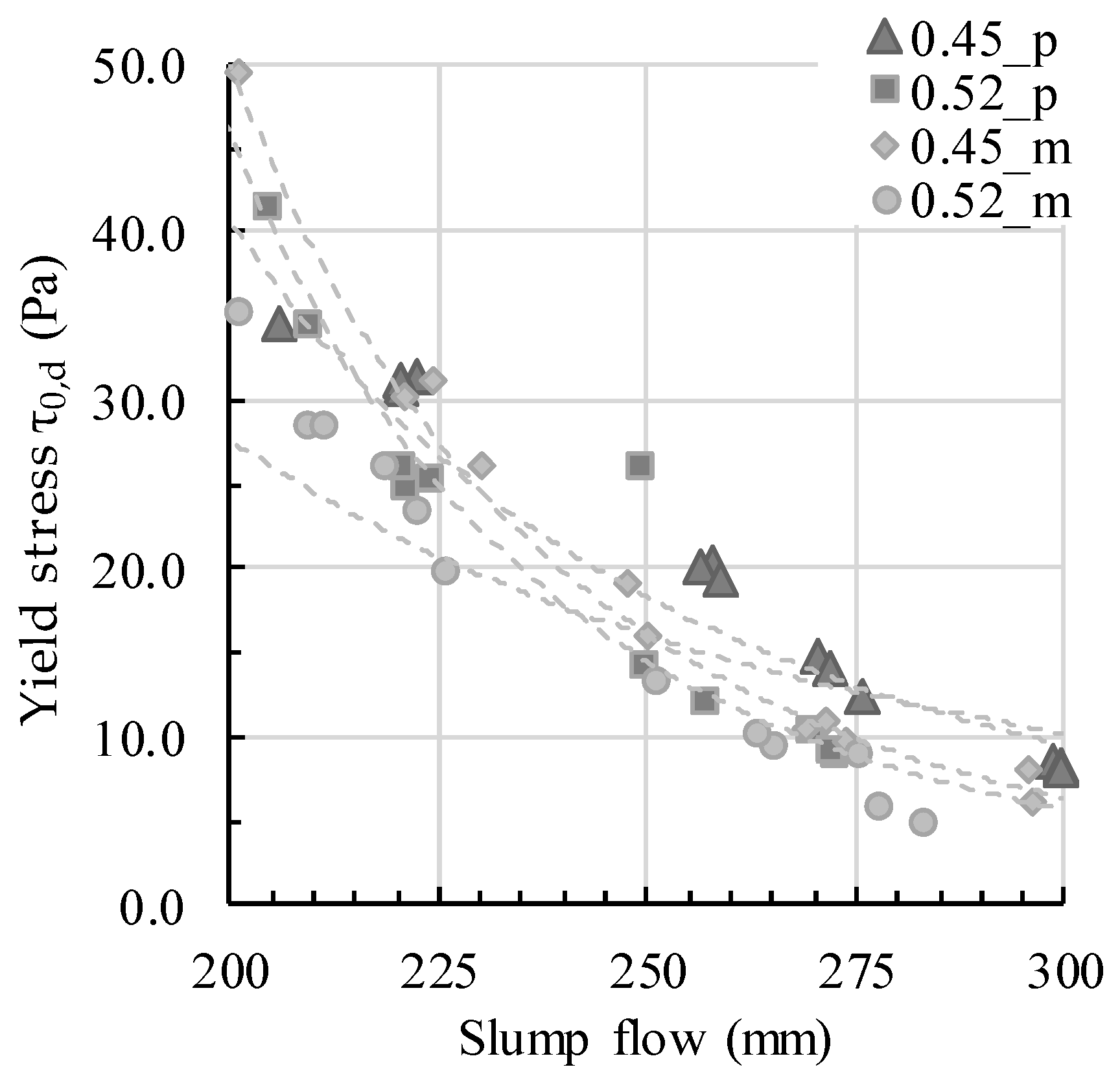
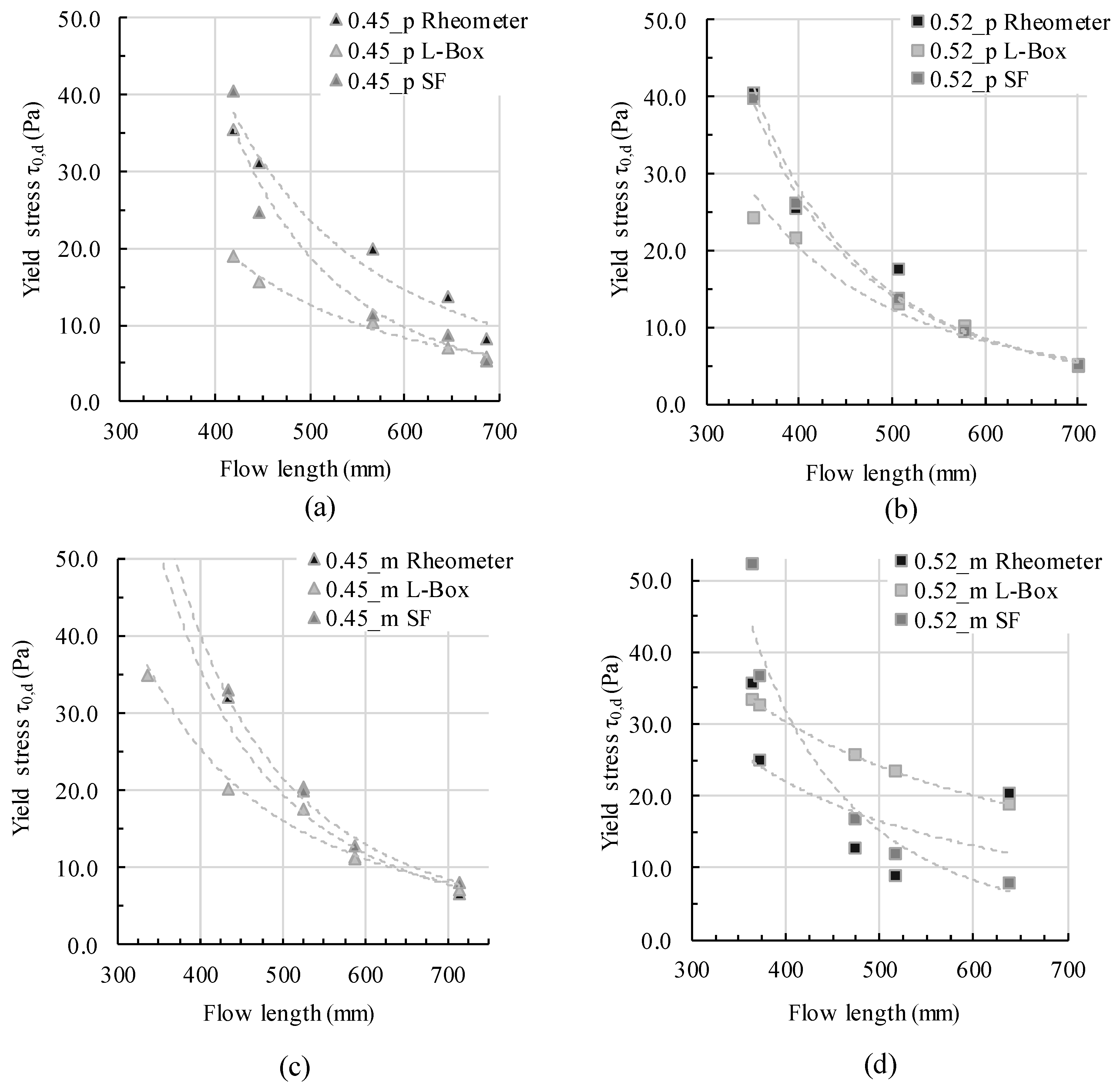
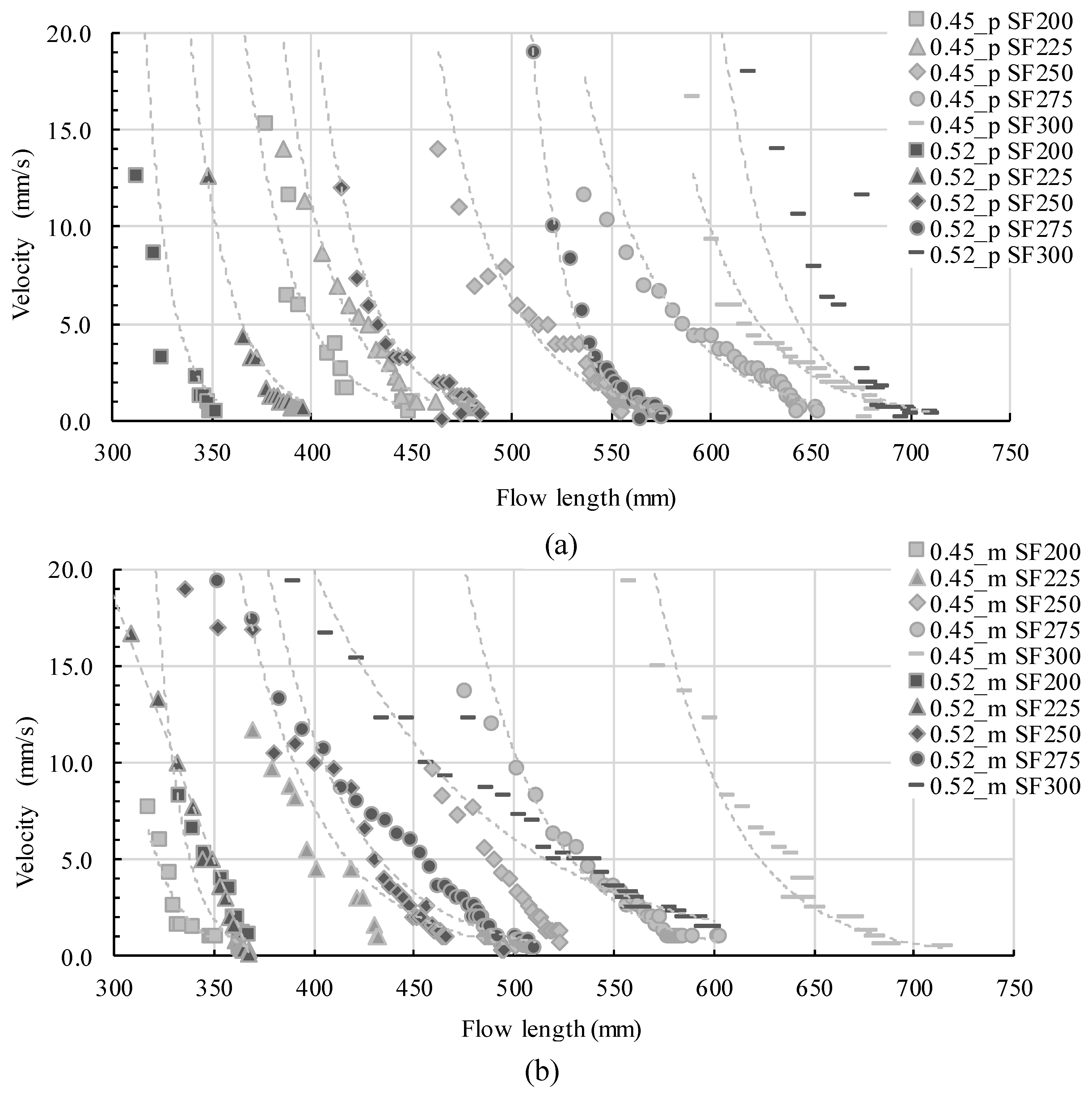
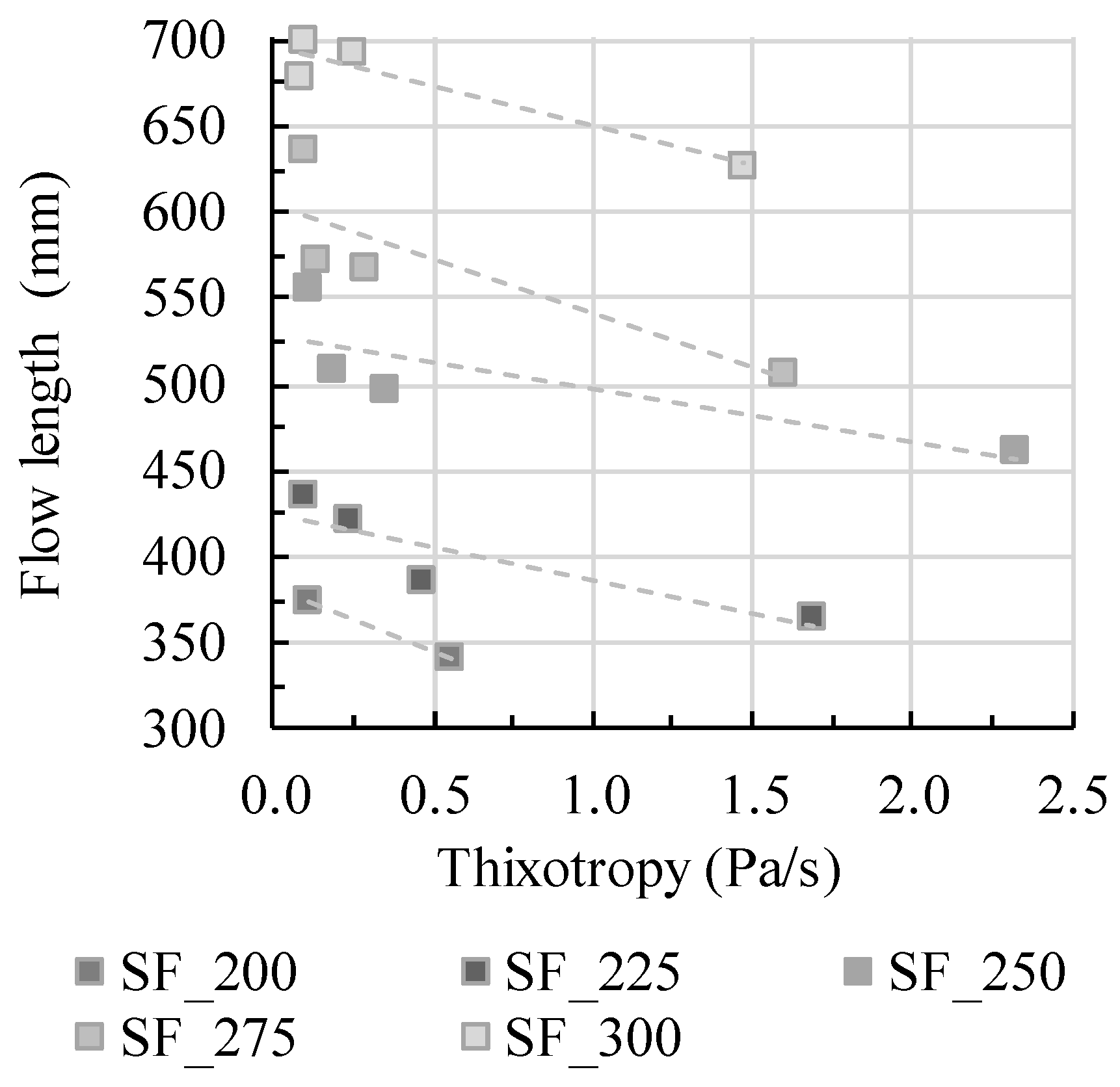
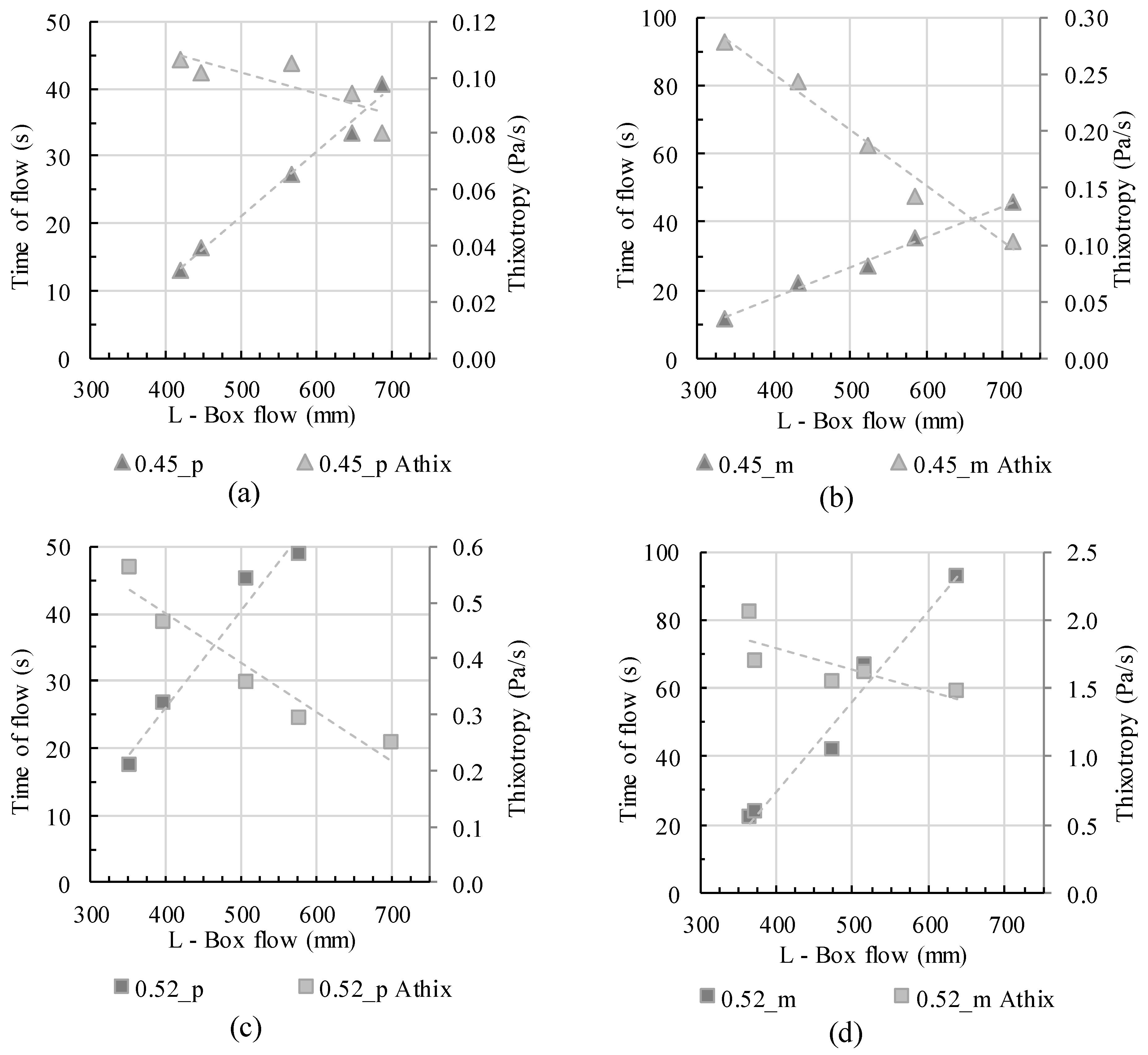
4.2. Flow Analysis
- -
- The rheometric dynamic yield stress measurement took place after the static yield stress measurement. The high shear of 30 seconds before the dynamic shear profile served for a homogenization and deagglomeration after the time of rest. Still, the agglomerate network within the colloidal paste changed over time and with rest, with a major impact on rheometric values (cf. [38])
- -
- The L-box flow was assumed as free flow. Still, within a short time of rest a low hydrodynamic pressure from the top to the bottom throughout the vertical column built up, which pushed the flow as soon as the gate was lifted.
- -
- The rheometric measurements were conducted with a vane-in-cup system using the Reiner–Riwlin equation for the calculation of shear stress from rotational torque. With increasing non-Bingham-like material behavior, the regression fits less.
- -
- Within the first two seconds, the flow length is different for each slump flow value. The higher the slump flow value, the higher the flow velocity and thus the initial flow length after two seconds
- -
- The velocity decreases tremendously but with a reduced rate during the experiment
- -
- The change of velocity decrease is more pronounced for highly flowable mixtures and for mortars than for pastes
- -
- Very slow flow takes place for the last few centimeters of flow
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bingham, E.C. An Investigation of the Law of Plastic Flow. Bull. Bur. Stand. 1916, 13, 309–353. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ferraris, C.F.; Galler, M.A.; Hansen, A.S.; Guynn, J.M. Influence of particle size distributions on yield stress and viscosity of cement–fly ash pastes. Cem. Concr. Res. 2012, 42, 404–409. [Google Scholar] [CrossRef]
- Larrard, F.; de Ferraris, C.F.; Sedran, T. Fresh concrete: A Herschel-Bulkley material. Mater. Struct. 1998, 31, 494–498. [Google Scholar] [CrossRef]
- Banfill, P.F.G. The Rheology of Fresh Cement and Concrete—A Review. In Proceedings of the 11th International Cement Chemistry Congress, Durban, South Africa, 11–16 May 2003. [Google Scholar]
- Koehler, E.P.; Fowler David, W. Summary of Concrete Workability Test Methods; 105 No. 1, 2001–2003; Research report, International Center for Aggregates Research; The University of Texas at Austin: Austin, TX, USA, 2003. [Google Scholar]
- Roussel, N. Rheology of fresh concrete: From measurements to predictions of casting processes. Mater. Struct. 2007, 40, 1001–1012. [Google Scholar] [CrossRef]
- Murata, J. Flow and deformation of fresh concrete. Mater. Struct. 1984, 17, 117–129. [Google Scholar] [CrossRef]
- Fataei, S.; Secrieru, E.; Mechtcherine, V. Influence of Aggregate Volume Fraction on Concrete Pumping Behaviour. In Rheology and Processing of Construction Materials; RILEM Bookseries 23; Mechtcherine, V., Khayat, K., Secrieru, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 303–310. ISBN 978-3-030-22565-0. [Google Scholar]
- Kovler, K.; Roussel, N. Properties of fresh and hardened concrete. Cem. Concr. Res. 2011, 41, 775–792. [Google Scholar] [CrossRef]
- Roussel, N.; Stefani, C.; Leroy, R. From mini-cone test to Abrams cone test: Measurement of cement-based materials yield stress using slump tests. Cem. Concr. Res. 2005, 35, 817–822. [Google Scholar] [CrossRef]
- Nguyen, T.L.H.; Roussel, N.; Coussot, P. Correlation between L-box test and rheological parameters of a homogeneous yield stress fluid. Cem. Concr. Res. 2006, 36, 1789–1796. [Google Scholar] [CrossRef]
- DIN EN 12350-10. Testing Fresh Concrete—Part 10: Self-Compacting Concrete—L Box Test, German version EN 12350-10:2010; German Institute for Standardisation (Deutsches Institut für Normung), Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Barnes, H.A. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Cheng, D.C.-H. Thixotropy. Int. J. Cosmet. Sci. 1987, 9, 151–191. [Google Scholar] [CrossRef]
- Dullaert, K.; Mewis, J. A model system for thixotropy studies. Rheol. Acta 2005, 45, 23–32. [Google Scholar] [CrossRef]
- Roussel, N. A thixotropy model for fresh fluid concretes: Theory, validation and applications. Cem. Concr. Res. 2006, 36, 1797–1806. [Google Scholar] [CrossRef]
- Glotzbach, C.; Lowke, D.; Kränkel, T.; Mazanec, O.; Schmidt, M.; Gehlen, C. Anwendungsorientierte Optimierung und Klassifizierung der rheologischen Eigenschaften von UHPC—Optimization and Classification of Rheological Properties of UHPC for its Application. In Nachhaltiges Bauen mit Ultrahochfestem Beton—Sustainable Building with Ultra-High Performance Concrete; Schriftenreihe Baustoffe und Massivbau—Structural Materials and Engineering Series; Schmidt, M., Fehling, E., Fröhlich, S., Thiemicke, J., Eds.; Kassel, Germany, 2014; pp. 355–362. ISBN 978-3-86219-480-3. [Google Scholar]
- Mujumdar, A.; Beris, A.N.; Metzner, A.B. Transient phenomena in thixotropic systems. J. Non-Newton. Fluid Mech. 2002, 102, 157–178. [Google Scholar] [CrossRef]
- Lowke, D.; Kränkel, T.; Gehlen, C.; Schießl, P. Effect of Cement on Superplasticizer Adsorption, Yield Stress, Thixotropy and Segregation Resistance. In Design, Production and Placement of Self-Consolidating Concrete; Khayat, K.H., Feys, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 91–101. ISBN 978-90-481-9663-0. [Google Scholar]
- Thrane, L.N. Form Filling with Self-Compacting Concrete. Ph.D.Thesis, TU Denmark, Lyngby, Denmark, 2007. [Google Scholar]
- Roussel, N.; Gram, A.; Cremonesi, M.; Ferrara, L.; Krenzer, K.; Mechtcherine, V.; Shyshko, S.; Skocec, J.; Spangenberg, J.; Svec, O.; et al. Numerical simulations of concrete flow: A benchmark comparison. Cem. Concr. Res. 2016, 79, 265–271. [Google Scholar] [CrossRef]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Rheology Series, 1; Elsevier: Amsterdam, The Netherlands, 1993; Volume 3, ISBN 0-444-87140-3. [Google Scholar]
- Barnes, H.A. The yield stress—A review or panta rei—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Choi, M.; Park, K.; Oh, T. Viscoelastic properties of Fresh Cement Paste to Study the Flow Behavior. Int. J. Concr. Struct. Mater. 2016, 10, 65–74. [Google Scholar] [CrossRef]
- Hafid, H.; Ovarlez, G.; Toussaint, F.; Jezequel, P.H.; Roussel, N. Effect of particle morphological parameters on sand grains packing properties and rheology of model mortars. Cem. Concr. Res. 2016, 80, 44–51. [Google Scholar] [CrossRef]
- Qian, Y.; Kawashima, S. Flow onset of fresh mortars in rheometers: Contribution of paste deflocculation and sand particle migration. Cem. Concr. Res. 2016, 90, 97–103. [Google Scholar] [CrossRef]
- Liu, D.-M. Particle packing and rheological property of highly-concentrated ceramic suspensions: Φm determination and viscosity prediction. J. Mater. Sci. 2000, 35, 5503–5507. [Google Scholar] [CrossRef]
- Genovese, D.B. Shear rheology of hard-sphere, dispersed, and aggregated suspensions, and filler-matrix composites. Adv. Colloid Interface Sci. 2012, 171–172, 1–16. [Google Scholar] [CrossRef]
- Da Cruz, F.; Chevoir, F.; Bonn, D.; Coussot, P. Viscosity bifurcation in granular materials, foams, and emulsions. Phys. Rev. E 2002, 66, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Firth, B.A.; Hunter, R.J. Flow Properties of Coagulated Colloidal Suspensions: Energy Dissipation in the Flow Units. J. Colloid Interface Sci. 1976, 57, 248–256. [Google Scholar] [CrossRef]
- Malkin, A.Y. Non-Newtonian viscosity in steady-state shear flows. J. Non-Newton. Fluid Mech. 2013, 192, 48–65. [Google Scholar] [CrossRef]
- Yammine, J.; Chaouche, M.; Guerinet, M.; Moranville, M.; Roussel, N. From ordinary rhelogy concrete to self compacting concrete: A transition between frictional and hydrodynamic interactions. Cem. Concr. Res. 2008, 38, 890–896. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Viscosity bifurcation in thixotropic, yielding fluids. J. Rheol. 2002, 46, 573–589. [Google Scholar] [CrossRef]
- Roussel, N.; Le Roy, R.; Coussot, P. Thixotropy modelling at local and macroscopic scales. J. Non-Newton. Fluid Mech. 2004, 117, 85–95. [Google Scholar] [CrossRef]
- Thiedeitz, M.; Kränkel, T.; Gehlen, C. Thixotropic Structural Build-Up of Cement Pastes at Low Shear Rates. In Proceedings of the International Conference on Sustainable Materials, Systems and Structures (SMSS2019), Rovinj, Croatia, 20–22 March 2019; pp. 272–279, ISBN 978-2-35158-218. [Google Scholar]
- Wallevik, O.H.; Feys, D.; Wallevik, J.E.; Khayat, K.H. Avoiding inaccurate interpretations of rheological measurements for cement-based materials. Cem. Concr. Res. 2015, 78, 100–109. [Google Scholar] [CrossRef]
- Thiedeitz, M.; Kränkel, T.; Gehlen, C. Effect of the mixing time on rheological parameters of cement pastes. In Proceedings of the Conference Proceedings Rheologische Messungen an Baustoffen 2019, Regensburg, Germany, 13 March 2019; pp. 14–25. [Google Scholar]
- Haist, M.E.A. Interlaboratory study on rheological properties of cement pastes and reference substances—Comparability of measurements performed with different rheometers and measurement geometries. Mater. Struct. 2020, in press. [Google Scholar]
- Feys, D.; Cepuritis, R.; Jacobsen, S.; Lesage, K.; Secrieru, E.; Yahia, A. Measuring Rheological Properties of Cement Pastes: Most common Techniques, Procedures and Challenges. Rilem. Tech. Lett. 2017, 2, 129–135. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Gram, A.; Krenzer, K.; Schwabe, J.-H.; Shyshko, S.; Roussel, N. Simulation of fresh concrete flow using Discrete Element Method (DEM): Theory and applications. Mater. Struct. 2014, 47, 615–630. [Google Scholar] [CrossRef]
- Flatt, R.J.; Bowen, P. Yield Stress of Multimodal Powder Suspensions: An Extension of the YODEL (Yield Stress mODEL). J. Am. Ceram. Soc. 2007, 90, 1038–1044. [Google Scholar] [CrossRef]
- Ukrainczyk, N.; Caggiano, A.; Schicchi, D.S.; Gilka-Bötzow, A.; Koenders, E. Hydrating Cement Particle Interaction Model for Yield Stress Analysis. In Rheology and Processing of Construction Materials; RILEM Bookseries 23; Mechtcherine, V., Khayat, K., Secrieru, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 636–643. ISBN 978-3-030-22565-0. [Google Scholar]
- DIN EN 1015-3:2007-05. Methods of Test for Mortar for Masonry—Part 3: Determination of Consistence of Fresh Mortar (by Flow Table); German Version EN 1015-3:1999+A1:2004+A2:2006; German Institute for Standardisation (Deutsches Institut für Normung), Beuth Verlag GmbH: Berlin, Germany, 2007. [Google Scholar]
- DIN EN 12350-8:2010-12. Testing Fresh Concrete—Part 8: Self-Compacting Concrete—Slump-Flow Test, German version EN 12350-8:2010; German Institute for Standardisation (Deutsches Institut für Normung), Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Roussel, N. The LCPC BOX: A cheap and simple technique for yield stress measurements of SCC. Mater. Struct. 2007, 40, 889–896. [Google Scholar] [CrossRef]
- Chaparian, E.; Nasouri, B. L-box—A tool for measuring the “yield stress”: A theoretical study. Phys. Fluids 2018, 30, 83101. [Google Scholar] [CrossRef]
- Shan, Z.; Yu, Z.; Shi, J. Experimental investigation of flow of fresh self-compacting concrete in improved L-box. Constr. Build. Mater. 2015, 84, 30–38. [Google Scholar] [CrossRef]
- Lowke, D.; Illguth, S.; Kränkel, T.; Gehlen, C. Rheological Optimization of Flowable Concretes Based on Computational Fluid Dynamics (CFD). In Proceedings of the 7th RILEM International Conference on Self-Compacting Concrete and of the 1st RILEM International Conference on Rheology and Processing of Construction Materials, Paris, France, 1–6 September 2013; Roussel, N., Bessaies-Bey, H., Eds.; [Google Scholar]
- Gram, A.; Silfwerbrand, J.; Lagerblad, B. Obtaining rheological parameters from flow test—Analytical, computational and lab test approach. Cem. Concr. Res. 2014, 63, 29–34. [Google Scholar] [CrossRef]
- Li, Z.; Cao, G.; Tan, Y. Prediction of time-dependent flow behaviors of fresh concrete. Constr. Build. Mater. 2016, 125, 510–519. [Google Scholar] [CrossRef]
- Tan, Y.; Cao, G.; Zhang, H.; Wang, J.; Deng, R.; Xiao, X.; Wu, B. Study on the Thixotropy of the Fresh Concrete Using DEM. Procedia Eng. 2015, 102, 1944–1950. [Google Scholar] [CrossRef][Green Version]
- Lu, Z.; Haist, M.; Ivanov, D.; Jakob, C.; Jansen, D.; Leinitz, S.; Link, J.; Mechtcherine, V.; Neubauer, J.; Plank, J.; et al. Characterization data of reference cement CEM I 42.5 R used for Priority Program DFG SPP 2005 “Opus Fluidum Futurum—Rheology of reactive, multiscale, multiphase construction materials”. Data Brief 2019, 27, 104699. [Google Scholar] [CrossRef]
- DIN EN 196-1:2016-11. Methods of Testing Cement—Part 1: Determination of Strength; German Version EN 196-1:2016; German Institute for Standardisation (Deutsches Institut für Normung), Beuth Verlag GmbH: Berlin, Germany, 2016. [Google Scholar]
- Eslami Pirharati, M.; Ivanov, D.; Krauss, H.-W.; Schilde, C.; Lowke, D. Numerical Simulation of the Flow Behavior of Newtonian Fluids in a Wide Gap Rheometer by CFD. In Rheology and Processing of Construction Materials; RILEM Bookseries 23; Mechtcherine, V., Khayat, K., Secrieru, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 588–595. ISBN 978-3-030-22565-0. [Google Scholar]
- Thiedeitz, M.; Kränkel, T.; Gehlen, C. Thixotropy-Dependent Form Filling Ability of Cement Paste. In Rheology and Processing of Construction Materials; RILEM Bookseries 23; Mechtcherine, V., Khayat, K., Secrieru, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 273–280. ISBN 978-3-030-22565-0. [Google Scholar]


| Mixture | w/c Ratio | Solid Concrete Φ [-] | Cement (kg/m3) | Water (kg/m3) 1 | Standard Sand (kg/m3) | PCE (wt. % by Cement) 2 |
|---|---|---|---|---|---|---|
| 0.45_p | 0.40 | 0.45 | 1395.1 | 551.4 | - | 0.13–0.34 |
| 0.45_m | 0.40 | 0.45 | 1088.2 | 430.1 | 1350 ± 5 | 0.32–0.57 |
| 0.52_p | 0.30 | 0.52 | 1615.2 | 480.1 | - | 0.68–1.24 |
| 0.52_m | 0.30 | 0.52 | 1259.9 | 375.9 | 1350 ± 5 | 2.78–5.44 |
| Average Slump Flow (mm) | 0.45_p | ||||||
|---|---|---|---|---|---|---|---|
| (Pa) | (Pas) | Flow Length (mm) | (s) | ||||
| 200.0 | 35.50 | 18.90 | 40.54 | 1.60 | 0.11 | 419 | 13.2 |
| 220.7 | 31.10 | 15.53 | 24.63 | 1.16 | 0.10 | 447 | 16.3 |
| 257.3 | 19.93 | 10.47 | 11.42 | 0.75 | 0.11 | 567 | 27.5 |
| 272.3 | 13.70 | 6.97 | 8.61 | 0.82 | 0.09 | 647 | 33.5 |
| 299.2 | 8.23 | 5.77 | 5.39 | 0.66 | 0.08 | 687 | 40.7 |
| Average slump flow (mm) | 0.52_p | ||||||
| (Pa) | (Pa) | (Pa) | (Pas) | (Pa/s) | Flow length (mm) | Flow time (s) | |
| 203.7 | 40.60 | 24.37 | 39.89 | 2.04 | 0.56 | 352 | 17.4 |
| 221.3 | 25.43 | 21.53 | 26.14 | 1.55 | 0.46 | 396 | 26.6 |
| 251.7 | 17.50 | 12.97 | 13.78 | 1.35 | 0.36 | 508 | 45.2 |
| 270.8 | 9.57 | 10.20 | 9.53 | 1.15 | 0.29 | 578 | 48.9 |
| 305.3 | 4.83 | 4.87 | 5.24 | 0.86 | 0.25 | 701 | 42.5 |
| Average slump flow (mm) | 0.45_m | ||||||
| (Pa) | (Pa) | (Pa) | (Pas) | (Pa/s) | Flow length (mm) | Flow time (s) | |
| 197.7 | 49.80 | 35.03 | 63.05 | 2.75 | 0.28 | 336 | 11.6 |
| 224.8 | 29.20 | 20.37 | 33.16 | 2.41 | 0.24 | 434 | 21.8 |
| 248.3 | 18.03 | 17.60 | 20.09 | 1.95 | 0.19 | 524 | 27.2 |
| 271.0 | 10.33 | 11.17 | 12.99 | 2.08 | 0.14 | 586 | 35.3 |
| 298.0 | 6.47 | 7.33 | 8.08 | 1.60 | 0.10 | 714 | 45.7 |
| Average slump flow (mm) | 0.52_m | ||||||
| (Pa) | (Pa) | (Pa) | (Pas) | (Pa/s) | Flow length (mm) | Flow time (s) | |
| 207.0 | 30.80 | 33.37 | 52.16 | 7.52 | 2.05 | 364 | 21.8 |
| 222.0 | 23.20 | 32.43 | 36.61 | 7.13 | 1.69 | 374 | 23.6 |
| 252.7 | 11.03 | 25.67 | 16.83 | 6.78 | 2.32 | 474 | 41.9 |
| 278.5 | 6.53 | 23.27 | 11.78 | 7.37 | 1.61 | 516 | 66.9 |
| 303.0 | 19.90 | 18.80 | 7.76 | 6.97 | 1.47 | 638 | 92.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiedeitz, M.; Habib, N.; Kränkel, T.; Gehlen, C. L-Box Form Filling of Thixotropic Cementitious Paste and Mortar. Materials 2020, 13, 1760. https://doi.org/10.3390/ma13071760
Thiedeitz M, Habib N, Kränkel T, Gehlen C. L-Box Form Filling of Thixotropic Cementitious Paste and Mortar. Materials. 2020; 13(7):1760. https://doi.org/10.3390/ma13071760
Chicago/Turabian StyleThiedeitz, Mareike, Nasime Habib, Thomas Kränkel, and Christoph Gehlen. 2020. "L-Box Form Filling of Thixotropic Cementitious Paste and Mortar" Materials 13, no. 7: 1760. https://doi.org/10.3390/ma13071760
APA StyleThiedeitz, M., Habib, N., Kränkel, T., & Gehlen, C. (2020). L-Box Form Filling of Thixotropic Cementitious Paste and Mortar. Materials, 13(7), 1760. https://doi.org/10.3390/ma13071760





