A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics
Abstract
1. Introduction
2. Material and Methods
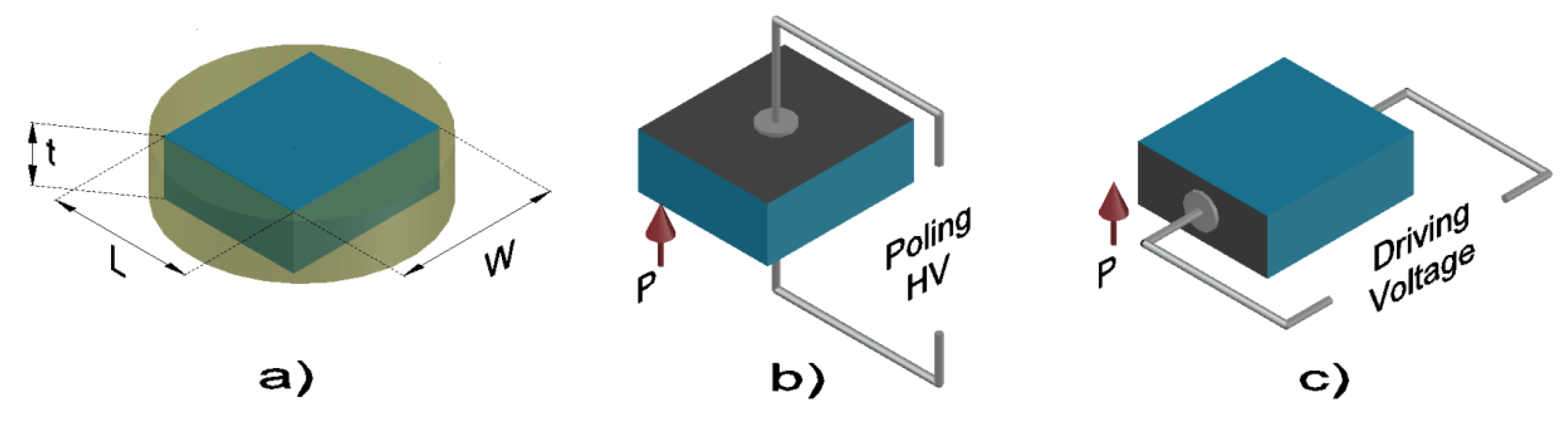
2.1. Material
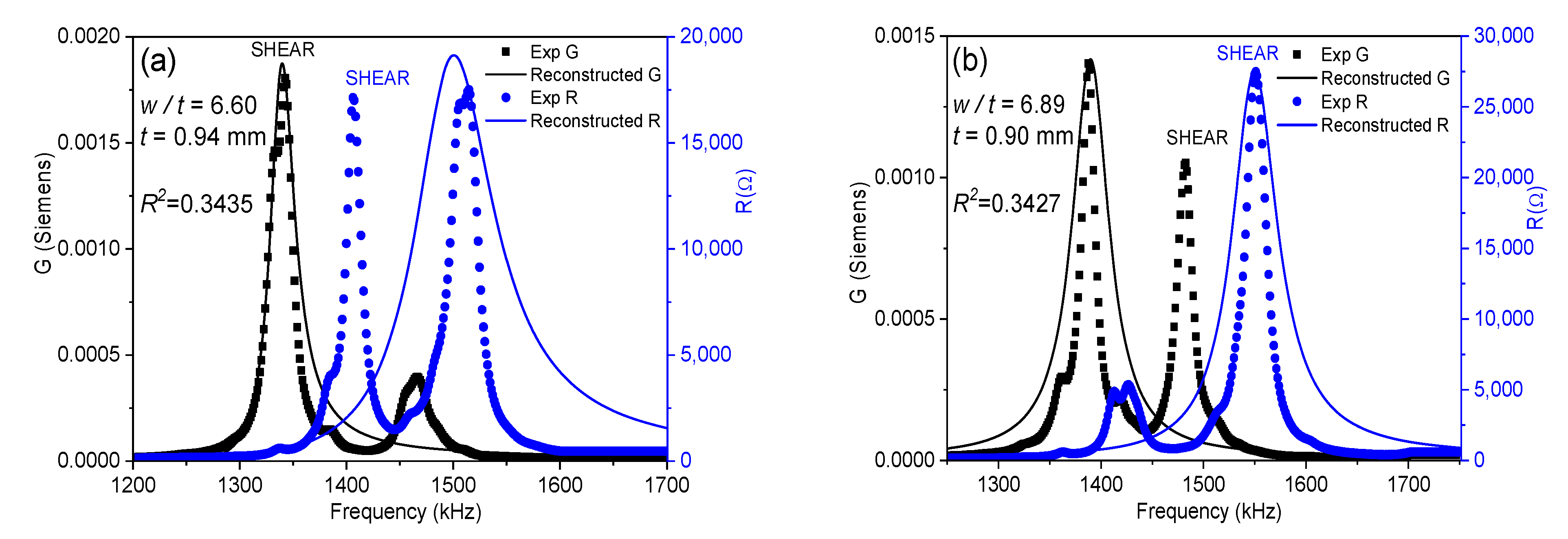
2.2. The Automatic Iterative Method for Analysis of Impedance Curves
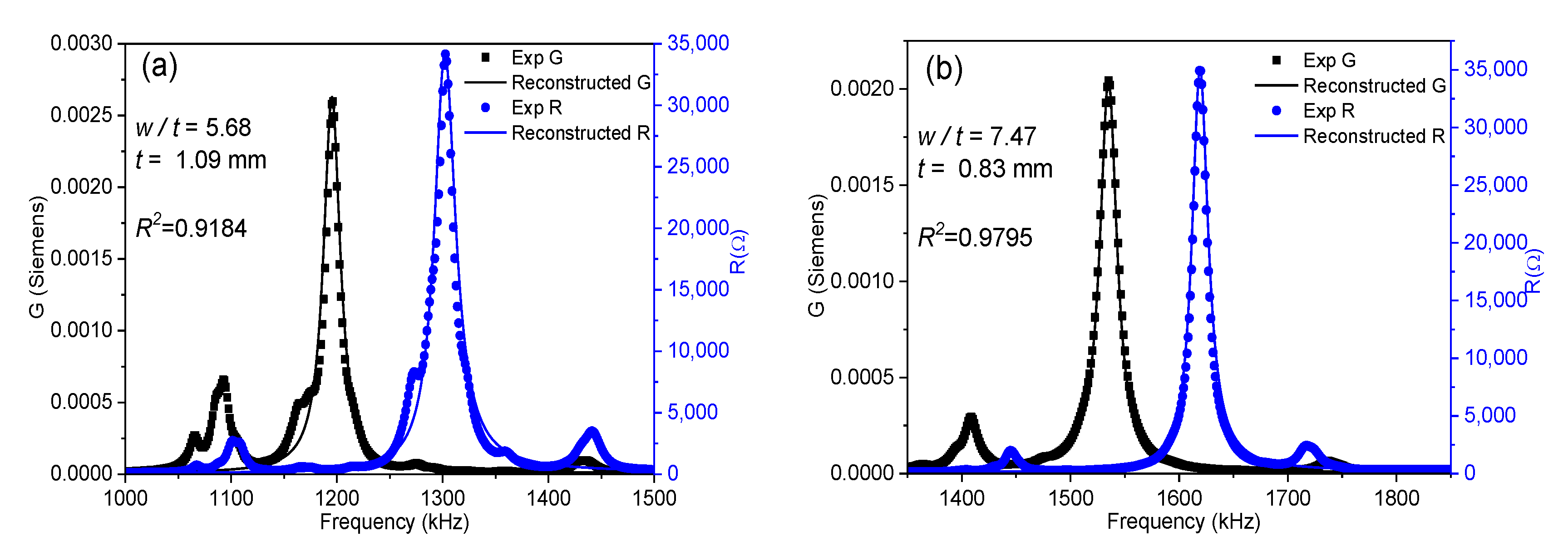
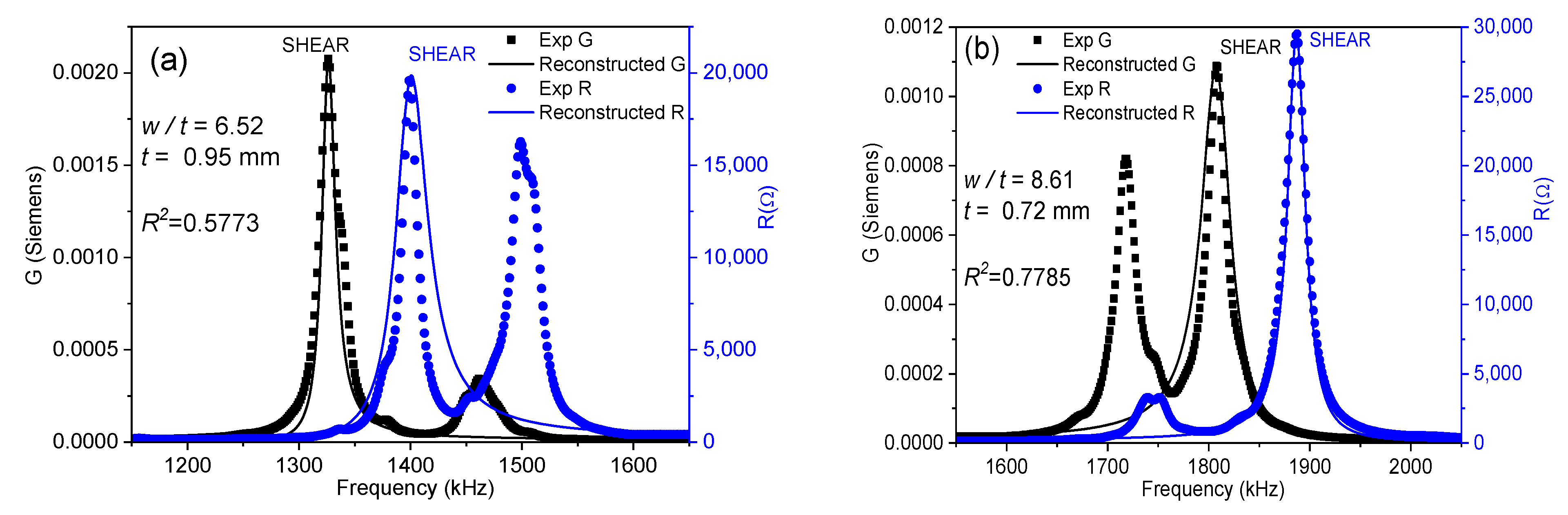
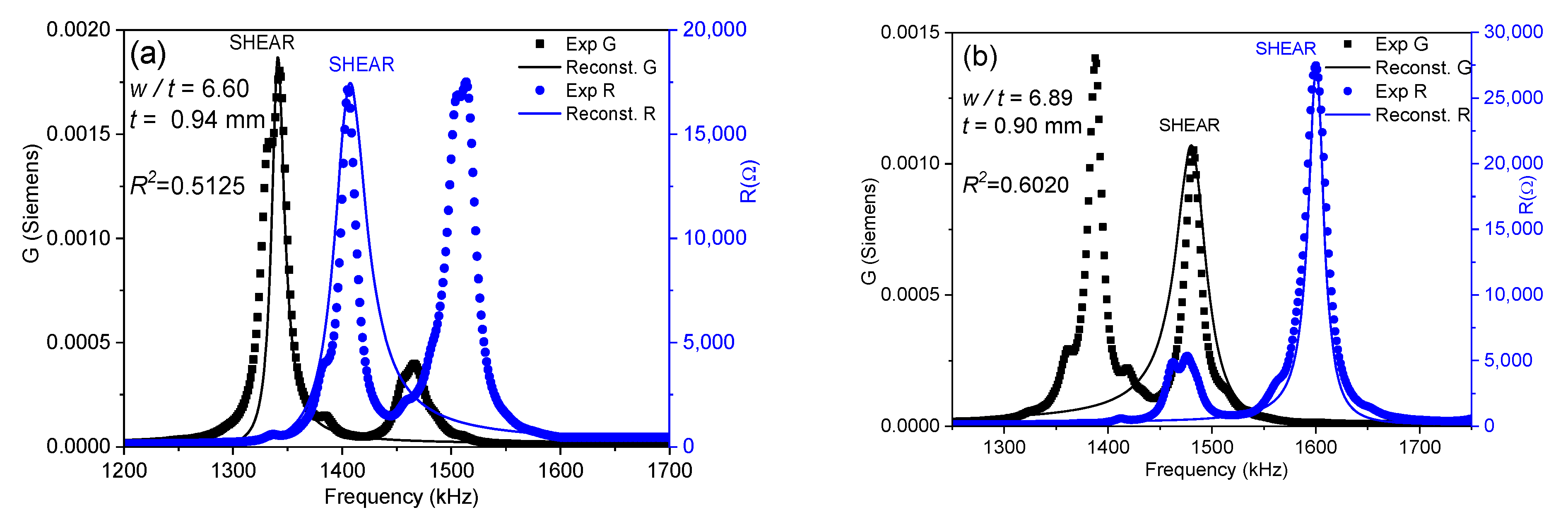
2.3. The Modified Automatic Iterative Method
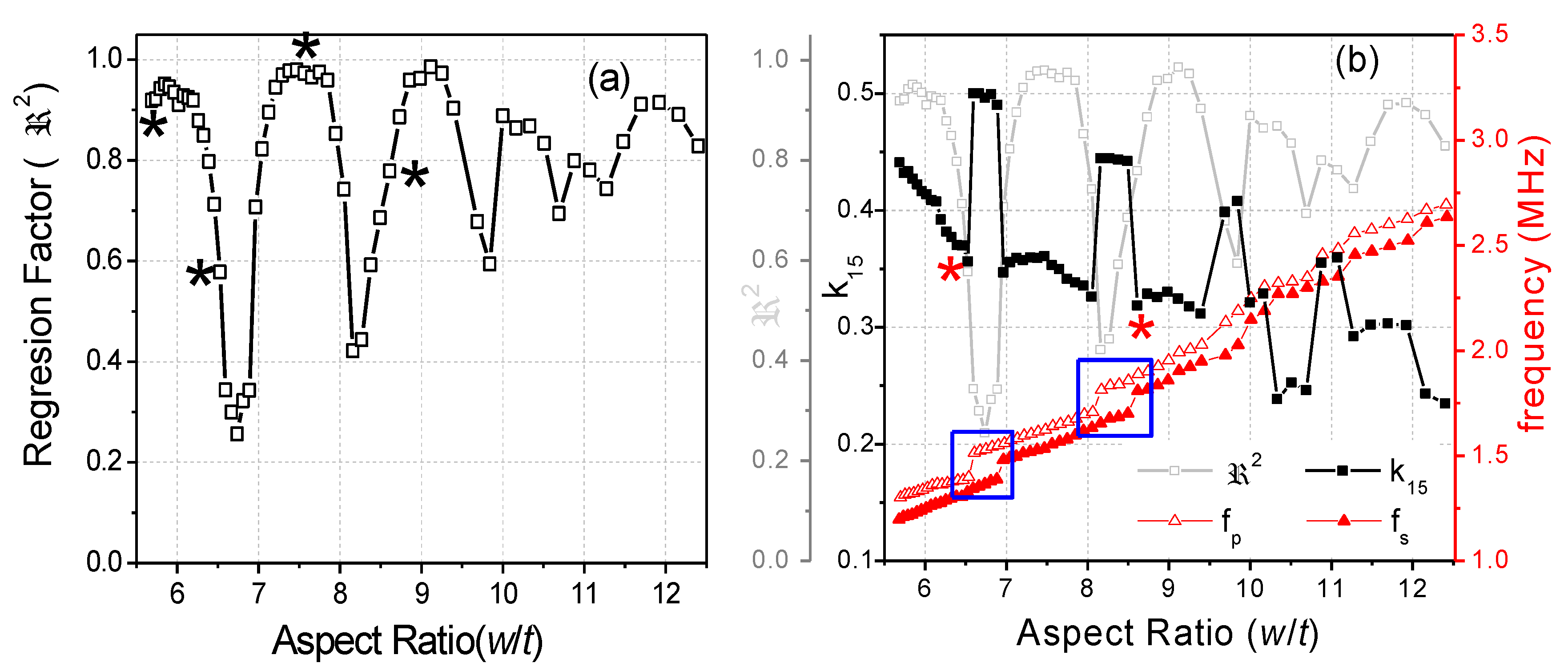
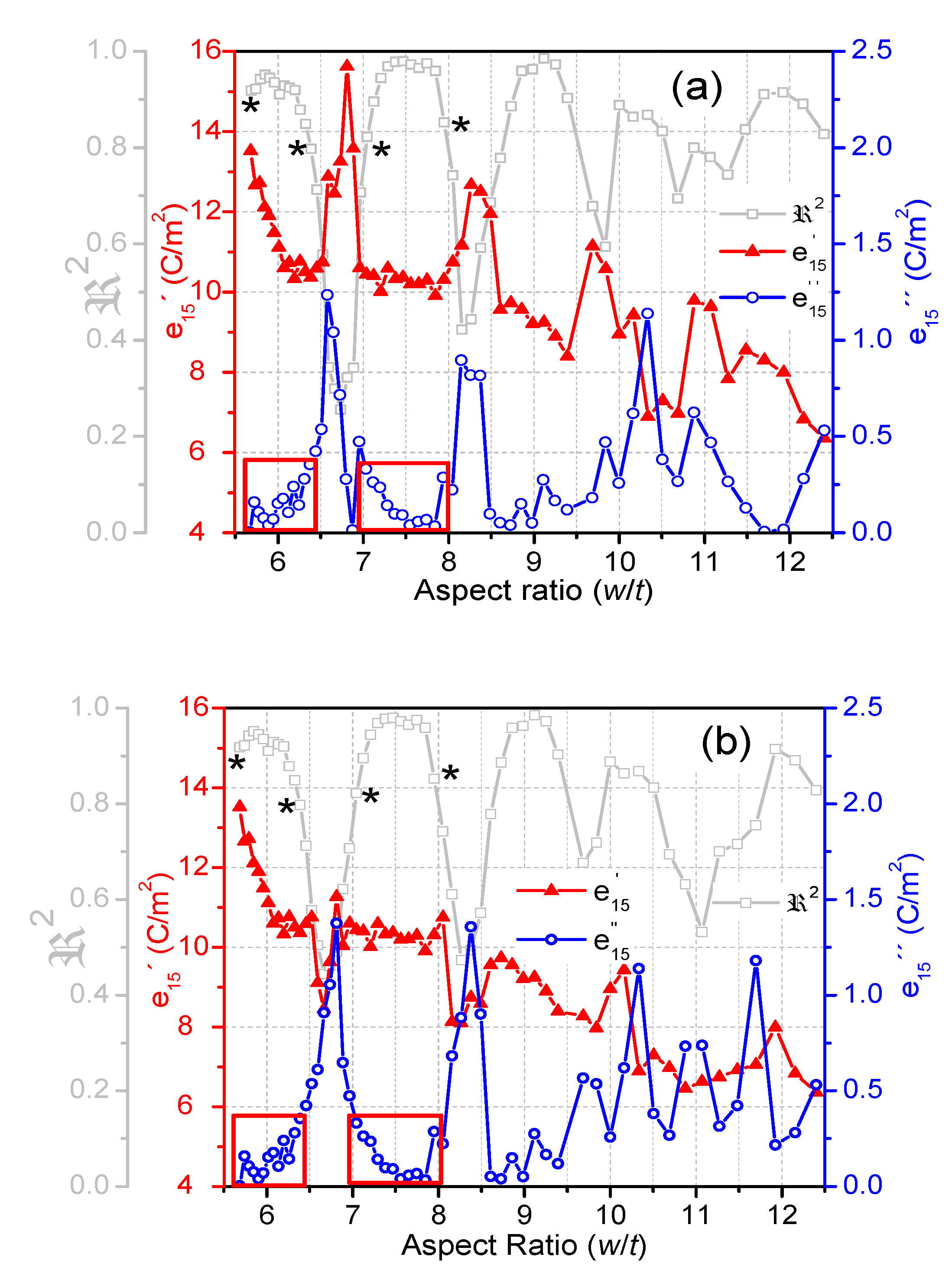
3. Results
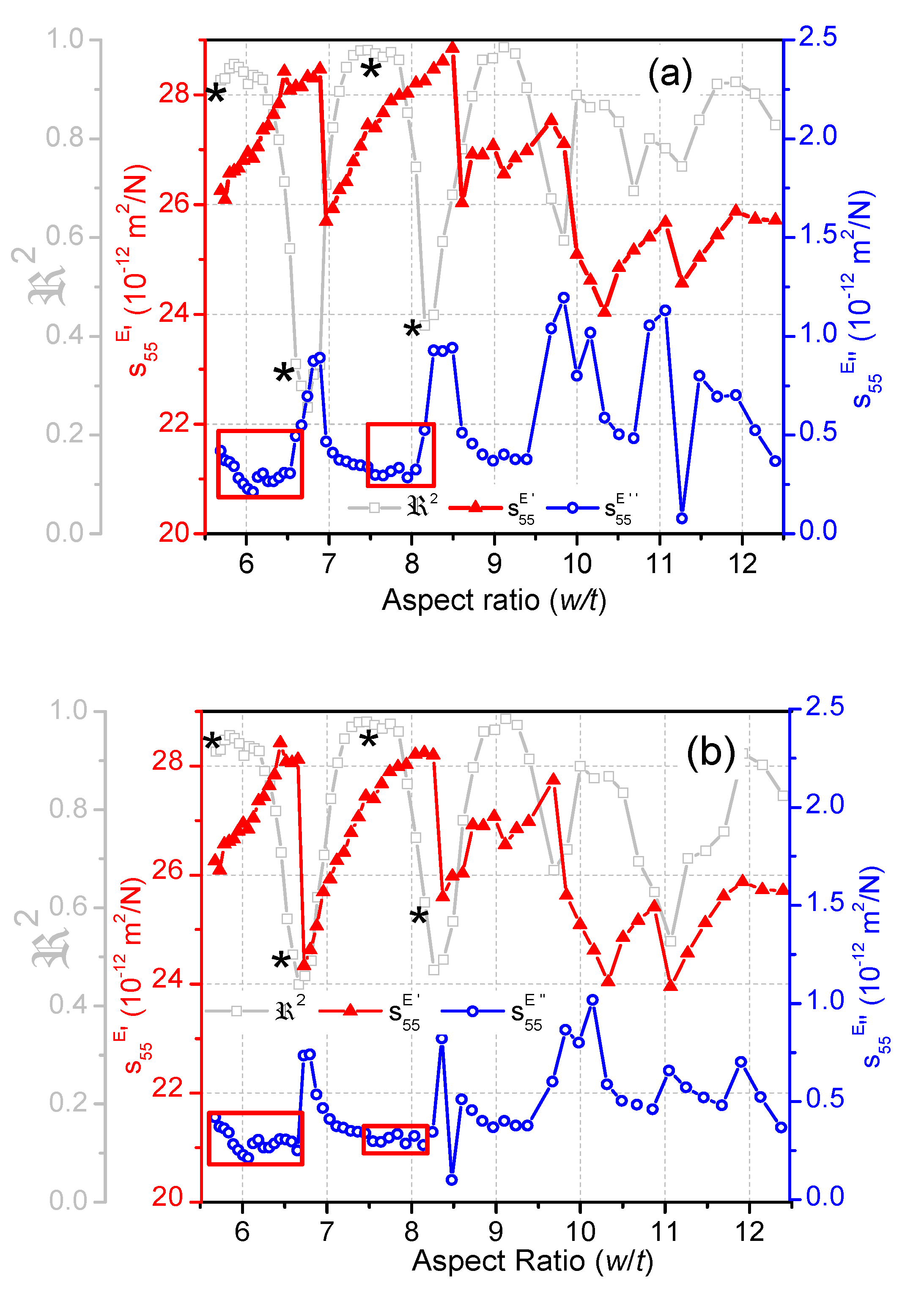
3.1. Elastic Properties
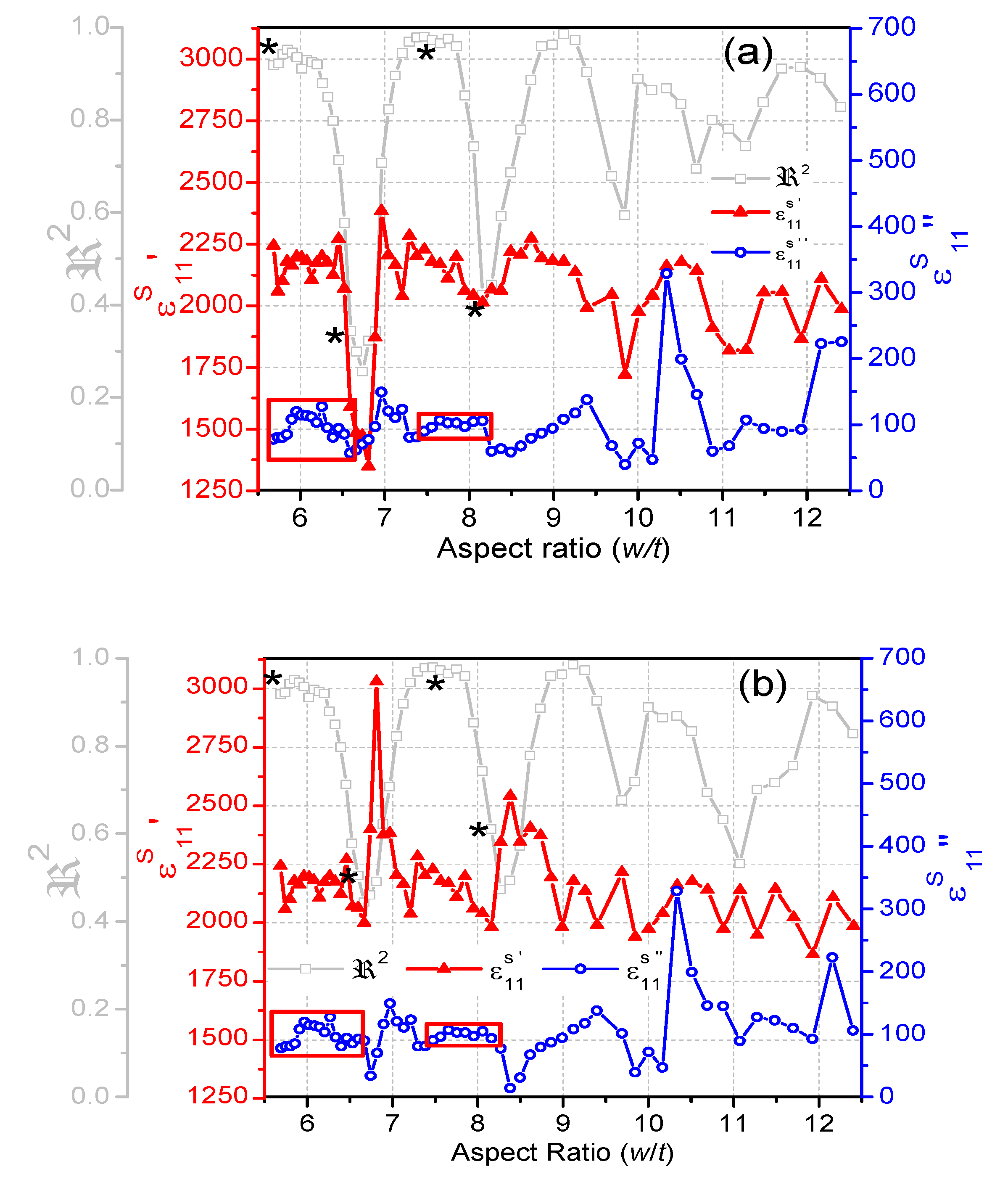
3.2. Dielectric Properties
3.3. Piezoelectric Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pardo, L.; Ricote, J. (Eds.) Multifunctional Polycrystalline Ferroelectric Materials; Springer Series in Materials Science vol. 140; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Villafuerte-Castrejón, M.E.; Morán, E.; Reyes-Montero, A.; Vivar-Ocampo, R.; Peña-Jiménez, J.A.; Rea-López, S.O.; Pardo, L. Towards Lead-Free Piezoceramics: Facing a Synthesis Challenge. Materials 2016, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Rodríguez, M.; Jiménez, F.J.; Pardo, L.; Ochoa, P.; González, A.M.; de Frutos, J. A New Prospect in Road Traffic Energy Harvesting Using Lead-Free Piezoceramics. Materials 2019, 12, 3725. [Google Scholar] [CrossRef] [PubMed]
- Ringgaard, E.; Wurlitzer, T. Lead-free piezoceramics based on alkali niobates. J. Eur. Ceram. Soc. 2005, 25, 2701. [Google Scholar] [CrossRef]
- Demartin Maeder, M.; Damjanovic, D.; Setter, N. Lead Free Piezoelectric Materials. J. Electroceram. 2004, 13, 385. [Google Scholar] [CrossRef]
- Gonzalez, A.M.; Garcia, Á.; Benavente-Peces, C.; Pardo, L. Revisiting the characterization of the losses in piezoelectric materials. Materials 2016, 9, 72. [Google Scholar] [CrossRef]
- Meeke, T.R. Publication and proposed revision of ANSI/IEEE standard 176-1987. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 717–772. [Google Scholar] [CrossRef]
- Electronic Materials Manufacturers Association of Japan. Japanese Industrial Standards EMAS-6100: Electronic Test Methods for the Characterisation of Piezoelectric Ceramic Oscillators; Electronic Materials Manufacturers Association of Japan: Tokyo, Japan.
- Pérez, N.; Buiochi, F.; Brizzotti Andrade, M.A.; Adamowski, J.C. Numerical Characterization of Piezoceramics Using Resonance Curves. Materials 2016, 9, 71. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Zhu, S.; Jiang, B. Analysis of the shear modes in a piezoelectric vibrator. J. Appl. Phys. 1998, 83, 4415. [Google Scholar] [CrossRef][Green Version]
- Hikita, K.; Hiruma, Y.; Nagata, H.; Takenaka, T. Shear-Mode Piezoelectric Properties of KNbO3—Based Ferroelectric Ceramics. Jpn. J. Appl. Phys. 2009, 48, 07GA05. [Google Scholar] [CrossRef]
- Brissaud, M. Modelling of coupling between shear and longitudinal modes of a bulky rectangular piezoelectric element. Mat. Res. Express 2019, 6, 095701. [Google Scholar] [CrossRef]
- Pardo, L.; Algueró, M.; Brebøl, K. Resonance modes in Standard Characterization of Piezoceramics: A discussion based on Finite Element Analysis. Ferroelectrics 2006, 336, 181. [Google Scholar] [CrossRef]
- Pardo, L.; de Espinosa, F.M.; Brebøl, K. Study by laser interferometry of the resonance modes of the shear plate used in the Standards characterization of piezoceramics. J. Electroceram. 2007, 19, 437. [Google Scholar] [CrossRef]
- Aurelle, N.; Roche, D.; Richard, C.; Gonnard, P. Sample aspect ratio influence on the shear coefficients measurements of a piezoelectric bar. In Proceedings of the 1994 IEEE International Symposium on Applications of Ferroelectrics, University Park, PA, USA, 7–10 August 1994; pp. 162–165. [Google Scholar] [CrossRef]
- Pardo, L.; García, A.; de Espinosa, F.M.; Brebøl, K. Shear Resonance Mode Decoupling to Determine the Characteristic Matrix of Piezoceramics for 3-D Modelling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 646–657. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Montero, A.; Pardo, L.; García, A.; González, A.M.; Villafuerte-Castrejón, M.E. Ba1−xCaxTi0.90Zr0·10O3 shear properties and their frequency dependence determined from ceramic plates by an effective method for resonance decoupling. J. Alloys Compd. 2019, 806, 428. [Google Scholar] [CrossRef]
- Alemany, C.; Pardo, L.; Jimenez, B.; Carmona, F.; Mendiola, J.; Gonzalez, A. Automatic iterative evaluation of complex material constants in piezoelectric ceramics. J. Phys. D Appl. Phys. 1994, 27, 148. [Google Scholar] [CrossRef]
- Alemany, C.; Gonzalez, A.M.; Pardo, L.; Jimenez, B.; Carmona, F.; Mendiola, J. Automatic determination of complex constants of piezoelectric lossy materials in the radial mode. J. Phys. D Appl. Phys. 1995, 28, 945–956. [Google Scholar] [CrossRef]
- Determination of Piezoelectric, Dielectric and Elastic Complex Coefficients in the Linear Range from the Electromechanical Resonance Modes of Poled Ferroelectric Ceramics. Available online: http://icmm.csic.es/gf2/medidas.htm (accessed on 20 February 2020).
- Nye, J.F. Physical Properties of Crystals. Their Representation by Tensors and Matrices; Clarendon Press: Oxford, UK, 1957. [Google Scholar]
- Villalobos-Portillo, E.E.; Fuentes-Montero, L.; Montero-Cabrera, M.E.; Burciaga-Valencia, D.E.; Fuentes- Cobas, L.E. Polycrystal piezoelectricity: Revisiting the Voigt-Reuss-Hill approximation. Mat. Res. Express 2019, 6, 115705. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, Y.; Bao, H.; Zhou, C.; Gao, J.; Ren, X. Elastic, piezoelectric, and dielectric properties of Ba(Zr0.2Ti0.8)O3-50(Ba0.7Ca0.3)TiO3 Pb-free ceramic at the morphotropic phase boundary. J. Appl. Phys. 2011, 109, 054110. [Google Scholar] [CrossRef]
- Reyes-Montero, A.; Pardo, L.; López-Juárez, R.; González, A.M.; Rea-López, S.O.; Cruz, M.P.; Villafuerte-Castrejón, M.E. Sub-10micron grain size Ba1−xCaxTi0.9Zr0.1O3(x = 0.10 and 0.15) piezoceramics processed using a reduced thermal treatment. Smart Mater. Struct. 2015, 24, 065033. [Google Scholar] [CrossRef]
- Ochoa, P.; González, A.M.; García, A.; Jiménez, F.J.; Vázquez-Rodríguez, M.; Pardo, L. FEA study of shear mode decoupling in non-standard thin plates of a lead-free piezoelectric ceramic. 2020; (Submitted for Publication). [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo, L.; Reyes-Montero, A.; García, Á.; Jacas-Rodríguez, A.; Ochoa, P.; González, A.M.; Jiménez, F.J.; Vázquez-Rodríguez, M.; Villafuerte-Castrejón, M.E. A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics. Materials 2020, 13, 1666. https://doi.org/10.3390/ma13071666
Pardo L, Reyes-Montero A, García Á, Jacas-Rodríguez A, Ochoa P, González AM, Jiménez FJ, Vázquez-Rodríguez M, Villafuerte-Castrejón ME. A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics. Materials. 2020; 13(7):1666. https://doi.org/10.3390/ma13071666
Chicago/Turabian StylePardo, Lorena, Armando Reyes-Montero, Álvaro García, Alfredo Jacas-Rodríguez, Pilar Ochoa, Amador M. González, Francisco J. Jiménez, Manuel Vázquez-Rodríguez, and María E. Villafuerte-Castrejón. 2020. "A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics" Materials 13, no. 7: 1666. https://doi.org/10.3390/ma13071666
APA StylePardo, L., Reyes-Montero, A., García, Á., Jacas-Rodríguez, A., Ochoa, P., González, A. M., Jiménez, F. J., Vázquez-Rodríguez, M., & Villafuerte-Castrejón, M. E. (2020). A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics. Materials, 13(7), 1666. https://doi.org/10.3390/ma13071666




