Homogenization and Equivalent Beam Model for Fiber-Reinforced Tubular Profiles
Abstract
1. Introduction
2. Motivation
3. Theoretical Background
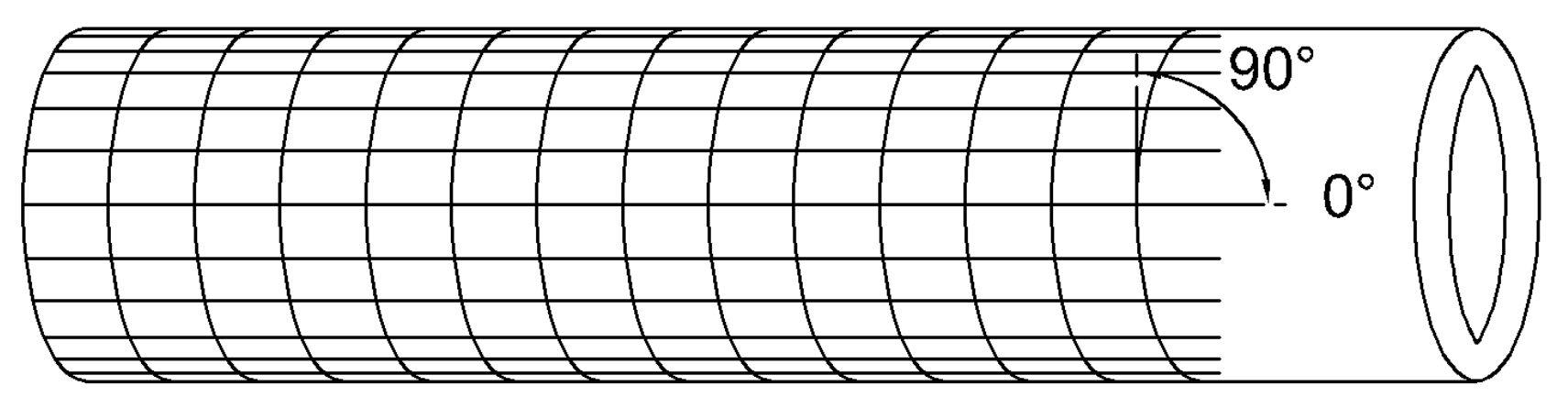
3.1. Cross-Ply Laminates
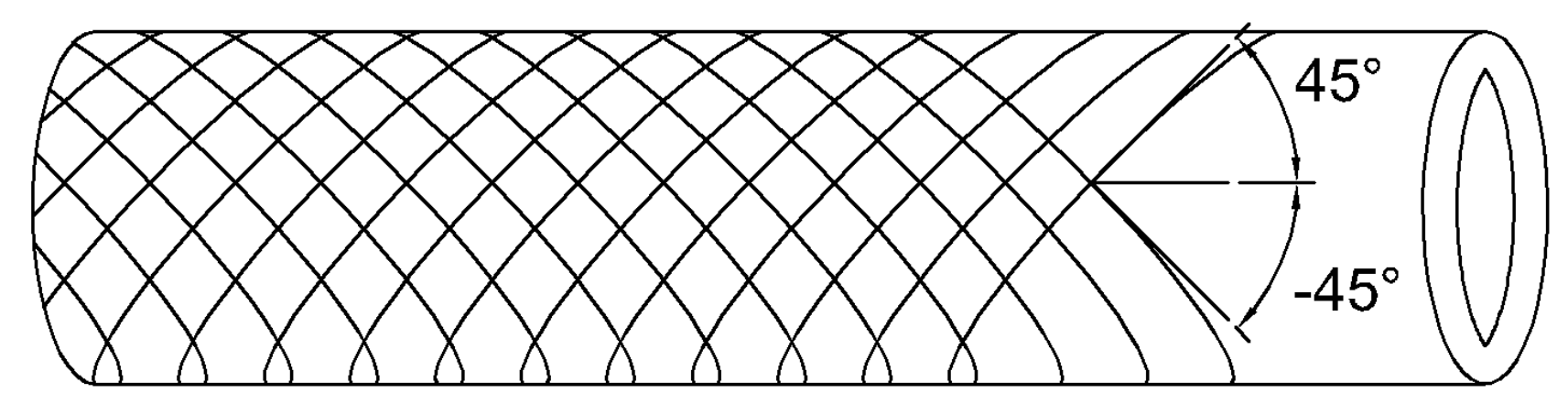
3.2. Angle-Ply Laminates
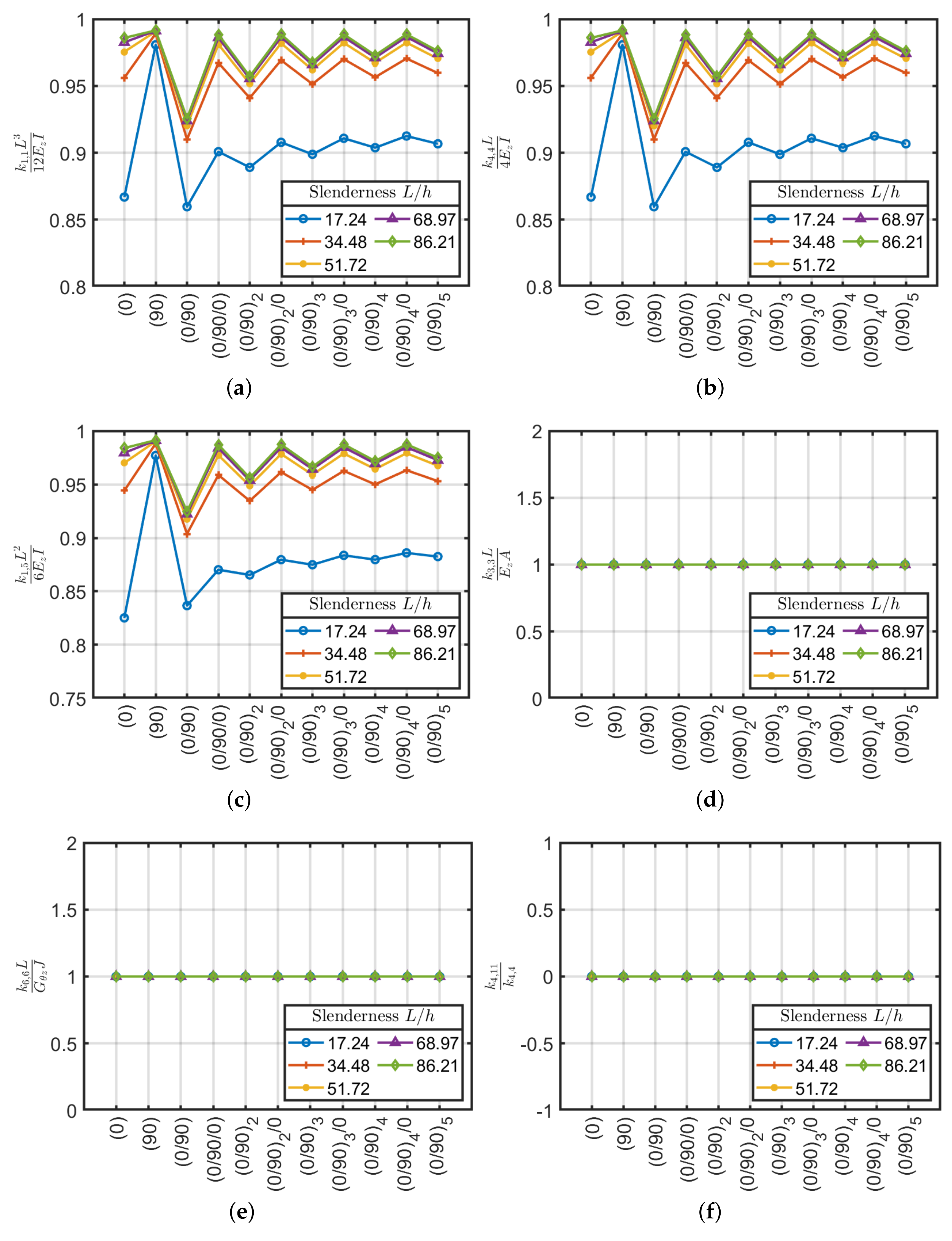
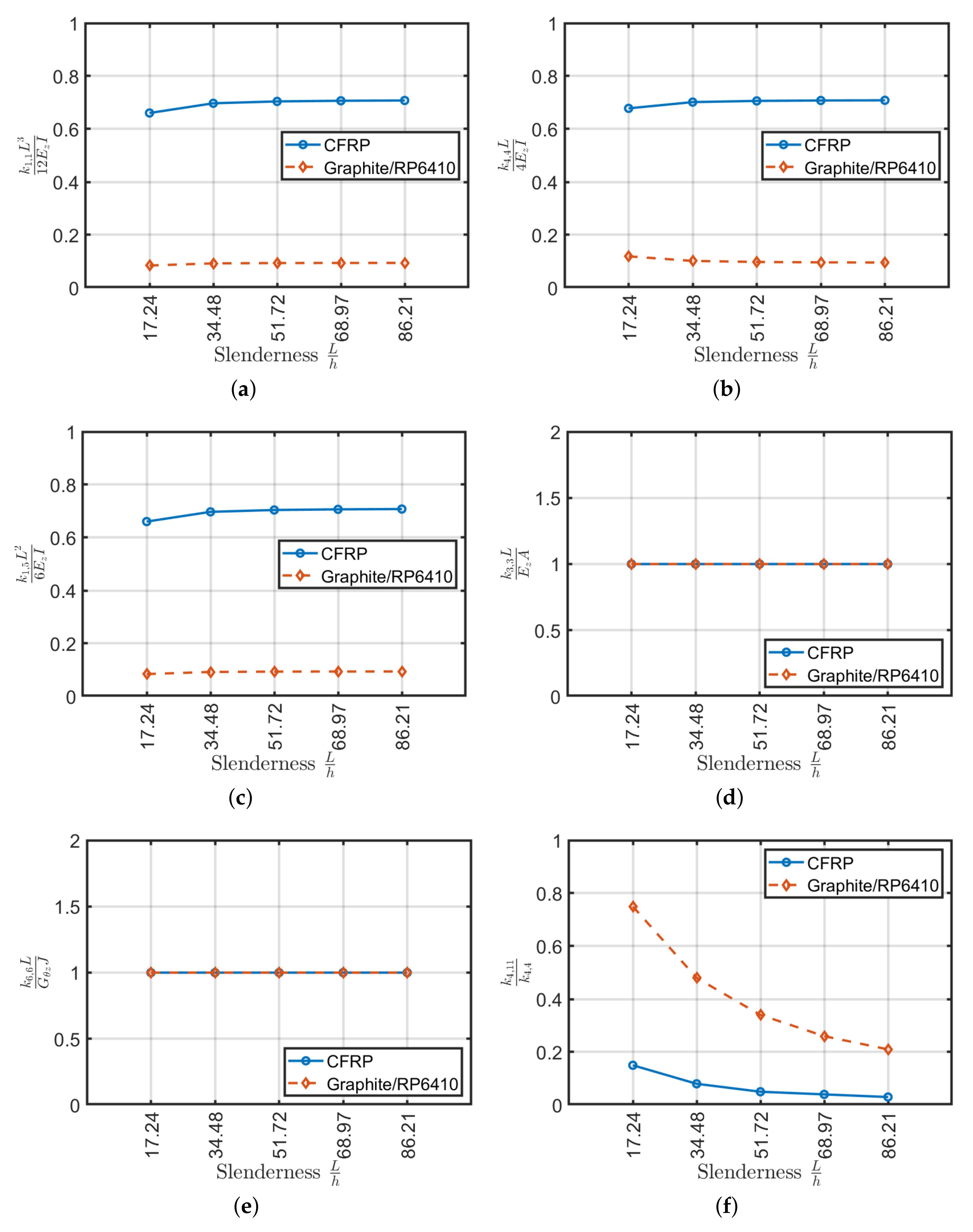
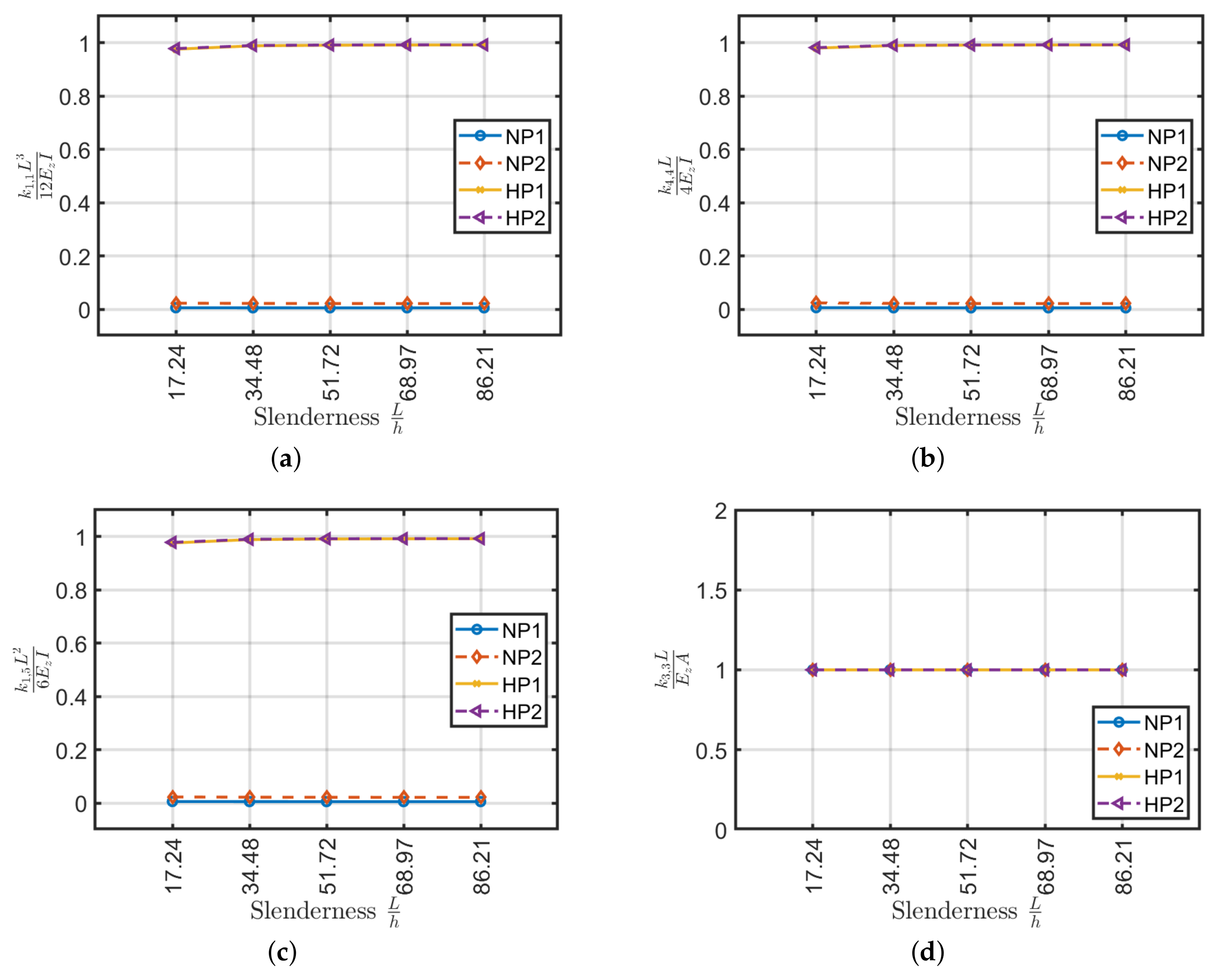
4. Beam Slenderness Effect
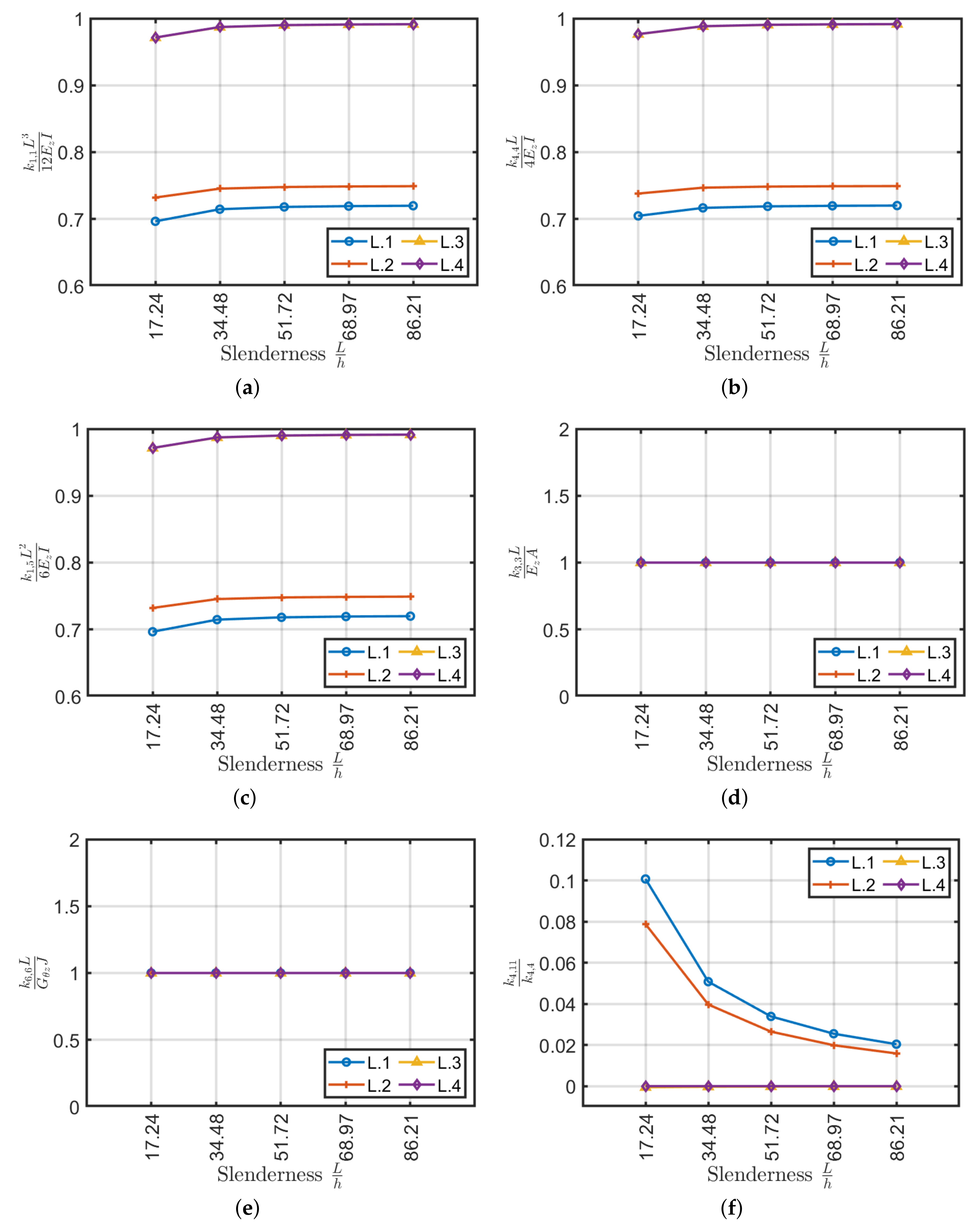
4.1. Cross-Ply Laminates
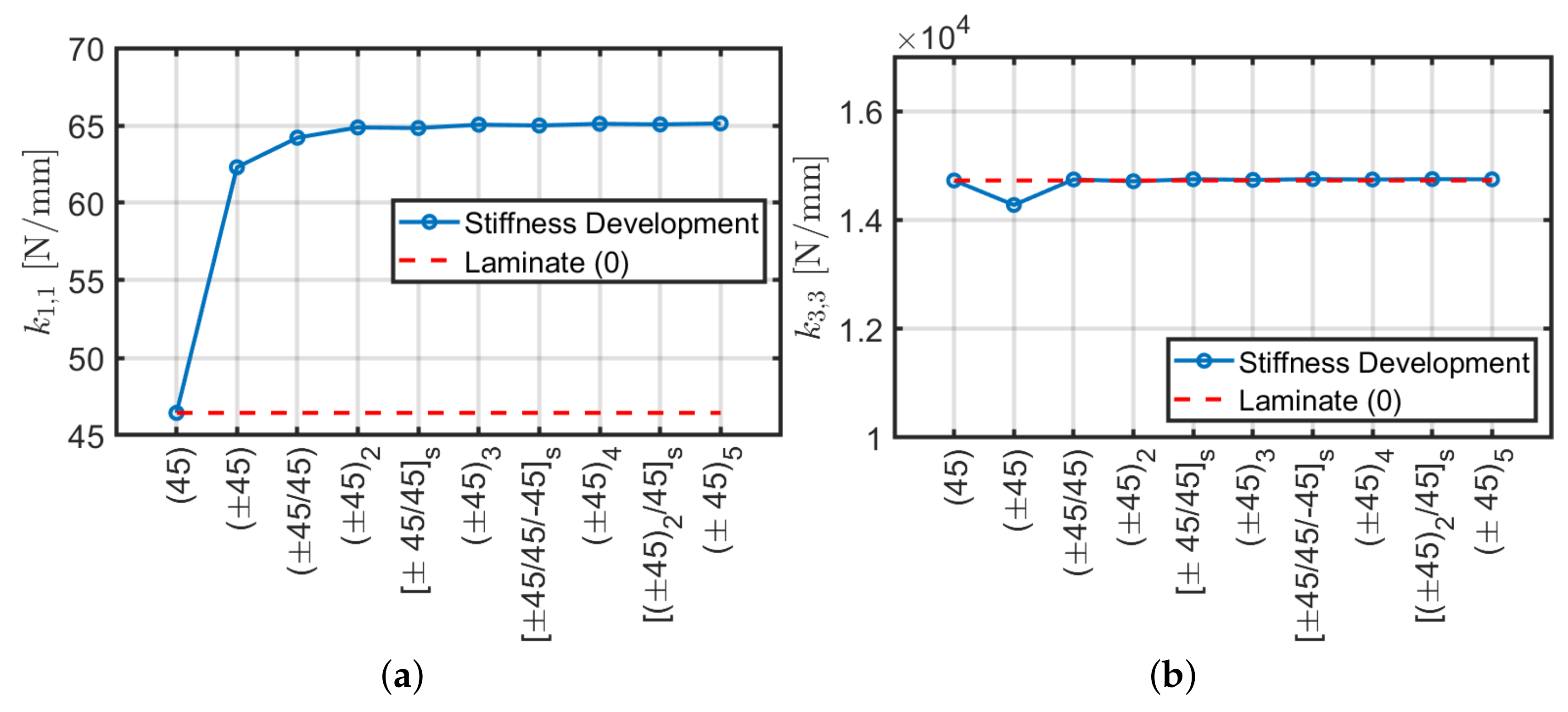
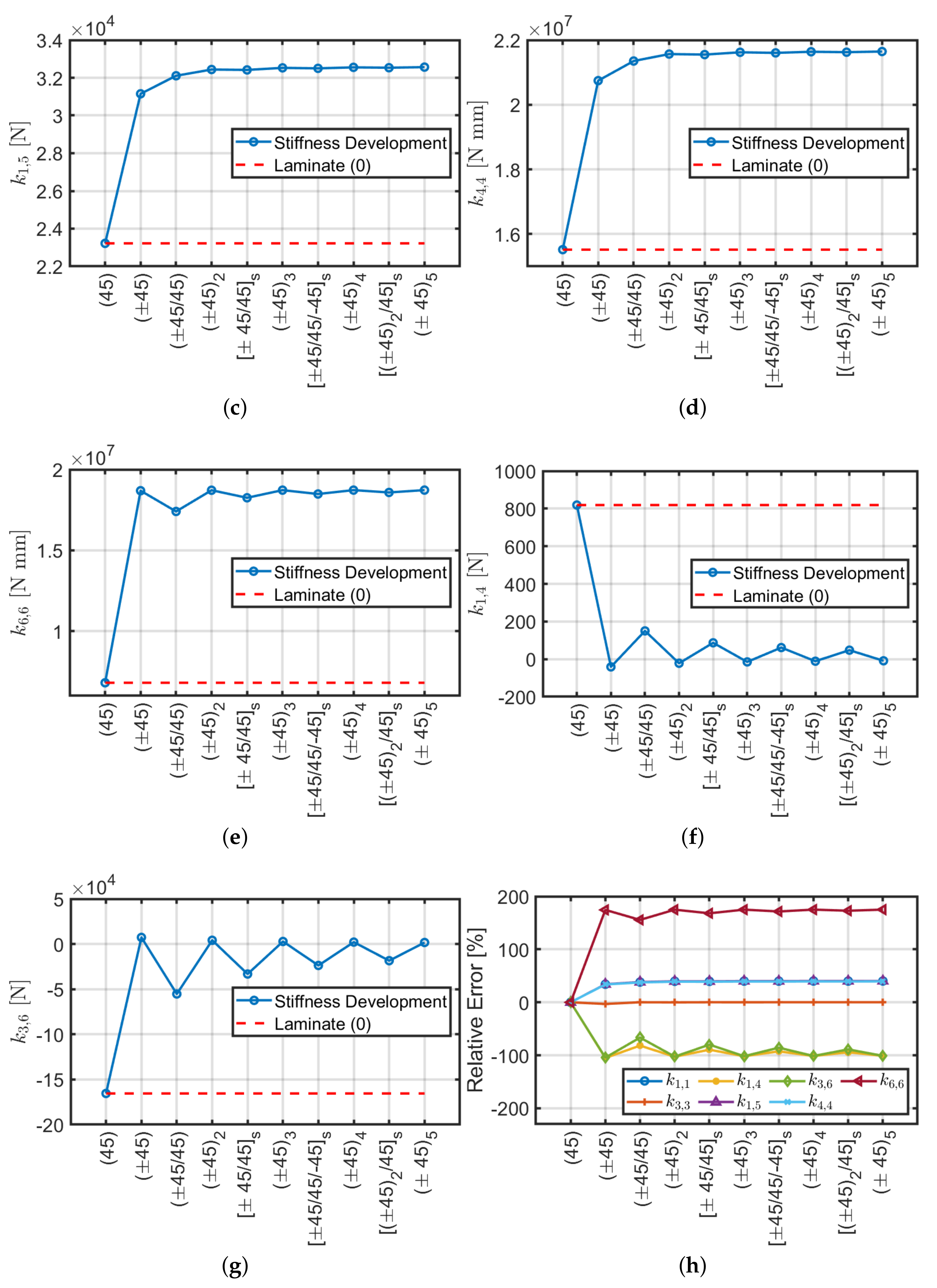
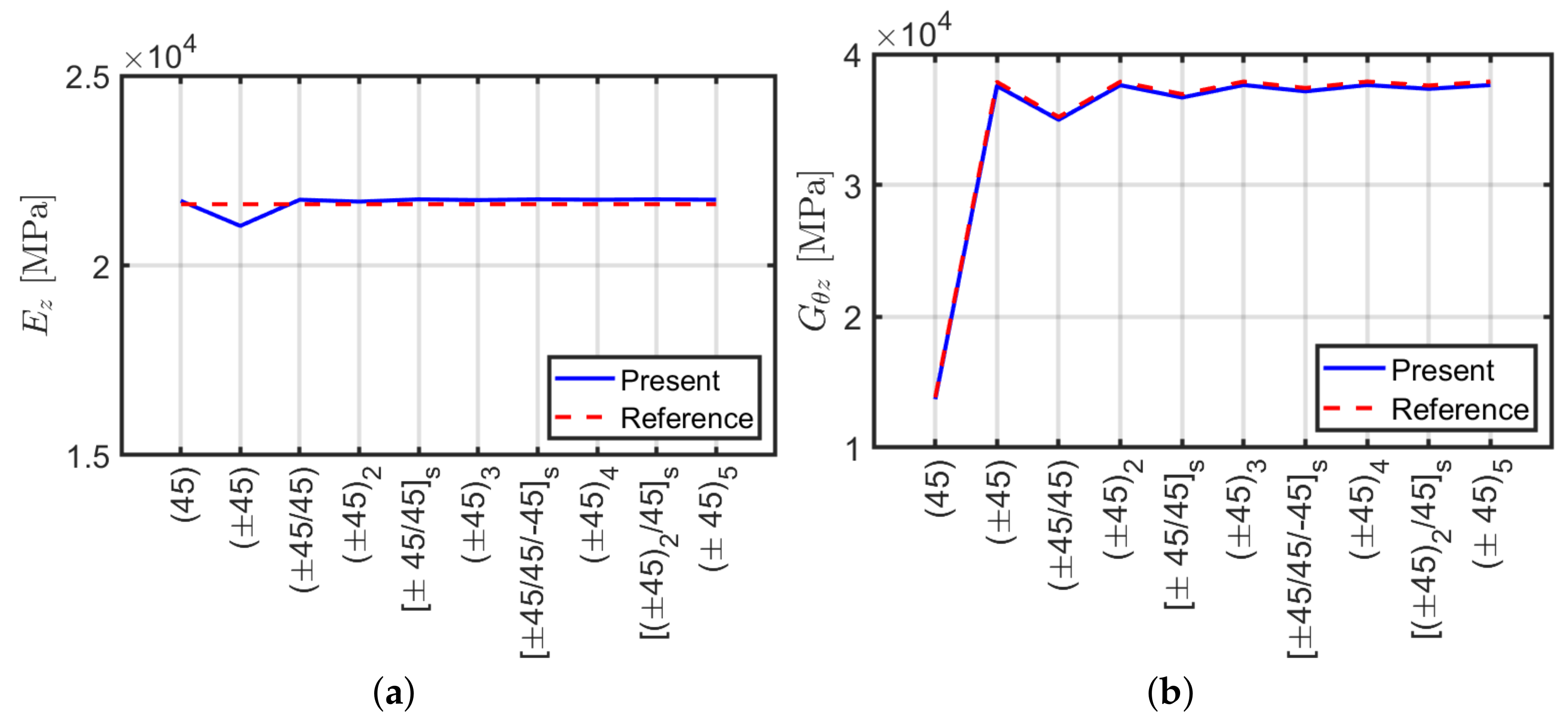
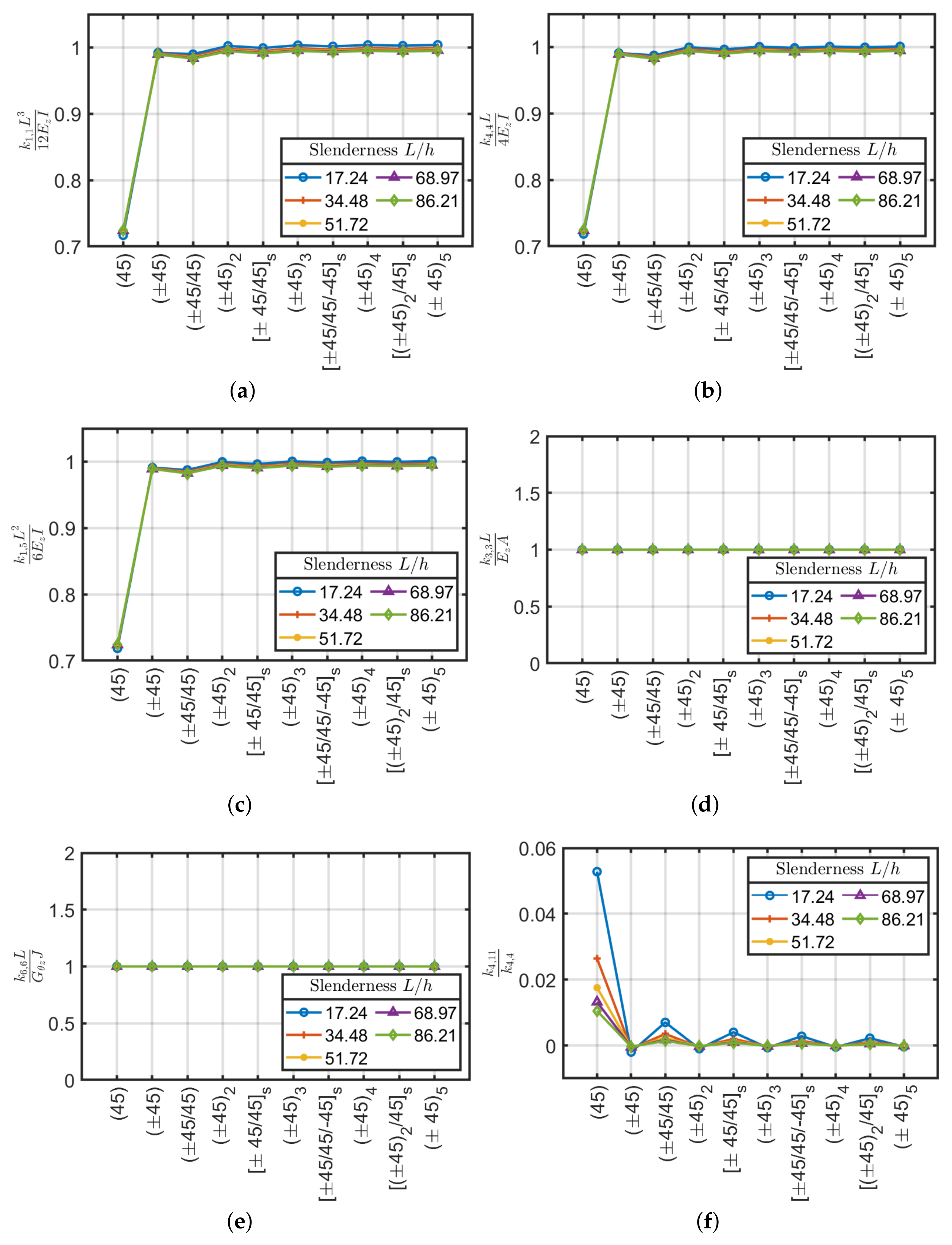
4.2. Angle-Ply Laminates
4.3. Quasi-Isotropic Configuration
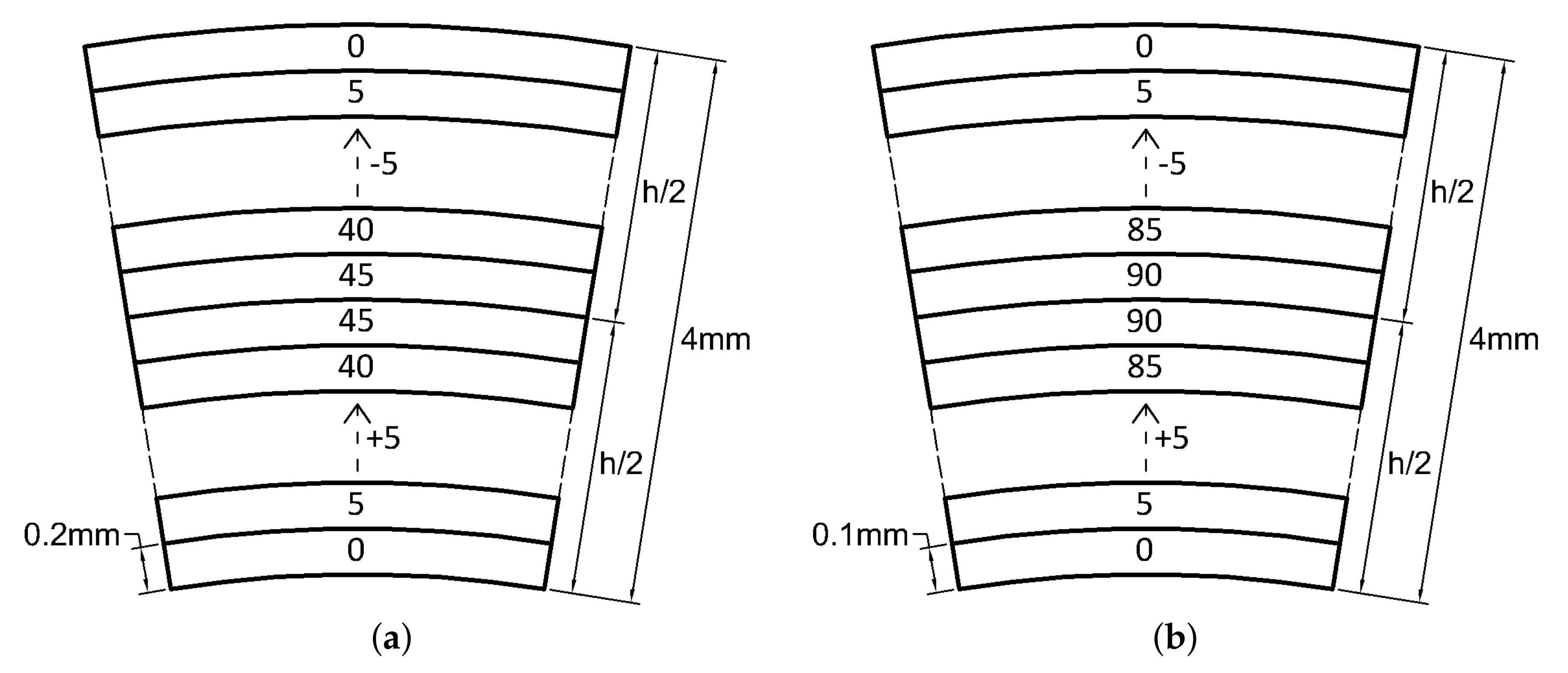
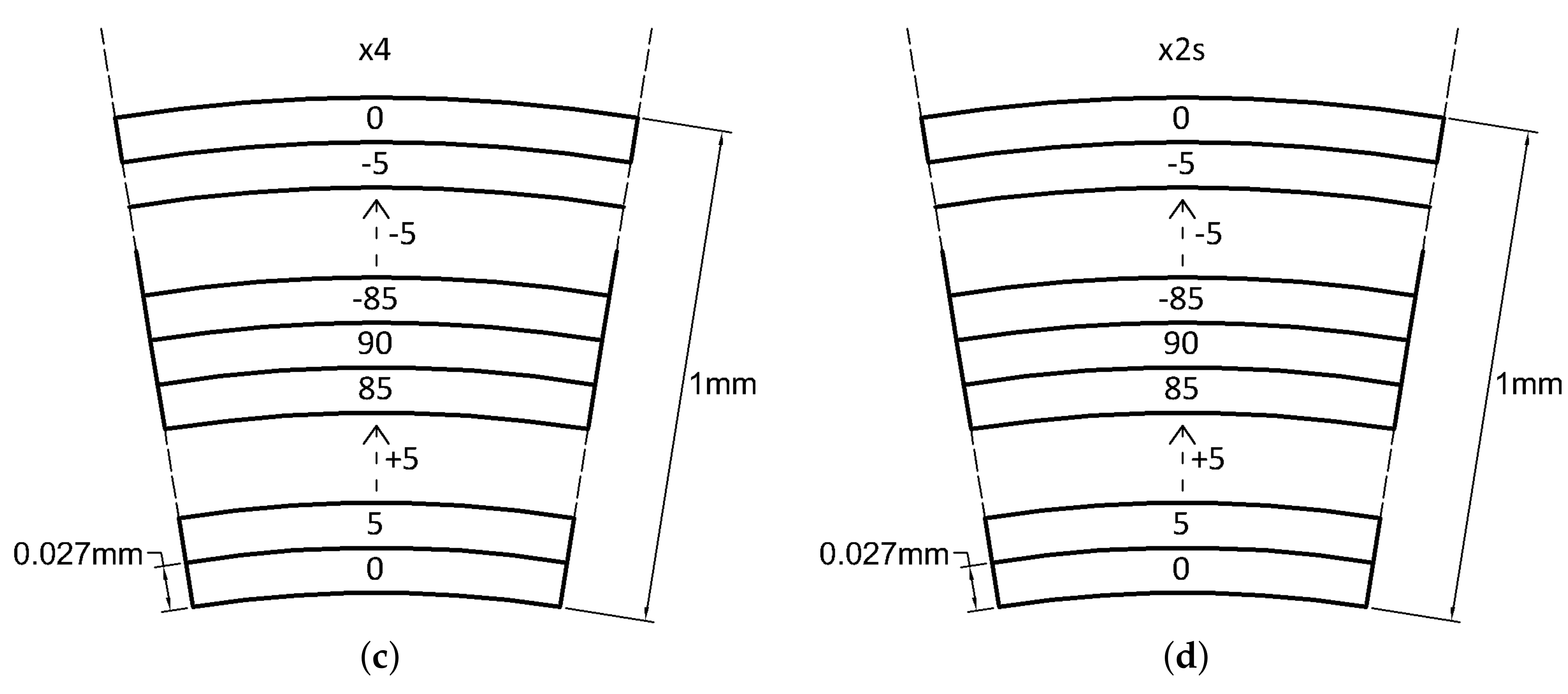
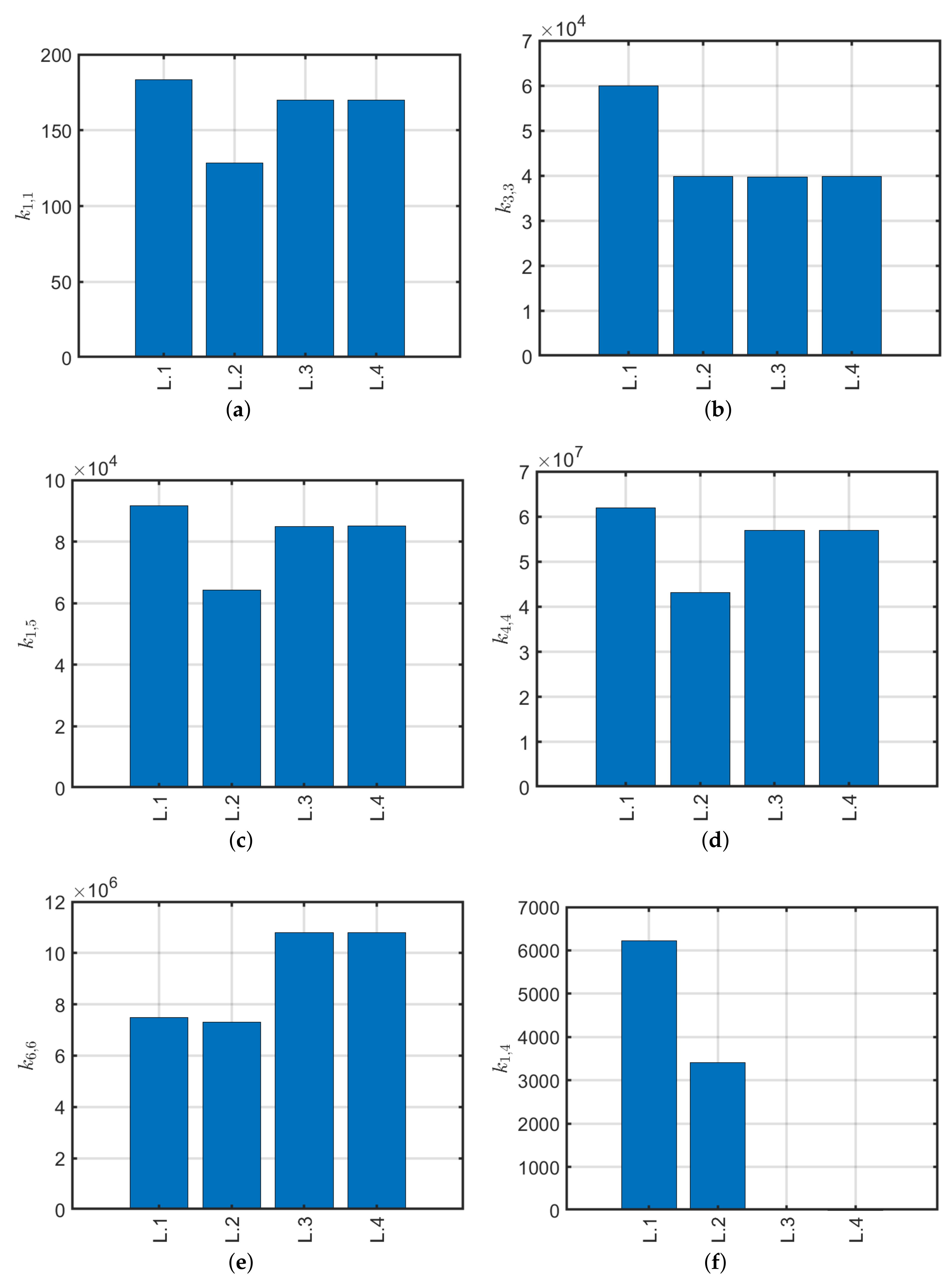
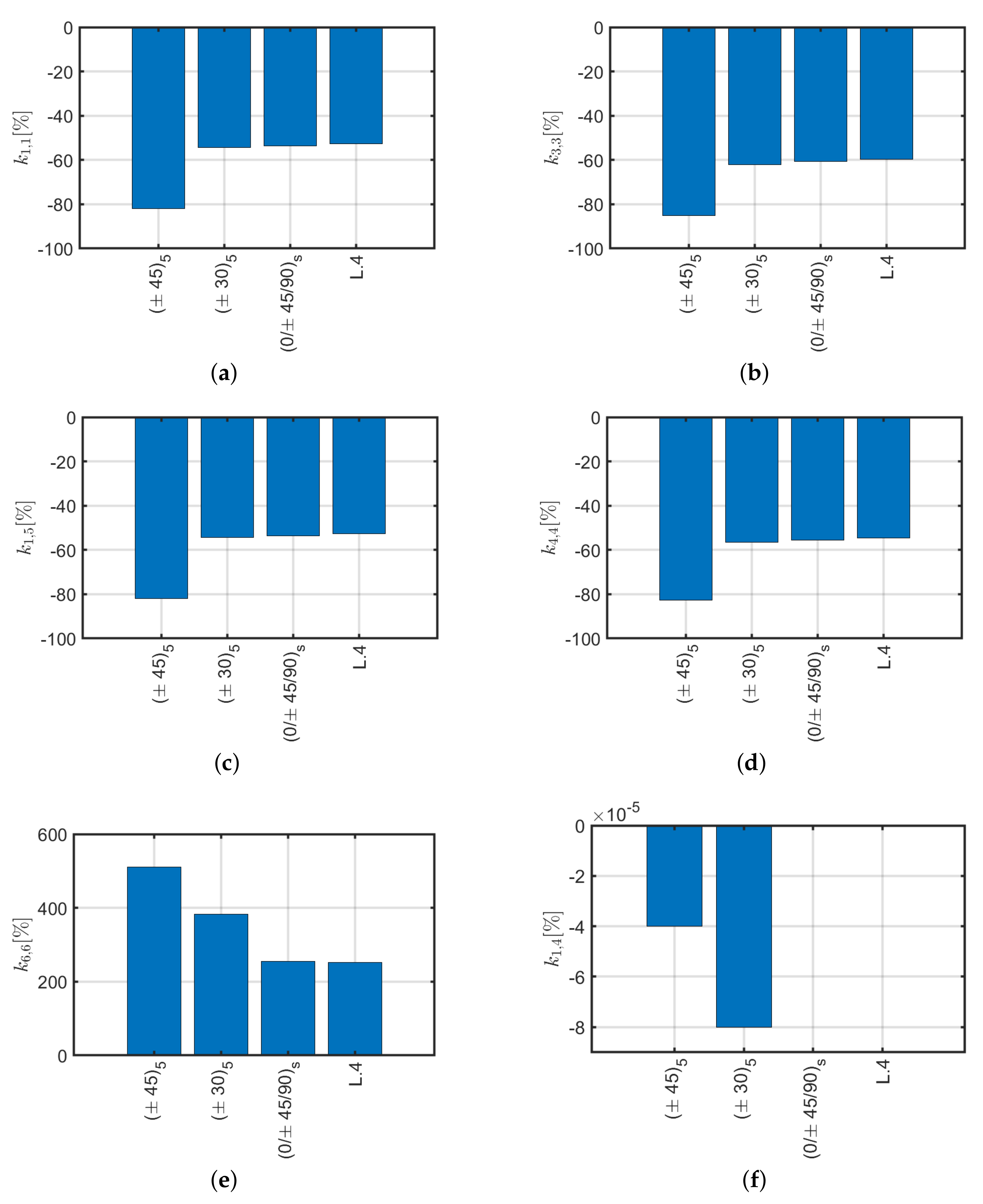
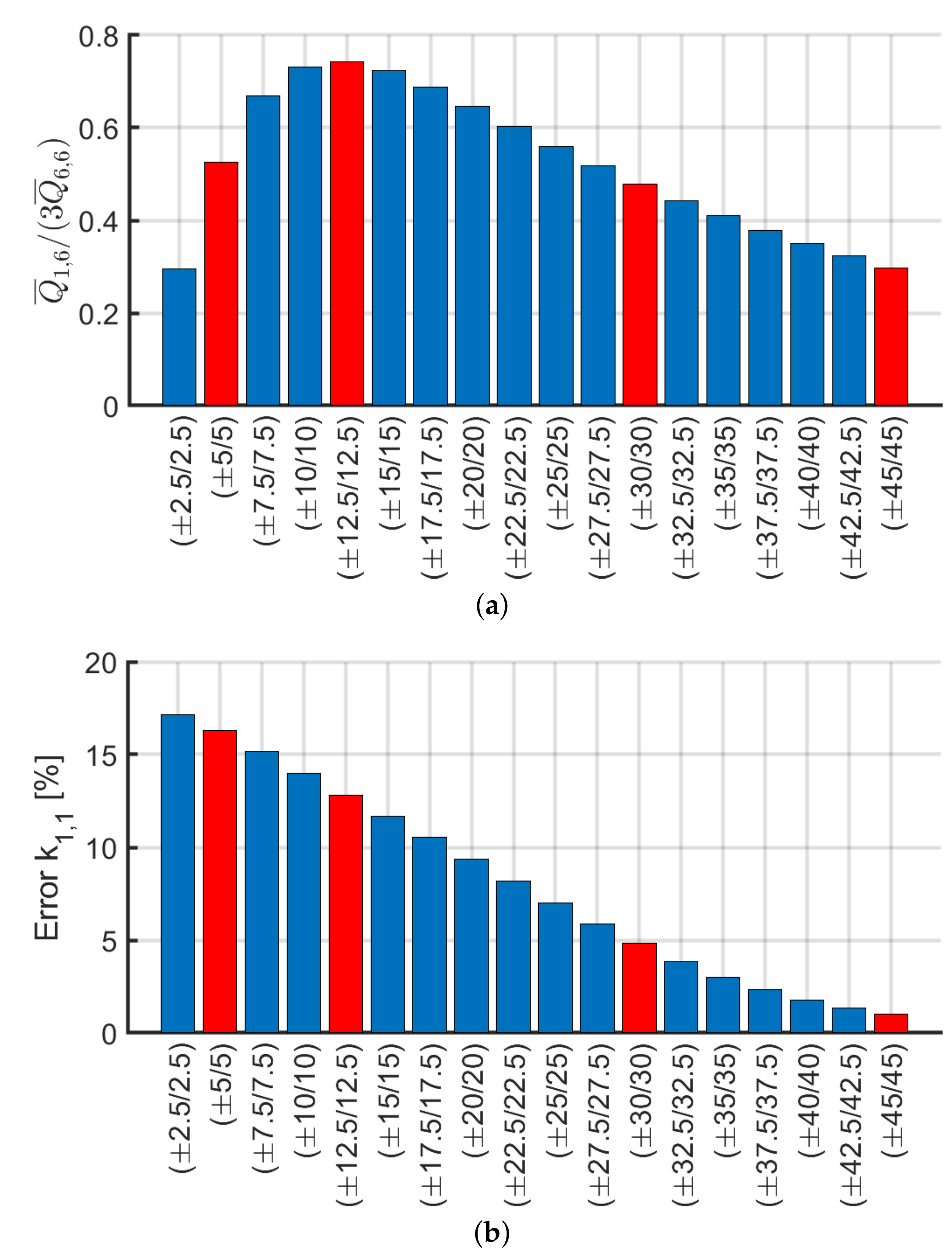
4.4. Bouligand Laminates
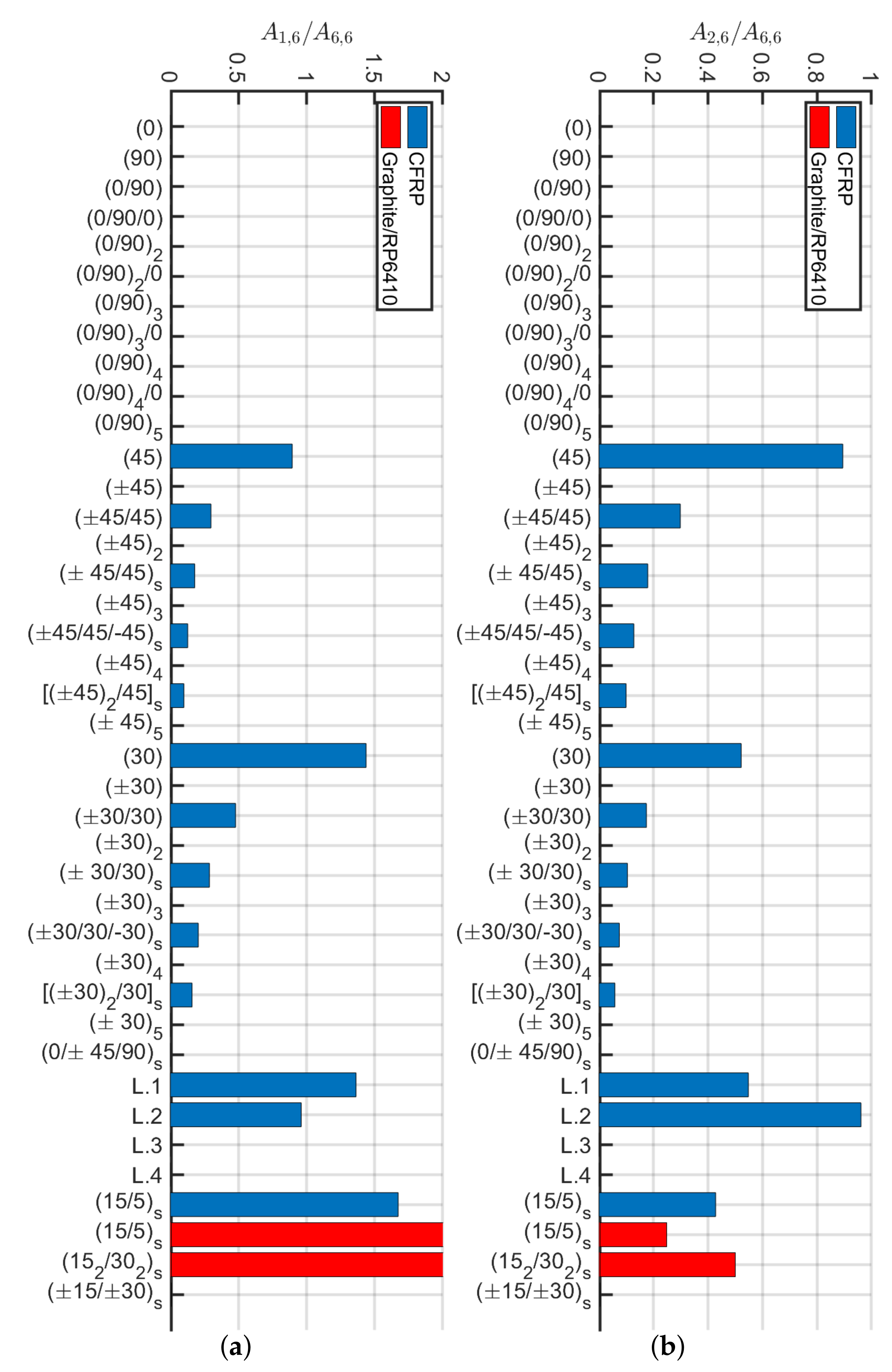
5. Comparison
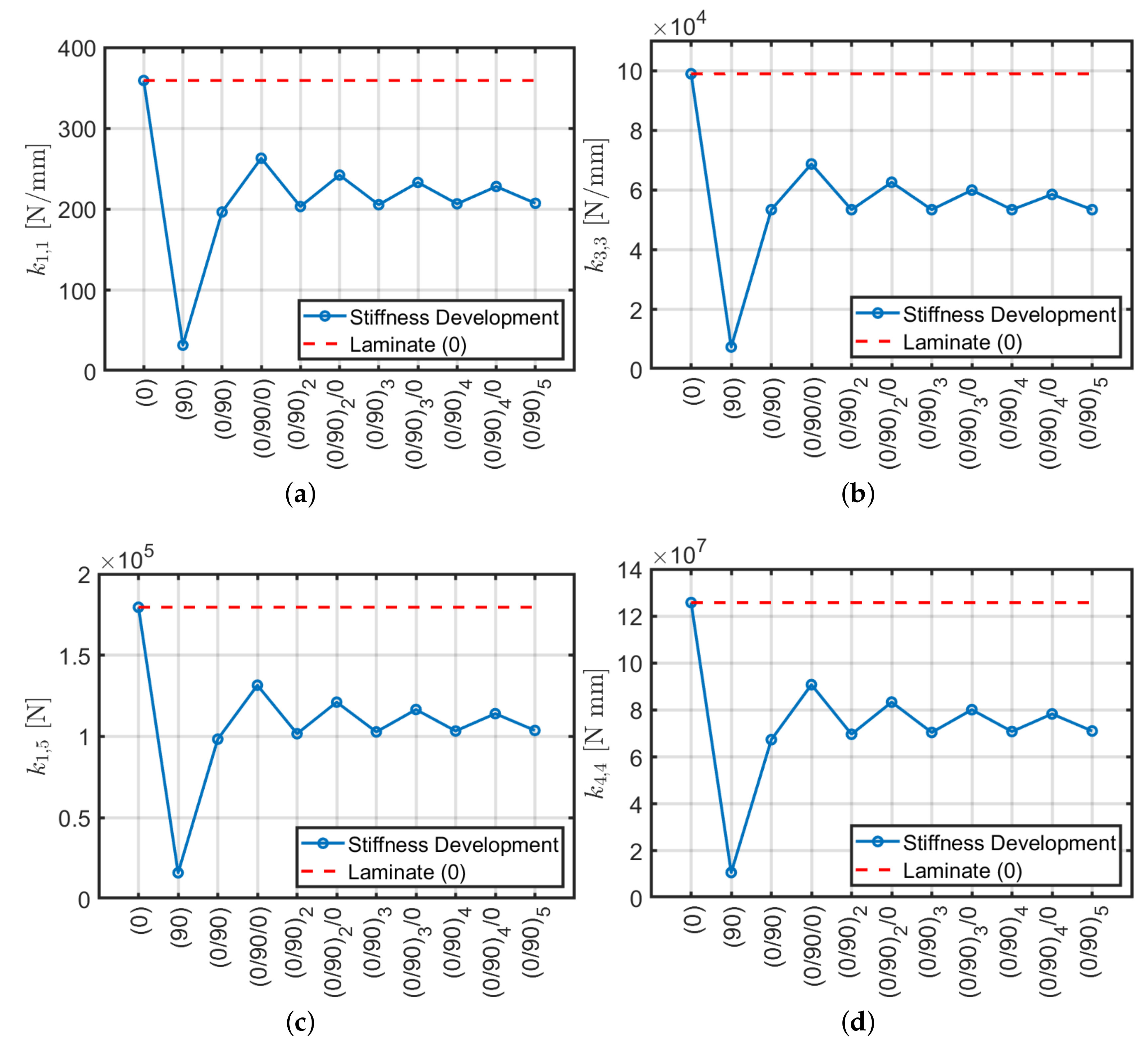
- All the stiffnesses tends to have a constant value by increasing beam slenderness.
- The orthotropic scheme (0) is very efficient if subjected to shear, axial and bending actions, but not for torsional ones. However, it has a significant variation while increasing slenderness. Furthermore, it suffers from delamination, because the fibers being all parallel, tend to form a preferential fracture plane.
- The angle-ply scheme works conversely with respect to the orthotropic configuration (0). It has high torsional stiffness, but low axial, shear and bending ones. For the present configuration, the shear-bending coupling is negligible. It is possible to use Sun et al. [40] formulae to homogenize equivalent properties because its properties do not depend on the beam slenderness.
- The angle-ply scheme represents an intermediate solution between the orthotropic (0) and the angle-ply configurations. It has a lower axial, shear and bending stiffness of 50–60% approximately and torsional stiffness of 80% with respect to (0). The present stack, as well as , has very low shear-bending coupling stiffness values which can be neglected and invariability of stiffness constants with respect to slenderness.
- The quasi-isotropic laminate (0/ has stiffness values similar to the laminate , except for the torsional stiffness which decreases by approximately 30%. Being a quasi-isotropic laminate, it has a negligible shear-bending coupling stiffness. In this case, the constants of the stiffness matrix vary slightly with increasing slenderness.
- The laminate, studied by Mencattelli and Pinho [63], with the only exception of the orthotropic configuration (0), presents slightly higher values for axial, shear and bending stiffnesses, but lower values for torsional stiffness with respect to the others. Coupling effects are minimal, and a very small dependency on the beam slenderness for the main stiffness components , , , and is observed.
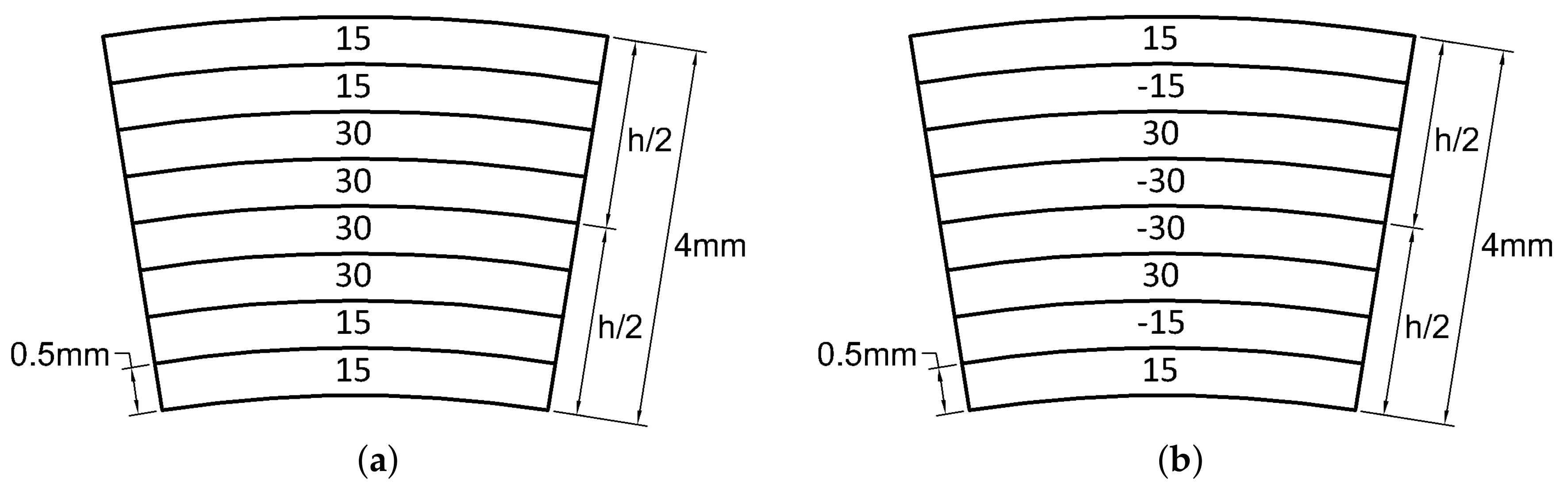
6. Laminates with Highly Positive and Negative Poisson Values
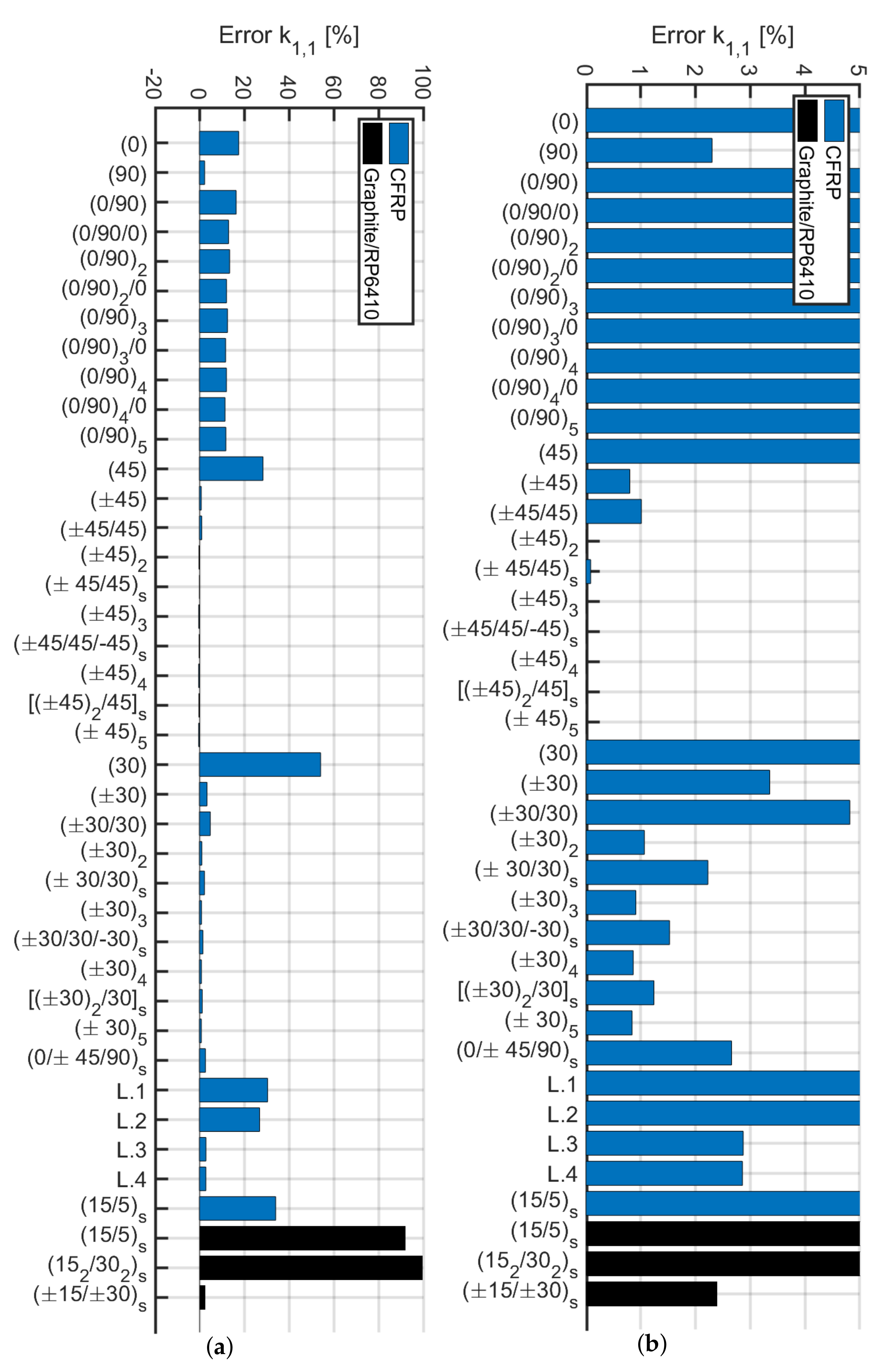
7. Validity and Limitations
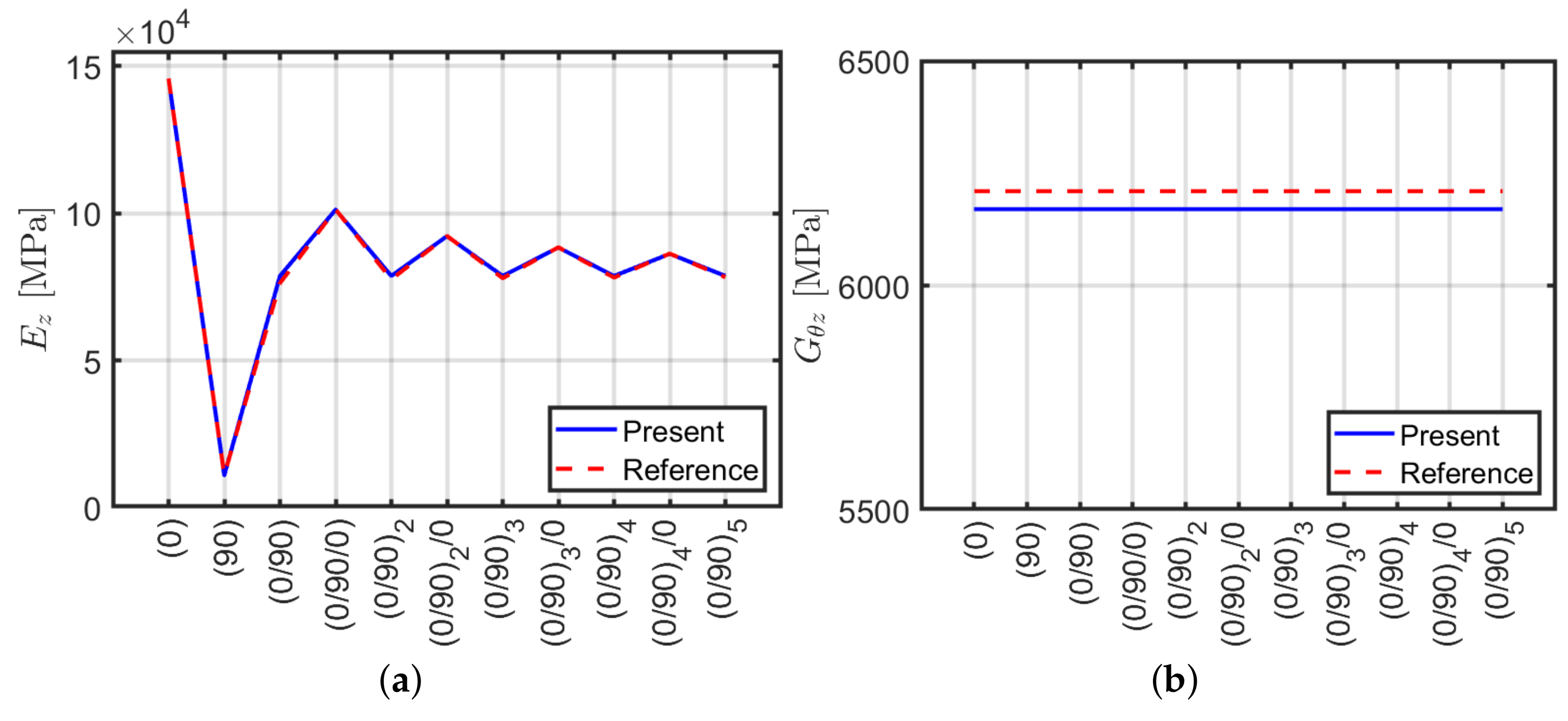
- cross-ply laminates, except laminate (90) have lower values, approximately 10% for m and highly variable as a function of slenderness with respect to the equivalent orthotropic model;
- scheme has lower values than the reference of about 30% and invariant with respect to beam slenderness;
- and scheme have lower values than the reference of about 55% and 5%, respectively, and they are invariant with respect to beam slenderness;
- unbalanced laminates with a fiber pitch angle of , and have values lower than the reference of approximately 30% and 25%, respectively;
- scheme has lower values than the reference of approximately 30% for the CFRP configuration and 90% for the Graphite/RP6410;
- scheme has values very large errors of about 100% and it is invariant with respect to beam slenderness.
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Leknitskii, S.G. Theory of Elasticity of an Anisotropic Body; Mir Publishers: Moscow, Russia, 1981. [Google Scholar]
- Jolicoeur, C.; Cardou, A. Analytical solution for bending of coaxial orthotropic cylinders. J. Eng. Mech. 1994, 120, 2556–2574. [Google Scholar] [CrossRef]
- Kollár, L.; Patterson, J.M.; Springer, G.S. Composite cylinders subjected to hygrothermal and mechanical loads. Int. J. Solids Struct. 1992, 29, 1519–1534. [Google Scholar] [CrossRef]
- Kollár, L.; Springer, G.S. Stress analysis of anisotropic laminated cylinders and cylindrical segments. Int. J. Solids Struct. 1992, 29, 1499–1517. [Google Scholar] [CrossRef]
- Bhaskar, K.; Varadan, T. Exact elasticity solution for laminated anisotropic cylindrical shells. J. Appl. Mech. 1993, 60, 41–47. [Google Scholar] [CrossRef]
- Xia, M.; Takayanagi, H.; Kemmochi, K. Analysis of multi-layered filament-wound composite pipes under internal pressure. Compos. Struct. 2001, 53, 483–491. [Google Scholar] [CrossRef]
- Xia, M.; Kemmochi, K.; Takayanagi, H. Analysis of filament-wound fiber-reinforced sandwich pipe under combined internal pressure and thermomechanical loading. Compos. Struct. 2001, 51, 273–283. [Google Scholar] [CrossRef]
- Çallıoğlu, H.; Ergun, E.; Demirdağ, O. Stress analysis of filament-Wound composite cylinders under combined internal pressure and thermal loading. Adv. Compos. Lett. 2008, 17, 096369350801700102. [Google Scholar] [CrossRef]
- Bakaiyan, H.; Hosseini, H.; Ameri, E. Analysis of multi-layered filament-wound composite pipes under combined internal pressure and thermomechanical loading with thermal variations. Compos. Struct. 2009, 88, 532–541. [Google Scholar] [CrossRef]
- Verijenko, V.E.; Adali, S.; Tabakov, P.Y. Stress distribution in continuously heterogeneous thick laminated pressure vessels. Compos. Struct. 2001, 54, 371–377. [Google Scholar] [CrossRef]
- Roque, C.; Ferreira, A. New developments in the radial basis functions analysis of composite shells. Compos. Struct. 2009, 87, 141–150. [Google Scholar] [CrossRef]
- Salahifar, R.; Mohareb, M. Finite element for cylindrical thin shells under harmonic forces. Finite Elem. Anal. Des. 2012, 52, 83–92. [Google Scholar] [CrossRef]
- Tarn, J.Q.; Wang, Y.M. Laminated composite tubes under extension, torsion, bending, shearing and pressuring: A state space approach. Int. J. Solids Struct. 2001, 38, 9053–9075. [Google Scholar] [CrossRef]
- Bai, Y.; Ruan, W.; Cheng, P.; Yu, B.; Xu, W. Buckling of reinforced thermoplastic pipe (RTP) under combined bending and tension. Ships Offshore Struct. 2014, 9, 525–539. [Google Scholar] [CrossRef]
- Derisi, B.; Hoa, S.V.; Xu, D.; Hojjati, M.; Fews, R. Mechanical behavior of Carbon/PEKK thermoplastic composite tube under bending load. J. Thermoplast. Compos. Mater. 2011, 24, 29–49. [Google Scholar] [CrossRef]
- Shadmehri, F.; Derisi, B.; Hoa, S. On bending stiffness of composite tubes. Compos. Struct. 2011, 93, 2173–2179. [Google Scholar] [CrossRef]
- Tings, T. New solutions to pressuring, shearing, torsion and extension of a cylindrically anisotropic elastic circular tube or bar. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 3527–3542. [Google Scholar] [CrossRef]
- Ting, T. Pressuring, shearing, torsion and extension of a circular tube or bar of cylindrically anisotropic material. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1996, 452, 2397–2421. [Google Scholar]
- Uchikawa, Y.; Itabashi, M.; Kawata, K. On crashworthiness of FRP thin-walled circular tubes under dynamic axial compression. Adv. Compos. Mater. 1997, 6, 239–252. [Google Scholar] [CrossRef]
- Silvestre, N. Non-classical effects in FRP composite tubes. Compos. Part B Eng. 2009, 40, 681–697. [Google Scholar] [CrossRef]
- Kardomateas, G.A. Elasticity solutions for sandwich orthotropic cylindrical shells under external/internal pressure or axial force. AIAA J. 2001, 39, 713–719. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, G.; Wan, B.; Han, B. Compressive Behavior of Circular Sawdust-Reinforced Ice-Filled Flax FRP Tubular Short Columns. Materials 2020, 13, 957. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Hoa, S.V.; Liu, P. A method to analyze the pure bending of tubes of cylindrically anisotropic layers with arbitrary angles including 0 or 90. Compos. Struct. 2014, 109, 57–67. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Sarvestani, M.Y. Free-edge stress analysis of general composite laminates under extension, torsion and bending. Appl. Math. Model. 2012, 36, 1570–1588. [Google Scholar] [CrossRef]
- Chen, T.; Chung, C.T.; Lin, W.L. A revisit of a cylindrically anisotropic tube subjected to pressuring, shearing, torsion, extension and a uniform temperature change. Int. J. Solids Struct. 2000, 37, 5143–5159. [Google Scholar] [CrossRef]
- Chouchaoui, C.; Ochoa, O. Similitude study for a laminated cylindrical tube under tensile, torsion, bending, internal and external pressure. Part I: governing equations. Compos. Struct. 1999, 44, 221–229. [Google Scholar] [CrossRef]
- Zhang, C.; Hoa, S.V. A limit-based approach to the stress analysis of cylindrically orthotropic composite cylinders (0/90) subjected to pure bending. Compos. Struct. 2012, 94, 2610–2619. [Google Scholar] [CrossRef]
- Guz, I.A.; Menshykova, M.; Paik, J.K. Thick-walled composite tubes for offshore applications: an example of stress and failure analysis for filament-wound multi-layered pipes. Ships Offshore Struct. 2017, 12, 304–322. [Google Scholar] [CrossRef]
- Menshykova, M.; Guz, I. Stress analysis of layered thick-walled composite pipes subjected to bending loading. Int. J. Mech. Sci. 2014, 88, 289–299. [Google Scholar] [CrossRef]
- Khalili, S.; Dehkordi, M.B.; Carrera, E. A nonlinear finite element model using a unified formulation for dynamic analysis of multilayer composite plate embedded with SMA wires. Compos. Struct. 2013, 106, 635–645. [Google Scholar] [CrossRef]
- Ascione, F.; Feo, L.; Maceri, F. An experimental investigation on the bearing failure load of glass fibre/epoxy laminates. Compos. Part B Eng. 2009, 40, 197–205. [Google Scholar] [CrossRef]
- Boscato, G.; Russo, S. Free vibrations of pultruded FRP elements: Mechanical characterization, analysis, and applications. J. Compos. Constr. 2009, 13, 565–574. [Google Scholar] [CrossRef]
- Philippidis, T.P.; Vassilopoulos, A. Fatigue of composite laminates under off-axis loading. Int. J. Fatigue 1999, 21, 253–262. [Google Scholar] [CrossRef]
- Quadrino, A.; Penna, R.; Feo, L.; Nisticò, N. Mechanical characterization of pultruded elements: Fiber orientation influence vs web-flange junction local problem. Experimental and numerical tests. Compos. Part B Eng. 2018, 142, 68–84. [Google Scholar] [CrossRef]
- Madenci, E.; Özkılıç, Y.O.; Gemi, L. Experimental and Theoretical Investigation on Flexure Performance of Pultruded GFRP Composite Beams with Damage Analyses. Compos. Struct. 2020, 242, 112162. [Google Scholar] [CrossRef]
- Xin, H.; Mosallam, A.; Liu, Y.; Xiao, Y.; He, J.; Wang, C.; Jiang, Z. Experimental and numerical investigation on in-plane compression and shear performance of a pultruded GFRP composite bridge deck. Compos. Struct. 2017, 180, 914–932. [Google Scholar] [CrossRef]
- Mayookh Lal, H.; Xian, G.; Thomas, S.; Zhang, L.; Zhang, Z.; Wang, H. Experimental Study on the Flexural Creep Behaviors of Pultruded Unidirectional Carbon/Glass Fiber-Reinforced Hybrid Bars. Materials 2020, 13, 976. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, T.; Zhu, H.; Chen, X. Experimental Identification of Statistical Correlation between Mechanical Properties of FRP Composite. Materials 2020, 13, 674. [Google Scholar] [CrossRef]
- Sun, C.T.; Li, S. Three-dimensional effective elastic constants for thick laminates. J. Compos. Mater. 1988, 22, 629–639. [Google Scholar] [CrossRef]
- Sun, X.S.; Tan, V.B.C.; Chen, Y.; Tan, L.B.; Jaiman, R.K.; Tay, T.E. Stress analysis of multi-layered hollow anisotropic composite cylindrical structures using the homogenization method. Acta Mech. 2014, 225, 1649–1672. [Google Scholar] [CrossRef]
- Ferdous, W.; Almutairi, A.D.; Huang, Y.; Bai, Y. Short-term flexural behaviour of concrete filled pultruded GFRP cellular and tubular sections with pin-eye connections for modular retaining wall construction. Compos. Struct. 2018, 206, 1–10. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Manalo, A.C.; Ferdous, W.; Zhuge, Y.; Vijay, P.; Pettigrew, J. Experimental and numerical evaluations on the behaviour of structures repaired using prefabricated FRP composites jacket. Eng. Struct. 2020, 210, 110358. [Google Scholar] [CrossRef]
- Al-Rubaye, M.; Manalo, A.; Alajarmeh, O.; Ferdous, W.; Lokuge, W.; Benmokrane, B.; Edoo, A. Flexural behaviour of concrete slabs reinforced with GFRP bars and hollow composite reinforcing systems. Compos. Struct. 2020, 236, 111836. [Google Scholar] [CrossRef]
- Babuška, I. Homogenization approach in engineering. In Computing Methods in Applied Sciences and Engineering; Springer: Berlin/Heidelberg, Germany, 1976; pp. 137–153. [Google Scholar]
- Sanchez-Palencia, E. Homogenization method for the study of composite media. In Asymptotic Analysis II; Springer: Berlin/Heidelberg, Germany, 1983; pp. 192–214. [Google Scholar]
- Sanchez-Palencia, E. Homogenization in mechanics. A survey of solved and open problems. Rend. Sem. Mat. Univ. Politec. Torino 1986, 44, 1–45. [Google Scholar]
- Kim, C.; White, S.R. Analysis of thick hollow composite beams under general loadings. Compos. Struct. 1996, 34, 263–277. [Google Scholar] [CrossRef]
- Yildiz, H.; Sarikanat, M. Finite-element analysis of thick composite beams and plates. Compos. Sci. Technol. 2001, 61, 1723–1727. [Google Scholar] [CrossRef]
- Ferreira, A. Thick composite beam analysis using a global meshless approximation based on radial basis functions. Mech. Adv. Mater. Struct. 2003, 10, 271–284. [Google Scholar] [CrossRef]
- Yazdani Sarvestani, H.; Hoa, S.V.; Hojjati, M. Stress analysis of thick orthotropic cantilever tubes under transverse loading. Adv. Compos. Mater. 2017, 26, 335–362. [Google Scholar] [CrossRef]
- Yazdani Sarvestani, H.; Hojjati, M. Effects of lay-up sequence in thick composite tubes for helicopter landing gears. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 2098–2110. [Google Scholar] [CrossRef]
- Berdichevsky, V.; Armanios, E.; Badir, A. Theory of anisotropic thin-walled closed-cross-section beams. Compos. Eng. 1992, 2, 411–432. [Google Scholar] [CrossRef]
- Kollar, L.P.; Pluzsik, A. Analysis of thin-walled composite beams with arbitrary layup. J. Reinf. Plast. Compos. 2002, 21, 1423–1465. [Google Scholar] [CrossRef]
- Jung, S.N.; Lee, J.Y. Closed-form analysis of thin-walled composite I-beams considering non-classical effects. Compos. Struct. 2003, 60, 9–17. [Google Scholar] [CrossRef]
- Lateral buckling analysis of thin-walled laminated composite beams with monosymmetric sections. Eng. Struct. 2006, 28, 1997–2009. [CrossRef]
- Boscato, G. Comparative study on dynamic parameters and seismic demand of pultruded FRP members and structures. Compos. Struct. 2017, 174, 399–419. [Google Scholar] [CrossRef]
- de Miranda, S.; Madeo, A.; Melchionda, D.; Patruno, L.; Ruggerini, A. A corotational based geometrically nonlinear Generalized Beam Theory: buckling FE analysis. Int. J. Solids Struct. 2017, 121, 212–227. [Google Scholar] [CrossRef]
- Ruggerini, A.; Madeo, A.; Gonçalves, R.; Camotim, D.; Ubertini, F.; de Miranda, S. GBT post-buckling analysis based on the Implicit Corotational Method. Int. J. Solids Struct. 2019, 163, 40–60. [Google Scholar] [CrossRef]
- Babamohammadi, S.; Fantuzzi, N.; Lonardi, G. Mechanical assessment of hollow-circular FRP beams. Compos. Struct. 2019, 227, 111313. [Google Scholar] [CrossRef]
- 2011 ABAQUS Version 6. 11: Analysis User’s Manual; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2011. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Gnoli, D. Studio di Profili Tubolari in FRP: Omogeneizzazione e Modello Trave Equivalente. Master’s Thesis, University of Bologna, Bologna, Italy, 2020. [Google Scholar]
- Mencattelli, L.; Pinho, S.T. Ultra-thin-ply CFRP Bouligand bio-inspired structures with enhanced load-bearing capacity, delayed catastrophic failure and high energy dissipation capability. Compos. Part A Appl. Sci. Manuf. 2019, 129, 105655. [Google Scholar] [CrossRef]
- Peel, L.D. Exploration of high and negative Poisson’s ratio elastomer-matrix laminates. Phys. Status Solidi (b) 2007, 244, 988–1003. [Google Scholar] [CrossRef]





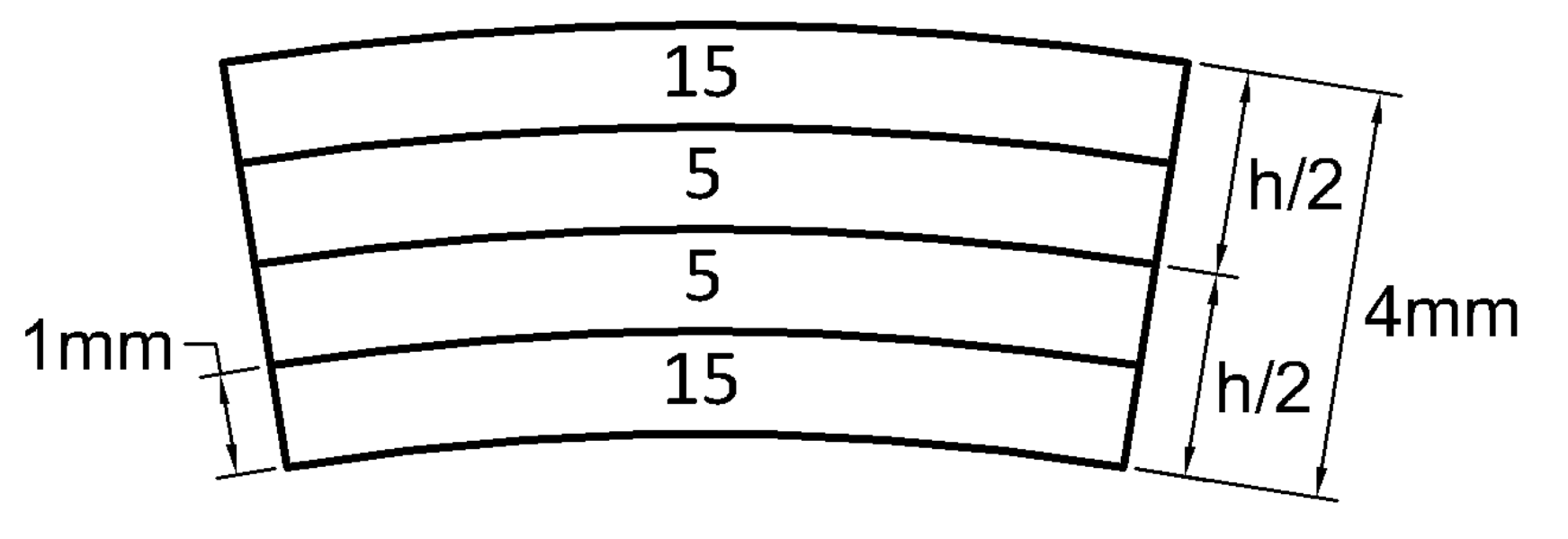

| Geometric | Mechanical | ||
|---|---|---|---|
| Average radius | 27 mm | 145,849.69 MPa | |
| Length | 1000 mm | 11,030 MPa | |
| Laminate thickness | 4 mm (Fixed) | 0.28 | |
| Layer thickness | Variable | 6209.89 MPa | |
| Area | 678.58 mm | 6209.89 MPa | |
| Polar inertia | 497,400 mm | 3860.5 MPa | |
| Inertia | 248,774.1516 mm |
| Materials | E [MPa] | [%] |
|---|---|---|
| RP6410 | 1.65 | 3.30 |
| RP6442 | 7.00 | 5.25 |
| Graphite | 276,000 | - |
| [MPa] | [MPa] | [MPa] | |||
|---|---|---|---|---|---|
| Graphite/RP6410 | 120,000 | 2.85 | 0.41 | 0.502 | 0.949 |
| Graphite/RP6442 | 126,600 | 12.02 | 0.41 | 0.504 | 4 |
| Graphite/RP6410 | CFRP | ||
|---|---|---|---|
| 4498.23 MPa | 94,509.78 MPa | ||
| 3.02 MPa | 11,234.40 MPa | ||
| −34.04 | 0.342 | ||
| −0.023 | 0.041 | ||
| 23.33 MPa | 7395.17 MPa |
| Laminates | Material | ||
|---|---|---|---|
| NP1 | Graphite/RP6410 | 42,800 | −6.38 |
| HP1 | Graphite/RP6410 | 42,800 | 3.73 |
| NP2 | Graphite/RP6442 | 10,530 | −6.15 |
| HP2 | Graphite/RP6442 | 10,530 | 3.72 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gnoli, D.; Babamohammadi, S.; Fantuzzi, N. Homogenization and Equivalent Beam Model for Fiber-Reinforced Tubular Profiles. Materials 2020, 13, 2069. https://doi.org/10.3390/ma13092069
Gnoli D, Babamohammadi S, Fantuzzi N. Homogenization and Equivalent Beam Model for Fiber-Reinforced Tubular Profiles. Materials. 2020; 13(9):2069. https://doi.org/10.3390/ma13092069
Chicago/Turabian StyleGnoli, Daniel, Sajjad Babamohammadi, and Nicholas Fantuzzi. 2020. "Homogenization and Equivalent Beam Model for Fiber-Reinforced Tubular Profiles" Materials 13, no. 9: 2069. https://doi.org/10.3390/ma13092069
APA StyleGnoli, D., Babamohammadi, S., & Fantuzzi, N. (2020). Homogenization and Equivalent Beam Model for Fiber-Reinforced Tubular Profiles. Materials, 13(9), 2069. https://doi.org/10.3390/ma13092069







