Determination of an Objective Criterion for the Assessment of the Feasibility of an Instrumented Indentation Test on Rough Surfaces
Abstract
1. Introduction
- (i)
- If the investigation of the material properties of a given component is required, then surface preparation may not be wished for to avoid affecting the surface properties or to avoid deteriorating the component.
- (ii)
- It is impossible to have a surface free of any roughness: whatever the surface preparation, there is always residual roughness that may impact the very small scales.
2. Materials and Methods
- -
- Surface roughness being stochastic, a large number of numerical simulations were required to obtain representative results. A semianalytical model was used to simulate numerous indentation tests on rough surfaces to get a high number of computations with low computation time.
- -
- Experimentally, it is impossible to change the morphology of a surface without impacting the subsurface properties. The use of the Weierstrass function was preferred to examine the influence of the characteristic parameters of the surface (e.g., amplitude, wavelength) independently of any material property changes. Inversely, the characteristic parameters of the surface can be modified without altering the mechanical properties of the surface.
- -
- This methodology avoided the introduction of any measurement noises or experimental artifacts.
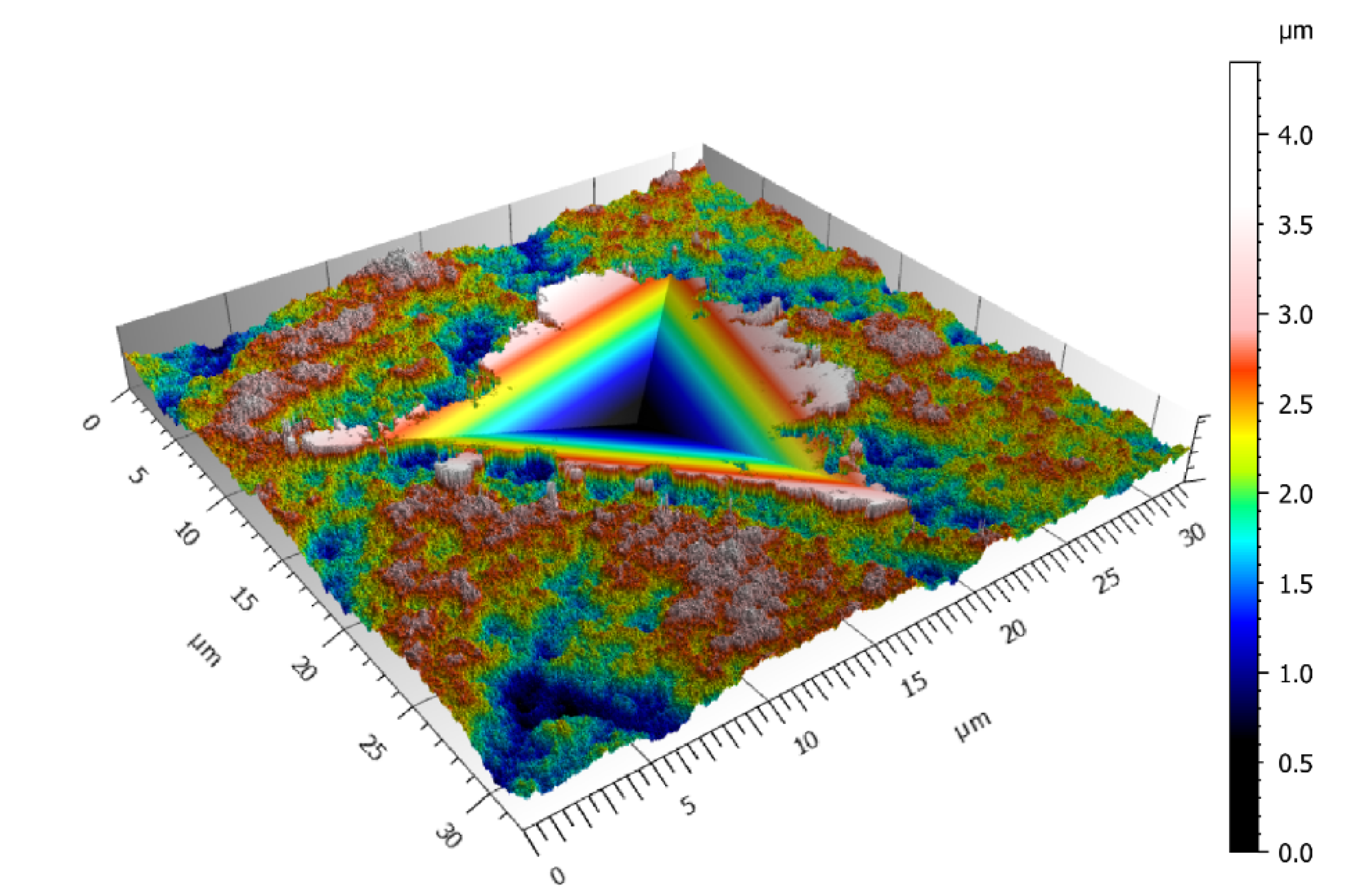
2.1. Surface Characteristics
- -
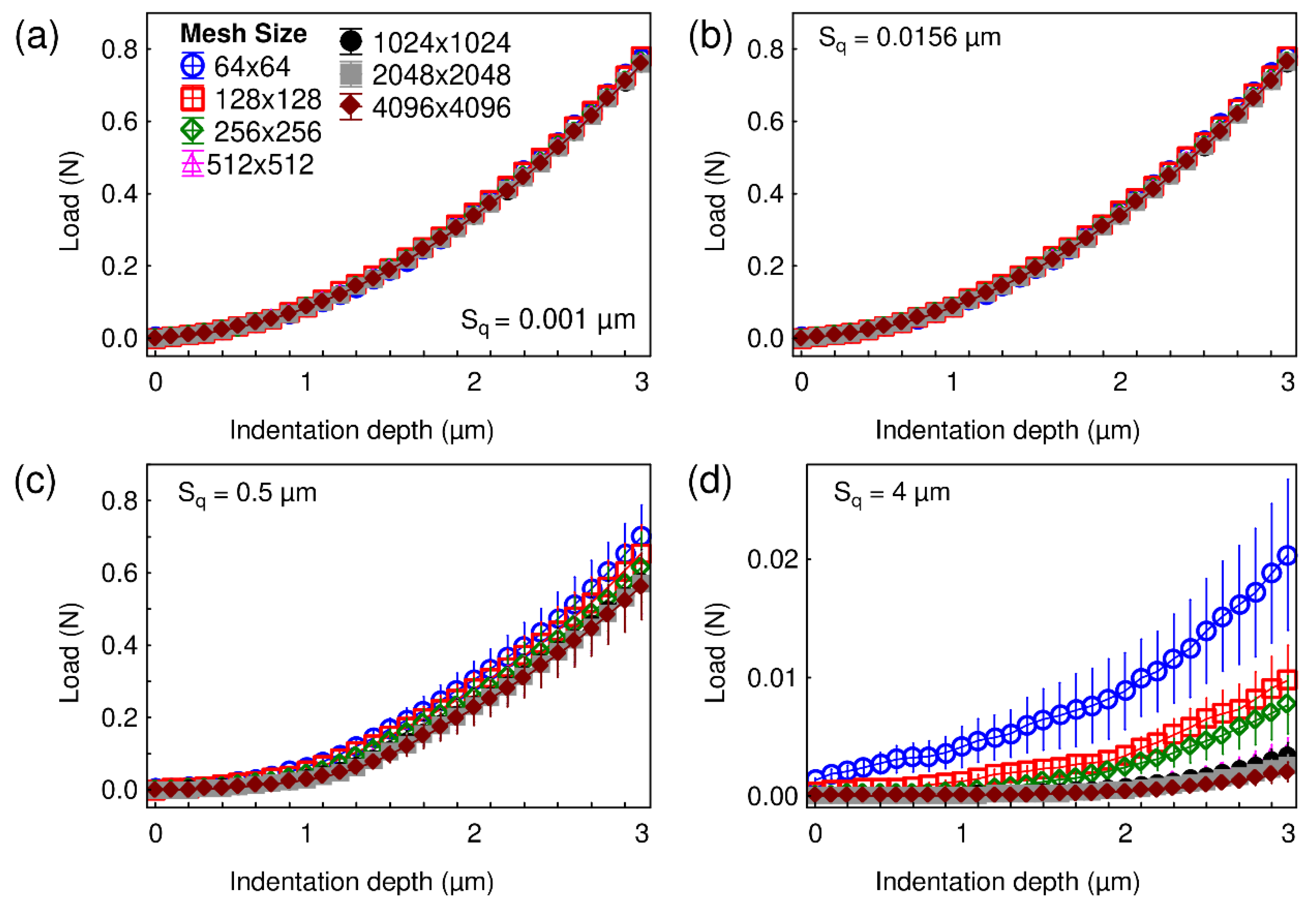
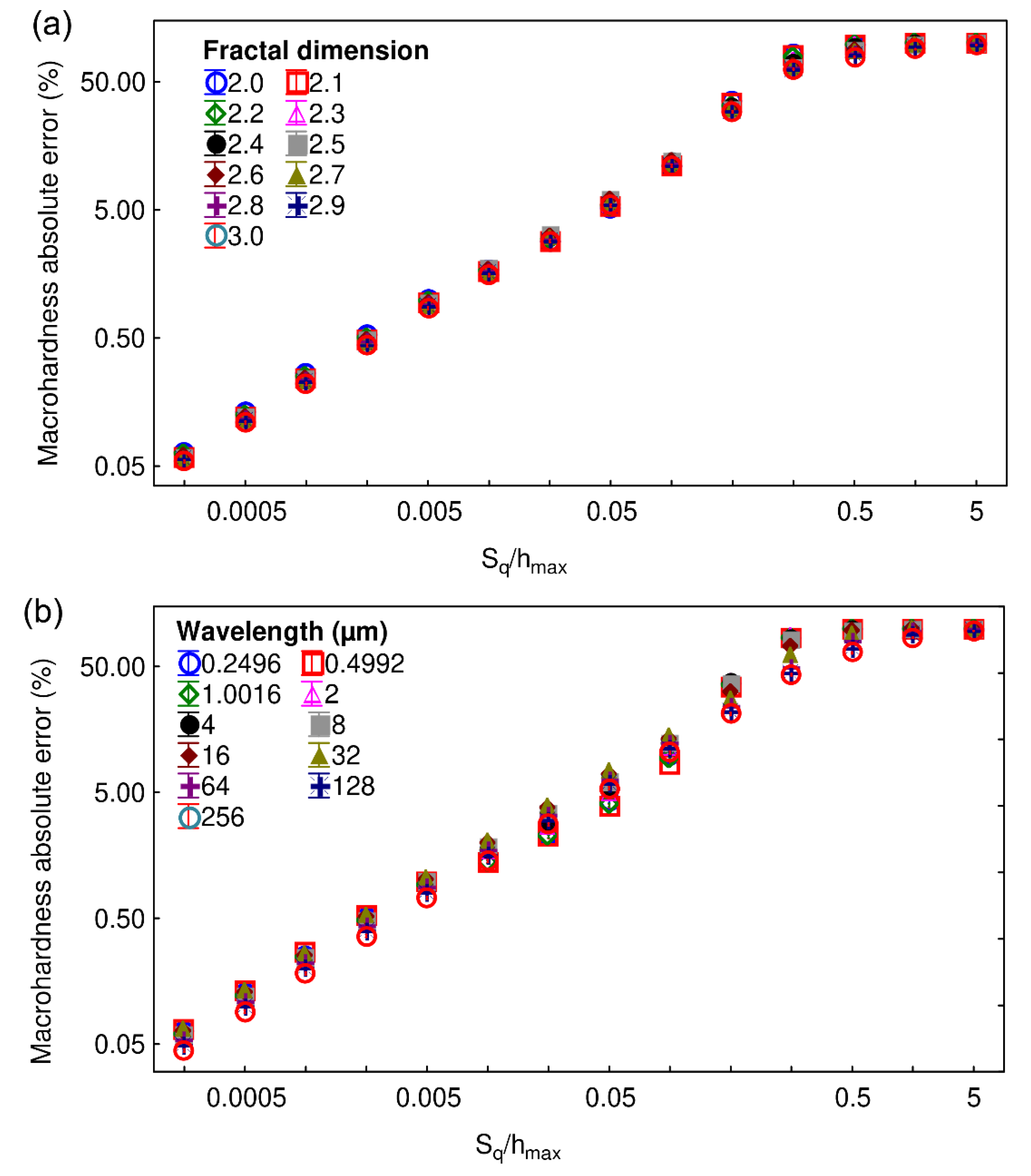
- The amplitude described by the root-mean-square deviation Sq, as described in [18]. The following values were tested: 0.001, 0.002, 0.0039, 0.0078, 0.0156, 0.0313, 0.0625, 0.125, 0.25, 0.5, 1, 2, 4, and 8 µm. It should be noted that very small values of Sq are only used as asymptotic values.
- -
- The wavelength. The following values were used: 0.2496, 0.4992, 1.0016, 2, 4, 8, 16, 32, 64, 128, and 256 µm. To be consistent with the standard, the wavelength was not defined by series truncation of Equation (5) but was obtained with the cut-off frequency of Gaussian high-pass filtering as defined in [19].
- -
- Fractal dimension. Values ranging from 2 to 3 using an increment of 0.1 were used.
2.2. Description of the Semianalytical Model Used for Simulating Indentation Testing
2.3. Hardness Computation Method
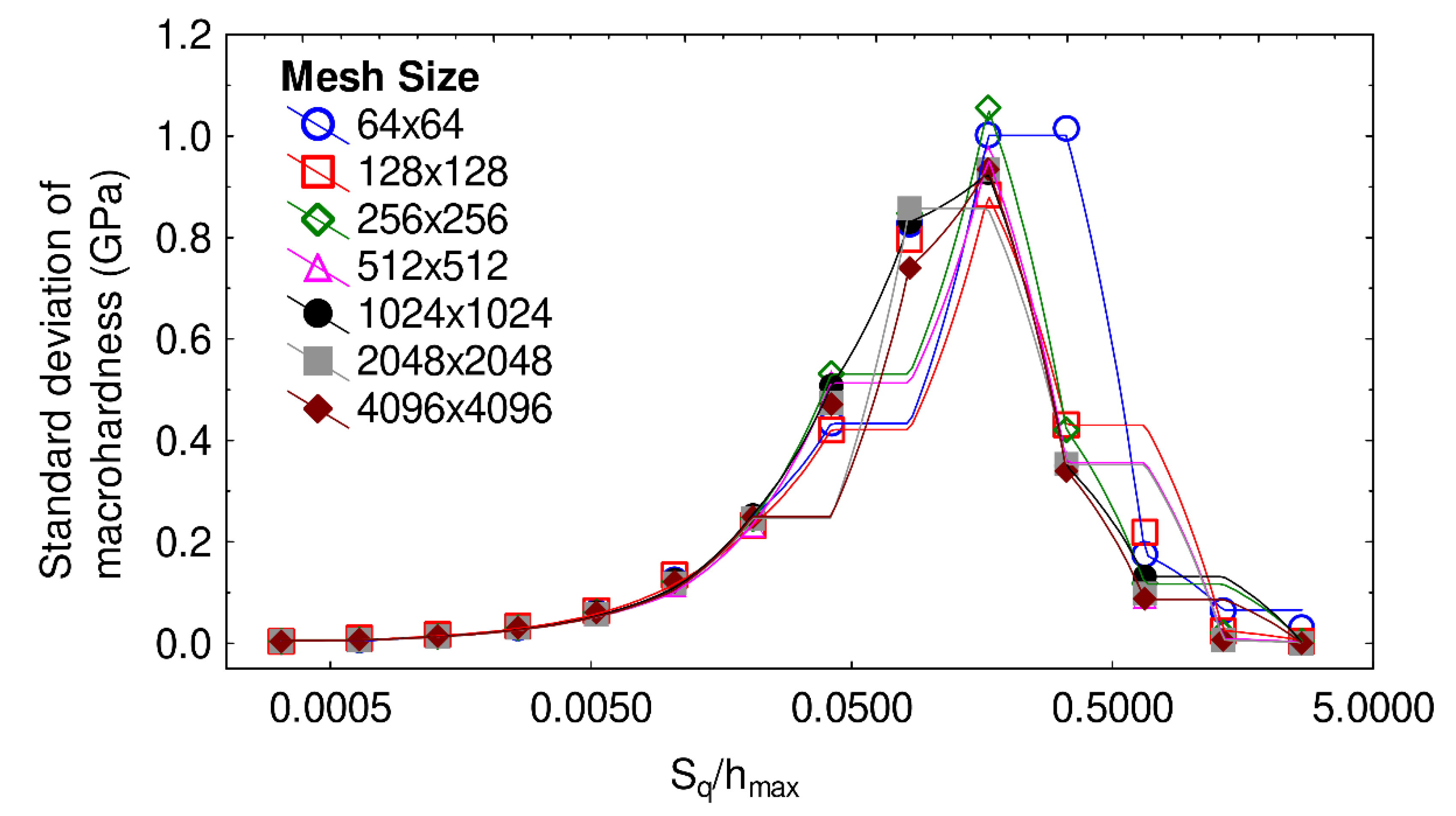
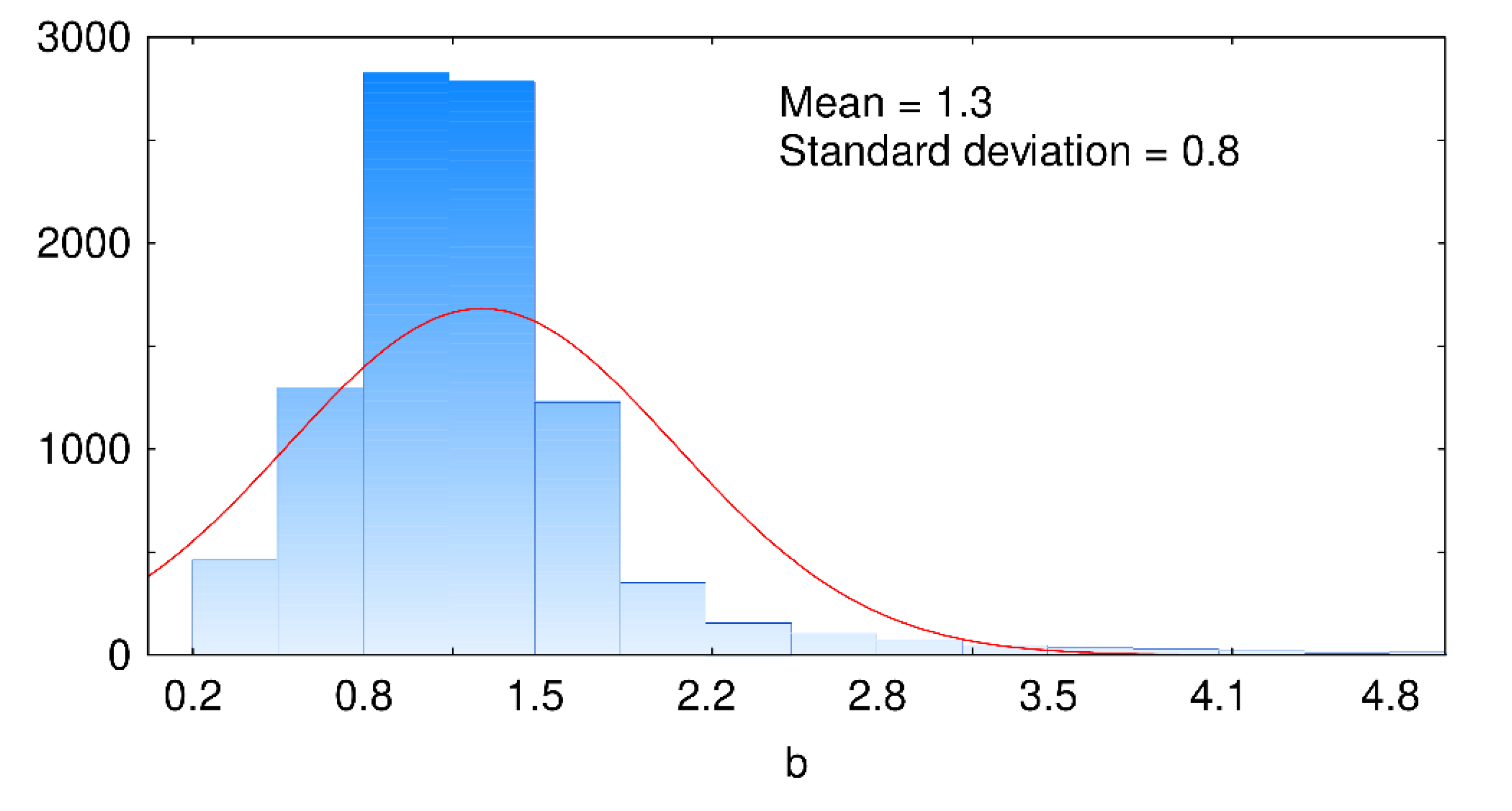
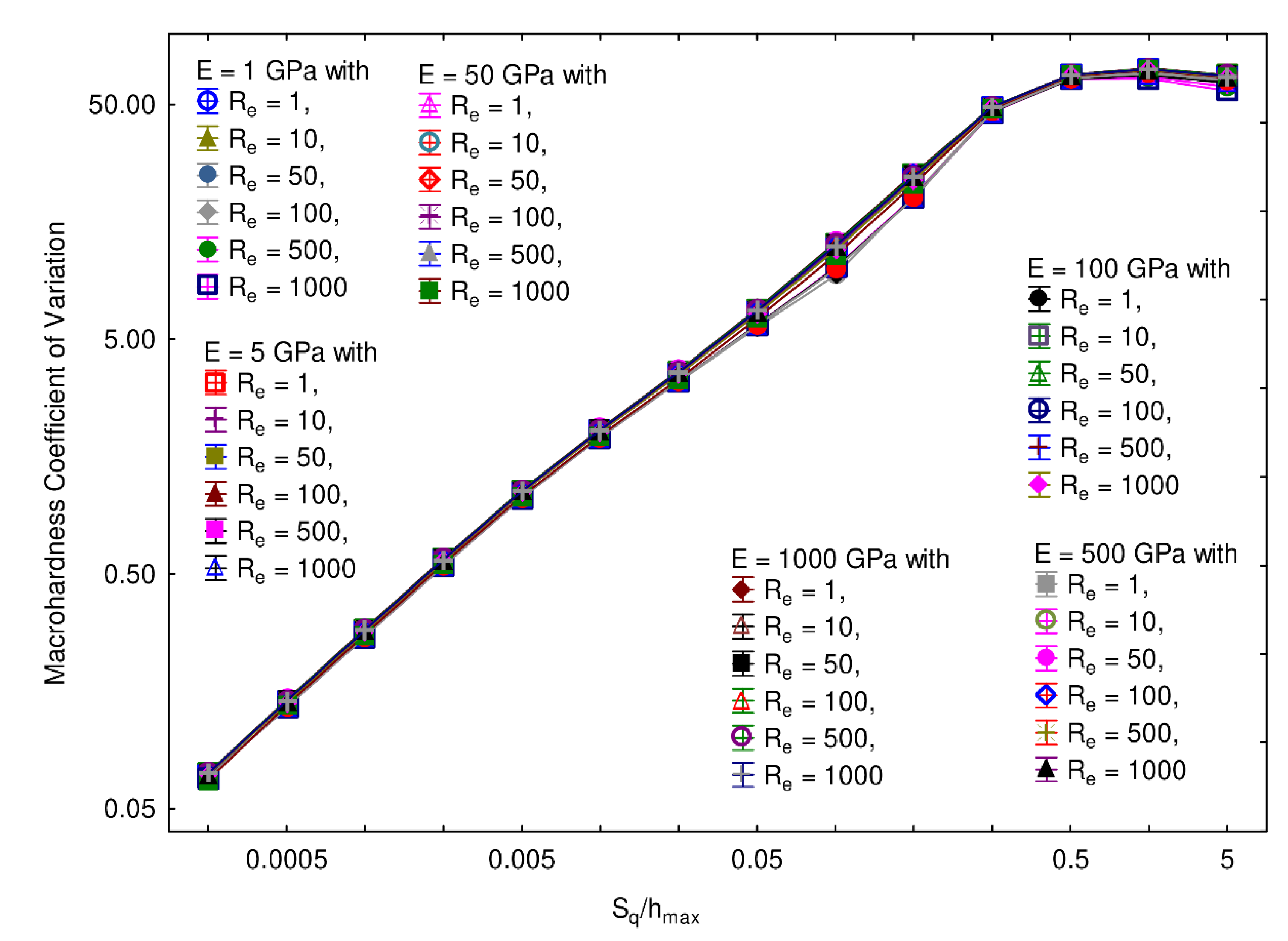
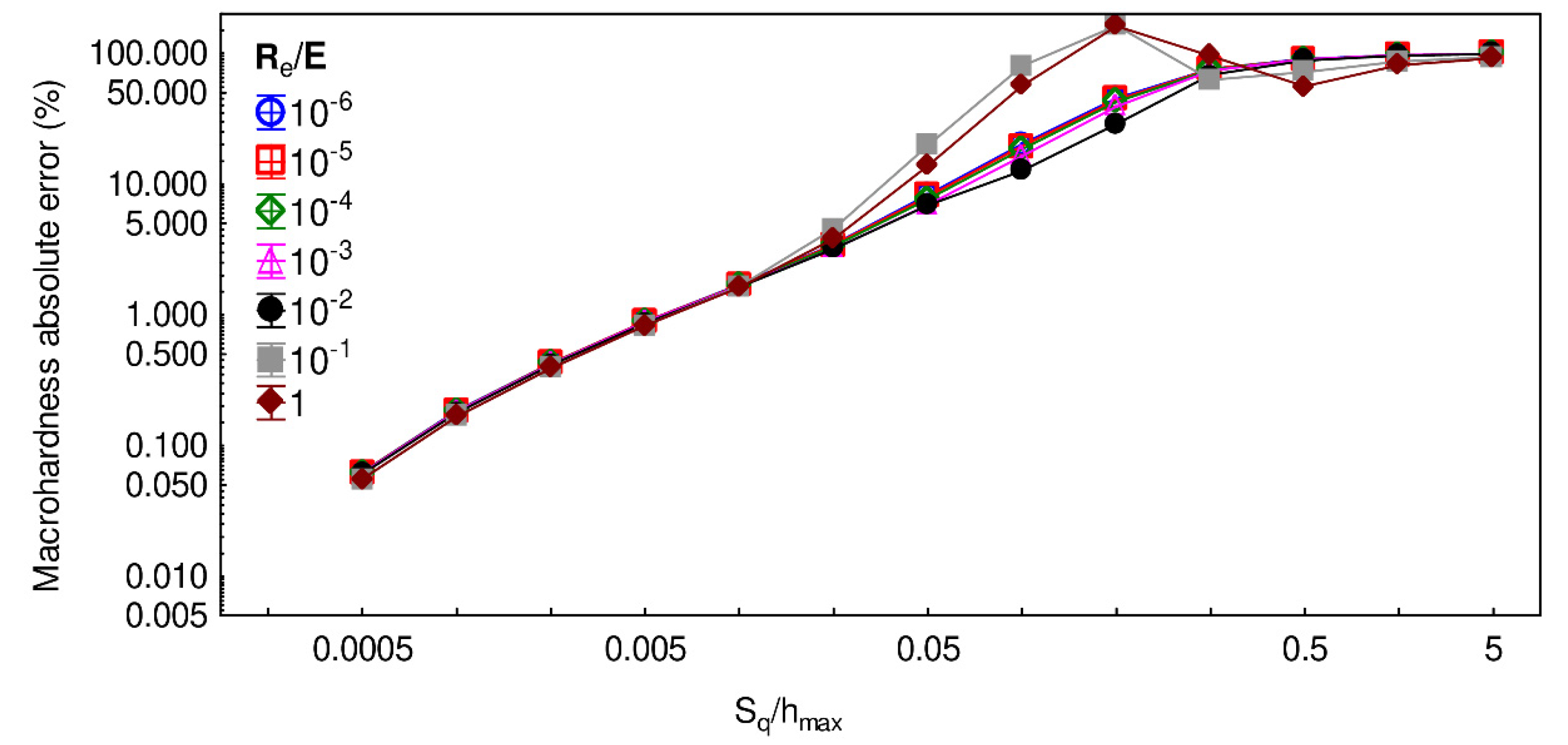
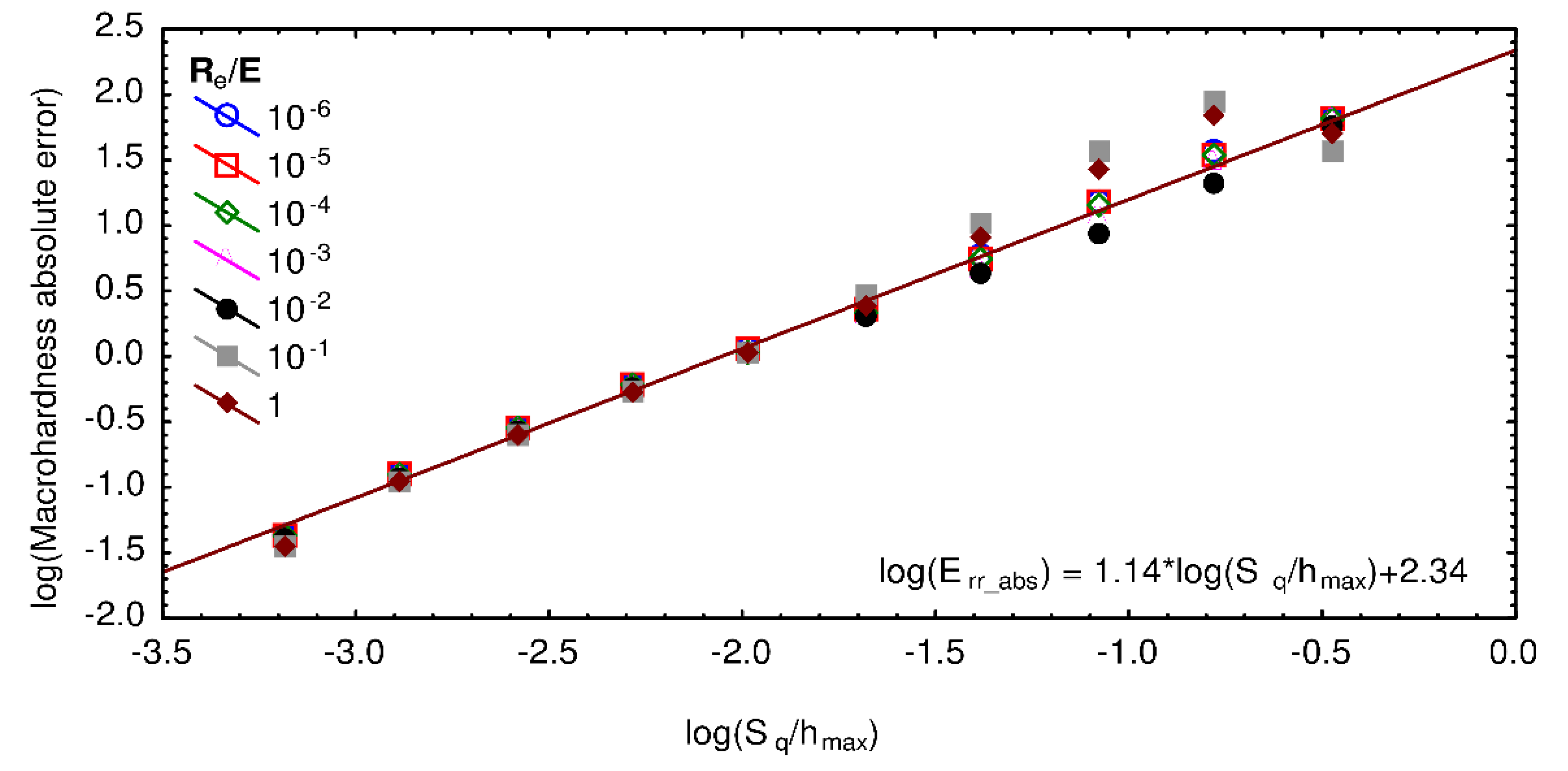
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| α | Constant linked to indenter geometry |
| aj, bj | Semiaxes of ellipse |
| b | Power-law exponent |
| CV | Coefficient of variation |
| Δhc | Discrepancy between Kick’s law and computed indentation curve |
| E | Young’s modulus |
| Err_abs | Macrohardness absolute error |
| Fj | Normal force |
| hc | Contact depth |
| hmax | Maximum indentation depth |
| H | Hölder exponent |
| Hth | Macrohardness of the material |
| H0 | Macrohardness computed with curve shifting methodology |
| pj | Local pressure |
| pjm | Mean pressure undergone by a given asperity j |
| P | Indentation load |
| Re | Elastic limit |
| Sq | Root-mean-square deviation |
| θ | Angle of attack |
References
- Marteau, J.; Bigerelle, M.; Bouvier, S.; Iost, A. Reflection on the measurement and use of the topography of the indentation imprint. Scanning 2014, 36, 115–126. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Walter, C.; Mitterer, C. 3D versus 2D finite element simulation of the effect of surface roughness on nanoindentation of hard coatings. Surf. Coat. Technol. 2009, 203, 3286–3290. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Li, M.; Chen, W.; Cheng, Y.-T.; Cheng, C.-M. Influence of contact geometry on hardness behavior in nano-indentation. Vacuum 2009, 84, 315–320. [Google Scholar] [CrossRef]
- Wei, P.J.; Tsai, P.W.; Lin, J.F. Micro-contact analysis for the initial contact in nanoindentation tests. Tribol. Int. 2008, 41, 1247–1254. [Google Scholar] [CrossRef]
- Qasmi, M.; Delobelle, P. Influence of the average roughness Rms on the precision of the Young’s modulus and hardness determination using nanoindentation technique with a Berkovich indenter. Surf. Coat. Technol. 2006, 201, 1191–1199. [Google Scholar] [CrossRef]
- Jiang, W.-G.; Su, J.-J.; Feng, X.-Q. Effect of surface roughness on nanoindentation test of thin films. Eng. Fract. Mech. 2008, 75, 4965–4972. [Google Scholar] [CrossRef]
- ISO. For ISO Standard 14577-1 2002 Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. Available online: https://www.iso.org/standard/30104.html (accessed on 19 March 2020).
- Wai, S.W.; Spinks, G.M.; Brown, H.R.; Swain, M. Surface roughness: Its implications and inference with regards to ultra microindentation measurements of polymer mechanical properties. Polym. Test. 2004, 23, 501–507. [Google Scholar] [CrossRef]
- Arivuoli, D.; Lawson, N.S.; Krier, A.; Attolini, G.; Pelosi, C. Nanoindentation studies of MOVPE grown GaAs/InP heterostructures. Mater. Chem. Phys. 2000, 66, 207–212. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Kang, S.-K.; Lee, J.-J.; Jang, J.; Lee, Y.-H.; Kwon, D. Influence of surface-roughness on indentation size effect. Acta Mater. 2007, 55, 3555–3562. [Google Scholar] [CrossRef]
- de Souza, G.B.; Mikowski, A.; Lepienski, C.M.; Foerster, C.E. Indentation hardness of rough surfaces produced by plasma-based ion implantation processes. Surf. Coat. Technol. 2010, 204, 3013–3017. [Google Scholar] [CrossRef]
- Chicot, D.; Ageorges, H.; Voda, M.; Louis, G.; Ben Dhia, M.A.; Palacio, C.C.; Kossman, S. Hardness of thermal sprayed coatings: Relevance of the scale of measurement. Surf. Coat. Technol. 2015, 268, 173–179. [Google Scholar] [CrossRef]
- Li, H.; Bradt, R.C. The effect of indentation-induced cracking on the apparent microhardness. J. Mater. Sci. 1996, 31, 1065–1070. [Google Scholar] [CrossRef]
- Bobji, M.S.; Biswas, S.K. Deconvolution of hardness from data obtained from nanoindentation of rough surfaces. J. Mater. Res. 1999, 14, 2259–2268. [Google Scholar] [CrossRef]
- Marteau, J.; Bigerelle, M.; Xia, Y.; Mazeran, P.E.; Bouvier, S. Quantification of first contact detection errors on hardness and indentation size effect measurements. Tribol. Int. 2013, 59, 154–162. [Google Scholar] [CrossRef]
- Marteau, J.; Bigerelle, M. Toward an understanding of the effect of surface roughness on instrumented indentation results. J. Mater. Sci. 2017, 52, 7239–7255. [Google Scholar] [CrossRef]
- Stout, K.J.; Matthia, T.; Sullivan, P.J.; Dong, W.P.; Mainsah, E.; Luo, N.; Zahouani, H. The Developments of Methods for the Characterisation of Roughness in Three Dimensions; Office for Official Publications of the European Communities: Luxembourg, 1993. [Google Scholar]
- ISO—ISO 16610-49:2015—Geometrical Product Specifications (GPS)—Filtration—Part 49: Morphological Profile Filters: Scale Space Techniques. Available online: https://www.iso.org/standard/61381.html (accessed on 19 March 2020).
- Johnson, K.L. Contact Mechanics; Cambridge University Press: London, UK, 1985. [Google Scholar]
- Jourani, A.; Dursapt, M.; Hamdi, H.; Rech, J.; Zahouani, H. Effect of the belt grinding on the surface texture: Modeling of the contact and abrasive wear. Wear 2005, 259, 1137–1143. [Google Scholar] [CrossRef]
- Kick, F. Das Gesetz der Proportionalen Widerstände und Seine Anwendungen: Nebst Versuchen Über das Verhalten Verschiedener Materialien bei Gleichen Formänderungen Sowohl Unter der Presse als dem Schlagwerk; Verlag von Arthur Felix: Leipzig, Germany, 1885. [Google Scholar]
- Marteau, J.; Mazeran, P.-E.; Bouvier, S.; Bigerelle, M. Zero-point correction method for nanoindentation tests to accurately quantify hardness and indentation size effect. Strain 2012, 48, 491–497. [Google Scholar] [CrossRef]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Cheng, Y.-T.; Cheng, C.-M. Scaling, dimensional analysis, and indentation measurements. Mater. Sci. Eng. R Rep. 2004, 44, 91–149. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marteau, J.; Jourani, A.; Bigerelle, M. Determination of an Objective Criterion for the Assessment of the Feasibility of an Instrumented Indentation Test on Rough Surfaces. Materials 2020, 13, 1589. https://doi.org/10.3390/ma13071589
Marteau J, Jourani A, Bigerelle M. Determination of an Objective Criterion for the Assessment of the Feasibility of an Instrumented Indentation Test on Rough Surfaces. Materials. 2020; 13(7):1589. https://doi.org/10.3390/ma13071589
Chicago/Turabian StyleMarteau, Julie, Abdeljalil Jourani, and Maxence Bigerelle. 2020. "Determination of an Objective Criterion for the Assessment of the Feasibility of an Instrumented Indentation Test on Rough Surfaces" Materials 13, no. 7: 1589. https://doi.org/10.3390/ma13071589
APA StyleMarteau, J., Jourani, A., & Bigerelle, M. (2020). Determination of an Objective Criterion for the Assessment of the Feasibility of an Instrumented Indentation Test on Rough Surfaces. Materials, 13(7), 1589. https://doi.org/10.3390/ma13071589





