Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of Concrete Mixtures
2.2. Determination of Packing Fraction
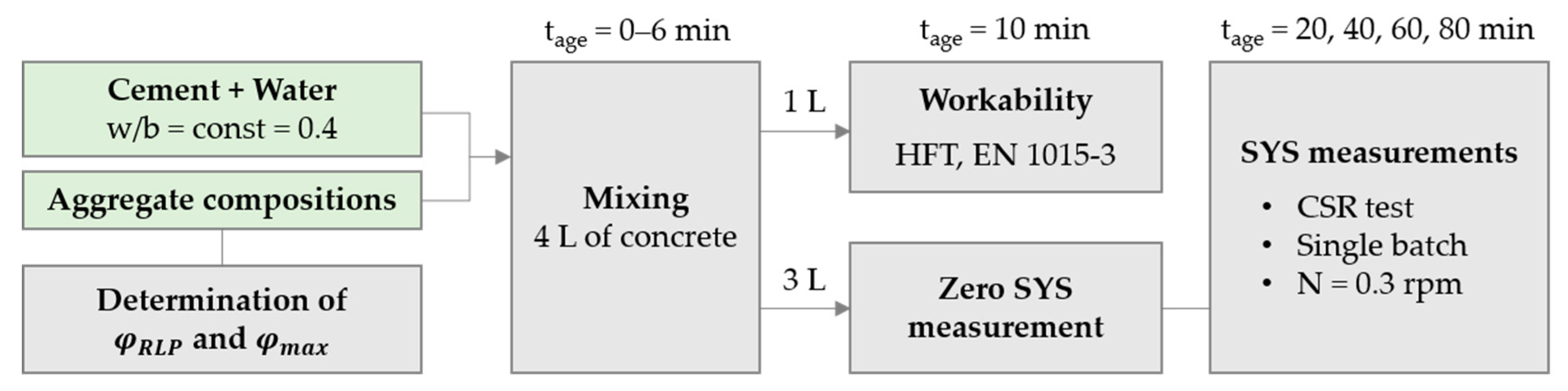
2.3. Determination of Workability and Static Rheological Properties
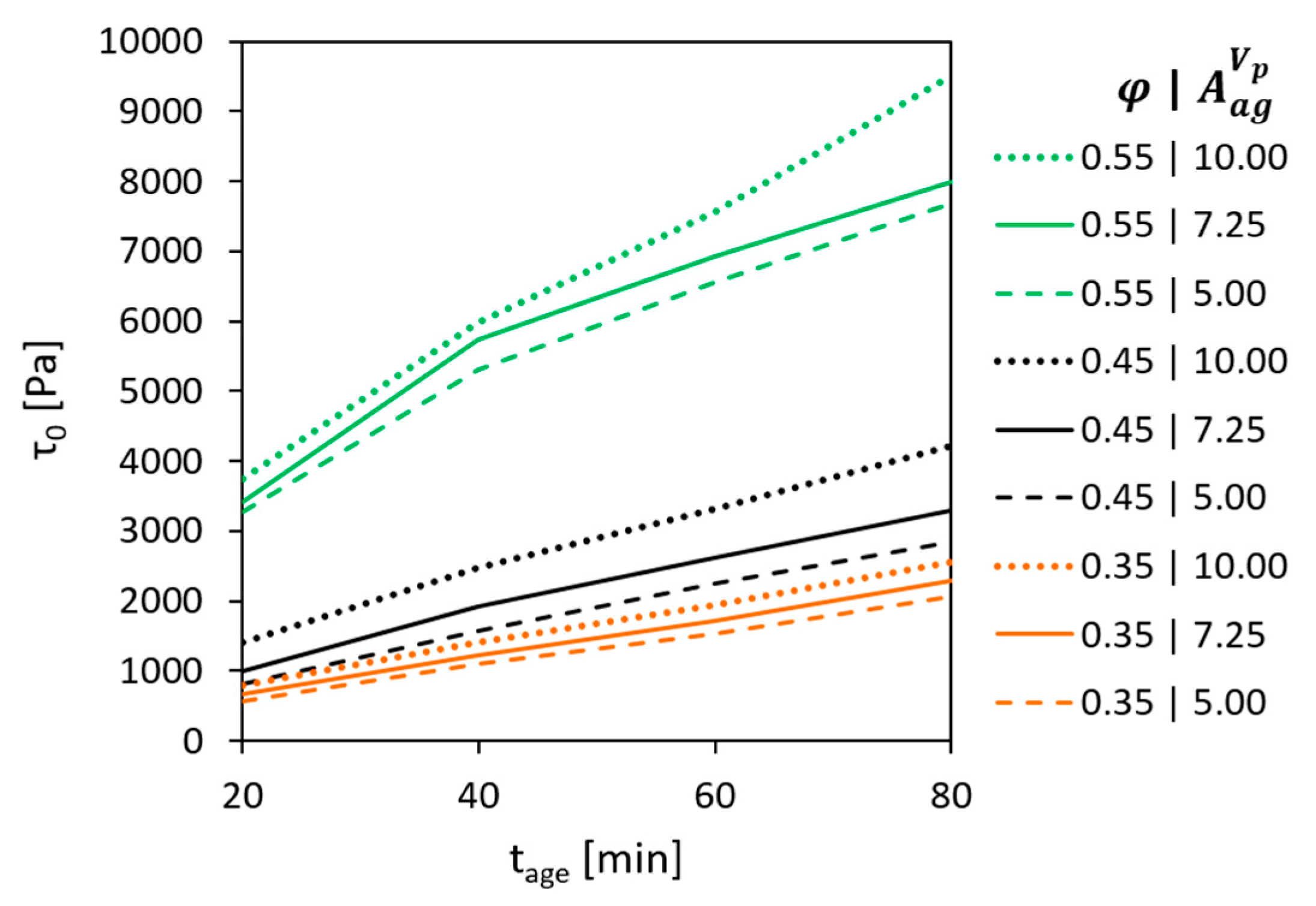
3. Results and Discussion
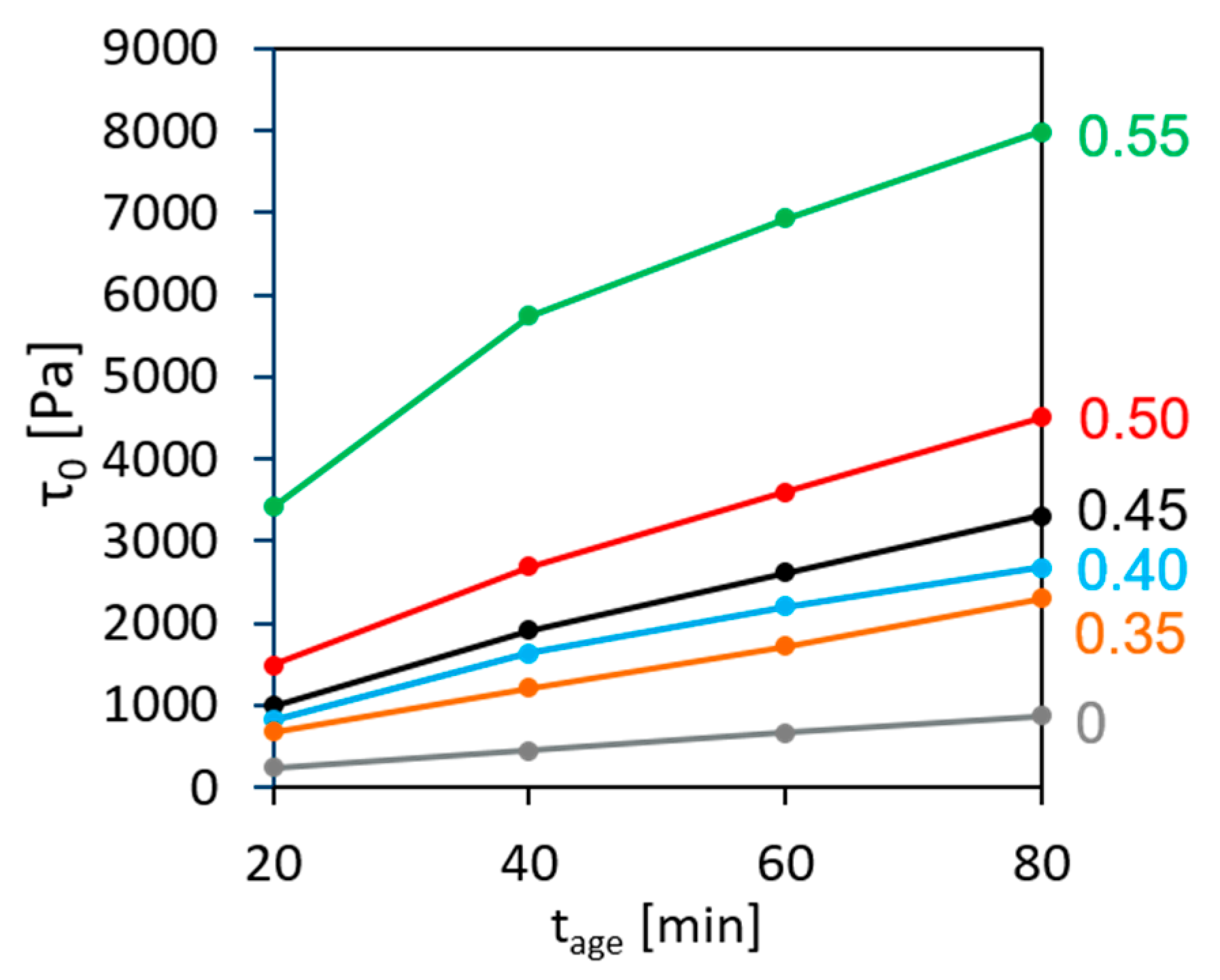
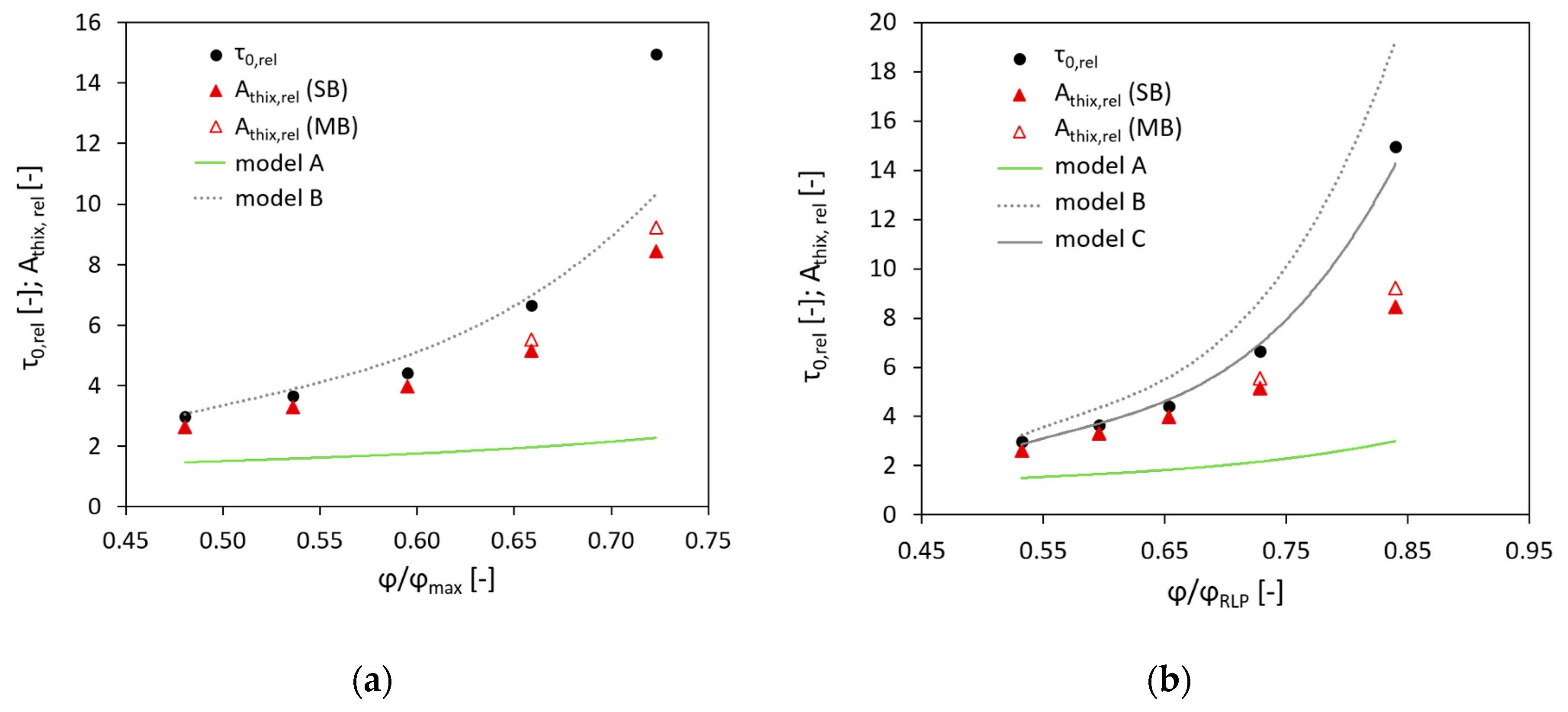
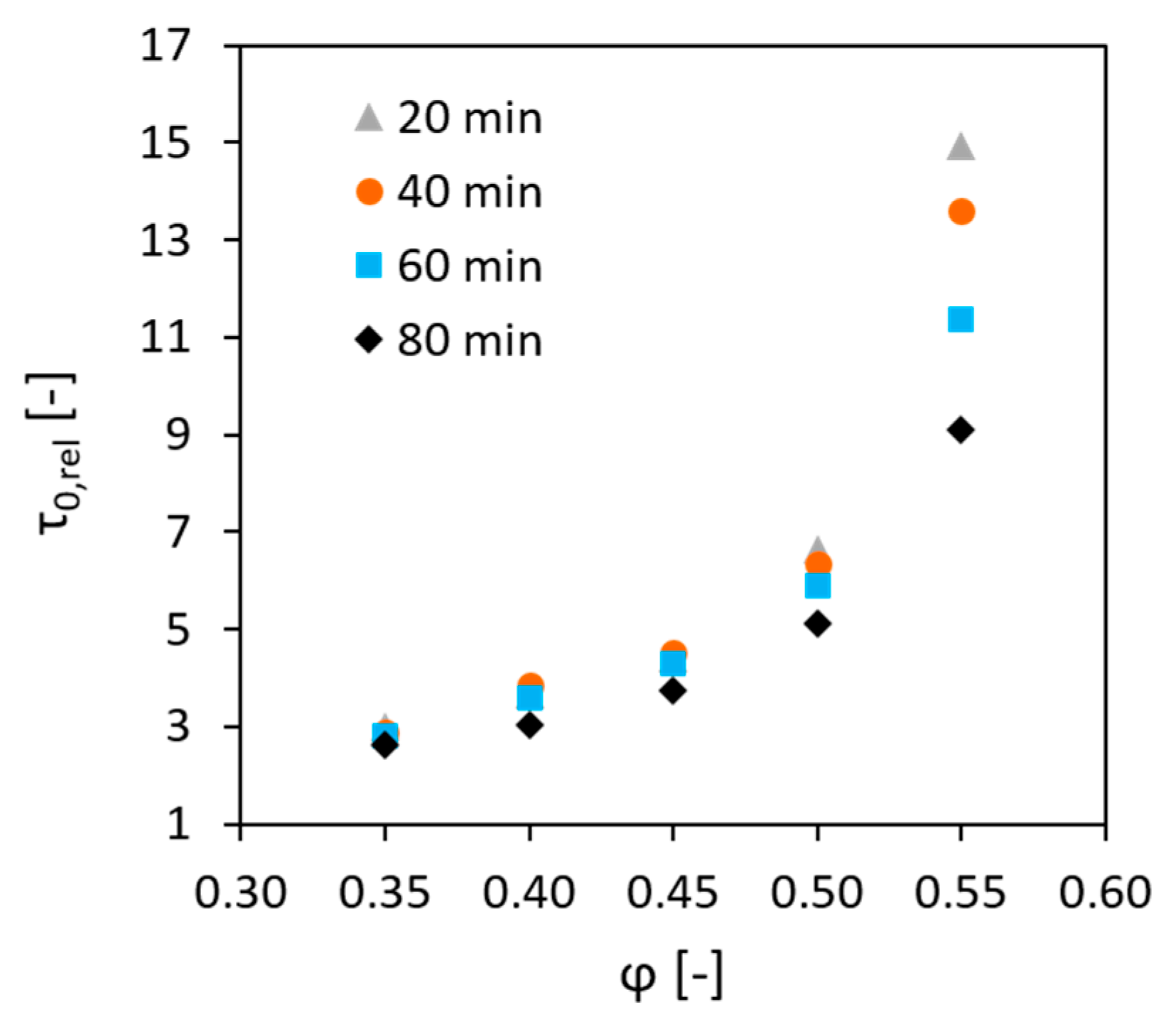
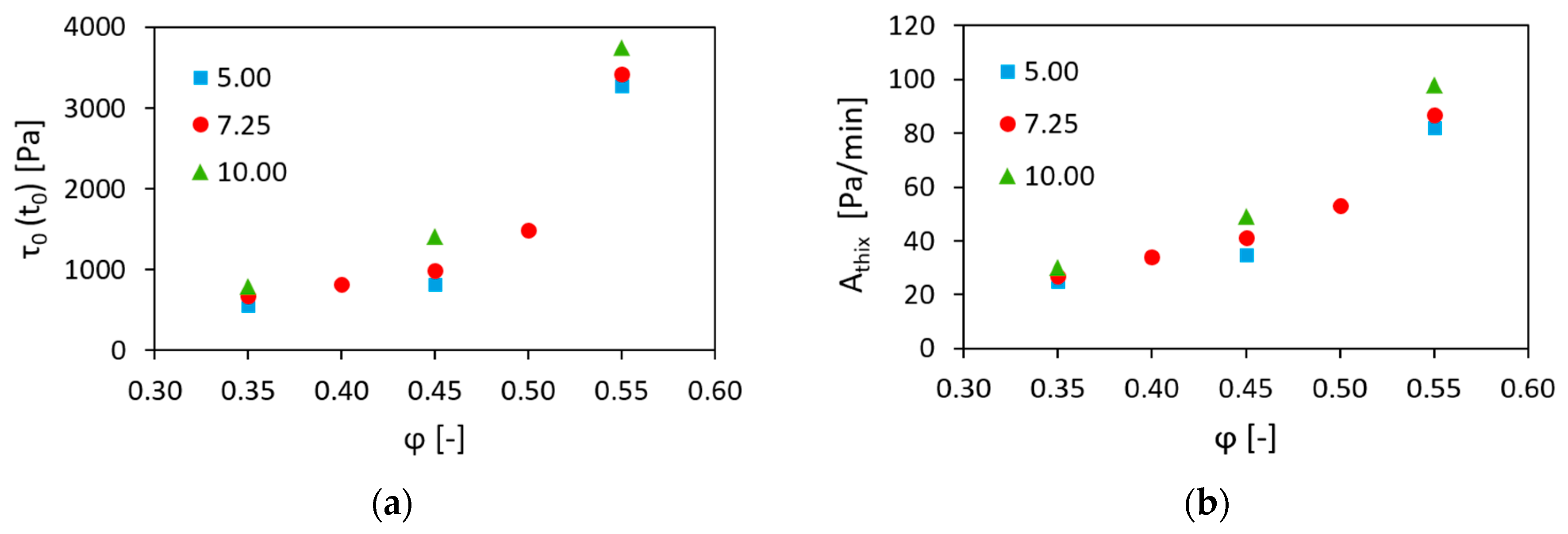
3.1. Effect of the Volume Fraction
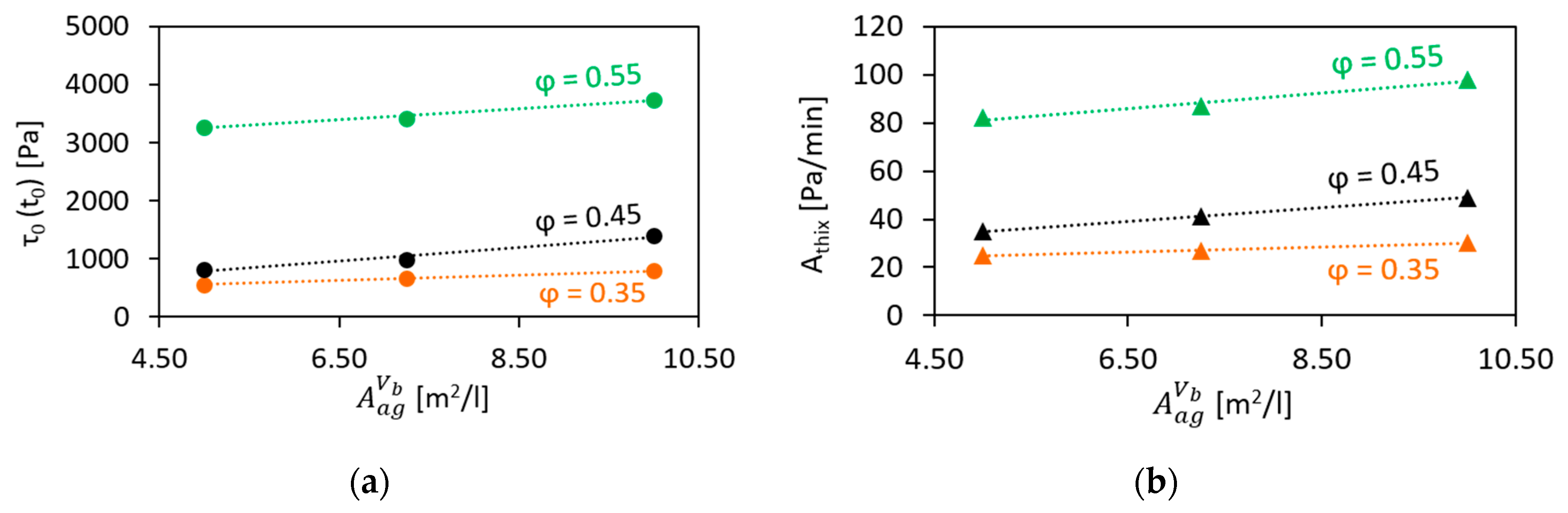
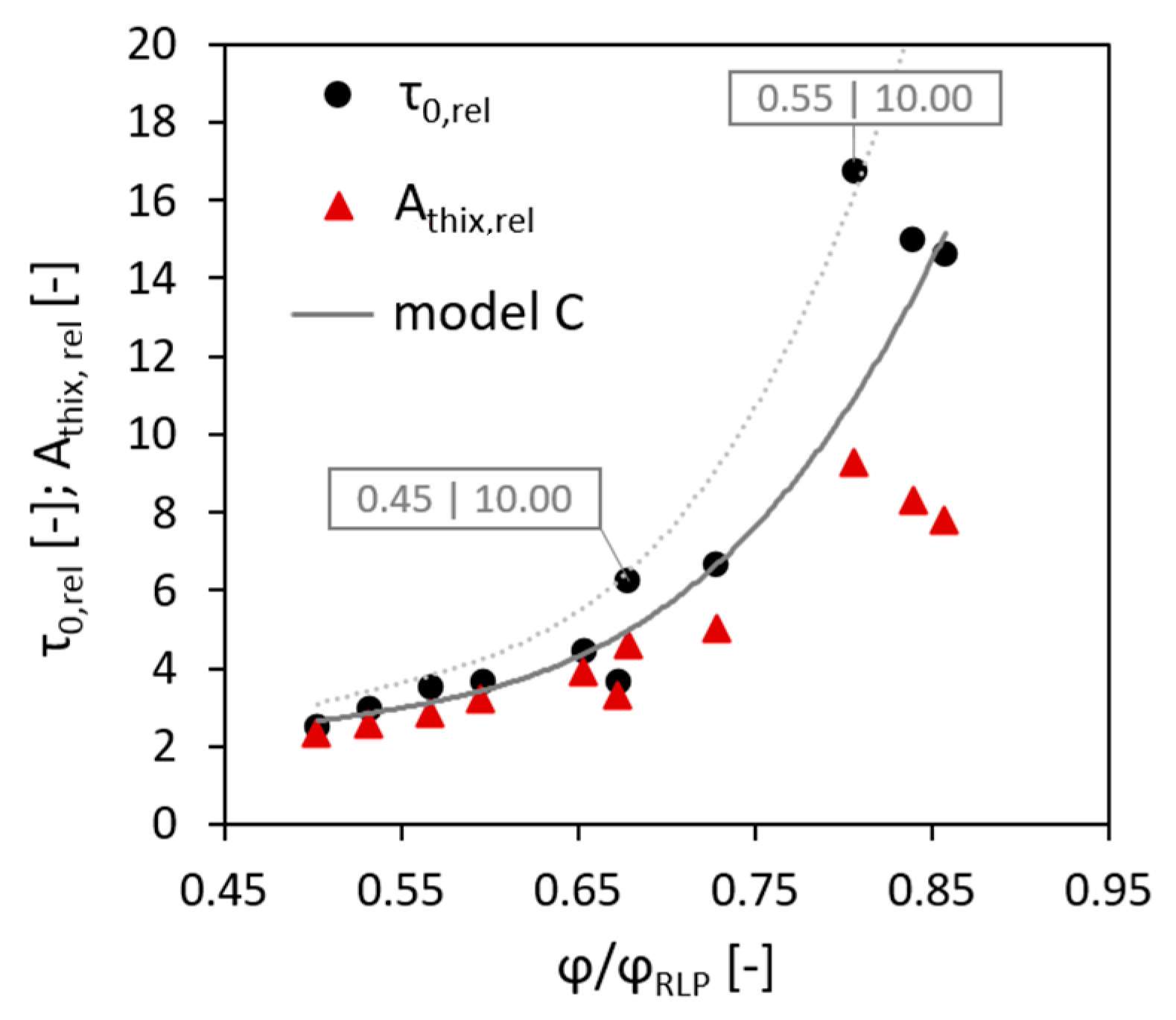
3.2. Effect of the Surface Area
4. Conclusion and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Terms and Definitions
| Volume fraction | Volume concentration of particles in the unit volume of material: e.g., suspension, concrete |
| Maximum volume fraction | Ratio of the true volume of particles to the volume occupied by them in a maximally compacted state |
| Random loose packing fraction | Ratio of the true volume of particles to the volume occupied by them in a random loose state, i.e., without compaction |
| Surface area of aggregate per unit volume of cement paste | Total area of surfaces of all aggregate particles distributed in the unit volume of cement paste |
| Sphericity | Ratio of the surface area of a sphere to the surface area of an actual, irregularly shaped particle of equivalent volume |
| Intrinsic viscosity | Measure of the effect of individual particles on the viscosity of suspensions; dependent on particle shape and concentration |
| Static yield stress | Stress which is required to initiate flow |
| Structural build-up | Evolution of rheological properties of a cementitious material over time due to flocculation and early hydration |
| Structural build-up rate | Rate of increase in the static yield stress of a cementitious material over time |
| Relative static yield stress | Ratio of the static yield stress of suspension, e.g., concrete, to the static yield stress of suspending medium, e.g., cement paste |
| Relative structural build-up rate | Ratio of the structural build-up rate of suspension, e.g., concrete, to the structural build-up rate of suspending medium, e.g., cement paste |
| Constant shear rate test | Rheometry method for measuring static yield stress; a low, constant shear rate is applied until shear stress reaches its peak or plateau value |
| Single-batch approach | A technique used to determine the evolution of static yield stress over time, in which the measurements of peak torque at all ages are performed on a single sample of material |
| Multi-batch approach | A technique used to determine the evolution of the static yield stress over time, in which measurement of peak torque at each particular age is performed on a discrete, individually prepared sample of the same material |
References
- Wangler, T.; Lloret, E.; Reiter, L.; Hack, N.; Gramazio, F.; Kohler, M.; Bernhard, M.; Dillenburger, B.; Buchli, J.; Roussel, N.; et al. Digital Concrete: Opportunities and Challenges. RILEM Tech. Lett. 2016, 1, 67–75. [Google Scholar] [CrossRef]
- Roussel, N. Rheological requirements for printable concretes. Cem. Concr. Res. 2018, 112, 76–85. [Google Scholar] [CrossRef]
- Reiter, L.; Wangler, T.; Roussel, N.; Flatt, R.J. The role of early age structural build-up in digital fabrication with concrete. Cem. Concr. Res. 2018, 112, 86–95. [Google Scholar] [CrossRef]
- Omran, A.F.; Khayat, K.H. Effect of SCC Mixture Composition on Thixotropy and Formwork Pressure Effect of SCC Mixture Composition on Thixotropy and Formwork Pressure. J. Mater. Civ. Eng. 2012. [Google Scholar] [CrossRef]
- Ovarlez, G.; Roussel, N. A physical model for the prediction of lateral stress exerted by self-compacting concrete on formwork, Mater. Struct. Constr. 2006, 36, 269–279. [Google Scholar] [CrossRef]
- Billberg, P.H.; Roussel, N.; Amziane, S.; Beitzel, M.; Charitou, G.; Freund, B.; Gardner, J.N.; Grampeix, G.; Graubner, C.A.; Keller, L.; et al. Field validation of models for predicting lateral form pressure exerted by SCC. Cem. Concr. Compos. 2014. [Google Scholar] [CrossRef]
- Tokhmechi, B.; Velayati, A.; Kazemzadeh, E.; Soltanian, H. Gas migration through cement slurries analysis: A comparative laboratory study. Int. J. Min. Geo-Eng. 2015, 49, 281–288. [Google Scholar] [CrossRef]
- Lloret, E.; Shahab, A.R.; Linus, M.; Flatt, R.J.; Gramazio, F.; Kohler, M.; Langenberg, S. Complex concrete structures: Merging existing casting techniques with digital fabrication. Comput. Des. 2015, 60, 40–49. [Google Scholar] [CrossRef]
- Buswell, R.A.; Leal de Silva, W.R.; Jones, S.Z.; Dirrenberger, J. 3D printing using concrete extrusion: A roadmap for research. Cem. Concr. Res. 2018, 112, 37–49. [Google Scholar] [CrossRef]
- Nerella, V.N.; Hempel, S.; Mechtcherine, V. Effects of layer-interface properties on mechanical performance of concrete elements produced by extrusion-based 3D-printing. Constr. Build. Mater. 2019, 205, 586–601. [Google Scholar] [CrossRef]
- Van Damme, H. Concrete material science: Past, present, and future innovations. Cem. Concr. Res. 2018, 112, 5–24. [Google Scholar] [CrossRef]
- Hafid, H.; Ovarlez, G.; Toussaint, F.; Jezequel, P.H.; Roussel, N. Effect of particle morphological parameters on sand grains packing properties and rheology of model mortars. Cem. Concr. Res. 2016. [Google Scholar] [CrossRef]
- Mehdipour, I.; Khayat, K.H. Understanding the role of particle packing characteristics in rheo-physical properties of cementitious suspensions: A literature review. Constr. Build. Mater. 2018, 161, 340–353. [Google Scholar] [CrossRef]
- Fuller, W.B.; Thompson, S.E. The laws of proportioning concrete. Trans. ASCE 1907, 59, 67–143. [Google Scholar]
- Andreasen, A.H.M. Ueber die Beziehung zwischen Kornabstufung und Zwischenraum in Produkten aus losen Körnern (mit einigen Experimenten). Kolloid-Zeitschrift 1930, 50, 217–228. [Google Scholar] [CrossRef]
- Funk, J.E.; Dinger, D. Predictive Control of Crowded Particulate Suspension Applied to Ceramic Manufacturing; Kluwer Academic Publishers: Springer, Boston, MA, USA, 1994. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1905. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of concentrated suspensions. J. Appl. Polym. Sci. 1971, 15, 2007–2021. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems and minimum energy dissipation principle—I. Viscosity-concentration relationship. Rheol. Acta 1977, 16, 82–94. [Google Scholar] [CrossRef]
- Farris, R.J. Prediction of the Viscosity of Multimodal Suspensions from Unimodal Viscosity Data. Trans. Soc. Rheol. 1968, 12, 281–301. [Google Scholar] [CrossRef]
- Choi, M.S.; Kim, Y.J.; Kim, J.K. Prediction of Concrete Pumping Using Various Rheological Models. Int. J. Concr. Struct. Mater. 2014, 8, 269–278. [Google Scholar] [CrossRef]
- Chateau, X.; Ovarlez, G. Homogenization approach to the behavior of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 2008. [Google Scholar] [CrossRef]
- Mahaut, F.; Mokéddem, S.; Chateau, X.; Roussel, N.; Ovarlez, G. Effect of coarse particle volume fraction on the yield stress and thixotropy of cementitious materials. Cem. Concr. Res. 2008. [Google Scholar] [CrossRef]
- Roussel, N. A thixotropy model for fresh fluid concretes: Theory, validation and applications. Cem. Concr. Res. 2006. [Google Scholar] [CrossRef]
- Lecompte, T.; Perrot, A.; Picandet, V.; Bellegou, H.; Amziane, S. Cement-based mixes: Shearing properties and pore pressure. Cem. Concr. Res. 2012, 42, 139–147. [Google Scholar] [CrossRef]
- Perrot, A.; Lecompte, T.; Estellé, P.; Amziane, S. Structural build-up of rigid fiber reinforced cement-based materials. Mater. Struct. Constr. 2013, 46, 1561–1568. [Google Scholar] [CrossRef]
- Le, T.T.; Austin, S.A.; Lim, S.; Buswell, R.A.; Gibb, A.G.F.; Thorpe, T. Mix design and fresh properties for high-performance printing concrete. Mater. Struct. 2012, 45, 1221–1232. [Google Scholar] [CrossRef]
- Lindemann, H.; Gerbers, R.; Ibrahim, S.; Dietrich, F.; Herrmann, E.; Dröder, K.; Raatz, A.; Kloft, H. Development of a Shotcrete 3D-Printing (SC3DP) Technology for Additive Manufacturing of Reinforced Freeform Concrete Structures. In RILEM Bookseries; Wangler, T., Flatt, R.J., Eds.; Springer: Cham, Switzerland, 2019; pp. 287–298. [Google Scholar] [CrossRef]
- Lowke, D. Interparticle Forces and Rheology of Cement Based Suspensions. In Nanotechnology in Construction 3; Bittnar, Z., Bartos, P.J.M., Němeček, J., Šmilauer, V., Zeman, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 295–301. [Google Scholar]
- Ivanova, I.; Mechtcherine, V. Evaluation of Structural Build-Up Rate of Cementitious Materials by Means of Constant Shear Rate Test: Parameter Study. In Rheology and Processing of Construction Materials; RILEM Bookseries; Springer: Cham, Switzerland, 2020; pp. 209–218. [Google Scholar] [CrossRef]
- Stark, J.; Wicht, B. Zement und Kalk: Der Baustoff als Werkstoff, F.A; Finger-Institut für Baustoffkunde derBauhaus-Universität Weimar: Weimar, Germany, 2000. [Google Scholar]
- Wadell, H. Sphericity and Roundness of Rock Particles. J. Geol. 1933, 41, 310–331. [Google Scholar] [CrossRef]
- De Larrard, F. Concrete Mixture Proportioning; E & FN Spon: London, UK, 1999. [Google Scholar]
- German Institute for Standardisation (Deutsches Institut für Normung). Methods of Test for Mortar for Masonry—Part 3: Determination of Consistence of Fresh Mortar (by Flow Table); EN 1015-3:2007; German Institute for Standardisation (Deutsches Institut für Normung): Berlin, Germany, 2007. [Google Scholar]
- Ivanova, I.; Mechtcherine, V. Possibilities and challenges of constant shear rate test for evaluation of structural build-up rate of cementitious materials. Cem. Concr. Res. 2020, 130. [Google Scholar] [CrossRef]
- Eslami Pirharati, M.; Ivanov, D.; Krauss, H.-W.; Schilde, C.; Lowke, D. Rheology and Processing of Composite Materials. In RILEM Bookseries; Springer: Cham, Switzerland, 2020; pp. 588–595. [Google Scholar] [CrossRef]
- Heirman, G.; Hendrickx, R.; Vandewalle, L.; Van Gemert, D.; Feys, D.; De Schutter, G.; Desmet, B.; Vantomme, J. Integration approach of the Couette inverse problem of powder type self-compacting concrete in a wide-gap concentric cylinder rheometer. Part II. Influence of mineral additions and chemical admixtures on the shear thickening flow behavior. Cem. Concr. Res. 2009. [Google Scholar] [CrossRef]
- Struble, L.; Sun, G.K. Viscosity of Portland cement paste as a function of concentration. Adv. Cem. Based Mater. 1995, 2, 62–69. [Google Scholar] [CrossRef]
- Szecsy, R.S. Concrete Rheology. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 1997. [Google Scholar]
| [-] | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | ||||||
| [m2/L] | 5.00 | 7.25 | 10.00 | 7.25 | 5.00 | 7.25 | 10.00 | 7.25 | 5.00 | 7.25 | 10.00 |
| Sieve Size [mm] | Percentage Passing [%] | ||||||||||
| 0.125 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.25 | 12.0 | 21.5 | 34.0 | 15.4 | 5.0 | 10.6 | 18.5 | 8.0 | 1.5 | 4.0 | 9.0 |
| 0.5 | 25.5 | 41.0 | 62.0 | 31.5 | 13.0 | 24.5 | 36.5 | 18.3 | 4.5 | 13.0 | 22.3 |
| 1 | 41.5 | 58.4 | 76.0 | 48.0 | 27.3 | 40.0 | 53.5 | 31.6 | 18.0 | 28.5 | 36.9 |
| 2 | 58.0 | 74.0 | 86.0 | 65.0 | 49.0 | 57.5 | 69.5 | 48.9 | 40.0 | 47.5 | 54.5 |
| 4 | 78.0 | 87.5 | 94.0 | 82.2 | 73.5 | 76.5 | 85.0 | 71.2 | 68.0 | 71.0 | 75.5 |
| 8 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Parameter | Value | ||||||||||
| [-] | 0.70 | 0.66 | 0.62 | 0.67 | 0.67 | 0.69 | 0.66 | 0.69 | 0.64 | 0.66 | 0.68 |
| [-] | 0.76 | 0.73 | 0.68 | 0.75 | 0.75 | 0.76 | 0.74 | 0.76 | 0.73 | 0.76 | 0.76 |
| [-] | 0.50 | 0.53 | 0.57 | 0.60 | 0.67 | 0.65 | 0.68 | 0.73 | 0.86 | 0.84 | 0.81 |
| [-] | 0.46 | 0.48 | 0.52 | 0.54 | 0.60 | 0.59 | 0.61 | 0.66 | 0.75 | 0.72 | 0.72 |
| [-] | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | Cement paste | ||||||
| [m2/L] | 5.00 | 7.25 | 10.00 | 7.25 | 5.00 | 7.25 | 10.00 | 7.25 | 5.00 | 7.25 | 10.00 | |
| Component | Amount per 4 L of Concrete [kg] | |||||||||||
| CEM I 42.5 R | 3.598 | 3.598 | 3.598 | 3.321 | 3.045 | 3.045 | 3.045 | 2.768 | 2.491 | 2.491 | 2.491 | 5.536 |
| Sand fr. 0.125–0.250 mm | 0.445 | 0.798 | 1.261 | 0.653 | 0.239 | 0.506 | 0.882 | 0.423 | 0.087 | 0.233 | 0.525 | - |
| Sand fr. 0.25–0.50 mm | 0.501 | 0.723 | 1.039 | 0.683 | 0.382 | 0.663 | 0.859 | 0.547 | 0.175 | 0.525 | 0.775 | - |
| Sand fr. 0.5–1.0 mm | 0.594 | 0.646 | 0.519 | 0.700 | 0.682 | 0.739 | 0.811 | 0.707 | 0.787 | 0.904 | 0.851 | - |
| Sand fr. 1–2 mm | 0.612 | 0.579 | 0.371 | 0.721 | 1.035 | 0.835 | 0.763 | 0.914 | 1.283 | 1.108 | 1.026 | - |
| Sand fr. 2–4 mm | 0.742 | 0.501 | 0.297 | 0.729 | 1.169 | 0.906 | 0.739 | 1.181 | 1.632 | 1.370 | 1.224 | - |
| Gravel fr. 4–8 mm | 0.816 | 0.464 | 0.223 | 0.755 | 1.264 | 1.121 | 0.716 | 1.527 | 1.866 | 1.691 | 1.428 | - |
| Water | 1.439 | 1.439 | 1.439 | 1.329 | 1.218 | 1.218 | 1.218 | 1.107 | 0.996 | 0.996 | 0.996 | 2.216 |
| Parameter | Value | |||||||||||
| Spread diameter [mm] | 220 | 210 | 210 | 210 | 210 | 210 | 200 | 188 | 177 | 168 | 166 | 235 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanova, I.; Mechtcherine, V. Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete. Materials 2020, 13, 1551. https://doi.org/10.3390/ma13071551
Ivanova I, Mechtcherine V. Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete. Materials. 2020; 13(7):1551. https://doi.org/10.3390/ma13071551
Chicago/Turabian StyleIvanova, Irina, and Viktor Mechtcherine. 2020. "Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete" Materials 13, no. 7: 1551. https://doi.org/10.3390/ma13071551
APA StyleIvanova, I., & Mechtcherine, V. (2020). Effects of Volume Fraction and Surface Area of Aggregates on the Static Yield Stress and Structural Build-Up of Fresh Concrete. Materials, 13(7), 1551. https://doi.org/10.3390/ma13071551





