Analysis of One-Dimensional Ivshin–Pence Shape Memory Alloy Constitutive Model for Sensitivity and Uncertainty
Abstract
1. Introduction
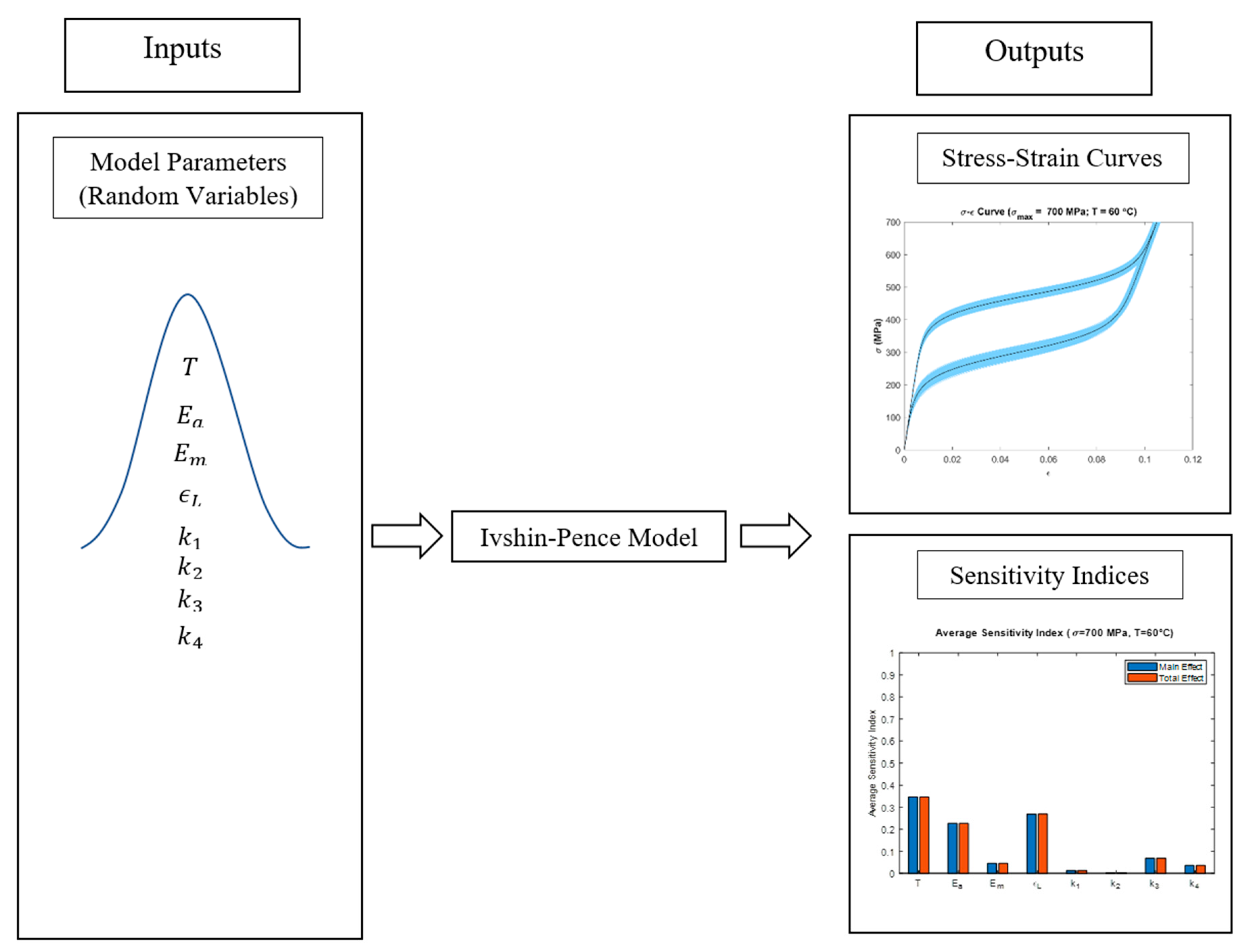
2. Ivshin–Pence SMA Model
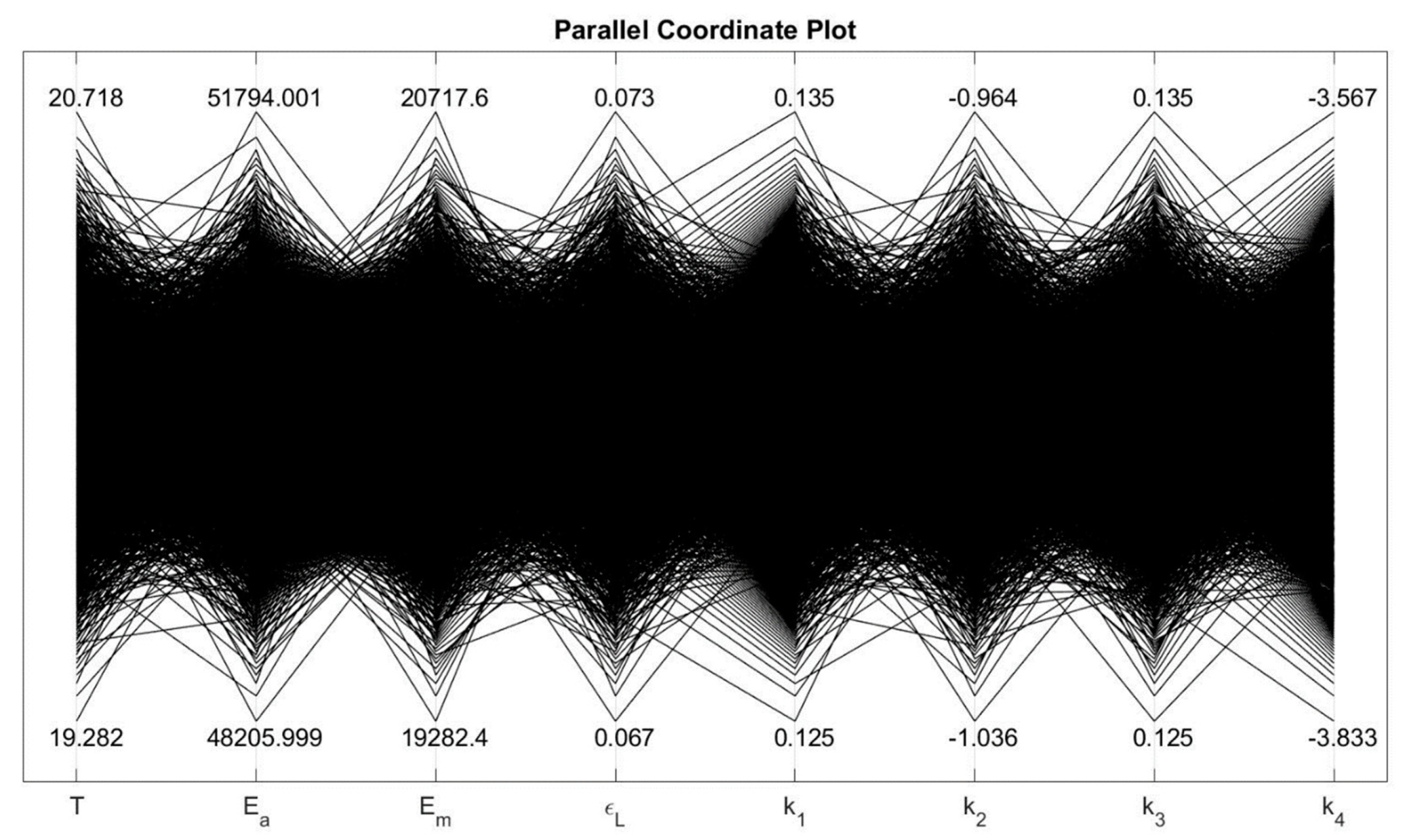
3. Methods
4. Results
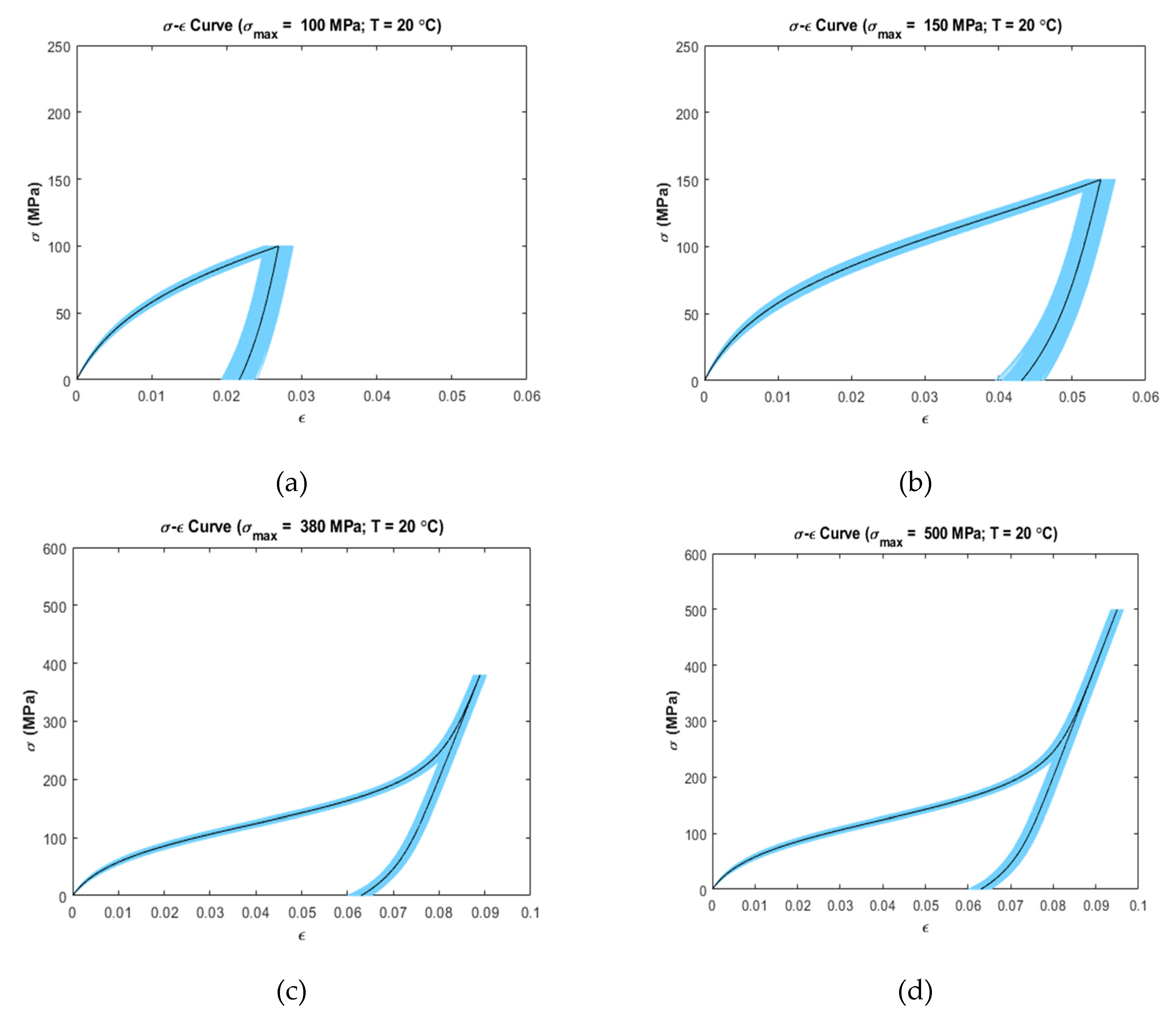
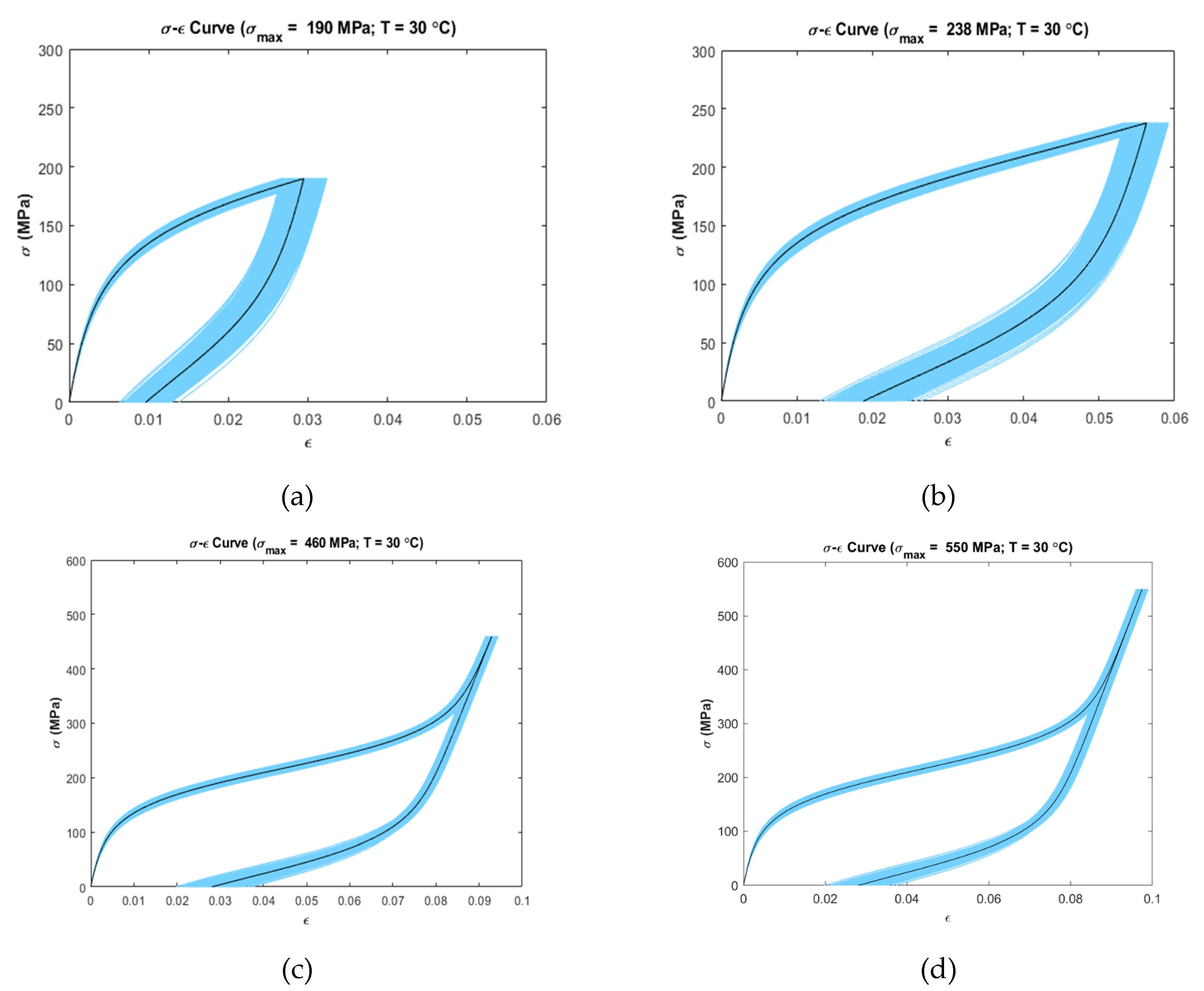
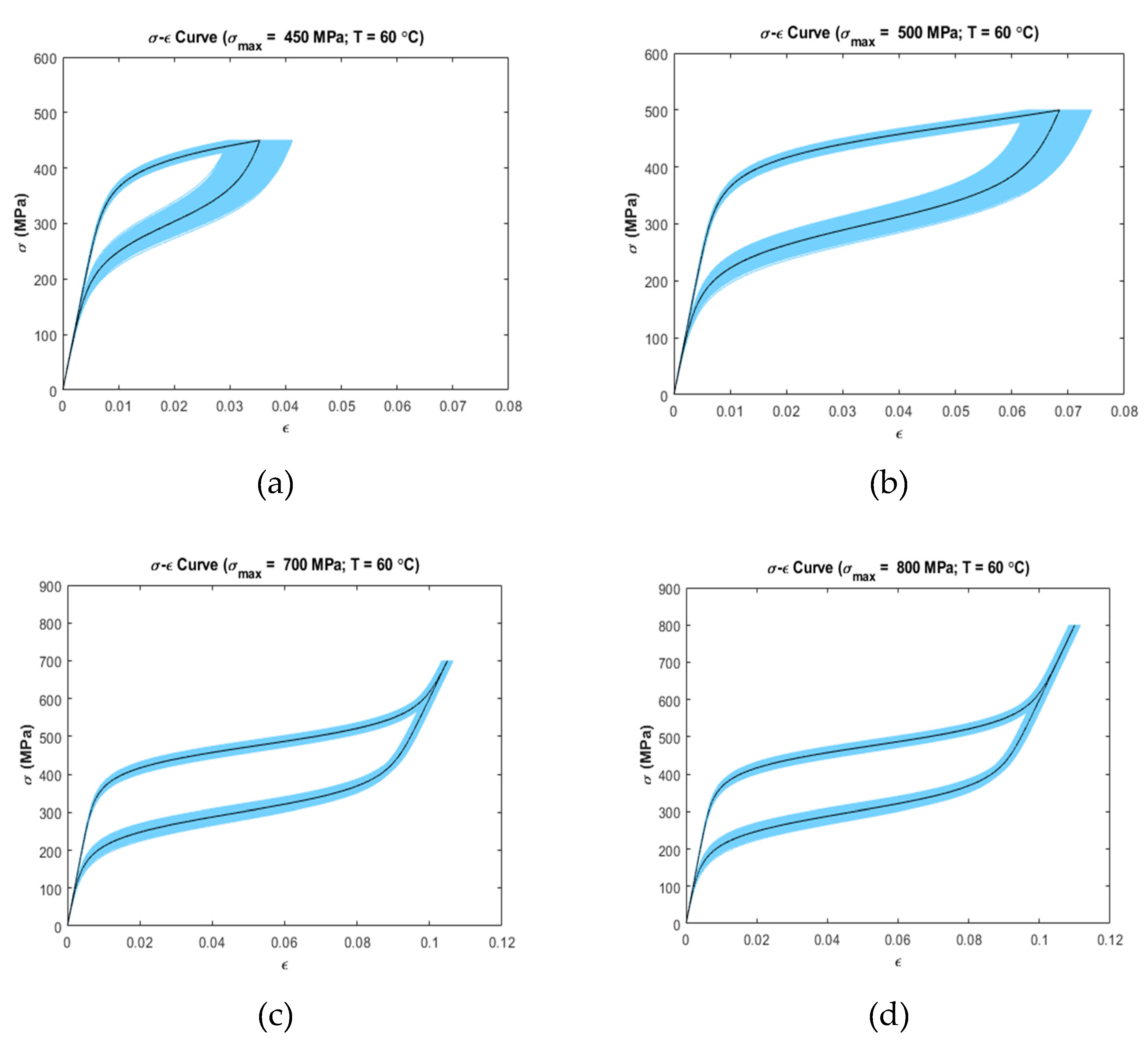
4.1. Uncertainty Analysis
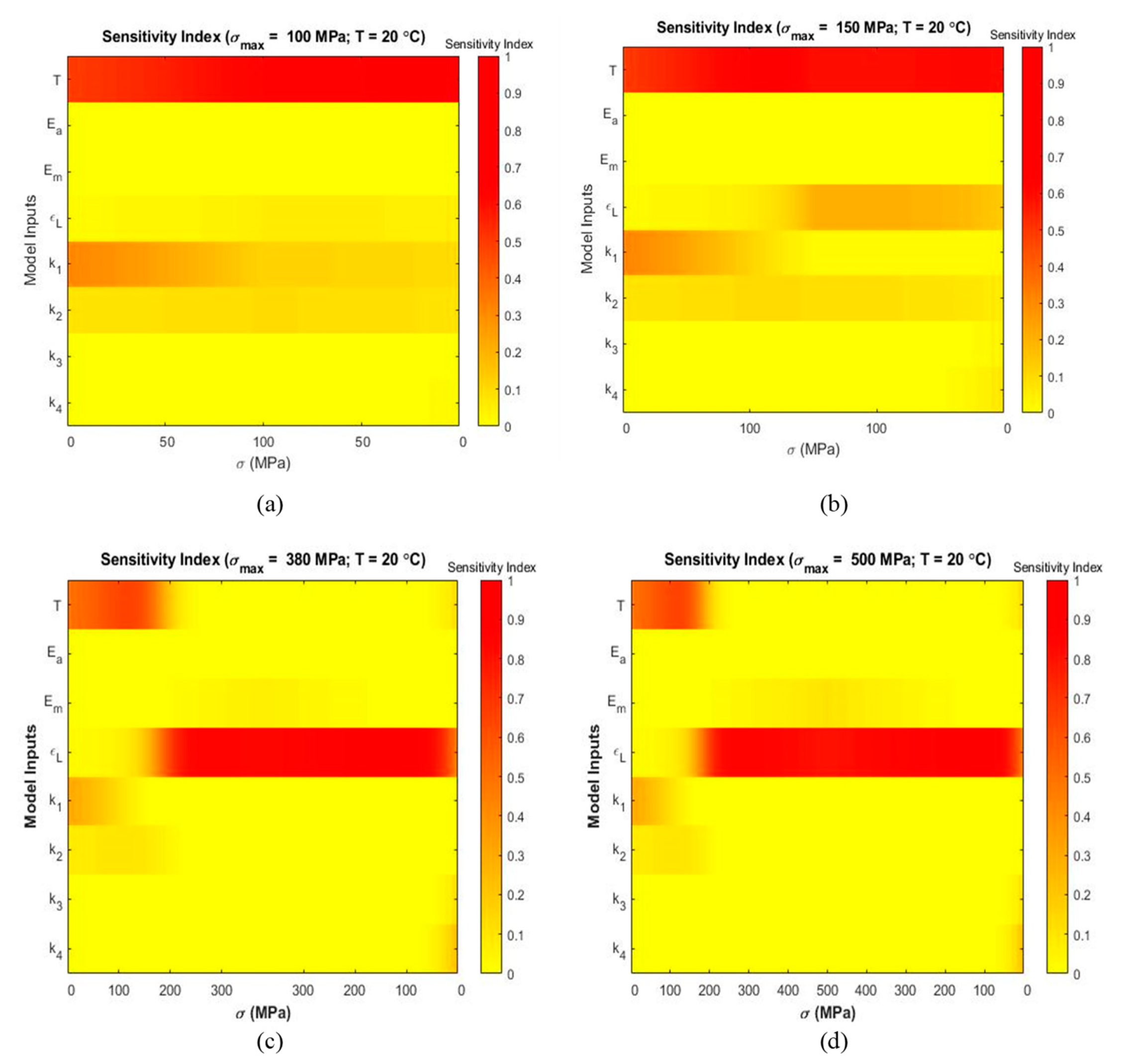
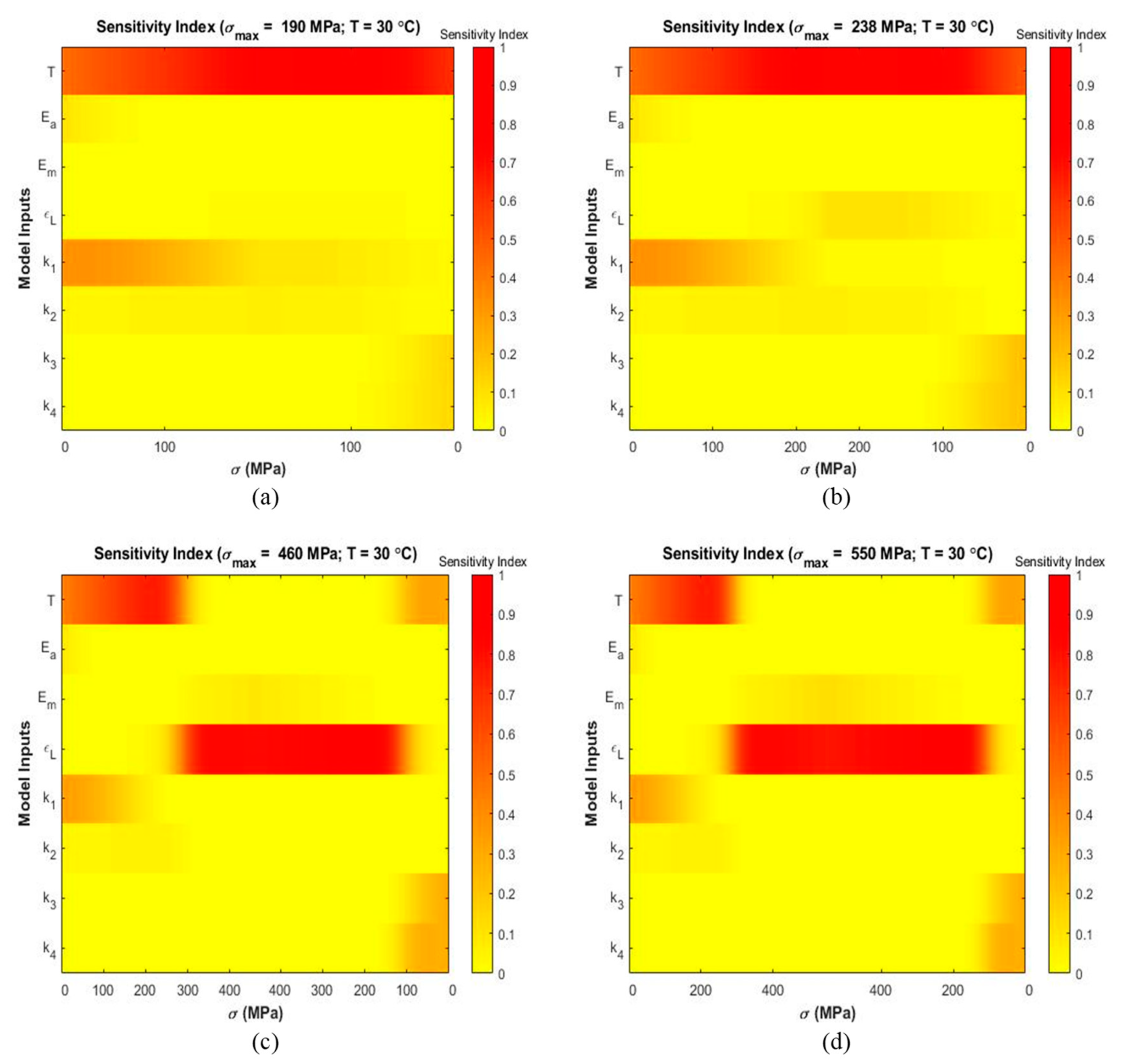
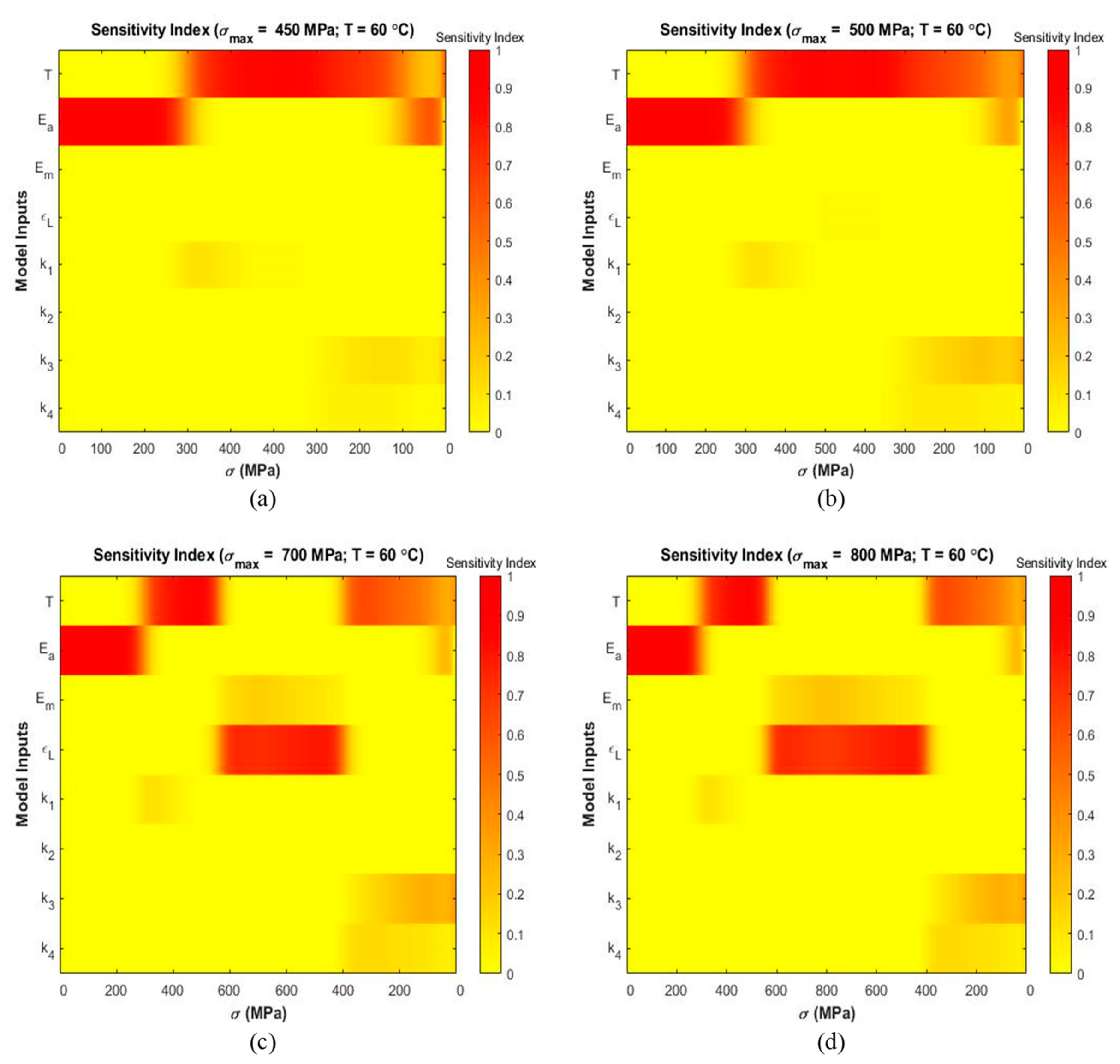
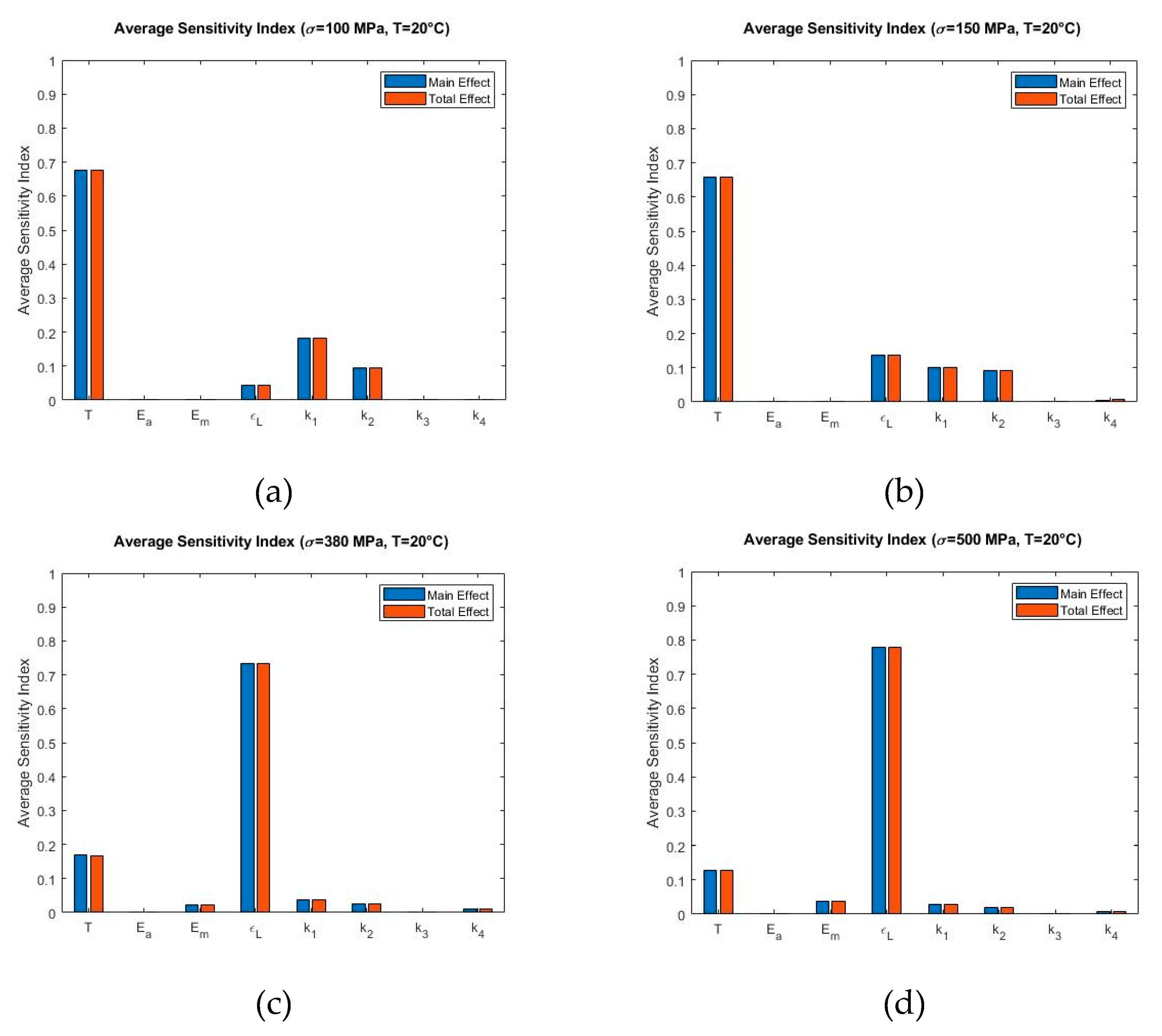
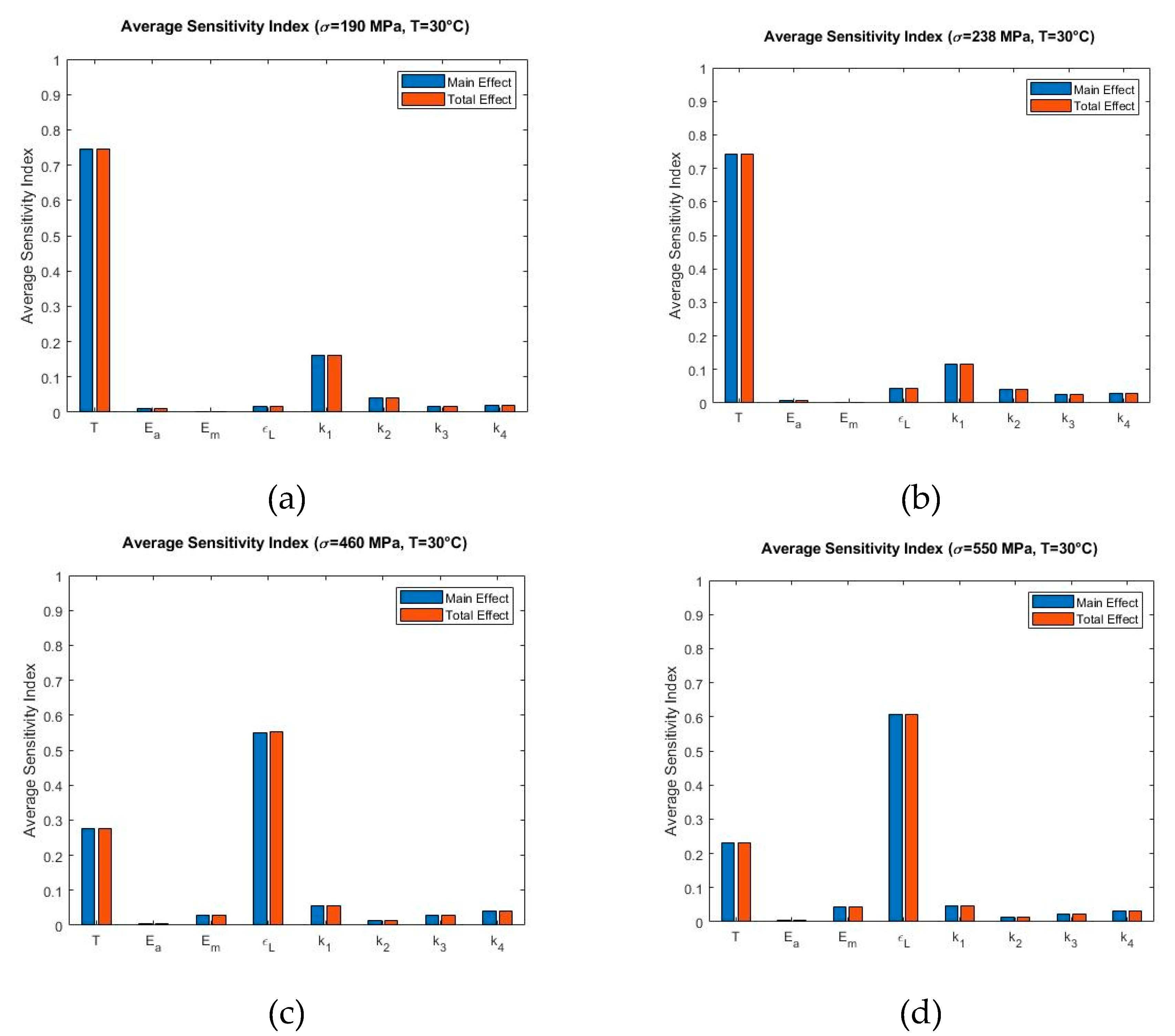
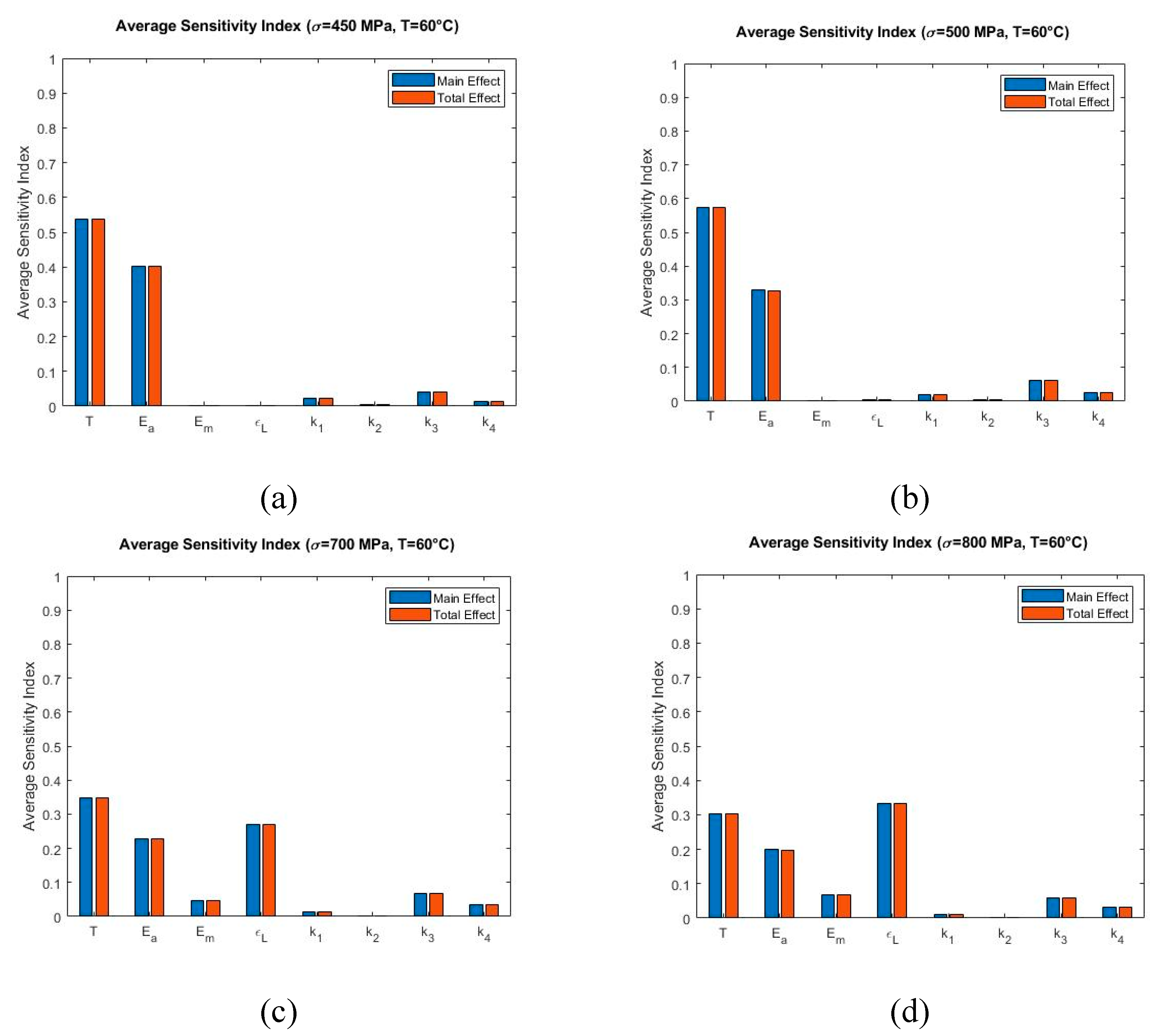
4.2. Sensitivity Analysis
5. Discussion
5.1. Uncertainty Analysis
5.2. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simaan, N.; Taylor, R.; Flint, P. A dexterous system for laryngeal surgery (multi-backbone bending snake-like slaves for teleoperated dexterous surgical tool manipulation). In Proceedings of the 2004 IEEE International Conference on Robotics & Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 351–357. [Google Scholar]
- Sreekumar, M.; Singaperumal, M.; Nagarajan, T.; Zoppi, M.; Molfino, R. Recent advances in nonlinear control technologies for shape memory alloy actuators. J. Zhejiang Univ. Sci. 2007, 8, 818–829. [Google Scholar]
- Mineta, T.; Mitsui, T.; Watanabe, Y.; Kobayashi, S.; Haga, Y.; Esashi, M. Batch fabricated flat mandering shape memory alloy actuator for active catheter. J. Sens. Actuators A 2001, 88, 112–120. [Google Scholar] [CrossRef]
- Carrozza, M.C.; Arena, A.; Accoto, D.; Menciassi, A.; Dario, P. A SMA-actuated miniature pressure regulator for a miniature robot for colonoscopy. J. Sens. Actuators A 2003, 105, 119–131. [Google Scholar] [CrossRef]
- Peirs, J.; Reynaerts, D.; Van Brussel, H. A miniature manipulator for integration in a selfpropelling endoscope. J. Sens. Actuators A 2001, 92, 343–349. [Google Scholar] [CrossRef]
- Morra, F.; Molfino, R.; Cedolina, F. Miniature gripping device. In Proceedings of the IEEE International Conference on Intelligent Manipulation and Grasping IMG 04, Genova, Italy, 1–2 July 2004. [Google Scholar]
- Büttgenbach, S.; Bütefisch, S.; Leester-Schädel, M.; Wogersien, A. Shape memory microactuators. J. Microsyst. Technol. 2001, 7, 165–170. [Google Scholar] [CrossRef]
- Kohl, M.; Krevet, B.; Just, E. SMA microgripper system. J. Sens. Actuators A 2002, 97, 646–652. [Google Scholar] [CrossRef]
- Kohl, M.; Just, E.; Pfleging, W.; Miyazaki, S. SMA micro gripper with integrated antagonism. J. Sens. Actuators 2000, 83, 208–213. [Google Scholar] [CrossRef]
- Reynaerts, D.; Peirs, J.; Van Brussel, H. An implantable drug delivery system based on shape memory alloy micro-actuation. J. Sens. Actuators A 1997, 61, 455–462. [Google Scholar] [CrossRef]
- Haga, Y.; Mizushima, M.; Matsunaga, T.; Esashi, M. Medical and welfare applications of shape memory alloy microcoil actuators. Smart Mater. Struct. 2005, 14, S266–S272. [Google Scholar] [CrossRef]
- Andreasen, G.F. Method and System for Orthodontic Moving of Teeth. U.S. Patent 4037324, 26 July 1977. [Google Scholar]
- Andreasen, G.F.; Hilleman, T.B. An evaluation of 55 cobalt substituted Nitinol wire for use in orthodontics. J. Am. Dent. Assoc. 1971, 82, 1373–1375. [Google Scholar] [CrossRef]
- Torrisi, L. The NiTi superelastic alloy application to the dentistry field. Bio-Med. Mater. Eng. 1999, 9, 39–47. [Google Scholar]
- Idelsohn, S.; Pena, J.; Lacroix, D.; Planell, J.A.; Gil, F.J.; Arcas, A. Continuous mandibular distraction osteogenesis using superelastic shape memory alloy (SMA). J. Mater. Sci. 2004, 15, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Torrisi, L.; Di Marco, G. Physical characterization of endodontic instruments in NiTi alloy. Mater. Sci. Forum 2000, 327, 75–78. [Google Scholar] [CrossRef]
- Parashos, P.; Messer, H.H. The diffusion of innovation in dentistry: A review using rotary nickel-titanium technology as an example. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endodontol. 2006, 101, 395–401. [Google Scholar] [CrossRef]
- Sattapan, B.; Palamara, J.E.; Messer, H.H. Torque during canal instrumentation using rotary nickel-titanium files. J. Endod. 2000, 26, 156–160. [Google Scholar] [CrossRef]
- Dai, K.R.; Hou, X.K.; Sun, Y.H.; Tang, R.G.; Qiu, S.J.; Ni, C. Treatment of intra-articular fractures with shape memory compression staples. Injury 1993, 24, 651–655. [Google Scholar] [CrossRef]
- Laster, Z.; MacBean, A.D.; Ayliffe, P.R.; Newlands, L.C. Fixation of a frontozygomatic fracture with a shape-memory staple. Br. J. Oral Maxillofac. Surg. 2001, 39, 324–325. [Google Scholar] [CrossRef]
- Schmerling, M.A.; Wilkor, M.A.; Sanders, A.E.; Woosley, J.E. A proposed medical application of the shape memory effect: An Ni-Ti Harrington rod for treatment of scoliosis. J. Biomed. Mater. Res. 1976, 10, 879–902. [Google Scholar] [CrossRef]
- Sanders, J.O.; Sanders, A.E.; More, R.; Ashman, R.B. A preliminary investigation of shape memory alloys in the surgical correction of scoliosis. Spine 1993, 18, 1640–1646. [Google Scholar] [CrossRef]
- Wever, D.; Elstrodt, J.; Veldhuizen, A.; Horn, J. Scoliosis correction with shape-memory metal: Results of an experimental study. Eur. Spine J. 2002, 11, 100–106. [Google Scholar] [CrossRef]
- Lipscomb, I.P.; Nokes, L.D.M. The Application of Shape Memory Alloys in Medicine; Paston Press Ltd.: Norfolk, VA, USA, 1996. [Google Scholar]
- Simon, M.; Kaplan, R.; Salzman, E.; Freiman, D. A vena cava filter using thermal shape memory alloy: Experimental aspects. Radiology 1977, 125, 89–94. [Google Scholar] [CrossRef]
- Engmann, E.; Asch, M.R. Clinical experience with the antecubital Simon nitinol IVC filter. J. Vasc. Interv. Radiol. 1998, 9, 774–778. [Google Scholar] [CrossRef]
- Poletti, P.A.; Becker, C.D.; Prina, L.; Ruijs, P.; Bounameaux, H.; Didier, D.; Terrier, F. Long-term results of the Simon nitinol inferior vena cava filter. Eur. Radiol. 1998, 8, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Stöckel, D. The Shape Memory Effect: Phenomenon, Alloys, Applications; Shape Memory Alloys for Power Systems (EPRI): Fremont, CA, USA, 1995; pp. 1–13. [Google Scholar]
- Dynalloy. Dynalloy Newsletters. 2006. Available online: https://www.dynalloy.com/newsletters.php (accessed on 6 January 2020).
- General, G.; Lightweight, C.D. ‘Smart Material’ on Corvette; General Motors News: Detroit, MI, USA, 2013. [Google Scholar]
- Jani, J.M.; Leary, M.; Subic, A. Shape Memory Alloys in Automotive Applications. Appl. Mech. Mater. 2014, 663, 248–253. [Google Scholar] [CrossRef]
- Butera, F.; Alessandretti, G. CRF Società Consortile per Azioni. EP Patent 0,972,676, 19 January 2000. [Google Scholar]
- Luchetti, T.; Zanella, A.; Biasiotto, M.; Saccagno, A. Electrically actuated antiglare rear-view mirror based on a shape memory alloy actuator. J. Mater. Eng. Perform. 2009, 18, 717–724. [Google Scholar] [CrossRef]
- Alacqua, S.; Butera, F.; Zanella, A.; Capretti, G. CRF Societa Consortile per Azioni. U.S. Patent 7625019B2, 1 December 2009. [Google Scholar]
- Kudva, J. Overview of the DARPA smart wing project. J. Intell. Mater. Syst. Struct. 2004, 15, 261–267. [Google Scholar] [CrossRef]
- Kudva, J.; Appa, K.; Martin, C.; Jardine, A. Design, fabrication, and testing of the DARPA/Wright lab ‘smart wing’ wind tunnel model. In Proceedings of the 38th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Kissimmee, FL, USA, 7–10 April 1997; pp. 1–6. [Google Scholar]
- Jardine, P.; Kudva, J.; Martin, C.; Appa, K. Shape memory alloy NiTi actuators for twist control of smart designs. In Proceedings of the SPIE, Smart Materials and Structures, San Diego, CA, USA, 1 May 1996; Volume 2717, pp. 160–165. [Google Scholar]
- Jardine, P.; Flanigan, J.; Martin, C. Smart wing shape memory alloy actuator design and performance. In Proceedings of the SPIE, Smart Structures and Materials, San Diego, CA, USA, 23 May 1997; Volume 3044, pp. 48–55. [Google Scholar]
- Mabe, J.; Cabell, R.; Butler, G. Design and control of a morphing chevron for takeoff and cruise noise reduction. In Proceedings of the 26th Annual AIAA Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; Volume 27, pp. 1–15. [Google Scholar]
- Mabe, J.H.; Calkins, F.; Butler, G. Boeing’s variable geometry chevron, morphing aerostructure for jet noise reduction. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Newport, RI, USA, 1–4 May 2006; Volume 28, pp. 1–19. [Google Scholar]
- Hartl, D.; Volk, B.; Lagoudas, D.C.; Calkins, F.T.; Mabe, J. Thermomechanical characterization and modeling of Ni60Ti40 SMA for acutated chevrons. In Proceedings of the ASME, International Mechanical Engineering Congress and Exposition (IMECE), Chicago, IL, USA, 5–10 November 2006; Volume 29, pp. 1–10. [Google Scholar]
- Hartl, D.; Lagoudas, D.C. Characterization and 3D modeling of Ni60Ti SMA for actuation of a variable geometry jet engine chevron. In Proceedings of the SPIE, Smart Structures and Materials, San Diego, CA, USA, 18 April 2007; Volume 6529, pp. 1–12. [Google Scholar]
- Birman, V. Review of mechanics of shape memory alloy structures. Appl. Mech. Rev. 1997, 50, 629–645. [Google Scholar] [CrossRef]
- Prahlad, H.; Chopra, I. Design of a variable twist tiltrotor blade using shape memory alloy (SMA) actuators. In Proceedings of the SPIE, Smart Structures and Materials, Newport Beach, CA, USA, 1–5 March 2001; Volume 4327, pp. 46–59. [Google Scholar]
- Wu, M.H.; Schetky, L.M. Industrial applications for shape memory alloys. In Proceedings of the International Conference on Shape Memory and Superelastic Technologies, Pacific Grove, CA, USA, 30 April–4 May 2000; pp. 171–182. [Google Scholar]
- Wu, M.H.; Ewing, W.A. Pilot-operated anti-scald safety valve: Design and actuator considerations. In Proceedings of the SMST-94, Pacific Grove, CA, USA, 7–10 March 1994; p. 311. [Google Scholar]
- Kheirikhah, M.; Rabiee, S.; Edalat, M. A review of shape memory alloy actuators in robotics. In Robo Cup Robot Soccer World Cup XIV; Ruiz-del-Solar, J., Chown, E., Plöger, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 206–217. [Google Scholar]
- Sreekumar, M.; Nagarajan, T.; Singaperumal, M.; Zoppi, M.; Molfino, R. Critical review of current trends in shape memory alloy actuators for intelligent robots. Ind. Robot Int. J. 2007, 34, 285–294. [Google Scholar] [CrossRef]
- Furuya, Y.; Shimada, H. Shape memory actuators for robotic applications. Mater. Des. 1991, 12, 21–28. [Google Scholar] [CrossRef]
- Huang, X.; Kumar, K.; Jawed, M.K.; Mohammadi Nasab, A.; Ye, Z.; Shan, W.; Majidi, C. Highly Dynamic Shape Memory Alloy Actuator for Fast Moving Soft Robots. Adv. Mater. Technol. 2019, 4, 1800540. [Google Scholar] [CrossRef]
- Mohammad, A.A.K.-L.; Anthony, D.D.; Zhang, J.; Alan, S.W.; John, A.S. Robotic jellyfish actuated with a shape memory alloy spring. In Proceedings of the SPIE 10965, Bioinspiration, Biomimetics, and Bioreplication IX, 1096504, Denver, CO, USA, 13 March 2019. [Google Scholar] [CrossRef]
- Tanaka, K.; Nagaki, S. A Thermomechanical Description of Materials with Internal Variables in the Process of Phase Transitions. Ing. Arch. 1982, 51, 287–299. [Google Scholar] [CrossRef]
- Tanaka, K.; Iwasaki, R. A Phenomenological Theory of Transformation Superplasticity. Eng. Fract. Mech. 1985, 21, 709–720. [Google Scholar] [CrossRef]
- Tanaka, K.; Kobayashi, S.; Sato, Y. Thermomechanics of Transformation Pseudoelasticity and Shape Memory Effect in Alloys. Int. J. Plast. 1986, 2, 59–72. [Google Scholar] [CrossRef]
- Sato, Y.; Tanaka, K. Estimation of Energy Dissipation in Alloys due to Stress-Induced Martensitic Transformation. Res. Mech. 1988, 23, 381–393. [Google Scholar]
- Liang, C.; Rogers, C.A. One-Dimensional Thermomechanical Constitutive Relations for Shape Memory Materials. J. Intell. Mater. Syst. Struct. 1990, 1, 207–234. [Google Scholar] [CrossRef]
- Brinson, L.C. One Dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-Constant Material Functions. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Ivshin, Y.; Pence, T.J. A thermomechanical model for a one variant shape memory material. J. Intell. Mater. Syst. Struct. 1994, 5, 455–473. [Google Scholar] [CrossRef]
- Pence, T.J.; Grummon, D.S.; Ivshin, Y. A macroscopic model for thermoelastic hysteresis in shape-memory materials. Mech. Phase Transform. Shape Mem. Alloy. 1994, 189, 45–58. [Google Scholar]
- Brinson, L.C.; Lammering, R. Finite Element Analysis of the Behavior of Shape Memory Alloys and their Application. Int. J. Solids Struct. 1993, 30, 3261–3280. [Google Scholar] [CrossRef]
- Boyd, J.G.; Lagoudas, D.C. Thermomechanical Response of Shape Memory Composites. J. Intell. Matl. Syst. Struct. 1994, 5, 333–346. [Google Scholar] [CrossRef]
- Patoor, E.; Eberhardt, A.; Berveiller, M. Thermomechanical Behavior of Shape Memory Alloys. Arch. Mech. 1988, 40, 775–794. [Google Scholar]
- Patoor, E.; Eberhardt, A.; Berveiller, M. Micromechanical modelling of the shape memory alloys. Pitman Res. Notes Math. Ser. 1993, 296, 38–54. [Google Scholar]
- Karadoğan, E. Probabilistic evaluation of the one-dimensional Brinson model’s sensitivity to uncertainty in input parameters. J. Intell. Mater. Syst. Struct. 2019, 30, 1070–1083. [Google Scholar] [CrossRef]
- Islam, A.B.M.R.; Karadoğan, E. Sensitivity and Uncertainty Analysis of One-Dimensional Tanaka and Liang-Rogers Shape Memory Alloy Constitutive Models. Materials 2019, 12, 1687. [Google Scholar] [CrossRef]
- Macki, J.W.; Nistri, P.; Zecca, P. Mathematical models for hysteresis. SIAM Rev. 1993, 35, 94–123. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Analysis for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 1407–1414. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Cukier, R.I.; Schaibly, J.H.; Shuler, K.E. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. III. Analysis of the approximations. J. Chem. Phys. 1978, 63, 1140–1149. [Google Scholar] [CrossRef]
- Xu, C.; Gertner, G. Understanding and comparisons of different sampling approaches for the Fourier amplitudes sensitivity test (FAST). Comput. Stat. Data Anal. 2011, 55, 184–198. [Google Scholar] [CrossRef] [PubMed]
- Jana, F.; Olivier, R.; Sonja, K. Total Interaction Index: A Variance-Based Sensitivity Index for Second-Order Interaction Screening. 2013. Available online: hal-00631066v5 (accessed on 6 January 2020).
| Parameter | Description | Deterministic Value | Unit |
|---|---|---|---|
| Temperature | 20, 30, 60 | °C | |
| Elastic modulus of Austenite | 50,000 | MPa | |
| Elastic modulus of Martensite | 20,000 | MPa | |
| Maximum residual strain | 0.07 | N/A | |
| Martensite Start Temperature | 22.00 | °C | |
| Martensite Finish Temperature | −7.00 | °C | |
| Austenite Start Temperature | 13.00 | °C | |
| Austenite Finish Temperature | 42.00 | °C | |
| Adjustable Fitting Parameter #1 | 0.13 | /°C | |
| Adjustable Fitting Parameter #2 | −1.00 | N/A | |
| Adjustable Fitting Parameter #3 | 0.13 | /°C | |
| Adjustable Fitting Parameter #4 | −3.70 | N/A |
| Temperature (°C) | Martensite Volume Fraction, ξ | Region | |
|---|---|---|---|
| 20 | 1/3 | 100 | |
| 2/3 | 150 | ||
| 1 | 380 | ||
| 1 | 500 | ||
| 30 | 1/3 | 190 | |
| 2/3 | 238 | ||
| 1 | 460 | ||
| 1 | 550 | ||
| 60 | 1/3 | 450 | |
| 2/3 | 500 | ||
| 1 | 700 | ||
| 1 | 800 |
| Parameter | Distribution | Mean Value | Standard Deviation | Unit |
|---|---|---|---|---|
| Normal | 20, 30, 60 | 0.20, 0.30, 0.60 | °C | |
| Normal | 50,000 | 500 | MPa | |
| Normal | 20,000 | 200 | MPa | |
| Normal | 0.07 | 0.0007 | N/A | |
| Normal | 0.13 | 0.0013 | /°C | |
| Normal | −1.00 | 0.01 | N/A | |
| Normal | 0.13 | 0.0013 | /°C | |
| Normal | −3.70 | 0.037 | N/A |
| Operating Temperature T(°C) | Maximum Variability |
|---|---|
| 20 | 15–18% |
| 30 | 38–48% |
| 60 | 53–168% |
| Temperature, T(°C) | Most Significant Model Parameter | SMA Behavior |
|---|---|---|
| 20 () | , , | Shape Memory Effect |
| 30 () | , , | |
| 60 ( | , , | Pseudoelastic Effect |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, A.B.M.R.; Karadoğan, E. Analysis of One-Dimensional Ivshin–Pence Shape Memory Alloy Constitutive Model for Sensitivity and Uncertainty. Materials 2020, 13, 1482. https://doi.org/10.3390/ma13061482
Islam ABMR, Karadoğan E. Analysis of One-Dimensional Ivshin–Pence Shape Memory Alloy Constitutive Model for Sensitivity and Uncertainty. Materials. 2020; 13(6):1482. https://doi.org/10.3390/ma13061482
Chicago/Turabian StyleIslam, A B M Rezaul, and Ernur Karadoğan. 2020. "Analysis of One-Dimensional Ivshin–Pence Shape Memory Alloy Constitutive Model for Sensitivity and Uncertainty" Materials 13, no. 6: 1482. https://doi.org/10.3390/ma13061482
APA StyleIslam, A. B. M. R., & Karadoğan, E. (2020). Analysis of One-Dimensional Ivshin–Pence Shape Memory Alloy Constitutive Model for Sensitivity and Uncertainty. Materials, 13(6), 1482. https://doi.org/10.3390/ma13061482





