Resistance Characteristics of SMA Actuator Based on the Variable Speed Phase Transformation Constitutive Model
Abstract
1. Introduction
2. Variable Speed Phase Transformation Constitutive Model
2.1. Phase Transformation Equation
2.2. Constitutive Equation
3. Resistance Characteristic Model
4. Parameter Identification
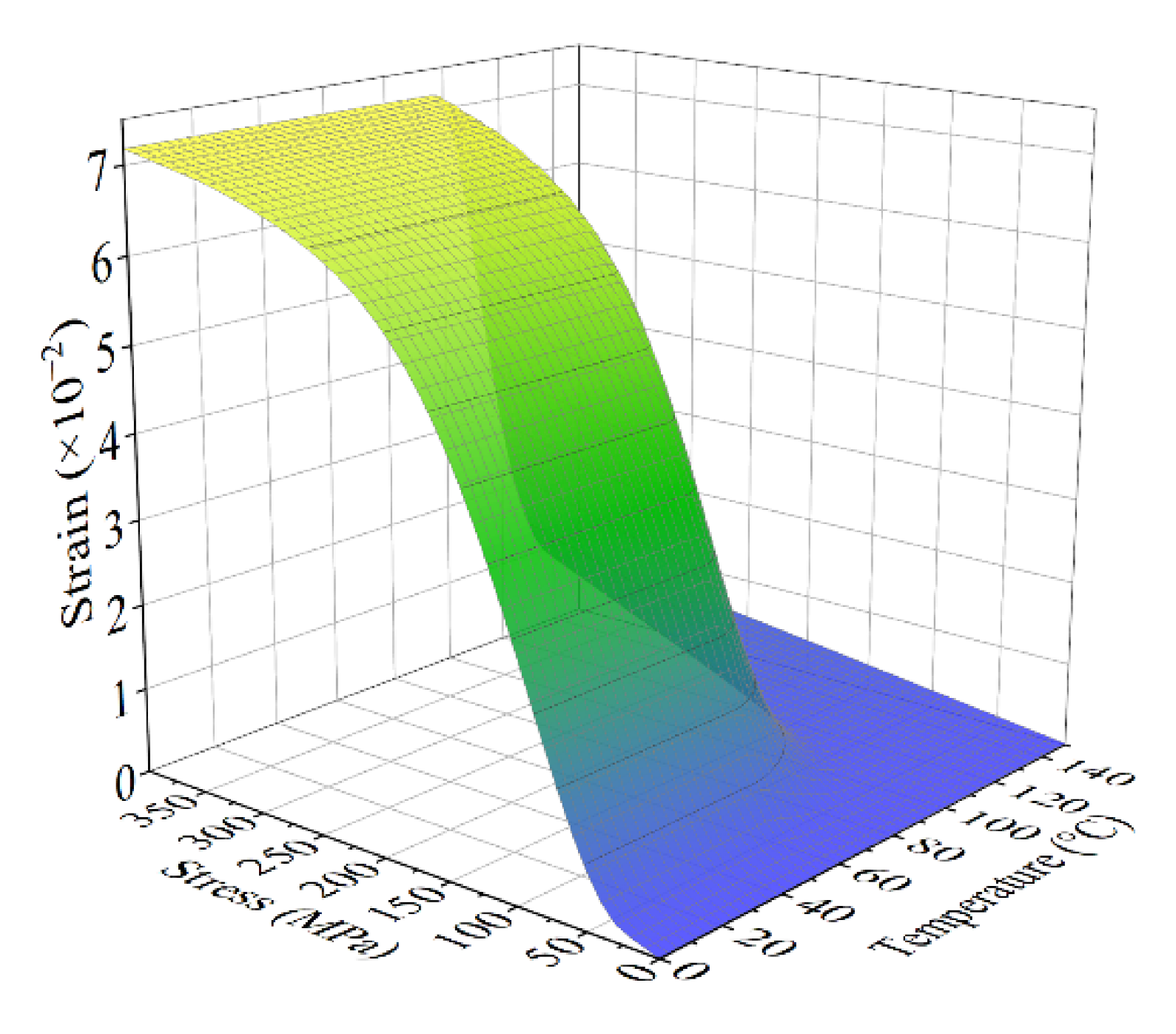
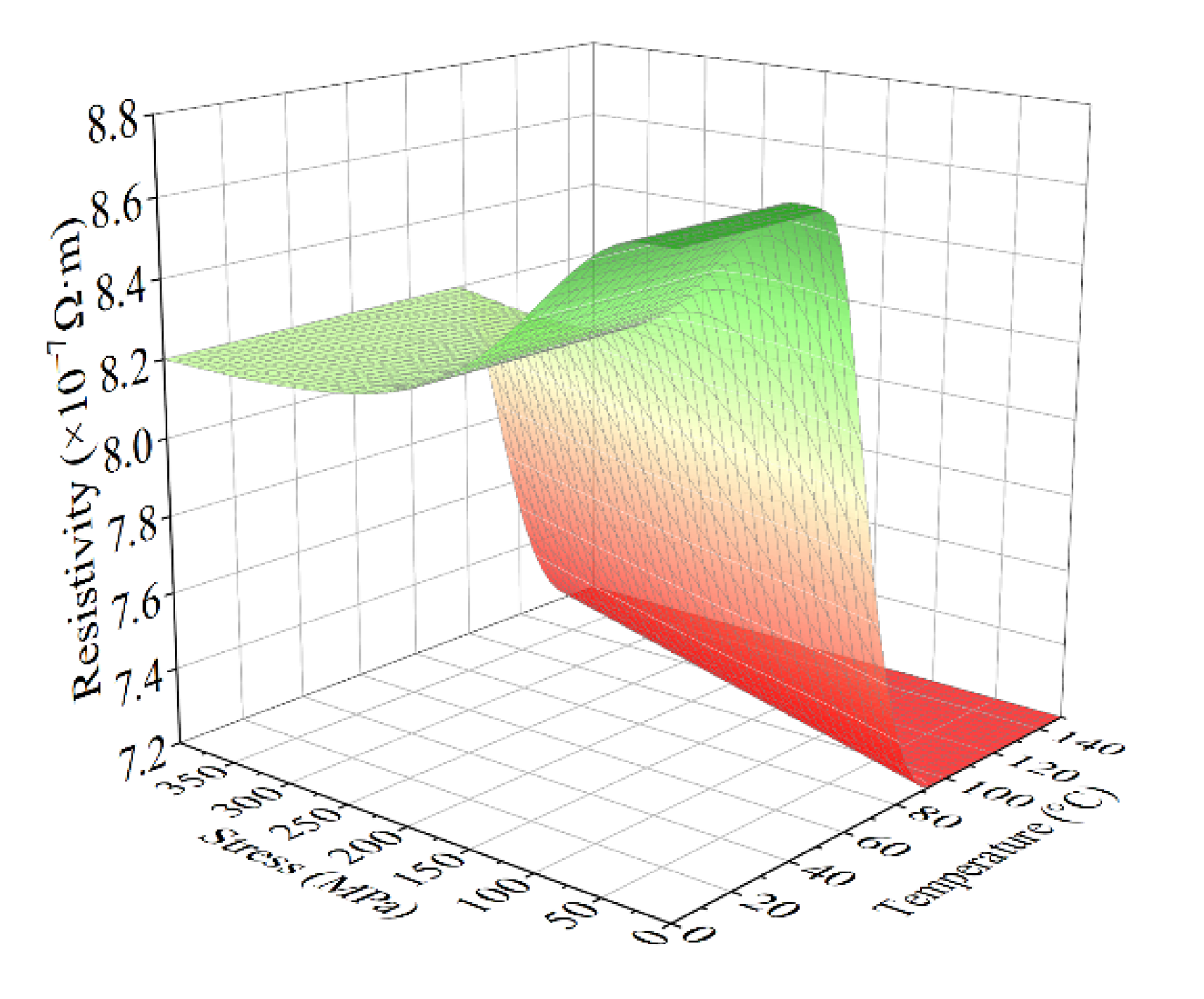
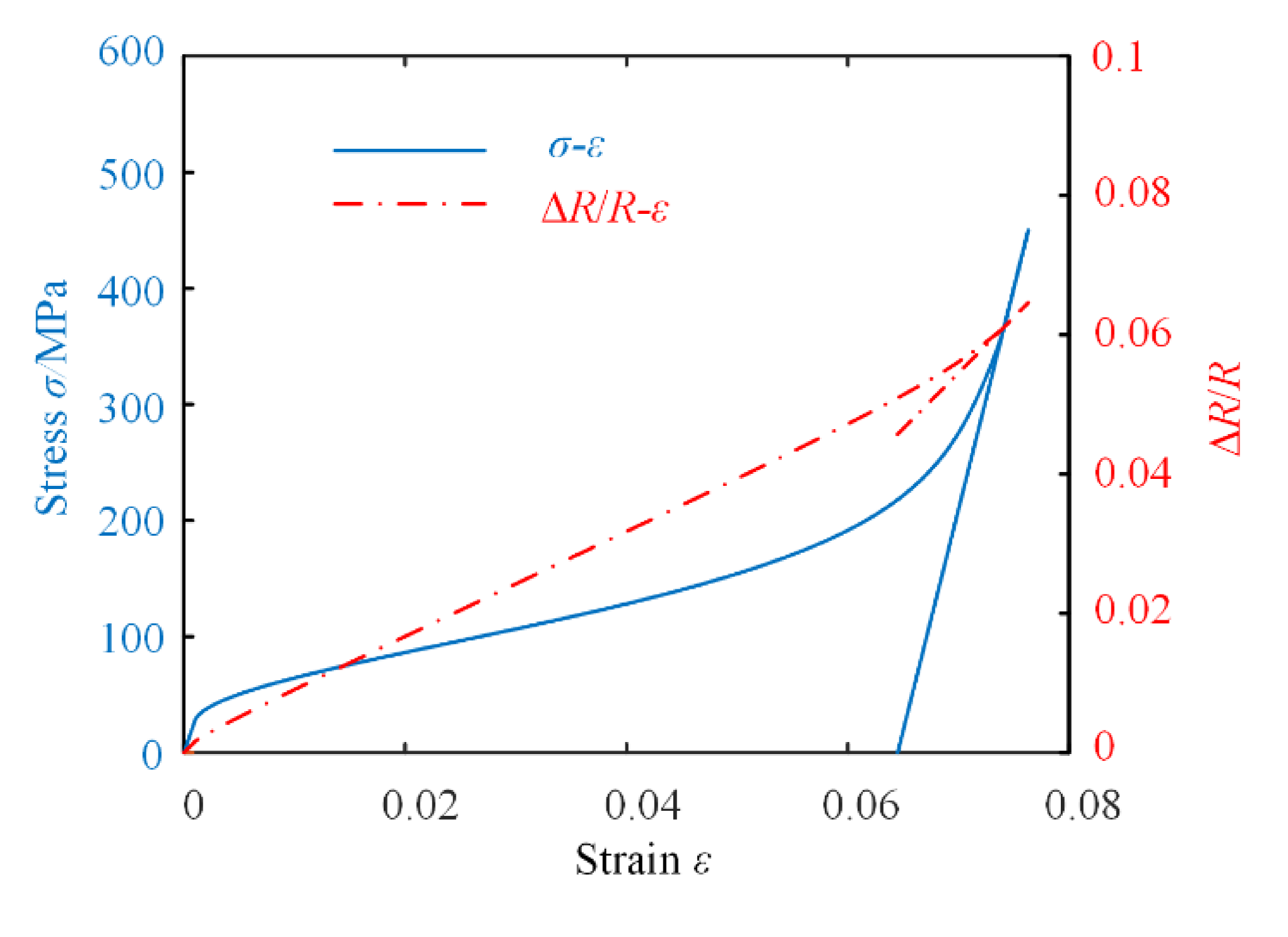
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| T | Temperature | k | Crystal variable speed coefficient |
| Ms | Martensite start temperature | K | Crystal variable speed function |
| Mf | Martensite finish temperature | A | Austenite |
| As | Austenite start temperature | DM | Detwinned martensite |
| Af | Austenite finish temperature | TM | Twinned martensite |
| Mp | Martensite peak temperature | Ψ | Transformation modulus |
| Ap | Austenite peak temperature | EA | Elastic modulus of austenite |
| σ | Stress | ETM | Elastic modulus of TM |
| σs | Starting stress | EDM | Elastic modulus of DM |
| σf | Finishing stress | ξA | Volume fraction of austenite |
| σp | Peaking stress | ξDM | Volume fraction of DM |
| ε | Strain | εL | Maximum residual strain |
| αM | Thermal expansion coefficient of martensite | αA | Thermal expansion coefficient of austenite |
| ν | Poisson’s ratio | a | Temperature coefficient of R |
| S | Cross-sectional area. | l | Length |
| ρ | Resistivity | ρTM | Resistivity of TM |
| ΡDM | Resistivity DM | ρA | Resistivity DM |
References
- Hartl, D.J.; Lagoudas, D.C. Aerospace applications of shape memory alloys. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2007, 221, 535–552. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Sellitto, A.; Riccio, A. Overview and Future Advanced Engineering Applications for Morphing Surfaces by Shape Memory Alloy Materials. Materials 2019, 12, 708. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Xie, Z.; Wang, J.; Yue, H.; Wu, M.; Liu, Y. A novel design of a parallel gripper actuated by a large-stroke shape memory alloy actuator. Int. J. Mech. Sci. 2019, 159, 74–80. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, Y.; Lu, Y.; Yang, F.; Yue, H. A reusable SMA actuated non-explosive lock-release mechanism for space application. Int. J. Smart Nano Mater. 2020, 1–13. [Google Scholar] [CrossRef]
- Wang, M.; Yu, H.; Shi, P.; Meng, Q. Design Method for Constant Force Components Based on Superelastic SMA. Materials 2019, 12, 2842. [Google Scholar] [CrossRef]
- Dhanalakshmi, K. Differential resistance feedback control of a self-sensing shape memory alloy actuated system. ISA Trans. 2014, 53, 289–297. [Google Scholar] [CrossRef]
- Furst, S.J.; Seelecke, S. Modeling and experimental characterization of the stress, strain, and resistance of shape memory alloy actuator wires with controlled power input. J. Intell. Mater. Syst. Struct. 2012, 23, 1233–1247. [Google Scholar] [CrossRef]
- Furst, S.J.; Crews, J.H.; Seelecke, S. Stress, strain, and resistance behavior of two opposing shape memory alloy actuator wires for resistance-based self-sensing applications. J. Intell. Mater. Syst. Struct. 2013, 24, 1951–1968. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Hagiwara, I.; Yasuhiro, M. Research on sensing and control of shape memory alloy embedded in intelligent material. Chin. J. Mech. Eng. 2005, 41, 221–225. [Google Scholar] [CrossRef]
- Nahm, S.H.; Kim, Y.J.; Kim, J.M.; Yoon, D.J. A study on the application of Ni-Ti shape memory alloy as a sensor. Mater. Sci. Forum 2005, 475, 2043–2046. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, Y.; Wang, W.; Yu, Z. Electrical Resistance-Strain Model for Shape Memory Alloys. J. Shenyang Jianzhu Univ. Nat. Sci. 2008, 24, 980–984. [Google Scholar]
- Cui, D.; Li, H.; Song, G. Study on electrical resistance properties of shape memory alloy. J. Build. Mater. 2008, 11, 567–573. [Google Scholar]
- Cui, D.; Song, G.; Li, H. Modeling of the electrical resistance of shape memory alloy wires. Smart Mater. Struct. 2010, 19, 055019. [Google Scholar] [CrossRef]
- Xu, L.; Wang, R.; Zhang, S. Electrical resistance properties of Ni-Ti shape memory alloy fiber in phase transformation. J. Text. Res. 2010, 31, 15–19. [Google Scholar]
- Zhang, J.; Chen, B.; Geng, L.; Chen, S.; Wu, H. Design of control system for SMA actuator based on resistance feedback. Microprocessors 2011, 35, 91–93. [Google Scholar]
- Lynch, B.; Jiang, X.X.; Ellery, A.; Nitzsche, F. Characterization, modeling, and control of Ni-Ti shape memory alloy based on electrical resistance feedback. J. Intell. Mater. Syst. Struct. 2016, 27, 2489–2507. [Google Scholar] [CrossRef]
- Brinson, L.C.; Huang, M.S. Simplifications and comparisons of shape memory alloy constitutive models. J. Intell. Mater. Syst. Struct. 1996, 7, 108–114. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C.A. One-dimensional thermomechanical constitutive relations for shape memory materials. J. Intell. Mater. Syst. Struct. 1997, 8, 285–302. [Google Scholar] [CrossRef]
- Cisse, C.; Zaki, W.; Zineb, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Zhou, B.; Yoon, S.H.; Leng, J.S. A three-dimensional constitutive model for shape memory alloy. Smart Mater. Struct. 2009, 18, 095016. [Google Scholar] [CrossRef]
- Zhou, B.; Yoon, S.H. A new phase transformation constitutive model of shape memory alloys. Smart Mater. Struct. 2006, 15, 1967–1973. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, R.; Xie, Z.; Yue, H.; Wang, L. A new variable speed phase transformation constitutive model of shape memory alloys. Mater. Res. Express 2019, 6, 105705. [Google Scholar] [CrossRef]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar] [CrossRef]




| Mf (°C) | Ms (°C) | As (°C) | Af (°C) | σs (MPa) | σf (MPa) |
| 35.8 | 62.8 | 47.6 | 81.9 | 26.5 | 326.8 |
| EA (GPa) | ETM (GPa) | EDM (GPa) | CM (MPa/°C) | CA (MPa/°C) | εL |
| 54.64 | 17.96 | 31.52 | 10.4 | 8.0 | 0.0645 |
| αM (°C−1) | αA (°C−1) | l0 (mm) | k1 | k2 | k3 |
| 2.73 × 10−7 | 9.16 × 10−7 | 100 | 1.15 | 1.28 | 7.88 |
| ν | a (°C−1) | ρTM (Ω∙m) | ρDM (Ω∙m) | ρA (Ω∙m) |
|---|---|---|---|---|
| 0.3 | 8.75 × 10−4 | 0.87 × 10−6 | 0.82 × 10−6 | 0.72 × 10−6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Zhang, R.; Xu, Y.; Wang, L.; Yue, H. Resistance Characteristics of SMA Actuator Based on the Variable Speed Phase Transformation Constitutive Model. Materials 2020, 13, 1479. https://doi.org/10.3390/ma13061479
Lu Y, Zhang R, Xu Y, Wang L, Yue H. Resistance Characteristics of SMA Actuator Based on the Variable Speed Phase Transformation Constitutive Model. Materials. 2020; 13(6):1479. https://doi.org/10.3390/ma13061479
Chicago/Turabian StyleLu, Yifan, Rongru Zhang, Ye Xu, Lei Wang, and Honghao Yue. 2020. "Resistance Characteristics of SMA Actuator Based on the Variable Speed Phase Transformation Constitutive Model" Materials 13, no. 6: 1479. https://doi.org/10.3390/ma13061479
APA StyleLu, Y., Zhang, R., Xu, Y., Wang, L., & Yue, H. (2020). Resistance Characteristics of SMA Actuator Based on the Variable Speed Phase Transformation Constitutive Model. Materials, 13(6), 1479. https://doi.org/10.3390/ma13061479






