A Numerical Study of the Effect of Component Dimensions on the Critical Buckling Load of a GFRP Composite Strut under Uniaxial Compression
Abstract
1. Introduction
2. Finite Element (FE) Model
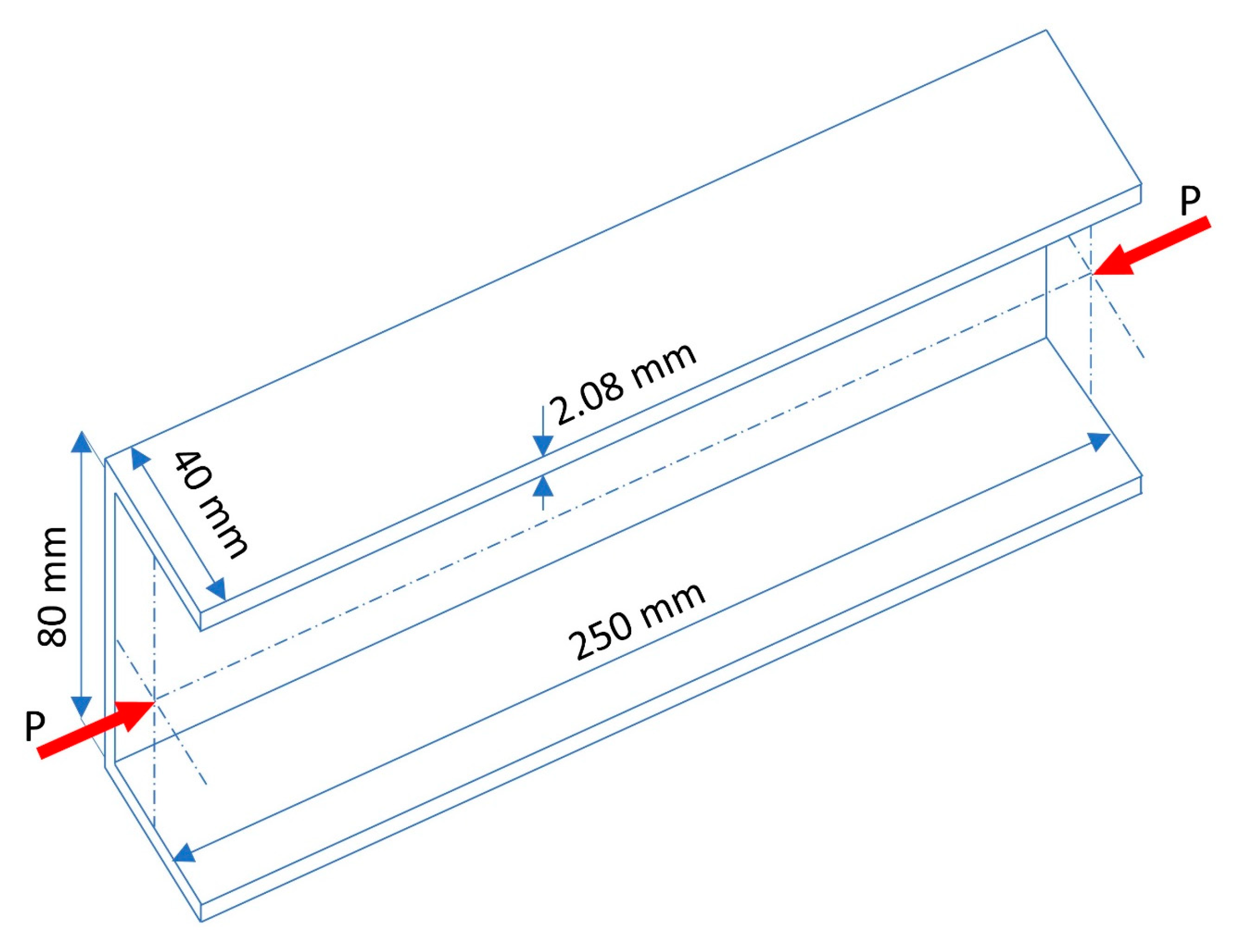
2.1. Studied Object and Scope
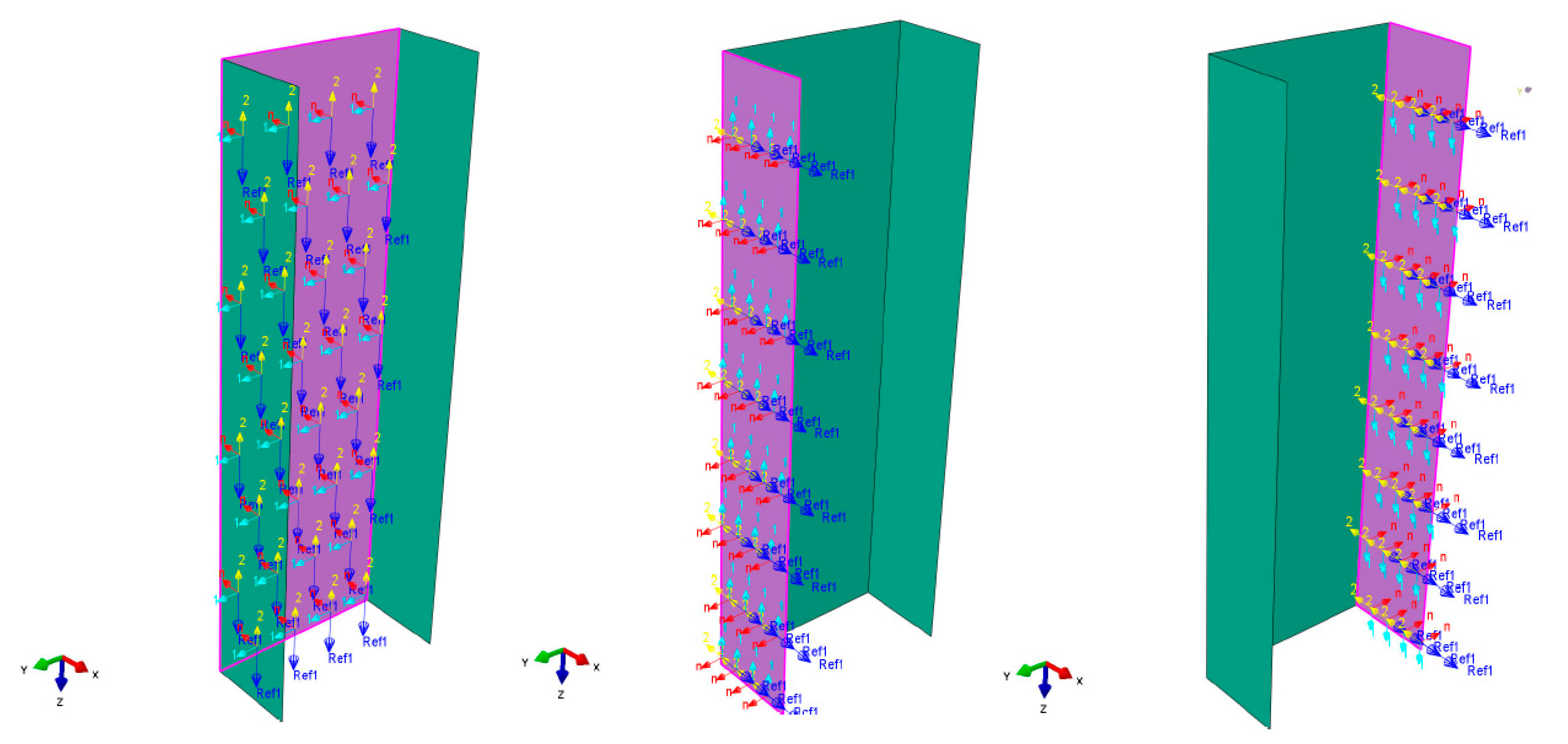
2.2. Discrete Models of Composite Struts
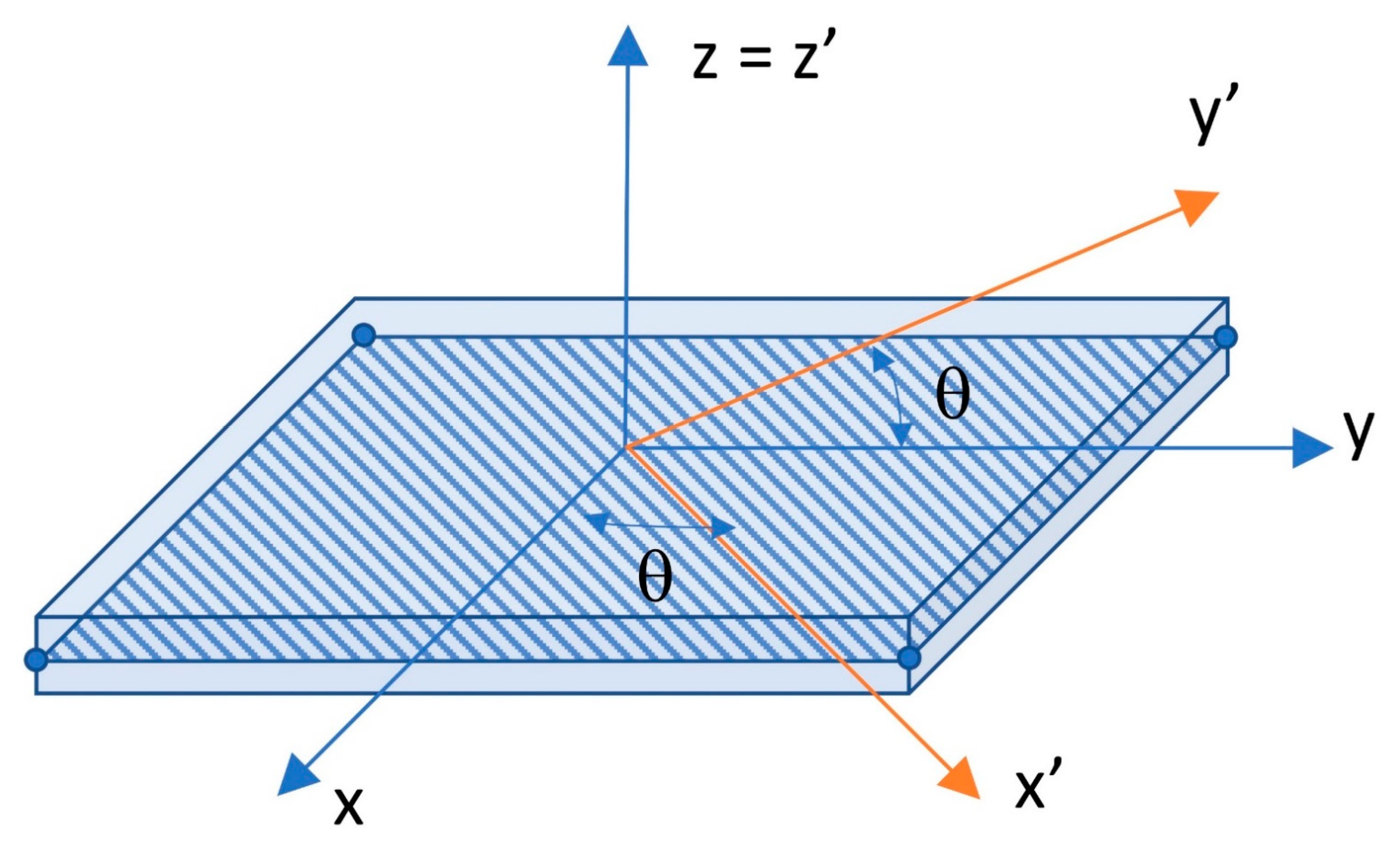
2.3. Model of GFRP Laminate Plate
2.4. Material Properties Model
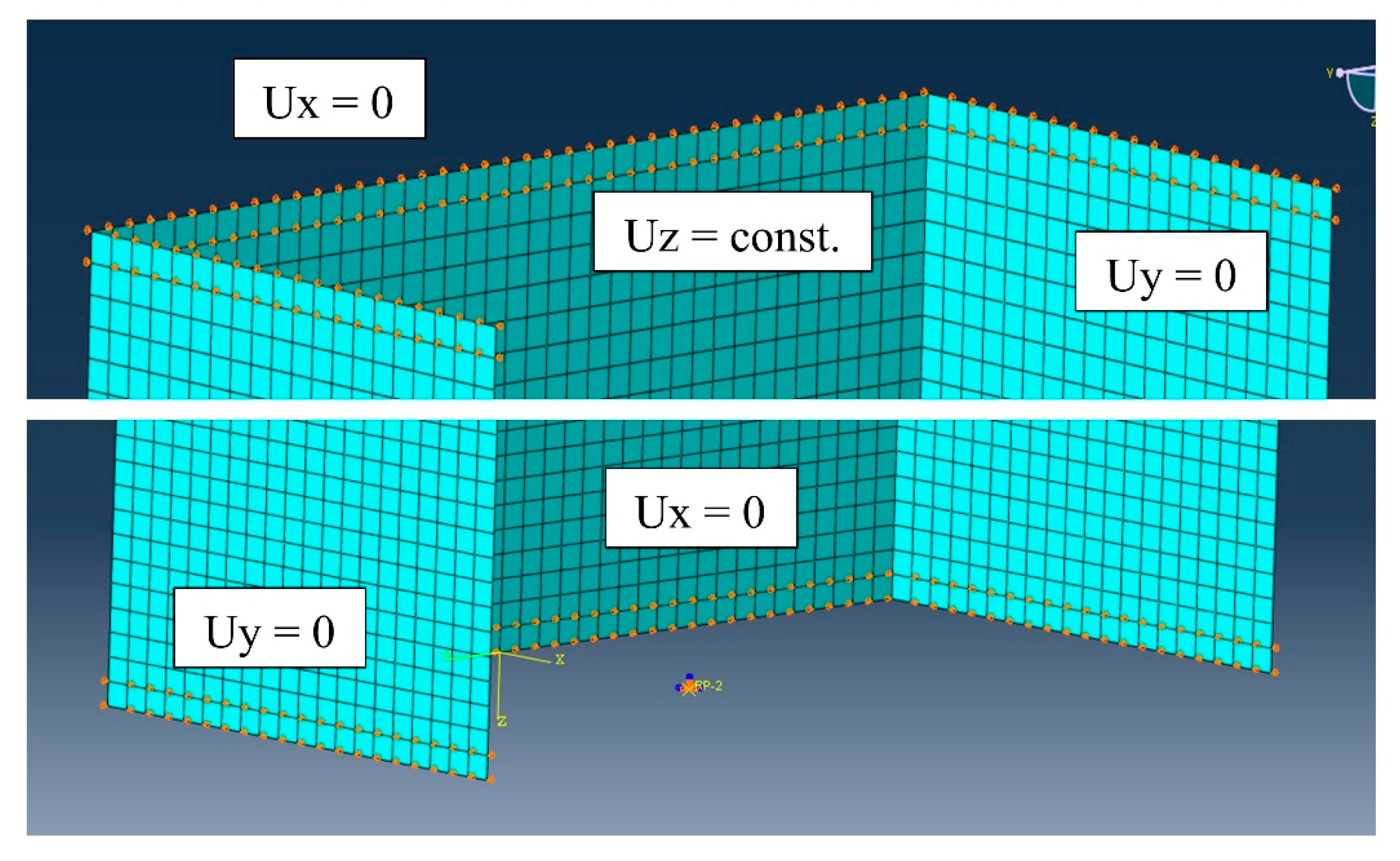
2.5. Model of the Boundary and Loading Conditions
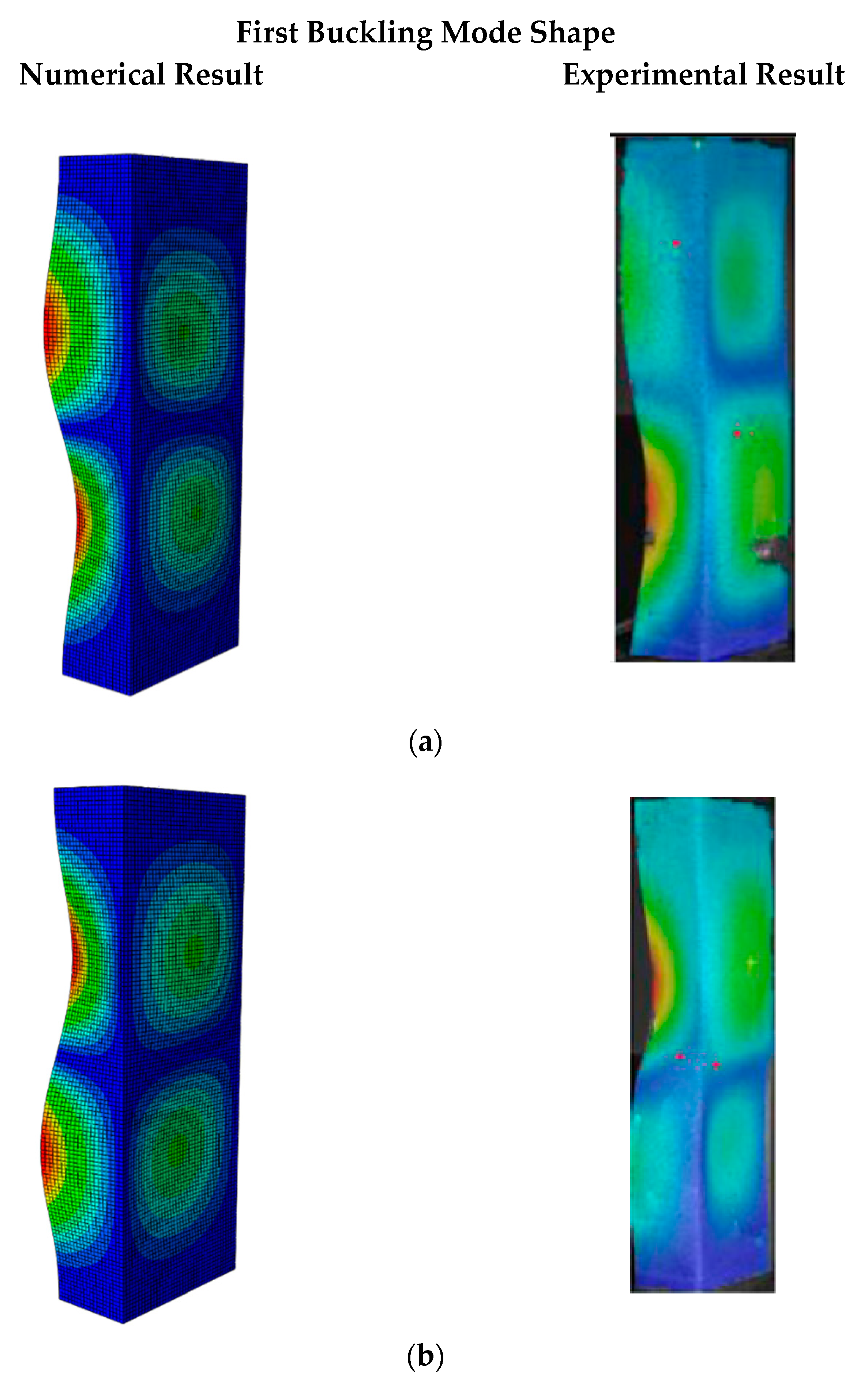
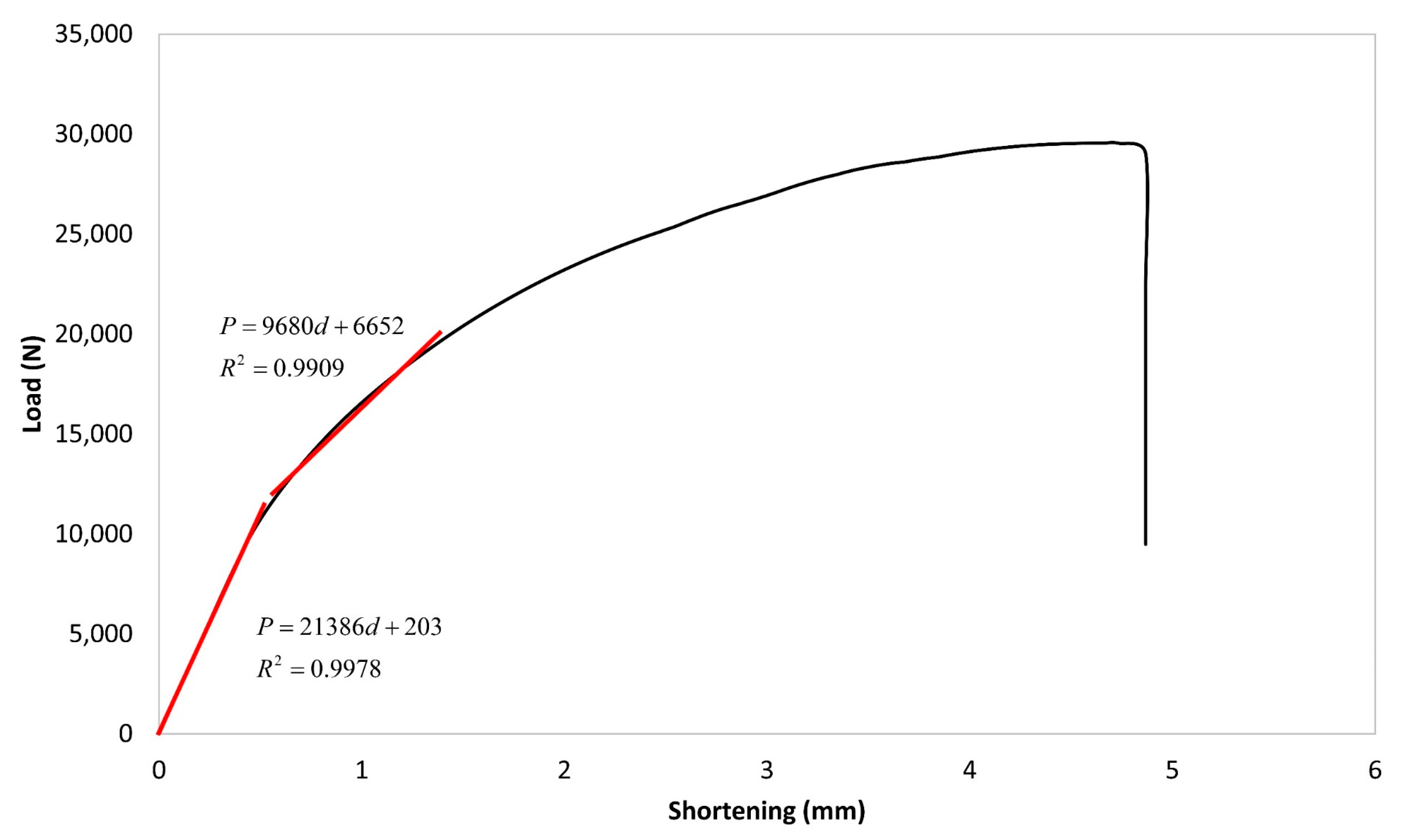
2.6. Verification of FE Model
3. Parametric Analysis and Proposal
3.1. Optimal Section Dimension
3.2. Optimal Thickness Ratio
3.3. Cost-Effective Design
3.4. Slenderness Ratio Effect and the Proposed Column Curve
4. Conclusions
- (1)
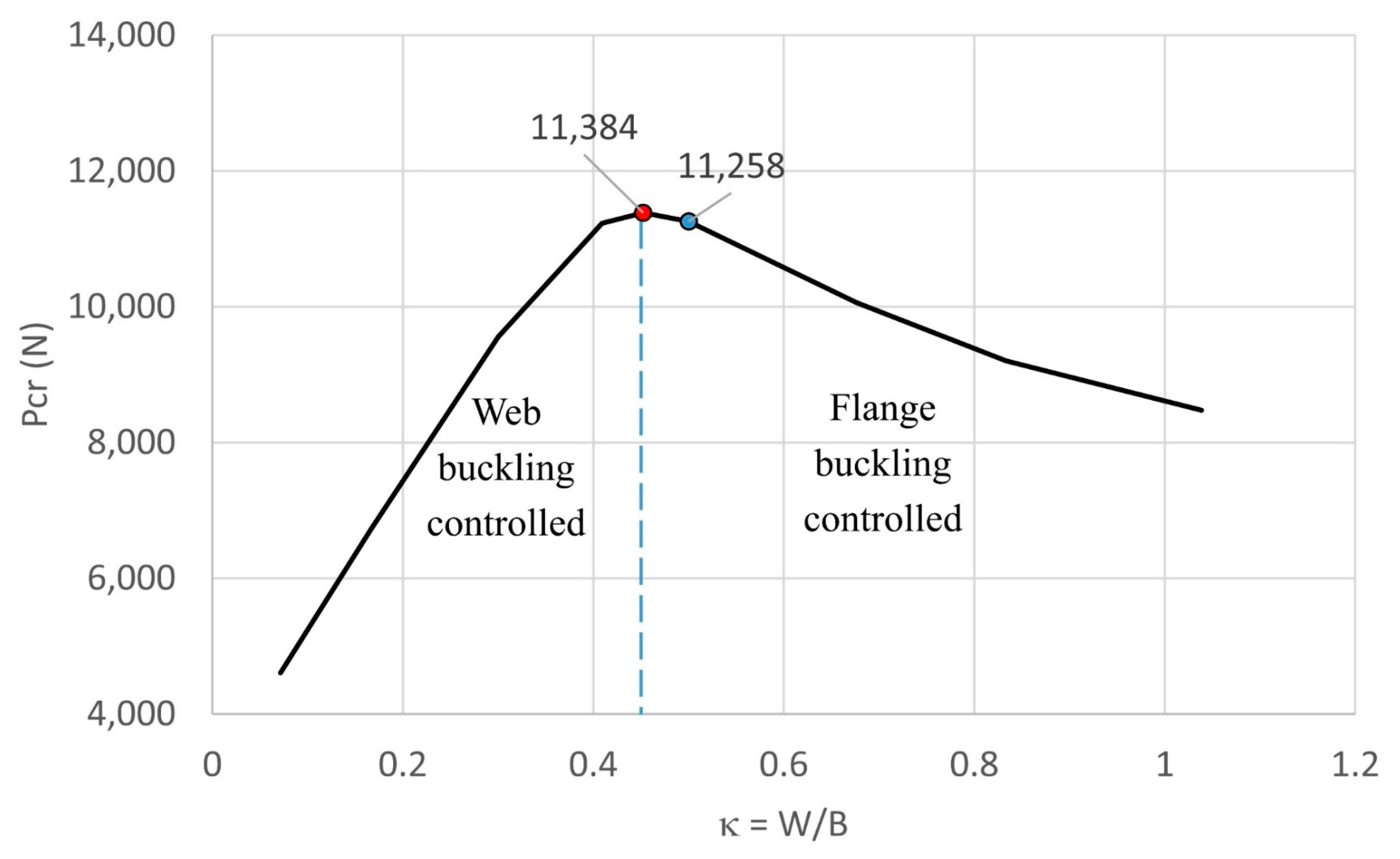
- The maximum critical buckling load was obtained when the length of the web was around 2.2 times greater than the flange length. The two-wave buckling mode shape, which contained three inflection points, withstood a higher buckling load.
- (2)
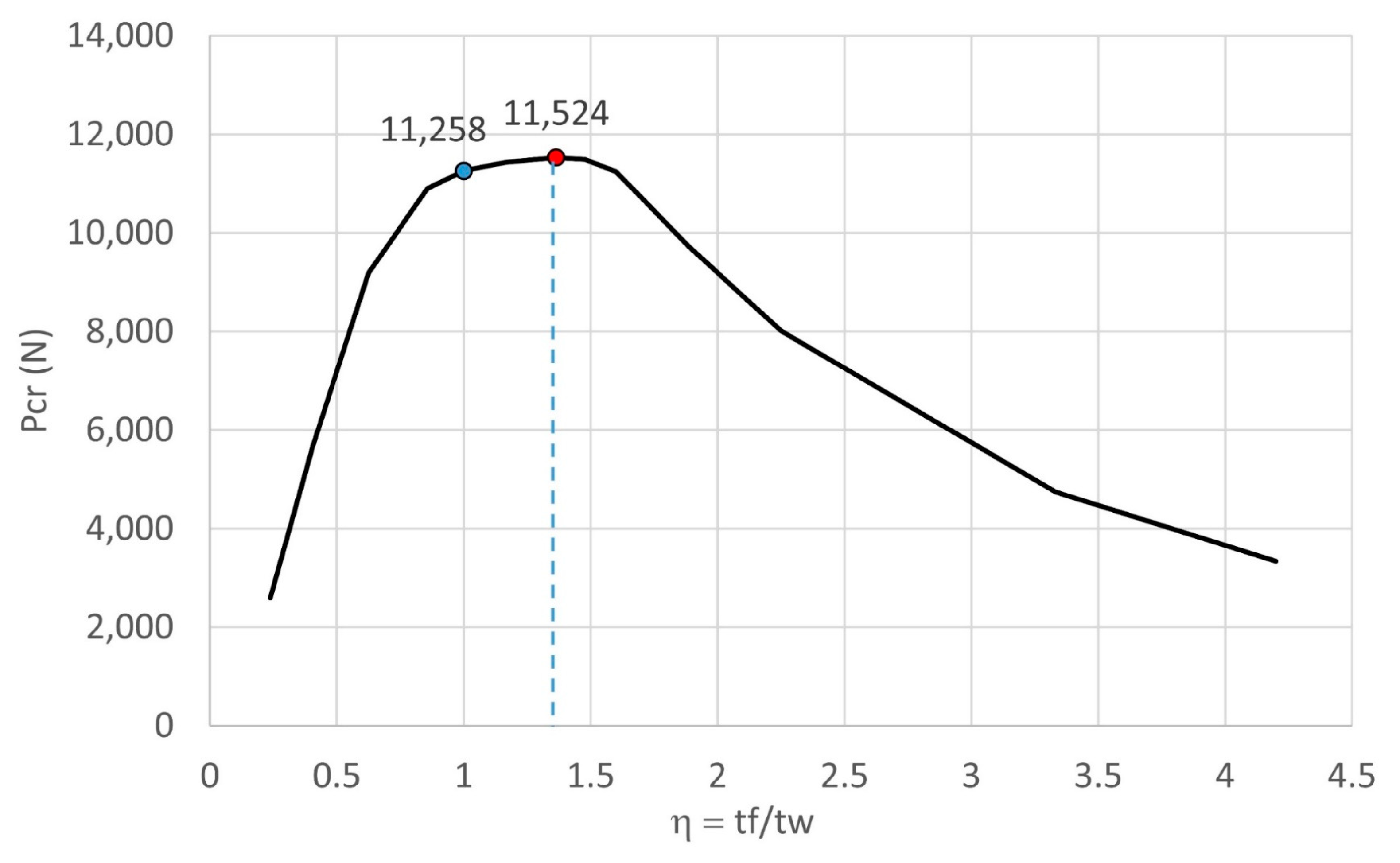
- When the thickness ratio between the web and the flange stayed in the range of 0.85–1.60, a good buckling load could be withstood.
- (3)
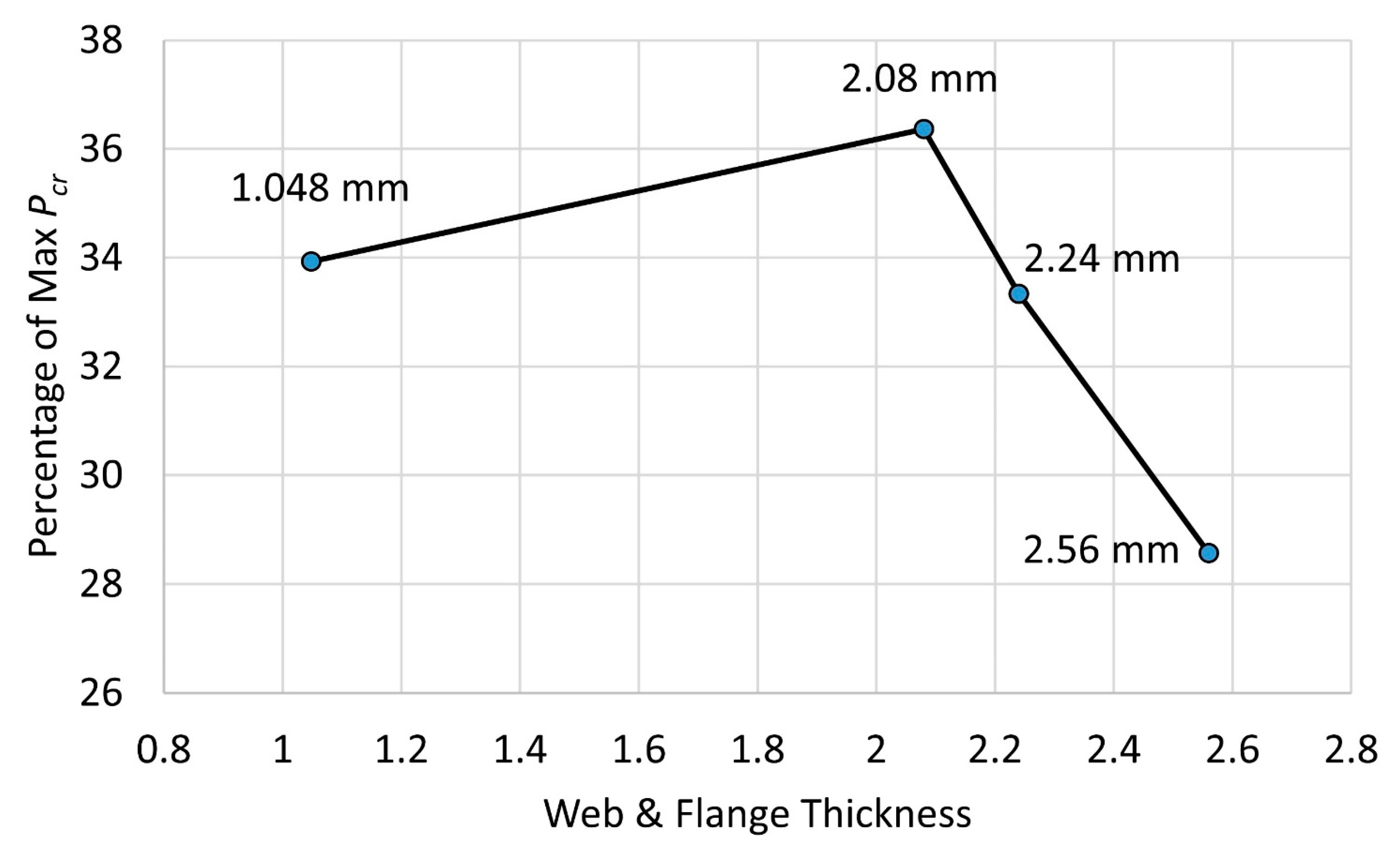
- A cost-effective design could be obtained when the thickness of the web and flange of mm was used.
- (4)
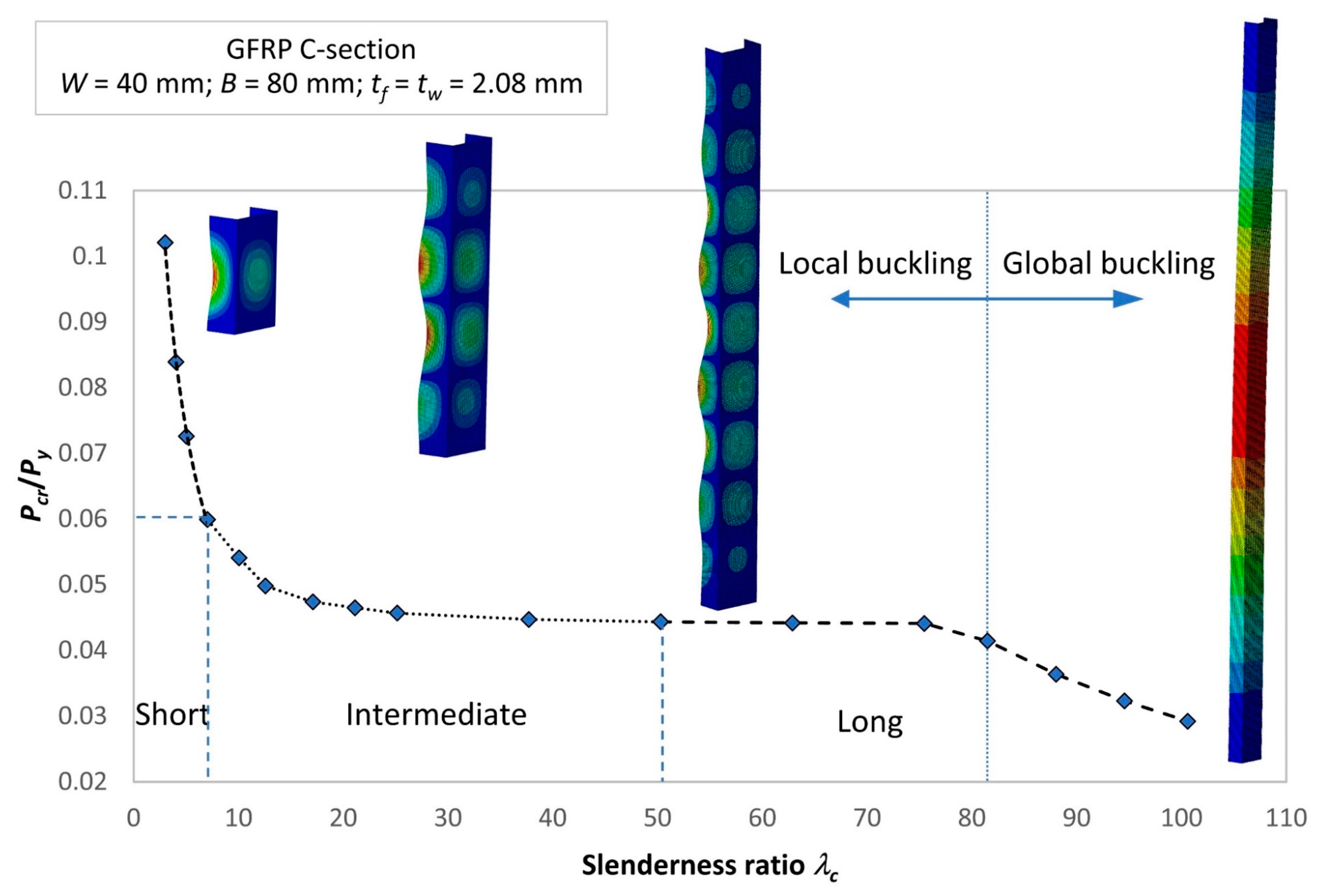
- The buckling behavior of the GFRP strut changed from local buckling to global buckling at a demarcation point with a slenderness ratio of .
- (5)
- The proposed design curve and equations for the GFRP strut provided a precise method for calculating the critical buckling load based on the input dimensions of the GFRP strut.
Author Contributions
Funding
Conflicts of Interest
References
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber–reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019, 105, 2289–2308. [Google Scholar] [CrossRef]
- Das, S.K.; Roy, S. Finite element analysis of aircraft wing using carbon fiber reinforced polymer and glass fiber reinforced polymer. IOP Conf. Ser. Mater. Sci. Eng. 2018, 402, 12077. [Google Scholar]
- Liu, S.; Zhou, Y.; Zhou, J.; Zhang, B.; Jin, F.; Zheng, Q.; Fan, H. Blast responses of concrete beams reinforced with GFRP bars: Experimental research and equivalent static analysis. Compos. Struct. 2019, 226, 111271. [Google Scholar] [CrossRef]
- Wang, W.; Song, Q.; Xu, C.; Gong, H. Mechanical behaviour of fully grouted GFRP rock bolts under the joint action of pre-tension load and blast dynamic load. Tunn. Undergr. Space Technol. 2018, 73, 82–91. [Google Scholar] [CrossRef]
- Grammatikos, S.A.; Jones, R.G.; Evernden, M.; Correia, J.R. Thermal cycling effects on the durability of a pultruded GFRP material for off-shore civil engineering structures. Compos. Struct. 2016, 153, 297–310. [Google Scholar] [CrossRef]
- Sankholkar, P.P.; Pantelides, C.P.; Hales, T.A. Confinement Model for Concrete Columns Reinforced with GFRP Spirals. J. Compos. Constr. 2018, 22, 4018007. [Google Scholar] [CrossRef]
- Wiater, A. Research on the lightweight concrete bridge deck slabs reinforced with GFRP composite bars. Arch. Civ. Eng. Environ. 2017, 10. [Google Scholar] [CrossRef]
- AlAjarmeh, O.S.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P.; Nguyen, K.T.Q. Compressive behavior of axially loaded circular hollow concrete columns reinforced with GFRP bars and spirals. Constr. Build. Mater. 2019, 194, 12–23. [Google Scholar] [CrossRef]
- Cardoso, D.C.T.; Togashi, B.S. Experimental investigation on the flexural-torsional buckling behavior of pultruded GFRP angle columns. Thin Wall Struct. 2018, 125, 269–280. [Google Scholar] [CrossRef]
- Hales, T.A.; Pantelides, C.P.; Reaveley, L.D. Analytical buckling model for slender FRP-reinforced concrete columns. Compos. Struct. 2017, 176, 33–42. [Google Scholar] [CrossRef]
- Kaya, A.; Dawood, M.; Gencturk, B. Repair of corroded and buckled short steel columns using concrete-filled GFRP jackets. Constr. Build. Mater. 2015, 94, 20–27. [Google Scholar] [CrossRef]
- Liu, T.; Harries, K.A. Flange local buckling of pultruded GFRP box beams. Compos. Struct. 2018, 189, 463–472. [Google Scholar] [CrossRef]
- Cintra, G.G.; Cardoso, D.C.T.; Vieira, J.D. Parameters affecting local buckling response of pultruded GFRP I-columns: Experimental and numerical investigation. Compos. Struct. 2019, 222, 110897. [Google Scholar] [CrossRef]
- Elchalakani, M.; Dong, M.; Karrech, A.; Li, G.; Mohamed Ali, M.S.; Yang, B. Experimental Investigation of Rectangular Air-Cured Geopolymer Concrete Columns Reinforced with GFRP Bars and Stirrups. J. Compos. Constr. 2019, 23, 4019011. [Google Scholar] [CrossRef]
- Elchalakani, M.; Karrech, A.; Dong, M.; Mohamed Ali, M.S.; Yang, B. Experiments and Finite Element Analysis of GFRP Reinforced Geopolymer Concrete Rectangular Columns Subjected to Concentric and Eccentric Axial Loading. Structures 2018, 14, 273–289. [Google Scholar] [CrossRef]
- D’Aguiar, S.C.M.; Parente Junior, E. Local buckling and post-critical behavior of thin-walled composite channel section columns. Lat. Am. J. Solids Struct. 2018, 15, 7. [Google Scholar]
- Debski, H. Numerical and experimental analysis of stability of thin-walled composite structures subjected to eccentric load. Arch. Civ. Mech. Eng. 2019, 19, 792–802. [Google Scholar] [CrossRef]
- Li, Y.-F.; Lai, J.-Y.; Yu, C.-C. The Push-Over Test and Numerical Analysis Study on the Mechanical Behavior of the GFRP Frame for Sustainable Prefabricated Houses. Sustainability 2019, 11, 6753. [Google Scholar] [CrossRef]
- Zhan, Y.; Wu, G. Global buckling capacity of pultruded FRP-I section columns under axial compression. Mech. Res. Commun. 2018, 90, 8–17. [Google Scholar] [CrossRef]
- Debski, H.; Kubiak, T.; Teter, A. Buckling and postbuckling behaviour of thin-walled composite channel section column. Compos. Struct. 2013, 100, 195–204. [Google Scholar] [CrossRef]
- Debski, H.; Jonak, J. Failure analysis of thin-walled composite channel section columns. Compos. Struct. 2015, 132, 567–574. [Google Scholar] [CrossRef]
- Gliszczynski, A.; Kubiak, T. Progressive failure analysis of thin-walled composite columns subjected to uniaxial compression. Compos. Struct. 2017, 169, 52–61. [Google Scholar] [CrossRef]
- Debski, H.; Rozylo, P.; Gliszczynski, A.; Kubiak, T. Numerical models for buckling, postbuckling and failure analysis of pre-damaged thin-walled composite struts subjected to uniform compression. Thin Wall Struct. 2019, 139, 53–65. [Google Scholar] [CrossRef]
- Abaqus Inc. ABAQUS/Standard, 6.14; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2014. [Google Scholar]
- Gliszczynski, A.; Kubiak, T.; Borkowski, L. Experimental investigation of pre-damaged thin-walled channel section column subjected to compression. Compos. B Eng. 2018, 147, 56–68. [Google Scholar] [CrossRef]
- Bienias, J.; Gliszczynski, A.; Jakubczak, P.; Kubiak, T.; Majerski, K. Influence of autoclaving process parameters on the buckling and postbuckling behaviour of thin-walled channel section beams. Thin Wall Struct. 2014, 85, 262–270. [Google Scholar] [CrossRef]
- Bieniaś, J.; Mania, R.J.; Jakubczak, P.; Majerski, K. The issues of manufacturing of geometrically complicated elements by using FML laminates. Compos. Theory Prac. 2015, 15, 243–249. [Google Scholar]
- Chapelle, D.; Bathe, K.J. The Finite Element Analysis of Shells-Fundamentals: Fundamentals, 2nd ed.; Springer: Heidelberg, Germany, 2003; p. 330. [Google Scholar]
- Gruttmann, F.; Wagner, W. Shear correction factors for layered plates and shells. Comput. Mech. 2017, 59, 129–146. [Google Scholar] [CrossRef]
- Debski, H.; Teter, A.; Kubiak, T.; Samborski, S. Local buckling, post-buckling and collapse of thin-walled channel section composite columns subjected to quasi-static compression. Compos. Struct. 2016, 136, 593–601. [Google Scholar] [CrossRef]
- Kubiak, T. Static and Dynamic Buckling of Thin-Walled Plate Structures; Springer: London, UK, 2013. [Google Scholar]
- Staab, G.H. Laminate analysis. In Laminar Composites, 2nd ed.; Jackson, D., Ed.; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Banat, D.; Kolakowski, Z.; Mania, R.J. Investigations of fml profile buckling and post-buckling behaviour under axial compression. Thin Wall Struct. 2016, 107, 335–344. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Size-dependent buckling and postbuckling analyses of first-order shear deformable magneto-electro-thermo elastic nanoplates based on the nonlocal elasticity theory. Int. J. Struct. Stab. Dyn. 2017, 17, 1750014. [Google Scholar] [CrossRef]
- Guo, Z.; Bažant, Z.P. Size effect on buckling strength of eccentrically compressed column with fixed or propagating transverse crack. Int. J. Fract. 2006, 142, 151–162. [Google Scholar] [CrossRef]
- Shojaee, T.; Mohammadi, B.; Madoliat, R. Experimental and numerical investigation of stiffener effects on buckling strength of composite laminates with circular cutout. J. Compos. Mater. 2019, 0021998319874101. [Google Scholar] [CrossRef]
- Teter, A.; Kolakowski, Z. Buckling of thin-walled composite structures with intermediate stiffeners. Compos. Struct. 2005, 69, 421–428. [Google Scholar] [CrossRef]
- Ramôa Correia, J. Pultrusion of advanced fibre-reinforced polymer (FRP) composites. In Advanced Fibre-Reinforced Polymer (FRP) Composites for Structural Applications; Bai, J.B.T., Ed.; Woodhead Publishing: Cambridge, UK, 2013. [Google Scholar]
- McIlhagger, A.; Archer, E.; McIlhagger, R. Manufacturing processes for composite materials and components for aerospace applications. In Polymer Composites in the Aerospace Industry; Irving, P.E., Soutis, C., Eds.; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- American Institute of Steel Construction (AISC)-Steel Construction Manual, 15th ed.; American Institute of Physics: College Park, MD, USA; Springer: Berlin, Germany, 2017.

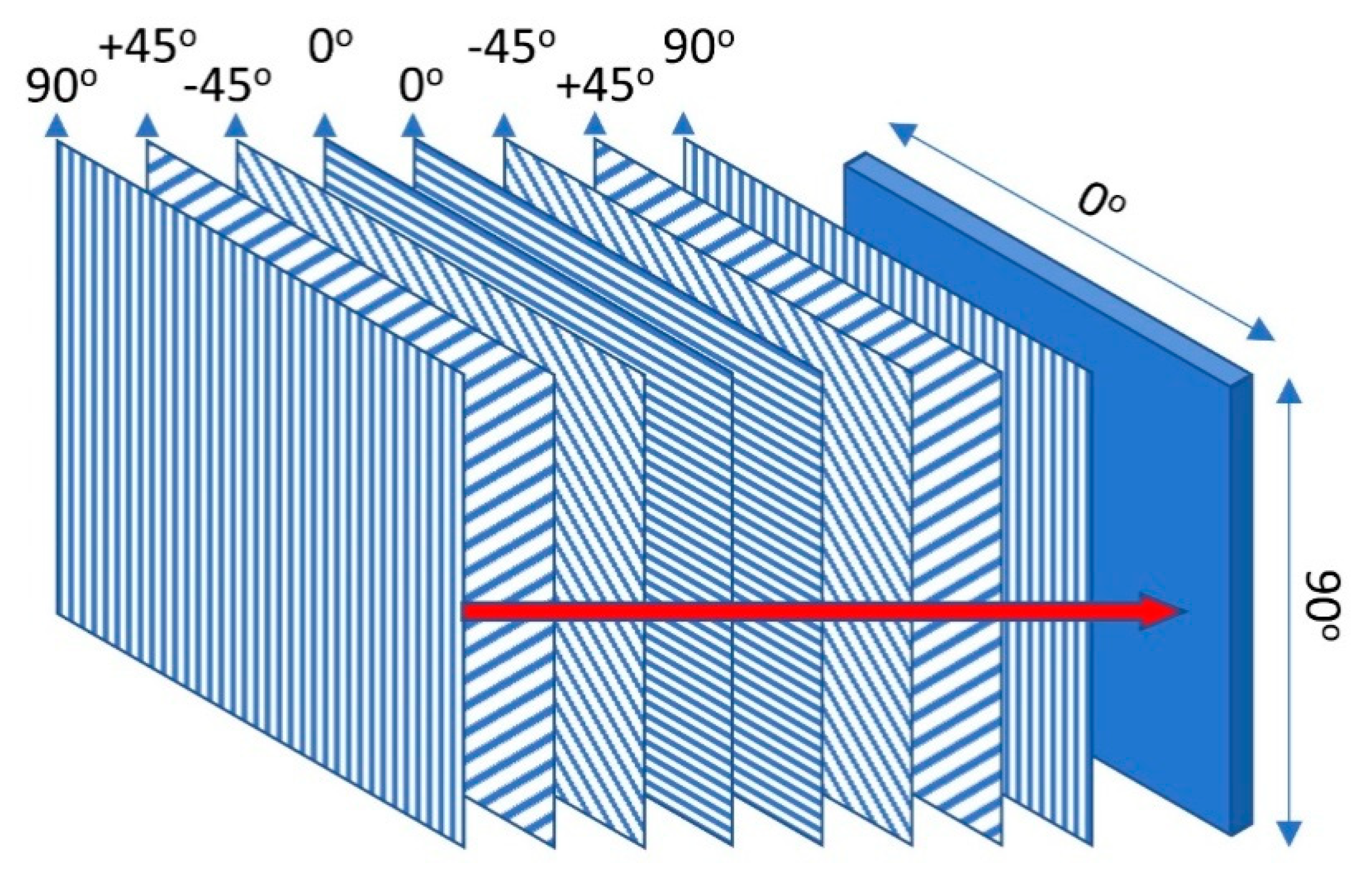
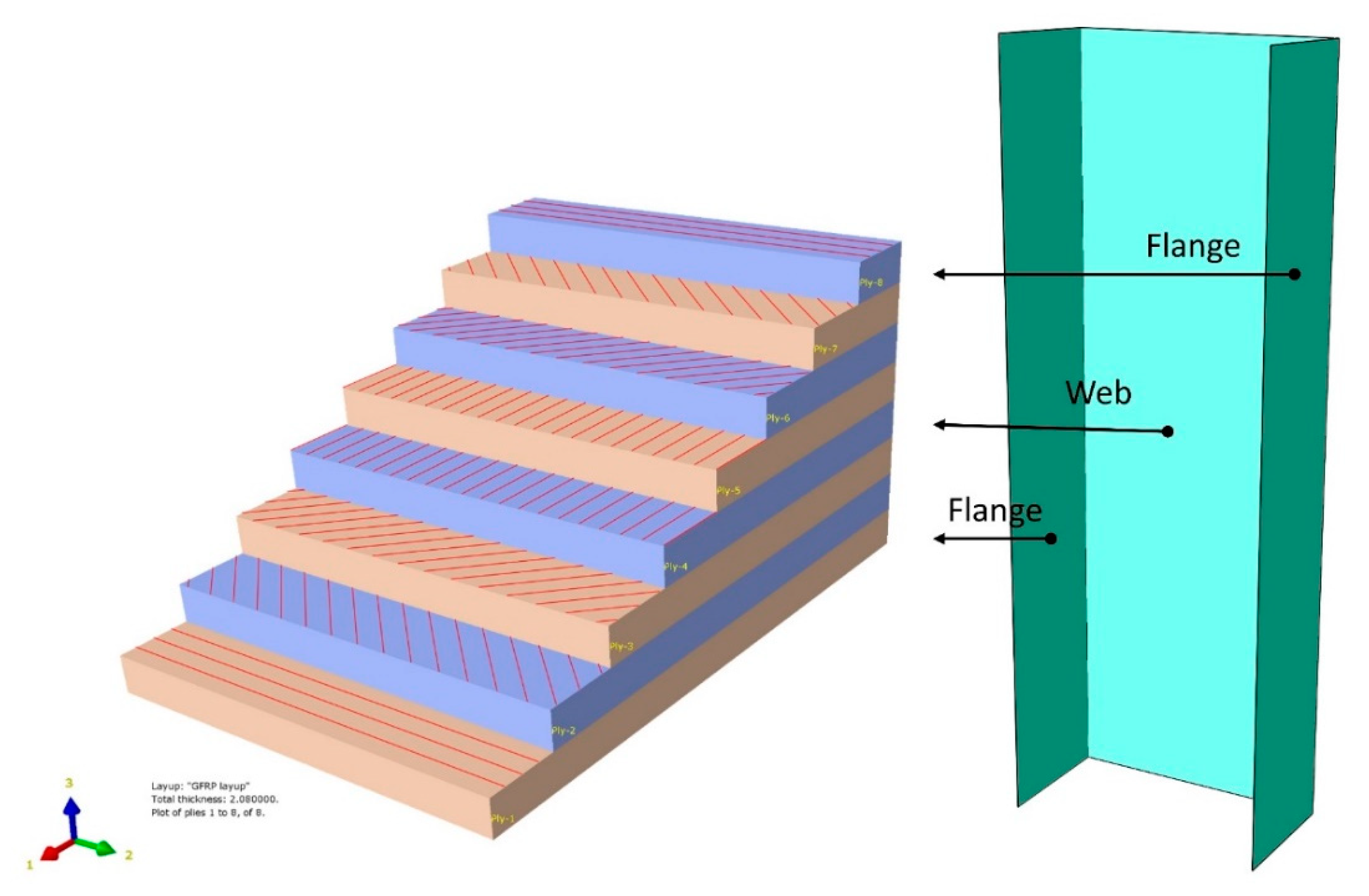

| Ply | 1 [90°] | 2 [45°] | 3 [−45°] | 4 [0°] | 5 [0°] | 6 [−45°] | 7 [45°] | 8 [90°] |
|---|---|---|---|---|---|---|---|---|
| Thickness (mm) | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 |
| 38,000 | 81,000 | 0.27 | 2000 | 2000 | 2000 |
| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | |
| 792 | 679 | 39 | 71 | 102 |
| Laminate Types | Critical Buckling Load (N) | |
|---|---|---|
| Numerical Results | Experiment Results | |
| Quasi-isotropic laminate [0/−45/+45/90]s | 11,285 | 10,500 ± 10% |
| Angle-ply laminate [+45/−45/+45/−45]s | 12,652 | 11,700 ± 10% |
| κ = W/B | 0.167 | 0.300 | 0.452 | 0.500 | 1.038 |
| Pcr (N) | 6727.8 | 9556.9 | 11384 | 11258 | 8476.2 |
| First Buckling Mode | 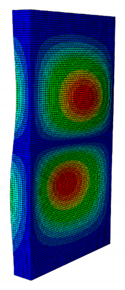 |  | 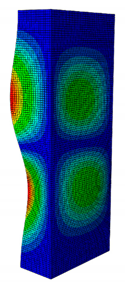 |  |  |
| 0.238 | 0.405 | 0.625 | 0.857 | 1.000 | |
| Pcr (N) | 2595.8 | 5678.5 | 9190.1 | 10,904 | 11,258 |
| First Buckling Mode | 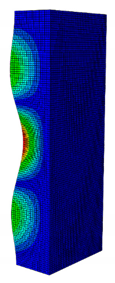 | 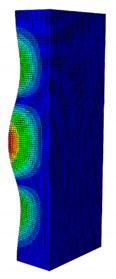 | 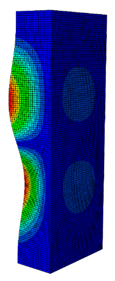 | 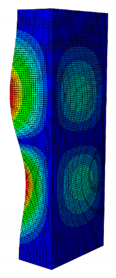 | 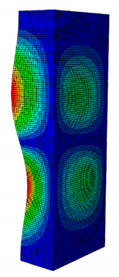 |
| 1.363 | 1.476 | 1.600 | 1.889 | 2.250 | |
| Pcr (N) | 11,524 | 11,492 | 11,244 | 9714.3 | 8009.3 |
| First Buckling Mode |  | 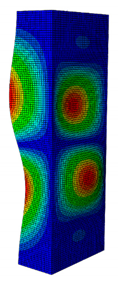 |  |  |  |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doan, Q.H.; Thai, D.-K.; Tran, N.L. A Numerical Study of the Effect of Component Dimensions on the Critical Buckling Load of a GFRP Composite Strut under Uniaxial Compression. Materials 2020, 13, 931. https://doi.org/10.3390/ma13040931
Doan QH, Thai D-K, Tran NL. A Numerical Study of the Effect of Component Dimensions on the Critical Buckling Load of a GFRP Composite Strut under Uniaxial Compression. Materials. 2020; 13(4):931. https://doi.org/10.3390/ma13040931
Chicago/Turabian StyleDoan, Quoc Hoan, Duc-Kien Thai, and Ngoc Long Tran. 2020. "A Numerical Study of the Effect of Component Dimensions on the Critical Buckling Load of a GFRP Composite Strut under Uniaxial Compression" Materials 13, no. 4: 931. https://doi.org/10.3390/ma13040931
APA StyleDoan, Q. H., Thai, D.-K., & Tran, N. L. (2020). A Numerical Study of the Effect of Component Dimensions on the Critical Buckling Load of a GFRP Composite Strut under Uniaxial Compression. Materials, 13(4), 931. https://doi.org/10.3390/ma13040931






