DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method
Abstract
1. Introduction
2. DEM, CM, and DECM Approaches to Model the Continuum
3. Basic Principles of the Discrete Elements Cell Method (DECM)
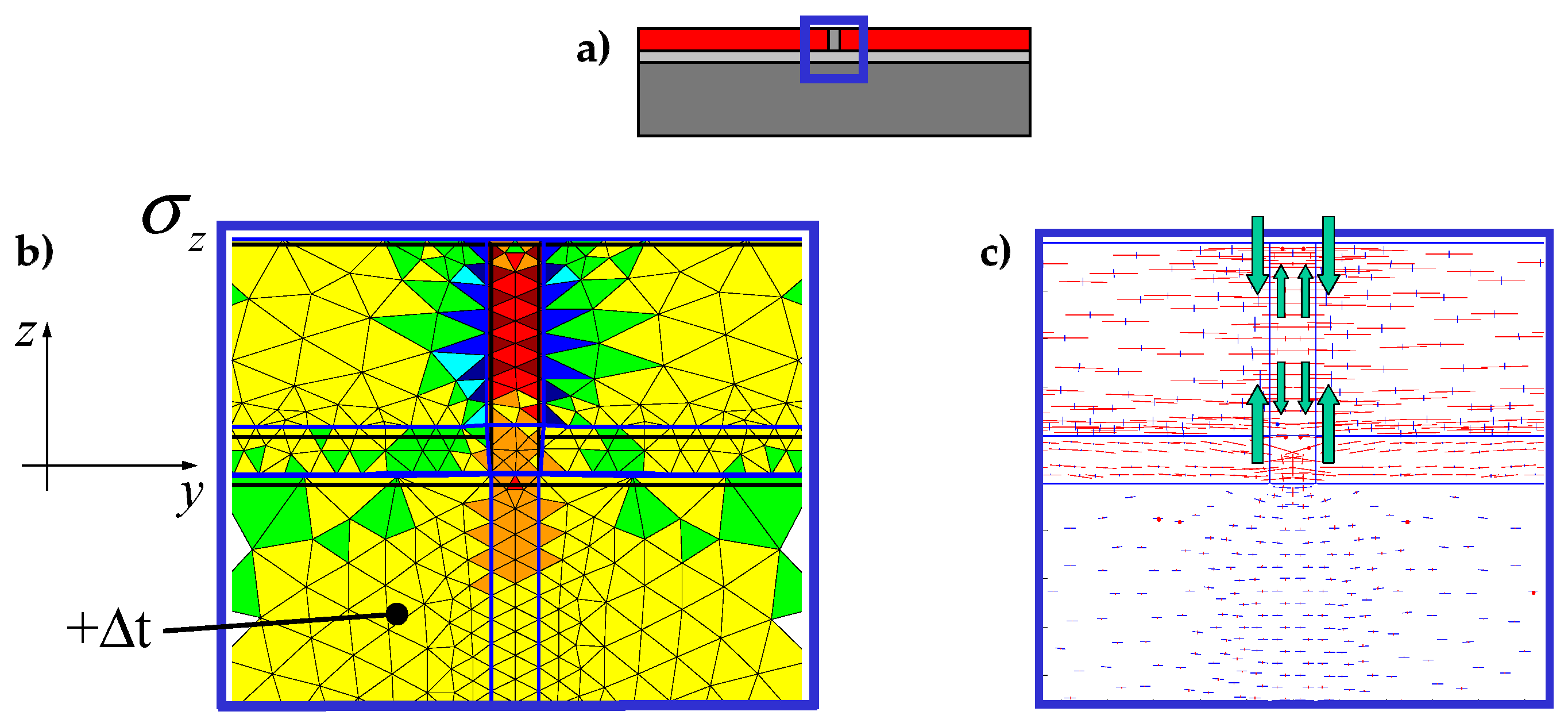
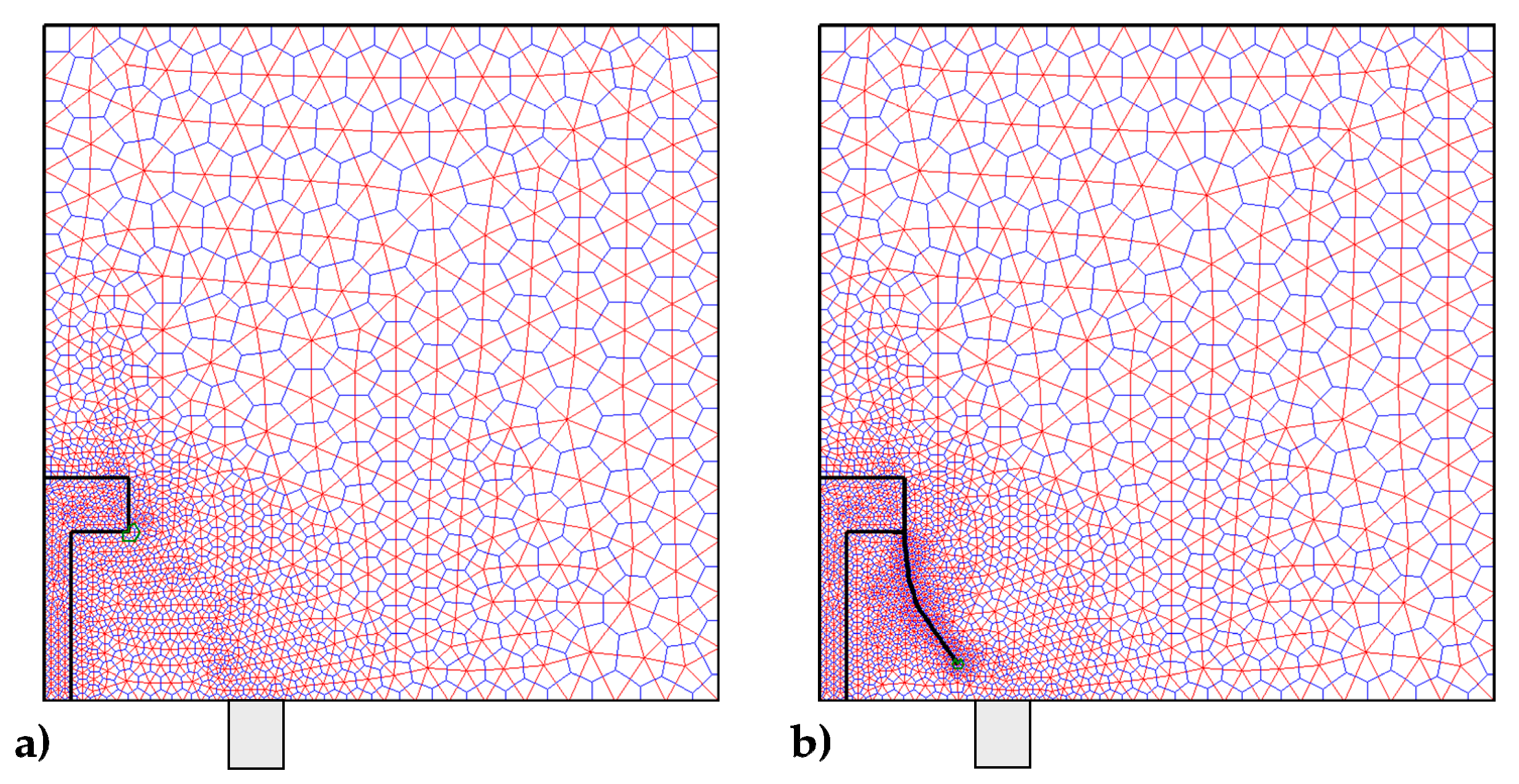
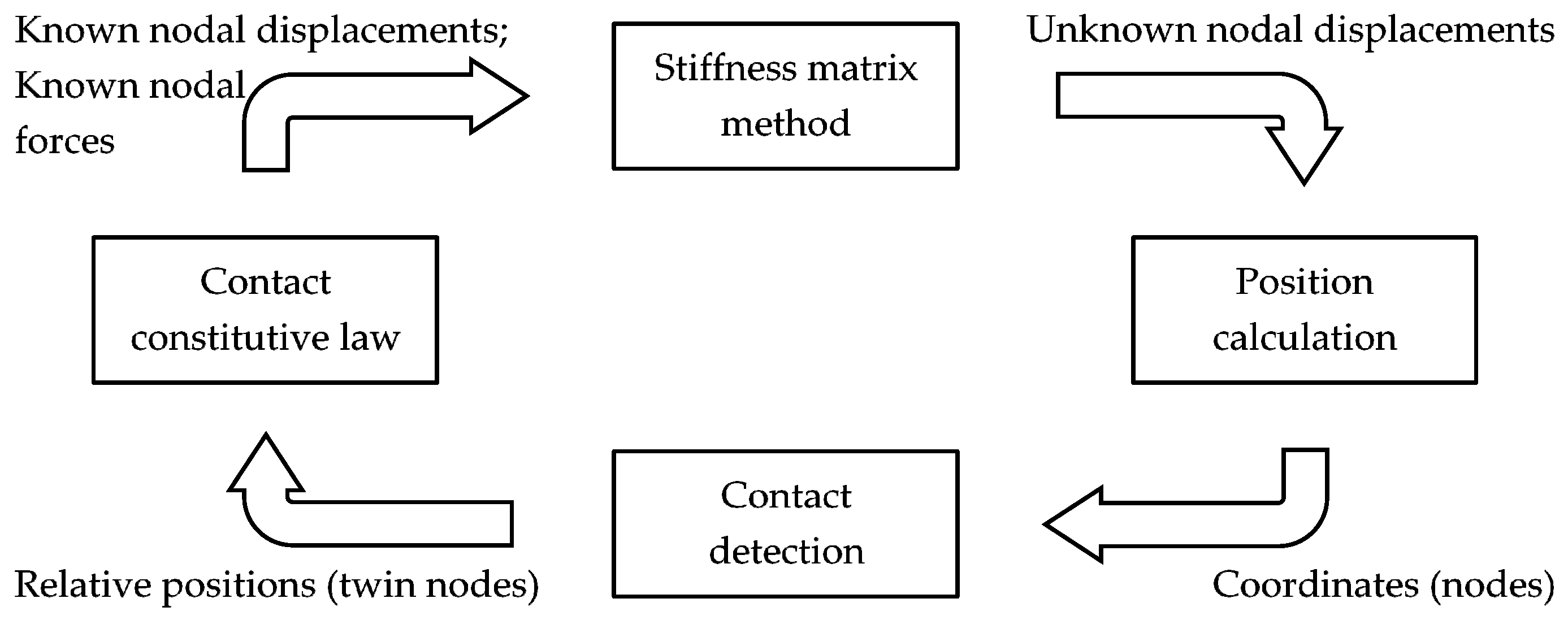
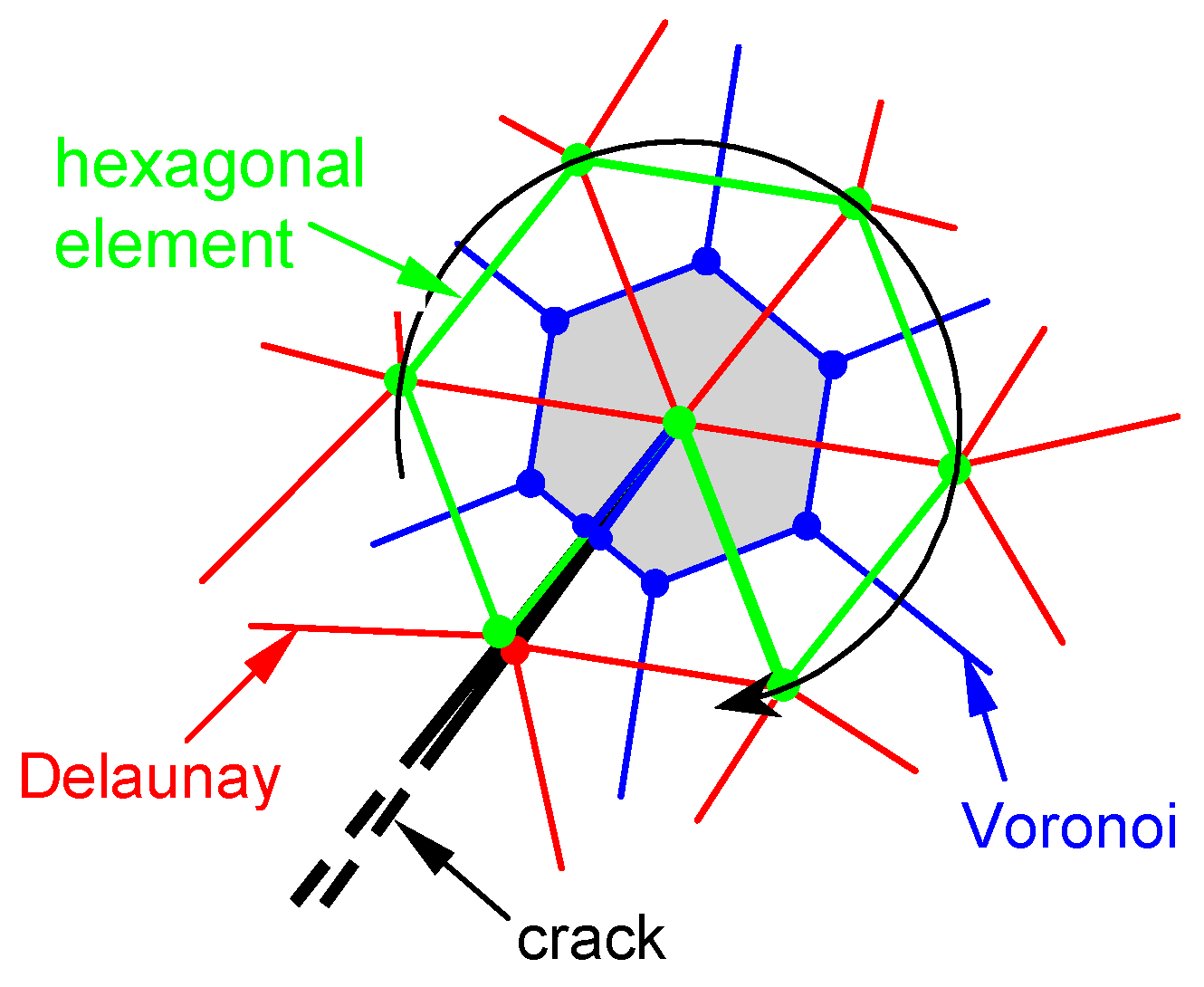
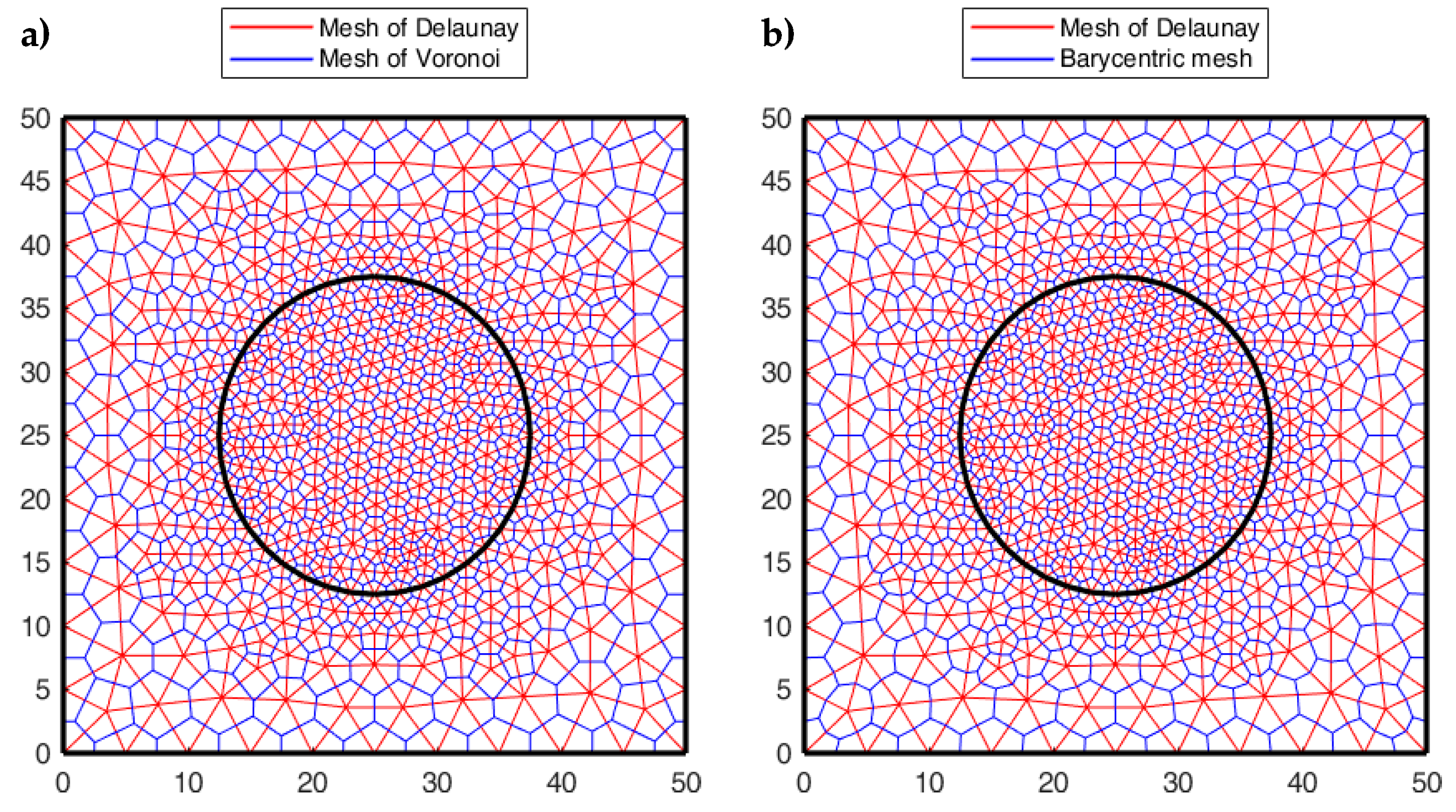
3.1. Contact Detection Algorithm
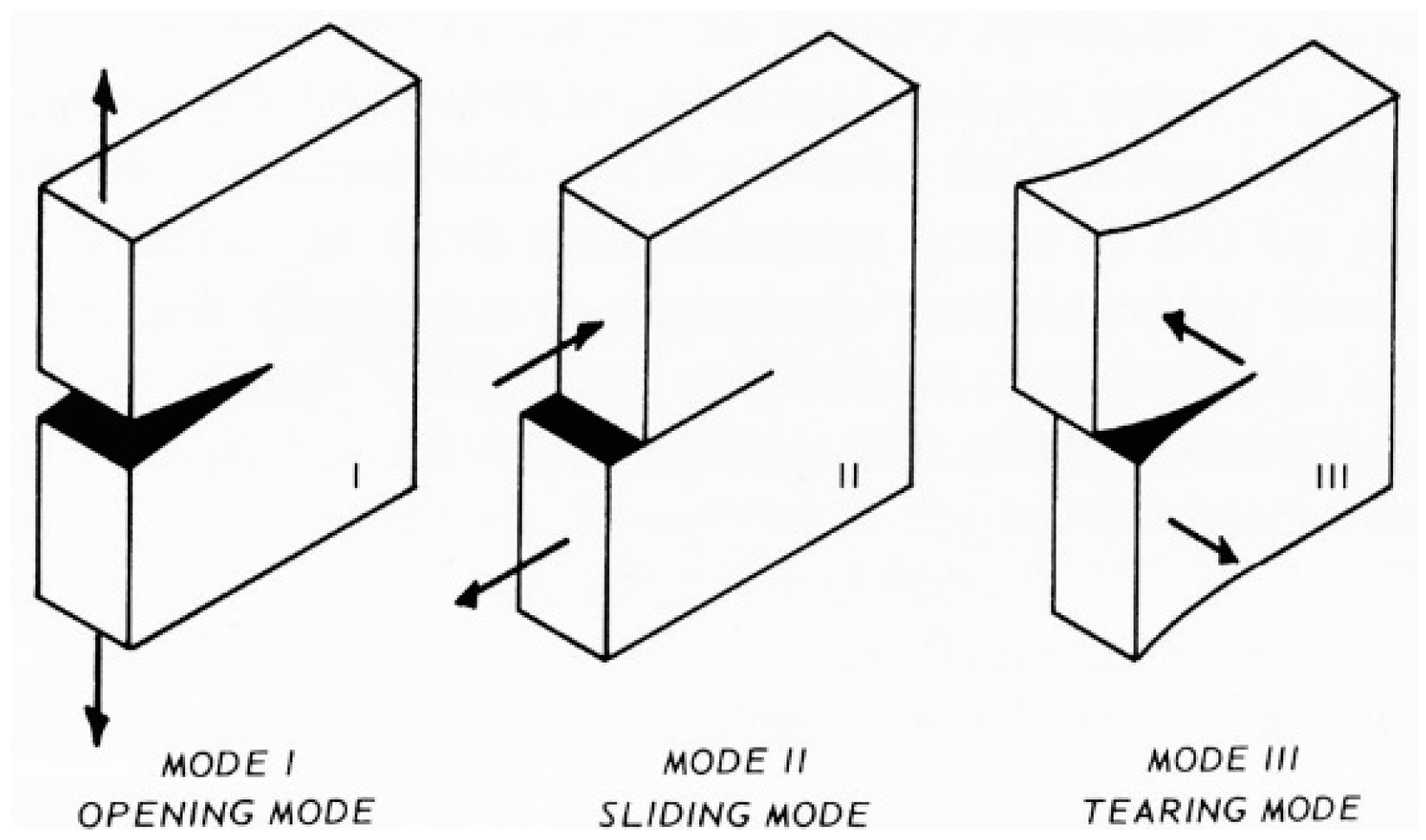
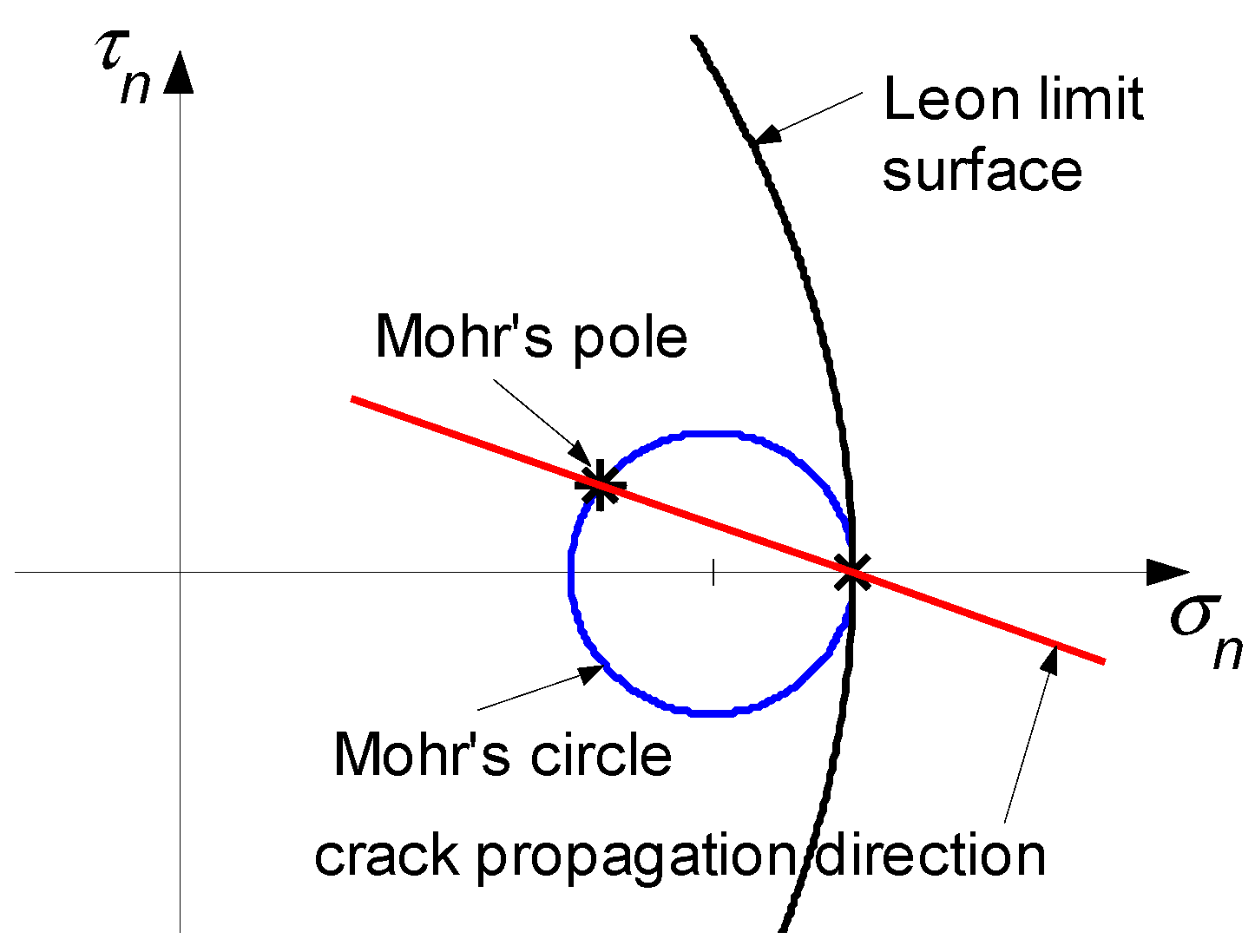
3.2. Direction of Crack Propagation
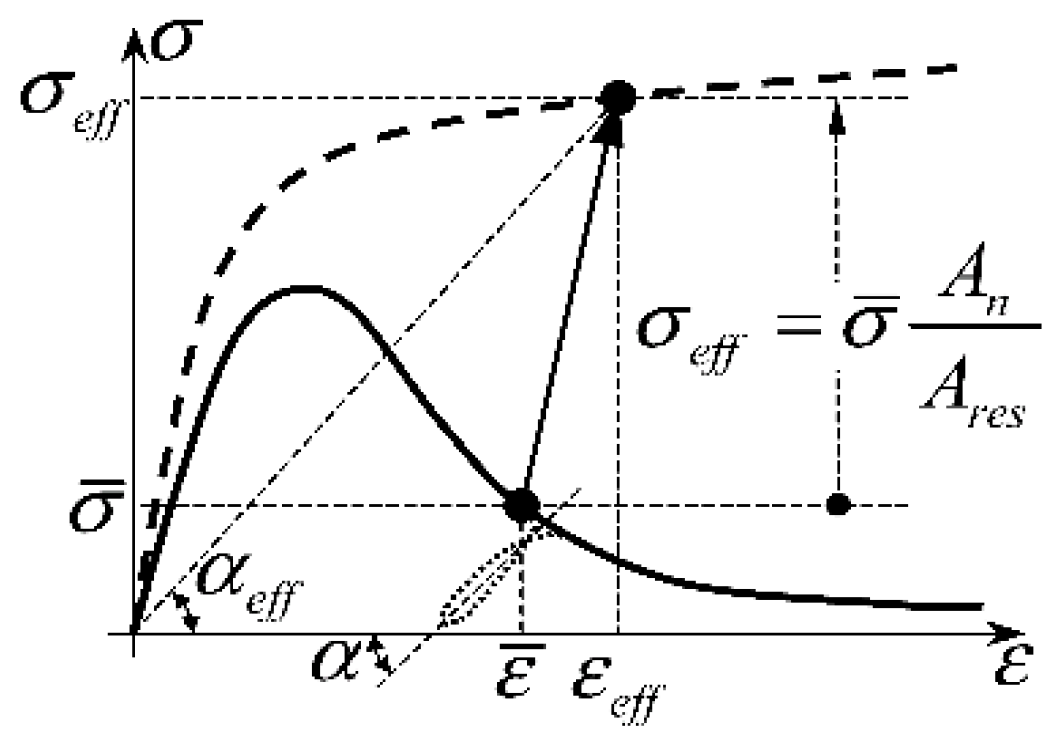
3.3. Constitutive Assumptions
4. DECM for Periodic Composite Continua
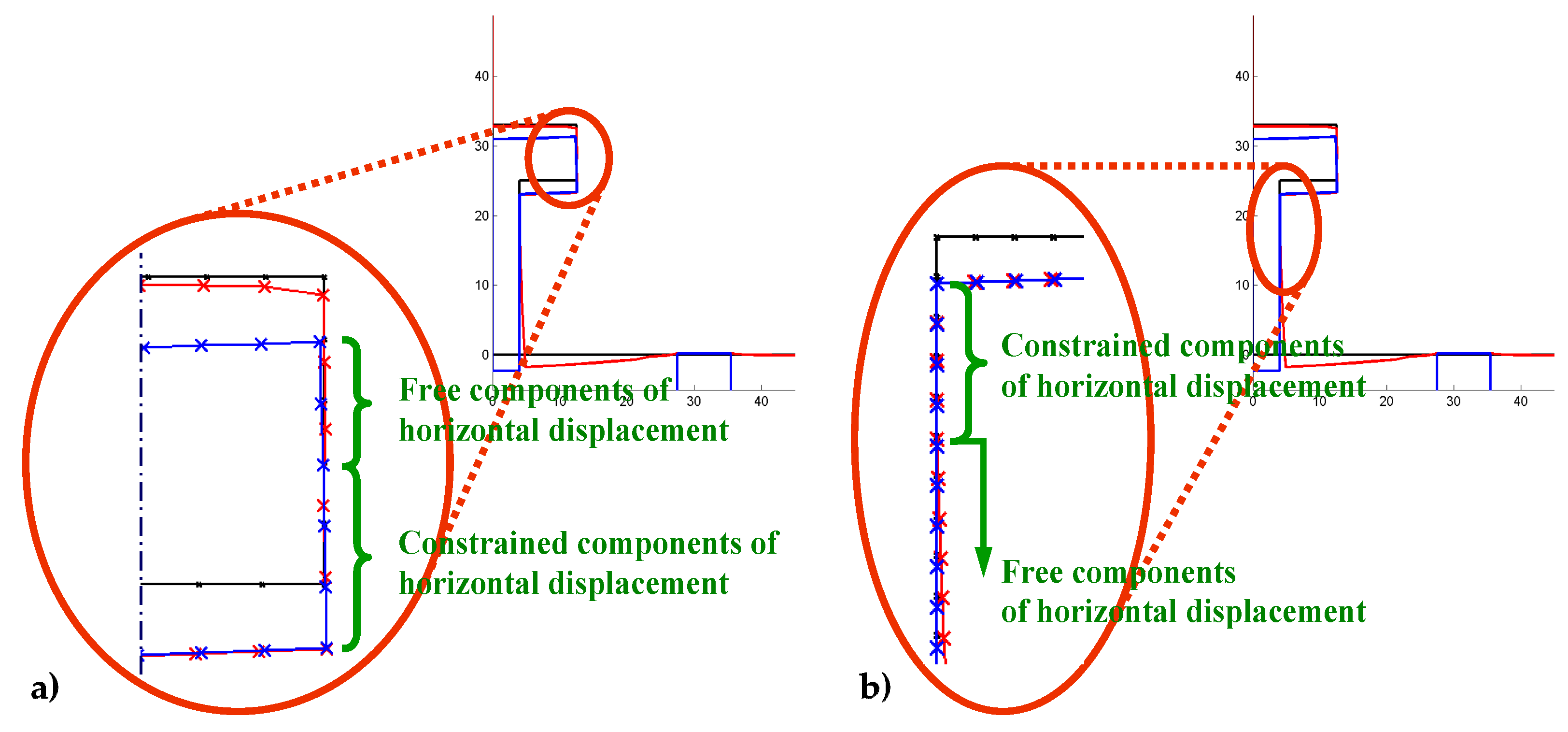
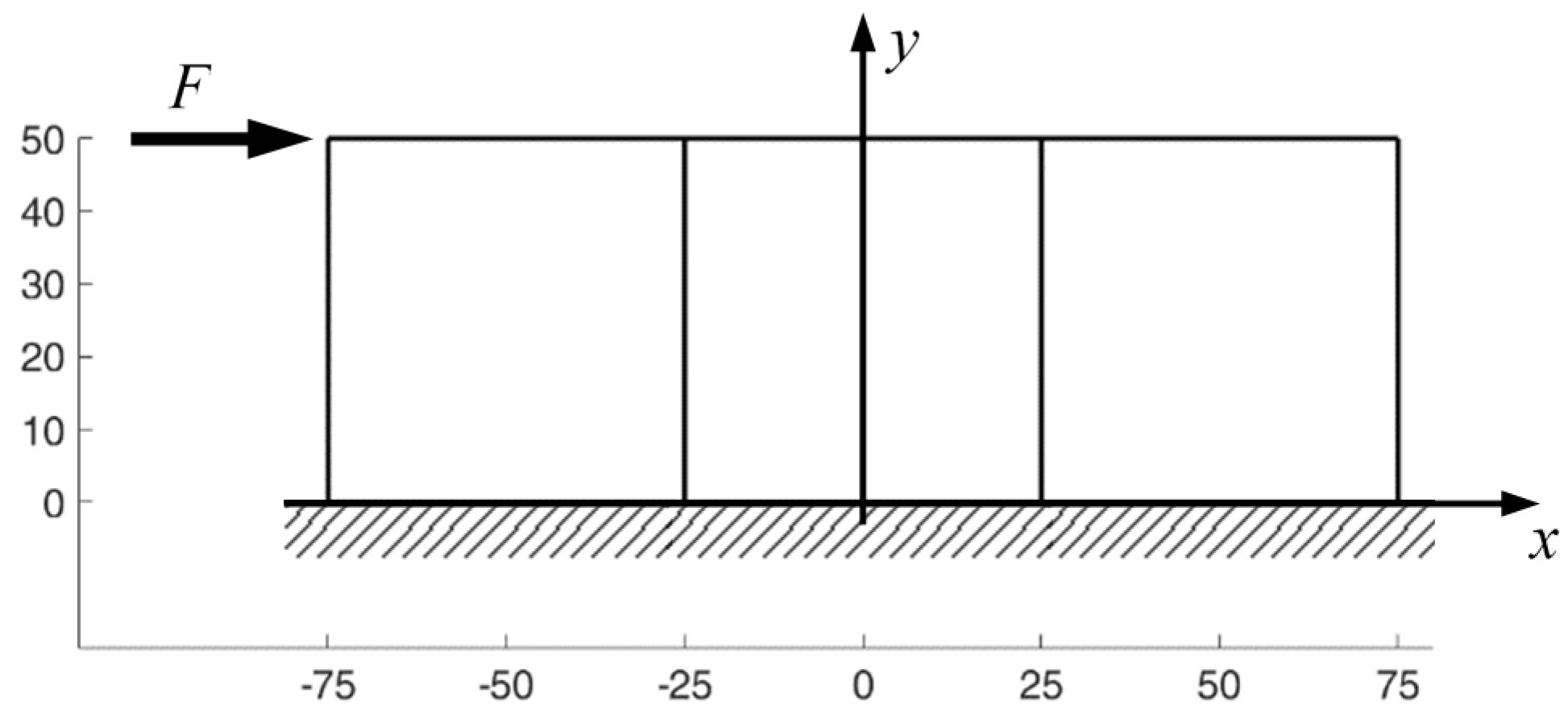
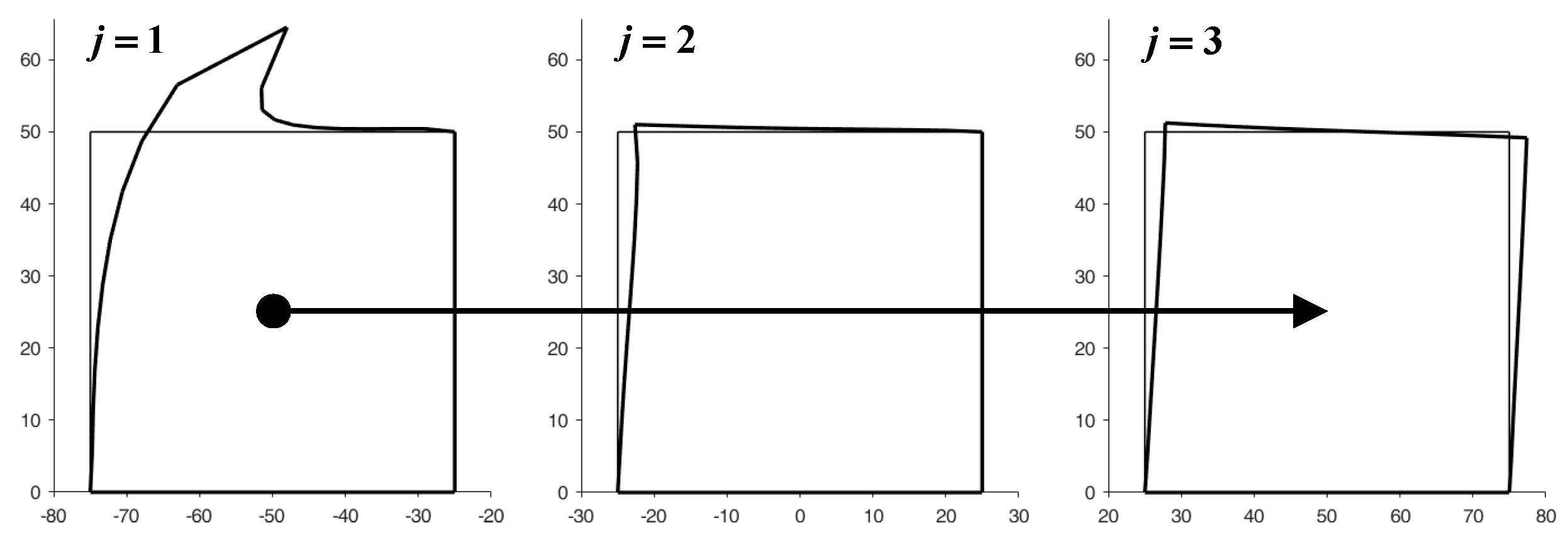
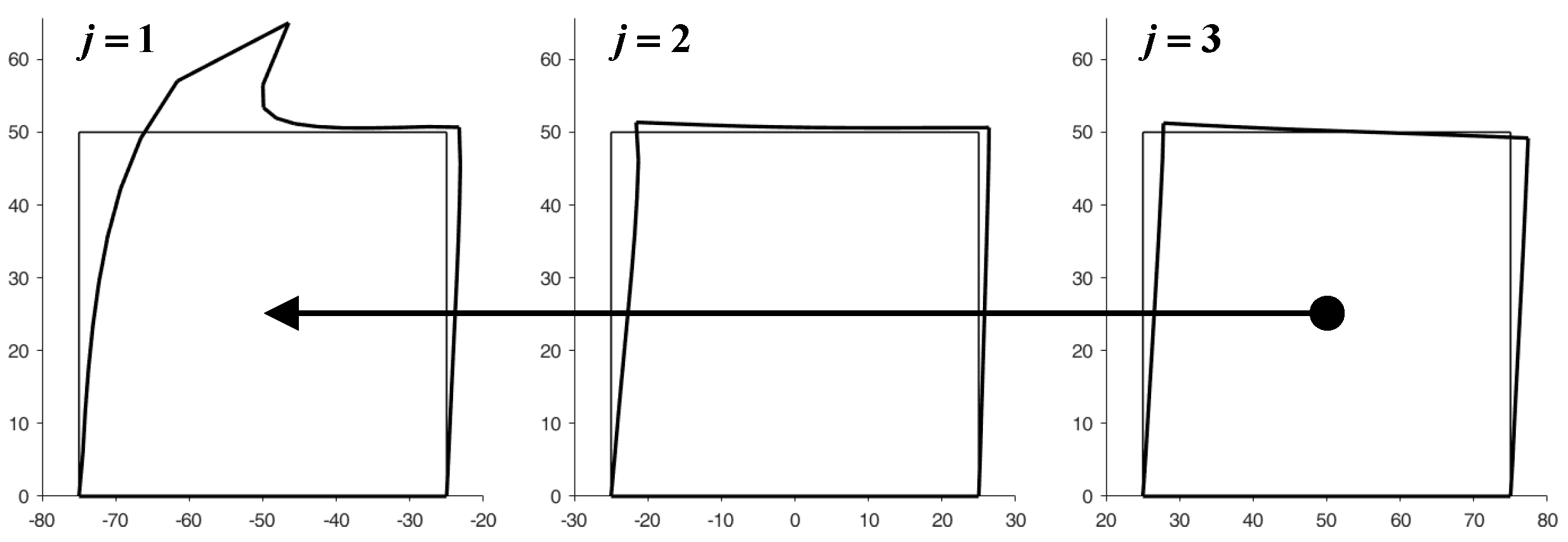
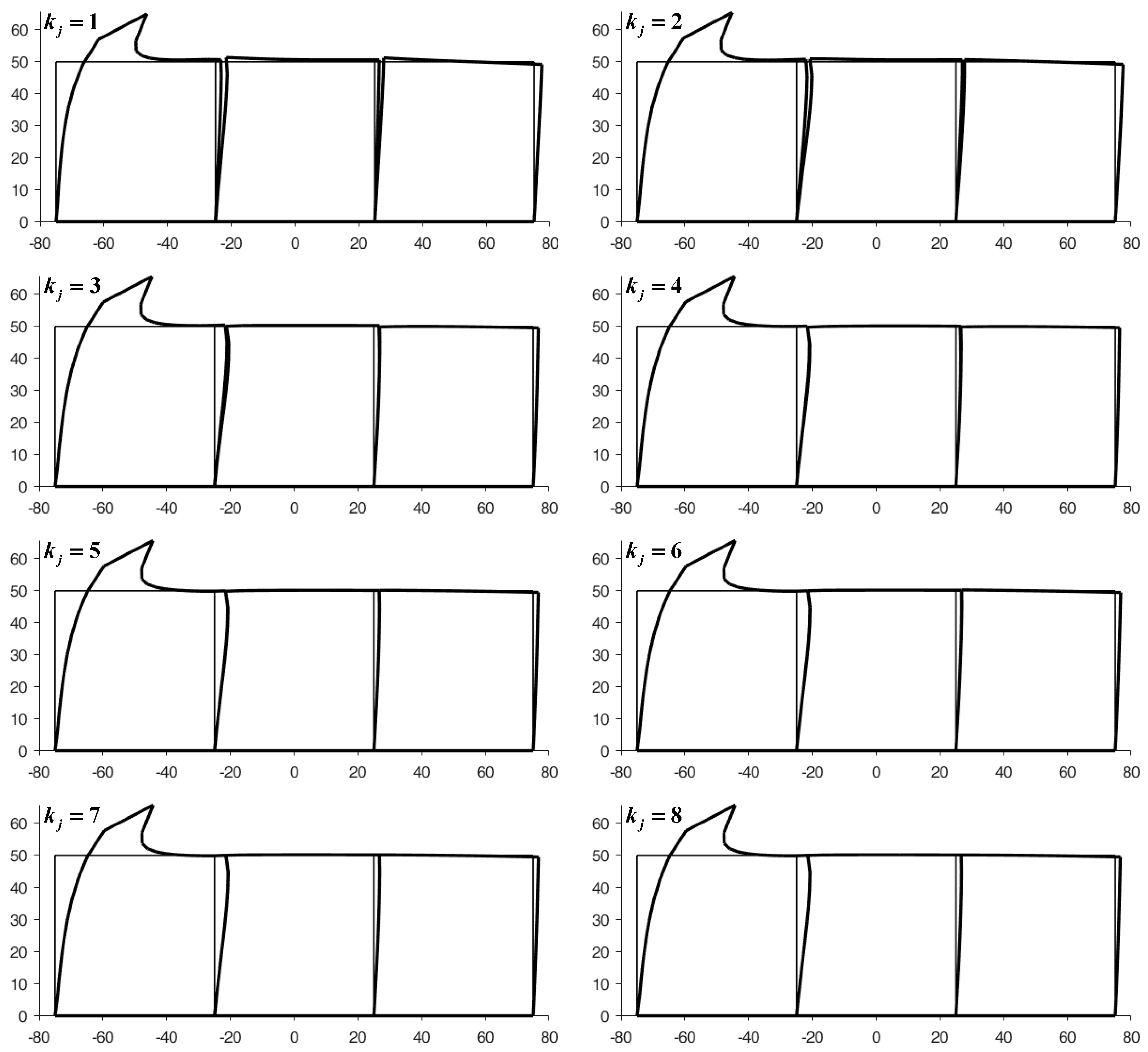
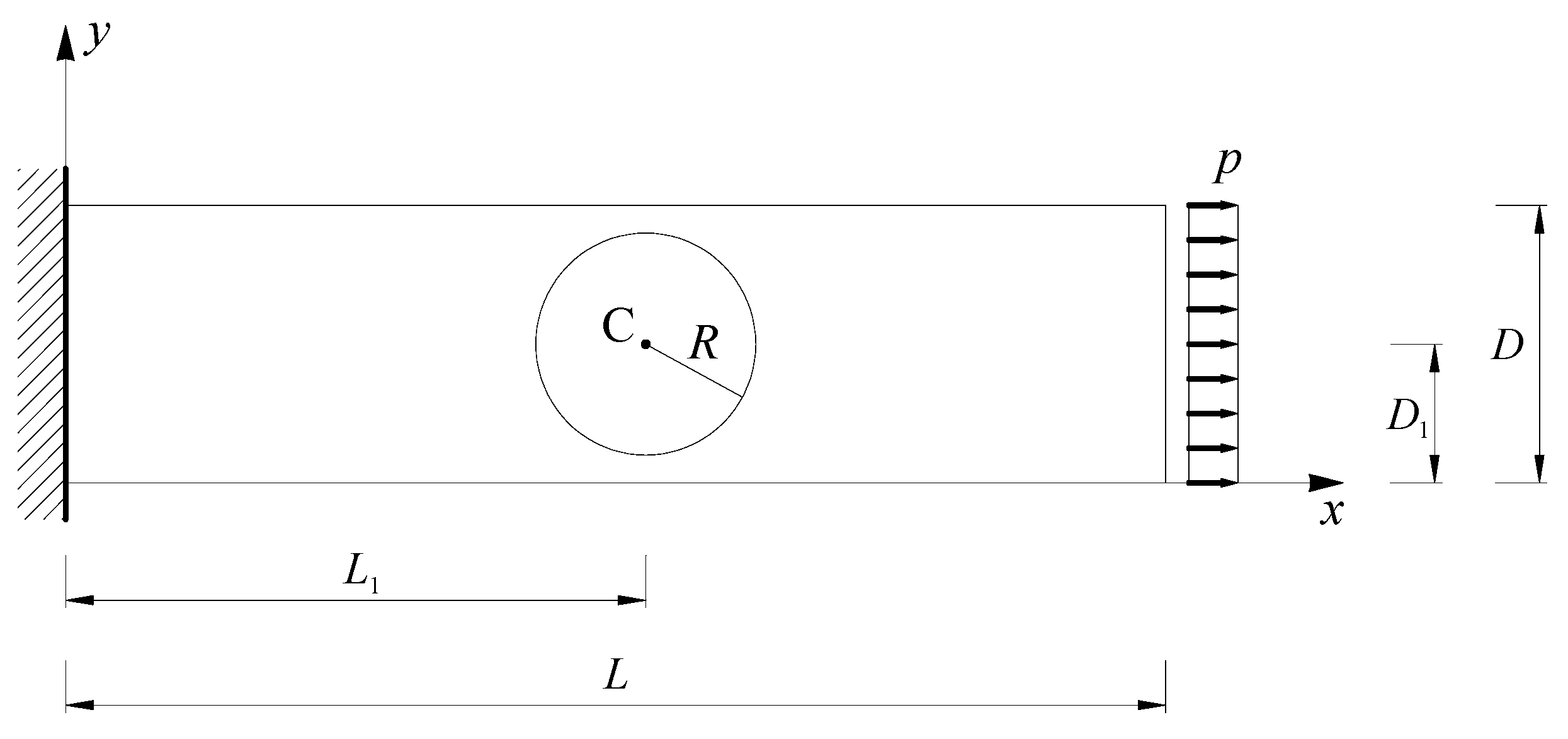
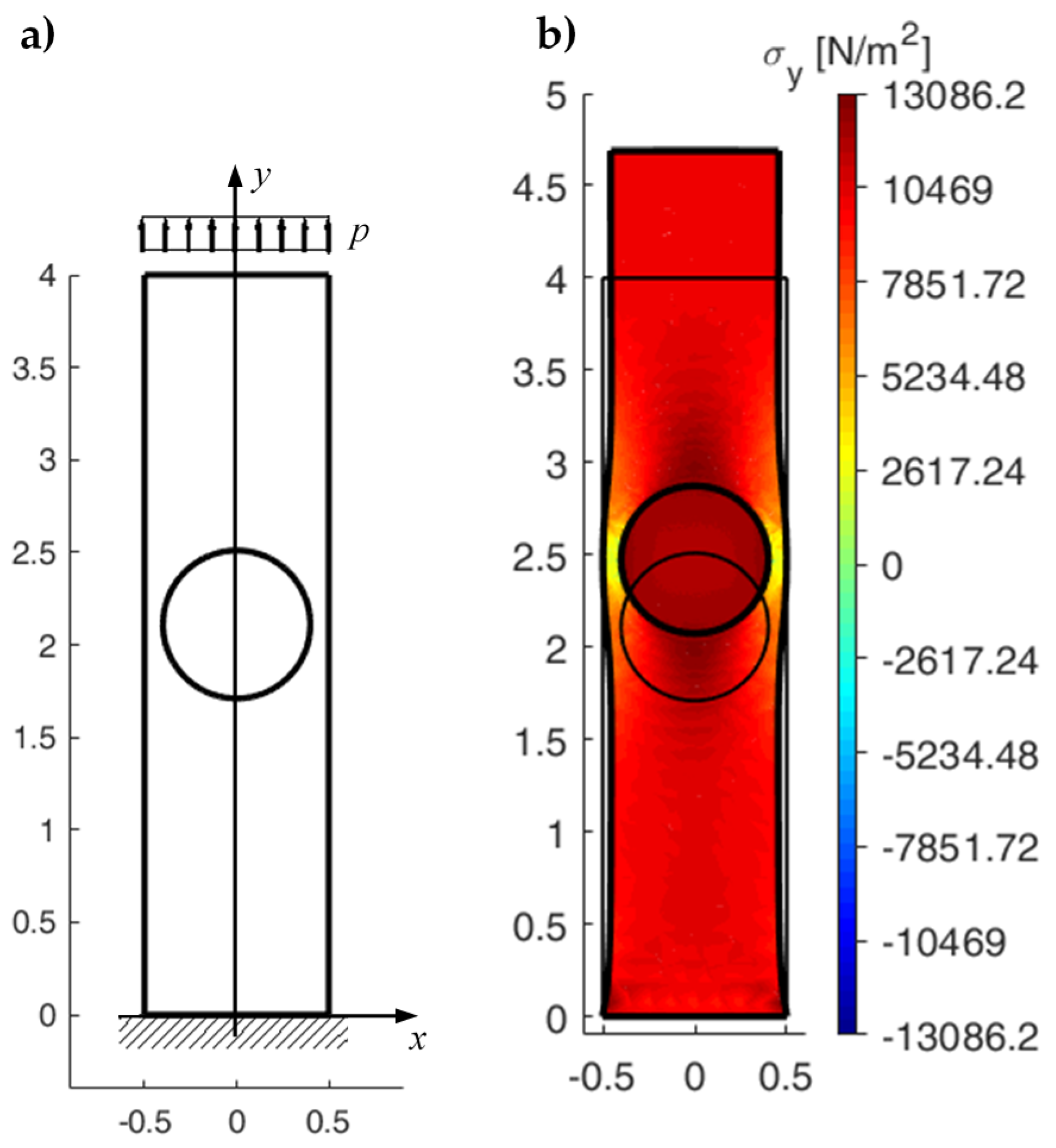
4.1. Two-Dimensional Problems
- The forces imposed on the nodes of the left side of the element, with , are half the differences (semi-differences) between the forces already present on the nodes and the forces calculated for the twin nodes on the right side of the element,
- The displacements imposed on the nodes of the right side of the element, with , are half the sums (semi-sums) of the displacements already calculated for the nodes and the displacements calculated for the twin nodes on the left side of the element.
- The forces imposed on the nodes of the upper sides of the row, with , are half the differences (semi-differences) between the forces already present on the nodes and the forces calculated for the twin nodes on the lower sides of the row,
- The displacements imposed on the nodes of the lower sides of the row, with , are half the sums (semi-sums) of the displacements already calculated for the nodes and the displacements calculated for the twin nodes on the upper sides of the row.
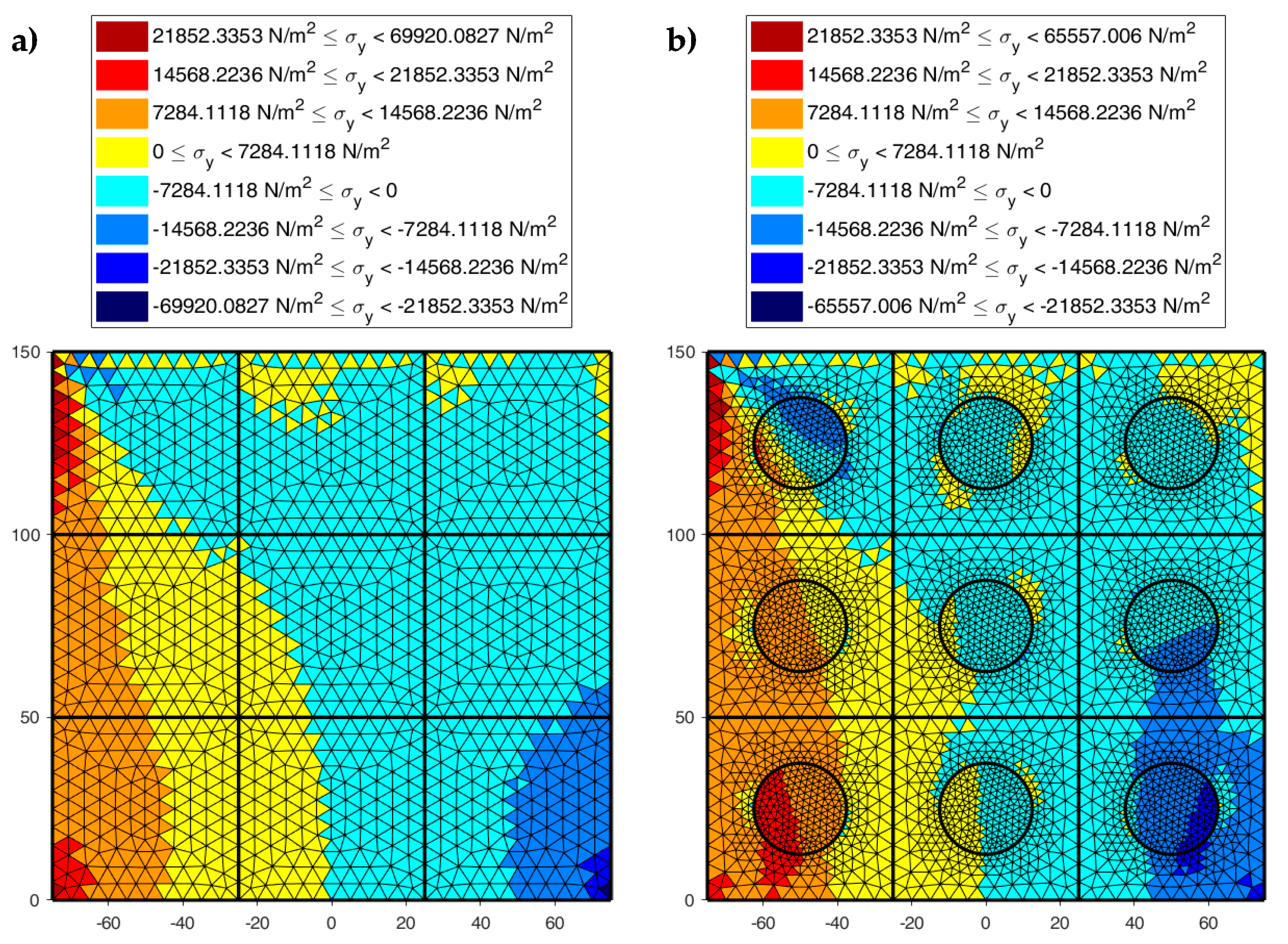
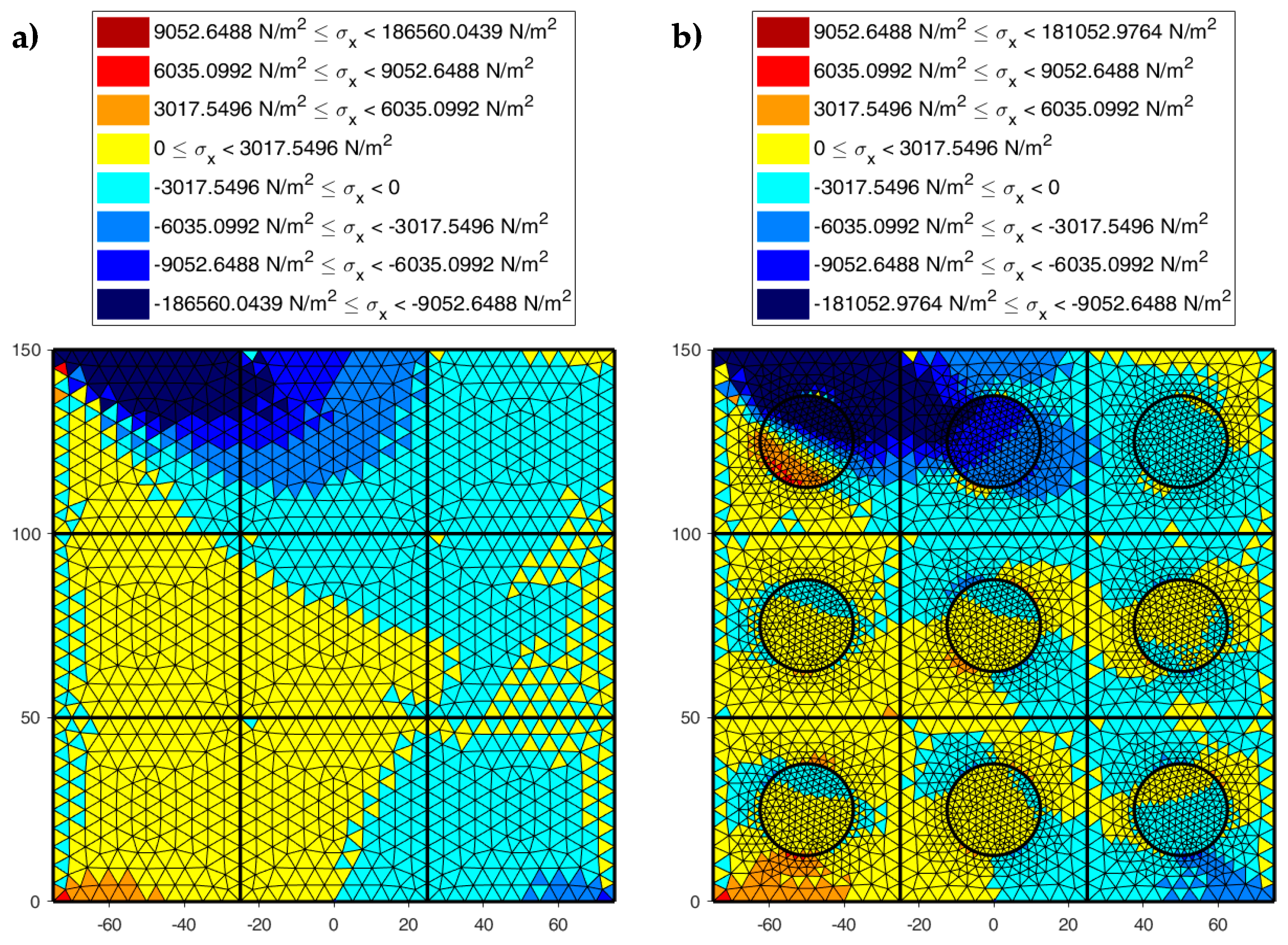
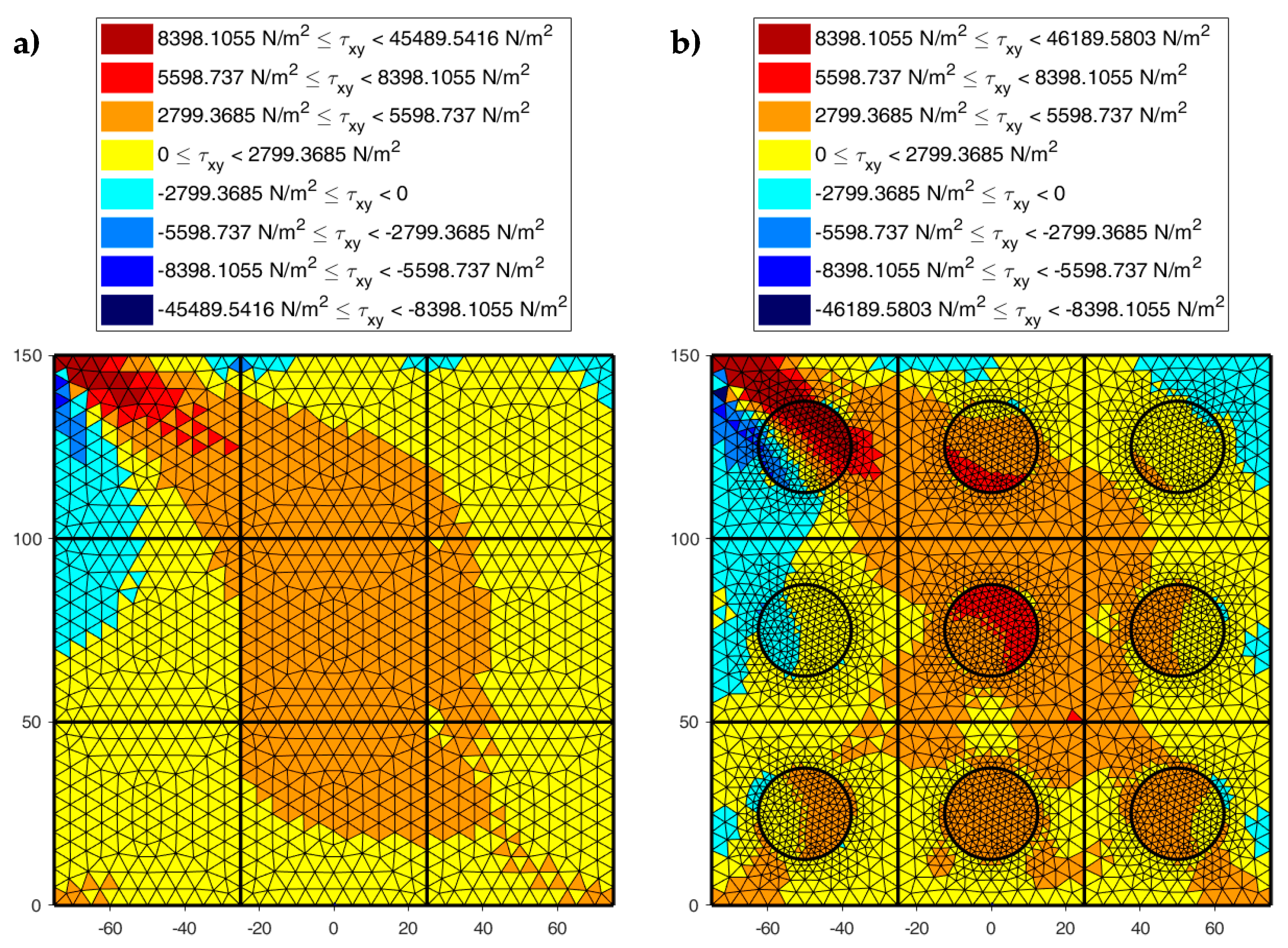
4.2. The Effect of the Inclusions for Shear Loads
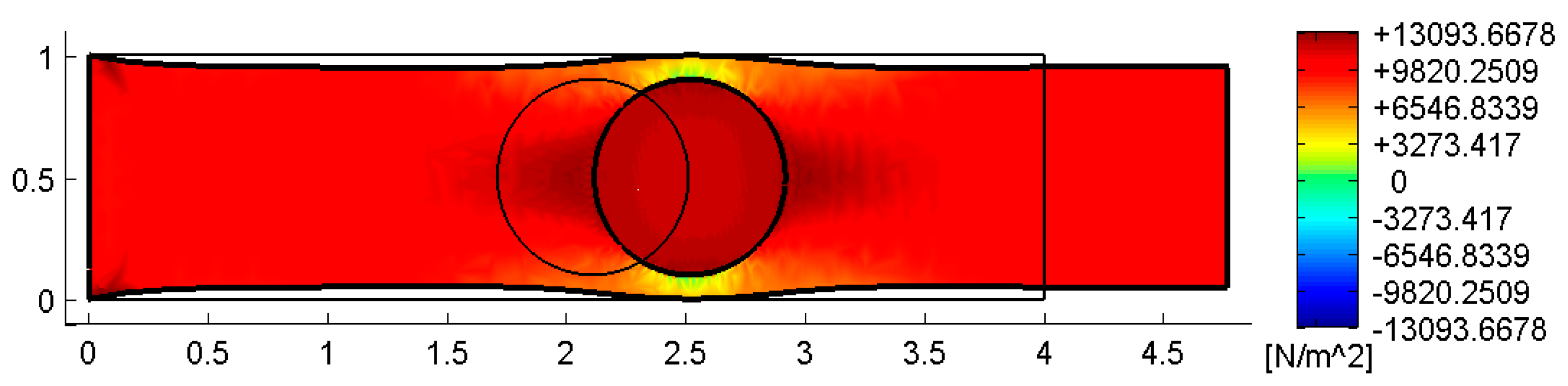
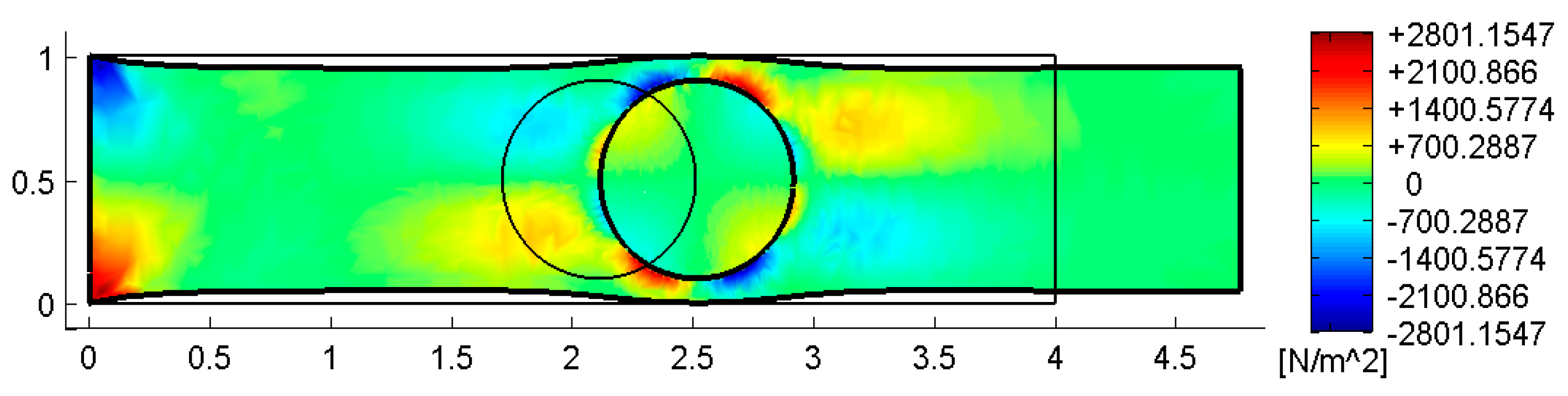
4.3. The Effect of the Inclusions for Axial Loads
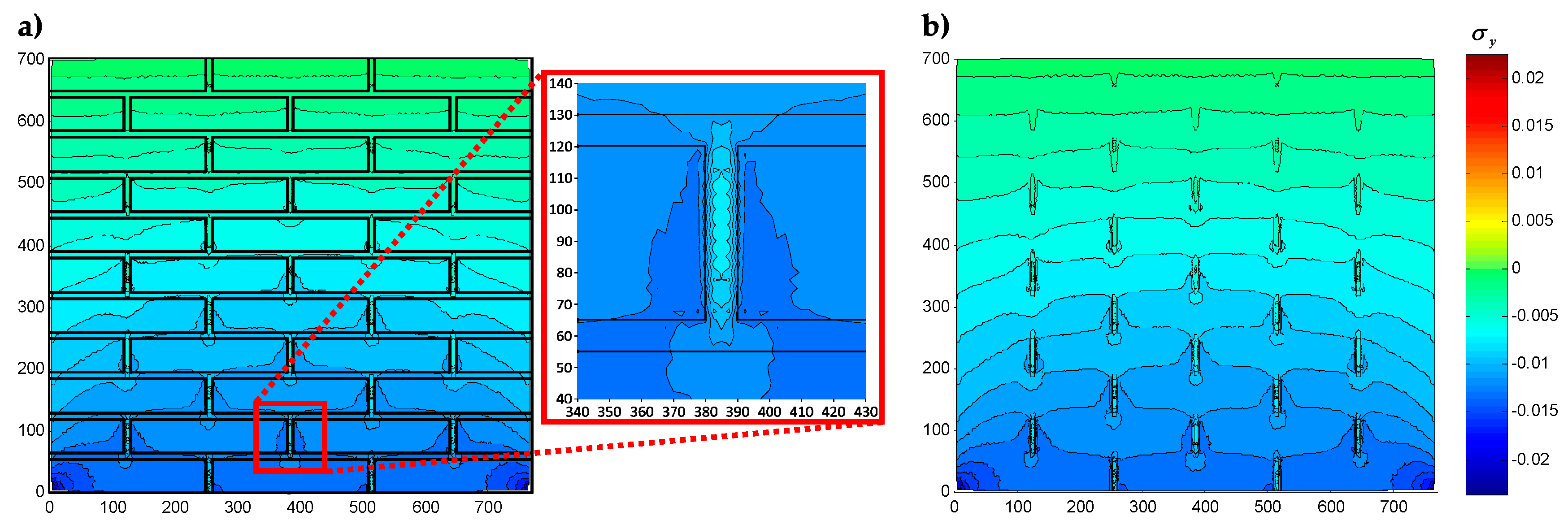
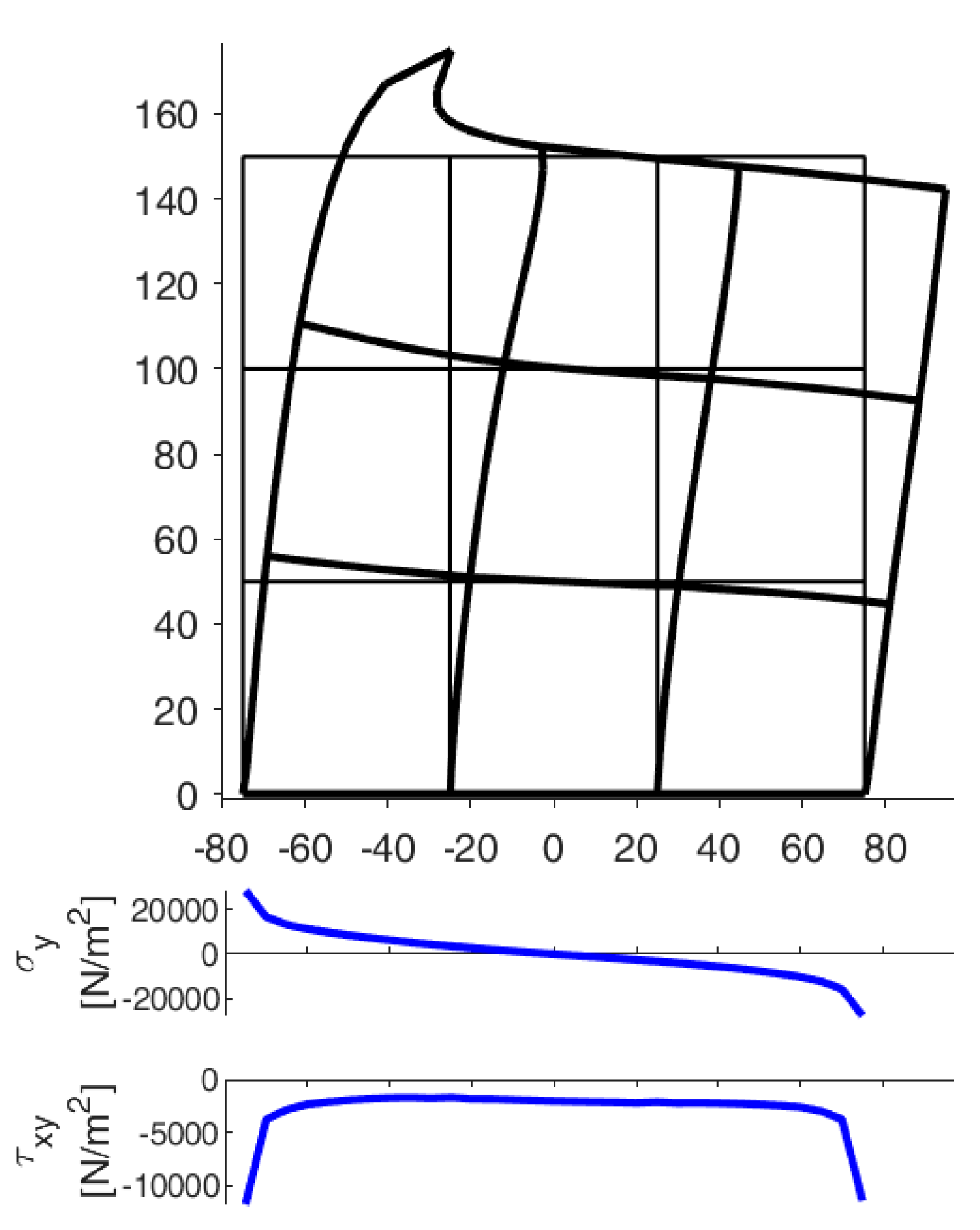
4.3.1. Comparison with the Results of a Previous CM Analysis
- Young’s modulus of both the inclusion and the matrix;
- Poisson’s ratio of both the inclusion and the matrix;
- Length of the base of the discrete element;
- Height of the discrete element (not necessarily equal to the base);
- Shape of the inclusion (no inclusion, round inclusion, polygonal inclusion with a randomly generated shape [107], or straight crack that form a random angle with the );
- Radius of the round inclusion, which also serves to generate the polygonal inclusion [107];
- Coordinates of the center of the inclusion;
- Number of subdivisions of the base (to generate the mesh);
- Number of subdivisions of the height (to generate the mesh);
- Number of subdivisions of the circular contour (in the case of round inclusion);
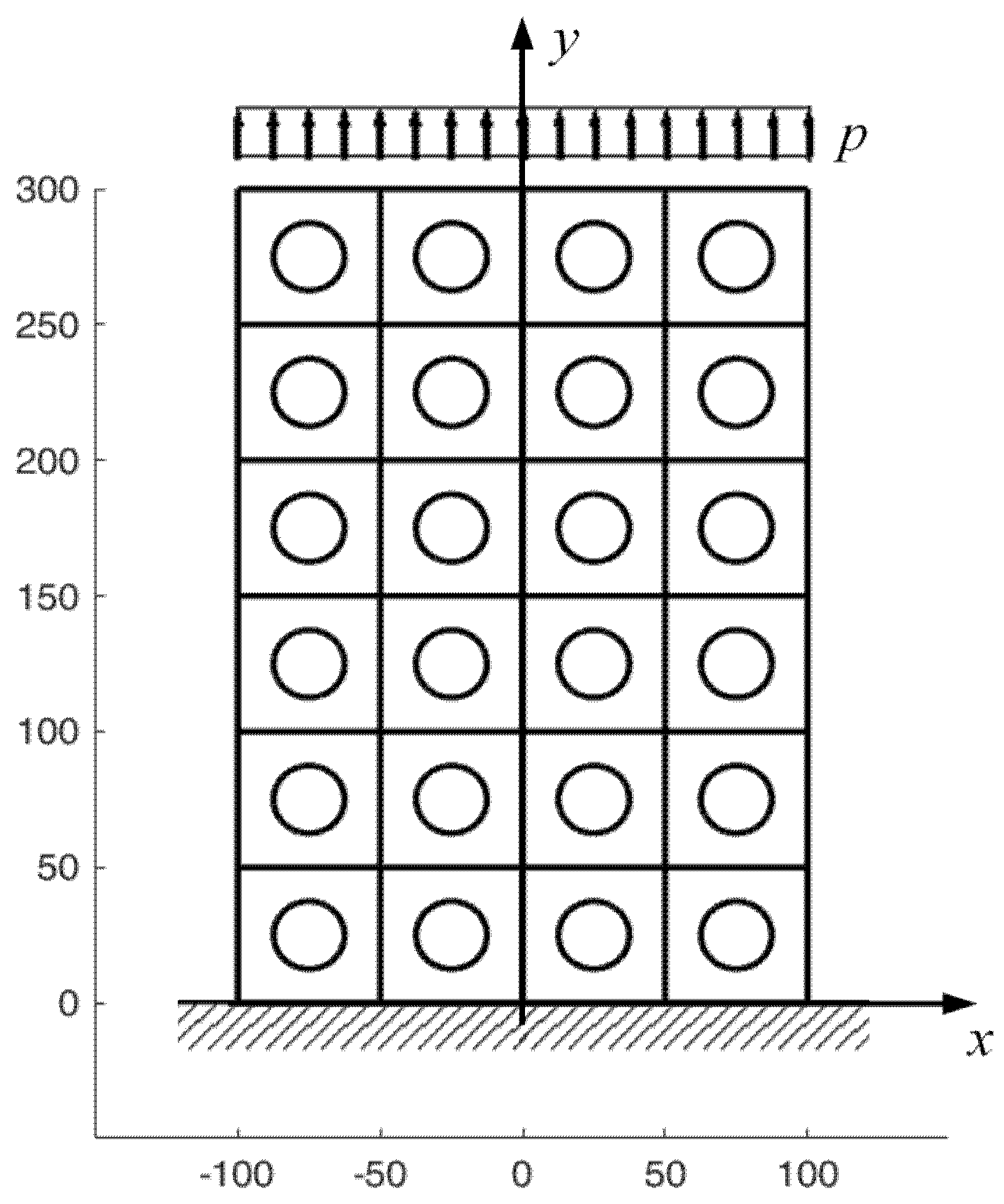
- Number of rows of the array;
- Number of columns of the array;
- Loading condition (concentrated force or distributed load);
- Position of the load (one of the two unconstrained corners or one of the midpoints of the three unconstrained sides, in the case of concentrated forces and one of the three unconstrained sides, in the case of distributed loads);
- Intensity of the load.
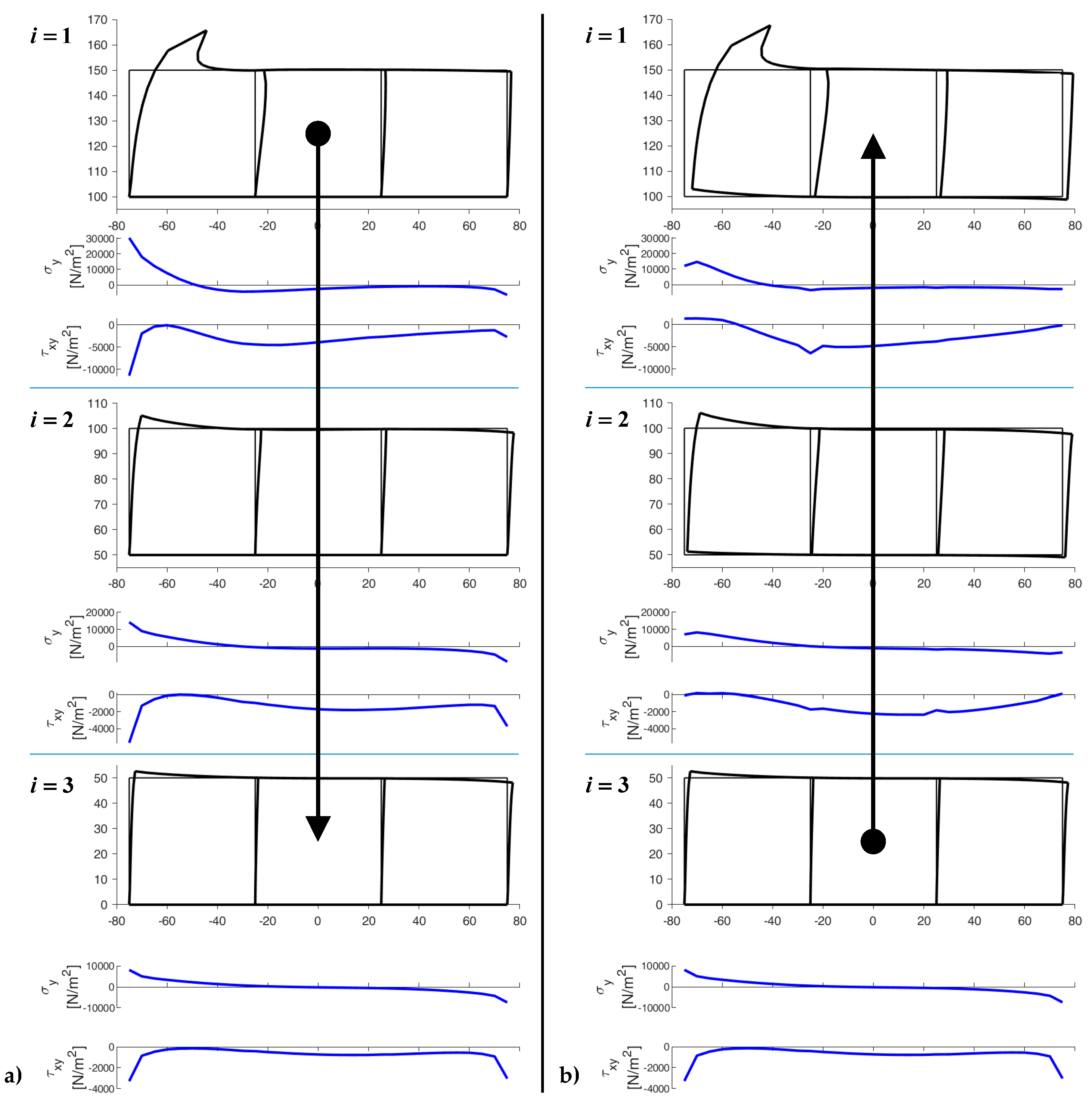
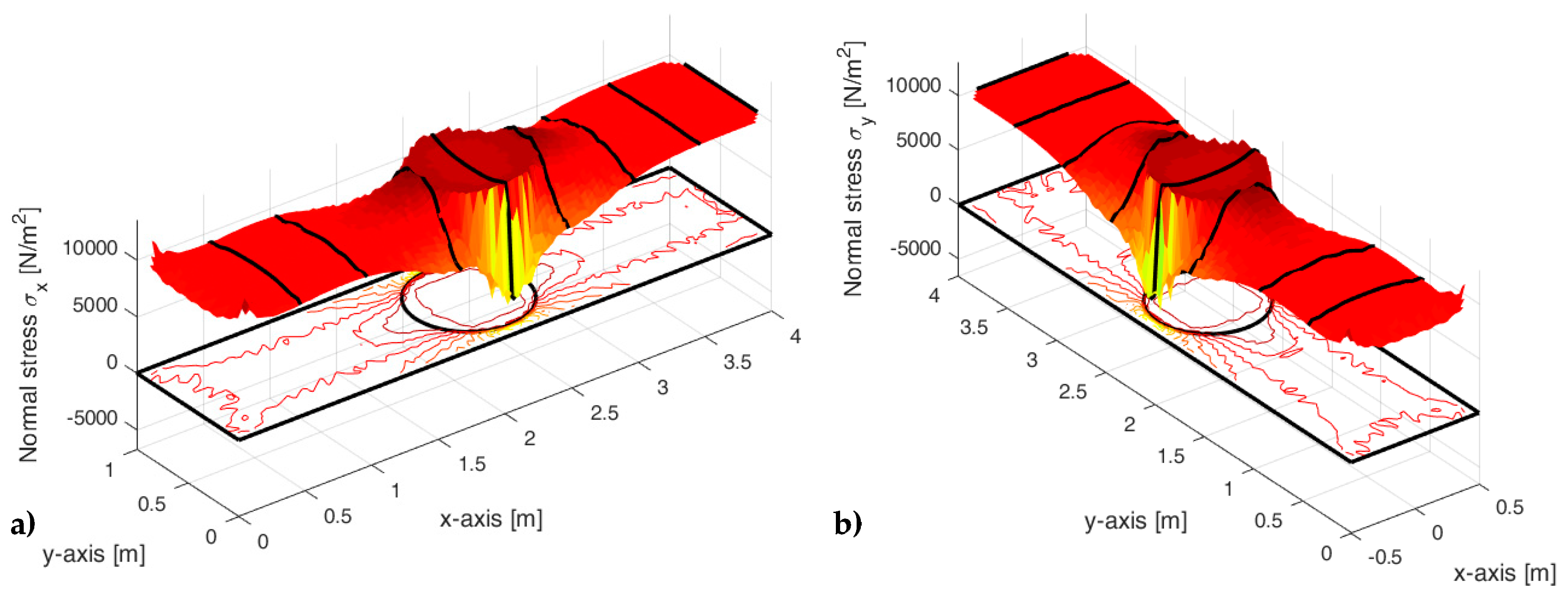
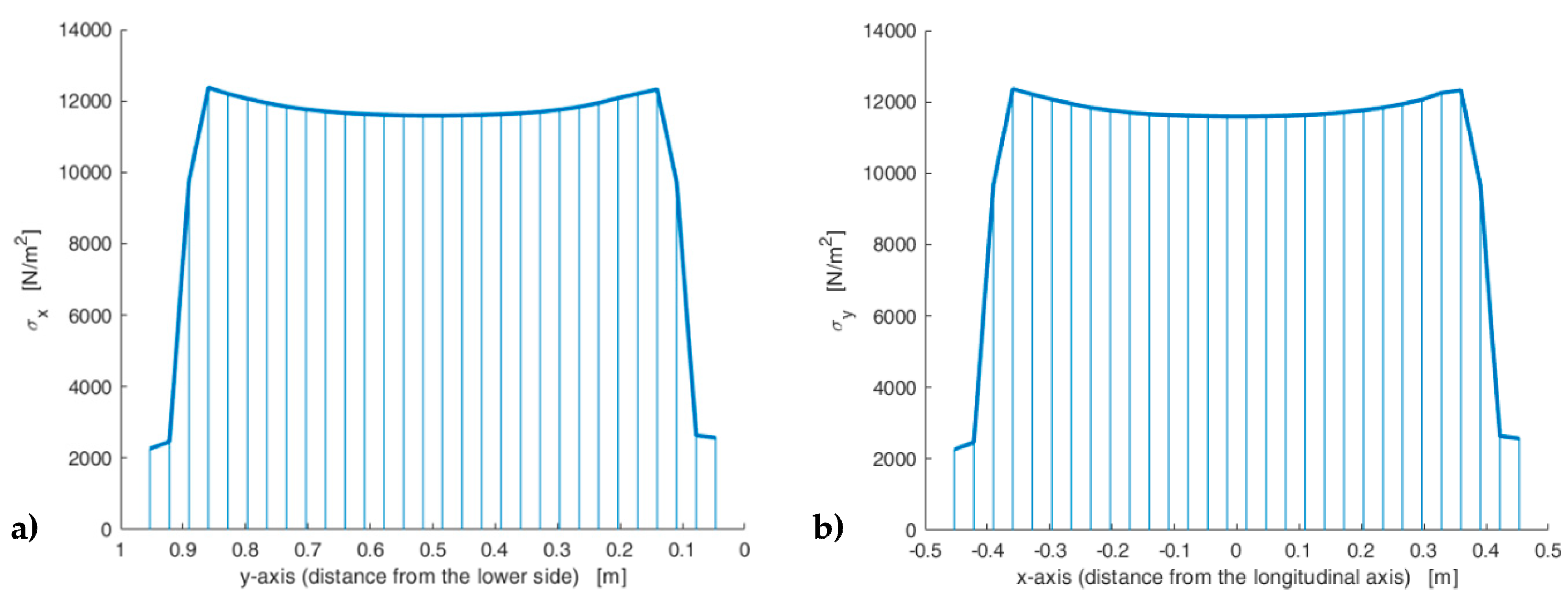
- (stresses calculated along a line at a distance equal to 1/8 of the longest side);
- (stresses calculated along a line at a distance equal to 1/4 of the longest side);
- (stresses calculated along a line tangent to the inclusion, on the constraint side);
- (stresses calculated along a line that passes through the center of the inclusion);
- (stresses calculated along a line tangent to the inclusion, on the opposite side of the constraint);
- (stresses calculated along a line at a distance equal to 3/4 of the longest side);
- (stresses calculated along a line at a distance equal to 7/8 of the longest side);
- (stresses calculated on the loaded side).
4.3.2. DECM Results for a Periodic Composite Specimen
5. Future Developments
6. Conclusions
- The DECM does not require the calibration of the stable time step, which is, instead, needed by the DEM to allow the convergence of the numerical solution;
- The DECM does not require a preliminary assessment of the minimum number of contact points to obtain the correct solution, which happens in the case of the DEM with deformable discrete elements to limit the computational cost of the dynamic relaxation technique.
Funding
Conflicts of Interest
References
- Barbero, E.J. Finite Element Analysis of Composite Materials; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2015. [Google Scholar]
- Giordano, A.; Mele, E.; De Luca, A. Modelling of historical masonry structures: Comparison of different approaches through a case study. Eng. Struct. 2002, 24, 1057–1069. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computations of historical masonry constructions. Prog. Struct. Eng. Mater. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- Tonti, E. A Direct Discrete Formulation of Field Laws: The Cell Method. CMES-Comp. Model. Eng. 2001, 2, 237–258. [Google Scholar]
- Ferretti, E. On the relationship between primal/dual cell complexes of the cell method and primal/dual vector spaces: An application to the cantilever elastic beam with elastic inclusion. Curved Layer. Struct. 2019, 6, 77–89. [Google Scholar] [CrossRef]
- Ferretti, E. The cell method: An overview on the main features. Curved and Layer. Struct. 2015, 2, 194–243. [Google Scholar] [CrossRef]
- Ferretti, E. The algebraic formulation: Why and how to use it. Curved and Layer. Struct. 2015, 2, 106–149. [Google Scholar] [CrossRef]
- Ferretti, E. The Cell Method: An enriched description of physics starting from the algebraic formulation. CMC-Comput. Mater. Con. 2013, 36, 49–71. [Google Scholar]
- Mohammadi, S. Discontinuum Mechanics Using Finite and Discrete Elements; WIT Press: Boston, MA, USA, 2003; ISBN 1-85312-959-3. [Google Scholar]
- Balevičius, R.; Džiugys, A.; Kačianauskas, R. Discrete element method and its application to the analysis of penetration into granular media. J. Civ. Eng. Manag. 2004, 10, 3–14. [Google Scholar] [CrossRef]
- Ardiç, Ö. Analysis of Bearing Capacity using Discrete Element Method. Master’s Thesis, Civil Engineering, Graduate School of Natural and Applied Sciences of Middle East Technical University, Çankaya/Ankara, Turkey, 2006. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive large scale movements in block rock systems. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- André, D.; Iordanoff, I.; Charles, J.-l.; Néauport, J. Discrete element method to simulate continuous material by using the cohesive beam model. Comput. Methods Appl. Mech. Energy 2012, 213, 113–125. [Google Scholar] [CrossRef]
- Deluzarche, R.; Cambou, B. Discrete numerical modelling of rockfill dams. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1075–1096. [Google Scholar] [CrossRef]
- Maynar, M.J.M.; Rodriguez, L.E.M. Discrete numerical model for analysis of earth pressure balance tunnel excavation. J. Geotech. Geoenviron. 2005, 131, 1234–1242. [Google Scholar] [CrossRef]
- Cheng, Y.P.; Nakata, Y.; Bolton, M.D. Discrete Element Simulation of Crushable Soil. Geotechnique 2003, 53, 633–641. [Google Scholar] [CrossRef]
- Hentz, S.; Daudeville, L.; Donzé, F.V. Discrete Element Modelling of Concrete and Identification of the Constitutive Behaviour. In Proceedings of the 15th ASCE Engineering Mechanics Conference, Columbia University, New York, NY, USA, 2–5 June 2002. [Google Scholar]
- Magnier, S.A.; Donze, F.V. Numerical simulations of impacts using a discrete element method. Mech. Cohesive Frict. Mater. 1998, 3, 257–276. [Google Scholar] [CrossRef]
- Tan, Y.; Yang, D.; Sheng, Y. Discrete element method (DEM) modeling of fracture and damage in the machining process of polycrystalline sic. J. Euro. Ceramic Soc. 2009, 29, 1029–1037. [Google Scholar] [CrossRef]
- Hentz, S.; Donzé, F.V.; Daudeville, L. Discrete element modelling of concrete submitted to dynamic loading at high strain rates. Comput. Struct. 2004, 82, 2509–2524. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Schauffert, A.; Cusatis, G. Lattice discrete particle model for fiber-reinforced concrete. I: Theory. J. Eng. Mech. 2012, 138, 826–833. [Google Scholar] [CrossRef]
- Bobet, A.; Fakhimi, A.; Johnson, S.; Morris, J.; Tonon, F.; Yeung, M.R. Numerical models in discontinuous media: Review of advances for rock mechanics applications. J. Geotech. Geoenviron. 2009, 135, 1547–1561. [Google Scholar] [CrossRef]
- Radi, K.; Jauffrès, D.; Deville, S.; Martin, C.L. Elasticity and fracture of brick and mortar materials using discrete element simulations. J. Mech. Phys. Solids 2019, 126, 101–116. [Google Scholar] [CrossRef]
- Radi, K.; Jauffrès, D.; Deville, S.; Martin, C.L. Strength and toughness trade-off optimization of nacre-like ceramic composites. Compos. B. Eng. 2020, 107699. [Google Scholar] [CrossRef]
- Schlangen, E.; Garboczi, E.J. Fracture simulations of concrete using lattice models: Computational aspects. Eng. Fract. Mech. 1997, 57, 319–332. [Google Scholar] [CrossRef]
- Leclerc, W. Discrete element method to simulate the elastic behavior of 3D heterogeneous continuous media. Int. J. Solids Struct. 2017, 121, 86–102. [Google Scholar] [CrossRef]
- Jebahi, M.; André, A.; Dau, F.; Charles, J.-l.; Iordanoff, I. Simulation of vickers indentation of silica glass. J. Non-Cryst. Solids 2013, 378, 15–24. [Google Scholar] [CrossRef]
- Leclerc, W.; Haddad, H.; Guessasma, M. On the suitability of a Discrete Element Method to simulate cracks initiation and propagation in heterogeneous media. Int. J. Solids Struct. 2017, 108, 98–114. [Google Scholar] [CrossRef]
- Potyondy, D.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Fakhimi, A.; Villegas, T. Application of dimensional analysis in calibration of a discrete element model for rock deformation and fracture. Rock Mech. Rock Eng. 2007, 40, 193–211. [Google Scholar] [CrossRef]
- Leclerc, W.; Haddad, H.; Guessasma, M. On a discrete element method to simulate thermal-induced damage in 2D composite materials. Comput. Struct. 2018, 196, 277–291. [Google Scholar] [CrossRef]
- Leclerc, W.; Haddad, H.; Guessasma, M. DEM-FEM coupling method to simulate thermally induced stresses and local damage in composite materials. Int. J. Solids Struct. 2019, 160, 276–292. [Google Scholar] [CrossRef]
- José, V.L. Discrete element modeling of masonry structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar]
- Sarhosis, V.; Bagi, K.; Lemos, J.V.; Milani, G. Computational Modelling of Masonry Structures Using the Discrete Element Method; Advances in Civil and Industrial Engineering (ACIE) Book Series; Engineering Science Reference (IGI Global): Hershey, PA, USA, 2016. [Google Scholar]
- Pulatsu, B.; Bretas, E.M.; Lourenço, P.B. Discrete element modeling of masonry structures: Validation and application. Earthq. Struct. 2016, 11, 563–582. [Google Scholar] [CrossRef]
- Sarhosis, V.; Lemos, J.V. Detailed micro-modelling of masonry using the discrete element method. Comput. Struct. 2018, 206, 66–81. [Google Scholar] [CrossRef]
- Sarhosis, V.; Forgcas, T.; Lemos, J.V. A discrete approach for modelling backfill material in masonry arch bridges. Comput. Struct. 2019, 224, 106–118. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Castori, G.; Sisti, R.; De Maria, A. Analysis of the collapse mechanisms of medieval churches struck by the 2016 Umbrian earthquake. Int. J. Archit. Herit. 2018, 1–14. [Google Scholar] [CrossRef]
- Castori, G.; Borri, A.; De Maria, A.; Corradi, M.; Sisti, R. Seismic vulnerability assessment of a monumental masonry building. Eng. Struct. 2017, 136, 454–465. [Google Scholar] [CrossRef]
- Castori, G.; Corradi, M.; Borri, A.; Sisti, R.; De Maria, A. Macroelement and dynamic seismic analysis of the medieval government building of Perugia, Italy. Int. J. Innov. Learn. (IJIL) 2019, 4, 297–310. [Google Scholar]
- Ferretti, D.; Coïsson, E.; Rozzi, M. A new numerical approach to the structural analysis of masonry vaults. Key Eng. Mater. 2017, 747, 52–59. [Google Scholar] [CrossRef]
- Obermayr, M.; Vrettos, C.; Eberhard, P. A discrete element model for cohesive soil. In Particle-based Methods III: Fundamentals and Applications. In Proceedings of the III International Conference on Particle-based Methods—Fundamentals and Applications, PARTICLES 3 2013, Stuttgart, Germany, 18–20 September 2013. [Google Scholar]
- Akhoundi, F.; Vasconcelos, G.; Lourenço, P.B. Experimental Out-Of-Plane Behavior of Brick Masonry Infilled Frames. Int. J. Archit. Herit. 2018. [Google Scholar] [CrossRef]
- Csikai, B.; Ramos, L.F.; Basto, P.; Moreira, S.; Lourenço, P.B. Flexural out-of-plane retrofitting technique for masonry walls in historical constructions. In Proceedings of the SAHC2014 9th International Conference on Structural Analysis of Historical Constructions, Mexico City, Mexico, 14–17 October 2014. [Google Scholar]
- Lourenço, P.B. Technologies for Seismic Retrofitting and Strengthening of Earthen and Masonry Structures: Assessment and Application. In Recent Advances in Earthquake Engineering in Europe, ECEE 2018, Geotechnical, Geological and Earthquake Engineering; Pitilakis, K., Ed.; Springer: Cham, Switzerland, 2018; Volume 46, pp. 501–518. [Google Scholar]
- Coïsson, E.; Ferrari, L.; Ferretti, D.; Rozzi, M. Non-Smooth Dynamic Analysis of Local Seismic Damage Mechanisms of the San Felice Fortress in Northern Italy. Procedia Eng. 2016, 161, 451–457. [Google Scholar] [CrossRef]
- Moukadiri, D.; Leclerc, W.; Khellil, K.; Aboura, Z.; Guessasma, M.; Bellenger, E.; Druesne, F. Halo approach to evaluate the stress distribution in 3D discrete element method simulation: Validation and application to flax/bio based epoxy composite. Modelling Simul. Mater. Sci. Eng. 2019, 27, 065005. [Google Scholar] [CrossRef]
- Ferretti, E. Some new findings on the mathematical structure of the cell method. Int. J. Math. Models Methods Appl. Sci. 2015, 9, 473–486. [Google Scholar]
- Ferretti, E. The mathematical foundations of the cell method. Int. J. Math. Models Methods Appl. Sci. 2015, 9, 362–379. [Google Scholar]
- Ferretti, E. Masonry walls under shear test: A CM modeling. CMES-Comp. Model. Eng. 2008, 30, 163–189. [Google Scholar]
- Ferretti, E. On nonlocality and Locality: Differential and Discrete Formulations. In Proceedings of the ICF11, 11th International Conference on Fracture 2005, Turin, Italy, 20–25 March 2005; Carpinteri, A., Ed.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; pp. 1728–1733. [Google Scholar]
- Huang, T.; Zheng, J.; Gong, W. The Group Effect on Negative Skin Friction on Piles. Procedia Eng. 2015, 116, 802–808. [Google Scholar] [CrossRef]
- Saha, A. The Influence of negative skin friction on piles and pile groups & settlement of existing structures. Int. J. Emerg. Technol. 2015, 6, 53–59. [Google Scholar]
- Sukumar, N.; Bolander, J.E. Numerical computation of discrete differential operators on non-uniform grid. CMES-Comp. Model. Eng. 2003, 4, 691–705. [Google Scholar]
- Bolander, J.E.; Sukumar, N. Irregular lattice model for quasistatic crack propagation. Phys. Rev. B 2005, 71, 094106. [Google Scholar] [CrossRef]
- Kang, J.; Bolander, J.E. Flow in fibrous composite materials: Numerical simulations. In Proceedings of the Conference on Computational Modelling of Concrete and Concrete Structures (EURO-C 2018), Bad Hofgastein, Austria, 26 February–1 March 2018. [Google Scholar]
- Ferretti, E. Crack propagation modeling by remeshing using the Cell Method (CM). CMES Comput. Model. Eng. 2003, 4, 51–72. [Google Scholar]
- Israelsson, J.I. Short Descriptions of UDEC and 3DEC. Dev. Geotech. Eng. 1996, 79, 523–528. [Google Scholar]
- Cundall, P.A.; Hart, R.D. Numerical modelling of discontinua. Eng. Comput. 1992, 9, 101–113. [Google Scholar] [CrossRef]
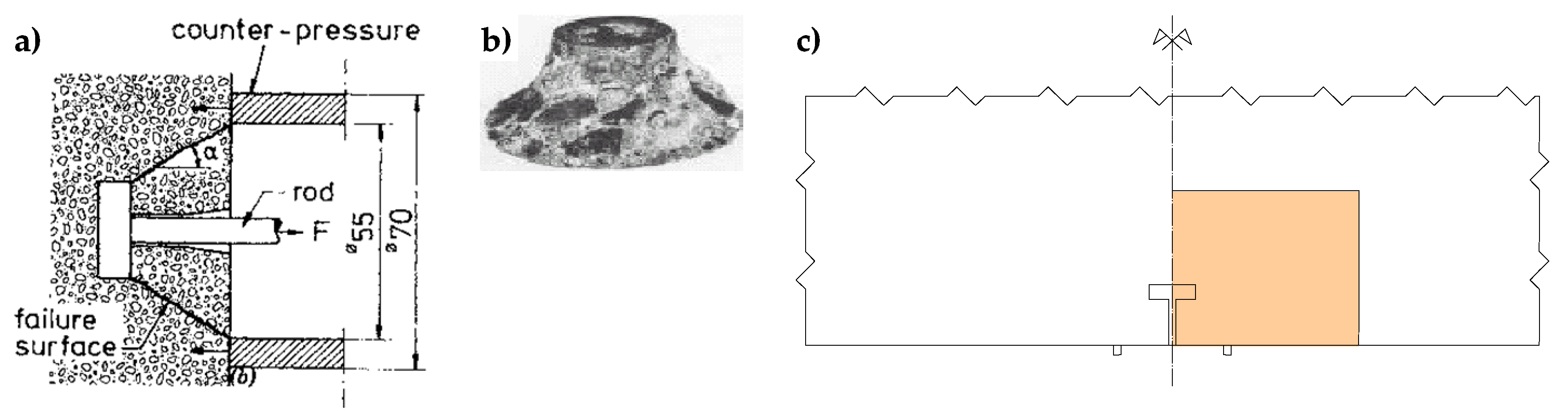
- Ferretti, E. Modeling of the pullout test through The Cell Method. In Proceedings of the International Conference on Restoration, Recycling and Rejuvenation Technology for Engineering and Architecture Application, RRRTE’04, Cesena, Italy, 7–11 June 2004; pp. 180–192. [Google Scholar]
- Ferretti, E. A Cell Method stress analysis in thin floor tiles subjected to temperature variation. CMC-Comput. Mater. Con. 2013, 36, 293–322. [Google Scholar]
- Mohebkhah, A.; Sarhosis, V.; Tavafi, E. Seismic behaviour of cube of Zoroaster tower using the Distinct Element Method. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. (JRMGE) 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Casolo, S.; Uva, G. Nonlinear analysis of out-of-plane masonry façades: Full dynamic versus pushover methods by rigid body and spring model. Earthq. Eng. Struct. Dyn. 2018, 42, 499–521. [Google Scholar] [CrossRef]
- Cherepanov, G.P. The contact problem of the mathematical theory of elasticity with stick and slip areas. The theory of rolling and tribology. J. Appl. Math. Mech. 2015, 79, 81–101. [Google Scholar] [CrossRef]
- Blázquez, A.; París, F. Effect of numerical artificial corners appearing when using BEM on contact stresses. Eng. Anal. Bound. Elem. 2011, 35, 1029–1037. [Google Scholar] [CrossRef]
- Hartmann, S.; Weyler, R.; Oliver, J.; Cante, J.C.; Hernández, J.A. A 3D frictionless contact domain method for large deformation problems. CMES Comput. Model. Eng. 2010, 55, 211–269. [Google Scholar]
- Imai, R.; Nakagawa, M. A reduction algorithm of contact problems for core seismic analysis of fast breeder reactors. CMES Comput. Model. Eng. 2012, 84, 253–281. [Google Scholar]
- Oner, E.; Yaylaci, M.; Birinci, A. Analytical solution of a contact problem and comparison with the results from FEM. Struct. Eng. Mech. 2015, 54, 607–622. [Google Scholar] [CrossRef]
- Santosa, D.B.V.; Bandeira, A.A. Numerical modeling of contact problems with the finite element method utilizing a B-Spline surface for contact surface smoothing. Lat. Am. J. Solids Stru. 2018, 15, e77. [Google Scholar] [CrossRef]
- Theilig, H. Efficient fracture analysis of 2D crack problems by the MVCCI method. SDHM Struct. Durab. Health Monit. 2010, 6, 239–271. [Google Scholar]
- Yun, C.; Junzhi, C.; Yufeng, N.; Yiqiang, L. A New Algorithm for the Thermo-Mechanical Coupled Frictional Contact Problem of Polycrystalline Aggregates Based on Plastic Slip Theory. CMES Comput. Model. Eng. 2011, 76, 189–206. [Google Scholar]
- Zhou, Y.-T.; Li, X.; Yu, D.-H.; Lee, K.-Y. Coupled crack/contact analysis for composite material containing periodic cracks under periodic rigid punches action. CMES Comput. Model. Eng. 2010, 63, 163–189. [Google Scholar]
- Lemos, J.V. Discrete Element Modeling of the Seismic Behavior of Masonry Construction. Buildings 2019, 9, 43. [Google Scholar] [CrossRef]
- Pham, A.T.; Pham, X.D.; Tan, K.H. Slab corner effect on torsional behaviourof perimeter beams under missing column scenario. Mag. Concr. Res. 2018, 71, 1–43. [Google Scholar]
- Ou, C.-Y.; Shiau, B.-Y. Analysis of the corner effect on excavation behaviors. Can. Geotech. J. 2011, 35, 532–540. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.A.; Zhao, D.; Ghaboussi, J. Shortest Link Method for Contact Detection in Discrete Element Method. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 783–801. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.A.; Zhao, D.; Ghaboussi, J. A Fast Contact Detection Algorithm for 3-D Discrete Element Method. Comput. Geotech. 2004, 31, 575–587. [Google Scholar] [CrossRef]
- Richard, H.A.; Schramm, B.; Schirmeisen, N.-H. Cracks on Mixed Mode loading—Theories, experiments, simulations. Int. J. Fatigue 2014, 62, 93–103. [Google Scholar] [CrossRef]
- Har, J. A New Scalable Parallel Finite Element Approach for Contact-Impact Problems. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1998. [Google Scholar]
- Papadopoulos, P.; Jones, R.E.; Solberg, J. A novel finite element formulation for frictionless contact problems. Int. J. Num. Meth. Engrg. 1995, 38, 2603–2617. [Google Scholar] [CrossRef]
- Zhong, Z.H. Finite Element Procedures for Contact-Impact Problems; Oxford Science Publications: Oxford, NY, USA; Tokyo, Japan, 1993. [Google Scholar]
- Ferretti, E.; Di Leo, A.; Viola, E. Computational Aspects and Numerical Simulations in the Elastic Constants Identification. In Problems in Structural Identification and Diagnostics: General Aspects and Applications; CISM Courses and Lectures No. 471; Davini, C., Viola, E., Eds.; Springer: Wien, Austria, 2003; pp. 133–147. [Google Scholar]
- Ferretti, E. Crack-path analysis for brittle and non-brittle cracks: A cell method approach. CMES-Comp. Model. Eng. 2004, 6, 227–244. [Google Scholar]
- Ferretti, E. Cell method analysis of crack propagation in tensioned concrete plates. CMES-Comp. Model. Eng. 2009, 54, 253–281. [Google Scholar]
- Cundall, P.A. A Discontinuous Future for Numerical Modelling in Geomechanics. Proc. Inst. Civil Eng. Geotech. Eng. 2001, 149, 41–47. [Google Scholar] [CrossRef]
- Ferretti, E. A discussion of strain-softening in concrete. Int. J. Fract. 2004, 126, L3–L10. [Google Scholar] [CrossRef]
- Alonso-Marroquin, F. Micromechanical Investigation of Soil Deformation: Incremental Response and Granular Ratcheting. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2004. [Google Scholar]
- Ferretti, E. Experimental procedure for verifying strain-softening in concrete. Int. J. Fract. 2004, 126, L27–L34. [Google Scholar] [CrossRef]
- Ferretti, E.; Di Leo, A. Cracking and creep role in displacements at constant load: Concrete solids in compression. CMC-Comput. Mater. Con. 2008, 7, 59–79. [Google Scholar]
- Daponte, P.; Olivito, R.S. Crack Detection Measurements in Concrete. In Proceedings of the ISMM International Conference Microcomputers Applications, Los Angeles, CA, USA, 14–16 December 1989; pp. 123–127. [Google Scholar]
- Ferretti, E. On Strain-softening in dynamics. Int. J. Fract. 2004, 126, L75–L82. [Google Scholar] [CrossRef]
- Ferretti, E.; Di Leo, A.; Viola, E. A Novel Approach for the Identification of Material Elastic Constants. In Problems in Structural Identification and Diagnostics: General Aspects and Applications; CISM Courses and Lectures No. 471; Davini, C., Viola, E., Eds.; Springer: Wien, Austria, 2003; pp. 117–131. [Google Scholar]
- Ferretti, E. Shape-effect in the effective laws of plain and rubberized concrete. CMC-Comput. Mater. Con. 2012, 30, 237–284. [Google Scholar]
- Rogula, D. Introduction to Nonlocal Theory of Material Media. In Nonlocal Theory of Material Media; CISM Courses and Lectures No. 268; Rogula, D., Ed.; Springer: Wien, Austria, 1982; pp. 125–222. [Google Scholar]
- Kröner, E. Elasticity theory of materials with long-range cohesive forces. Int. J. Solids Struct. 1968, 3, 731–742. [Google Scholar] [CrossRef]
- Eringen, A.C. A unified theory of thermomechanical materials. Int. J. Eng. Sci. 1966, 4, 179–202. [Google Scholar] [CrossRef]
- Kunin, I.A. Theory of elasticity with spatial dispersion. Prikl. Mat. Mekh. 1966, 30, 866. [Google Scholar]
- Krumhansl, J.A. Generalized Continuum Field Representation for Lattice Vibrations. In Lattice Dynamics; Wallis, R.F., Ed.; Pergamon: London, UK, 1965; pp. 627–634. [Google Scholar]
- Rogula, D. Influence of spatial acoustic dispersion on dynamical properties of dislocations. Bull. l’Académie Pol. Sci. Séries Sci. Tech. 1965, 13, 337–343. [Google Scholar]
- Duhem, P. Le potentiel thermodynamique et la pression hydrostatique. Ann. Sci. Ecole Norm. S. 1893, 10, 183–230. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Chang, T.P. Is Strain-Softening Mathematically Admissible? In Volume 2: Engineering Mechanics in Civil Engineering. In Proceedings of the 5th Engineering Mechanics Division Specialty Conference, Laramie, WY, USA, 1–3 August 1984; Boresi, A.P., Chong, K.P., Eds.; American Society of Civil Engineers: New York, NY, USA, 1984; pp. 1377–1380. [Google Scholar]
- Bažant, Z.P.; Jirásek, M. nonlocal integral formulations of plasticity and damage: survey of progress. J. Eng. Mech. 2002, 128, 1119–1149. [Google Scholar] [CrossRef]
- Ferretti, E. A discrete nonlocal formulation using local constitutive laws. Int. J. Fract. 2004, 130, L175–L182. [Google Scholar] [CrossRef]
- Ferretti, E. Multiscale Modeling of Composite Materials with DECM Approach: Shape Effect of Inclusions. Int. J. Mech. 2019, 13, 114–128. [Google Scholar]
- Ferretti, E. Parallel Computing for Multiscale Modeling with the DECM. In prepared.


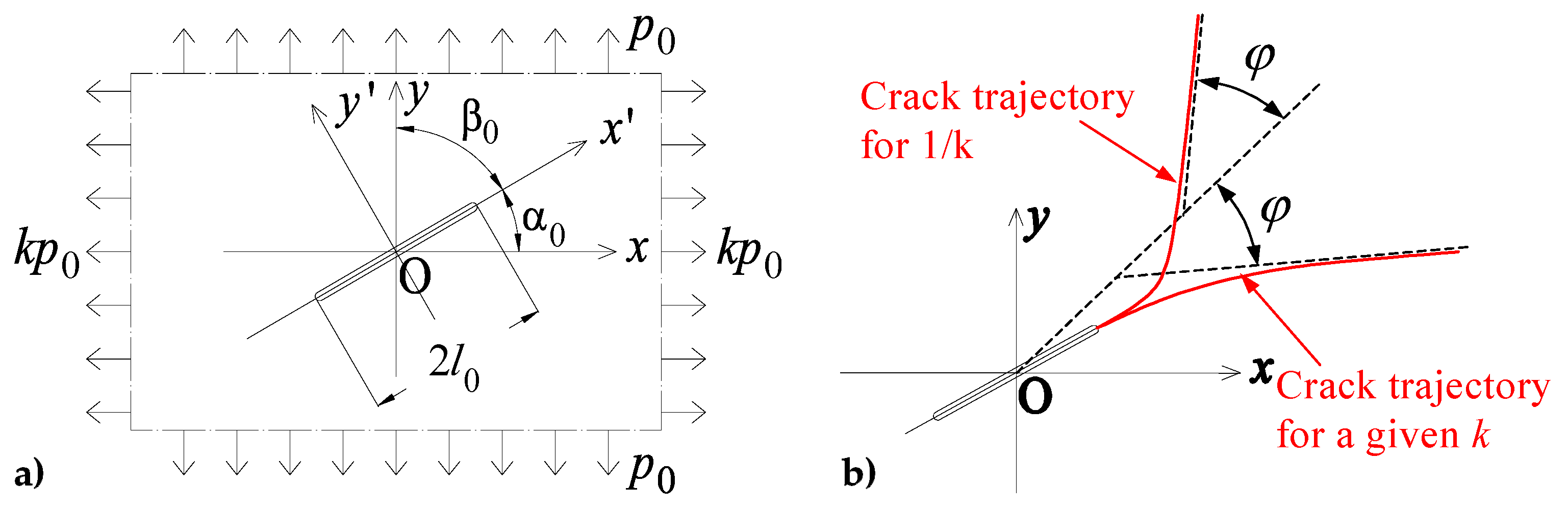



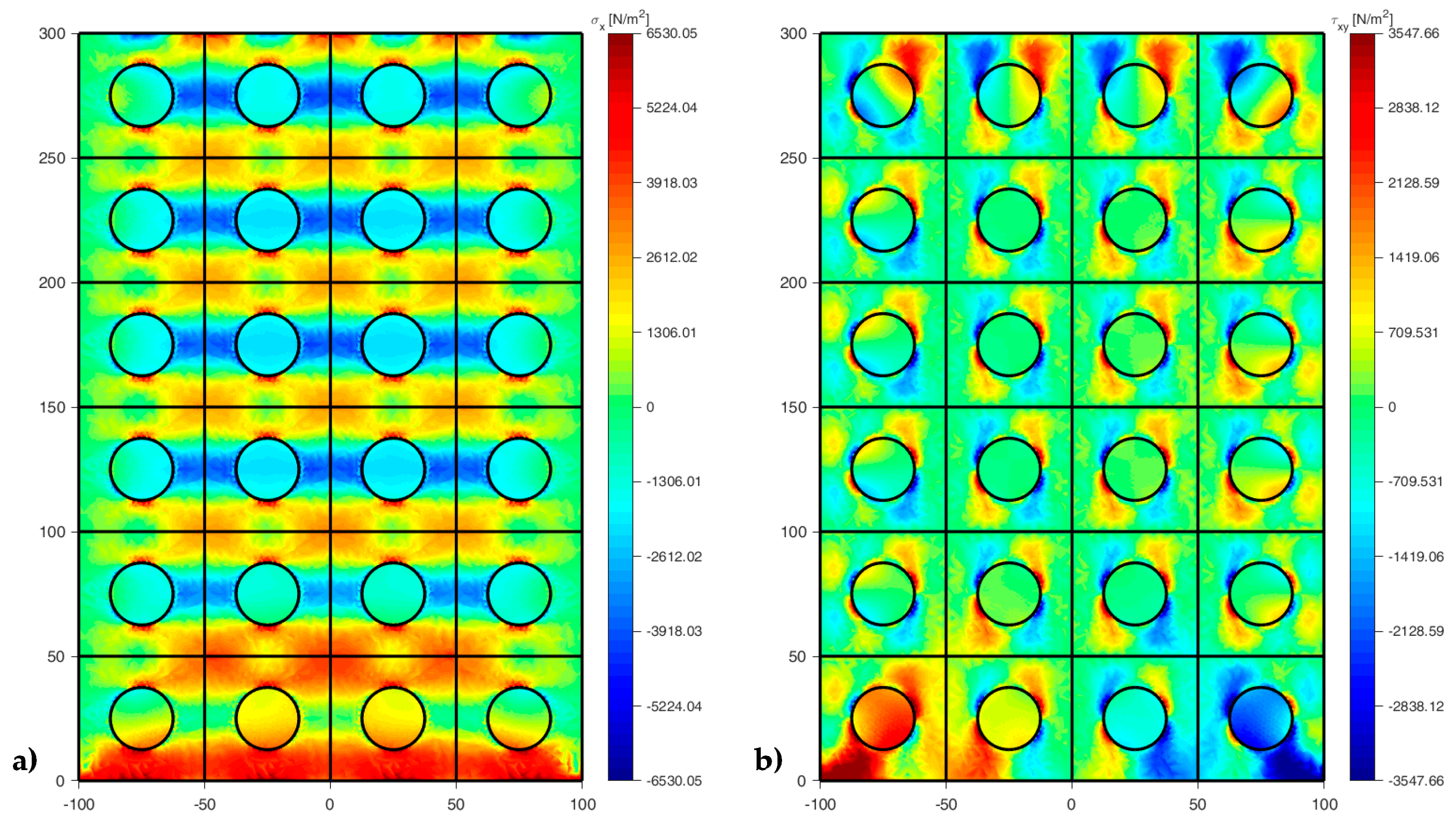
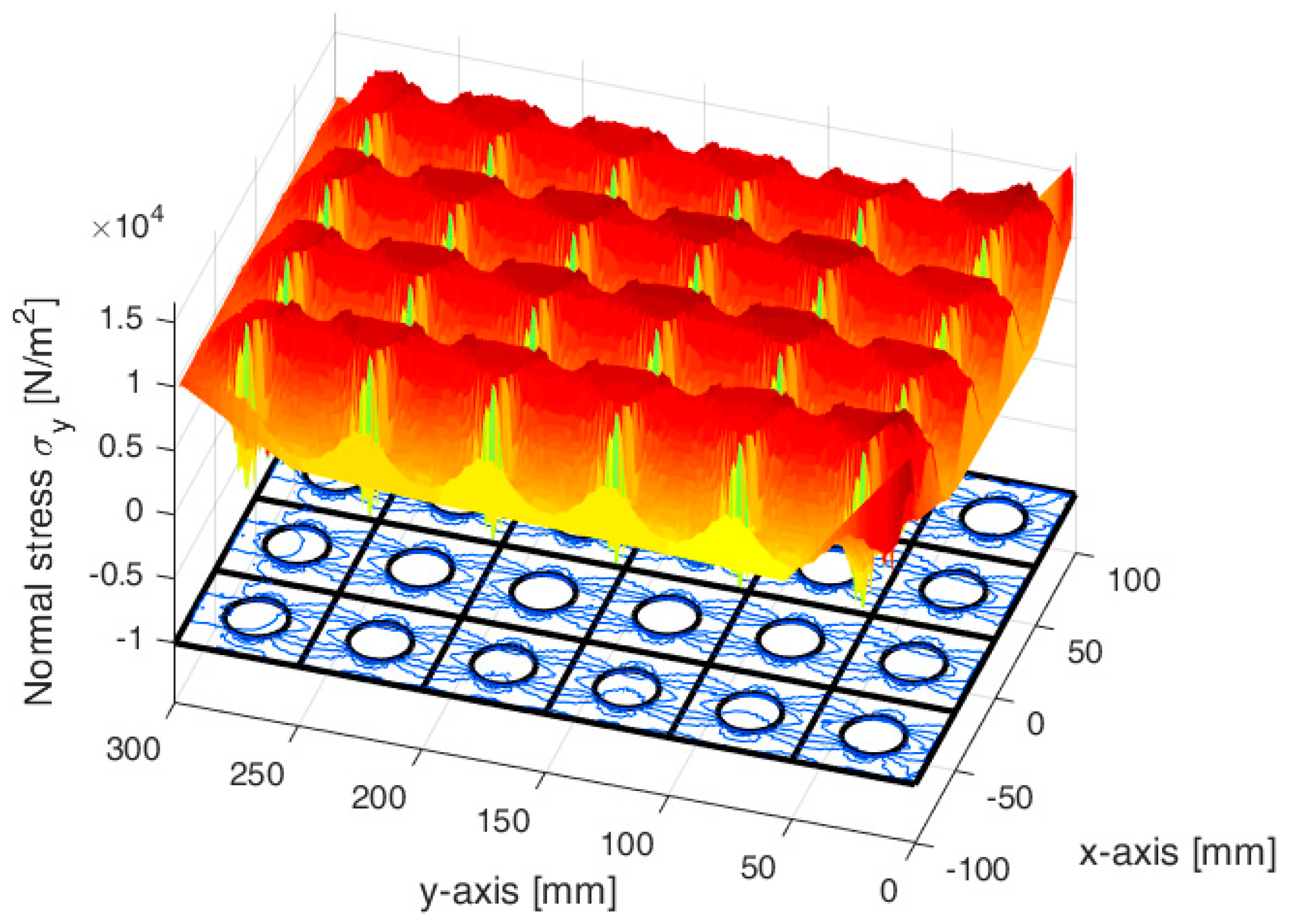
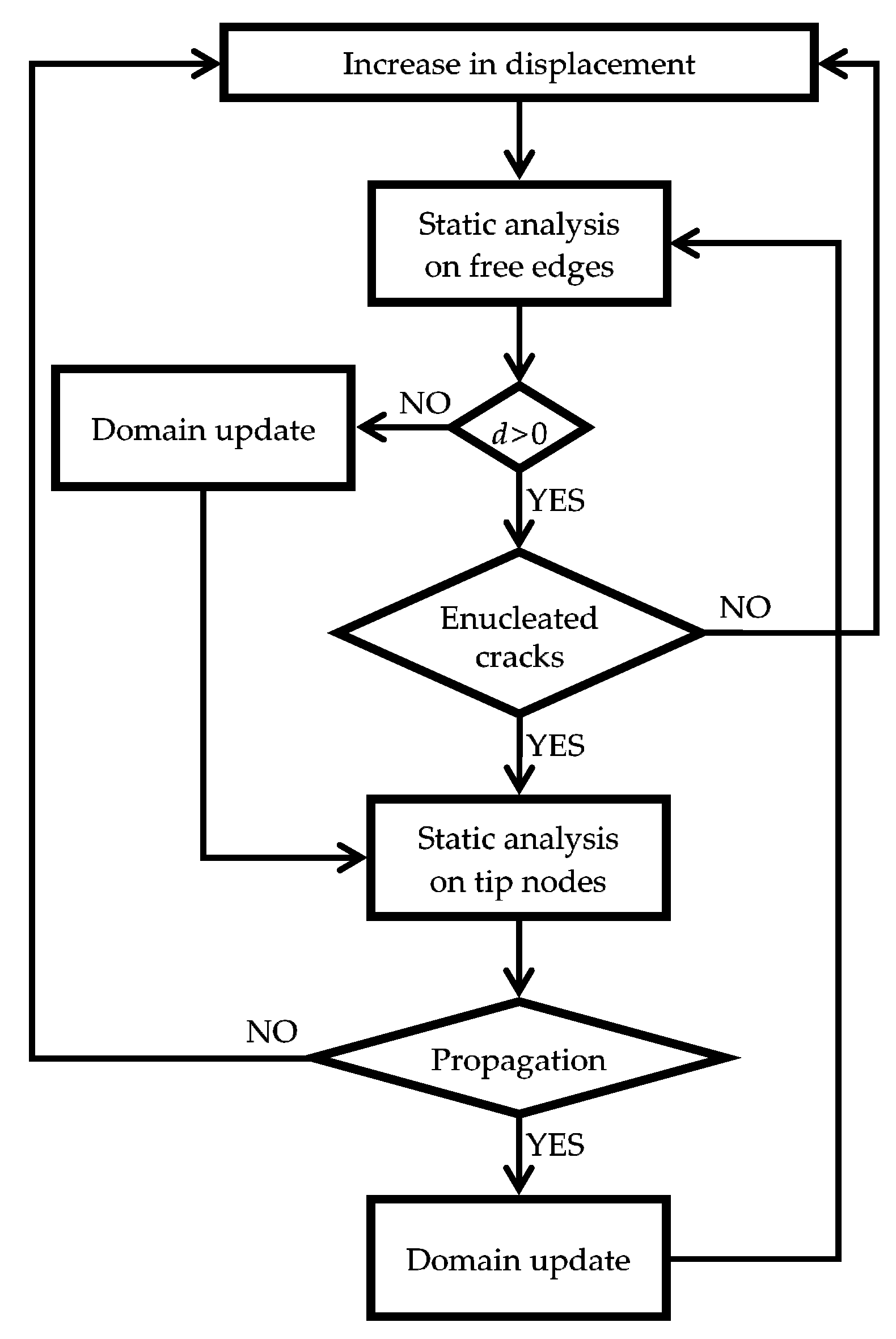


| Symbol | Description | Value |
|---|---|---|
| Base | ||
| Height | ||
| Radius of the round inclusion | ||
| Distance of the center C from the left side | ||
| Distance of the center C from the lower side | ||
| Number of subdivisions of the base | 32 | |
| Number of subdivisions of the height | 8 | |
| Number of subdivisions of the circular contour | 80 |
| Symbol | Description | Value |
|---|---|---|
| Base | ||
| Height | ||
| Radius of the round inclusion | ||
| Distance of the center of the inclusion from the lower side | ||
| Distance of the center of the inclusion from the left side | ||
| Number of subdivisions of the base | 8 | |
| Number of subdivisions of the height | 32 | |
| Number of subdivisions of the circular contour | 80 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, E. DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method. Materials 2020, 13, 880. https://doi.org/10.3390/ma13040880
Ferretti E. DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method. Materials. 2020; 13(4):880. https://doi.org/10.3390/ma13040880
Chicago/Turabian StyleFerretti, Elena. 2020. "DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method" Materials 13, no. 4: 880. https://doi.org/10.3390/ma13040880
APA StyleFerretti, E. (2020). DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method. Materials, 13(4), 880. https://doi.org/10.3390/ma13040880





