1. Introduction
Compression tests on spherical micro samples are usually performed as single-grain or single-particle experiments or experiments on agglomerates for the characterization of particles in powders, granules or medical products. There are several publications about compression tests on small particles in which the complex state of stress as well as crack and breakage behavior due to compression are investigated [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]. Particle fracture and breakage behavior [
1,
2,
3,
4,
5,
6], the development of stress and strain during compression of spheres [
2,
7,
8,
9] and energy absorption at different strain rates [
10] are often described in finite element models and are underlined with experimental investigations [
1,
2,
3,
4,
5,
8,
10]. The experimental particle compression testing is performed with either static or cyclic loading. The main challenge due to geometrical boundary constraints (i.e., the contact problem of sphere and plane and the influence of stiffness and rigidity of the contact partners) is well described. The most relevant influences on particle breakage behavior is related to the material and conditions of the contact partners [
5,
9], particle size, form (roundness) and porosity of the particles due to manufacturing processes [
6,
7,
12]. Within the experimental investigations, different materials and particle sizes are evaluated (e.g., granules like quartz, aluminum oxide, silica, zirconium and sodium chloride or acrylic glass), but no structural materials like steel alloys. The particle diameters in these studies range from exemplary 20 to 60 µm [
9], 500 to 700 µm [
6], 1 to 4 mm [
11] and up to 50 mm [
7], with varying loading forces from 1 to 30 N. Nevertheless, the aim of those investigations usually is the examination of a particle as one constituent in bulk material and the interactions of those particles during transportation, processing and storage (e.g., impact stress and abrasion).
A material characterization by particle crushing is possible as it is shown for sand particles. The mechanical behavior of quartz can be described even for particles with irregular morphology in a diameter range of 1 to 4 mm [
11]. Additionally, a finite element model is developed for the characterization of the hoop strength assuming linear elastic and brittle material behavior of a compressed spherical sample [
3]. The prediction of the material behavior of a metal particle during compression is more complex, since non-linear elasticity can occur as well as plasticity caused by motion of dislocations, stress-induced phase transformation and twinning. Phase-field models are developed for crystalline materials and focus on mechanisms during elastic and plastic deformation. Those phase-field models are used to describe material behavior and properties (e.g., stress-induced martensitic phase transformation) [
13]. One investigated mechanism is, for instance, multiple twinning, which occurs for low temperatures, high strain rates and small grains, and is evaluated on a nanoscale [
14]. For a comparison of the existing models and simulations and the published experimental investigations of compression tests, the difference in evaluated length scale needs to be considered, since the technological and geometrical size effect is a challenge in mechanical testing and material characterization. However, the focus of this study is on the development of a test method to perform a mechanical material characterization for structural materials, like steel alloys, by compression of spherical micro samples.
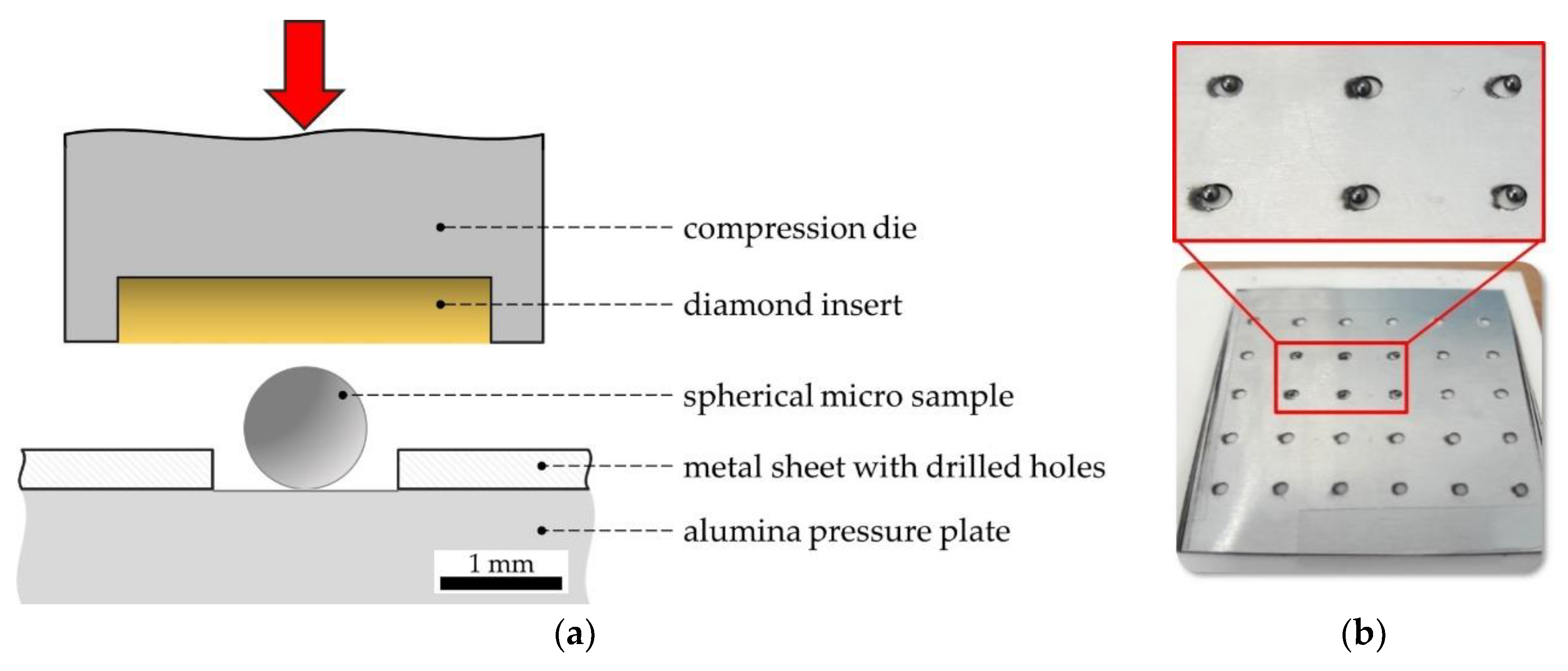
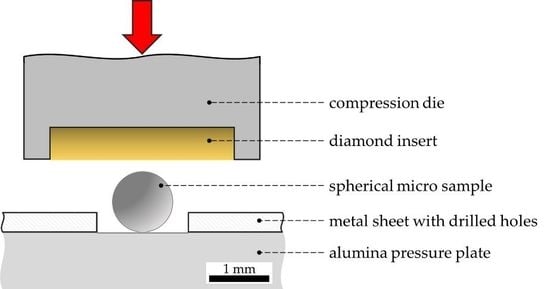
For the establishment of a novel development process of new structural materials within the Collaborative Research Center “Farbige Zustände” (CRC 1232), micro samples are used for a cost- and resource-efficient material variation [
15,
16]. The mass of a conventional flat tensile specimen (5.37 g) is equal to the mass of 1315 spherical micro samples (
Figure 1). The spherical micro samples are provided by single droplet generators, as described in [
17], which enable a fast manufacturing of a high number of samples. A compression test on spherical micro samples is introduced to investigate the elastic-plastic deformation behavior. So-called descriptors (characteristic values) are delivered to enable a comparison of values of short-term characterization techniques to conventional material properties. The descriptor-based high-throughput approach of material characterization of the CRC 1232 is explained in detail in [
18].
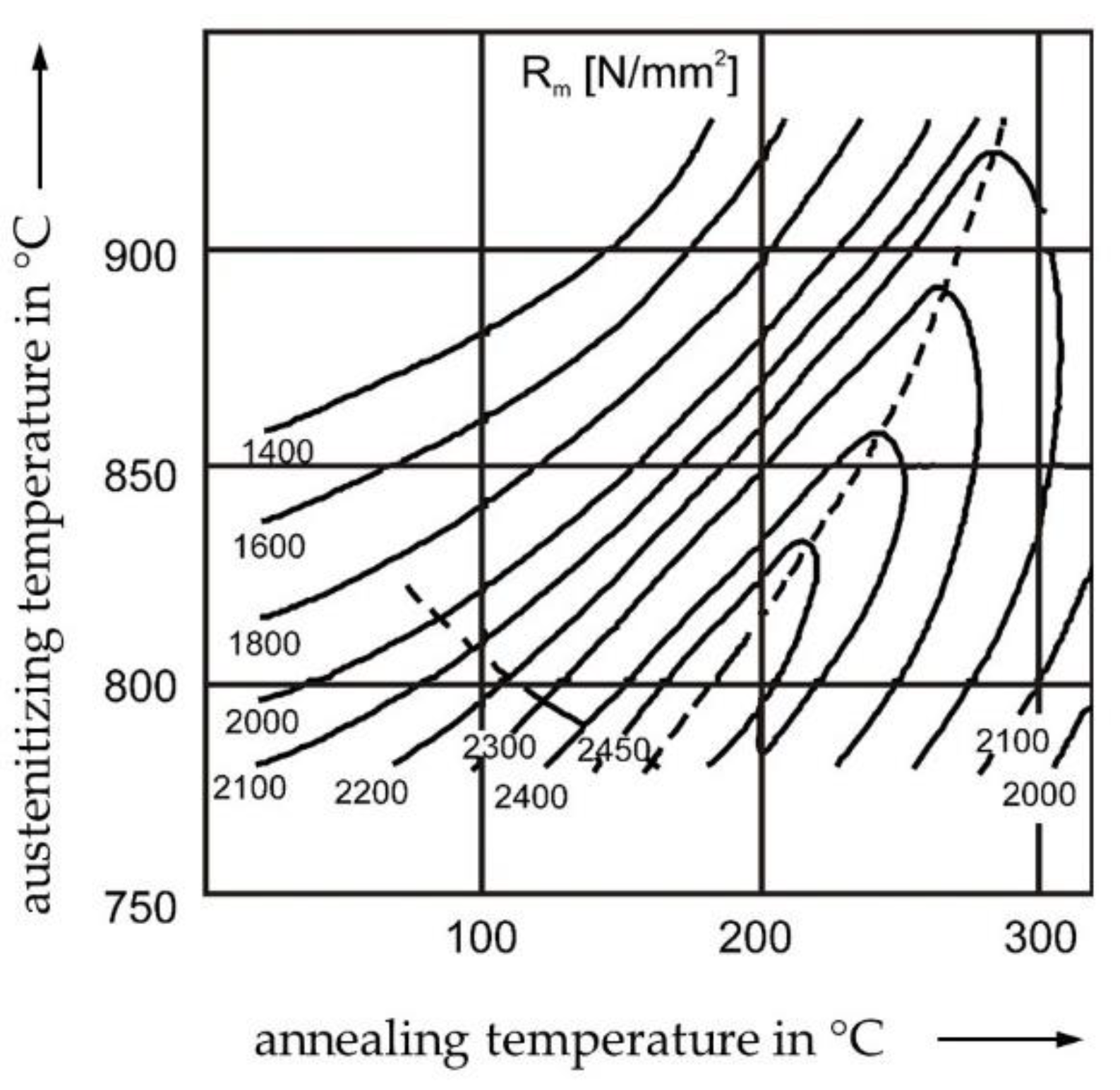
Material properties like strength, ductility and hardness are a result of the microstructure of the material. The complex changes of the tensile strength
Rm of conventional tensile tests due to heat treatment is shown in
Figure 2 using 100Cr6 as an exemplary alloy in the Fe-C-Cr system. Due to the superposition of different effects on the microstructure during heat treatment, the development of the tensile strength in dependence of austenitizing and annealing temperatures is resulting in the displayed trend [
19].
Micro samples can not only be generated very fast but are also easily further processed in terms of heat treatment using a differential scanning calorimetry (DSC) process. Calorimetry offers precise temperature adjustment possibilities so that tempering in the DSC process of previously hardened microspheres is an adequate heat treatment facility regarding ecological sustainability.
The main aim of this paper is to introduce the micro compression test method as a descriptor providing short-term characterization method within the CRC 1232 to improve and simplify the development of new structural materials. Results of this newly developed micro compression test are compared to the tensile strength of conventional tensile tests.
4. Discussion
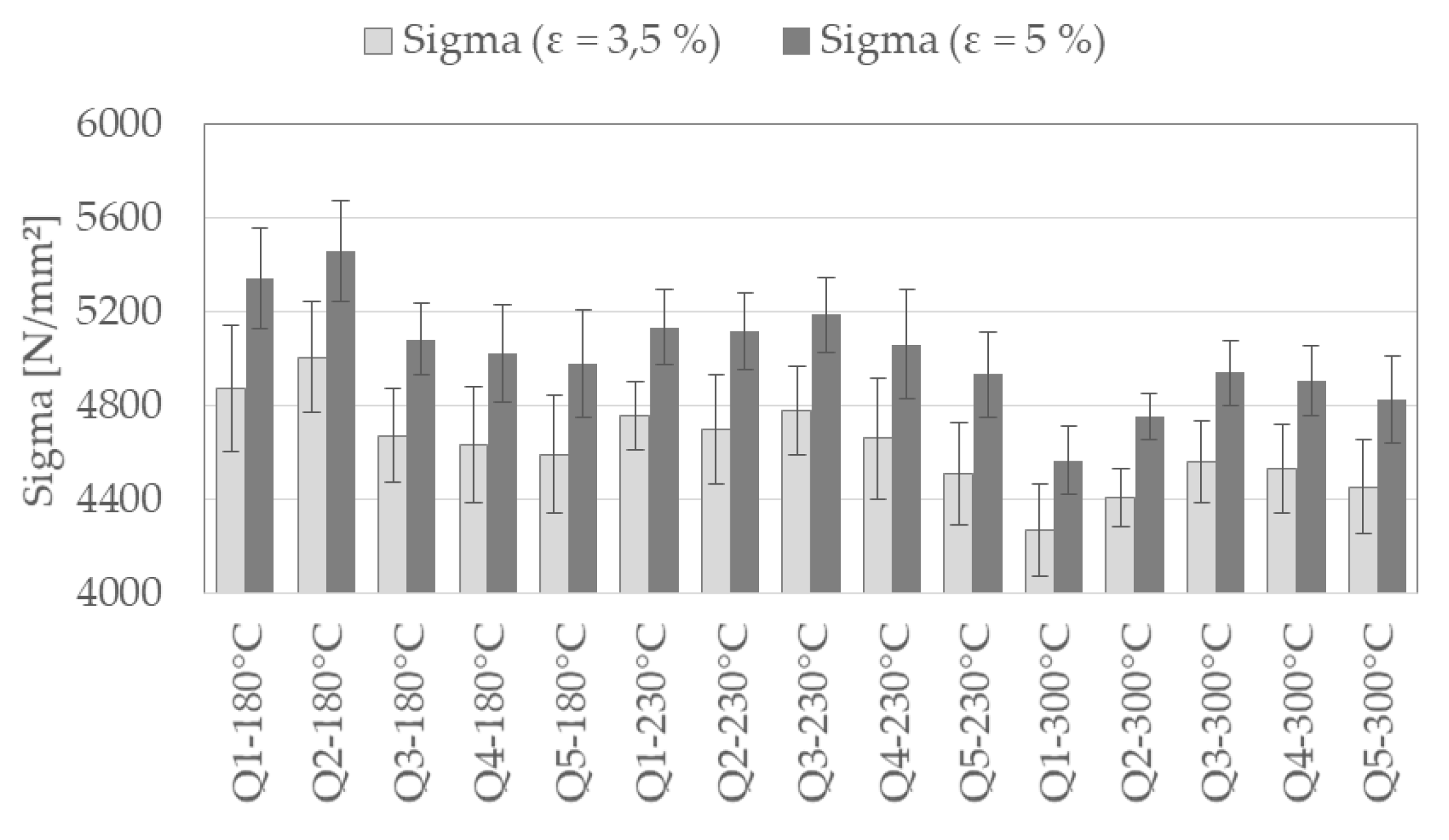
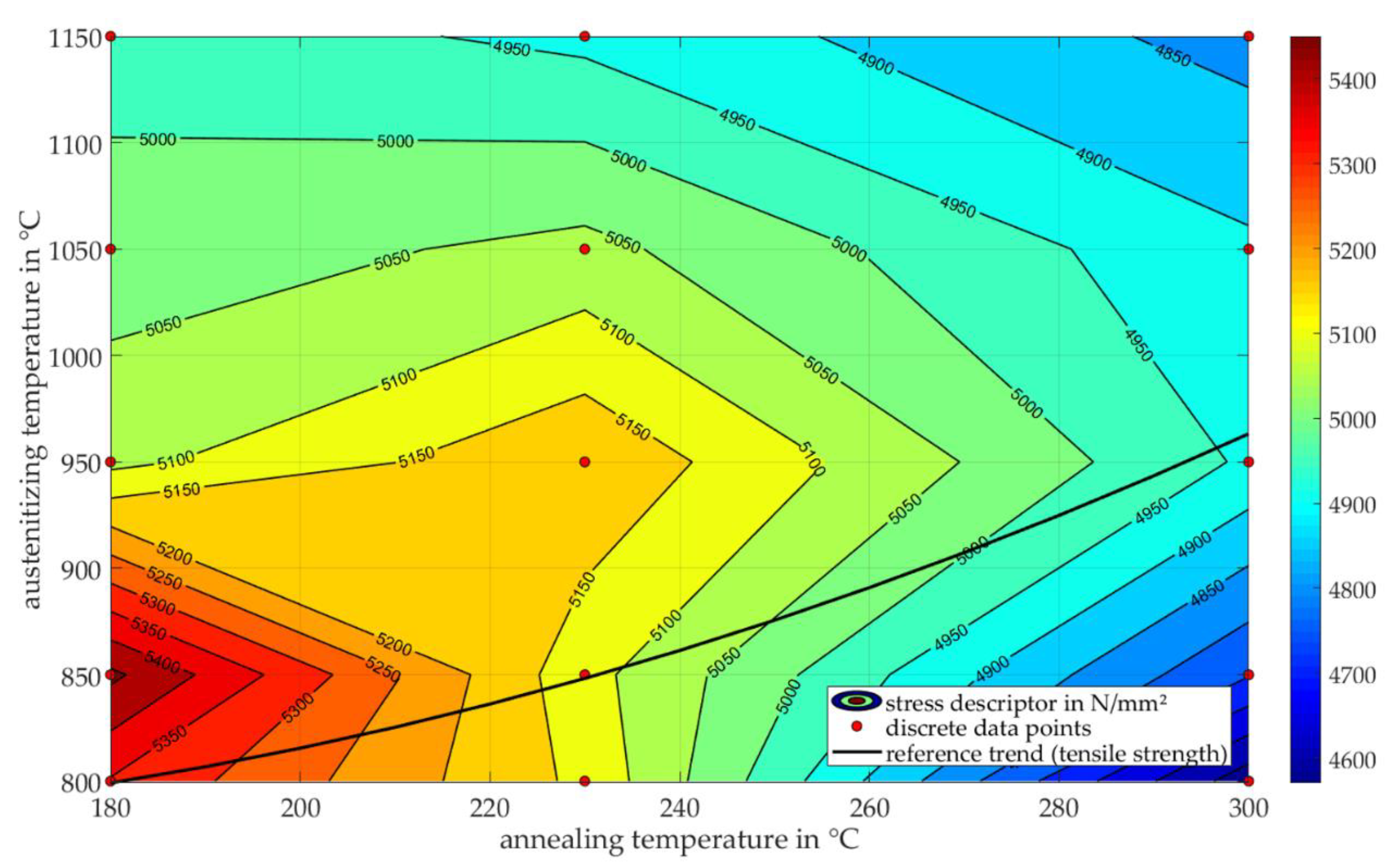
All the presented descriptors, which can be determined by the newly developed micro compression testing method of spherical samples, show a significant sensitivity in dependence of the heat treatment condition. However, the visualization of the obtained data can be improved. Inspired by the contour plot of the tensile strength
Rm in dependence of austenitizing temperature and annealing temperature (
Figure 2), the stress descriptor,
at a strain of
is used to create an analog interpolated graphic (
Figure 9) for the investigated annealing temperatures
TT = 180–360 °C and austenitizing temperatures of
TA = 800–1150 °C, revealing a much more informative visualization of the data. The contour plot of
of the micro compression test is generated by interpolating the 15 discrete data points (arithmetic mean values) of the examined heat treatment conditions, which are marked as red dots in
Figure 9.
With the help of this contour plot, the effects of heat treatment on the mechanical response of the material condition can be classified and evaluated. First of all, there is a maximum of
at the austenitizing temperature of 850 °C at the lowest annealing temperature (Q2-180 °C). This maximum corresponds to the increase of hardness with increasing dissolved carbon content, since the dissolvability of carbon and chromium is increasing with increasing austenitizing temperatures. Above
TA = 850 °C, the increasing dissolvability of carbon causes the martensite finish temperature to fall below room temperature which results in a higher retained austenite content. The increasing austenitizing temperature of course also involves a decrease in the amount of carbides. These effects and the aforementioned (in
Section 2.1) grain growth with increasing austenitizing temperature therefore lead to a decrease of hardness as well as strength of the material. The main effect of annealing is the relaxation of residual stresses due to diffusion of atoms, motion of dislocations and voids, as well as the formation of carbides. At low annealing temperatures, the hardness only slightly decreases as the tetragonal martensite transforms into cubic martensite. With higher annealing temperatures, the precipitation of finely-distributed carbides is enhanced due to higher diffusion rates, resulting in reduced hardness and higher ductility. There is an opposed effect at higher austenitizing temperatures, since for hardened conditions, with higher retained austenite contents, the transformation of retained austenite to martensite increases the hardness with increasing annealing temperatures (e.g., Q3-230 °C and Q4-230 °C) until the relaxation effects of carbide formation predominate.
Regarding the expected mechanical properties of the different heat treatment conditions of 100Cr6, the trends of tensile strength values
Rm out of conventional tensile tests (
Figure 2) are considered as a validation approach of the compression test on spherical micro samples. Note that, since the stress value
of compression tests is only a descriptor, absolute values should not be compared to those of standardized tensile tests. Due to superposition of different effects during heat treatment of 100Cr6, the development of the stress descriptor
is similar to the resulting trend of the tensile strength in dependence of austenitizing and annealing temperatures in
Figure 2. Although the amount of experimental data points of the descriptor of compression tests is not sufficient to replicate the whole material data of 100Cr6, as in [
19], the analog trend is still discernible. The dashed line of
Figure 2 is recreated by using the online tool WebPlotDigitizer (version 4.2, Ankit Rohatgi, San Francisco, CA, USA) [
22] and is displayed as a black reference line in
Figure 9. The interrelation between the stress descriptor of micro compression tests and the tensile strength seem to be not linear and shifted. Variations in the chemical composition of the examined alloys might explain the differences in the contour plots, as the carbon content of the tensile specimens was slightly lower (0.97 wt.%) [
19]. Furthermore, the initial material condition before heat treatment (e.g., the amount of carbides) highly influences the resulting microstructure. However, transferability and scalability from a compression test on micro samples to a material property on the macro level seem possible.
Additional experiments are needed to further validate the trend of the mechanical material property of 100Cr6 in areas of special interest, for example, of material conditions with the expected highest values of the stress descriptor in the range of temperatures of TA = 800–950 °C and TT = 180–230 °C.
In general, during micro compression test on spherical samples, mechanical effects and material-specific influences superpose and affect resulting descriptor values. The mechanical effects include the contact mechanics of sphere and plane with point contact at the beginning of the test, complex stress development due to sample geometry, friction and surface roughness of contact partners. Influences like diffusion, motion of dislocations, residual stresses, local distribution of carbides, grain boundaries, stress-induced phase transformation and alloy dependencies belong to the material-specific effects occurring during mechanical loading. For a better understanding of these effects and the improvement of the interpretation of the extracted descriptors, a simulation of the micro compression test will be part of future research work.
5. Conclusions
In this work, the relevance of micro compression testing for the determination of mechanical descriptors in a short-term characterization method on spherical micro samples, as in the CRC 1232, was demonstrated.
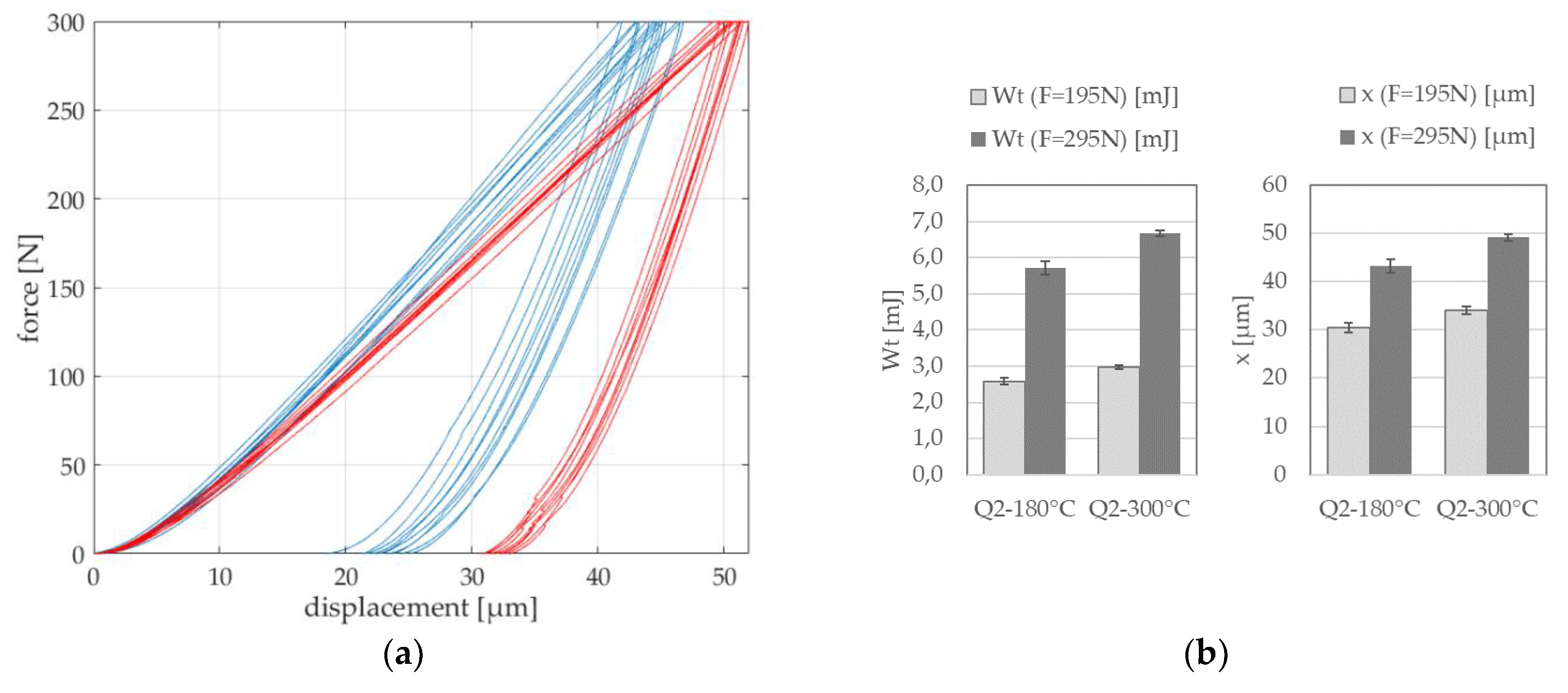
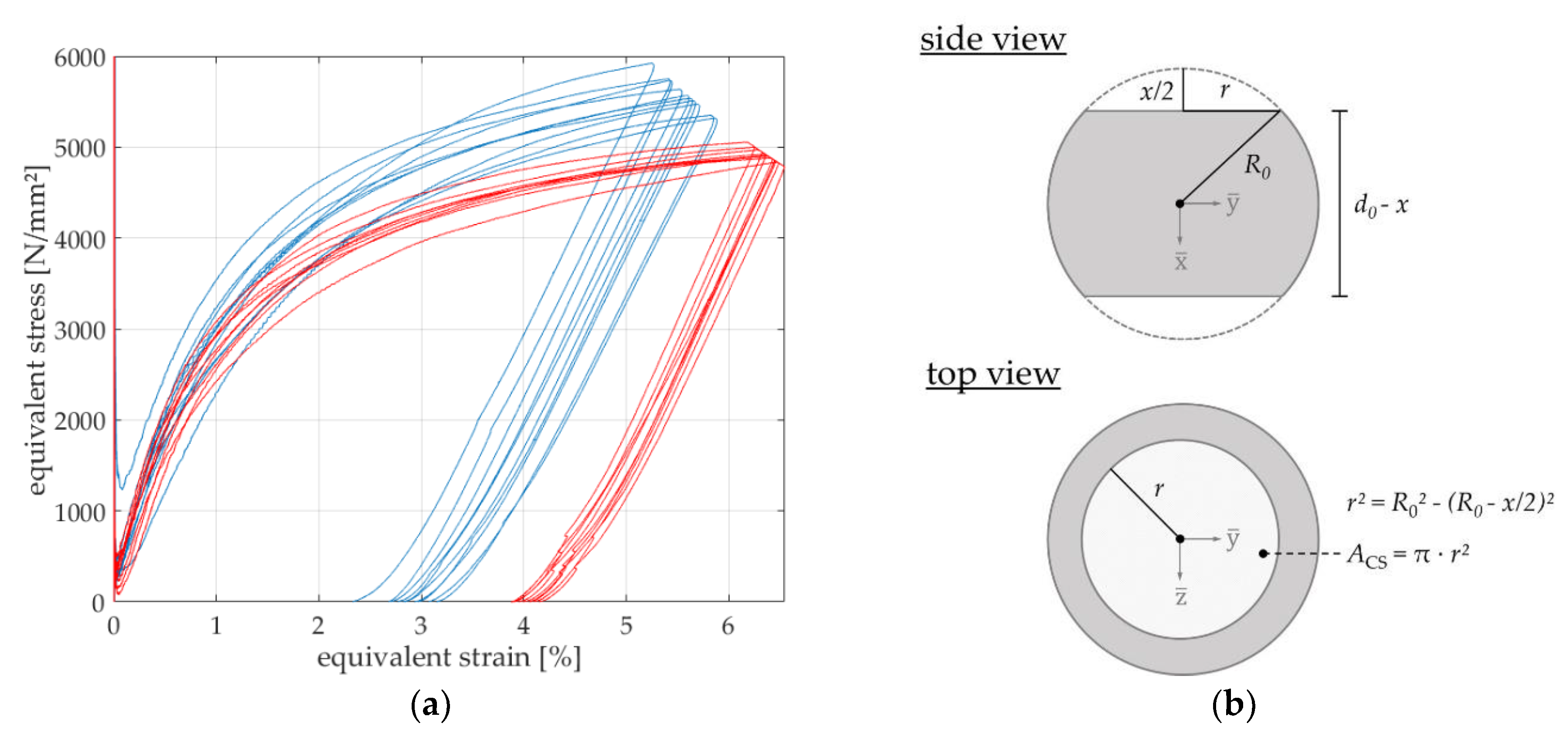
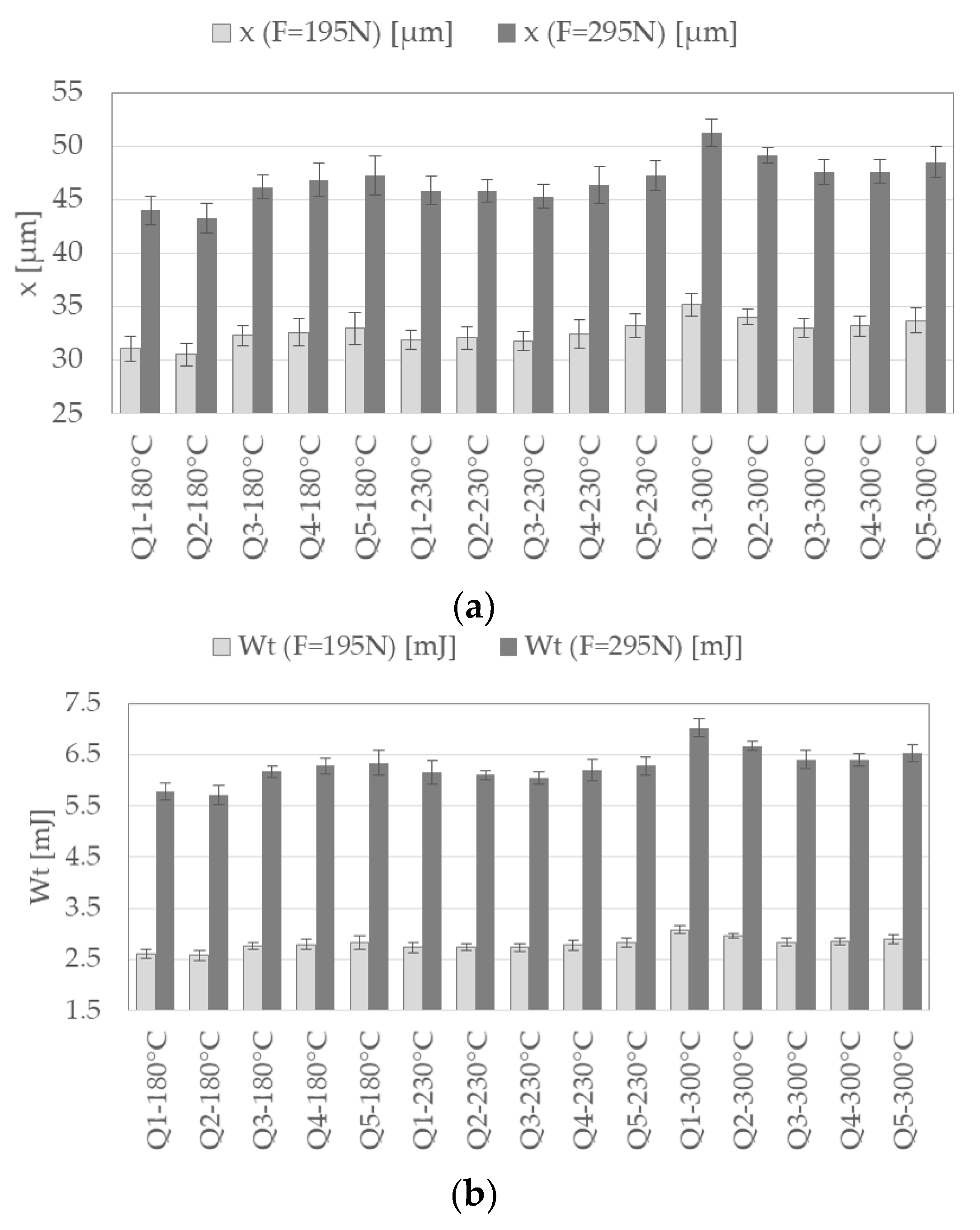
The evaluation of descriptors extracted from force-displacement curves and calculated stress-strain relations proves the robustness of this testing method, because scatter and standard deviations are small. Due to the sample geometry, descriptors at higher load levels show less scattering and examined trends tend to be more pronounced than for lower load levels. Due to a greater deformation of the sample and a bigger loaded sample volume, small errors (e.g., due to surface roughness or deviations in geometry accuracy) can be compensated. In this study it is shown that the descriptors of the micro compression testing method are sensitive to heat treatment changes and different microstructures. However, the higher the load, the greater the possible detection of differences between different investigated materials. Nevertheless, it should be noted that there is a maximum limit of loading, since with greater deformations the geometry of the sphere transforms into a disc, resulting in higher frictional influences, thus affecting the results significantly.
Regarding the transferability of mechanical material characterization by compression test on microspheres to conventional material properties of macro material, a transfer is found to be promising, as the examined trend of a stress descriptor interrelates with the trend of tensile strength from literature. Of course, since there is yet only a small area investigated by micro compression tests, it is necessary to perform further investigations to determine a direct correlation between descriptors of a fast characterization technique on micro samples and a material property on a macro scale. This study can therefore be extended with experiments on additional heat treatments of 100Cr6 in areas of special interest (e.g., maximum descriptor values), but also with investigations of different alloy compositions. All in all, the micro compression test on spherical samples can then be used in high throughput-based screening processes for the development of new alloys, as in the CRC 1232, since it provides useful descriptors very fast compared to conventional material testing methods.