Accounting for the Local Field When Determining the Dielectric Loss Spectra of Metals in the Region of the Frequencies of Volume, Surface and Localized Plasmon Oscillations
Abstract
1. Theoretical Considerations
1.1. Intermolecular Interactions in a Condensed Medium
1.2. The Manifestation of the Spectral Differences of the Effective and Average Fields in a Condensed Medium
1.3. Consideration of the Differences between the Effective Eeff(ν) and the Average Eav(ν) Fields in a Condensed Medium
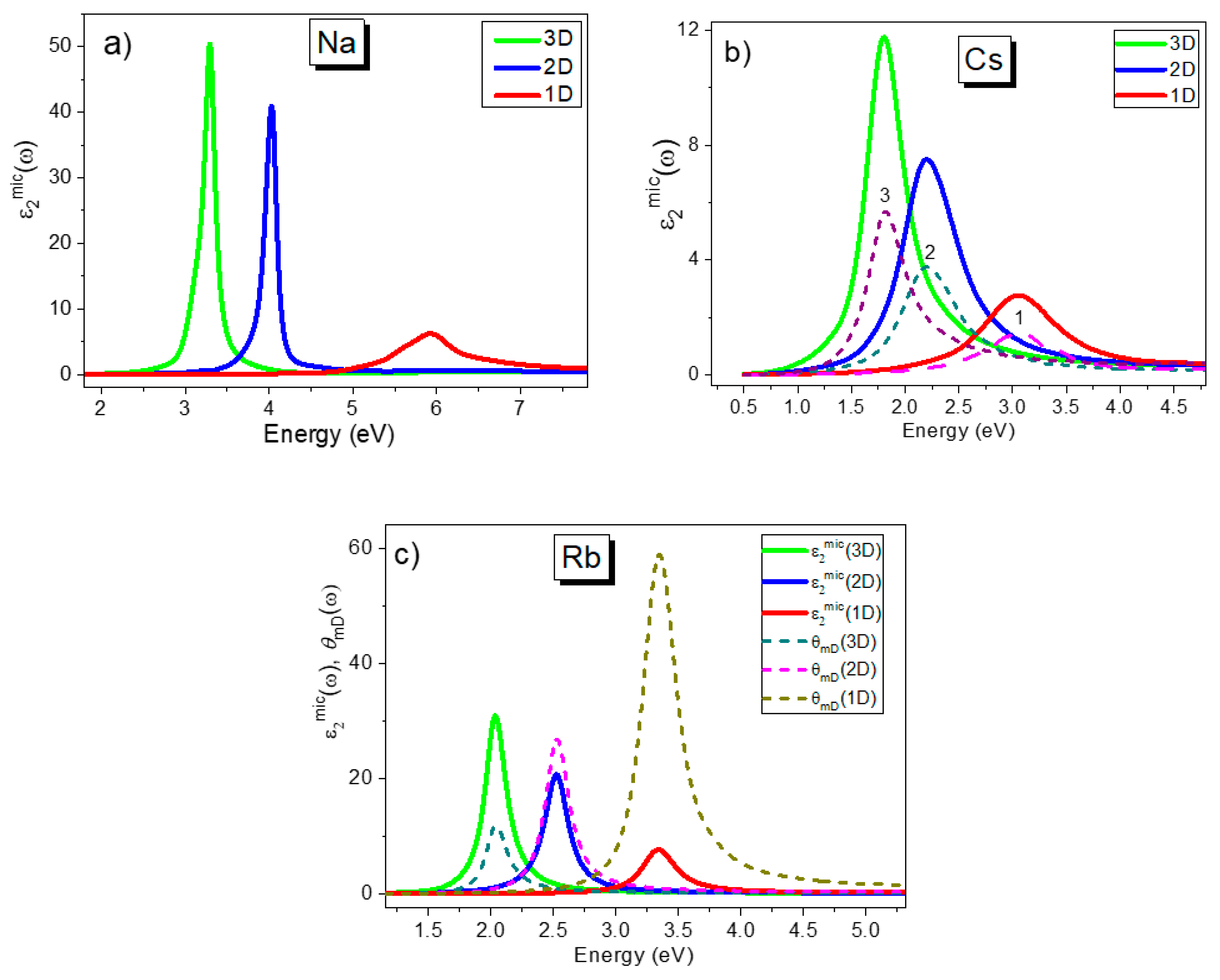
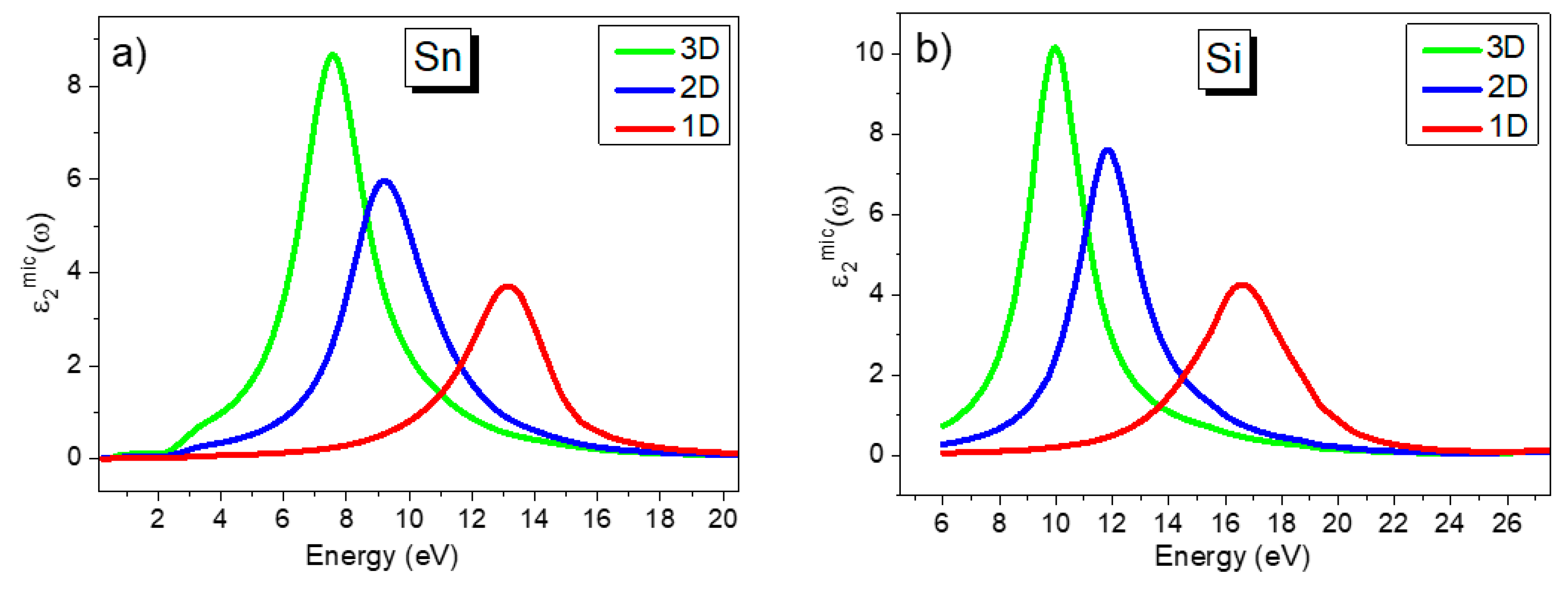
2. Results of Model Calculations
2.1. Three-Dimensional Dielectric Confinement
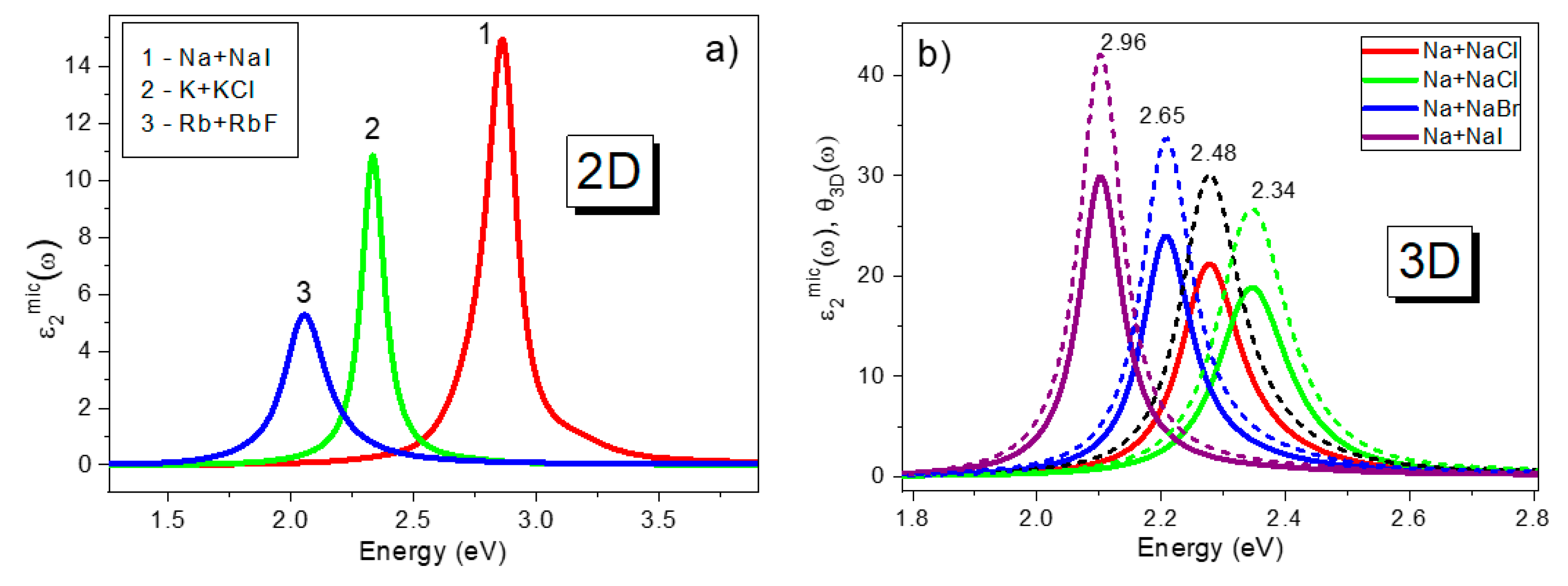
2.2. Two-Dimensional Dielectric Confinement
2.3. One-Dimensional Dielectric Confinement
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College Publishing: Troy, Missouri, 1976. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Elsevier: Cambridge, UK, 1999. [Google Scholar]
- Elyashevich, M.A. Atomic and Molecular Spectroscopy; Mir: Moscow, Russia, 1962. [Google Scholar]
- Buckingham, E. Intermolecular Interactions: From Diatomics to Biopolymers; Pullman, B., Ed.; John Wiley & Sons: Chichester, UK; New York, NY, USA; Brisbane, Australia; Toronto, ON, Canada, 1978; p. 447. [Google Scholar]
- Bakhshiev, N.G.; Girin, O.P.; Libov, V.S. Relation between the observed and true absorption spectra of molecules in a solid medium. II. Methods for determining the correction of a universal effect of the effective (internal) field. Opt. Spektrosk. 1963, 14, 745. [Google Scholar]
- Clifford, A.A.; Crowford, B., Jr. Vibrational Intensities. XIV. The Relation of Optical Constants to Molecular Parameters. J. Phys. Chem. 1966, 70, 1536–1543. [Google Scholar] [CrossRef]
- Bakhshiev, N.G. Photophysics of Dipole–Dipole Interactions; SPB SU Publishing: Saint Petersburg, Russia, 2005; p. 500. [Google Scholar]
- Libov, V.S. Advancements and perspectives in use of local field method to study spectral manifestation of resonance interactions in condensed medium. Rus. J. Phys. Chem. 1980, 54, 817. [Google Scholar]
- Perova, T.S.; Shaganov, I.I.; Unnikrishnan, S.; Moore, R.A. Spectroscopic Characteristics of Nano-Composite Structures in 3D, 2D and 1D Size Confinement. Proc. SPIE 2005, 5826, 387–396. [Google Scholar]
- Shaganov, I.I.; Perova, T.S.; Melnikov, V.A.; Dyakov, S.; Berwick, K. Size effect on the infrared spectra of condensed media under condition of 1D, 2D and 3D dielectric confinement. J. Phys. Chem. C 2010, 114, 16071–16081. [Google Scholar] [CrossRef]
- Shaganov, I.I.; Perova, T.S.; Mukhina, M.V.; Martynenko, I.V.; Baranov, A.V.; Fedorov, A.V.; Gerard, V.; Gun’ko, Y.K. Influence of intermolecular interactions on spectroscopic characteristics of metal nanoparticles and their composites. Phys. Chem. Chem. Phys. 2014, 16, 24536–24548. [Google Scholar] [CrossRef]
- Shaganov, I.I.; Perova, T.S.; Moore, R.A.; Berwick, K. Effect of the internal field on the IR absorption spectra of small particles in the case of 3D, 2D and 1D size confinement. J. Phys. Chem. B 2005, 109, 9885–9891. [Google Scholar] [CrossRef]
- Shaganov, I.I.; Perova, T.S.; Berwick, K. The effect of the local field and dipole-dipole interactions on the absorption spectra of noble metals and the plasmon resonance of their nanoparticles. Photon. Nanostruc. Fundam. Appl. 2017, 27, 24–31. [Google Scholar] [CrossRef][Green Version]
- Ghiner, A.V.; Surdutovich, G.I. Method of integral equations and an extinction theorem for two-dimensional problems in nonlinear optics. Phys. Rev. A 1994, 50, 714. [Google Scholar] [CrossRef] [PubMed]
- Aspnes, D.E. Local field effects and effective-medium theory: A microscopic perspective. Am. J. Phys. 1984, 50, 704. [Google Scholar] [CrossRef]
- Garnett JCM, VII Colours in metal glasses, in metallic films, and in metallic solutions—II. Philos. Trans. R. Soc. London A 1906, 205, 237–288.
- Handbook of Optical Constants of Solid, Part I; Palik, E.D., Ed.; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Handbook of Optical Constants of Solids, Part II; Palik, E.D., Ed.; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Adachi, S. The Handbook on Optical Constants of Metals: In Tables and Figures; World Scientific: Singapore, 2012. [Google Scholar]
- Hagemann, H.-J.; Gudat, W.; Kunz, C. Optical constants from the far infrared to the x-ray region: Mg, Al, Cu, Ag, Au, Bi, C, and A12O3. J. Opt. Soc. Am. 1975, 65, 742–744. [Google Scholar] [CrossRef]
- Jezequel, G.; Lemonnier, J.C.; Thomas, J. Optical properties of gallium films between 2 and 15 eV. J. Phys. F Met. Phys. 1977, 7, 1613–1622. [Google Scholar] [CrossRef]
- MacRae, R.A.; Arakawa, T.; Williams, M.W. Optical Properties of Vacuum Evaporated White Tin. Phys. Rev. 1967, 162, 615–620. [Google Scholar] [CrossRef]
- Stahrenberg, K.; Herrmann, T.; Wilmers, K.; Esser, N.; Richter, W. Optical Properties of copper and silver in the energy range 2.5–9.0 eV. Phys. Rev. B 2001, 64, 115111. [Google Scholar] [CrossRef]
- Salem, M.A. Studies on the opto-electronic constants of alkali-halide crystals. Ind. J. Pure Appl.Phys. 2003, 41, 384–388. [Google Scholar]
- Doyle, W.T. Coagulations, Optical Absorption and Photoconductivity of Colloid Centres in Alkai Halides. Proc. Phys. Soc. 1960, 75, 649–663. [Google Scholar] [CrossRef]
- Kreibig, U.; Volmer, M. Optical Properties of Metal Clusters; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1995; p. 533. [Google Scholar]
- Savostianowa, M. Über die kolloidale Natur der färbenden Substanz im verfärbten Steinsalz. Z. Phys. 1930, 64, 262–278. [Google Scholar] [CrossRef]
- Scott, A.B.; Smith, W.A.; Thompson, M.A. Alkali halides colored by colloidal metal. J. Phys. Chem. 1953, 57, 757–761. [Google Scholar] [CrossRef]
- Creuzburg, M. Entstehung von Alkalimetallen bei der Elektronenbestrahlung von Alkalihalogeniden. Z. Phys. 1966, 194, 211–218. [Google Scholar] [CrossRef]
- Fujimoto, F.; Komaki, K.-I. Plasma Oscillations Excited by a Fast Electron in a Metallic Particle. J. Phys. Soc. Jpn. 1968, 25, 1679–1687. [Google Scholar] [CrossRef]
- Seitz, F. Color Centers in Alkali Halide Crystals. II. Rev. Mod. Phys. 1954, 26, 7–94. [Google Scholar] [CrossRef]
- Doyle, W.T.; Ingram, D.J.E.; Smith, M.J.A. Detection of colloidal centers in lithium hydride by electron resonance. Phys. Rev. Lett. 1959, 2, 497–498. [Google Scholar] [CrossRef]
- Doyle, W.T. Absorption of Light by Colloids in Alkali Halide Crystals. Phys. Rev. 1958, 111, 1067. [Google Scholar] [CrossRef]
- Tonks, L. Plasma-electron resonance, plasma resonance and plasma shape. Phys. Rev. 1931, 38, 1219–1223. [Google Scholar] [CrossRef]
- Hughes, A.F.; Jain, S.C. Metal colloids in ionic crystals. Adv. Phys. 1979, 28, 717–828. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Shaganov, I.I.; Berwick, K.; Perova, T.S. Influence of the local field and dipole-dipole interactions on the spectral characteristics of simple metals and their nanoparticles. Plasmonics 2019, 14, 1443–1451. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron-Energy-Loss Spectroscopy in the Electron Microscopy, 3rd ed.; Springer Science+Business Media, LLC: New York, NY, USA, 2011. [Google Scholar]
- Powell, C.J. The origin of the characteristic electron energy losses in ten elements. Proc. Phys. Soc. 1960, 76, 593–610. [Google Scholar] [CrossRef]
- Pines, D. Collective Energy Losses in Solids. Rev. Mod. Phys. 1956, 28, 184–199. [Google Scholar] [CrossRef]
- Rocca, M. Low-energy EELS investigation of electronic excitations on metals. Sur. Sci. Rep. 1995, 22, 1–71. [Google Scholar] [CrossRef]
- Strawbridge, B.; Singh, R.K.; Beach, C.; Mahajan, S.; Newman, N. Effect of surface topography on reflection electron energy loss plasmon spectra of group III metals. J. Vac. Sci. Techn. A 2006, 24, 1776–1781. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; London, UK; Paris, France; Tokyo, Japan, 1988. [Google Scholar]
- Ritchie, R.H. Plasma Losses by fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Ferrell, R.A. Predicted radiation of plasma oscillations in metal films. Phys. Rev. 1958, 111, 1214–1222. [Google Scholar] [CrossRef]
- Steinmann, W. Optical Plasma Resonances in Solids. Phys. Stat. Sol. 1968, 28, 437–462. [Google Scholar] [CrossRef]
- Fröhlich, H.; Pelzer, H. Plasma oscillations and energy loss of charged particles in solids. Proc. Phys. Soc. A 1955, 68, 525–529. [Google Scholar] [CrossRef]
- Wilson, C.B. A phenomenological theory of the characteristic energy losses of fast electrons in metals. Proc. Phys. Soc. 1960, 76, 481–488. [Google Scholar] [CrossRef]
- Lehmann, A. Theory of Infrared Transmission Spectra of Thin Insulating Films. Phys. Stat. Sol. B 1988, 148, 401–405. [Google Scholar] [CrossRef]
- Oates, T.W.H.; Wormeester, H.; Arwin, H. Characterisation of plasmonic effects in thin films and metamaterials using spectroscopic ellipsometry. Prog. Surf. Sci. 2011, 86, 328–376. [Google Scholar] [CrossRef]
- Berreman, D.W. Infrared absorption at longitudinal optic frequency in cubic crystal films. Phys. Rev. 1963, 130, 2193. [Google Scholar] [CrossRef]
- McAlister, A.J.; Stern, E.A. Plasma Resonance Absorption in Thin Metal Films. Phys. Rev. 1963, 132, 1599–1602. [Google Scholar] [CrossRef]
- Melnyk, A.R.; Harrison, M.J. Theory of Optical Excitations of Plasmon in Metals. Phys. Rev. B 1970, 2, 835–850. [Google Scholar] [CrossRef]
- Sytchkova, A. Complex materials with subwavelength inclusions for optical thin film applications. Ch. 5. In Optical Thin Films and Coatings: From Materials and Applications; Piegari, A., Flory, F., Eds.; Elsevier Ltd.; Woodhead Publishing: Sawston, UK, 2018; pp. 143–186. [Google Scholar]
- Jana, J.; Gangulyb, M.; Pal, T. Enlightening surface plasmon resonance effect of metal nanoparticles for practical spectroscopic application. RSC Adv. 2016, 6, 86174–86211. [Google Scholar] [CrossRef]
- Ginsburg, V.L.; Frank, I.M. Radiation of a uniformly moving electron arising from its transition from one medium to another. Soviet Phys. JETP 1946, 16, 15–28. [Google Scholar]
- Silin, V.P.; Fetisov, E.P. Interpretation of the electromagnetic radiation from electron passage through metal films. Phys. Rev. Lett. 1961, 7, 374–377. [Google Scholar] [CrossRef]
- Frank, I.M. Transition Radiation and Optical Properties of Matter. Soviet Phys. – Uspekhi 1966, 8, 729–742. [Google Scholar] [CrossRef]
- Yamaguchi, S. Theory of the Optical Properties of Very Thin Inhomogeneous Films. Phys. Soc. Jap. 1962, 17, 184–193. [Google Scholar] [CrossRef]
- Matsudaira, N. Interaction of Solid State Plasmon with Radiation. II. Optical Absorption of Thin Metal Films. J. Phys. Soc. Jap. 1963, 18, 380–387. [Google Scholar] [CrossRef]
- Yamaguchi, S. The Resonance Type Absorption of Very Thin Silver and Gold Films. J. Phys. Soc. Jap. 1960, 15, 1577–1585. [Google Scholar] [CrossRef]
- Howie, A.; Walsh, C. Interpretation of valence loss spectra from composite media. Microsc. Microanal. Microstruct. 1991, 2, 171–181. [Google Scholar] [CrossRef][Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science + Business Media, LLC: New York, NY, USA, 2007. [Google Scholar]
- Wang, Y.; Plummer, E.W.; Kempa, K. Foundations of Plasmonics. Adv. Phys. 2011, 60, 799–898. [Google Scholar] [CrossRef]
- Rivera, V.A.G.; Silva, O.B.; Ledemi, Y.; Messaddeq, Y.; Marega, E., Jr. Collective Plasmon–Modes in Gain Media. Quantum Emitters and Plasmonic Nanostructures.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Sarid, D.; Challener, W.A. Modern Introduction to Surface Plasmons; Cambridge University Press: New York, NY, USA, 2010; p. 371. [Google Scholar]
- Langer, J.; Jimenez de Aberasturi, D.; Aizpurua, J.; Alvarez-Puebla, R.A.; Auguié, B.; Baumberg, J.J.; Bazan, G.C.; Bell, S.E.; Boisen, A.; Brolo, A.G.; et al. Present and Future of Surface-Enhanced Raman Scattering. ACS Nano 2019. [Google Scholar] [CrossRef] [PubMed]

| Solid Colloids | ωmax(eV) of ε2mic(ω) Spectra, Calculations | ωl, eV Opt. Transm. | ωl, eV [30,31] | ωl, eV [35] | ωl, eV EELS exp. [29] | ε∞ [24] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [30] | 3D | 2D | 1D | [25,33]. | Calculat. | Exp. | Exp. | 1st peak ωs | 2nd peak ωp | εh | ||
| Exp. | Calc | l = 1; | l = ∞ | |||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | ||
| Na+NaCl | 2.28 | 3.01 | 5.9 | 2.23 | 2.43 | 2.39 | 2.2 | 2.2 | 2.48 | |||
| 2.35 [26] | 2.2 | |||||||||||
| Na+NaBr | 2.25 | 2.95 | 5.9 | 2.1 | 2.25; | 2.95 | 2.11 | 2.2 | 5.7 | 2.65 | ||
| Na+NaI | 2.15 | 2.86 | 5.9 | 2.15; | 2.85 | 2.07 | 2.3 | 5.7 | 2.96 | |||
| K+KF | 1.8 | 2.33 | 3.8 | 1.89 | 1.8; | 2.25 | 2.3 | 3.4 | 1.89 | |||
| K+KCl | 1.67 | 2.17 | 3.8 | 1.7; | 1.72 | 1.7; | 2.09 + | 1.6 | 1.7 | 2.32 | ||
| K+KBr | 1.64 | 2.13 | 3.8 | 1.61; | 1.65 | 1.63; | 2.05 + | 1.46 | 1.68 | 2.44 | ||
| K+KI | 1.58 | 2.06 | 3.8 | 1.4; | 1.55 | 1.55; | 1.99 + | 1.4 | 1.54–1.46 | 2.66 | ||
| Rb+RbF | 1.6 | 2.05 | 3.4 | 1.54; | 1.98 + | 2.1 | 3.4 | 1.94 | ||||
| Rb+RbI | 1.42 | 1.84 | 3.36 | 1.36; | 1.79 + | 1.52-1.35 | 2.63 | |||||
| CsBr | 1.2 | 1.6 | 3.08 | 1.12; | 4.05 + | 1.18 | 2.83 | |||||
| LiF | 2.1 | 2.75 | 6.9 | 2.76-2.54 | 2.04 | |||||||
| LiH | 2.1 | 2.75 | 6.9 | 1.91 [33] | 2.4; | 3.21 + | 3.6 | |||||
| 2.02 | 2.66 | 6.9 | 2.3; | 3.1 + | 3.94 | |||||||
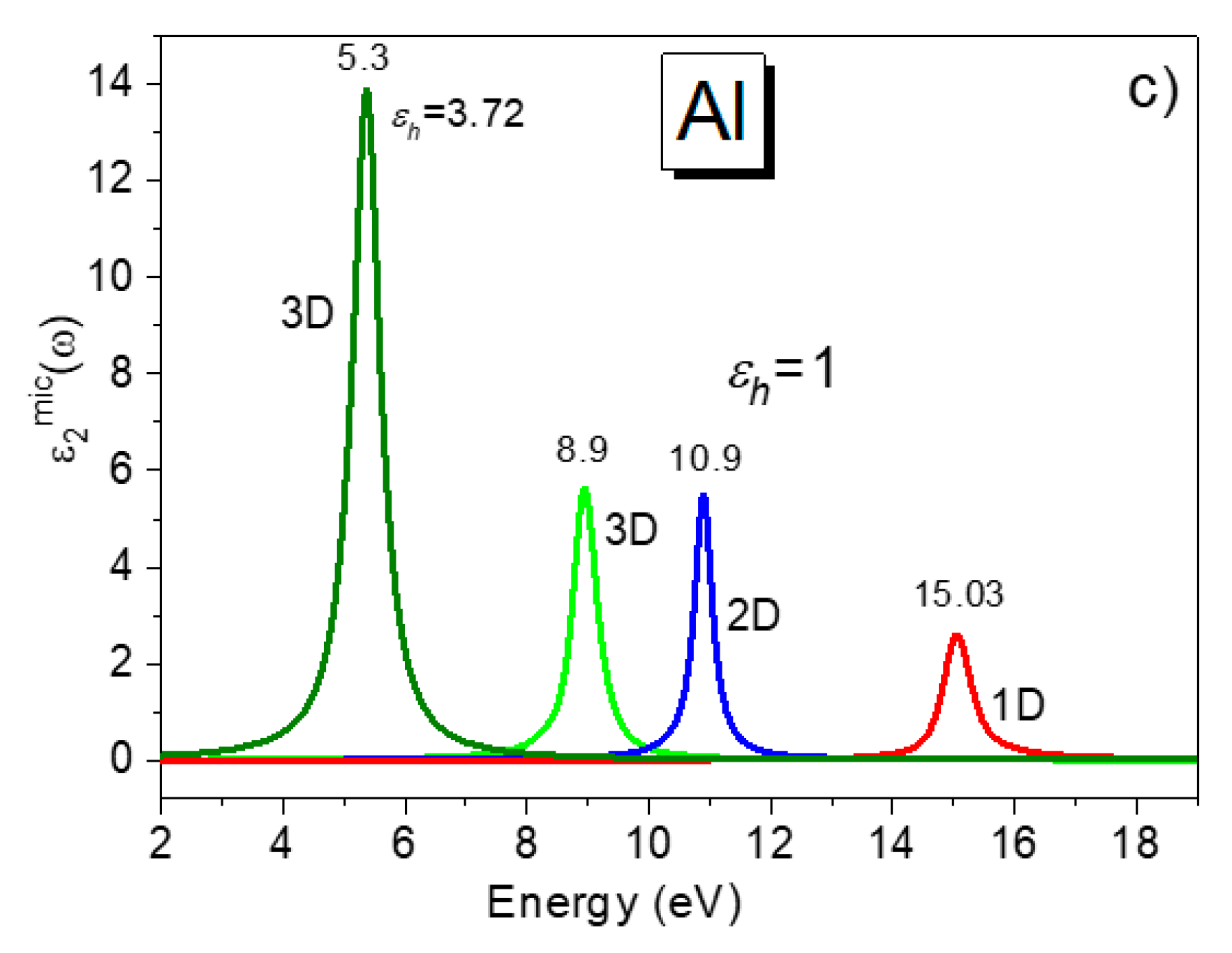
| Al+Al2O3 | 8.9 | 10.9 | 15.03 | 8.8; | 10.8 | 10.3 [39,41] | 15.3 [38,39] | 1 | ||||
| 5.3 | 15.03 | 5.14 | 3.72 | |||||||||
| Metal | ε∞ | 1D—ωp, eV | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EELS ωp, eV | ωp at ε1(ω) = 0 | ε2mic(ω1D) = Im[1/ε(ω)] | Exper. EELS | ωp/√2 | ωS at ε1(ω) = −1 | ε2mic(ω2D) = Im[1/ε + 1] | ωp/√3 | ωF at ε1(ω) = −2 | Mie Eq.(11) | ε2mic(ω3D) = Im[1/ε(ω)] | ||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII |
| Li | 1.02 | 7.1 a 8.2 c | 6.7 | 7 | 4.7 a 4.28 d | 5.04 | 4.64 | 4.83 | 4.1 | 3.5 | 3.65 | 3.56 |
| Na | 1.06 | 5.7 a 5.4 c | 6 | 5.92 | 3.98 d | 4.04 | 4 | 3.97 | 3.3 | 3.3 | 3.3 | 3.29 |
| K | 1.06 | 3.8 c | 3.9 | 3.87 | 2.73 d | 2.6 | 2.85 | 2.84 | 2.15 | 2.3 | 2.29 | 2.28 |
| Rb | 1 | 3.41 a | 3.36 | 3.34 | 2.46 d | 2.43 | 2.5 | 2.52 | 1.99 | 2.02 | 2.04 | 2.03 |
| Cs | 1 | 2.9 a | 3.07 | 3.08 | 1.99 d | 2.43 | 2.2 | 2.2 | 1.98 | 1.8 | 1.81 | 1.81 |
| Al | 1.11 | 15.0 a 15.3 b | 15.1 | 15.04 | 10.3 d 10.3 b | 10.8 | 11 | 10.9 | 8.8 | 8.9 | 8.87 | 8.94 |
| Be | 1.02 | 18.7 a 18.4 b | 17.5 | 18.1 | 11.9 b | 13.1 | 12.2 | 12.5 | 10.7 | 9.9 | 10.55 | 10.4 |
| Mg | 1.01 | 10.3 a 10.6 b | 10.8 | 10.7 | 7.38 d 7.1 b | 7.5 | 8.3 | 8.27 | 6.12 | 6.3 | 6.3 | 6.3 |
| Ga | 1.0 | 13.8 a | 14.1 | 14.07 | 10.2 e | 9.8 | 10.1 | 10.2 | 8.03 | 8.3 | 8.33 | 8.4 |
| In | 1.0 | 11.4 a 11.3 c | 11.44 | 11.43 | 8.7 e | 8.13 | 9.0 | 8.92 | 6.6 | 7.4 | 7.52 | 7.4 |
| Sn | 1.203 | 13.7 a 14.3 b | 13.0 | 13.2 | 10.5 b | 9.5 | 9.0 | 9.2 | 7.6 | 7.3 | 7.7 | 7.54 |
| Si | 16.7 a 17.0 c | 16.3 | 16.7 | 11 a | 12 | 11.7 | 11.8 | 9.8 | 9.8 | 10 | 9.97 | |
| Plasmon Type | N | Effect | References From [46] | Optical Spectra, Peak Position, eV | EELS Data Bulk Surface (SPR) | Calculation ωl, eV | |
|---|---|---|---|---|---|---|---|
| Radiative | 1 | Plasma radiation | Ag: [34,35,36,37,38,39] Al: [43,44,45] | Ag: 3.54–3.75 Al: 15.2–15.5 | 15.3 [39,42] | 10.3 [39,42] | 15.9 [39] |
| Radiative | 2 | Optical plasma Resonance in transmission | Ag: [40,59,60,89] K: [12,61,72] Al: [62,63,66,67] Mg: [86] | Ag: 3.75–3.8 K: 3.54–3.82 Al: 14.8–14.9 Mg: 10.1 | 3.8 [40] 10.5 *; 10.6 [39] | 7.1 [39] | 10.9; 7.7 [39] |
| Radiative | 3 | Optical plasma Resonance in reflection | Al: [90,91] | Al: 15.3 | |||
| Radiative | 4 | Optical plasma Resonance in photoemission | K–Cs: [70,71,72] Al: [66,67,73,91,92] | K–3.7; Na–5.9; Rb–3.1; Cs–2.87; Al: 14.85–14.9 | Li—9.5; Na—5.4 [40]; K—3.8 [40]; Cs—2.9 [41]; Rb—3.41 [38] | Na—3.8 [40]; Rb—2.46 [42]; Cs—1.99 [42] | Li—8.0; 5.7 [39]; Li—8.1; Na—6.0 [40]; K—4.4; Rb—4.0 [42]; Cs—3.6 [40] |
| Radiative | 5 | Plasma radiation excited by light | Ag: [75,76,77,78,83] K: [79,87] | Ag: 3.77–3.8 K: 3.76 | Ag—DEF, this work 3.5, 3.7, 3.78 | ||
| Non-Radiative | 6 | Frustrated total Reflection | Ag: [99] | Ag: 3.6 | |||
| Non-Radiative | 7 | Radiative decay of tangential Surface plasmon | Ag: [27,28,29,50,51,53,93] Al: [53,100] | Ag: 3.49–3.82 Al: 9.7 (2D) | 15 [40] | 10.3 [41] | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perova, T.; Shaganov, I.; Berwick, K. Accounting for the Local Field When Determining the Dielectric Loss Spectra of Metals in the Region of the Frequencies of Volume, Surface and Localized Plasmon Oscillations. Materials 2020, 13, 631. https://doi.org/10.3390/ma13030631
Perova T, Shaganov I, Berwick K. Accounting for the Local Field When Determining the Dielectric Loss Spectra of Metals in the Region of the Frequencies of Volume, Surface and Localized Plasmon Oscillations. Materials. 2020; 13(3):631. https://doi.org/10.3390/ma13030631
Chicago/Turabian StylePerova, Tatiana, Igor Shaganov, and Kevin Berwick. 2020. "Accounting for the Local Field When Determining the Dielectric Loss Spectra of Metals in the Region of the Frequencies of Volume, Surface and Localized Plasmon Oscillations" Materials 13, no. 3: 631. https://doi.org/10.3390/ma13030631
APA StylePerova, T., Shaganov, I., & Berwick, K. (2020). Accounting for the Local Field When Determining the Dielectric Loss Spectra of Metals in the Region of the Frequencies of Volume, Surface and Localized Plasmon Oscillations. Materials, 13(3), 631. https://doi.org/10.3390/ma13030631






