Determination of the Forming Limit for a ZIRLO™ Sheet with High Anisotropy
Abstract
1. Introduction
2. Experimental Setup
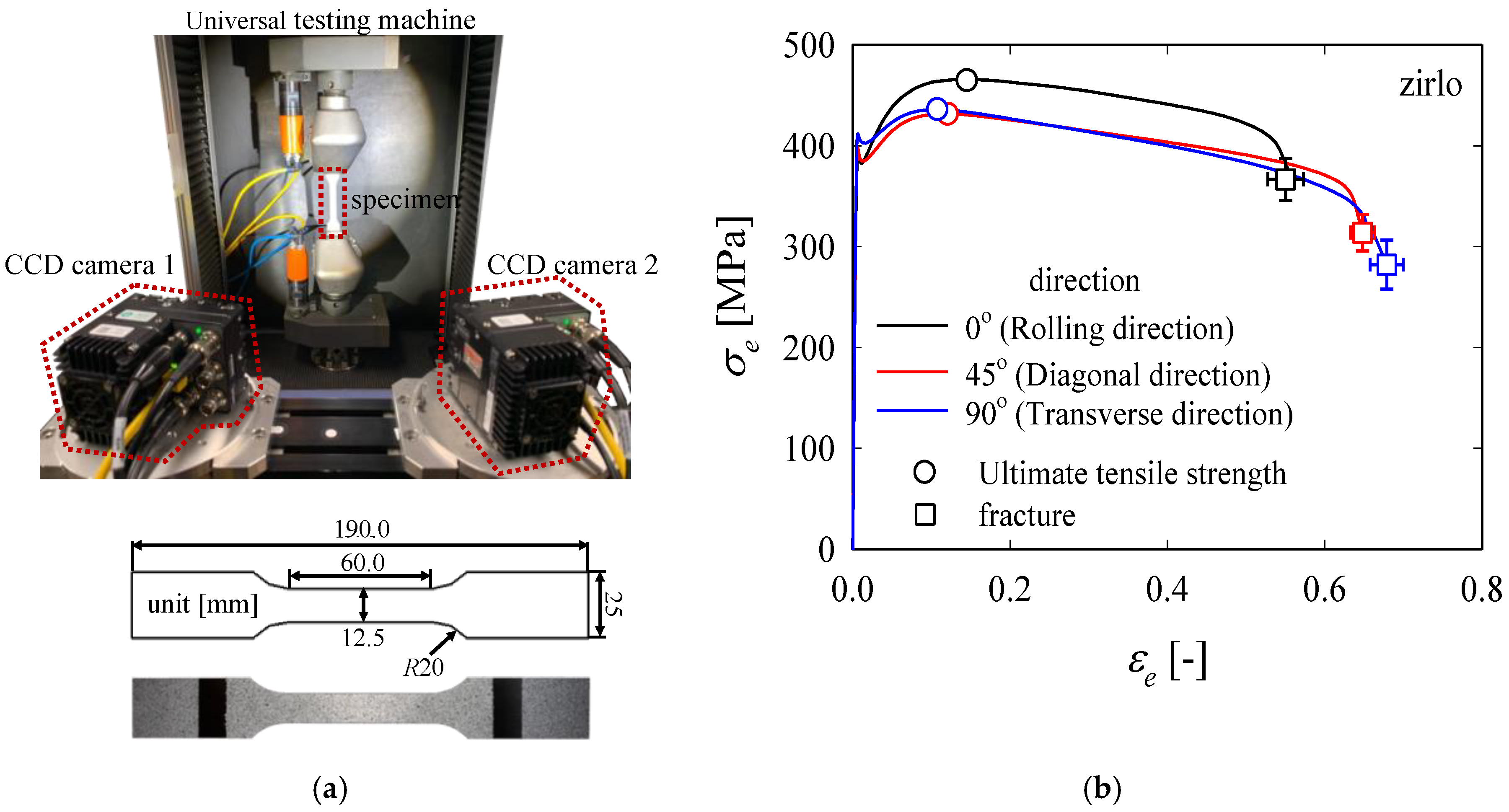
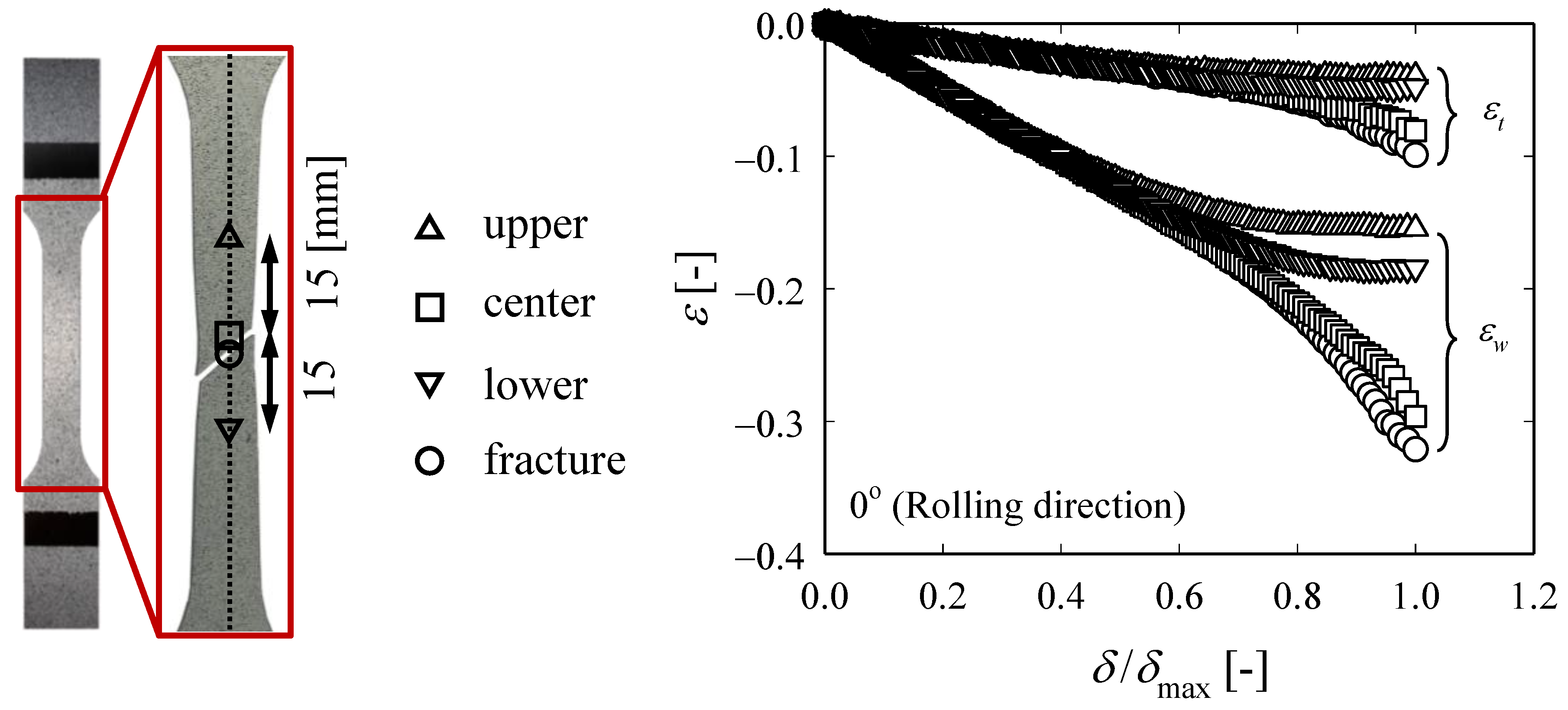
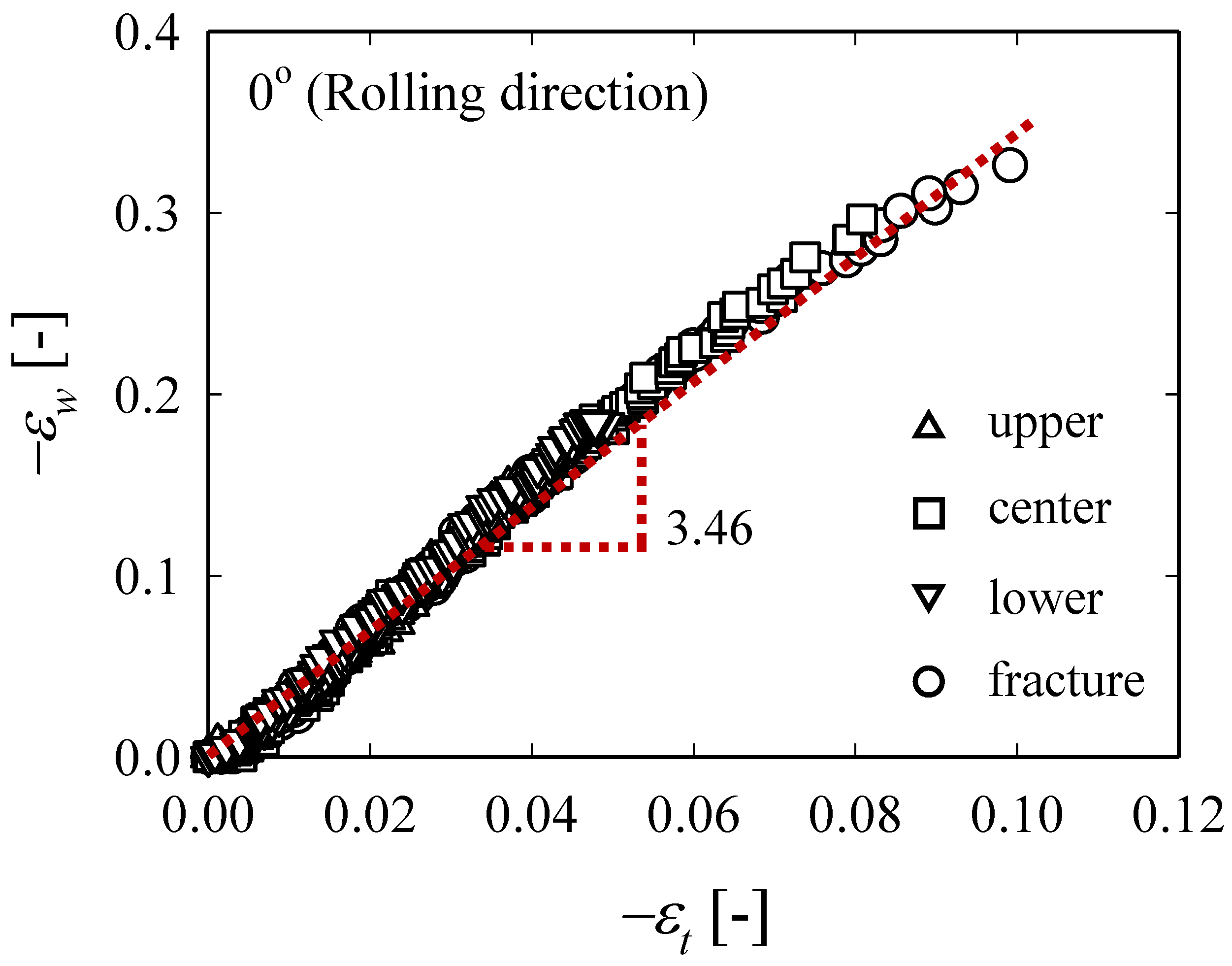
2.1. Tensile Tests
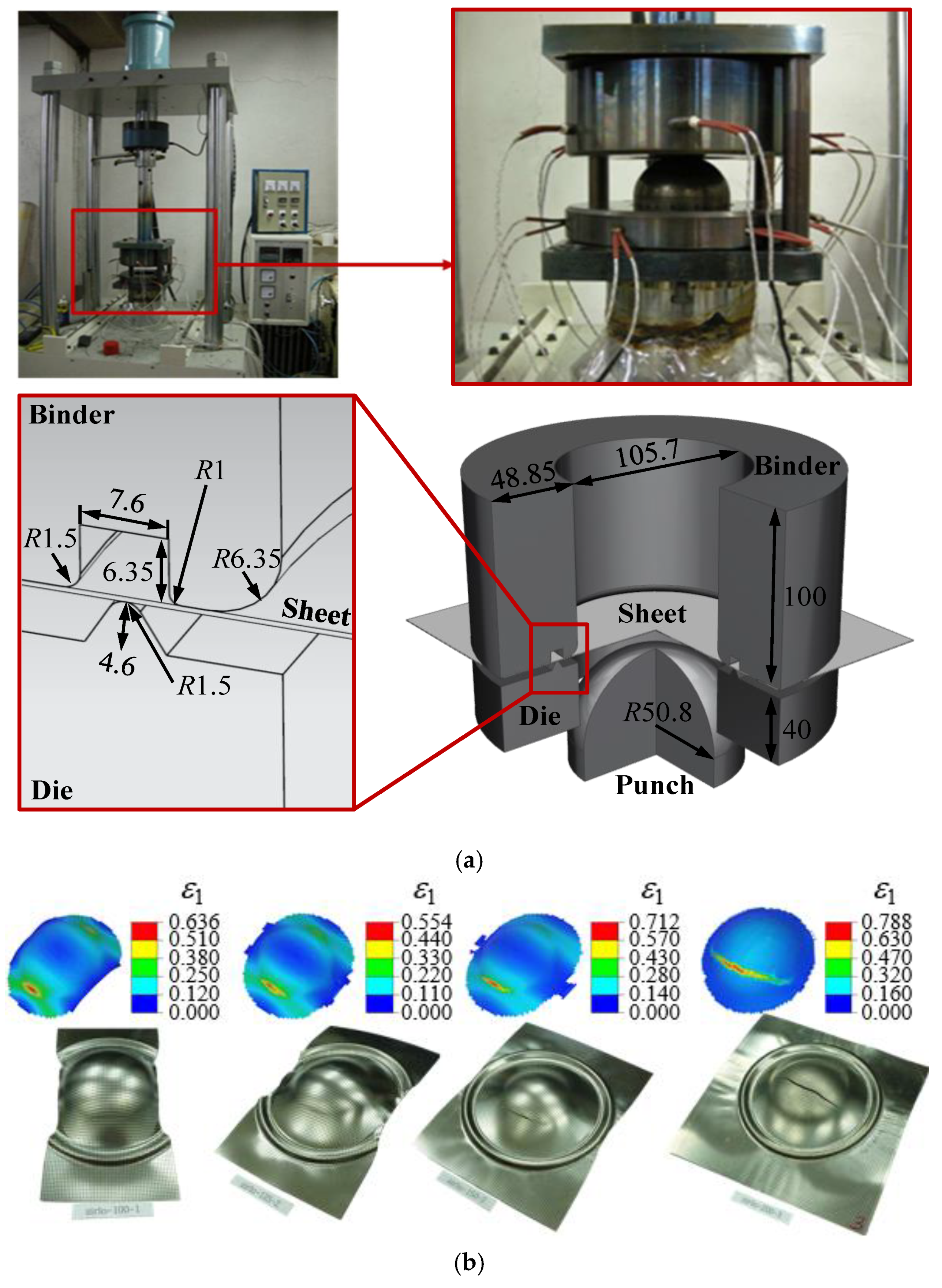
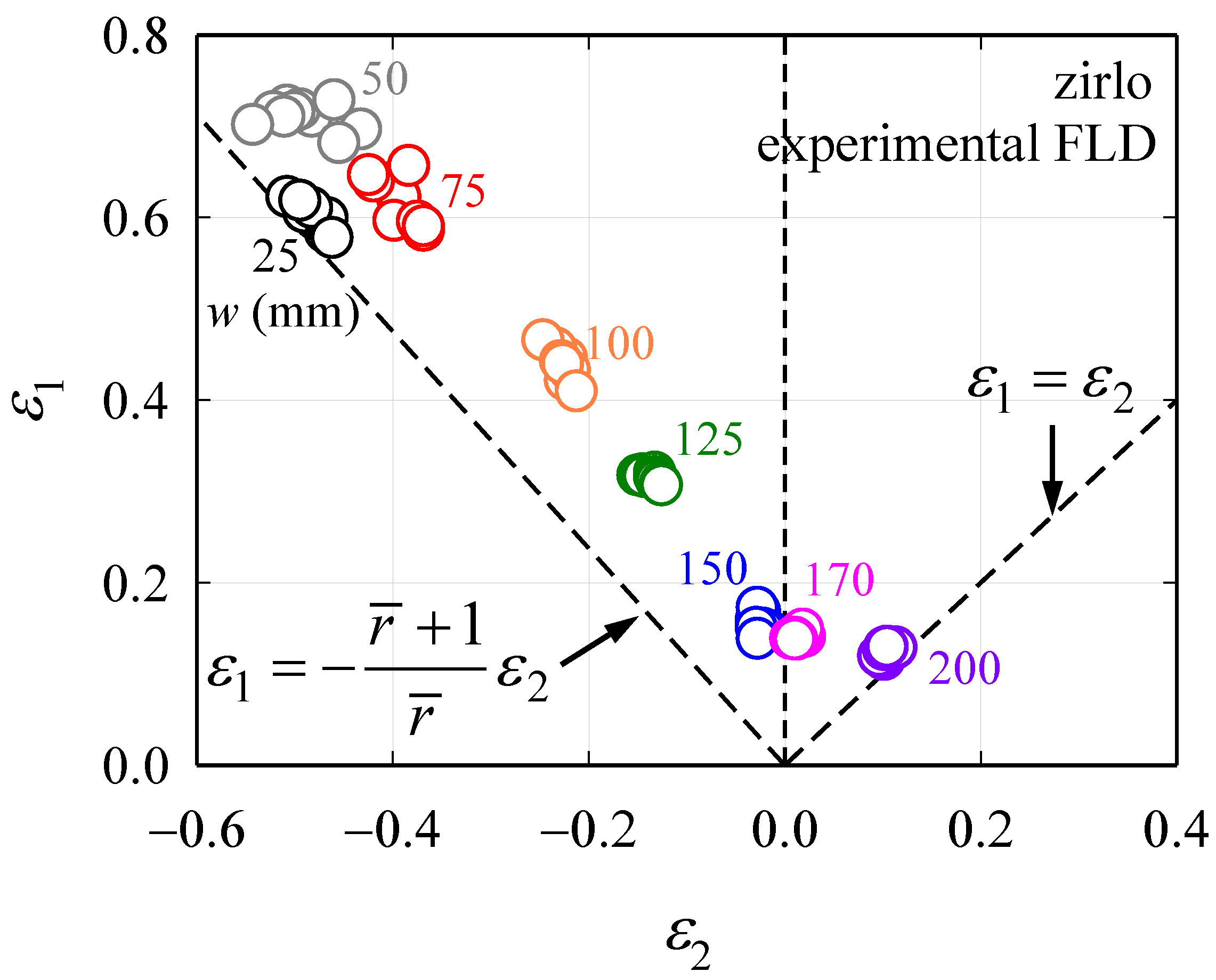
2.2. Limit Dome Height Test
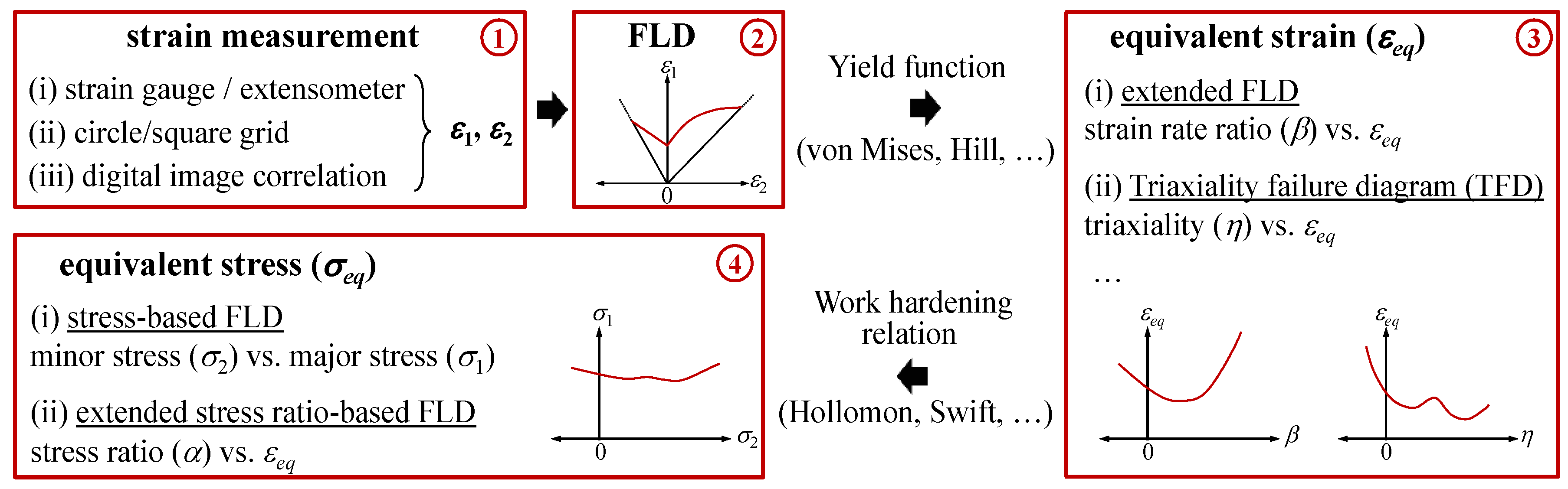
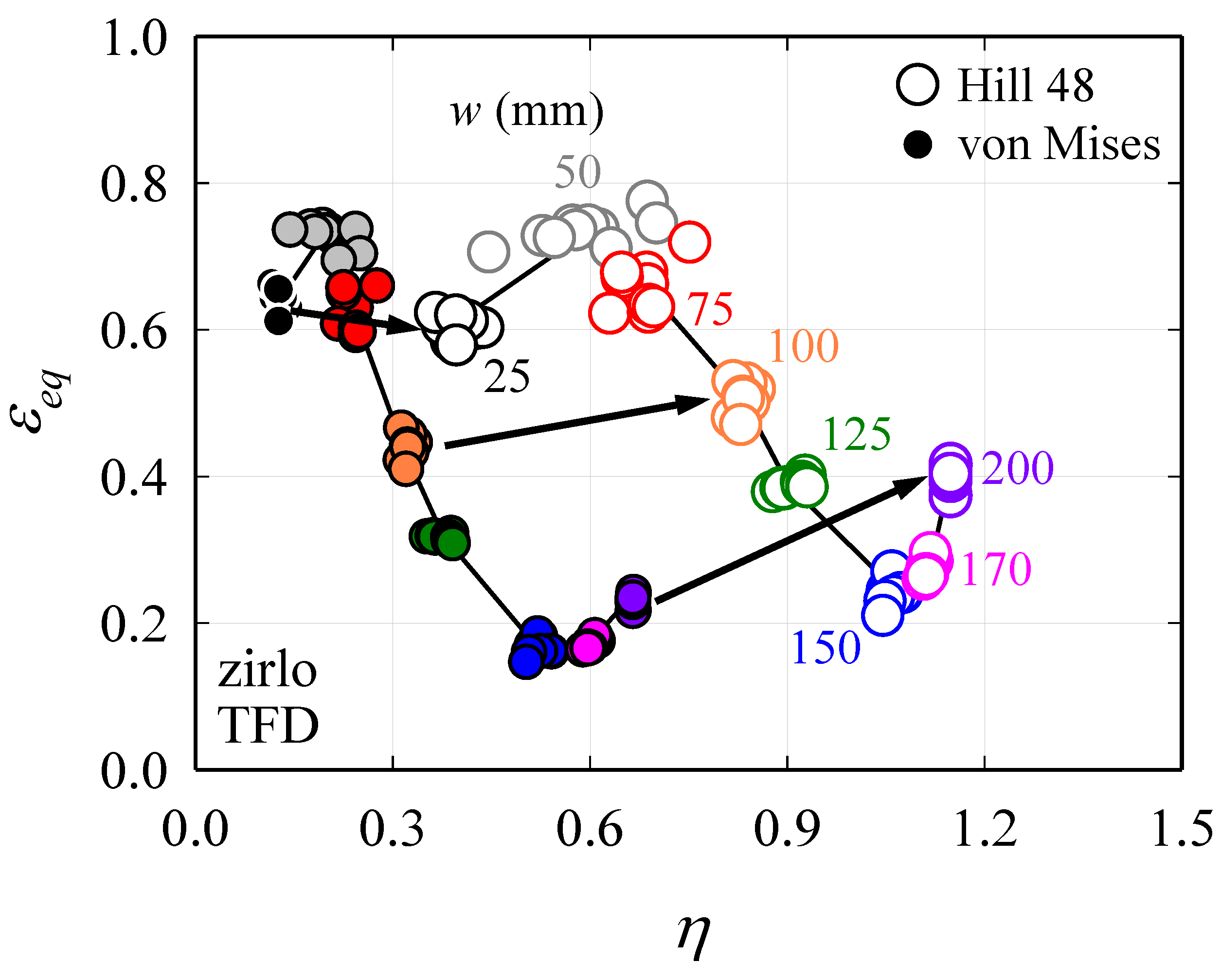
3. TFD with Anisotropy
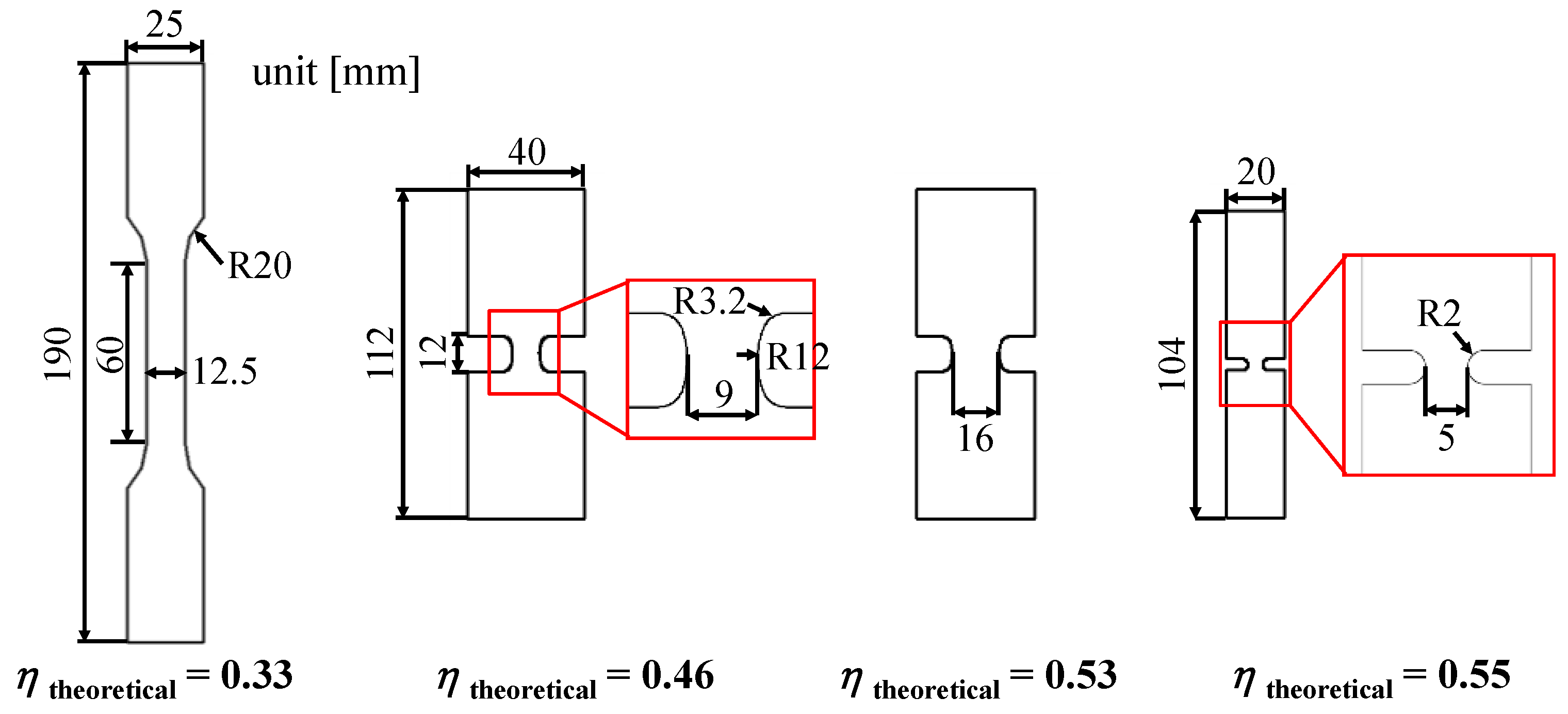
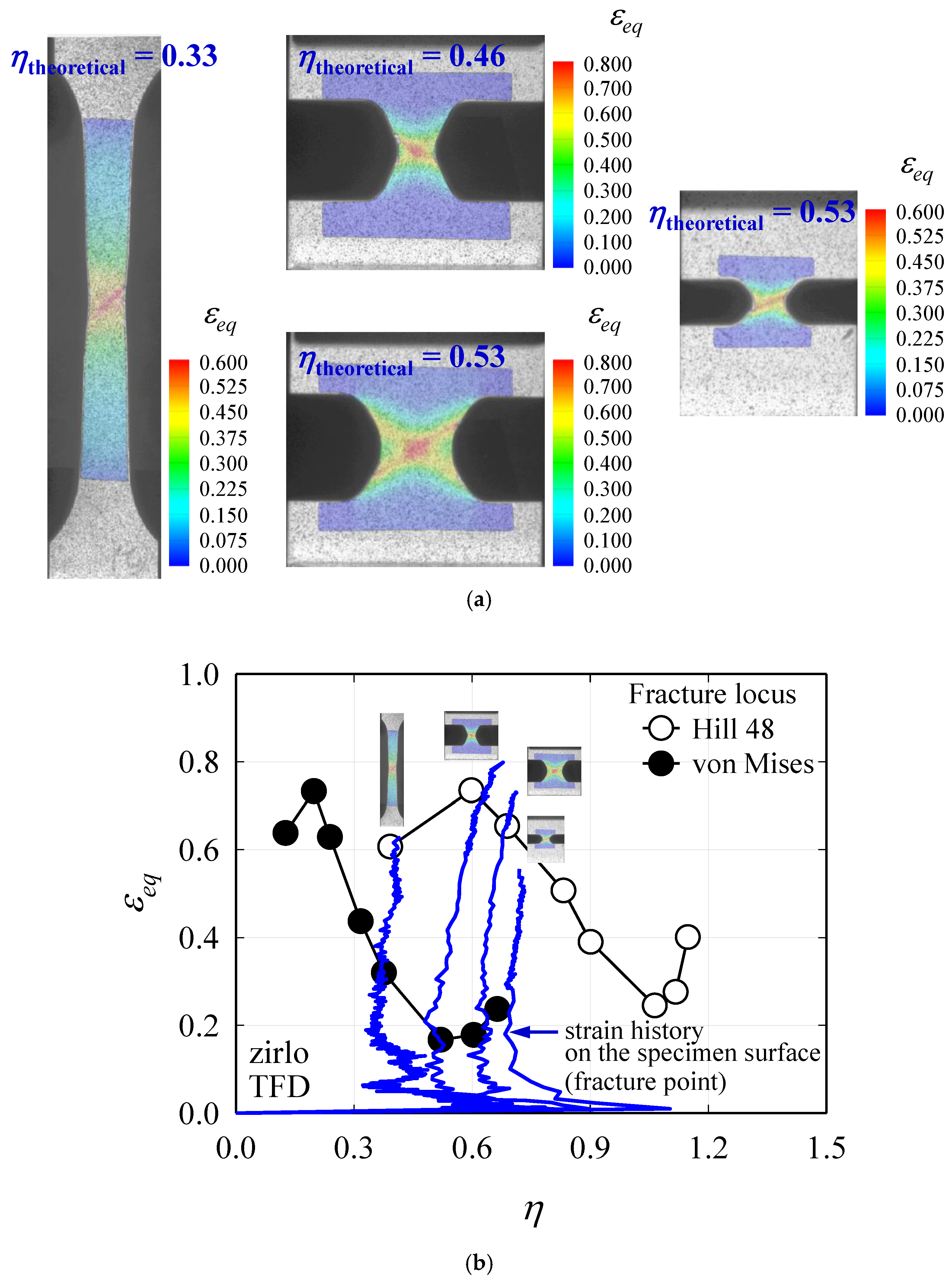
4. Validation through Tensile Tests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Keeler, S.P.; Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. ASM Trans. Quart. 1963, 56, 25–48. [Google Scholar]
- Goodwin, G.M. Application of strain analysis to sheet metal forming problems in the press shop. SAE Tech. Paper 1968, 680093. [Google Scholar] [CrossRef]
- ISO 12004. Metallic materials-sheet and strip-determination of the forming limit curves. In Part 2: Determination of FLCs in the Laboratory; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Kim, M.; Rickhey, F.; Lee, H.; Kim, N. Analytical determination of forming limit curve for zirlo and its experimental validation. J. Manuf. Process. 2016, 23, 122–129. [Google Scholar] [CrossRef]
- Ko, Y.K.; Lee, J.S.; Huh, H.; Kim, H.K.; Park, S.H. Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion. J. Mater. Process. Technol. 2007, 187, 358–362. [Google Scholar] [CrossRef]
- Narayanasamy, R.; Narayanan, C.S.; Padmanabhan, P.; Venugopalan, T. Effect of mechanical and fractographic properties on hole expandability of various automobile steels during hole expansion test. Int. J. Adv. Manuf. Technol. 2010, 47, 365–380. [Google Scholar] [CrossRef]
- Allwood, J.M.; Shouler, D.R. Generalised forming limit diagrams showing increased forming limits with non-planar stress states. Int. J. Plast. 2009, 25, 1207–1230. [Google Scholar] [CrossRef]
- Wu, P.D.; Embury, J.D.; Lloyd, D.J.; Huang, Y.; Neale, K.W. Effects of superimposed hydrostatic pressure on sheet metal formability. Int. J. Plast. 2009, 25, 1711–1725. [Google Scholar] [CrossRef]
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczynski, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–612. [Google Scholar] [CrossRef]
- Hora, P.; Tong, L.; Berisha, B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form. 2013, 6, 267–279. [Google Scholar] [CrossRef]
- Paul, S.K. Predicting the flow behavior of metals under different strain rate and temperature through phenomenological modeling. Comput. Mater. Sci. 2012, 65, 91–99. [Google Scholar] [CrossRef]
- Kim, M.; Gu, B.; Hong, S. Determination of post-necking stress-strain relationship for zirconium low-oxidation based on actual cross-section measurements by DIC. J. Mech. Sci. Technol. 2020, 34, 4211–4217. [Google Scholar] [CrossRef]
- Paul, S.K. Path independent limiting criteria in sheet metal forming. J. Manuf. Process. 2015, 20, 291–303. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. A 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Gabory, B.D.; Motta, A.T.; Wang, K. Transmission electron microscopy characterization of Zircaloy-4 and ZIRLO™ oxide layers. J. Nucl. Mater. 2015, 456, 272–280. [Google Scholar] [CrossRef]
- Azaroff, L.V. Introduction to Solids; McGraw-Hill Company: New York, NY, USA, 1960. [Google Scholar]
- ISO 10113. Metallic Materials—Sheet and Strip—Determination of Plastic Strain Ratio; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- ASTM E517-19. Standard Test Method for Plastic Strain Ratio r for Sheet Metal; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- ARAMIS. User’s Manual-Software v2019; GOM-Gesellschaft für Optische Messtechnik mbH: Braunschweig, Germany, 2019. [Google Scholar]
- KS B 0801. Test pieces for tensile test for metallic materials. In Korean Industrial Standards; Korean Standards Association: Seoul, Korea, 2017. [Google Scholar]
- Lee, J.K.; Kinzel, G.L.; Wagoner, R.H. LDH benchmark. In Proceedings of the Numisheet 96, 3rd International Conference, Numerical Simulation of 3-D Sheet Metal Forming Processes, Dearborn, MI, USA, 29 September–3 October 1996. [Google Scholar]
- ARGUS. Optical forming analysis. In User’s Manual-Software v4.7.4-2; GOM-Gesellschaft für Optische Messtechnik mbH: Braunschweig, Germany, 2001. [Google Scholar]
- Kim, M.; Rickhey, F.; Lee, H.; Kim, N. Numerical approach to the evaluation of forming limit curves for zircaloy-4 sheet. J. Mater. Res. 2015, 30, 3277–3287. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bao, Y.B.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr-Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation. J. Mater. Process. Technol. 2013, 213, 1284–1302. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Trans. AIME 1945, 162, 268–290. [Google Scholar]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Hong, S.; Kim, J.; Jun, T. Failure prediction for the tearing of a pin-loaded dual phase steel (DP980) adjusting guide. Appl. Sci. 2019, 9, 5460. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.; Hong, S. Experimental determination of the failure surface for DP980 high-strength metal sheets considering stress triaxiality and Lode angle. Int. J. Adv. Manuf. Technol. 2019, 100, 2775–2784. [Google Scholar] [CrossRef]
- Panich, S.; Barlat, F.; Uthaisangsuk, V.; Suranuntchai, S.; Jirathearanat, S. Experimental and theoretical formability analysis using strain and stress based forming limit diagram for advanced high strength steels. Mater. Des. 2013, 51, 756–766. [Google Scholar] [CrossRef]
- Li, S.; He, J.; Gu, B.; Zeng, D.; Xia, Z.C.; Zhao, Y.; Lin, Z. Anisotropic fracture of advanced high strength steel sheets: Experiment and theory. Int. J. Plast. 2018, 103, 95–118. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Hong, S. Determination of the Forming Limit for a ZIRLO™ Sheet with High Anisotropy. Materials 2020, 13, 5743. https://doi.org/10.3390/ma13245743
Kim M, Hong S. Determination of the Forming Limit for a ZIRLO™ Sheet with High Anisotropy. Materials. 2020; 13(24):5743. https://doi.org/10.3390/ma13245743
Chicago/Turabian StyleKim, Minsoo, and Seokmoo Hong. 2020. "Determination of the Forming Limit for a ZIRLO™ Sheet with High Anisotropy" Materials 13, no. 24: 5743. https://doi.org/10.3390/ma13245743
APA StyleKim, M., & Hong, S. (2020). Determination of the Forming Limit for a ZIRLO™ Sheet with High Anisotropy. Materials, 13(24), 5743. https://doi.org/10.3390/ma13245743




