Band Gaps Characteristics Analysis of Periodic Oscillator Coupled Damping Beam
Abstract
1. Introduction
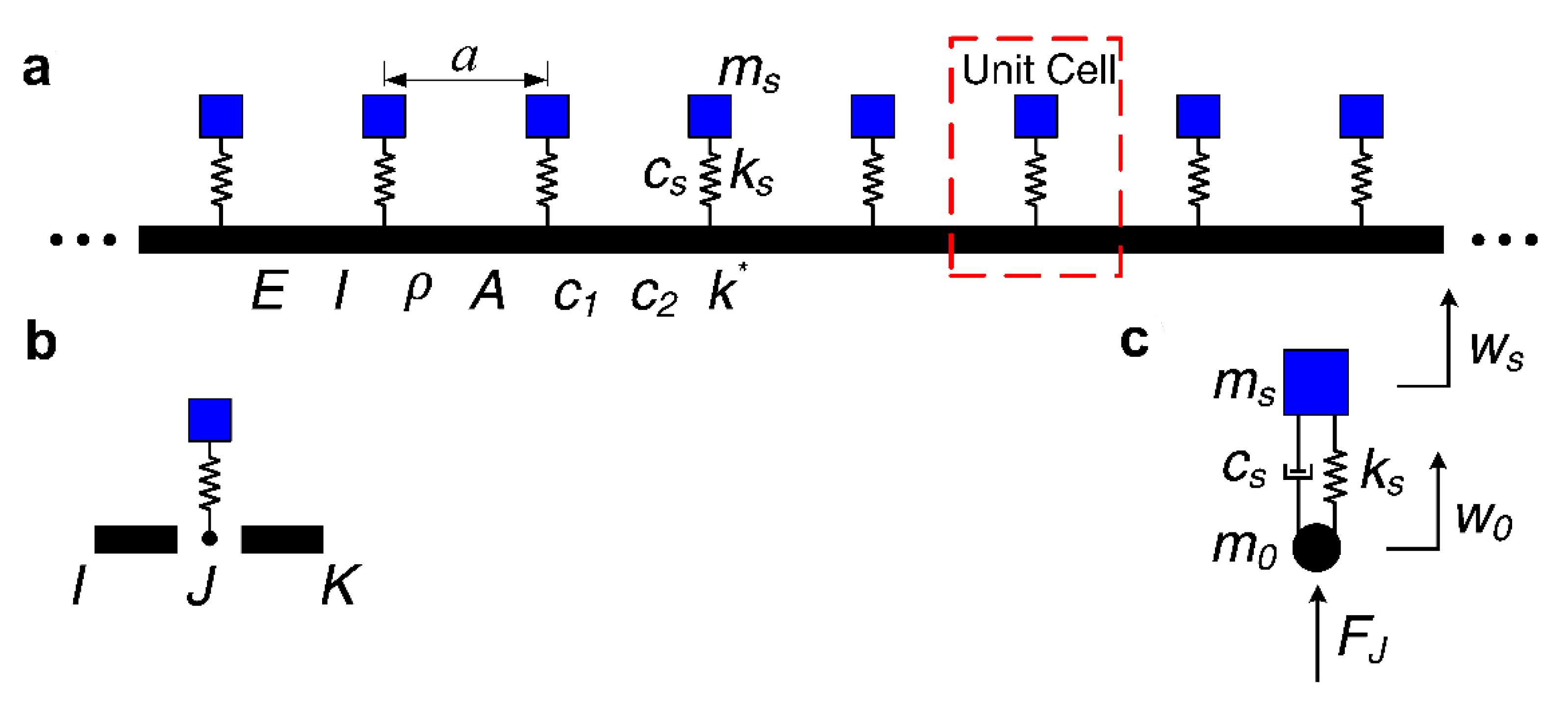
2. Physics Model and Calculation
3. Results and Discussion
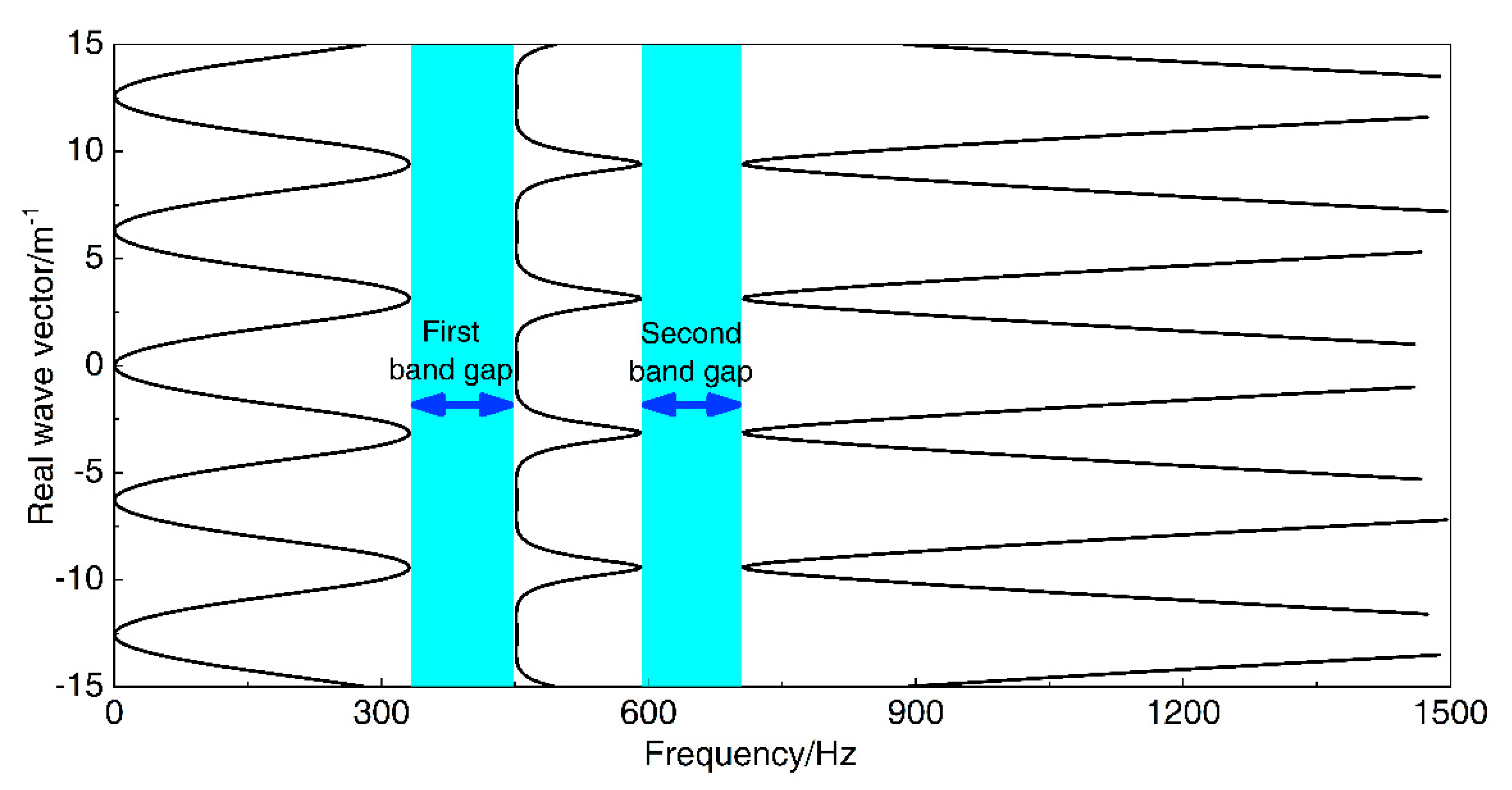
3.1. The Bad Gaps of Infinite Long Periodic Oscillator Coupled Damping Beam
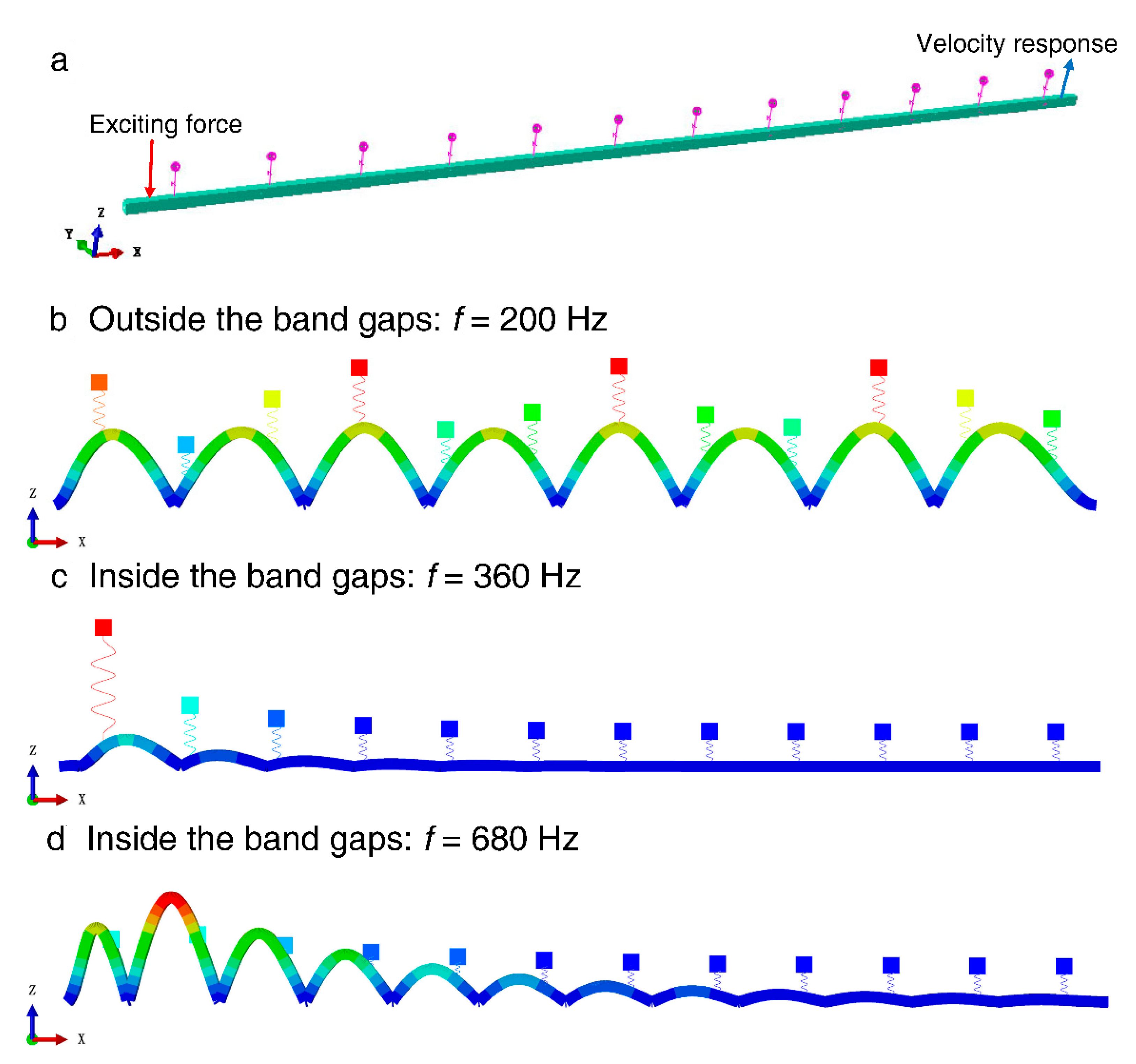
3.2. Numerical Calculation Validation Based on Finite Element Method
3.3. Parametric Study
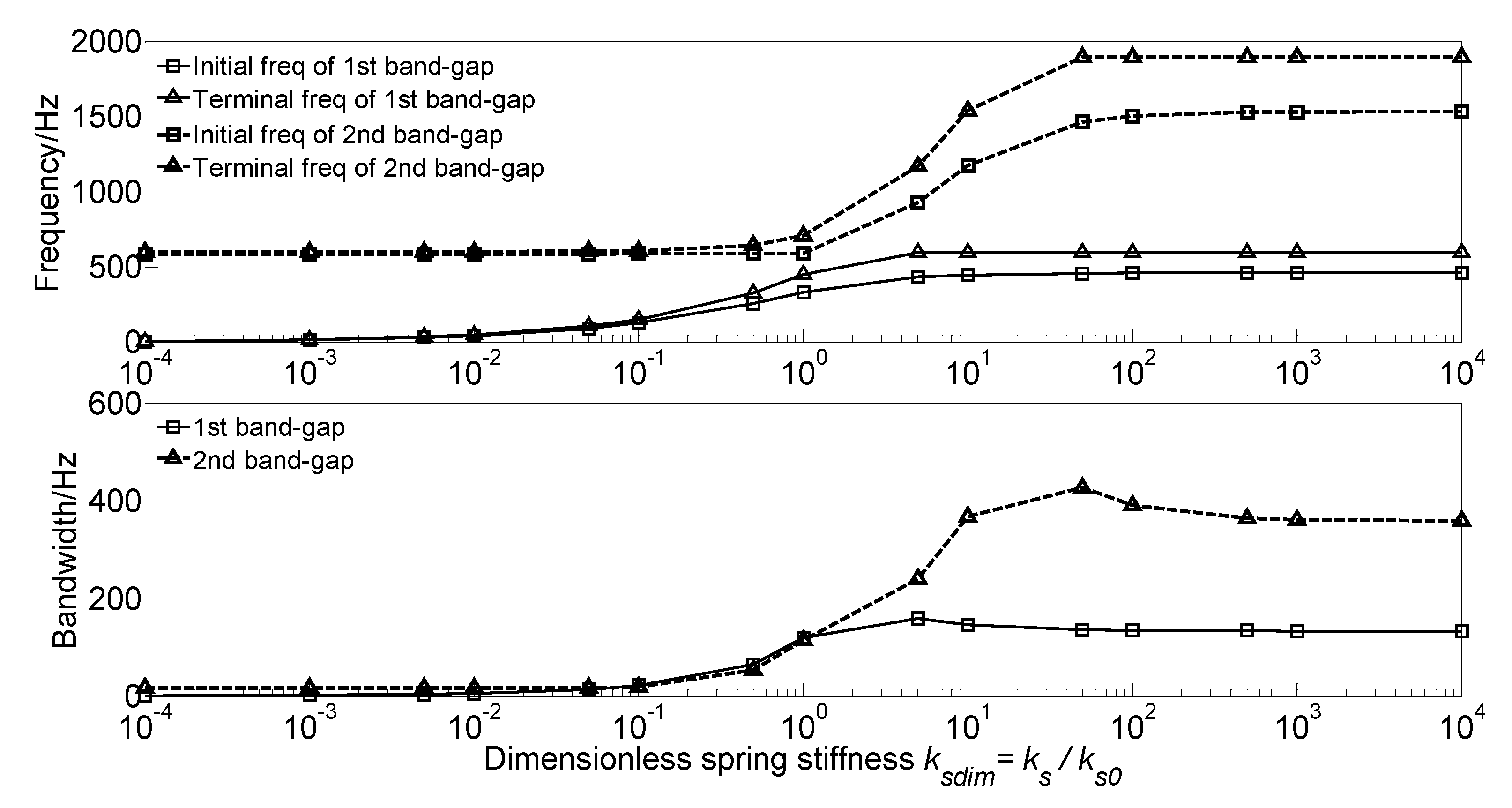
3.3.1. Effect of Spring Stiffness on the Band Gaps
3.3.2. Effect of Spring-Mass Oscillator Mass on the Band Gaps
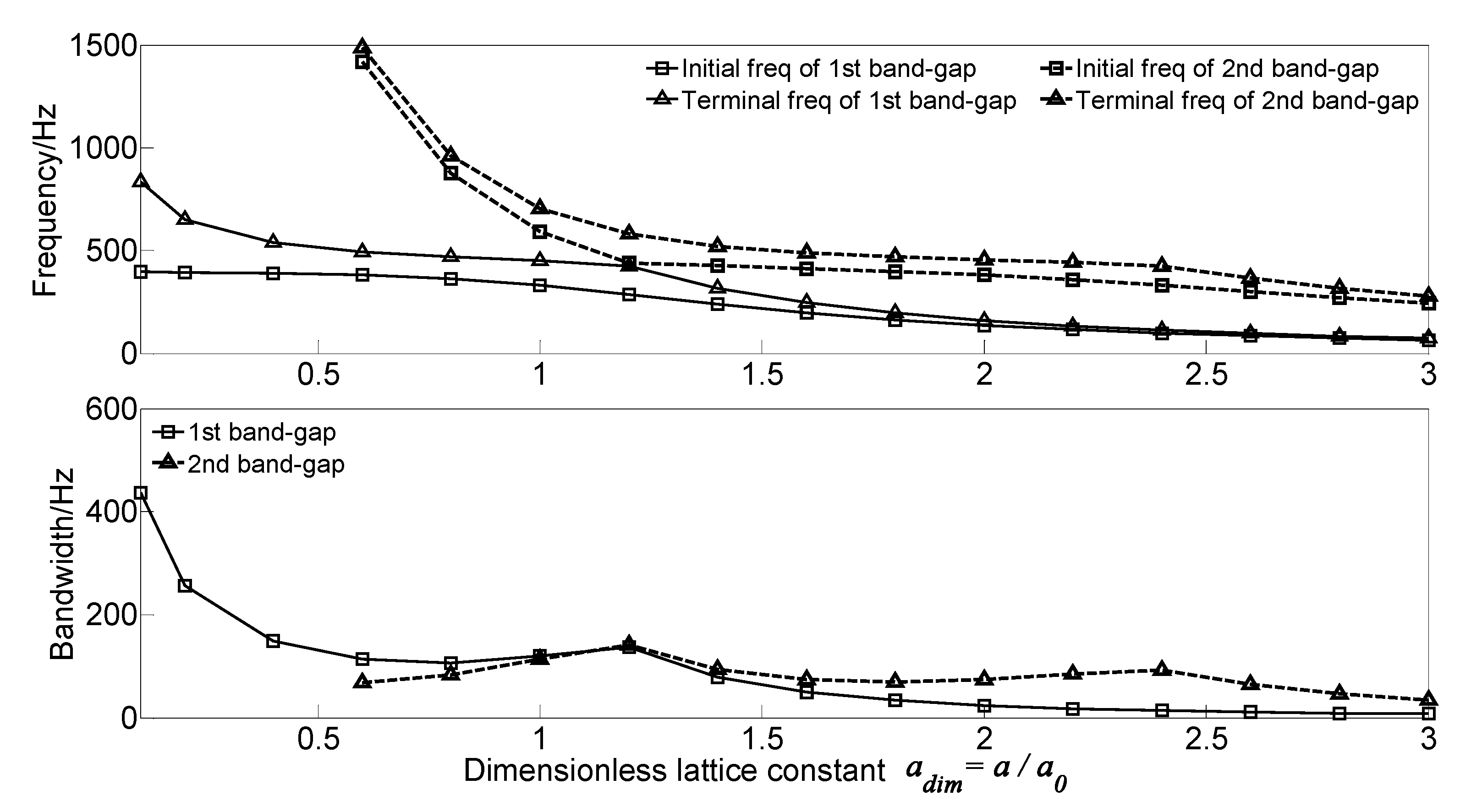
3.3.3. Effect of Lattice Constant on the Band Gaps
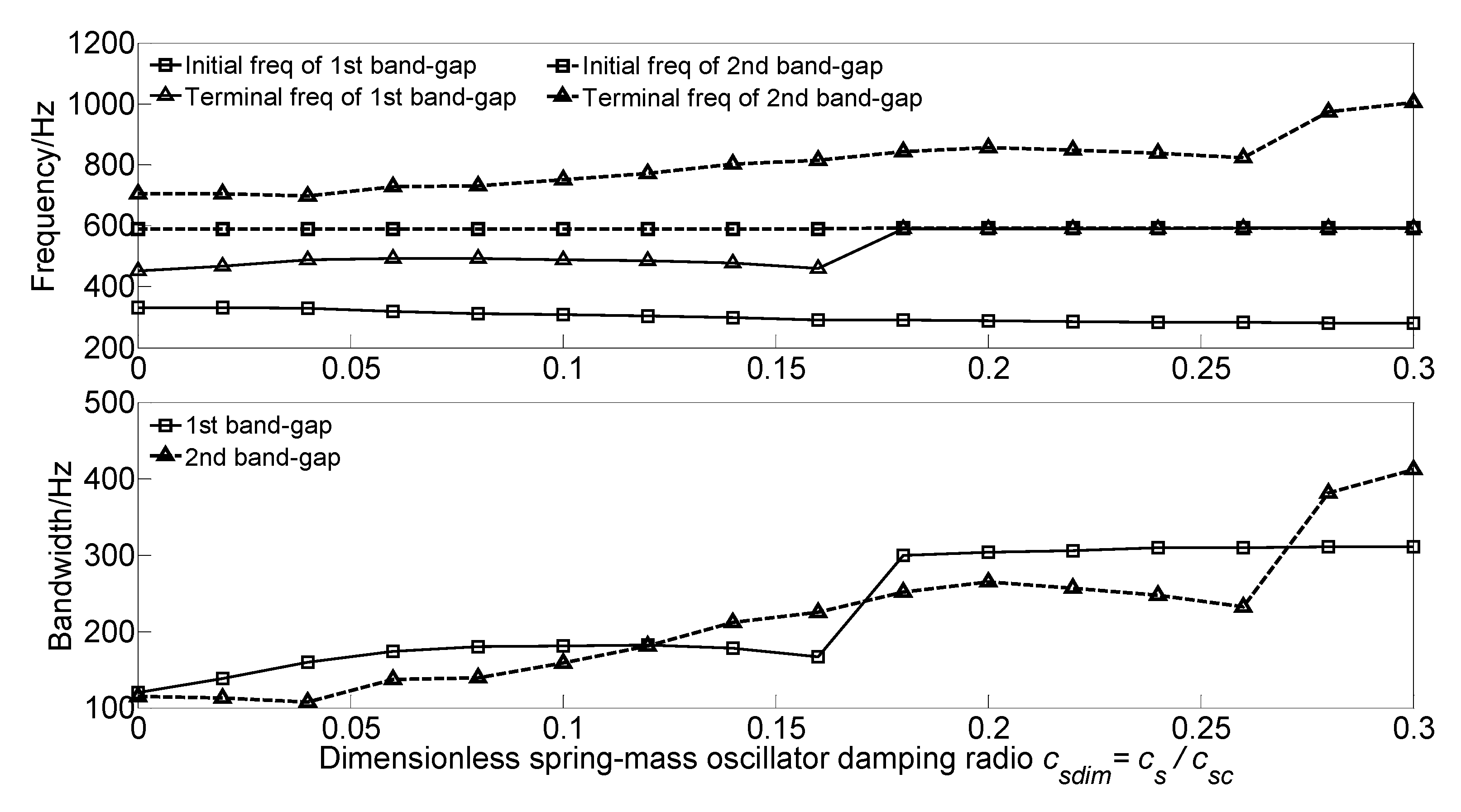
3.3.4. Effect of Spring-Mass Oscillator Damping on the Band Gaps
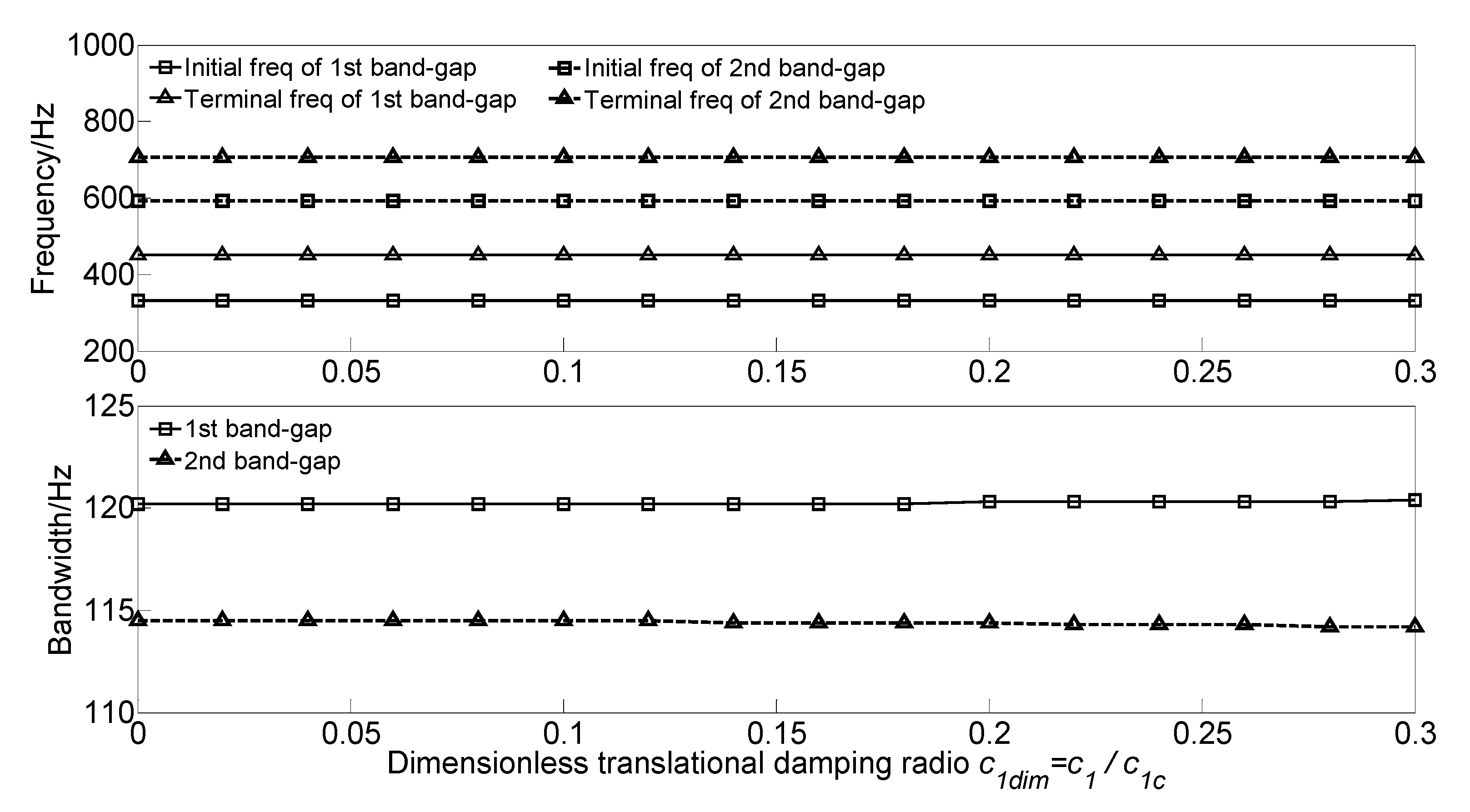
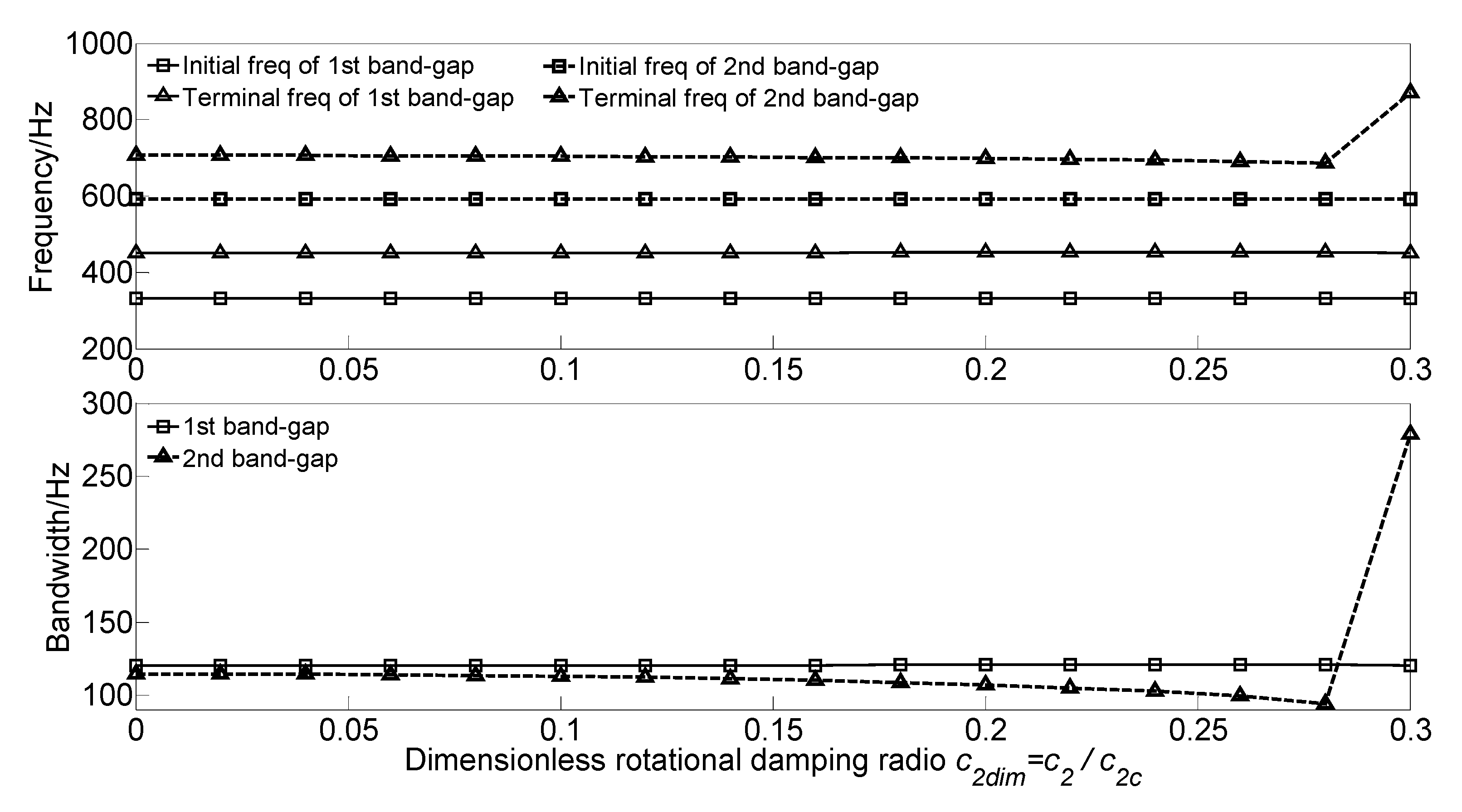
3.3.5. Effect of Beam Damping on the Band Gaps
3.3.6. Effect of Section Moment of Inertia on the Band Gaps
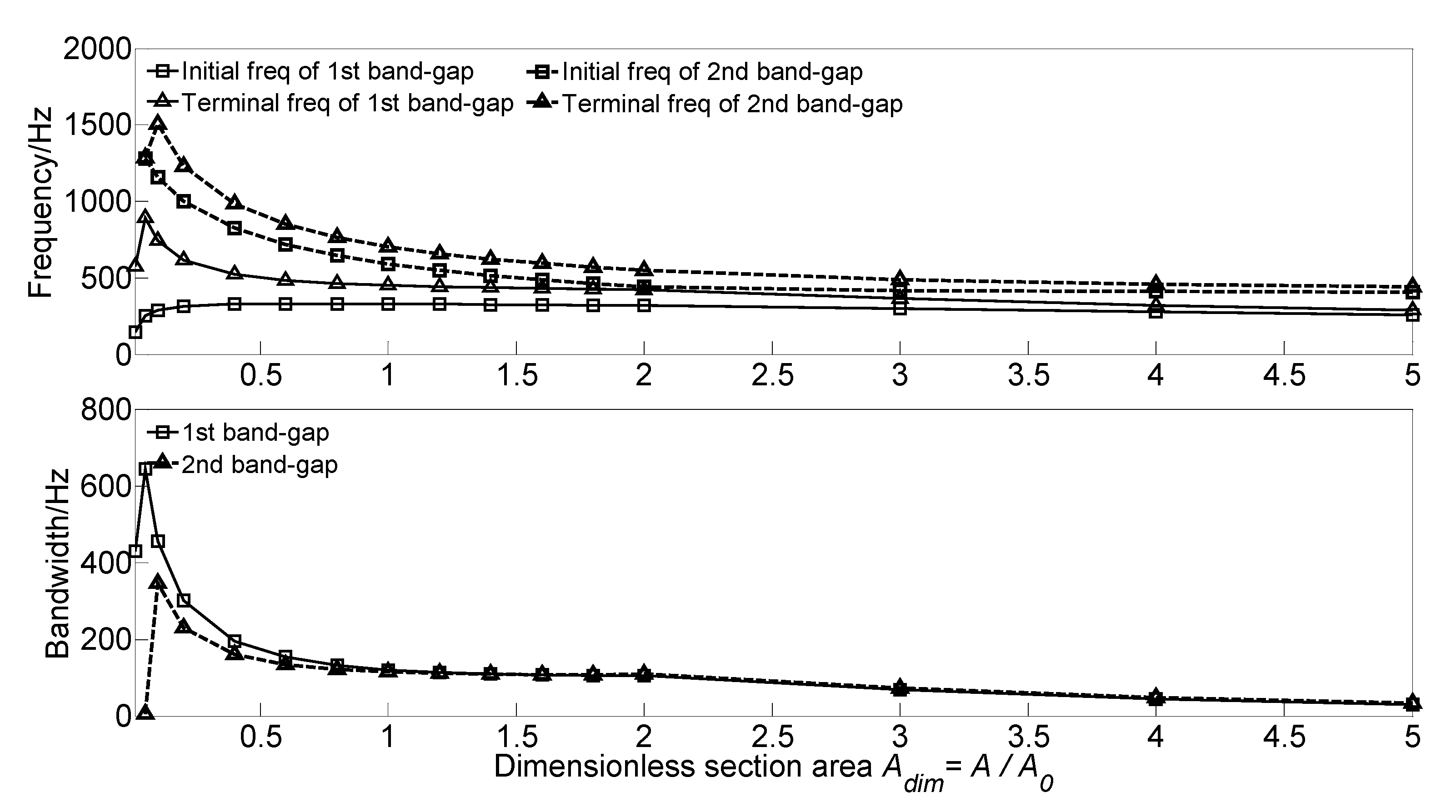
3.3.7. Effect of Section Area on the Band Gaps
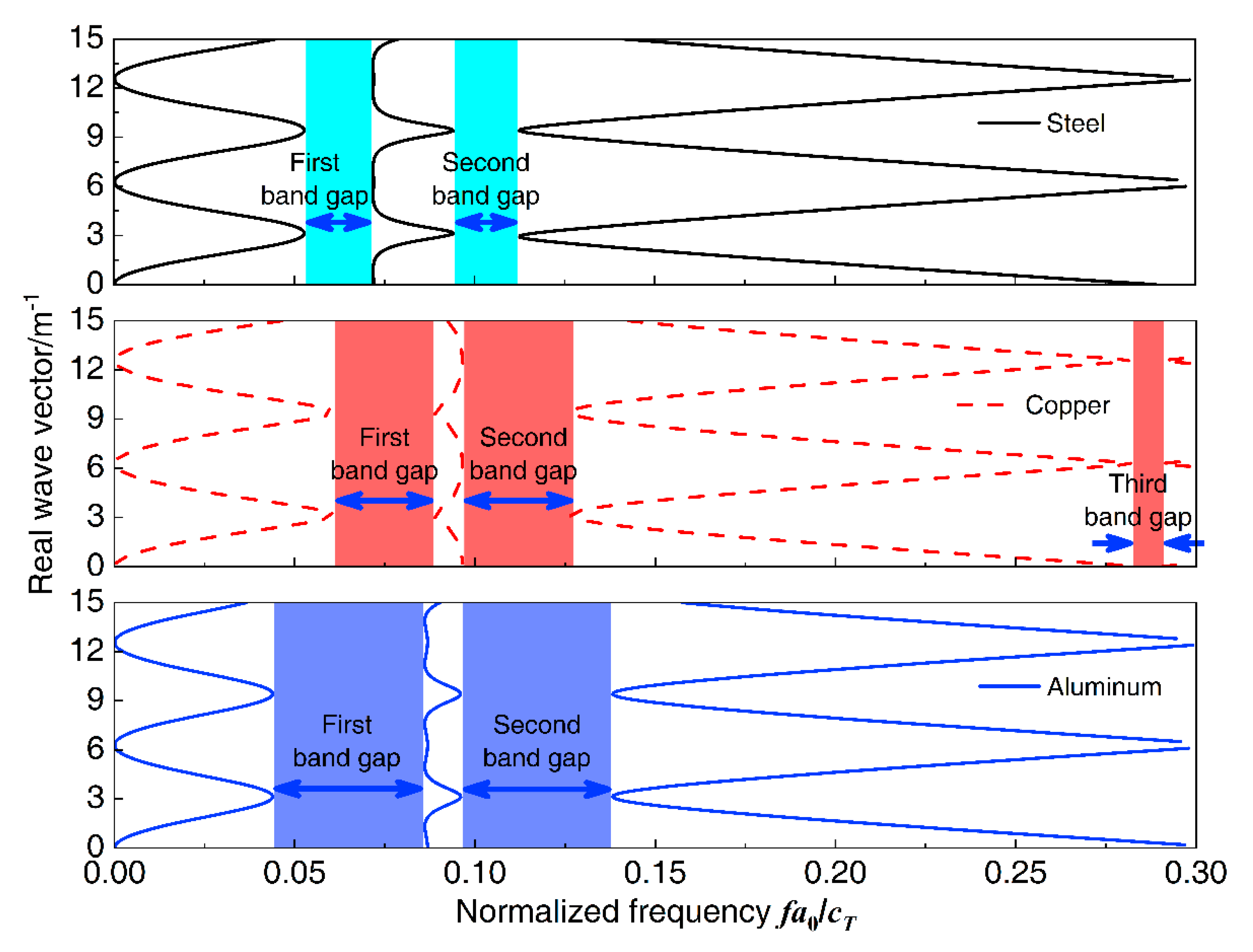
3.3.8. Effect of Material Parameters on the Band Gaps
4. Conclusions
- As the study of the effect of spring stiffness on the band gaps, the initial frequencies, terminal frequencies, and bandwidths of the band gaps increase in a multistep manner. The band gaps’ frequencies have a significant increase when the spring stiffness in the range of 105~108 N·m2, which is equivalent to the beam stiffness EI = 4.2 × 106 N·m2, while the band gaps characteristics almost remain unchanged when the spring stiffness outside the range.
- The dimensionless mass msdim increase cause the frequencies of the band gaps gradually decrease, while there is a critical dimensionless mass value msdim = 0.6, the terminal frequency of the first band gap remains unchanged when the dimensionless mass msdim < 0.6, and the initial frequency and terminal frequency of the second band gap are almost unchanged when the dimensionless mass msdim > 0.6.
- As the damping absorbs and consumes the flexural wave vibration energy but did not change the spectrum characteristics, the translational damping c1 and rotational damping c2 of the homogeneous straight damping beam have little effect on the band gaps characteristics. While the effects of spring-mass oscillator damping on the band gaps are due to the proposed damping changes in the reaction force of the spring-mass oscillator acting on the beam.
- The effects of section moment of inertia I and section area A on the band gaps are similar; the band gaps have significant changes when the dimensionless parametric ratios are less than the critical values, whereas almost remain unchanged when the dimensionless parametric ratios are greater than the critical values. Thus, it is not conducive to applying band gap characteristics to the structural vibration reduction design in engineering.
- The spring stiffness ks and lattice constant a have great effects on band gaps characteristics; with the increase of the dimensionless spring stiffness and dimensionless lattice constant, the initial frequencies and terminal frequencies gradually change. This is conducive to applying band gap characteristics by tuning the geometrical parameters for structural vibration reduction design.
Author Contributions
Funding
Conflicts of Interest
References
- Mead, D. Free wave propagation in periodically supported, infinite beams. J. Sound Vib. 1970, 11, 181–197. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P.; Janevski, G. Exact closed-form solutions for the natural frequencies and stability of elastically connected multiple beam system using Timoshenko and high-order shear deformation theory. J. Sound Vib. 2013, 332, 563–576. [Google Scholar] [CrossRef]
- Wesolowski, M.; Ruchwa, M.; Skukis, E.; Kovalovs, A. Numerical and Experimental Extraction of Dynamic Parameters for Pyramidal Truss Core Sandwich Beams with Laminated Face Sheets. Materials 2020, 13, 5199. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Wang, X.; Wu, N.; Chu, F.; Luo, J. A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core. Matererials 2019, 12, 3390. [Google Scholar] [CrossRef] [PubMed]
- Kandasamy, R.; Cui, F.; Townsend, N.; Foo, C.C.; Guo, J.; Shenoi, A.; Xiong, Y. A review of vibration control methods for marine offshore structures. Ocean Eng. 2016, 127, 279–297. [Google Scholar] [CrossRef]
- Shen, H. Flexural vibration property of periodic pipe system conveying fluid based on Timoshenko beam equation. Acta Phys. Sin. 2009, 58, 8357–8363. [Google Scholar]
- Wu, Q.; Wang, M. Study on the Dynamic Mechanical Properties of Viscoelastic Materials Based on Asymmetrical Sandwich Beams. Appl. Sci. 2018, 8, 1359. [Google Scholar] [CrossRef]
- Zhang, Y.; Ni, Z.-Q.; Jiang, L.-H.; Han, L.; Kang, X.-W. Study of the bending vibration characteristic of phononic crystals beam-foundation structures by Timoshenko beam theory. Int. J. Mod. Phys. B 2015, 29, 1550136. [Google Scholar] [CrossRef]
- Wen, J.H. Lumped-mass method on calculation of elastic band gaps of one-dimensional phononic crystals. Acta Phys. Sin. 2004, 53, 3384–3389. [Google Scholar]
- Cai, L.; Han, X.-Y. Study of the band-structure and the uncoupled modes in two-dimensional phononic crystals with the multiple-scattering theory. Acta Phys. Sin. 2006, 55, 5866–5872. [Google Scholar]
- Jiang, H.; Zhang, M.; Liu, Y.; Pei, D.; Chen, M.; Wang, Y.-R. Band Gaps and Vibration Isolation of a Three-Dimensional Metamaterial with a Star Structure. Materials 2020, 13, 3812. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Yang, L. Transmission of Low-Frequency Acoustic Waves in Seawater Piping Systems with Periodical and Adjustable Helmholtz Resonator. J. Mar. Sci. Eng. 2017, 5, 56. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Super Lattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P.; Goertzen, A.L.; Page, J.H. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446–2457. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P. Three-component elastic wave band-gap material. Phys. Rev. B 2002, 65, 165116–1651166. [Google Scholar] [CrossRef]
- Faiz, M.S.; Addouche, M.; Zain, A.R.M.; Siow, K.S.; Chaalane, A.; Khelif, A. Experimental Demonstration of a Multichannel Elastic Wave Filter in a Phononic Crystal Slab. Appl. Sci. 2020, 10, 4594. [Google Scholar] [CrossRef]
- Boechler, N.; Eliason, J.K.; Kumar, A.; Maznev, A.A.; Nelson, K.A.; Fang, N. Interaction of a Contact Resonance of Microspheres with Surface Acoustic Waves. Phys. Rev. Lett. 2013, 111, 036103. [Google Scholar] [CrossRef]
- Graczykowski, B.; Vogel, N.; Bley, K.; Butt, H.-J.; Fytas, G. Multiband Hypersound Filtering in Two-Dimensional Colloidal Crystals: Adhesion, Resonances, and Periodicity. Nano Lett. 2020, 20, 1883–1889. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Wen, J.; Yu, D.; Wen, X. The vibrational properties of a periodic composite pipe in 3D space. J. Sound Vib. 2009, 328, 57–70. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Zhao, H.; Liu, Y.; Wen, X. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J. Sound Vib. 2008, 318, 193–205. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.; Wen, X. Broadband locally resonant beams containing multiple periodic arrays of attached resonators. Phys. Lett. A 2012, 376, 1384–1390. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Shen, H.; Xiao, Y.; Wen, X. Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 2012, 376, 626–630. [Google Scholar] [CrossRef]
- Ruzzene, M.; Tsopelas, P. Control of Wave Propagation in Sandwich Plate Rows with Periodic Honeycomb Core. J. Eng. Mech. 2003, 129, 975–986. [Google Scholar] [CrossRef]
- Xiao, W.; Zeng, G.; Cheng, Y. Flexural vibration band gaps in a thin plate containing a periodic array of hemmed discs. Appl. Acoust. 2008, 69, 255–261. [Google Scholar] [CrossRef]
- Wu, J. Low frequency band gaps and vibration reduction properties of a multi-frequency locally resonant phononic plate. Acta Phys. Sin. 2016, 65, 5. [Google Scholar]
- Chen, Z.; Xie, W.-C. Vibration localization in plates rib-stiffened in two orthogonal directions. J. Sound Vib. 2005, 280, 235–262. [Google Scholar] [CrossRef]
- Ledet, L.S.; Ershova, O. Analysis of the energy transmission in compound cylindrical shells with and without internal heavy fluid loading by boundary integral equations and by Floquet theory. J. Sound Vib. 2006, 291, 81–99. [Google Scholar] [CrossRef]
- Dian-Long, Y.; Gang, W.; Yao-Zong, L.; Ji-Hong, W.; Jing, Q. Flexural vibration band gaps in thin plates with two-dimensional binary locally resonant structures. Chin. Phys. 2006, 15, 266–271. [Google Scholar] [CrossRef]
- Wang, G. Research on the Mechanism and the Vibration Attenuation Characteristic of Locally Resonant Band Gap in Phononic Crystals; National University of Defense Technology: Changsha, China, 2015. [Google Scholar]
- Cho, D.-S.; Kim, B.-H.; Kim, J.-H.; Choi, T.M.; Vladimir, N. Free vibration analysis of stiffened panels with lumped mass and stiffness attachments. Ocean Eng. 2016, 124, 84–93. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.Y.; Shao, X.; Wang, S.; Tian, Y. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin-Walled Struct. 2014, 82, 115–123. [Google Scholar] [CrossRef]
- Cao, Y.J.; Yun, G.H.; Narsu, B. Band-structure calculations of two-dimesional magnonic crystals with plane-wave expansion method. Acta Phys. Sin. 2011, 60, 50. [Google Scholar]
- Kafesaki, M.; Sigalas, M.M.; García, N. Frequency Modulation in the Transmittivity of Wave Guides in Elastic-Wave Band-Gap Materials. Phys. Rev. Lett. 2000, 85, 4044–4047. [Google Scholar] [CrossRef]
- Psarobas, I.E.; Stefanou, N.; Modinos, A. Phononic crystals with planar defects. Phys. Rev. B 2000, 62, 5536–5540. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.; Liu, Y.; Wen, X. Lumped-mass method for the study of band structure in two-dimensional phononic crystals. Phys. Rev. B 2004, 69, 184302. [Google Scholar] [CrossRef]
- Mencik, J.-M. A model reduction strategy for computing the forced response of elastic waveguides using the wave finite element method. Comput. Methods Appl. Mech. Eng. 2012, 229, 68–86. [Google Scholar] [CrossRef]
- Liu, C.R.; Wu, J.H.; Lu, K.; Zhao, Z.T.; Huang, Z. Acoustical siphon effect for reducing the thickness in membrane-type metamaterials with low-frequency broadband absorption. Appl. Acoust. 2019, 148, 1–8. [Google Scholar] [CrossRef]
- Richards, D.; Pines, D. Passive reduction of gear mesh vibration using a periodic drive shaft. J. Sound Vib. 2003, 264, 317–342. [Google Scholar] [CrossRef]
- Singh, A.; Pines, D. Active/Passive Vibration Reduction of Periodic 1-D Structures Using Piezoelectric Actuators. Struct. Struct. Dyn. Mater. Conf. 2002, 13, 698. [Google Scholar] [CrossRef]
- Yeh, J.-Y.; Chen, L.-W. Wave propagations of a periodic sandwich beam by FEM and the transfer matrix method. Compos. Struct. 2006, 73, 53–60. [Google Scholar] [CrossRef]
- Wu, M.-L.; Wu, L.-Y.; Yang, W.-P.; Chen, L.-W. Elastic wave band gaps of one-dimensional phononic crystals with functionally graded materials. Smart Mater. Struct. 2009, 18, 115013. [Google Scholar] [CrossRef]
- Tang, D.; Yao, X.; Wu, G.; Peng, Y. Free and forced vibration analysis of multi-stepped circular cylindrical shells with arbitrary boundary conditions by the method of reverberation-ray matrix. Thin-Walled Struct. 2017, 116, 154–168. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhao, X.Y.; Li, H. Green’s functions of the forced vibration of Timoshenko beams with damping effect. J. Sound Vib. 2014, 333, 1781–1795. [Google Scholar] [CrossRef]
- Nobrega, E.; Gautier, F.; Pelat, A.; Dos Santos, J. Vibration band gaps for elastic metamaterial rods using wave finite element method. Mech. Syst. Signal Process. 2016, 79, 192–202. [Google Scholar] [CrossRef]
- Waki, Y.; Mace, B.R.; Brennan, M. Numerical issues concerning the wave and finite element method for free and forced vibrations of waveguides. J. Sound Vib. 2009, 327, 92–108. [Google Scholar] [CrossRef]
- Xiang, H.; Ma, X.; Xiang, J. Band Gaps and Transmission Characteristics Analysis on a Two-Dimensional Multiple-Scatter Phononic Crystal Structure. Materials 2020, 13, 2106. [Google Scholar] [CrossRef]
- Zhou, C.W.; Lainé, J.P.; Ichchou, M.N.; Zine, A.M. Wave Finite Element Method Based on Reduced Model for One-Dimensional Periodic Structures. Int. J. Appl. Mech. 2015, 7. [Google Scholar] [CrossRef]




| Parameter | ks0 | ms0 | a0 | cs0 | c1 | c2 | I0 | A0 |
|---|---|---|---|---|---|---|---|---|
| Value | 5.0 × 107 N/m | 8 kg | 0.5 m | 0 N·s/m | 0 N·s/m | 0 N·s/m | 2.0 × 10−5 m4 | 3.0 × 10−3 m2 |
| Steel | Copper | Aluminum | |
|---|---|---|---|
| Young’s modulus E/Pa | 2.1 × 1011 | 1.1 × 1011 | 7.0 × 1010 |
| Mass density ρ/kg·m−3 | 7850 | 8900 | 2600 |
| Poisson’s ratio ν | 0.28 | 0.34 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Yao, X.; Wu, G.; Tang, D. Band Gaps Characteristics Analysis of Periodic Oscillator Coupled Damping Beam. Materials 2020, 13, 5748. https://doi.org/10.3390/ma13245748
Tang L, Yao X, Wu G, Tang D. Band Gaps Characteristics Analysis of Periodic Oscillator Coupled Damping Beam. Materials. 2020; 13(24):5748. https://doi.org/10.3390/ma13245748
Chicago/Turabian StyleTang, Li, Xiongliang Yao, Guoxun Wu, and Dong Tang. 2020. "Band Gaps Characteristics Analysis of Periodic Oscillator Coupled Damping Beam" Materials 13, no. 24: 5748. https://doi.org/10.3390/ma13245748
APA StyleTang, L., Yao, X., Wu, G., & Tang, D. (2020). Band Gaps Characteristics Analysis of Periodic Oscillator Coupled Damping Beam. Materials, 13(24), 5748. https://doi.org/10.3390/ma13245748





