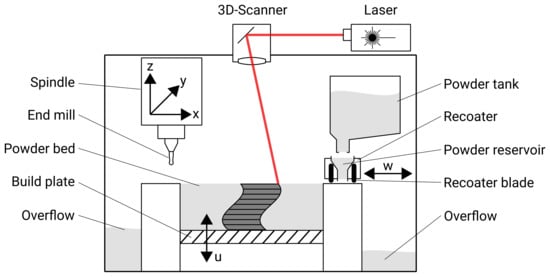
Four test series were evaluated, since the unmachined and milled components were each measured on the vertical and horizontal surfaces.
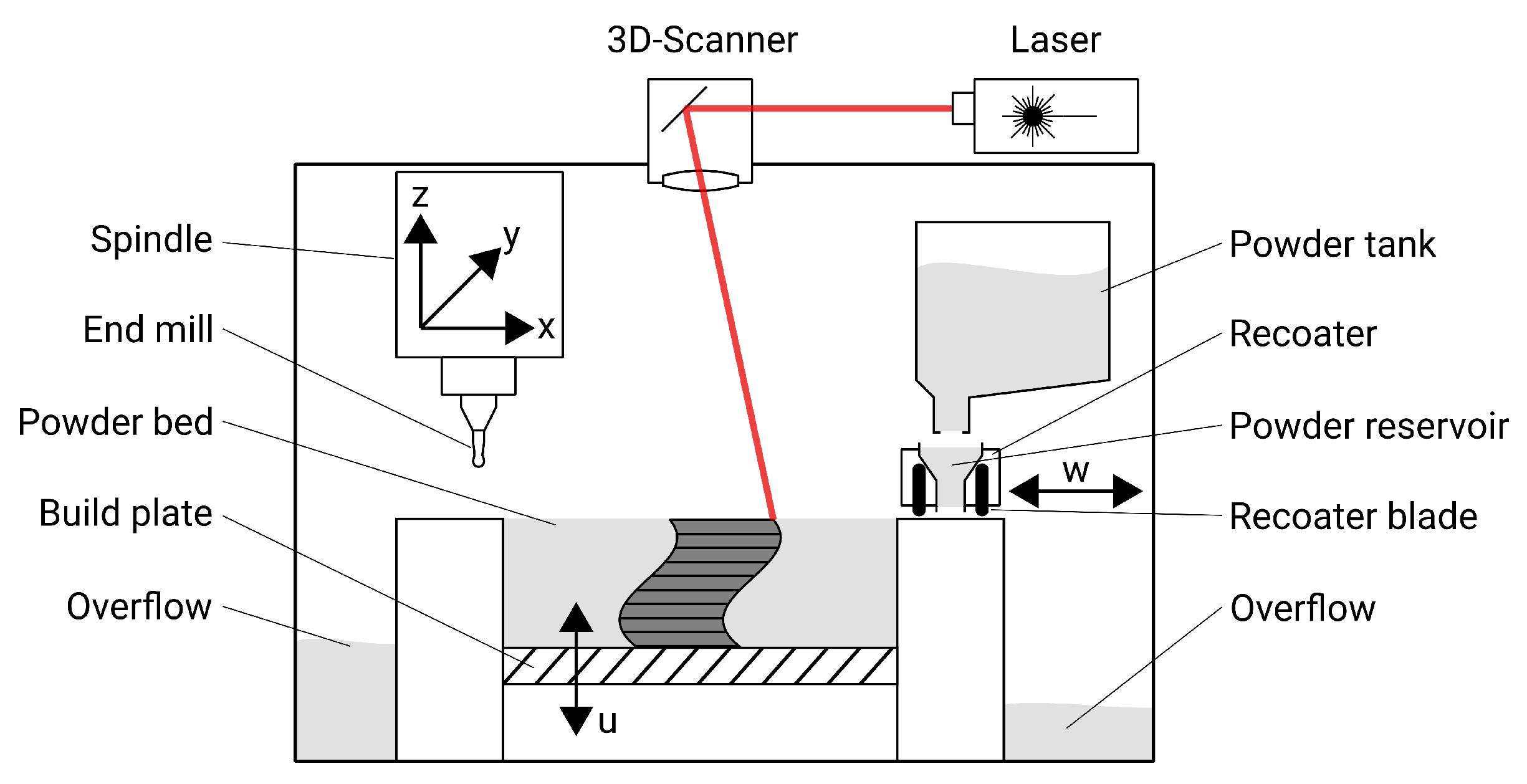
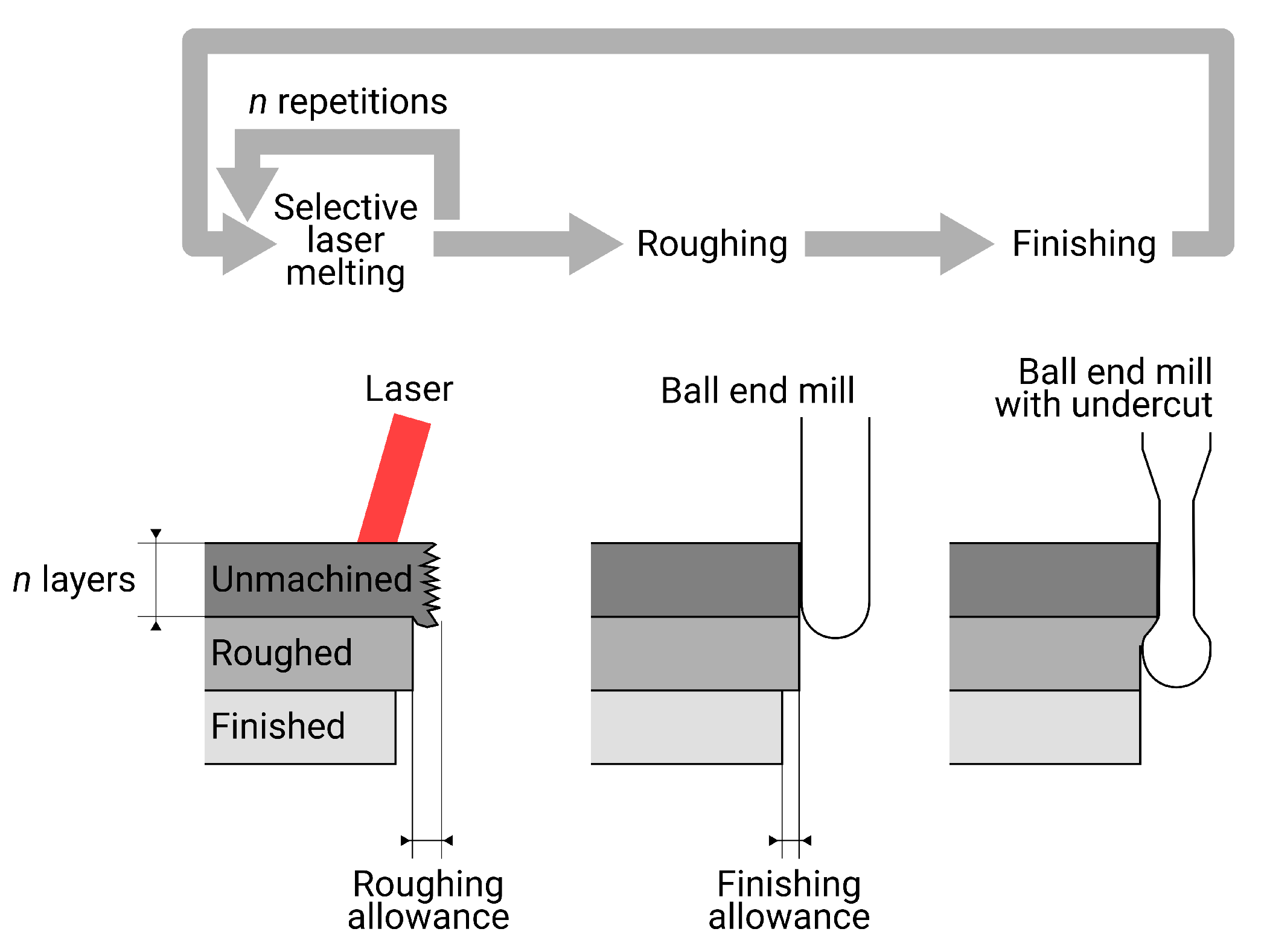
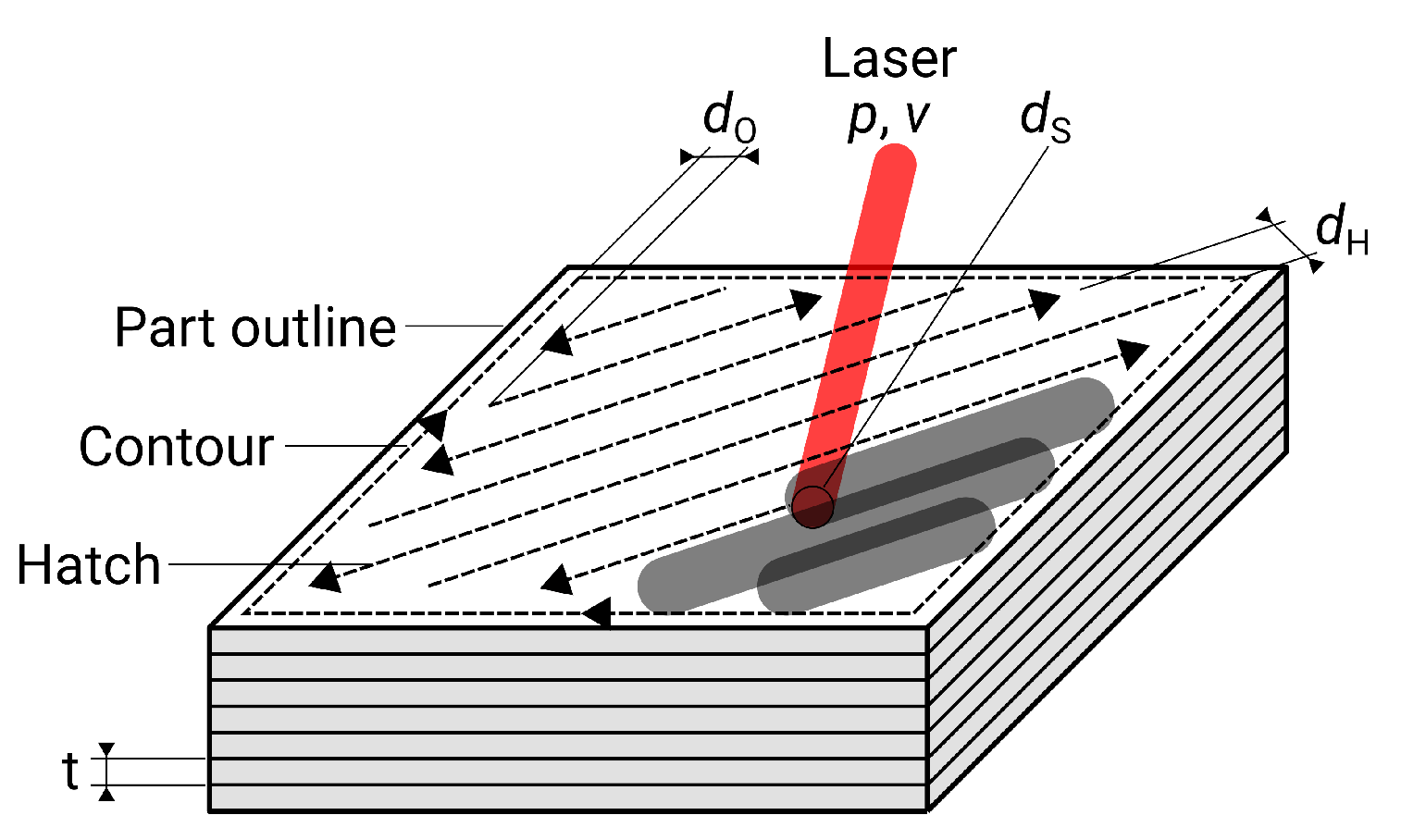
3.1. Selective Laser Melting
For vertical surfaces, i.e., contours, the performed test combinations, the respective energy density and the corresponding results can be found in
Table 4. The
p-value of the ANOVA (see
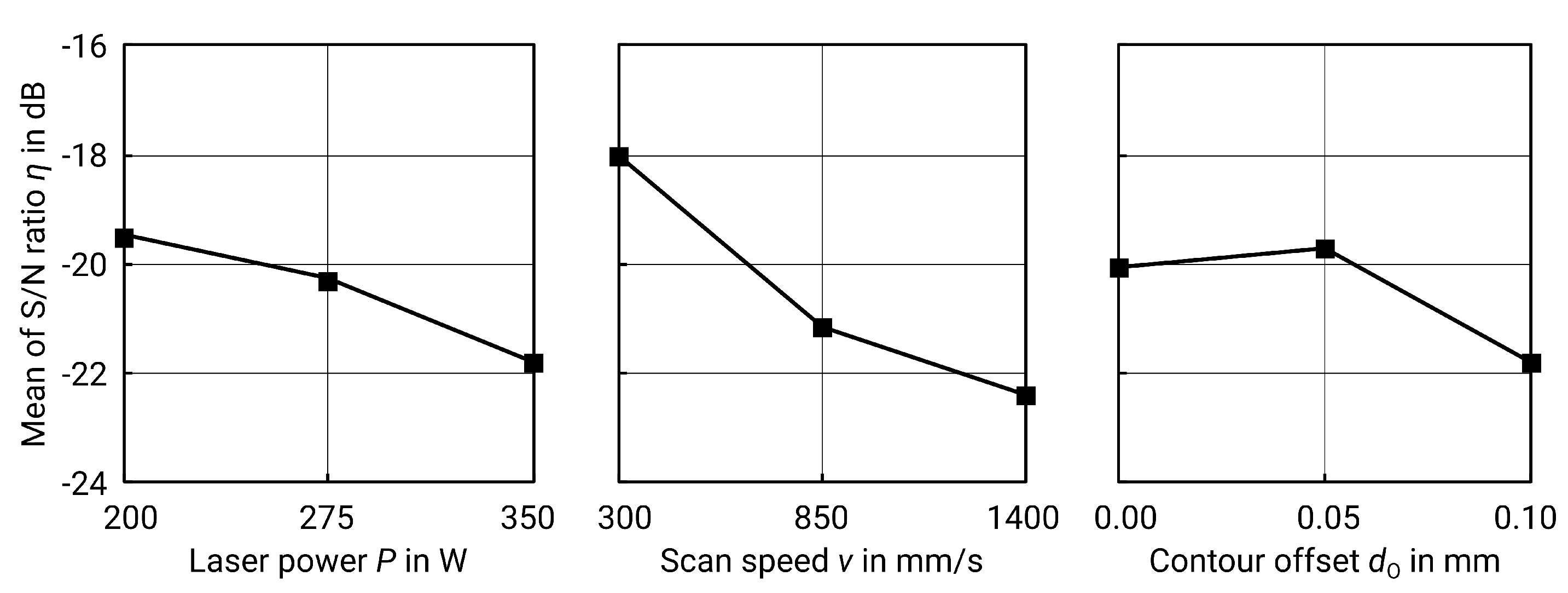
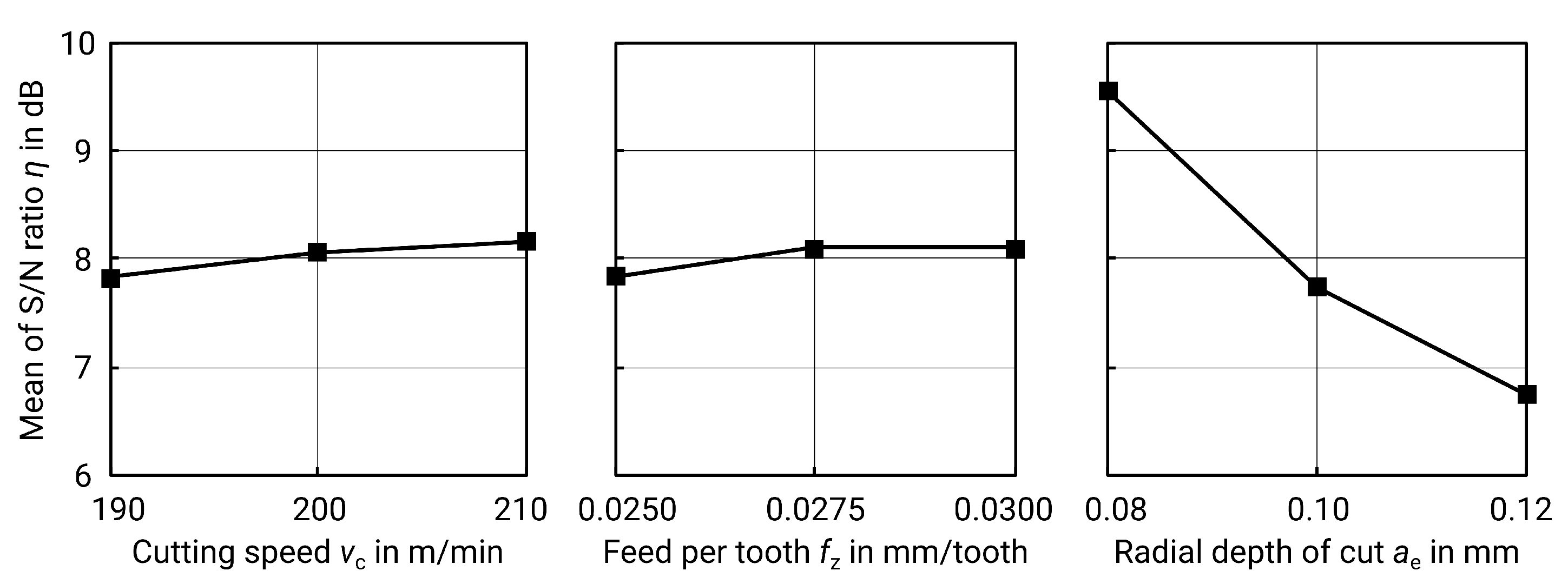
Table 5) shows that the scan speed
v is the most important factor. The delta S/N value (spreading of S/N values, see
Table 6 and
Figure 6) confirms this because the larger the spread, the stronger the influence of the factor.
The best result of the test series is specimen no. 1 (see
Table 4) with an obtained roughness
of 6.5
. However, the individual best factor levels result in a theoretical optimum at
,
and
. The resulting roughness from these factor levels can be predicted using linear regression using formula (
8) and results in
:
In order to validate the result, a further test specimen was produced and tested with the optimum factor levels. The
measured is 7.50
which is in good agreement with the afore predicted value. However, both the calculated and the measured
are not the best values of the test series. In order to achieve the lowest possible roughness, the factor levels from experiment number one should therefore be used (see
Table 4). The only difference between the parameters is the contour offset
, which is zero in the actual optimum. An interpretation of the statistical data supports the assumption that
can be set to zero: The
p-value of ANOVA shows that
is the least significant parameter. Abele and Kniepkamp confirm the assumption that
can be neglected, either due to the dominant effect of energy or due to insufficient spread of the design space [
5]. This shows that the model is a very good approximation but is also accompanied by certain errors, though only in the range of one micron.
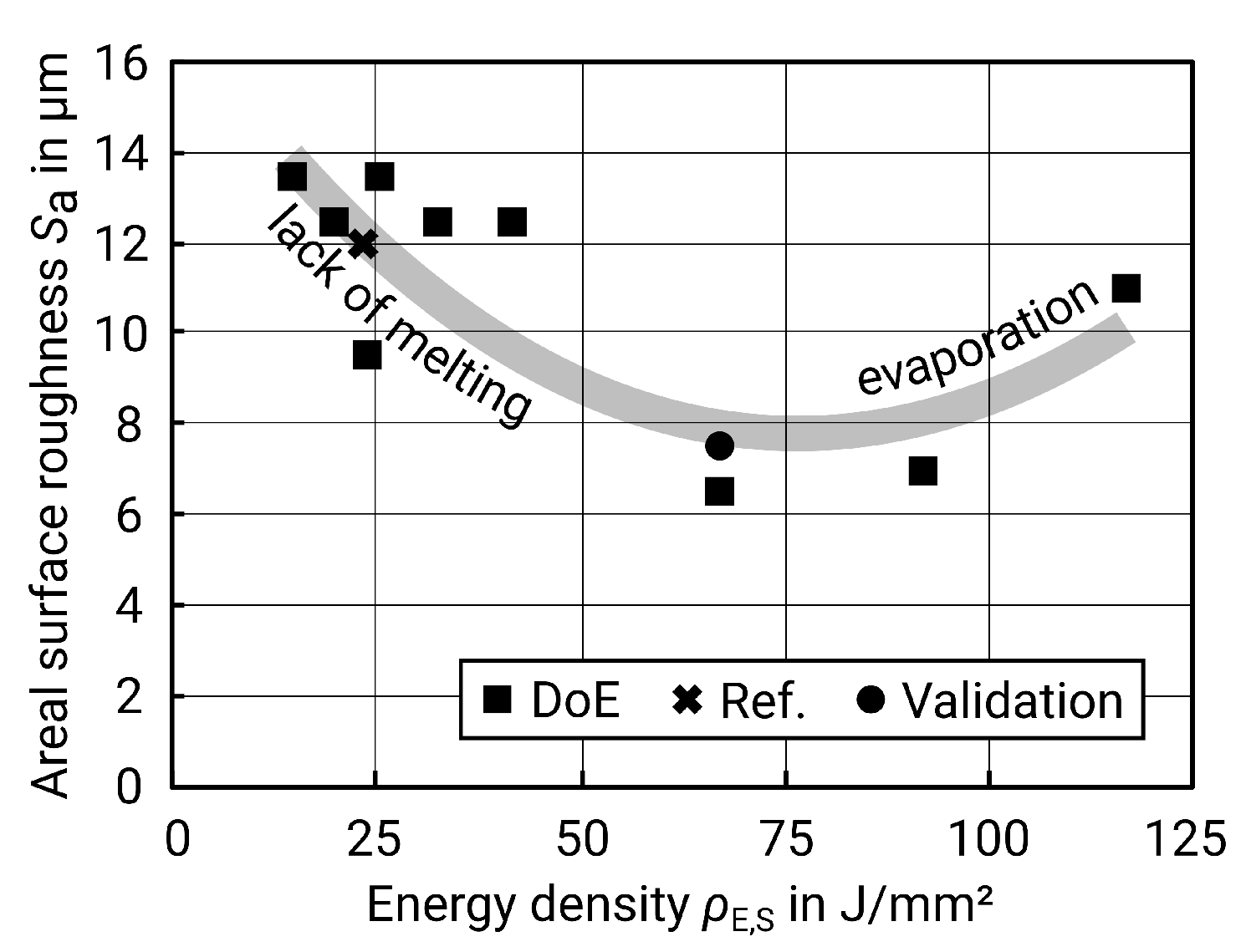
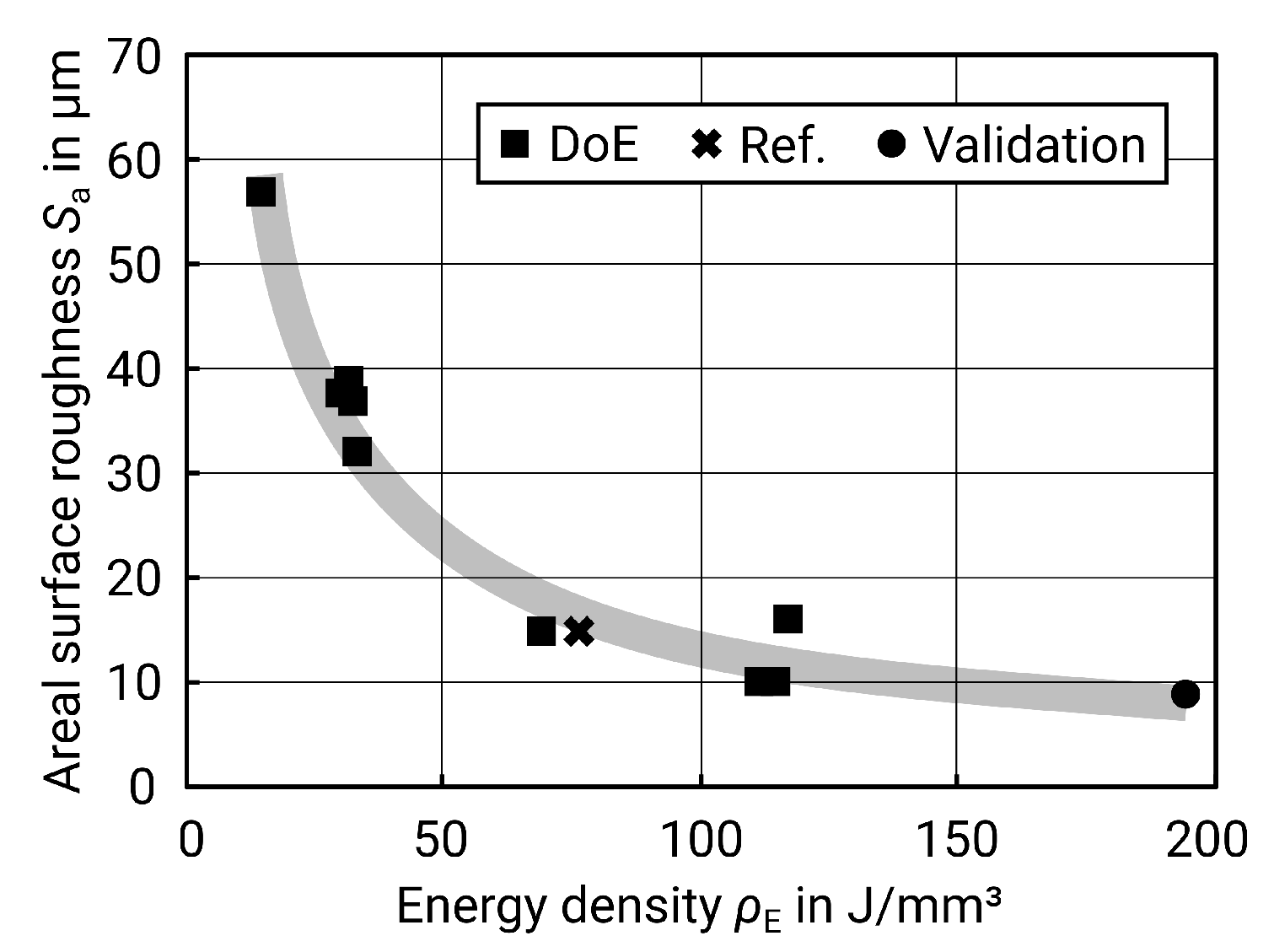
When considering energy density, the result meets the expectations as well: too low energy density leads to an instable track with lack of melting and balling and thus increases the roughness [
5,
24]. On the other hand, too much energy causes evaporation and also leads to high roughness [
25].
Figure 7 below illustrates this relationship.
Upskin surfaces are presented and evaluated in the same way as contour surfaces. The experiments conducted, energy density, and measurement results can be found in
Table 7. Again, the
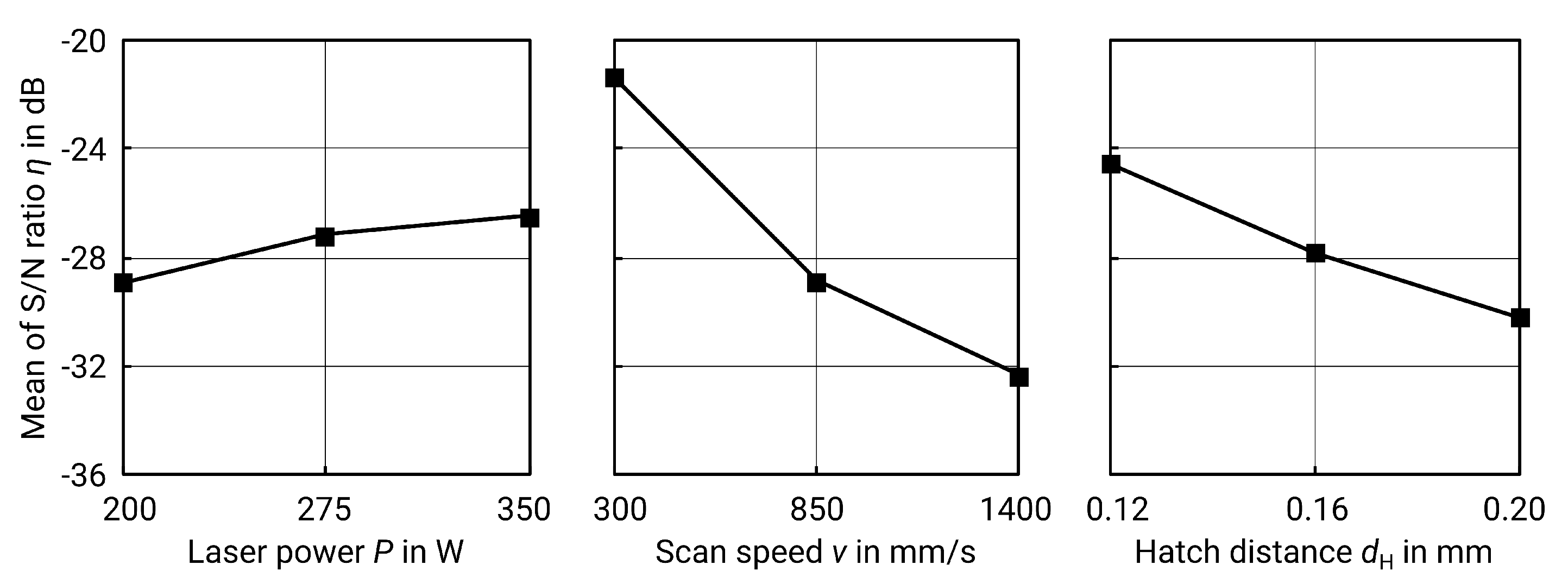
p-value of the ANOVA (see
Table 8) and the delta S/N-value (see
Table 9 and
Figure 8) show that the scanning speed
v is the most significant factor.
The best results of the test series are no. 1 and no. 4 (see
Table 7) with
and 275 W,
and
. The best levels for each factor, following the respective maximum S/N-value, result in a theoretical optimum for
at
,
and
.
The
-value for these factor levels can be predicted using regression. However, a simple linear regression might cause negative values in this case. Since this is physically impossible for surface roughness values, the model must be modified. A quadratic transformation was performed for this purpose, resulting in the following equation:
The predicted roughness for the combination of factor levels is . To validate the prediction and the previous optimization, another test specimen was produced. The roughness determined in this case is 9 and thus lower than in all previous tests, even if there is a deviation from the prediction. The prediction by regression should, however, be considered carefully. If a logarithmic transformation is chosen instead of a quadratic transformation, the fit is not as accurate (). However, the predicted value is closer to reality (). Hence, a validation is essential.
Regarding the roughness as a function of the energy density, the same effects occur as on the contour surfaces. A certain energy density is necessary to fully melt a continuous track, but, if the energy is too high, evaporation occurs [
5,
24,
25]. However, this area of too much energy did not become evident in the tests carried out, as
Figure 9 shows. Due to the underlying layers of solidified material, the heat is dissipated better at the upskin surfaces, which is why the region of evaporation is not reached here. On the contour surfaces, however, a larger amount of heat is dissipated by the surrounding powder bed, which conducts heat less well than solid material. A further increase of the energy density, however, may not be appropriate, as the energy input would otherwise be too high and the surface roughness would increase again due to evaporation.
A high energy density is helpful in achieving low surface roughness. Due to the resulting higher temperatures, the melt pool has more time to flatten during cooling. In addition, a low hatch distance, which also increases the energy density according to formula (
1), leads to a high overlap between the melt paths. This results in fewer peaks and valleys, which smoothens the surface as well [
24]. The importance of the hatch distance on roughness is also evident from the ANOVA, where the
p-value of
ranks second.
Table 10 summarizes the optimized values for both the contour and upskin surfaces produced by SLM.
3.2. Milling
The combinations of the various factor levels for ball end milling of vertical surfaces can be found in
Table 11. In addition, the spindle speed
n and the feed rate
, calculated using formulas (
3) and (
4), are given. For milling of the vertical side surfaces, both the
p-value of ANOVA (see
Table 12) and delta S/N (see
Table 13 and
Figure 10) show that the radial depth of cut
is the most important factor.
Based on the best factor levels, a theoretical optimum is obtained which corresponds to a test already conducted. The best surface quality results from the combination of cutting speed
m/min,
mm/tooth and
mm, corresponding to specimen no. 8 with a surface roughness
of 0.327
. In machining processes, however, the line roughness is usually specified. For this reason, these values are given as well. For these factor levels, the corresponding
is 0.292
and
is 1.943
(cut off
mm,
). The results from measurement and statistics meet the expectations and results of previous work: on one hand, a high cutting speed leads to better surfaces; on the other hand, the radial depth of cut is the most important parameter [
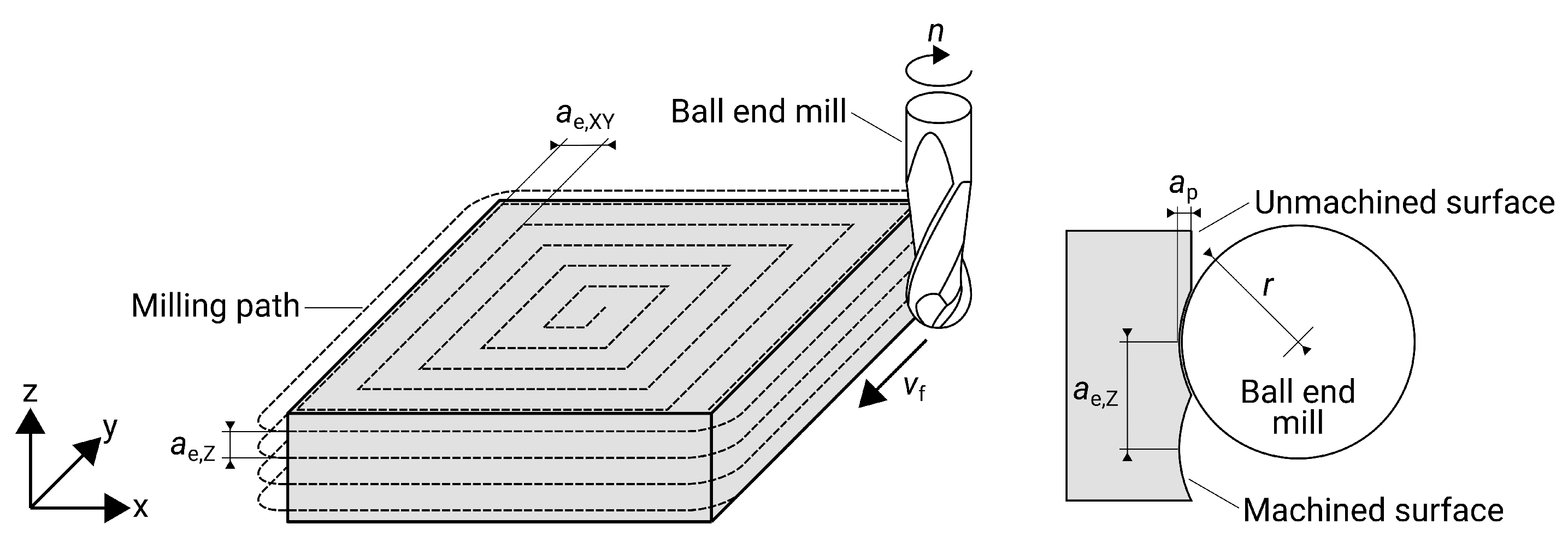
14]. The influence of the depth of cut can be explained by the geometry of the milling cutter and the z-constant milling process. The result is an undulating surface that is mainly dependent on radial depth of cut and the radius of the milling cutter (see
Figure 4). According to Peterka, the theoretical roughness
for the specified parameters is calculated according to the formulae below [
26]:
For tool radius
mm and
mm, a
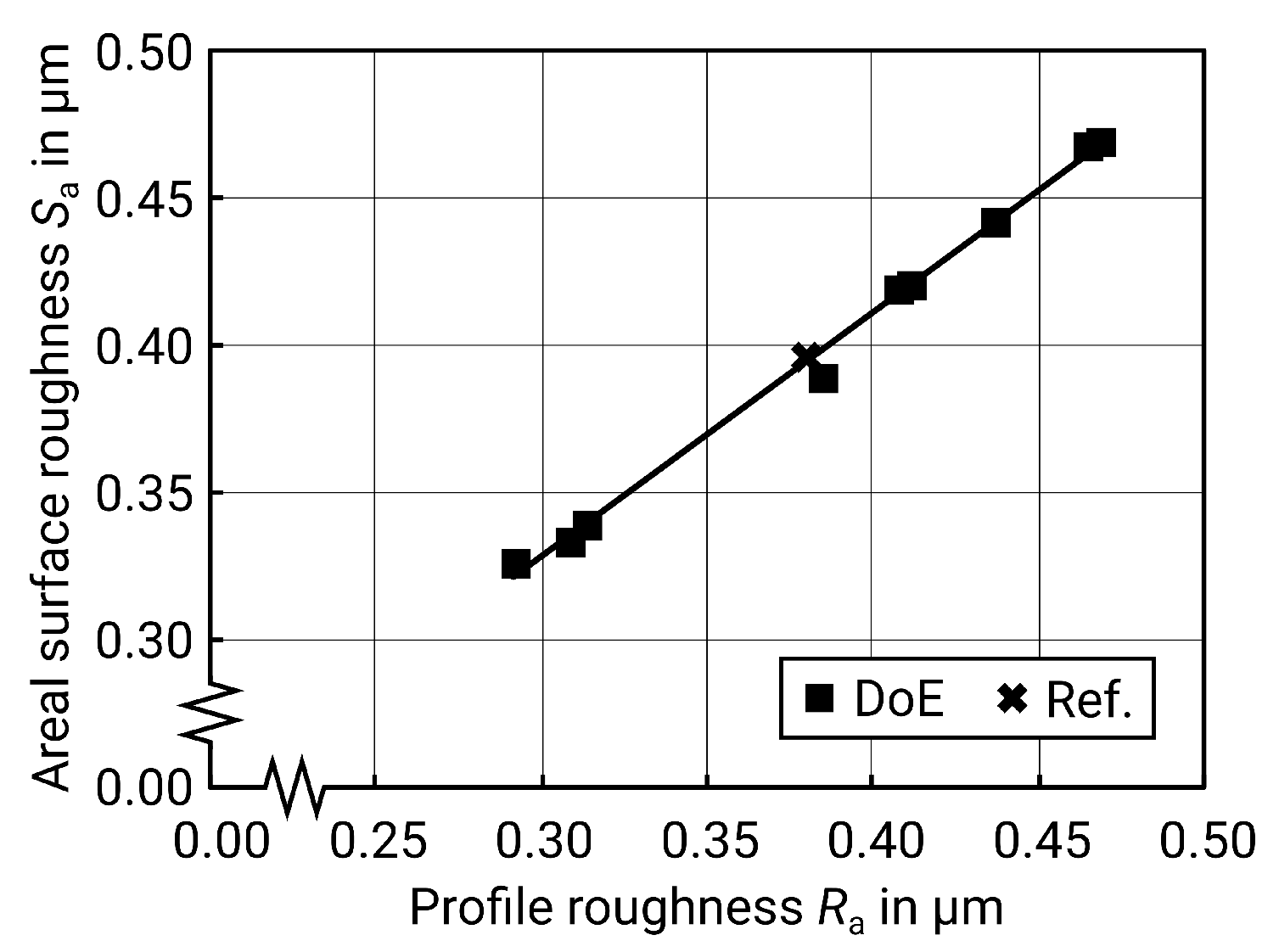
is obtained. As Harcarik and Jankovych describe, this value for profile roughness
can be converted to surface roughness
using a coefficient resulting from linear regression (see
Figure 11) and the formula below [
20]:
This results in . The deviation between measured and calculated values may result from a process- and machine-dependent coefficient, since, for example, the rigidity of the machine and the workpiece need to be taken into account as well. It can therefore be assumed that the optimum is reached at this point with the given factor levels.
Since the optimal combination of factor levels has already been evaluated, in this case, a regression to predict the roughness from all three factor levels and a further validation can be omitted.
The examination of the horizontal milled surfaces shows considerable differences. The respective variations and their corresponding surface roughness values can be found in
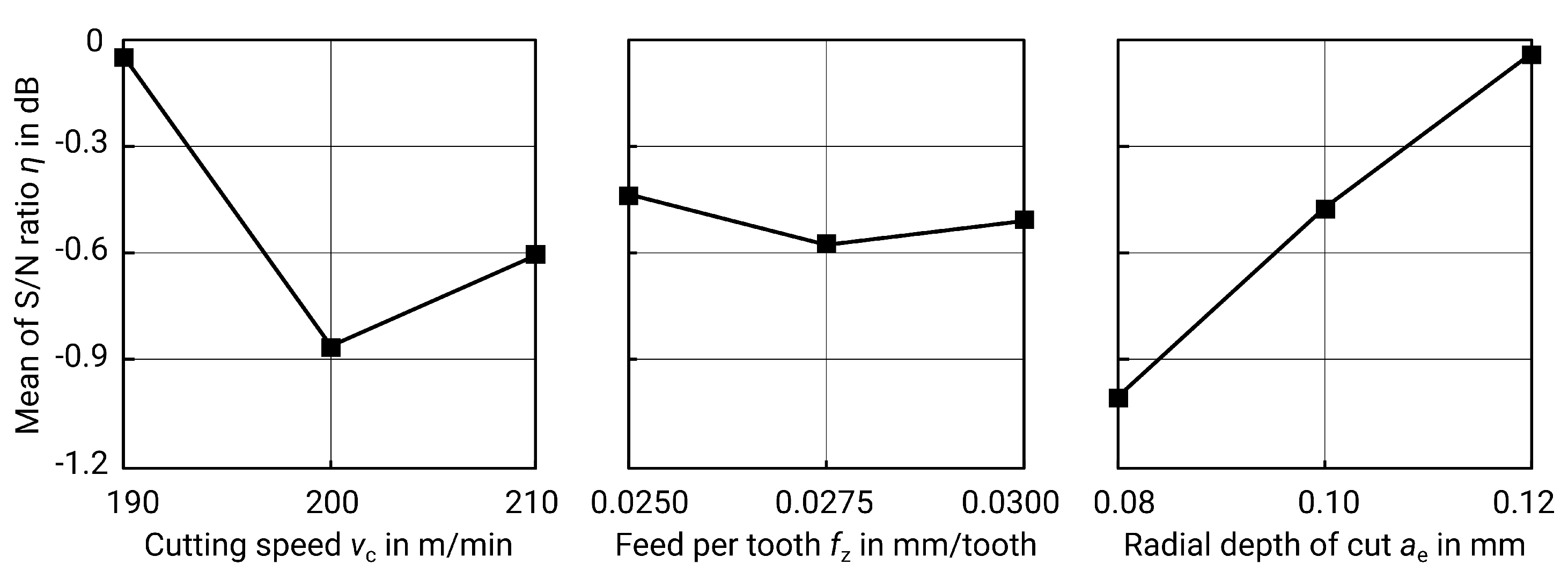
Table 14. Once again, the most significant factor is the radial depth of cut
, according to the
p-value from the ANOVA in
Table 15 and the spread of the S/N values from
Table 16 and
Figure 12.
However, the curve of the mean S/N values is contrary to the expectations. Due to the geometric relationship between the roughness and the depth of cut shown above, a minimum as an optimum should also be expected here. The statistical analysis reveals though that a high value for seems to be desirable. Thus, the statistics do not correspond to the real behaviour to be expected. Since the ANOVA shows that is the only significant parameter, and assuming that the actual roughness results from the theoretical roughness and a process- and machine-specific coefficient, this means that other factors play a role in milling of horizontal surfaces with a ball end mill and the parameters examined in this paper. This can include, for example, the rigidity of the machine, the tool, and the workpiece. The reliability of the statistics is therefore limited in this case.
The best surface roughness is obtained for test number 3 with cutting speed m/min, mm/tooth and mm, resulting in . Using the best factor levels in each case, a theoretical optimum is obtained at m/min, mm/tooth and mm.
The linear regression, which results according to formula (
14), also reflects the insufficient predictability, since
is only 73.04%. An adjustment of the regression model towards a higher
is possible, but this does not change the physically difficult circumstances of the milling process:
In order to evaluate the result with the optimal factor levels, another specimen was produced. The measured surface roughness for the optimum factor levels is and so it is lower than the previously measured values and also close to the value obtained by regression of , but these values must be viewed critically.
This is because milling the horizontal surfaces represents the greatest challenge for ball end milling on a machine with three axes. In this case, the central cutting edge of the milling cutter is used. However, this part of the cutting edge has no velocity because it is in the axis of rotation. This means that the material is deformed rather than cut in this area and the surface quality deteriorates. In addition, it is to be expected that the surface quality increases with the cutting speed. However, the actual cutting speed is lower than the set speed because it is calculated using the larger outer radius instead of the radius actually used.
An increasing radial depth of cut reduces the number of toolpaths in which the material is deformed instead of milled. In addition, a larger amount of the cutter’s radius is engaged, which means that the actual cutting speed is higher. Thus, when ball-milling horizontal surfaces, in the given range of values, a larger may lead to a better surface quality. However, this relationship is only valid within the range examined in this paper because above a certain the influence of geometry becomes dominant due to the z-constant milling strategy with the ball end mill, which leads to an undulating surface.
A further improvement may possibly be achieved with a different type of end mill. However, a variation of the milling tools is beyond the scope of this work and the selected range of parameters for optimization.
Table 17 summarizes the optimized values for both the vertical and horizontal surfaces produced by milling in the hybrid AM process. The photograph in
Figure 13 shows the different surfaces that have been achieved, with the unmachined surfaces in particular showing visible differences.