Development and Characterization of Titanium Dioxide Ceramic Substrates with High Dielectric Permittivities
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nair, K.M.; Guo, R.; Bhalla, A.S.; Hirano, S.-I.; Suvorov, D. Developments in Dielectric Materials and Electronic Devices: Proceedings of the 106th Annual Meeting of the American Ceramic Society; John Wiley & Sons: Indianapolis, IN, USA, 2004. [Google Scholar]
- Jang, Y.; Kim, J.; Kim, S.; Lee, K. Design and fabrication of a compact 3-dimensional stacked type dielectric ceramic waveguide bandpass filter. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 665–667. [Google Scholar] [CrossRef]
- Paul, M.C.; Dhar, A.; Das, S.; Pal, M.; Bhadra, S.K.; Markom, A.M.; Rosli, N.S.; Hamzah, A.; Ahmad, H.; Harun, S.W. Enhanced erbium-zirconia-yttria-aluminum co-doped fiber amplifier. IEEE Photonics J. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Antipov, O.L.; Novikov, A.A.; Eranov, I.D.; Kolker, D.B. High-efficiency oscillations at 1940 nm and 2070 nm in diode-pumped Tm: Lu2O3 ceramics lasers and their OPO frequency converision. In Proceedings of the 2014 International Conference Laser Optics, St. Petersburg, Russia, 30 June–4 July 2014. [Google Scholar]
- Ghosh, I.; Hilgers, A.; Schlenker, T.; Porath, R. Ceramic microwave antennas for mobile applications. J. Eur. Ceram. Soc. 2001, 21, 2621–2628. [Google Scholar] [CrossRef]
- Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M.; Reece, M.; Schrapel, K. Effect of porosity and grain size on the microwave dielectric properties of sintered alumina. J. Am. Ceram. Soc. 1997, 80, 1885–1888. [Google Scholar] [CrossRef]
- Kretly, L.C.; Almeida, A.F.L.; Fechine, P.B.A.; De Oliveira, R.S.; Sombra, A.S.B. Dielectric permittivity and loss of CaCu3Ti4O12 (CCTO) substrates for microwave devices and antennas. J. Mater. Sci. Mater. Electron. 2004, 15, 657–663. [Google Scholar] [CrossRef]
- Deschamps, G.A. Microstrip microwave antennas. In Proceedings of the 3rd USAF Symposium on Antennas, Champaign, IL, USA, 18–22 October 1953. [Google Scholar]
- Howell, J.Q. Microstrip antennas. IEEE Trans. Antennas Propag. 1975, 23, 90–93. [Google Scholar] [CrossRef]
- Herscovici, N. New considerations in the design of microstrip antennas. IEEE Trans. Antennas Propag. 1998, 46, 807–812. [Google Scholar] [CrossRef]
- Araujo, H.X.; Silva, G.M.B.; Oliveira, R.M.; Freitas, A.; Prata, D.N. Design and analysis of uwb antenna for use in aeronautical radio navigation. Int. J. Dev. Res. 2018, 8, 23698–23702. [Google Scholar]
- Lacerda, C.M.S.; Freitas, A.; Prata, D.N.P.; Araújo, H.X. Design of a circular fractal antenna for satellites applications. Int. J. Dev. Res. 2018, 8, 24718–24722. [Google Scholar]
- Agale, T.; Khanapurkar, M. A review on design approach for performance enhancement techniques of microstrip patch antenna. In Proceedings of the 2017 Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2017. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Araujo, H. Multiband antenna design comprising the future 5G mobile technology. Przegląd Elektrotechniczny 2019, 95, 108–111. [Google Scholar] [CrossRef]
- Filho, R.C.; Araujo, J.H.; Ginani, M.F.; D’Assunção, A.G.; Mendonça, L.M. Experimental and simulation analysis of microstrip patch antennas on BiNbO4 ceramic substrates. In Proceedings of the 2009 IEEE Antennas and Propagation Society International Symposium, Charleston, SC, USA, 1–5 July 2009. [Google Scholar]
- Silveira, J.H.A. Antena Discreta Com Patch Circular Confeccionada Sobre Substrato Dielétrico Cerâmico à Base de Pentóxido de Nióbio Nb2O5. Master’s Thesis, Federal Rural University of the Semi-Arid Region, Mossoró, Brazil, February 2015. [Google Scholar]
- Oliveira, E.E.C. Desenvolvimento de Antenas de Microfita e Antenas DRA Broadband/UltraWideBand Para Sistemas de Comunicação Sem Fio Utilizando Pós Cerâmicos Nanoestruturados. Ph.D. Thesis, Universidade Federal do Rio Grande do Norte, Natal, Brazil, September 2011. [Google Scholar]
- Sharma, A.; Chahal, J.S. Design of compact microstrip antenna using ceramic substrate. JEC & AS 2013, 2, 2319–5606. [Google Scholar]
- Medeiros, J.L.G.; D’Assunção, A.G.; Mendonça, L.M. Microstrip fractal patch antennas using high permittivity ceramic substrate. In Proceedings of the 2012 IEEE International Symposium on Antennas and Propagation, Chicago, IL, USA, 8–14 July 2012. [Google Scholar]
- Ramamurti, T.V.; Ganapathy, C.V.; Saran, S. Low-temperature sintering of titanium dioxide for ceramic capacitors. Nature 1954, 174, 1187. [Google Scholar] [CrossRef]
- Hakki, B.W.; Coleman, P.D.A. Dielectric resonator method of measuring inductive capacities in the millimeter range. IRE Trans. Microw. Theory Tech. 1960, 8, 402–410. [Google Scholar] [CrossRef]
- Patterson, A.L. The scherrer formula for x-ray particle size determination. Phys Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Torres, H.S.S.; Varajão, A.F.D.C.; Sabioni, A.C.S. Technological properties of ceramic produced from steatite (soapstone) residues–kaolinite clay ceramic composites. Appl. Clay Sci. 2015, 112, 53–61. [Google Scholar] [CrossRef]
- Kuang, X.; Carotenuto, G.; Nicolais, L. A review of ceramic sintering and suggestions on reducing sintering temperatures. Adv. Perform. Mater. 1997, 4, 257–274. [Google Scholar] [CrossRef]
- Hahn, H.; Logas, J.; Averback, R.S. Sintering characteristics of nanocrystalline TiO2. J. Mater. Res. 1990, 5, 609–614. [Google Scholar] [CrossRef]
- Mohammed, N.; Afsar, M.N. Precise Milimeter–wave Measurements of Complex Refractive Index, Complex Dieletric Permittivity and Loss Tangent of GaAs, Si, SiO2, Al2O3, Beo, Macor and Glass. IEEE Trans. Microw. Theory Tech. 1983, 31, 217–223. [Google Scholar]
- Rêgo Segundo, A.K.; Pinto, E.; Almeida, G.; Monteiro, P. Capacitive impedance measurement: Dual-frequency approach. Sensors 2019, 19, 2539. [Google Scholar] [CrossRef]
- Kuo, C.-G.; Liao, Y.-J.; Wu, C.-C.; Chen, C.-Y.; Meen, T.-H.; Huang, C.-J.; Wu, M.-C. Printing a novel compact triple-band monopole antenna on ceramic substrate. In Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011. [Google Scholar]
- Souza, J.A.M. Efeitos Do Uso de Substrato de Alta Permissividade Dielétrica Em Diversos Tipos de Antenas de Micro-Ondas. Ph.D. Thesis, Pontifícia Universidade Católica, Rio de Janeiro, Brazil, June 2015. [Google Scholar]
- Barsoum, M.W. Fundamentals of Ceramics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Mudinepalli, V.; Feng, L.; Lin, W.-C.; Murty, B. Effect of grain size on dielectric and ferroelectric properties of nanostructured Ba0.8Sr0.2TiO3 ceramics. J. Adv. Ceram. 2015, 4, 46–53. [Google Scholar] [CrossRef]
- El-razek, A.A.; Saed, E.M.; Gergs, M.K. Effect of grain size on the dielectric properties of lanthanum-doped PbTiO3 perovskite ceramics. J. Appl. Phys. 2014, 6, 20–29. [Google Scholar]
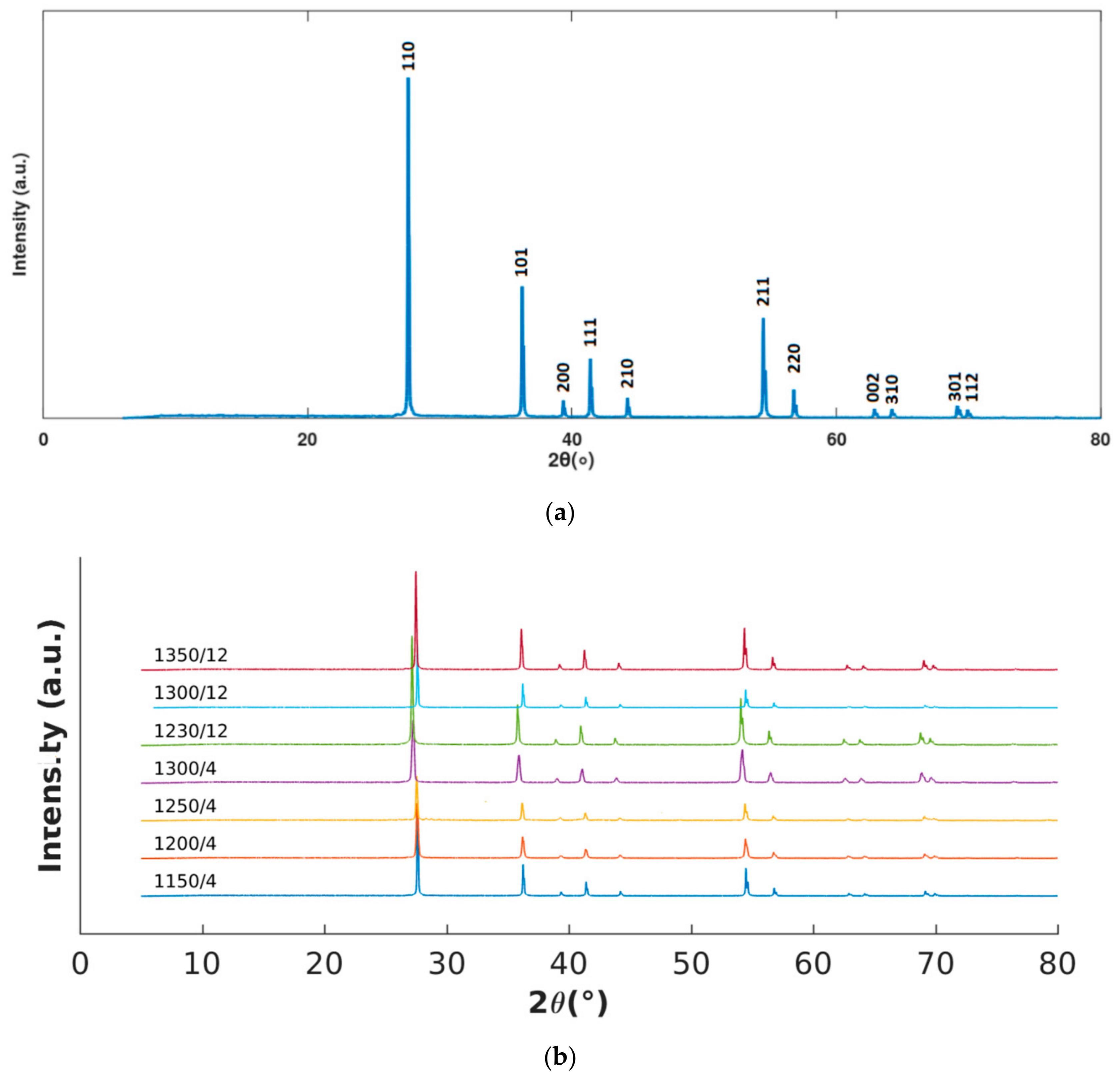

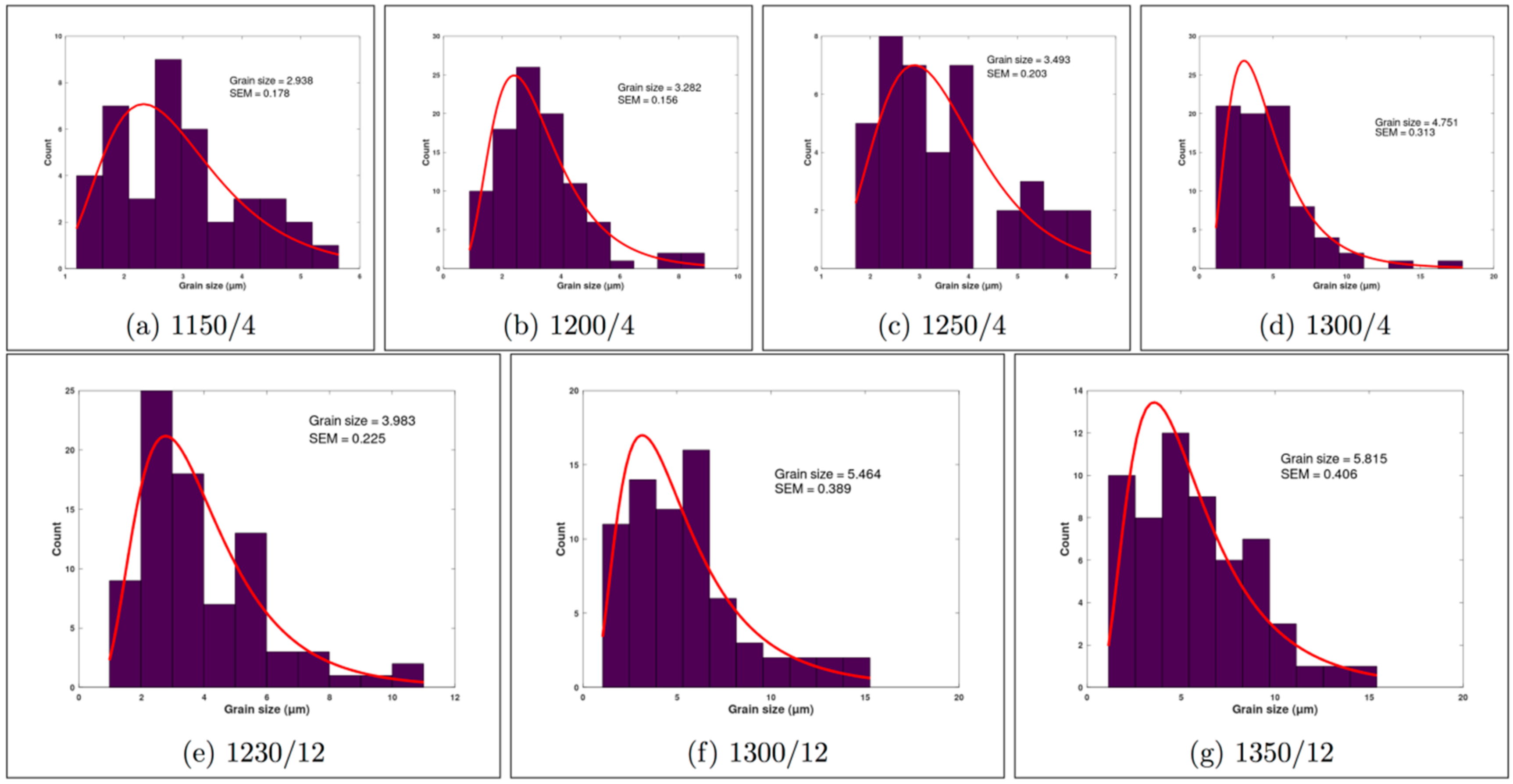
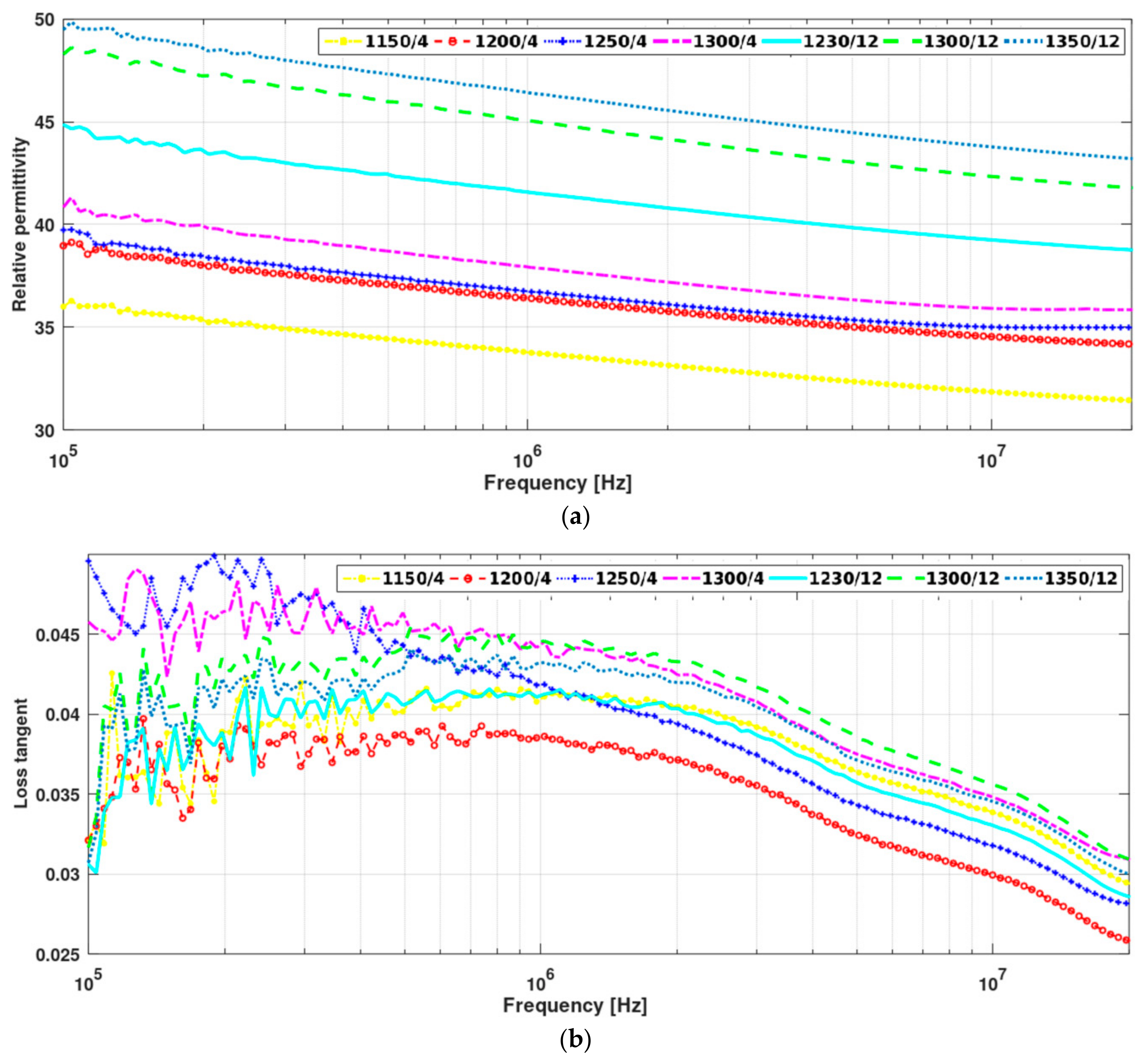
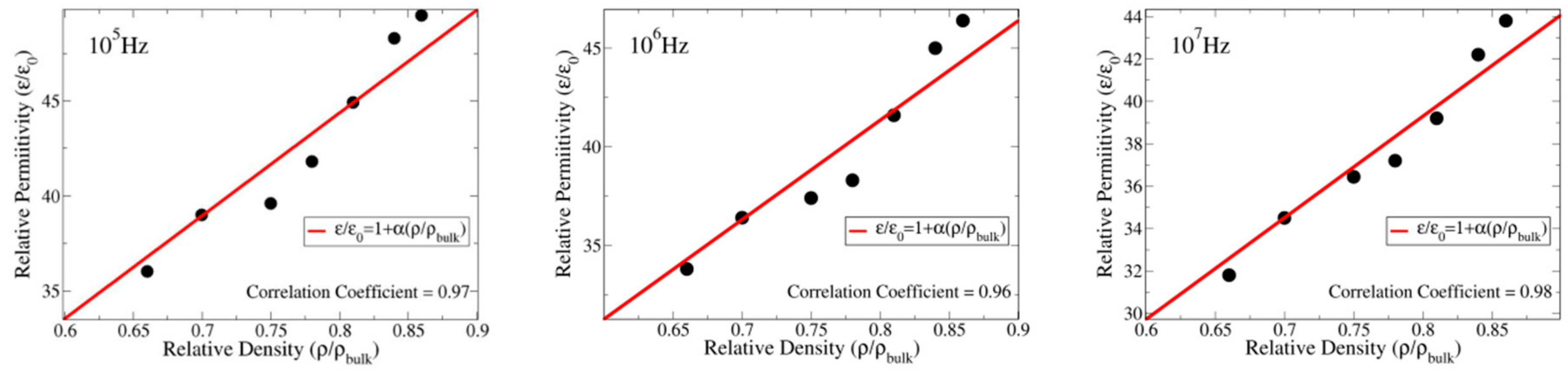
| Sintering Condition (Temperature/Time) | 1150/4 | 1200/4 | 1250/4 | 1300/4 | 1230/12 | 1300/12 | 1350/12 |
|---|---|---|---|---|---|---|---|
| Crystallite size (nm) | 48.0 | 49.6 | 58 | 59.5 | 62.7 | 68.8 | 69.0 |
| Sample Surface | 1150/4 | 1200/4 | 1250/4 | 1300/4 | 1230/12 | 1300/12 | 1350/12 |
|---|---|---|---|---|---|---|---|
| Grain Size (µm)/ SEM | 2.94/0.18 | 3.28/0.16 | 3.49/0.20 | 4.75/0.31 | 3.98/0.23 | 5.46/0.39 | 5.81/0.41 |
| Pore Size (µm)/ SEM | 3.16/0.21 | 2.71/0.21 | 2.02/0.16 | 1.68/0.23 | 1.53/0.16 | 1.46/0.15 | 1.87/0.26 |
| Sample | 1150/4 | 1200/4 | 1250/4 | 1300/4 | 1230/12 | 1300/12 | 1350/12 | Green Body |
|---|---|---|---|---|---|---|---|---|
| Density (g/cm3) | 3.1 | 3.3 | 3.5 | 3.7 | 3.8 | 3.9 | 4.0 | 3.0 |
| Relative Density | 0.66 | 0.70 | 0.75 | 0.78 | 0.81 | 0.84 | 0.86 | 0.64 |
| Total Porosity | 0.34 | 0.30 | 0.25 | 0.22 | 0.19 | 0.16 | 0.14 | 0.36 |
| Frequency | Sample | ||||||
|---|---|---|---|---|---|---|---|
| 1150/4 | 1200/4 | 1250/4 | 1300/4 | 1230/12 | 1300/12 | 1350/12 | |
| 105 Hz | 36.0 | 39.0 | 39.6 | 41.8 | 44.9 | 48.3 | 49.5 |
| 106 Hz | 33.8 | 36.4 | 37.4 | 38.3 | 41.6 | 45.0 | 46.4 |
| 107 Hz | 31.8 | 34.5 | 36.44 | 37.2 | 39.2 | 42.3 | 43.8 |
| 1.29 GHz | - | - | - | - | - | - | 59.9 |
| 2 GHz | - | - | - | - | - | - | 58.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freitas, A.E.; Manhabosco, T.M.; Batista, R.J.C.; Segundo, A.K.R.; Araújo, H.X.; Araújo, F.G.S.; Costa, A.R. Development and Characterization of Titanium Dioxide Ceramic Substrates with High Dielectric Permittivities. Materials 2020, 13, 386. https://doi.org/10.3390/ma13020386
Freitas AE, Manhabosco TM, Batista RJC, Segundo AKR, Araújo HX, Araújo FGS, Costa AR. Development and Characterization of Titanium Dioxide Ceramic Substrates with High Dielectric Permittivities. Materials. 2020; 13(2):386. https://doi.org/10.3390/ma13020386
Chicago/Turabian StyleFreitas, Antonio E., Taise M. Manhabosco, Ronaldo J. C. Batista, Alan K. Rêgo Segundo, Humberto X. Araújo, Fernando Gabriel S. Araújo, and Adilson R. Costa. 2020. "Development and Characterization of Titanium Dioxide Ceramic Substrates with High Dielectric Permittivities" Materials 13, no. 2: 386. https://doi.org/10.3390/ma13020386
APA StyleFreitas, A. E., Manhabosco, T. M., Batista, R. J. C., Segundo, A. K. R., Araújo, H. X., Araújo, F. G. S., & Costa, A. R. (2020). Development and Characterization of Titanium Dioxide Ceramic Substrates with High Dielectric Permittivities. Materials, 13(2), 386. https://doi.org/10.3390/ma13020386





