Simple Model for Corrugation in Surface Alloys Based on First-Principles Calculations
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
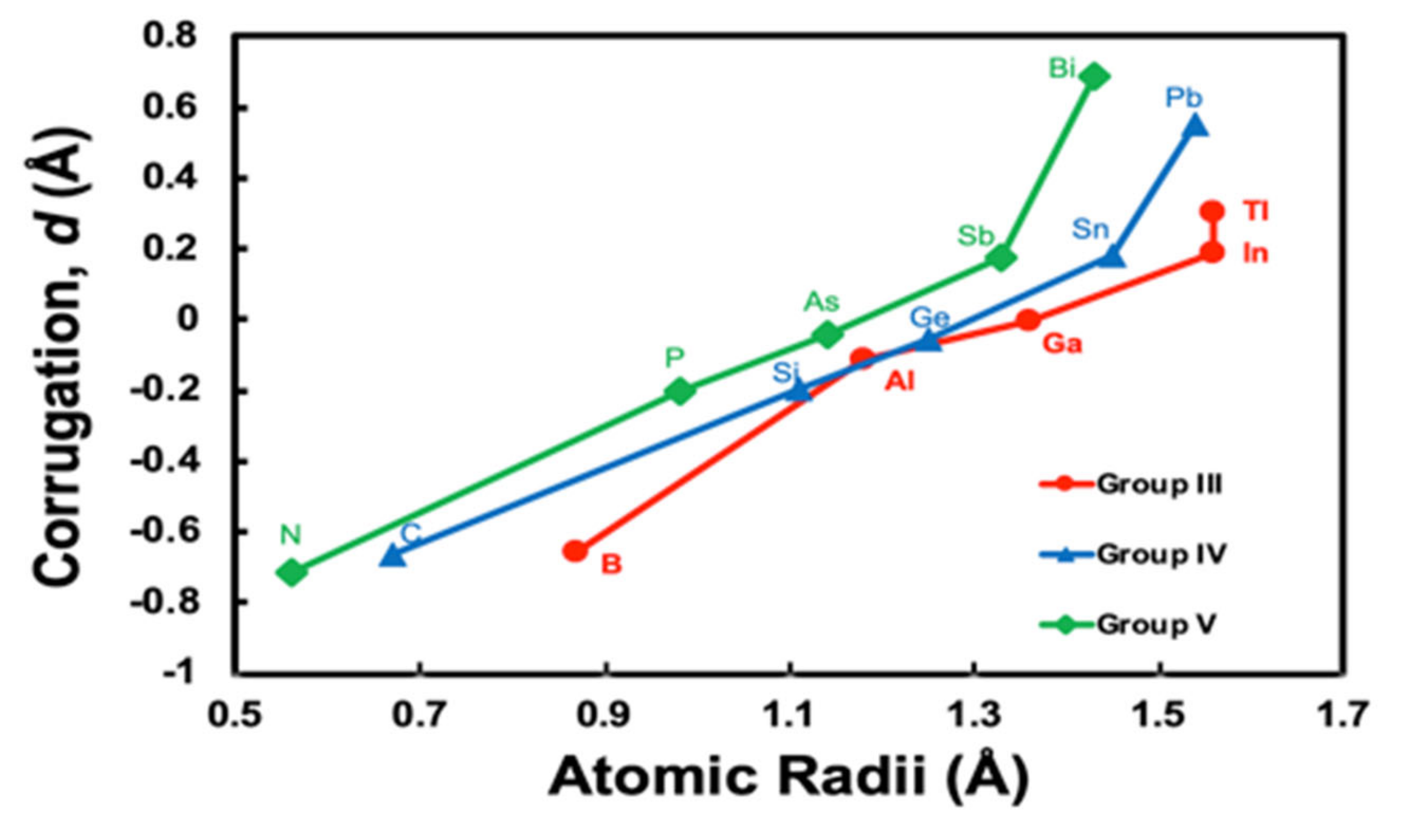
3.1. Corrugation Parameter of M/Ag(111)–
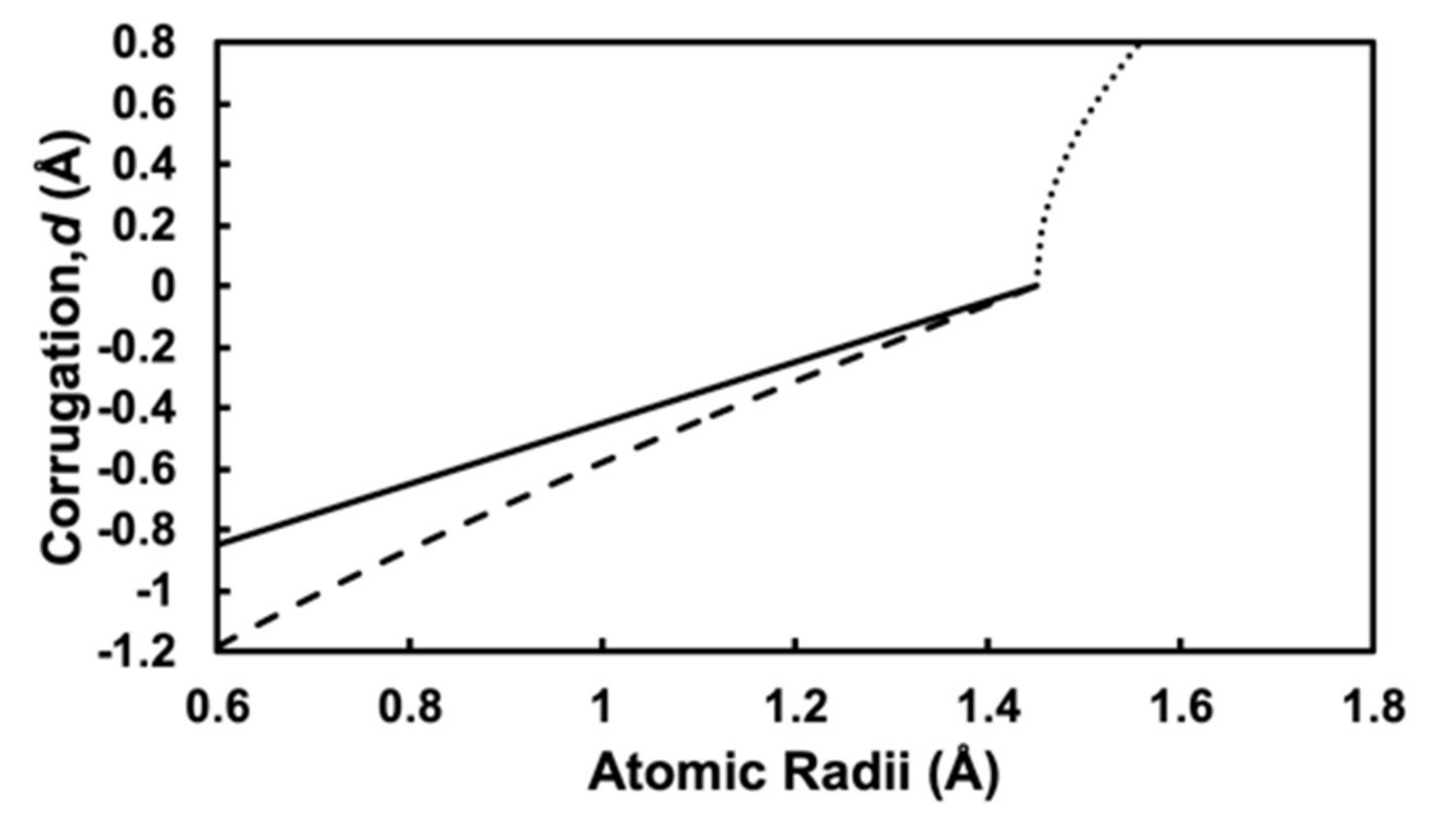
3.2. Simple Hard Spherical Atomic Model for Surface Corrugations
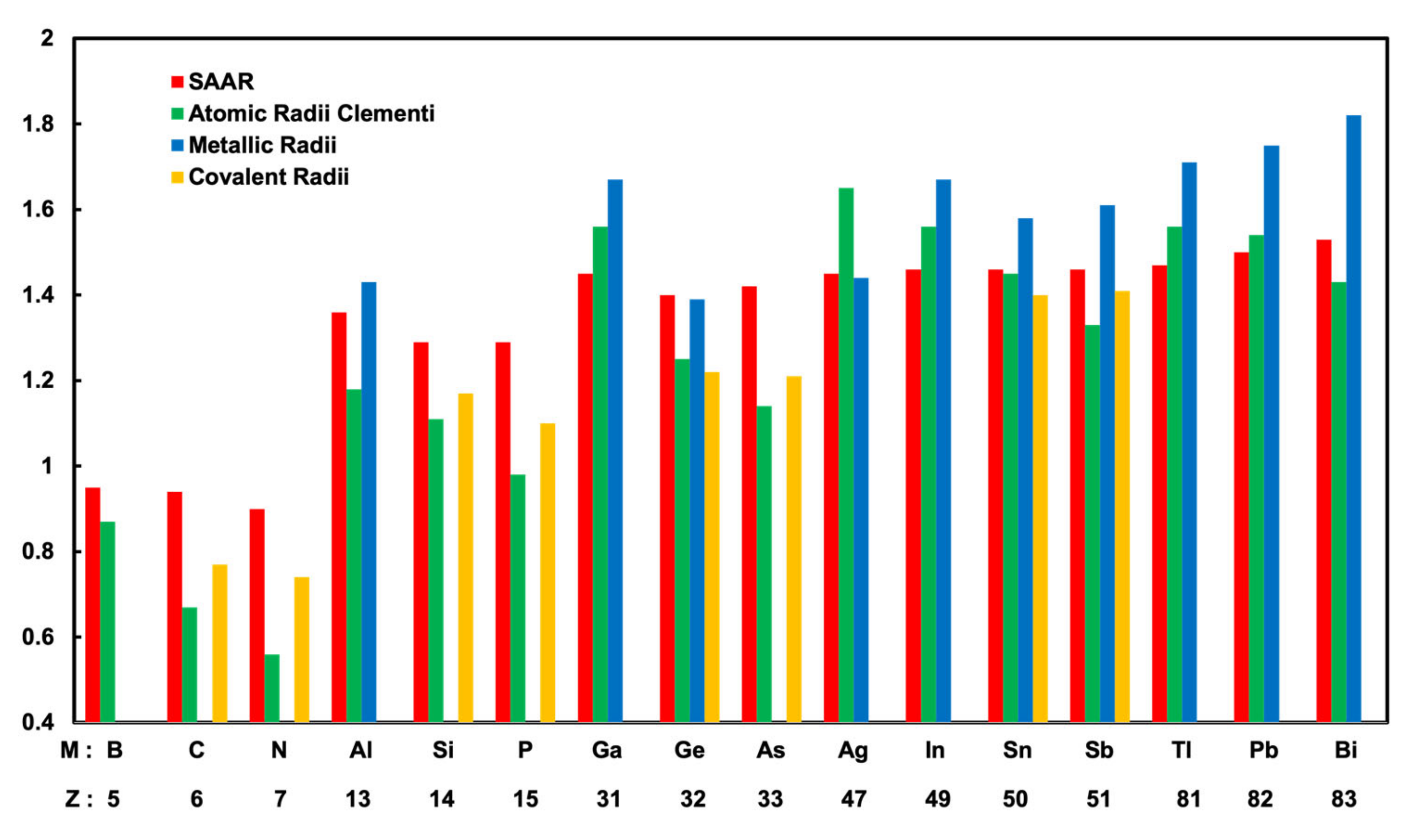
3.3. Determination of Surface Alloy Atomic Radii
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Woodruff, D.P.; Brown, D.; Quinn, P.D.; Noakes, T.C.Q.; Bailey, P.; Meth, B. Structure determination of surface adsorption and surface alloy phases using medium energy ion scattering. Nucl. Instrum. 2001, 183, 128–139. [Google Scholar] [CrossRef]
- Ast, C.R.; Henk, J.; Ernst, A.; Moreschini, L.; Falub, M.C.; Pacilé, D.; Bruno, P.; Kern, K.; Grioni, M. Giant Spin Splitting through Surface Alloying. Phys. Rev. Lett. 2007, 98, 186807. [Google Scholar] [CrossRef] [PubMed]
- Ou, M.G.; Lu, G.W.; Shen, H.; Descamps, A.; Marquette, C.A.; Blum, L.J.; Ledoux, G.; Roux, S.; Tillement, O.; Cheng, B.L.; et al. Catalytic Performance of Nanoscale-Corrugated Gold and Silver Films for Surface-Enhanced Chemiluminescence. Adv. Funct. Mater. 2007, 17, 1903–1909. [Google Scholar] [CrossRef]
- Bian, G.; Zhang, L.; Liu, Y.; Miller, T.; Chiang, T.C. Illuminating the Surface Spin Texture of the Giant-Rashba Quantum-Well System Bi/Ag (111) by Circularly Polarized Photoemission. Phys. Rev. Lett. 2012, 108, 186403. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liu, S.; Li, D.J.; Wang, S.; Guo, J.; Shen, Y. Ab initio atomistic thermodynamics study on the oxidation mechanism of binary and ternary alloy surfaces. J. Chem. Phys. 2015, 142, 06470. [Google Scholar] [CrossRef]
- Woodruff, D.P.; Robinson, J. Some structural issues in surface alloys and alloy surfaces: Rumpling, stacking faults and disorder. Appl. Surf. Sci. 2003, 219, 1–10. [Google Scholar] [CrossRef]
- Sawaya, S.; Goniakowski, J.; Tréglia, G. Ge deposition on Ag surfaces: Dependence of the adsorption characteristics on the surface orientation. Phys. Rev. B 2000, 61, 8469–8474. [Google Scholar] [CrossRef]
- Pacilé, D.; Ast, C.R.; Papagno, M.; Da Silva, C.; Moreschini, L.; Falub, M.; Seitsonen, A.P.; Grioni, M. Electronic structure of an ordered Pb∕Ag (111) surface alloy: Theory and experiment. Phys. Rev. B 2006, 73, 245429. [Google Scholar]
- McLeod, I.M.; Dhanak, V.R.; Matilainen, A.; Lahti, M.; Pussi, K.; Zhang, K.H.L. Structure determination of the p- Bi–Ag (111) surface alloy using LEED I–V and DFT analyses. Surf. Sci. 2010, 604, 1395–1399. [Google Scholar] [CrossRef]
- Osiecki, J.R.; Uhrberg, R.I.G. Alloying of Sn in the surface layer of Ag (111). Phys. Rev. B 2013, 87, 075441. [Google Scholar] [CrossRef]
- Tayran, C.; Çakmak, M. Electronic structure of the Pd2Sn surface alloy on Pd (111)-. Eur. Phys. J. B 2019, 92, 240. [Google Scholar] [CrossRef]
- Pancotti, A.; de Siervo, A.; Carazzolle, M.F.; Silva, J.J.; Nascente, P.A.P.; Landers, R. Surface structure characterization by X-ray photoelectron diffraction of Sn ultra-thin films deposited on Pd (111). Surf. Sci. 2019, 685, 7–12. [Google Scholar] [CrossRef]
- Tayran, C. Electronic structure of Lanthanum induced π-bonded Seiwatz chains on the Si (111)-(2 × 3) surface. Surf. Sci. 2019, 679, 214–217. [Google Scholar] [CrossRef]
- Bian, G.; Wang, X.; Miller, T.; Chiang, T.C. Origin of giant Rashba spin splitting in Bi/Ag surface alloys. Phys. Rev. B 2013, 88, 085427. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Morrison, I.; Bylander, D.M.; Kleinman, L. Nonlocal Hermitian norm-conserving Vanderbilt pseudopotential. Phys. Rev. B 1993, 47, 6728–6731. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Van Ingen, R.P.; Fastenau, R.H.J.; Mittemeijer, E.J. Formation of crystalline AgxNi1-x solid solutions of unusually high supersaturation by laser ablation deposition. Phys. Rev. Lett. 1994, 72, 3116–3119. [Google Scholar] [CrossRef]
- Oughaddou, H.; Sawaya, S.; Goniakowski, J.; Aufray, B.; Le Lay, G.; Gay, J.M.; Tréglia, G.; Bibérian, J.P.; Barrett, N.; Guillot, C.; et al. Ge/Ag (111) semiconductor-on-metal growth: Formation of an Ag2Ge surface alloy. Phys. Rev. B 2000, 62, 16653–16656. [Google Scholar] [CrossRef]
- McLeod, I.M.; Dhanak, V.R.; Lahti, M.; Matilainen, A.; Pussi, K.; Zhang, K.H.L. LEED I–V and DFT structure determination of the Pb–Ag(111) surface alloy. J. Phys. Condens. Matter 2011, 23, 265006. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, N.; Kotaka, H.; Ishii, F. First-principles study of Rashba effect in ultra-thin bismuth surface alloys. J. Cryst. Growth 2017, 468, 688–690. [Google Scholar] [CrossRef]
- Gierz, I.; Stadtmüller, B.; Vuorinen, J.; Lindroos, M.; Meier, F.; Dil, J.H.; Kern, K.; Ast, C.R. Structural influence on the Rashba-type spin splitting in surface alloys. Phys. Rev. B 2010, 81, 245430. [Google Scholar] [CrossRef]
- Clementi, E.; Raimondi, D.L.; Reinhardt, W.P. Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons. J. Chem. Phys. 1967, 47, 1300–1307. [Google Scholar] [CrossRef]
- Wells, A.F. Structural Inorganic Chemistry; Oxford University Press: Oxford, UK, 1984. [Google Scholar]
- Chausov, M.; Khyzhun, O.; Brezinová, J.; Maruschak, P.; Pylypenko, A.; Brezina, J.; Buzová, K.; Lopat’ko, K. Improving of Mechanical Properties of Titanium Alloy VT23 due to Impact-Oscillatory Loading and the Use of Carbon Nano-Solution. Metals 2019, 9, 652. [Google Scholar] [CrossRef]



| Z | Atom | d (Corrugation Parameter) (Å) | Reference (Å) | |
|---|---|---|---|---|
| (Theoretical) | (Experimental) | |||
| 5 | B | −0.654 | - | |
| 6 | C | −0.664 | - | |
| 7 | N | −0.712 | - | |
| 13 | Al | −0.115 | - | |
| 14 | Si | −0.199 | - | |
| 15 | P | −0.202 | - | |
| 31 | Ga | −0.002 | - | |
| 32 | Ge | −0.055 | - | 0.3 [21] |
| 33 | As | −0.040 | - | |
| 49 | In | 0.190 | - | |
| 50 | Sn | 0.184 | - | |
| 51 | Sb | 0.178 | - | |
| 81 | Tl | 0.306 | - | |
| 82 | Pb | 0.556 | 0.59 [22] | 0.42 [22] |
| 83 | Bi | 0.690 | 0.69 [23]; 0.61 [9]; 0.65 [24]; 0.8 [14] | 0.57 [9] |
| Atoms | Surface Alloy Atomic radii (Å) | Clementi’s Atomic Radii (Å) [25] | Metallic Radii (Å) [26] | Covalent Radii(Å) [26] |
|---|---|---|---|---|
| Ag | 1.45 | 1.65 | 1.44 | - |
| B | 0.95 | 0.87 | - | - |
| C | 0.94 | 0.67 | - | 0.77 |
| N | 0.9 | 0.56 | - | 0.74 |
| Al | 1.36 | 1.18 | 1.43 | - |
| Si | 1.29 | 1.11 | - | 1.17 |
| P | 1.29 | 0.98 | - | 1.1 |
| Ga | 1.45 | 1.36 | 1.53 | - |
| Ge | 1.40 | 1.25 | 1.39 | 1.22 |
| As | 1.42 | 1.14 | - | 1.21 |
| In | 1.46 | 1.56 | 1.67 | - |
| Sn | 1.46 | 1.45 | 1.58 | 1.40 |
| Sb | 1.46 | 1.33 | 1.61 | 1.41 |
| Tl | 1.47 | 1.56 | 1.71 | - |
| Pb | 1.5 | 1.54 | 1.75 | - |
| Bi | 1.53 | 1.43 | 1.82 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nur, M.; Yamaguchi, N.; Ishii, F. Simple Model for Corrugation in Surface Alloys Based on First-Principles Calculations. Materials 2020, 13, 4444. https://doi.org/10.3390/ma13194444
Nur M, Yamaguchi N, Ishii F. Simple Model for Corrugation in Surface Alloys Based on First-Principles Calculations. Materials. 2020; 13(19):4444. https://doi.org/10.3390/ma13194444
Chicago/Turabian StyleNur, Monika, Naoya Yamaguchi, and Fumiyuki Ishii. 2020. "Simple Model for Corrugation in Surface Alloys Based on First-Principles Calculations" Materials 13, no. 19: 4444. https://doi.org/10.3390/ma13194444
APA StyleNur, M., Yamaguchi, N., & Ishii, F. (2020). Simple Model for Corrugation in Surface Alloys Based on First-Principles Calculations. Materials, 13(19), 4444. https://doi.org/10.3390/ma13194444





