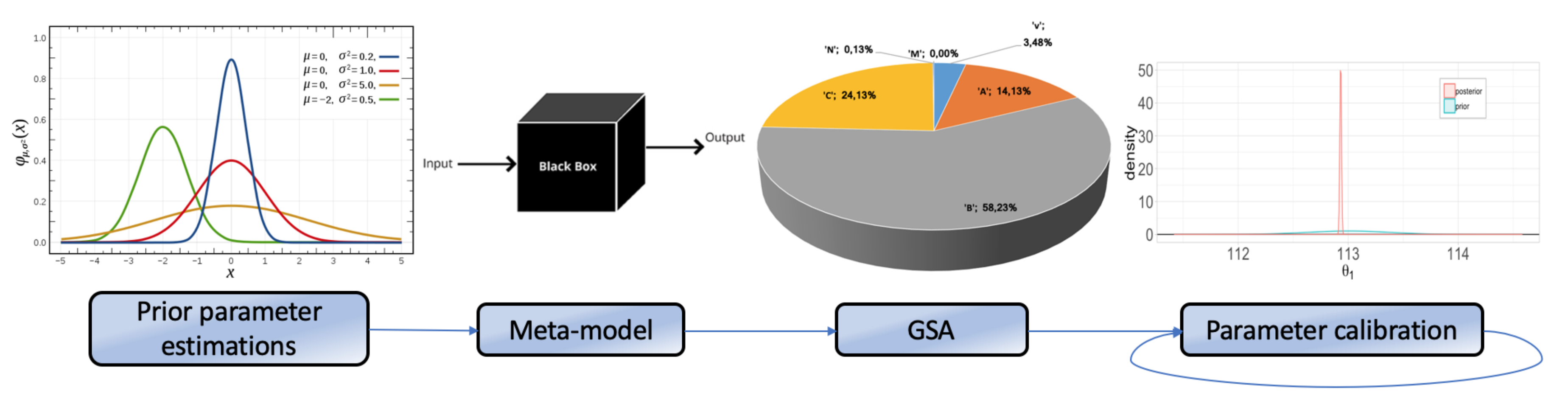
2.1. Global Sensitivity Analysis
Global Sensitivity Analysis (GSA) refers to a collection of techniques that allow identifying the most relevant variables in a model with respect to given Quantities of Interest (QoIs). They focus on apportioning the output’s uncertainty to the different sources of uncertain parameters [
2] and define qualitative and quantitative mappings between the multi-dimensional space of stochastic variables in the input and the output. The most popular GSA techniques are based on the decomposition of the variance’s output probability distribution and allow the calculation of Sobol’s sensitivity indices.
According to Sobol’s decomposition theory, a function can be approximated as the sum of functions of increasing dimensionality and orthogonal with respect to the standard
inner product. Hence, given a mathematical model
with
n parameters arranged in the input vector
x, the decomposition can be expressed as:
where
is a constant and
are functions with domains of increasing dimensionality. If we consider that
f is defined on random variables
, then the model output is itself a random variable with variance
Integrating Equation (
1) and using the orthogonality property of the functions
, we note that the variance itself can be decomposed in the sum
This expression motivates the definition of the Sobol indices
that trivially satisfy
This decomposition of the total variance
D reveals the main metrics employed to assess the relevance of each parameter in the scatter of the quantity of interest
f. The relative variances
are referred to as the first order indices or main effects and gauge the influence of the
i-th parameter on the model’s output. The total effect or total order sensitivities associated with the
—parameter, including its influence when combined with other parameters, is calculated as
The widespread use of the main and total effects as sensitivity measures is due to the relative simplicity of the formulas and algorithms that can be employed to calculate or approximate them ([
2], Chapter 4). Specifically, the number of simulations required to evaluate these measures is
, where
is the so-called base sample, a number that depends on the model complexity varying from a few hundreds to several thousands, and
n is, as before, the number of parameters of the model (we refer to ([
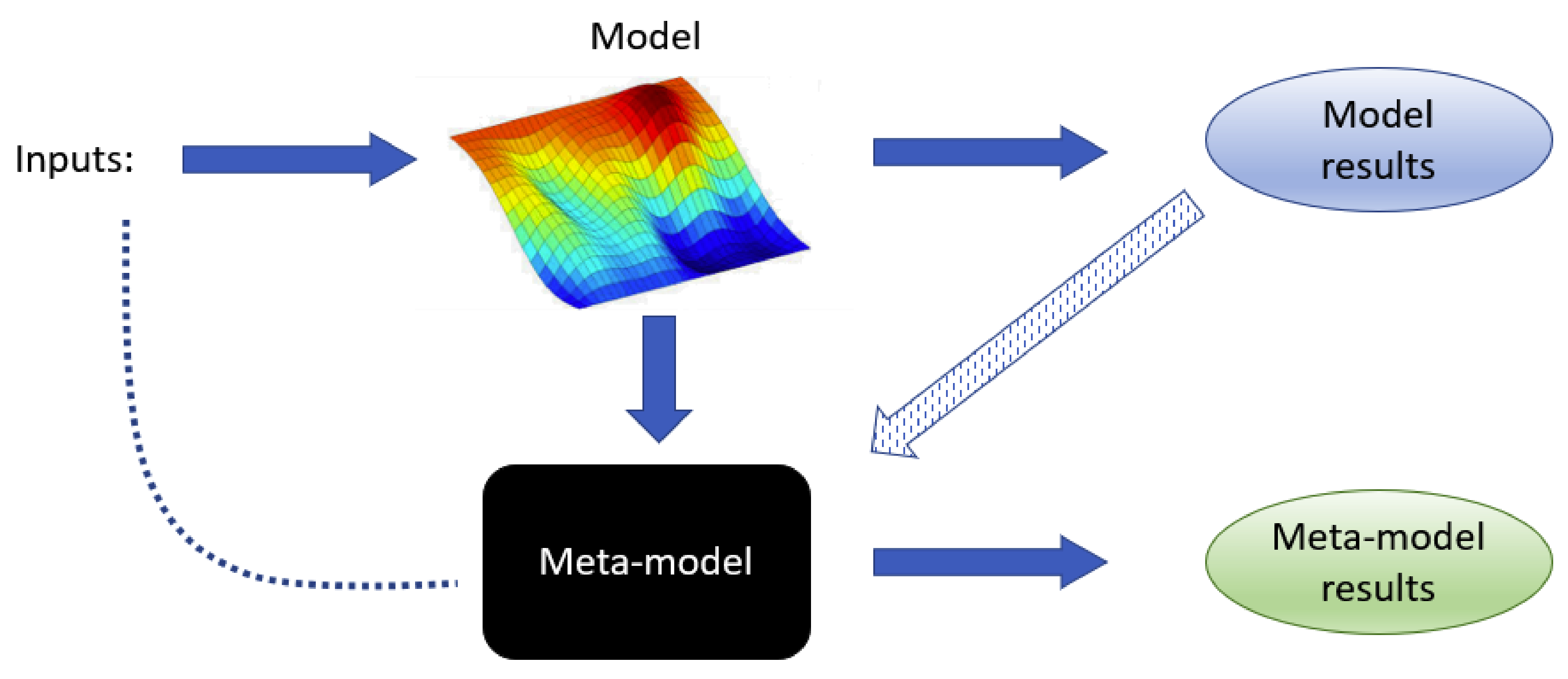
2], Chapter 4) for details on these figures). To calculate sensitivity indices, it proves essential to first create a simple meta-model that approximates the true model, because a limited set of runs is supposed to suffice for building a surrogate that, demanding far fewer computational resources, can then be run a large number of times to complete the GSA.
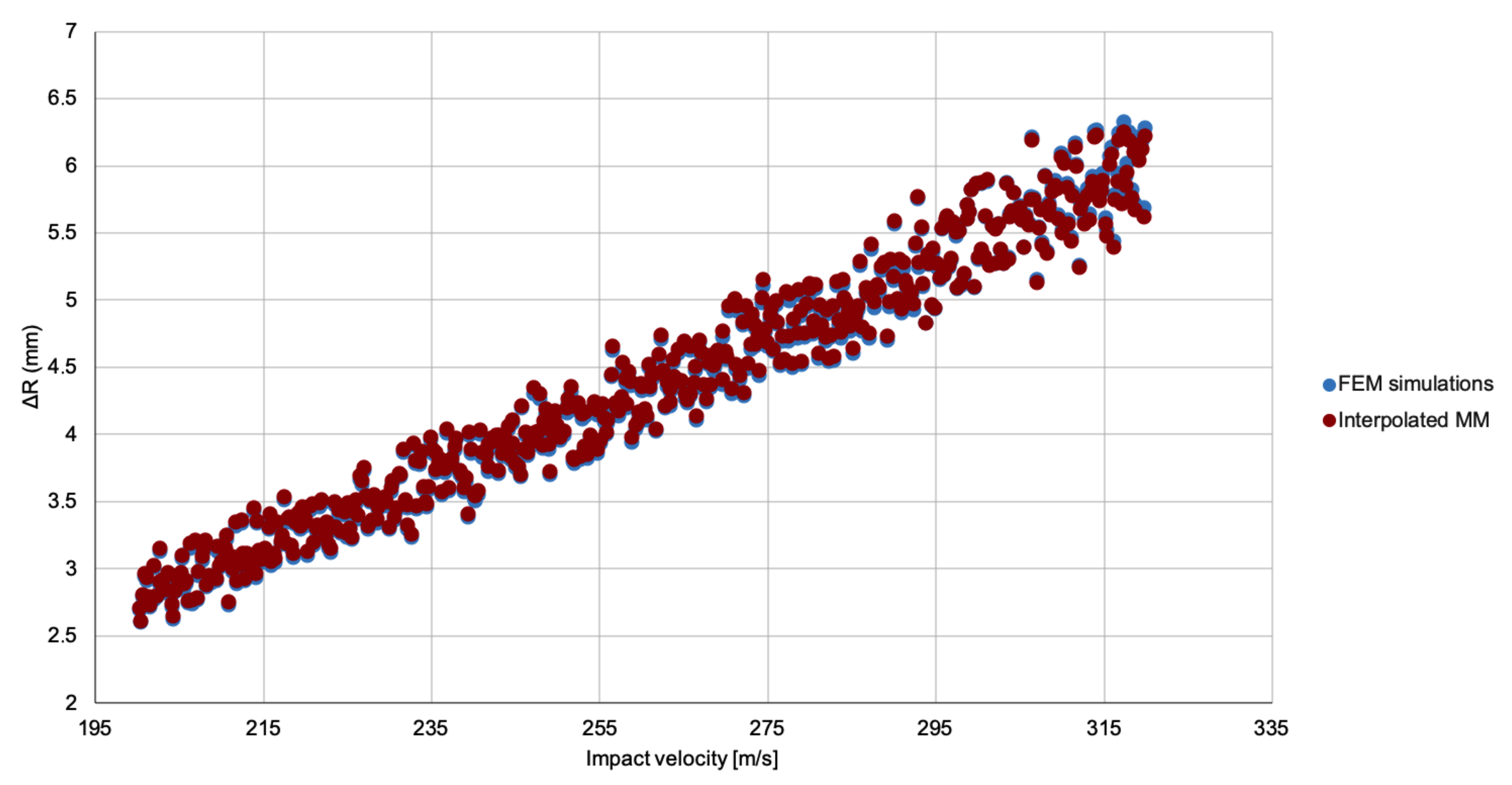
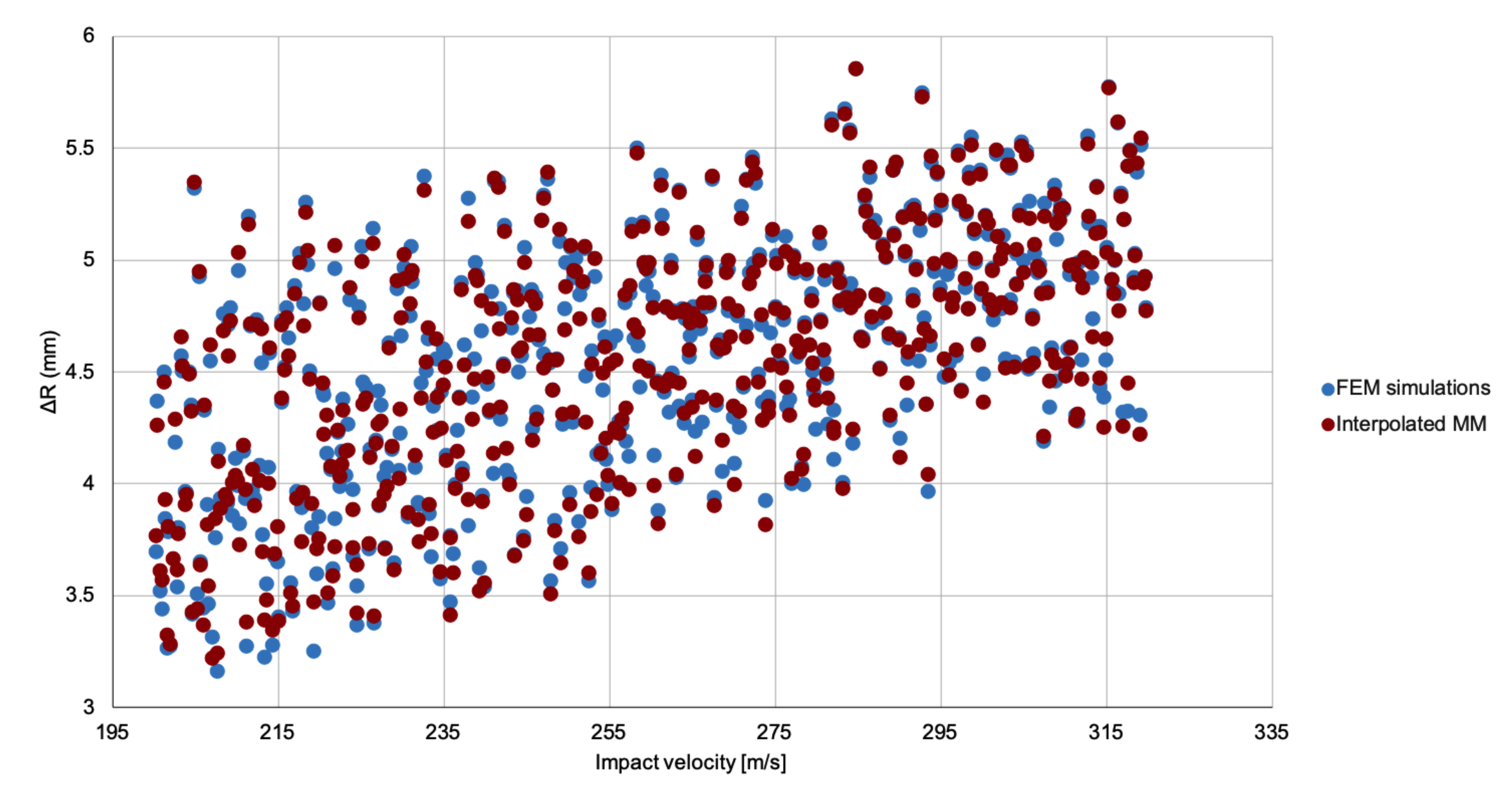
2.2. Meta-Models
A meta-model is a model for another model. That is, a much-simplified version of a given model that can provide, however, similar predictions as the original one for the same values of the parameters. In this work, we restrict our study to linear meta-models. To describe them, let us assume that the model we are trying to simplify depends on
parameters and we denote the quantity of interest, assumed for simplicity to be a scalar, as
y. For any collection of parameters
, we define
to be the corresponding value of the quantity of interest and slightly abusing the notation we write
where
N is the number of samples and
is an array of
N samples of the parameters. Then, a meta-model is a function
that approximates
and is of the form
In this equation, and later,
are the kernels of the approximation and
refer to the weights. Abusing slightly the notation again, we express the relation between the model and its meta-model as
or in compact form,
where
H is the so-called kernel matrix that collects all the kernel functions.
The precise definition of a meta-model depends, hence, on the number and type of kernel functions
and the value of the regression coefficients
. Given an a priori choice for the kernels, the weights can be obtained from a set of model evaluations
employing a least-squares minimization. Given, as before, an array of sample parameters
and their model evaluation
, the vector
can be calculated in closed form with the solution of the normal equations to the approximation. That is,
As previously indicated, the kernel functions belong to a set that must be selected a priori. In the literature, several classes of kernel have been proposed for approximating purposes and in this work we select anisotropic Radial Basis Functions (RBF). This type of kernel has shown improved accuracy as compared with standard RBF, particularly when only a limited set of model evaluations is available [
23].
A standard RBF is a map
of the form
where
is a monotonically decreasing function and
is the Euclidean distance. The anisotropic radial kernels redefine the function
K to be of the form
where
is a diagonal, positive definite matrix that scales anisotropically the contribution of each direction in the difference
, and
is the shape parameter of the kernel.
2.3. Bayesian Inference and Gaussian Processes
Bayesian inference is a mathematical technique used to improve the knowledge of probability distributions extracting information from sampled data [
24]. It is successfully employed for a wide variety of applications in data science and applied sciences. For instance, it has been used in conjunction with techniques such as machine learning and deep learning in fields like medicine [
25], robotics [
26], earth sciences [
27], and more. In this article, we employ Bayesian methods to find the optimal value of model parameters as a function of prior information and observed data. More specifically, we are concerned with model calibration and using it in combination with meta-models to obtain realistic parameter values for complex constitutive relations and their uncertainty quantification, with an affordable computational cost.
Some of the most robust techniques for calibration are based on non-parametric models for nonlinear regression [
28]. Here, we will employ Gaussian processes to represent in an abstract fashion the response of a simulation code to a complex mechanical problem employing the material models that we are set to study. We summarize next the main concepts behind these processes.
A Gaussian process is a set of random variables such that any finite subset of them has a Gaussian multivariate distribution [
28]. Such a process is completely defined by its mean and covariance, which are functions. If the set of random variables is indexed by points
, then when the random variables have a scalar value
, the standard notation employed is
where
and
are, respectively, the mean and covariance. The mean function can be arbitrary, but the covariance must be a positive function. Often these two functions are given explicit expressions depending on hyperparameters. In simple cases, the average is assumed to be zero, but often it is assumed to be of the form
where
is a vector of known basis functions and
is a vector of basis coefficients. The choice of the covariance function is the key aspect that determines the properties of the Gaussian process. It is often selected to be stationary, that is, depending only on a distance
. In particular, we will employ a covariance function such as
where
is a variance hyperparameter and
has been chosen as the Màtern
function, an isotropic, differentiable, stationary kernel commonly used in statistical fitting that is of the form
that uses a length-scale hyperparameter
. For the Gaussian process described, the collection of hyperparameters can be collected as
.
Let us now describe in which sense Bayesian analysis can be used for model calibration. The value of a computer model depends on the value of some input variables
that are measurable, and some parameters
that are difficult to determine because they are not directly measurable. Let us assume that
is the true value of the parameters, which is unknown and we would like to determine based on available data. Given some input variable
, a physical experiment of the problem we want to model will produce a scalar output
z and it will verify
In this equation, is the value of the computer model evaluated at the input variable and the true parameter , is the so-called model inadequacy and is the observation error. This last term can be taken to be a random variable with a Gaussian probability distribution . The functions and are completely unknown so we can assume them to be Gaussian processes with hyperparameters and , respectively.
If
were known, we could study the multivariate probability distribution of the output
z using Equation (
18) for any set of inputs
. However, we are interested in solving the inverse problem: we have a set of experimental and computational data and we would like to determine the most likely probability distribution for
and the hyperparameters, a problem that can be effectively addressed using Bayes’ theorem.
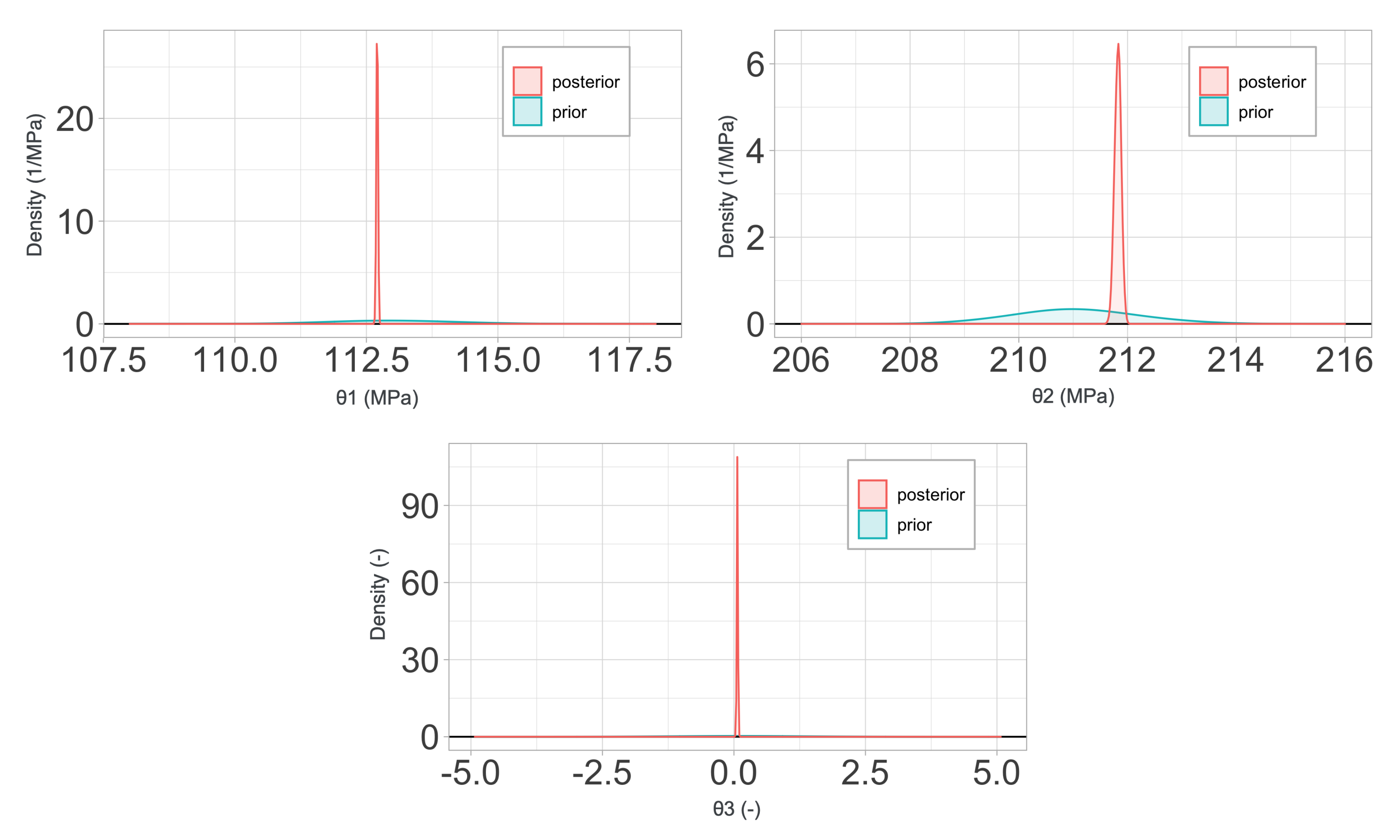
Bayes’ theorem states that, given a prior probability for the parameters
indicated as
, the posterior probability density function for these parameters after obtaining the data
is
The prior for the parameters and hyperparameters can be taken as Gaussian, or any other probability distribution that fits our initial knowledge. Assuming that the parameters and hyperparameters are independent, we have in any case that
In addition, since Equation (
18) indicates that the output is the sum of three random variables with Gaussian distributions,
z itself is a Gaussian.
To apply Bayes’ theorem, it remains to calculate the likelihood
. To this end, the hyperparameters of
and
are collected together with the observation error
and we assume that the conditioned random variable
has a normal probability distribution of the form
Here,
and
refer to the expectation and variance, respectively. Finally, in order to obtain the segregated posterior probability density of the parameters
, we should integrate out
and
; but, due to the high computational cost involved, this is typically done using Monte Carlo methods [
29]. Details of this process fall outside the scope of the present work and can be found in standard references [
12].
2.4. Material Models
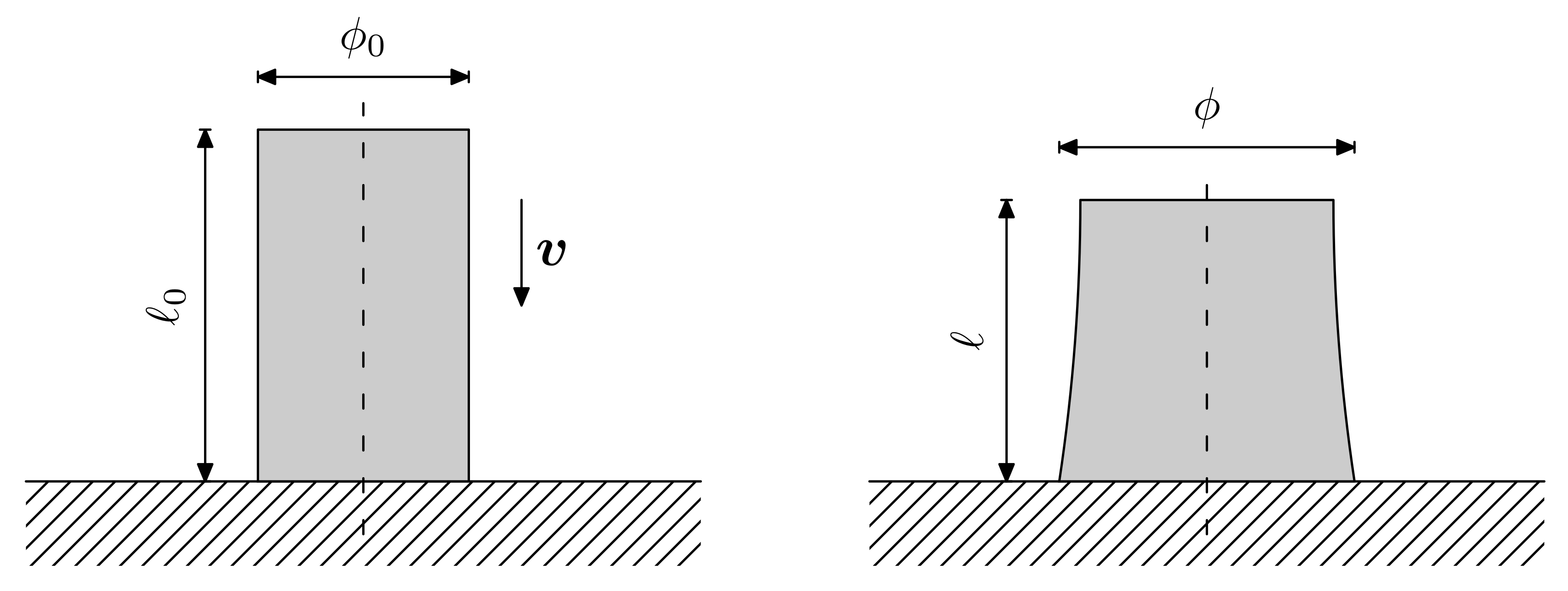
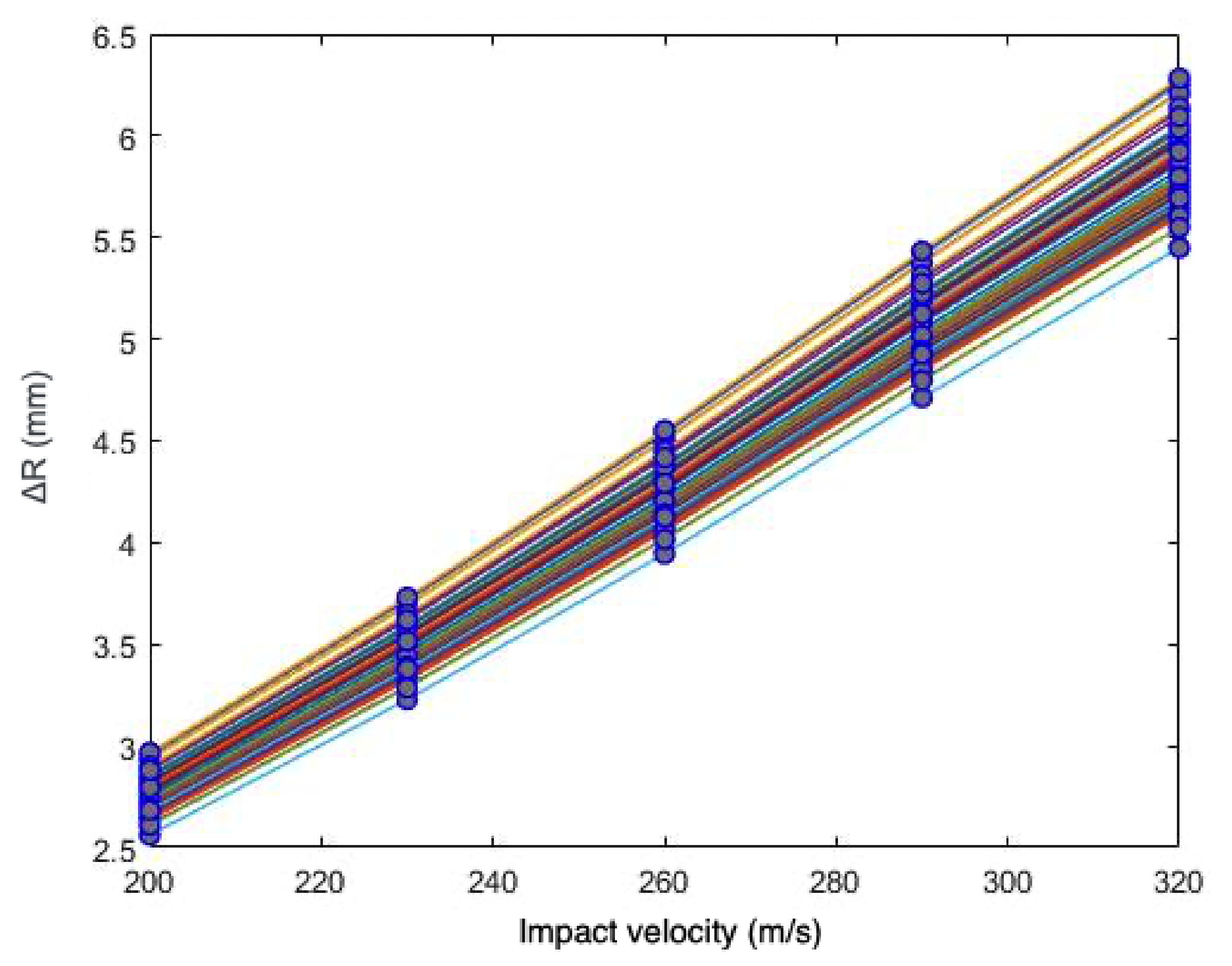
In
Section 4, a sensitivity and calibration procedure is applied to three relatively complex material models employed in advanced industrial applications. Here, we summarize them, listing all the parameters involved in their description. The remainder of the article will focus on ranking the significance of these parameters, their influence in the predictions, and the determination of their probability distributions.
2.4.1. Johnson–Cook Constitutive Relations
The Johnson–Cook (JC) constitutive model [
17] is commonly used to reproduce the behavior of metals subjected to large strains, high strain rates, and high temperatures. It is not extremely accurate in all ranges of strain rates and temperatures, but it is simple to implement, robust, and, as a result, has been employed over the years in a large number of applications [
30,
31,
32].
Johnson–Cook’s model is a
classical plasticity constitutive law in which the yield stress
is assumed to be of the form:
where
refers to the equivalent plastic strain. The first term in expression (
22) accounts for the quasistatic hardening, including the initial yield stress,
A, and the constants representing the strain hardening,
B, and the exponent
n. The second term in (
22) is related to the hardening due to strain rate effects, containing the strain rate constant,
C and also the dimensionless plastic strain rate,
, where
is a reference plastic strain rate, often taken to be equal to 1. Finally, the third term accounts for the effects of temperature, including the thermal softening exponent,
m, and also the so-called “homologous temperature”
Here, is the experimental temperature at which the material is being modeled, is the melting temperature of the material and is the ambient temperature.
2.4.2. Zerilli–Armstrong Constitutive Relations
The Zerilli–Armstrong (ZA) model [
18] was conceived as a new approach to the metal plasticity modeling, using a finite deformation formulation based on constitutive relations related to the physical phenomenon of dislocation mechanics, in contrast to other purely phenomenological constitutive relations, such as the previously described Johnson–Cook model. These relations have been proved to be well suited for the modeling of the response of metals to high strains, strain rates, and temperatures. Its numerical implementation, although more complicated than the JC model, is still relatively simple, justifying its popularity.
The ZA relations were developed in order to respond to the need of a physical-based model that could include the high dependence of the flow stress of metals and alloys on dislocation mechanics. For instance, aspects like the grain size, thermal activation energy, or the characteristic crystal unit cell structure have a dramatic effect in the plastic response of these materials, according to experimental data. Hence, the ZA model is still a
plasticity model in which the yield stress becomes a function of strain, strain rate, and temperature, but with their relative contributions weighted by constants that have physical meaning. The yield stress is assumed to be
In this relation, are constants. The constants represent, respectively, the contributions to the yield stress due to solutes, the initial dislocation density, and the average grain diameter. The remaining constants are selected to distribute the contribution to the hardening of the plastic strain, its rate, and the temperature. Based on the crystallographic structure of the metal under study, some of the constants will be set to zero. For example, fcc metals such as copper will have . Iron and other bcc metals will be represented with equations that have . These differences are mainly based on the physical influence of the effects of strain on each type of structure, which is especially dominant when it comes to modeling fcc metals, whereas the strain-rate hardening, thermal softening, and grain size have a greater effect on bcc metals.
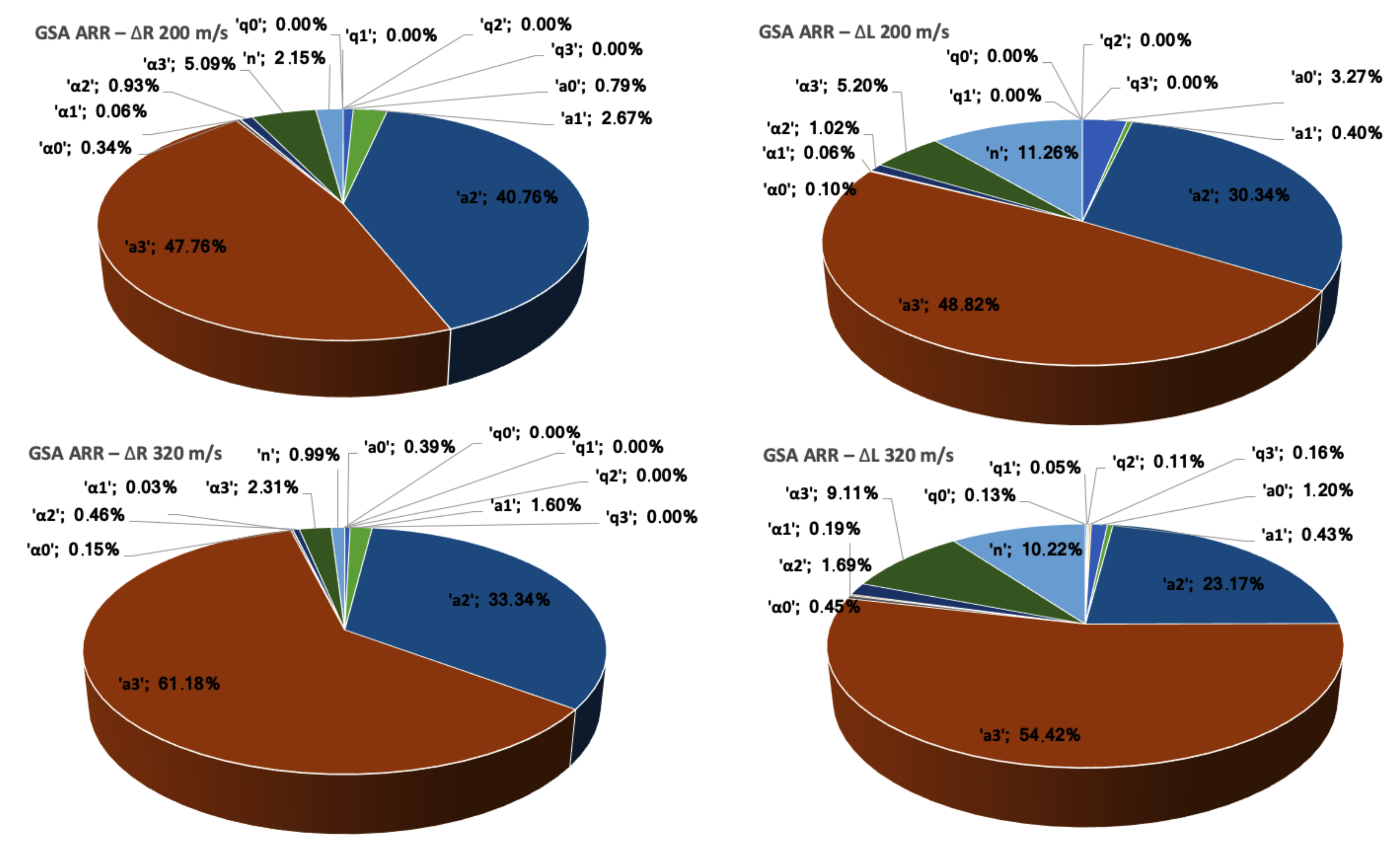
2.4.3. Arrhenius-Type Model Constitutive Relations
Last, we consider an Arrhenius-type (AR) constitutive model [
19], a strain-compensated equation aiming to reproduce the behavior of metals at high temperature. As in the previous constitutive laws, the AR model is a classical
plasticity model with an elaborated expression for the yield stress
. In this case, it is defined as
where
and
are two functions employed to represent the influence of the plastic strain on the response and
n is a material exponent. On the other hand,
is the so-called Zener–Holloman function, accounts for the effects of strain rate
and temperature
T, and is defined as
where
R is the universal gas constant and
is the activation energy, assumed to be a third-order polynomial.
The scalar functions that enter the definition of the yield function are thus
and
Q. The three are defined parametrically as
where
,
, and
are material constants determined experimentally. Depending on the author, these three functions might adopt slightly different forms leading to potentially higher accuracy at the expense of more difficulties for their calibration.