Novel Approach and Interpretation for the Determination of Electromagnetic Forming Limits
Abstract
1. Introduction
1.1. Forming Limits in High-Speed Processes
1.2. Problems in Determining Forming Limits in High-Speed Processes
- Difficulty in achieving constant strain paths: Due to the use of “conventional” tools such as straight or spiral coils, a uniform pressure distribution is not achieved in the specimen, leading to bending and non-constant strain paths.
- Failure/fracture in regions apart from the apex of the specimen: It is expected for the FLC determination that the peak strains in the specimens occur at the apex. However, in many instances, failures occur at regions other than the apex, which lead to a non-constant strain path. This can be observed in the results of Li et al. [10], where failure is seen at the die entry radius. In electrohydraulic forming, Rohatgi et al. [11] observed fracture at the ligament in cruciform-shaped specimens. In explosive forming, Wood [9] explains that after the third critical velocity, the fracture observed in the specimens is primarily circumferential.
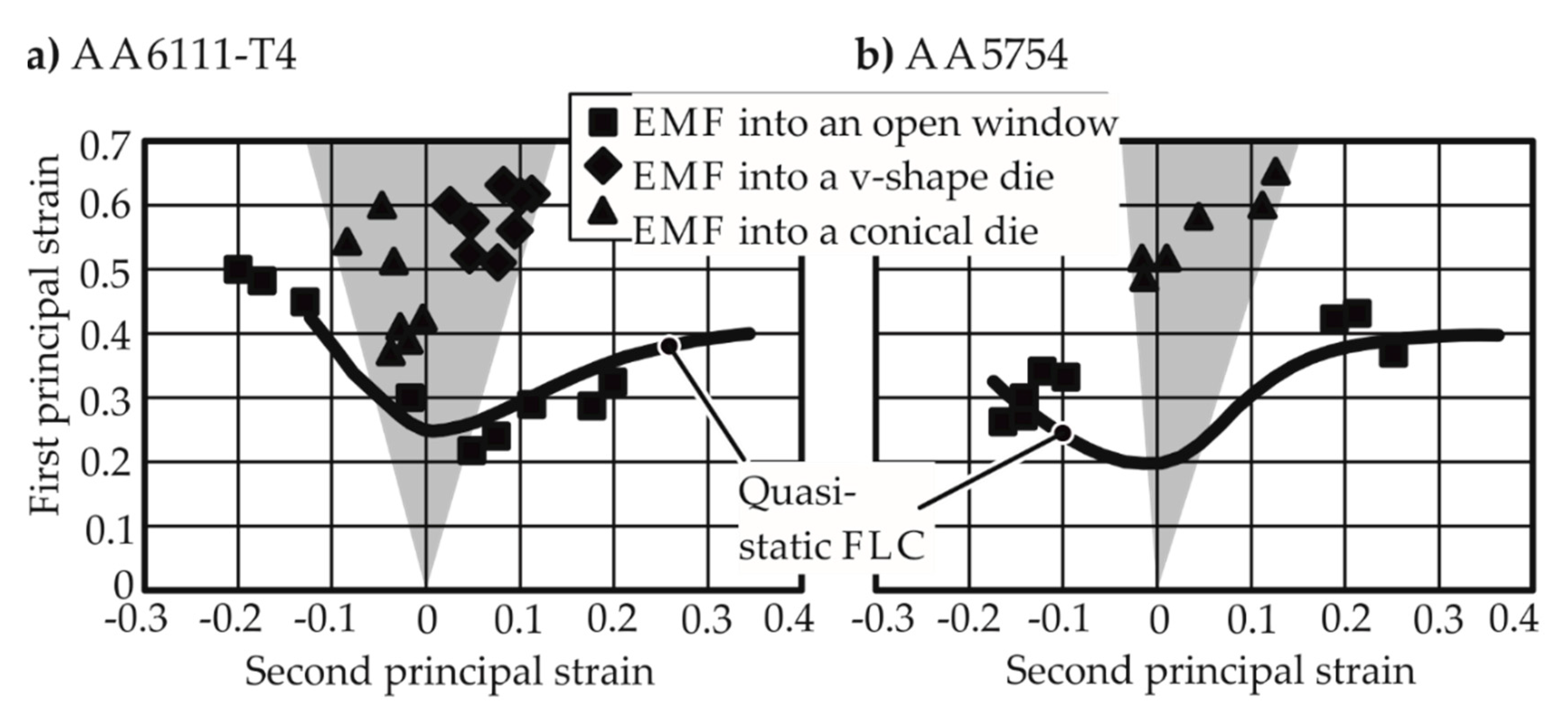
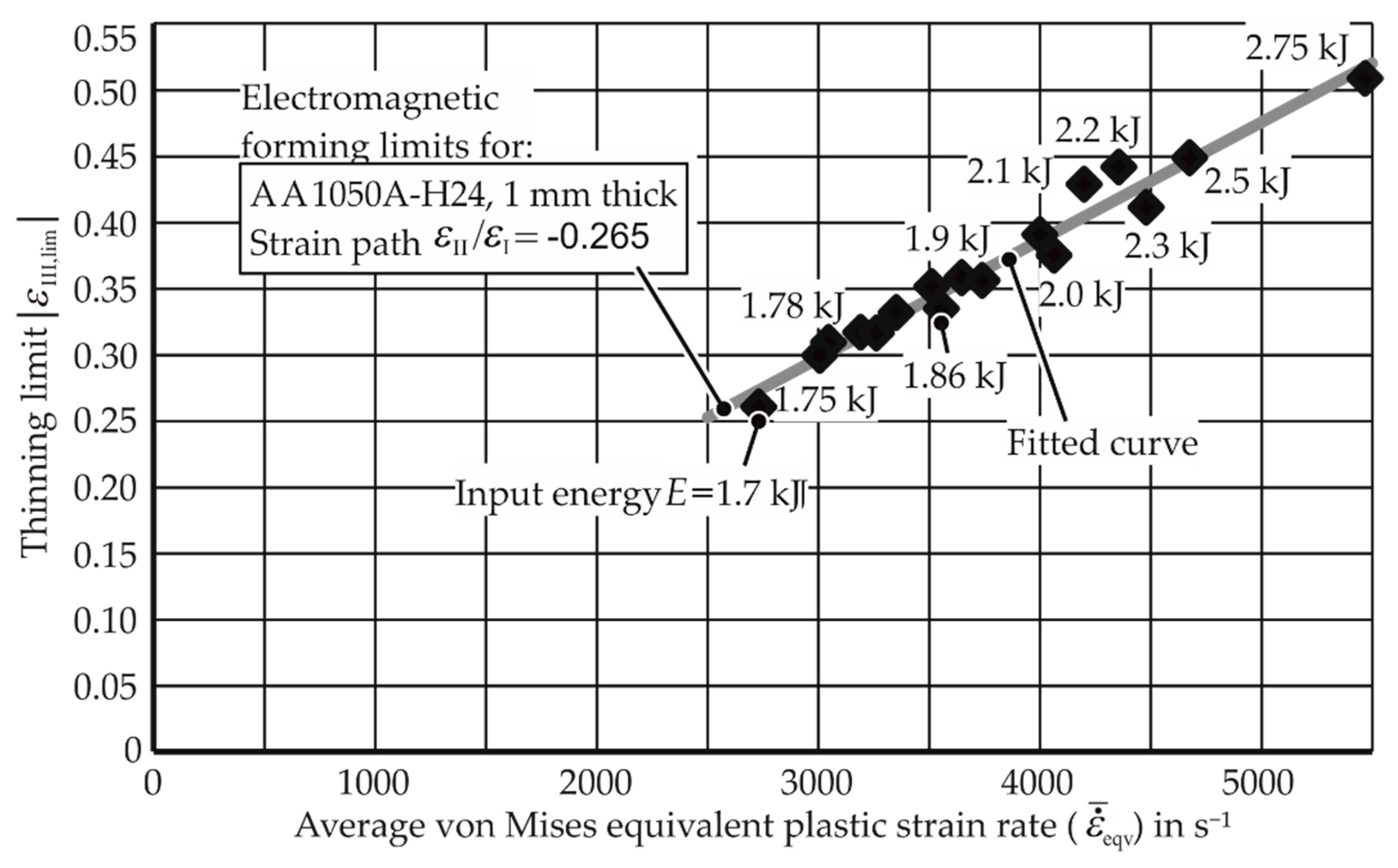
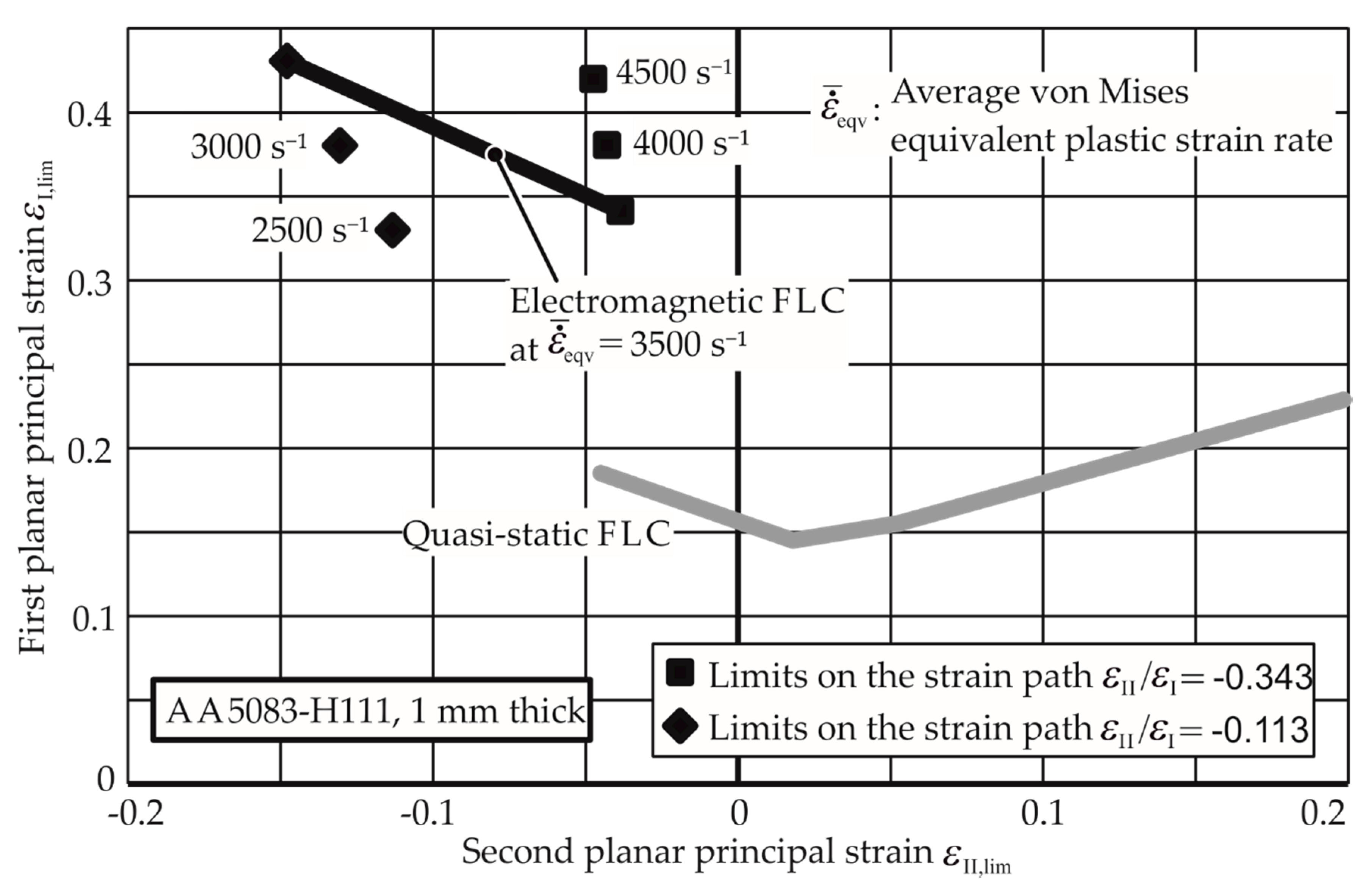
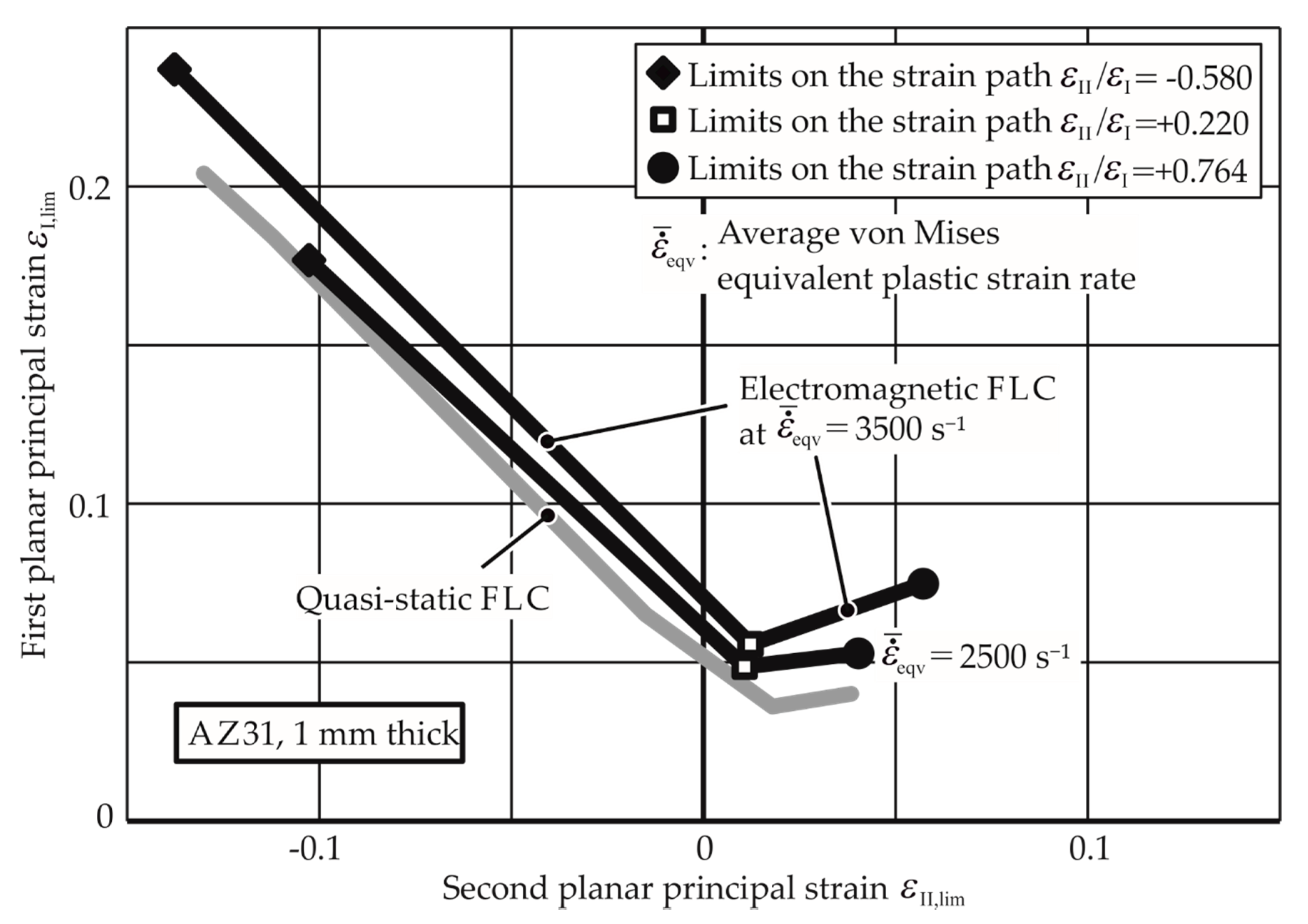
- Strain rate during the determination of the FLC: In electrohydraulic forming, the results produced by Maris et al. [12] show higher FLCs. However, the points on the higher FLC come from different experiments with different strain rates. As the quasi-static FLC is produced at a constant strain rate, the points for an FLC in high-speed processes should also be determined for specific strain rates, e.g., at least identical average strain rates.
1.3. Possible Reasons for Higher Forming Limits in Impulse Forming
1.3.1. Die–Sheet Interaction
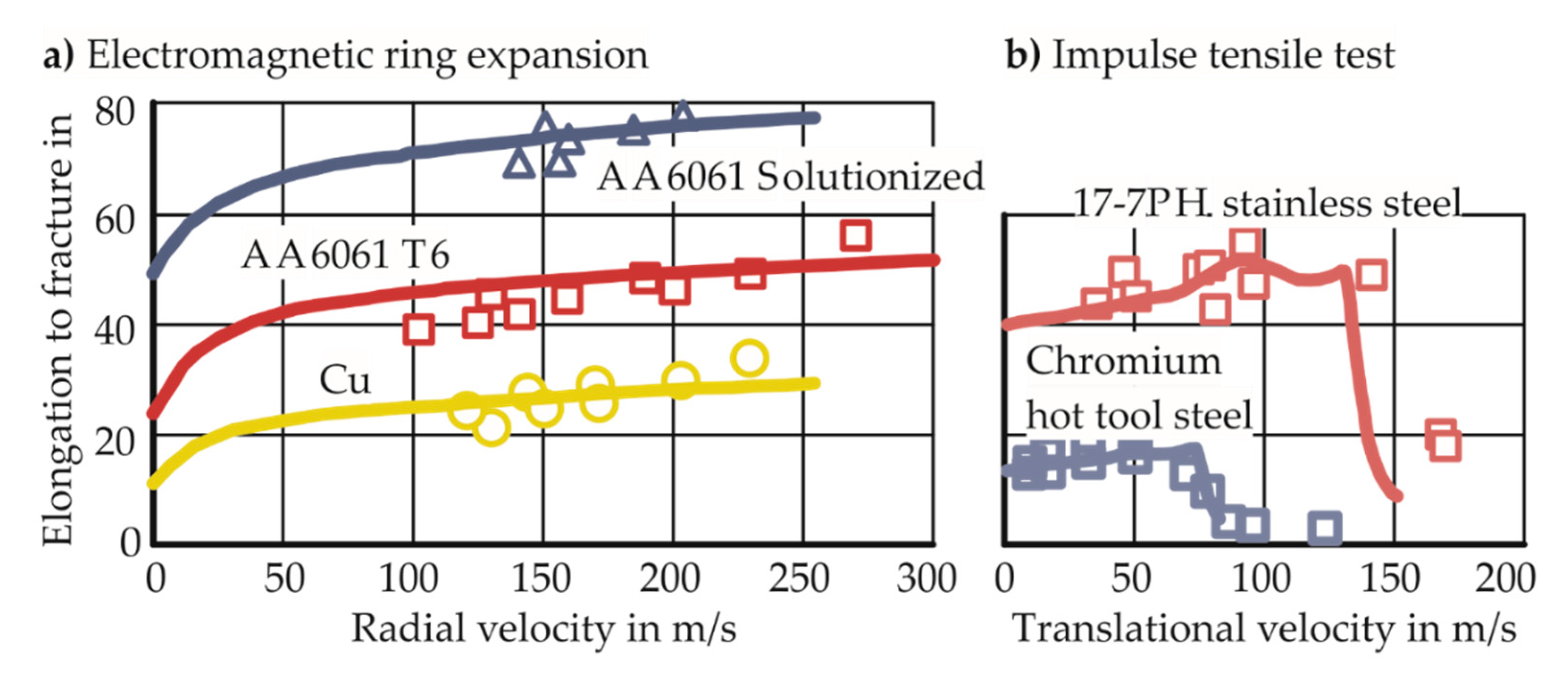
1.3.2. Inertial Stabilization
1.3.3. Strain Rate Hardening
1.3.4. Change in Failure Mechanism
1.4. Purpose of the Work
- To deform the specimens on constant strain paths between uniaxial and biaxial tension under free-forming conditions
- To deform the specimens without excessive bending
- To achieve failure in the apex of the specimens and avoiding failure at the periphery, specimen cutouts, or die radius
- Ensure identical average strain rates for different points of a particular FLC.
2. Materials and Methods
2.1. Numerical Model for Experimental Design
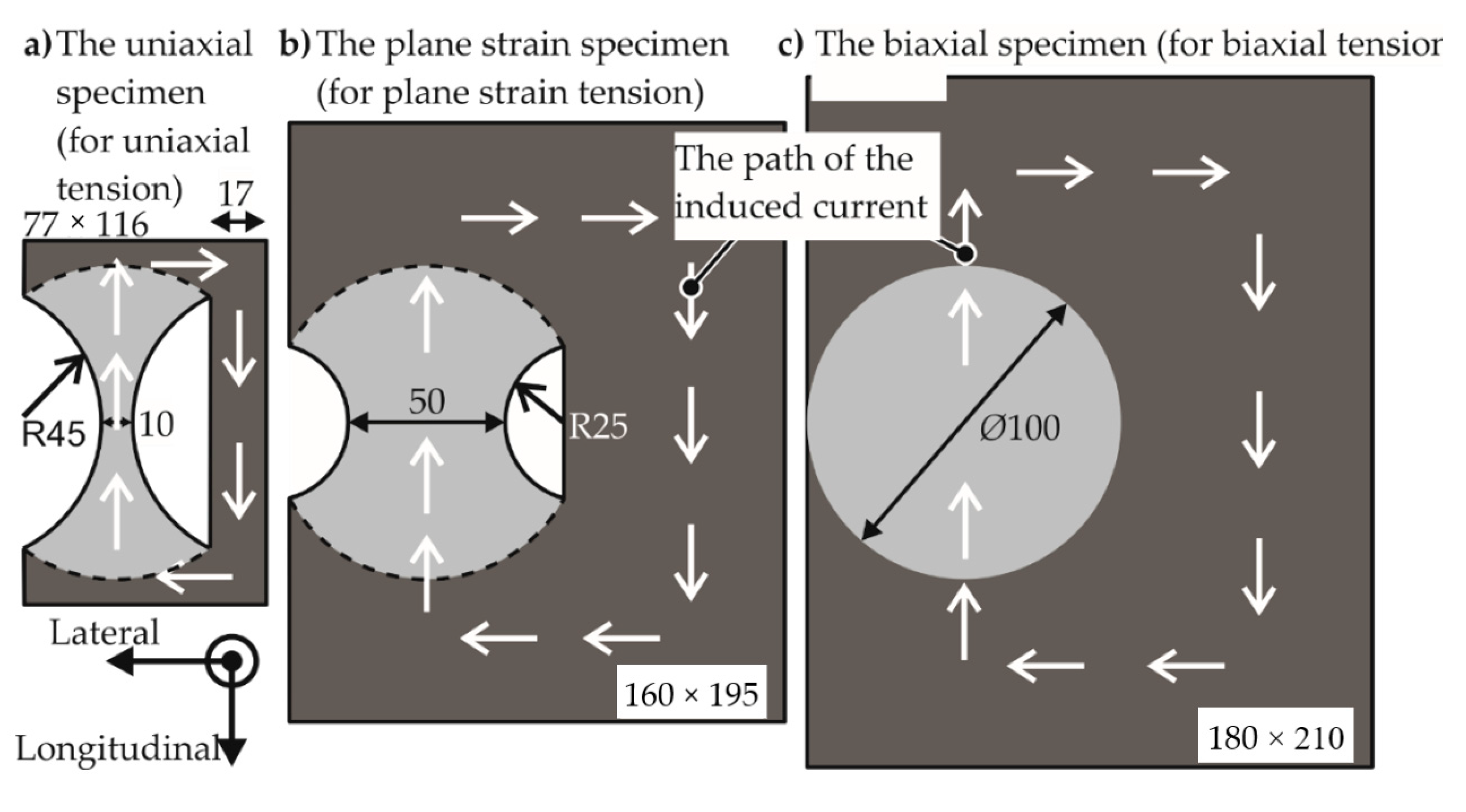
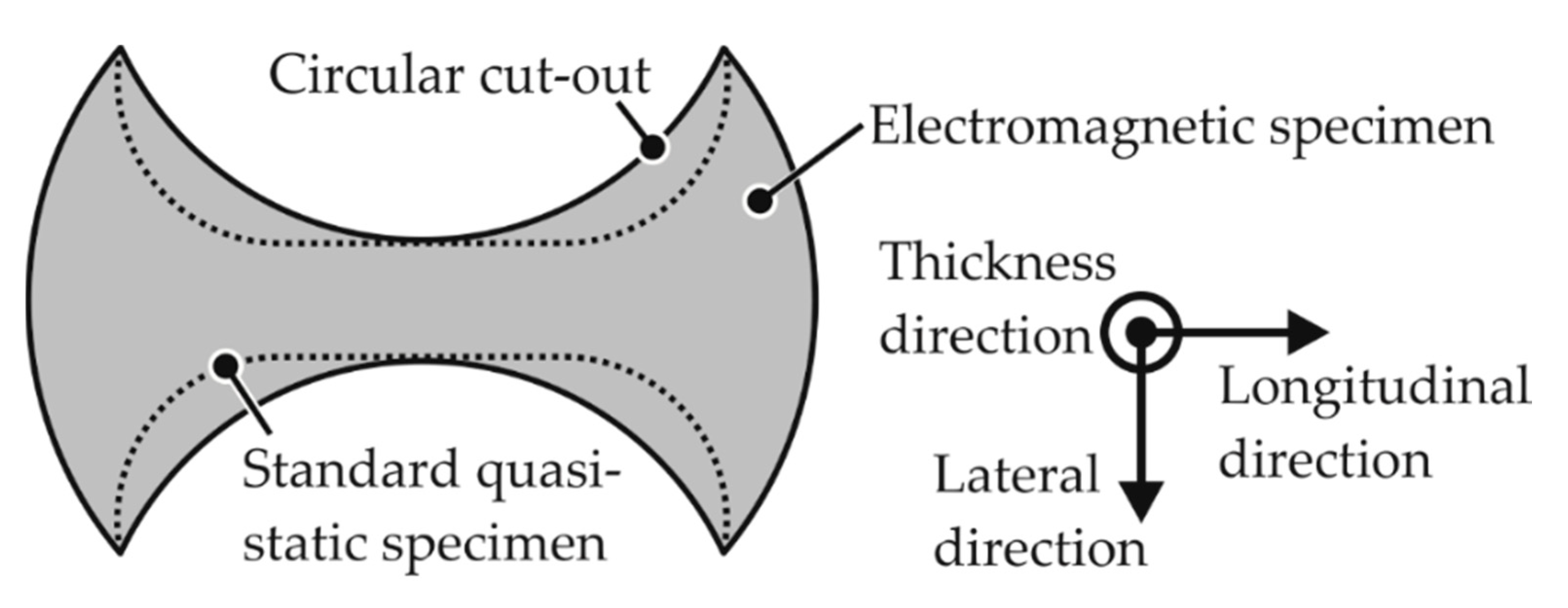
2.1.1. Specimen Design
- The standard specifies an Ø105 mm die opening and a Ø200 mm specimen diameter.
- The electromagnetic forming limit test halves these values to reduce the required voltage to let the specimen fracture within the capacity of the electrical equipment.
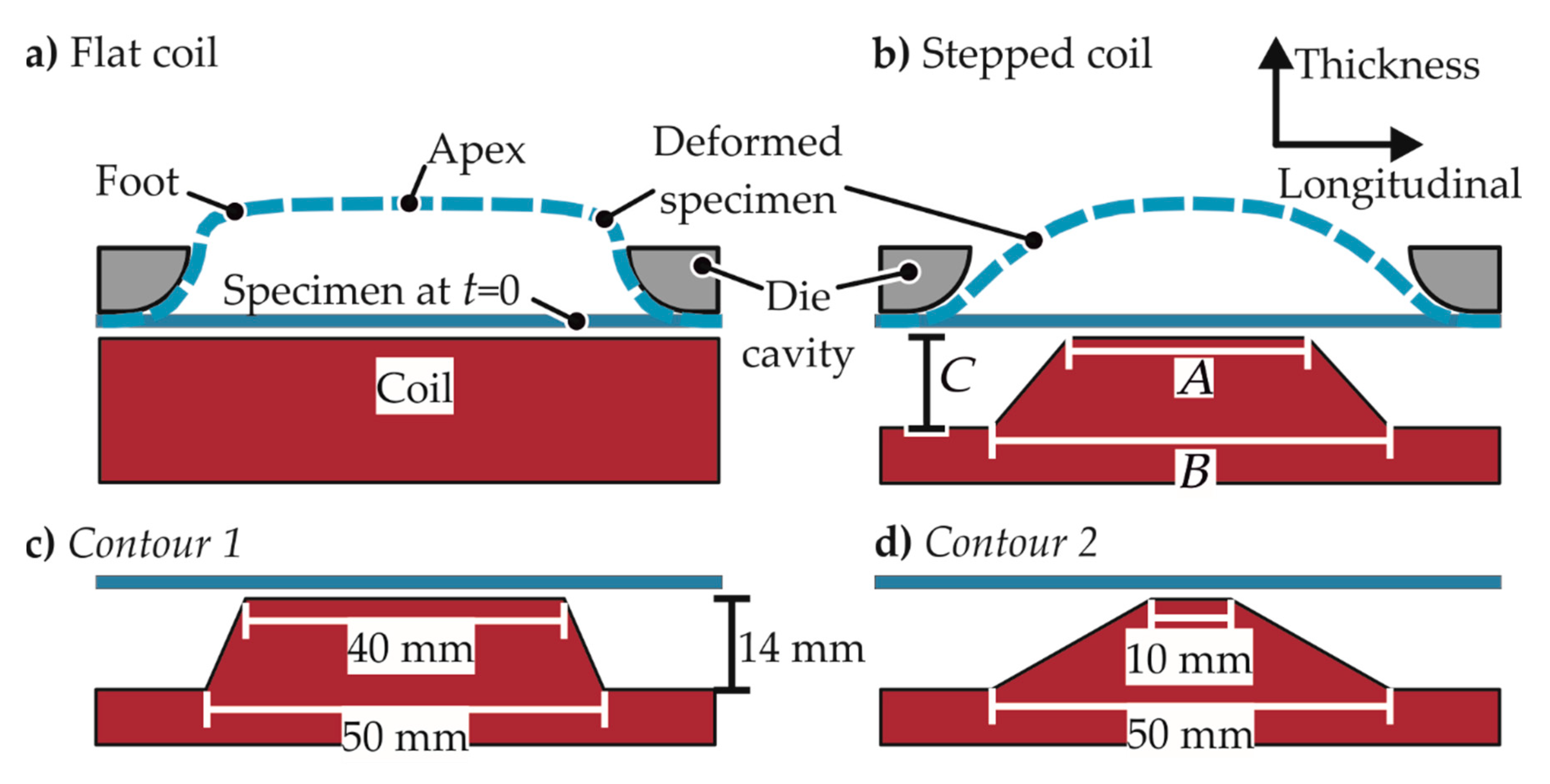
2.1.2. Coil Design
2.1.3. Die Design
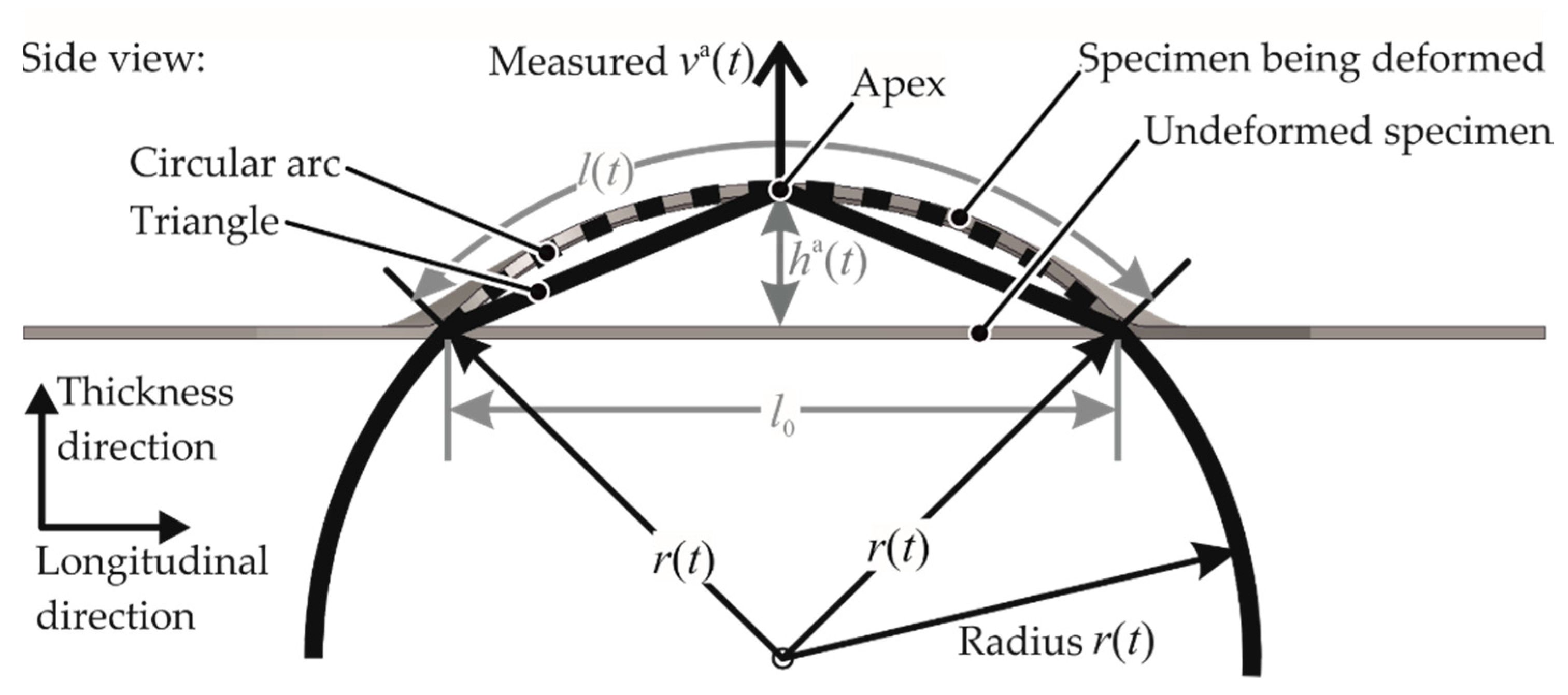
2.2. Experimental Setup and Measurement Systems
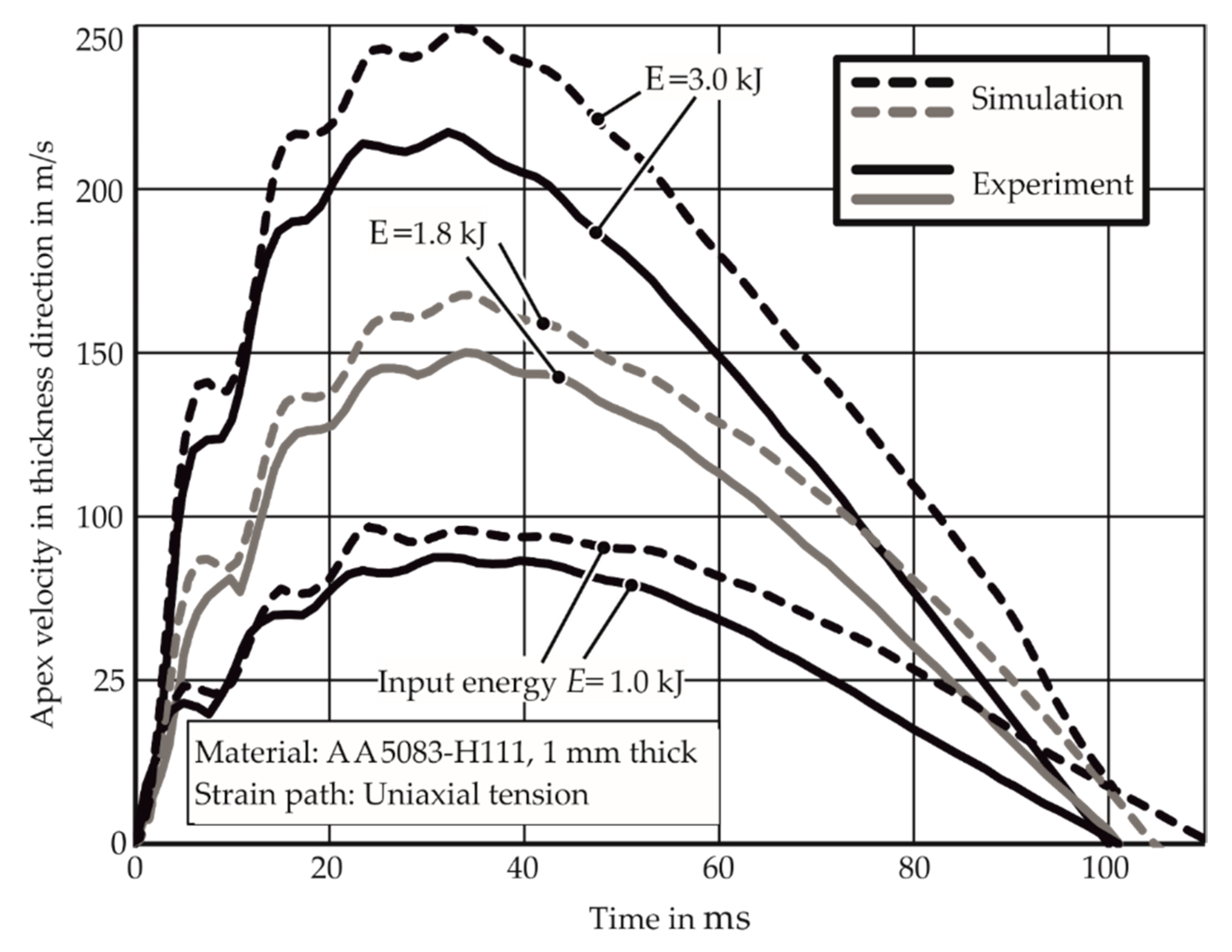
2.3. Determination of Strain Rates for the Tests
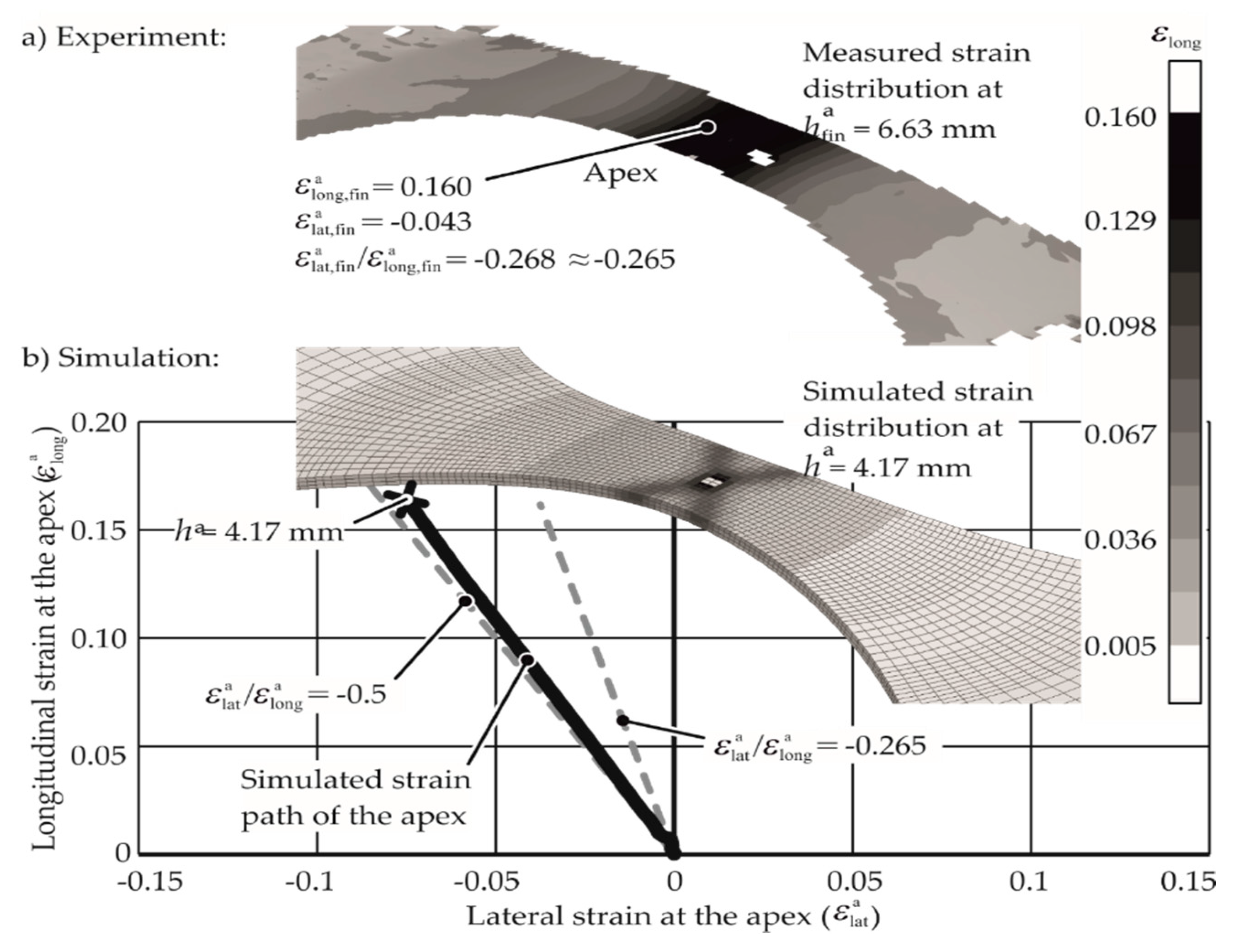
2.4. Validation and Usage of the Simulation Approach
3. Results
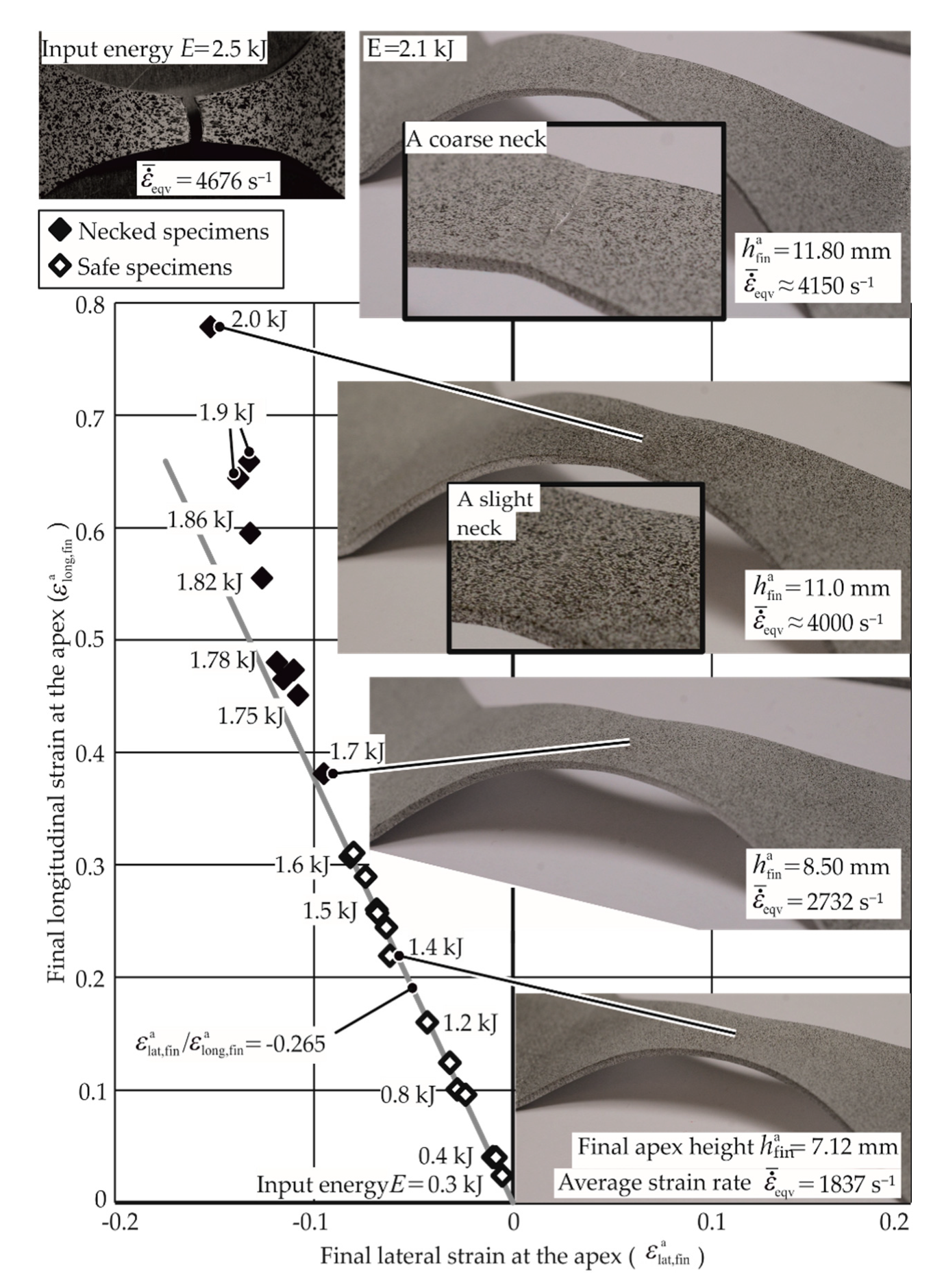
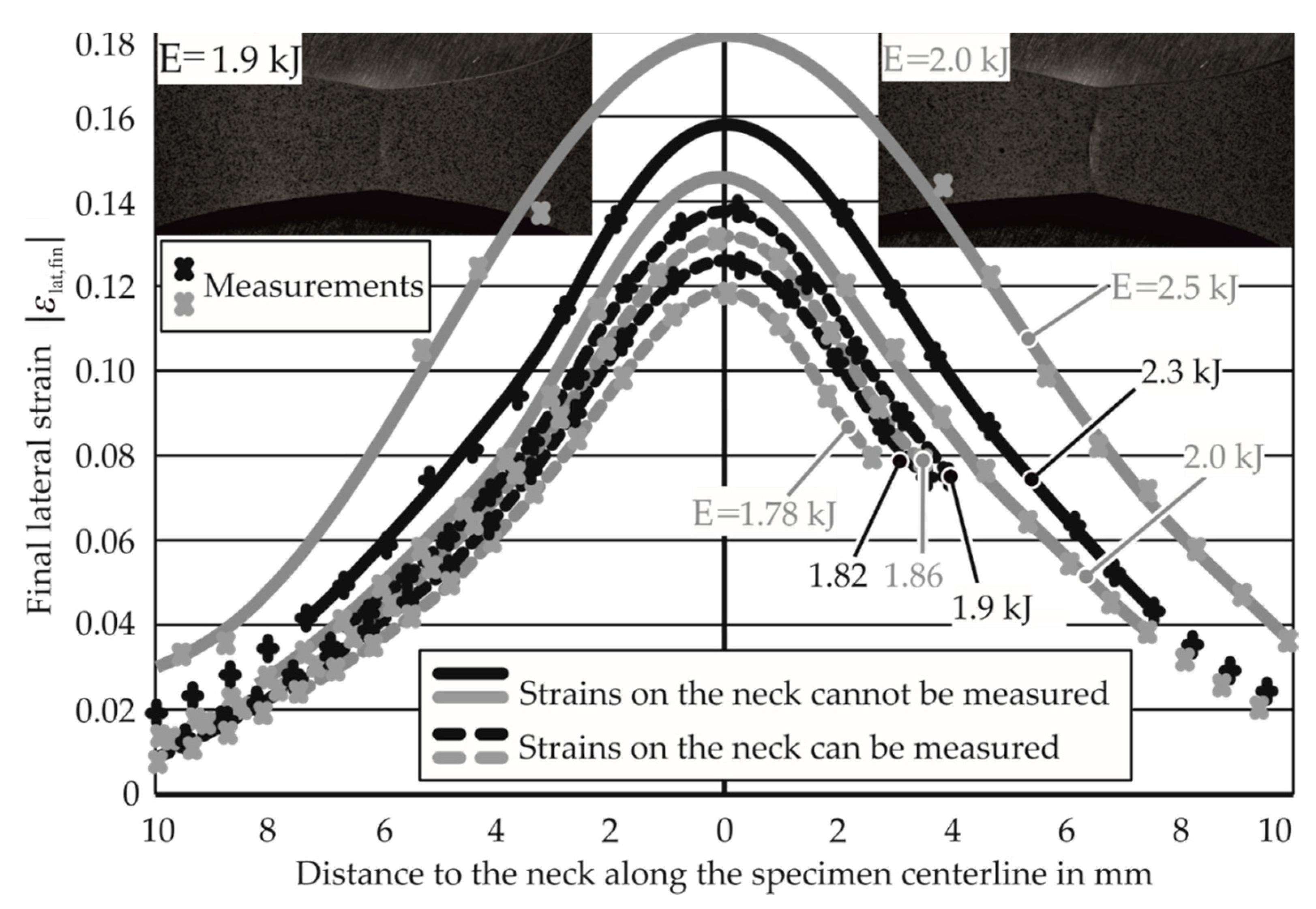
3.1. Necking Limits for Tests Where Apex Strains Could Not Be Measured
3.2. EM-FLCs for Different Average Strain Rates and Materials
4. Discussion
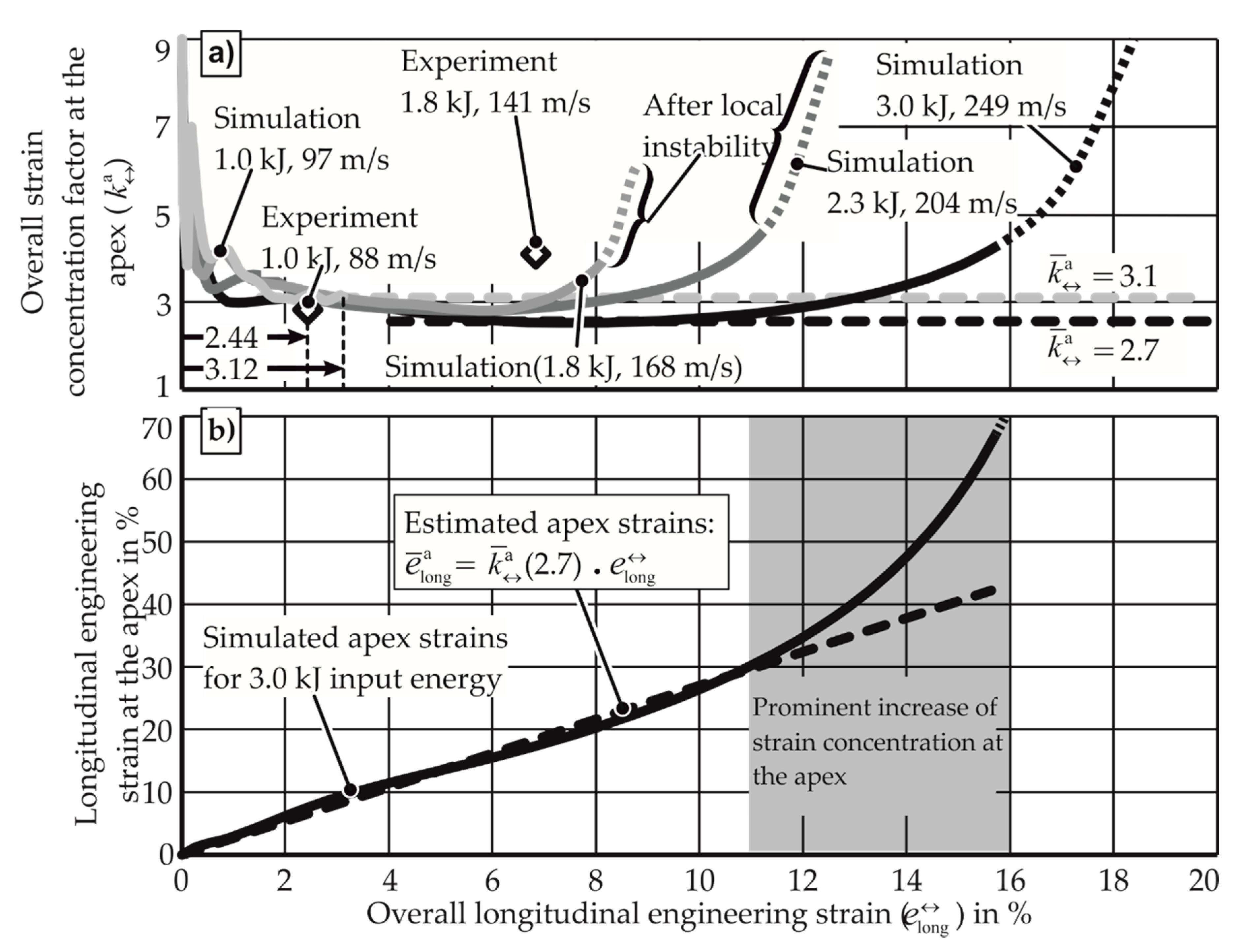
4.1. Assumptions in EM-FLC Calculations
4.2. Reasons for Higher Forming Limits in EMF
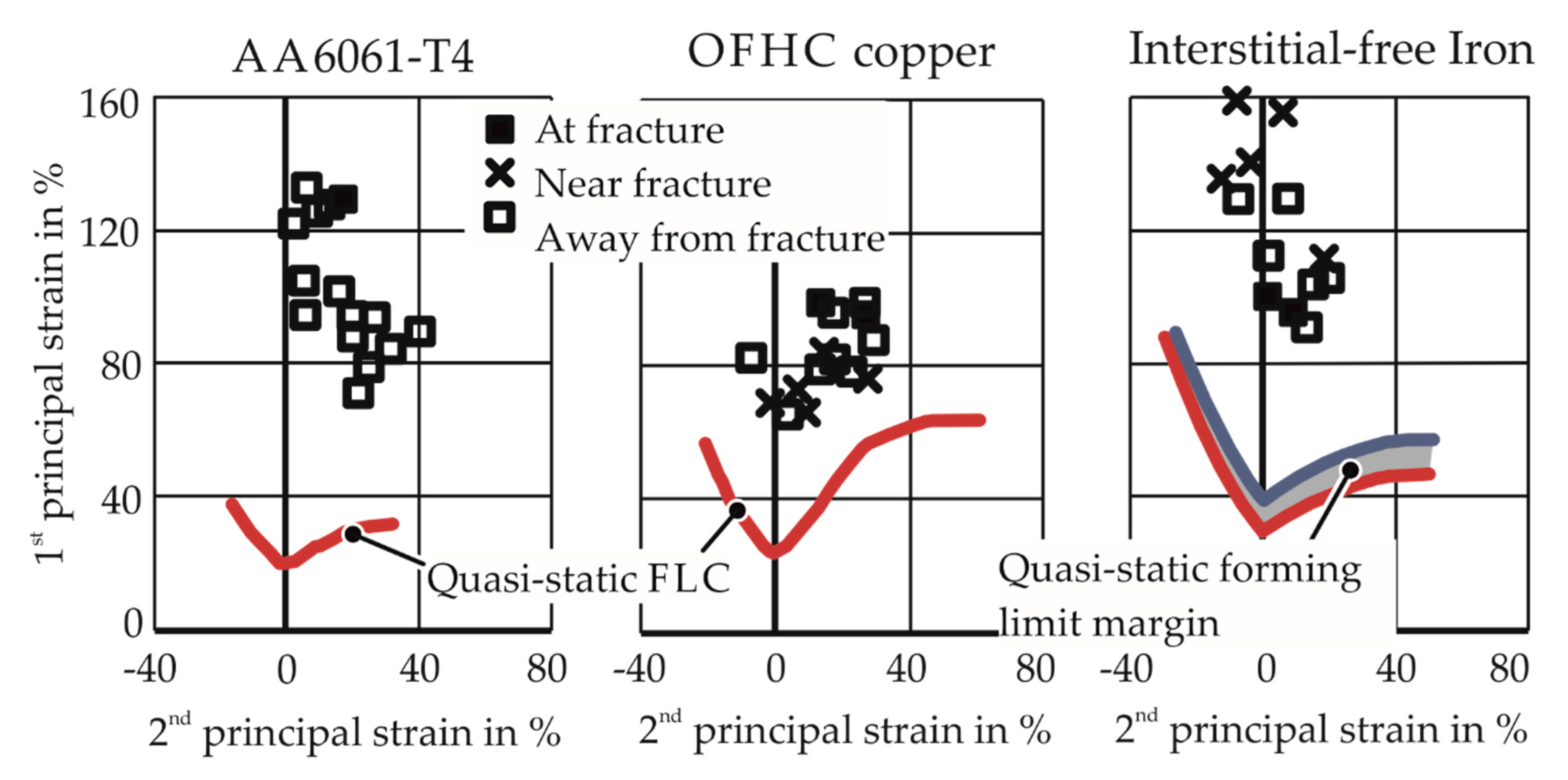
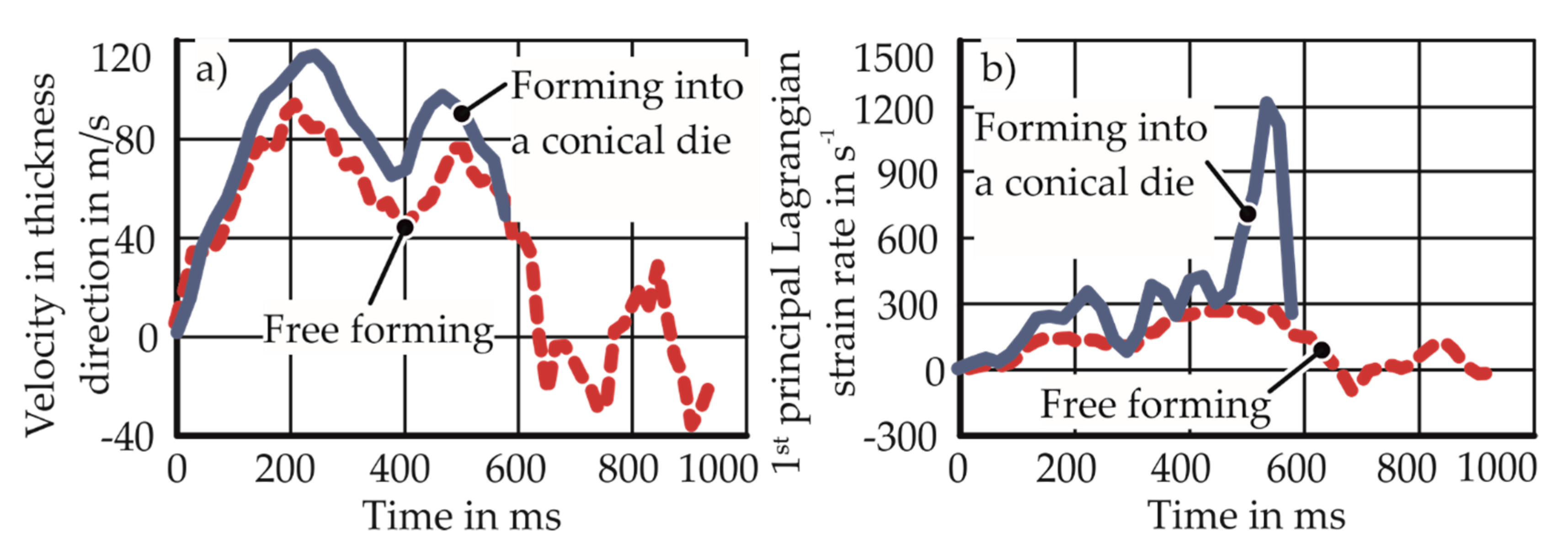
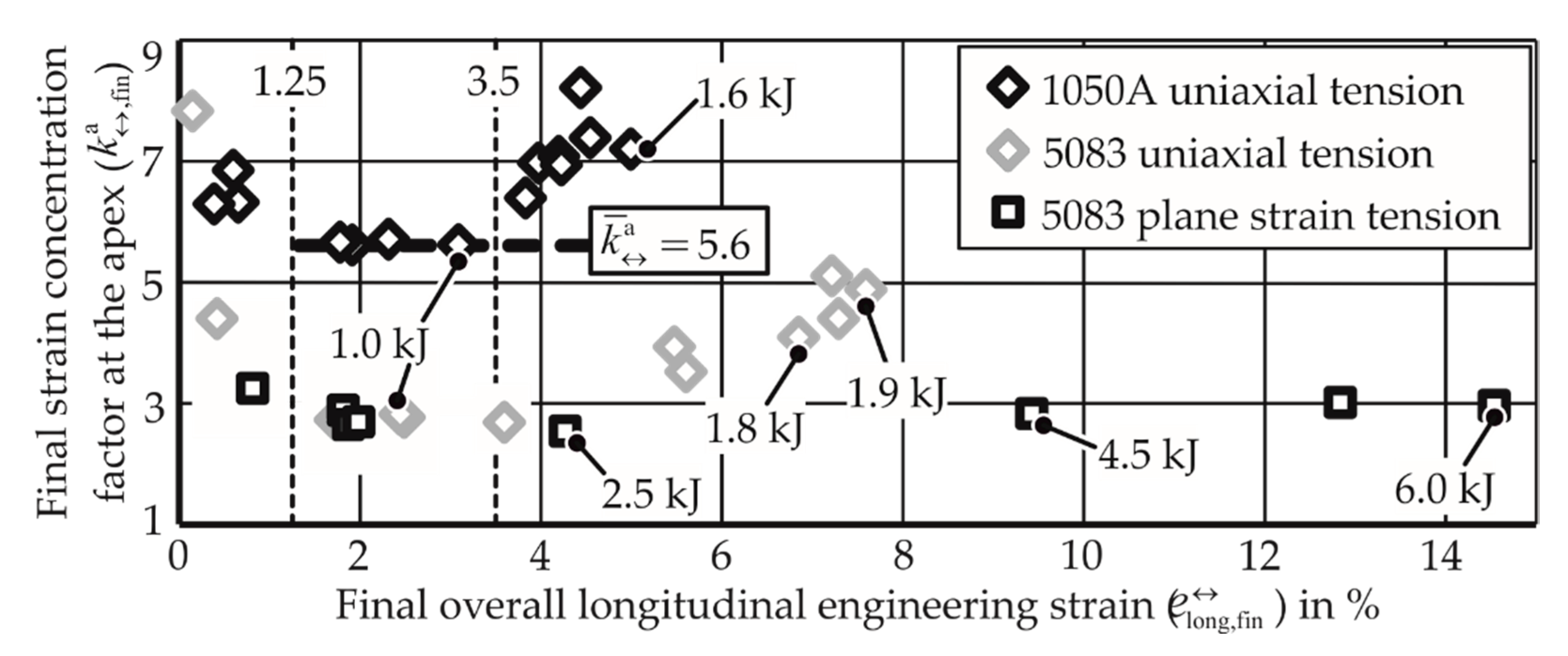
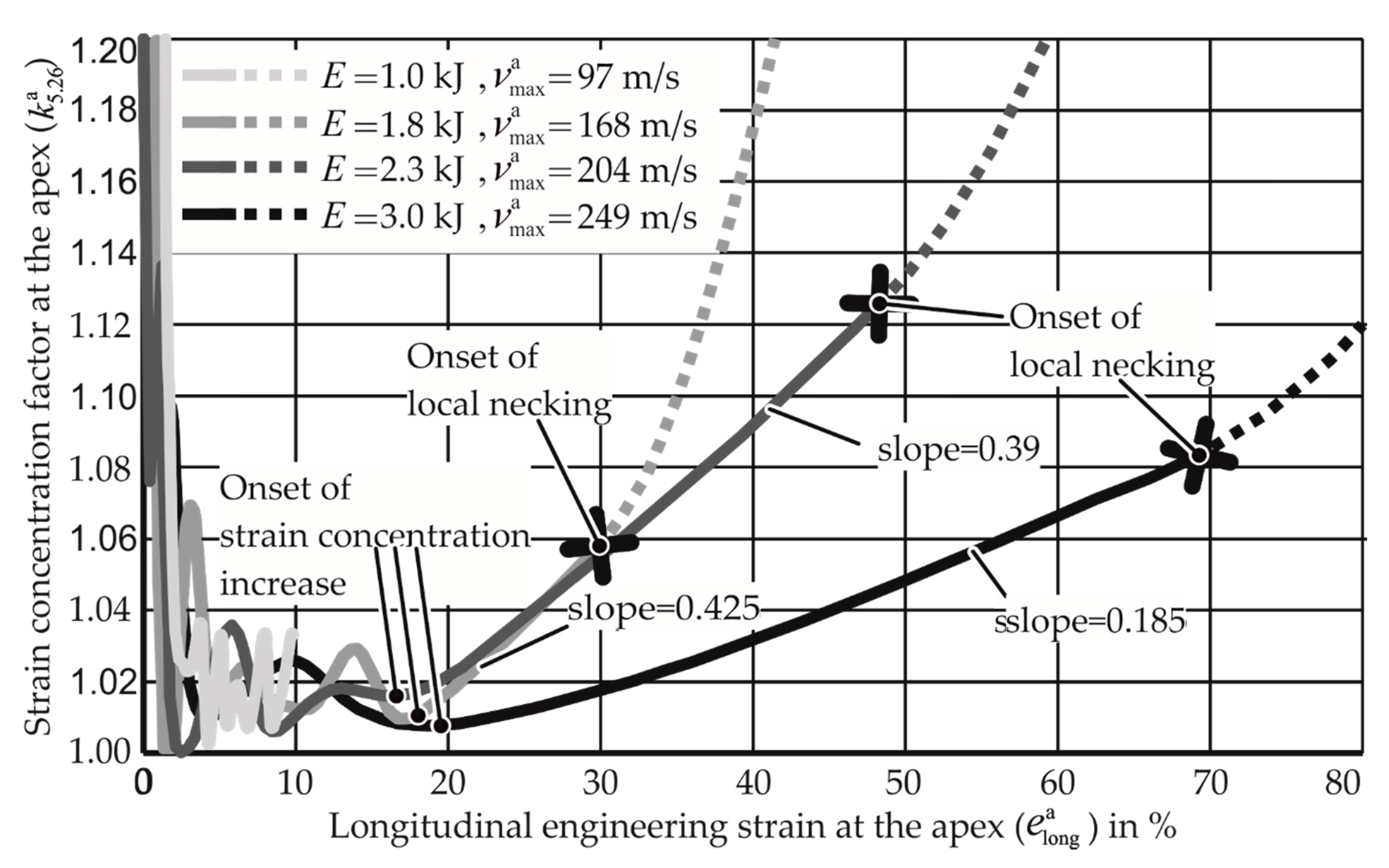
4.2.1. Strain Localization
- reduces
- The end phase of deformation (where rises again) starts at a higher overall strain
- Apex strain: to be observed as the strain concentration starts to increase. This indicates whether for higher strain rates, the strain concentration starts to increase at a higher value of apex strain or not.
- Increase of strain concentration per unit increase of apex strain: This indicates whether the strain localization happens at a slower rate for higher strain rates compared to low strain rate cases.
- Strain concentration at the onset of necking: This indicates if the material can tolerate a higher strain concentration before a local neck emerges.
4.2.2. Fracture Surface Assessment
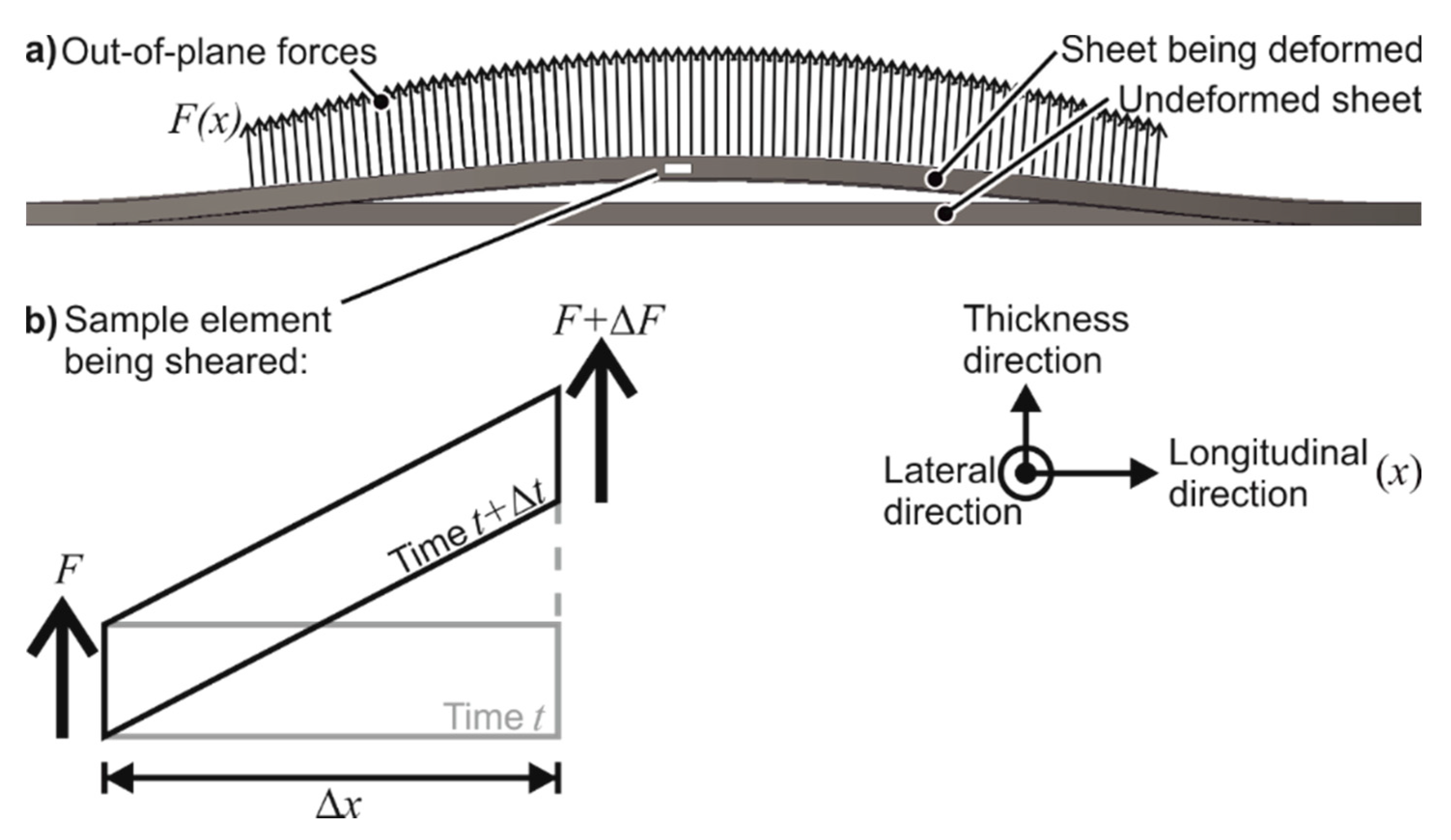
4.2.3. Out-of-Plane Shear Stresses
4.2.4. Higher Limits of Mg AZ31-O
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
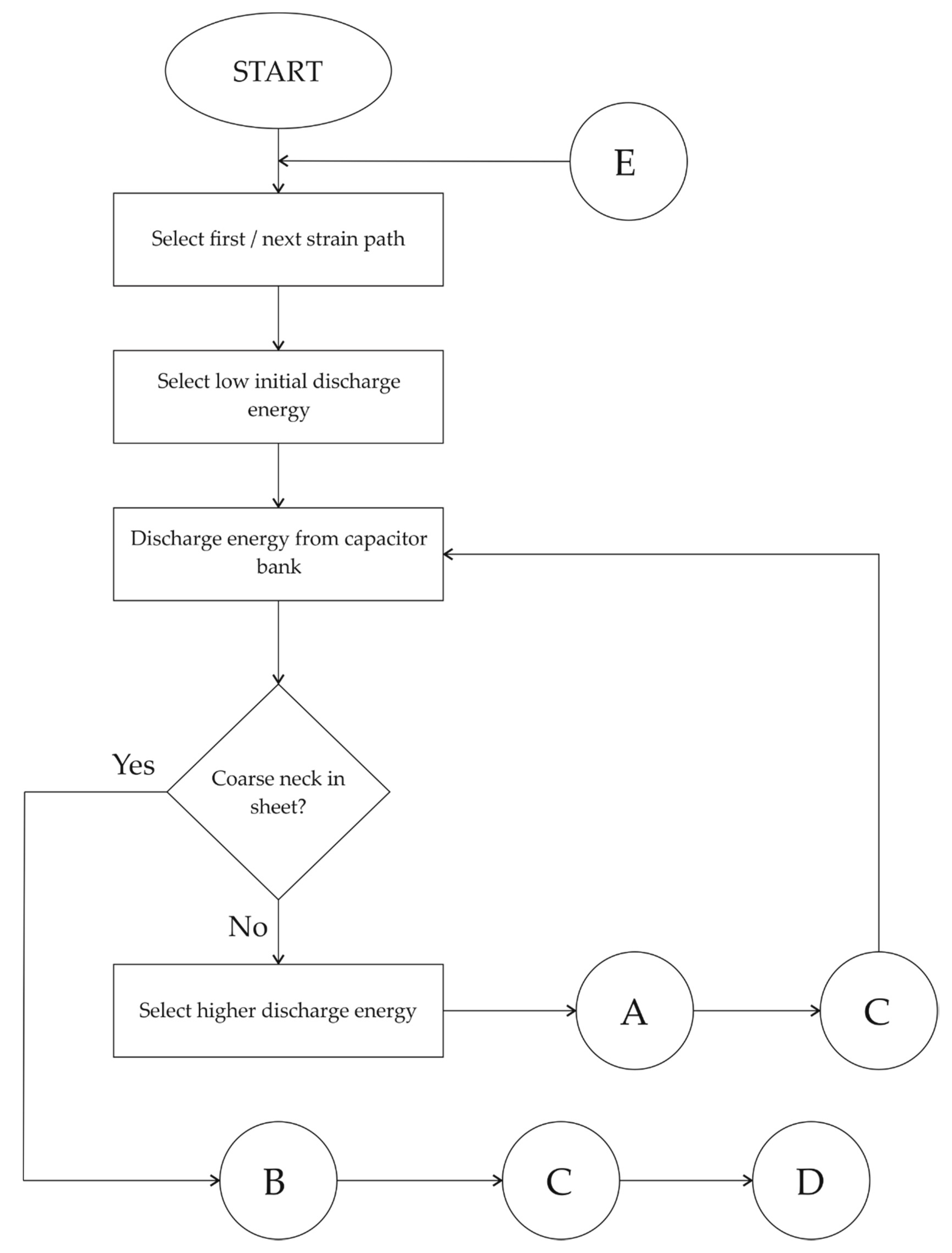

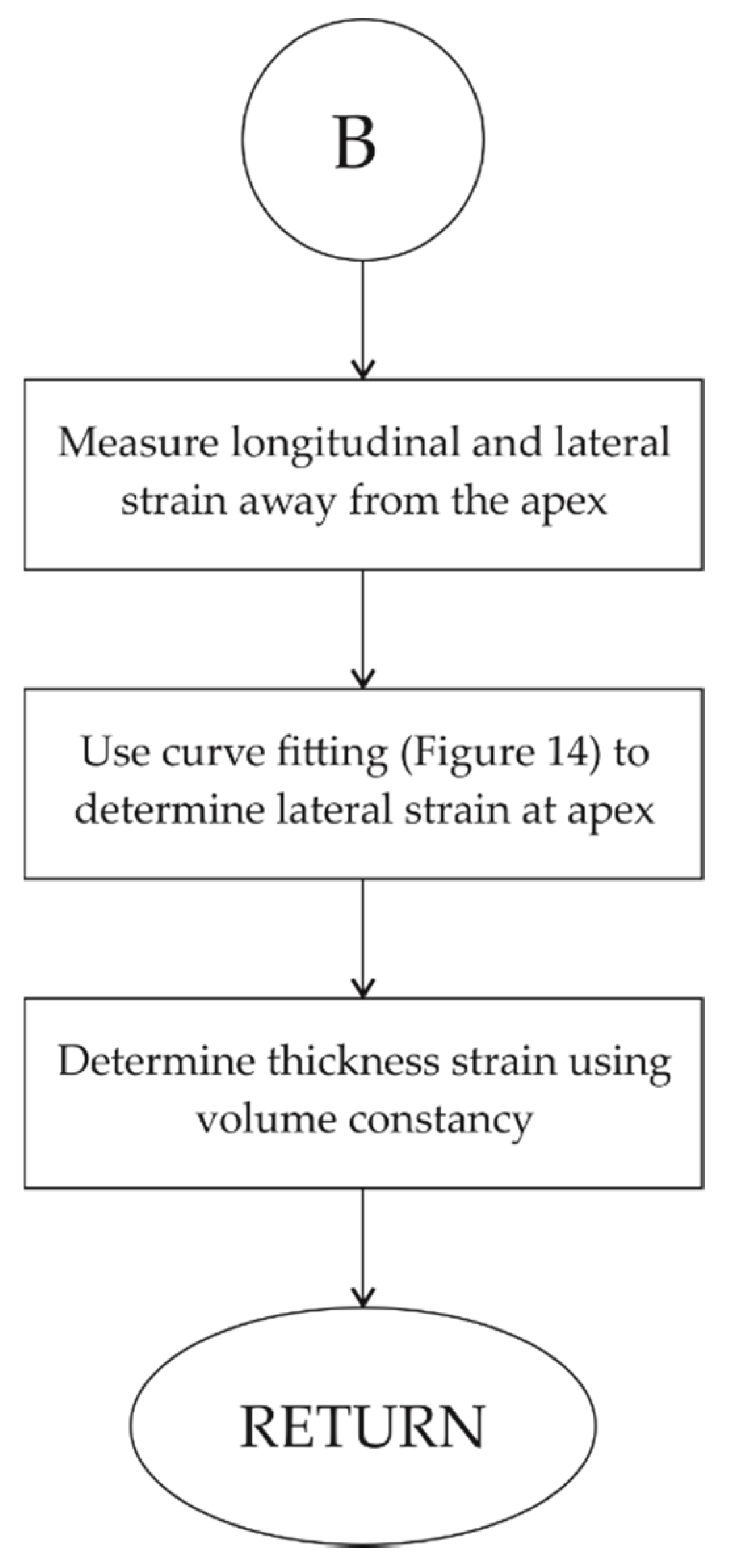
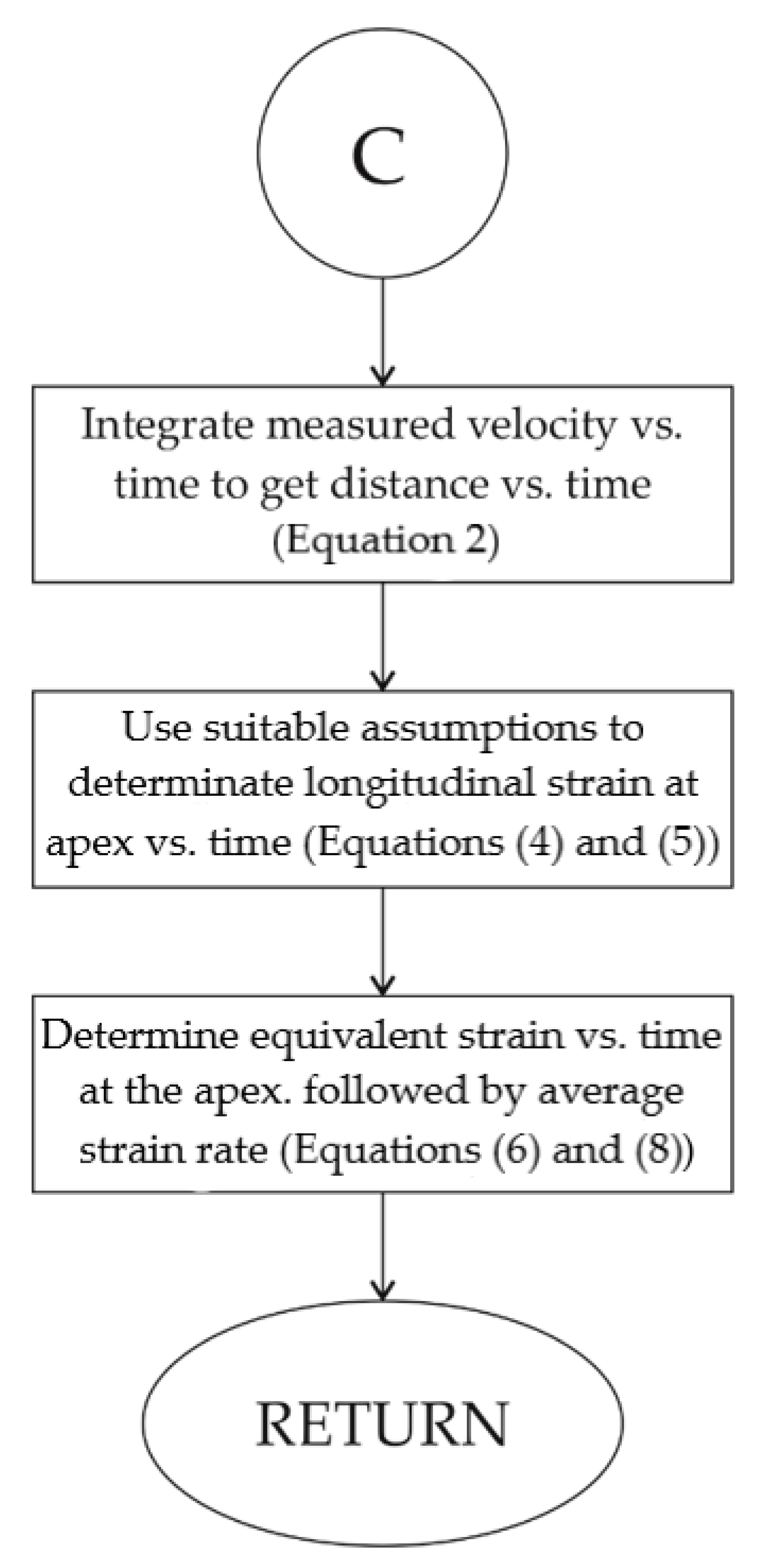
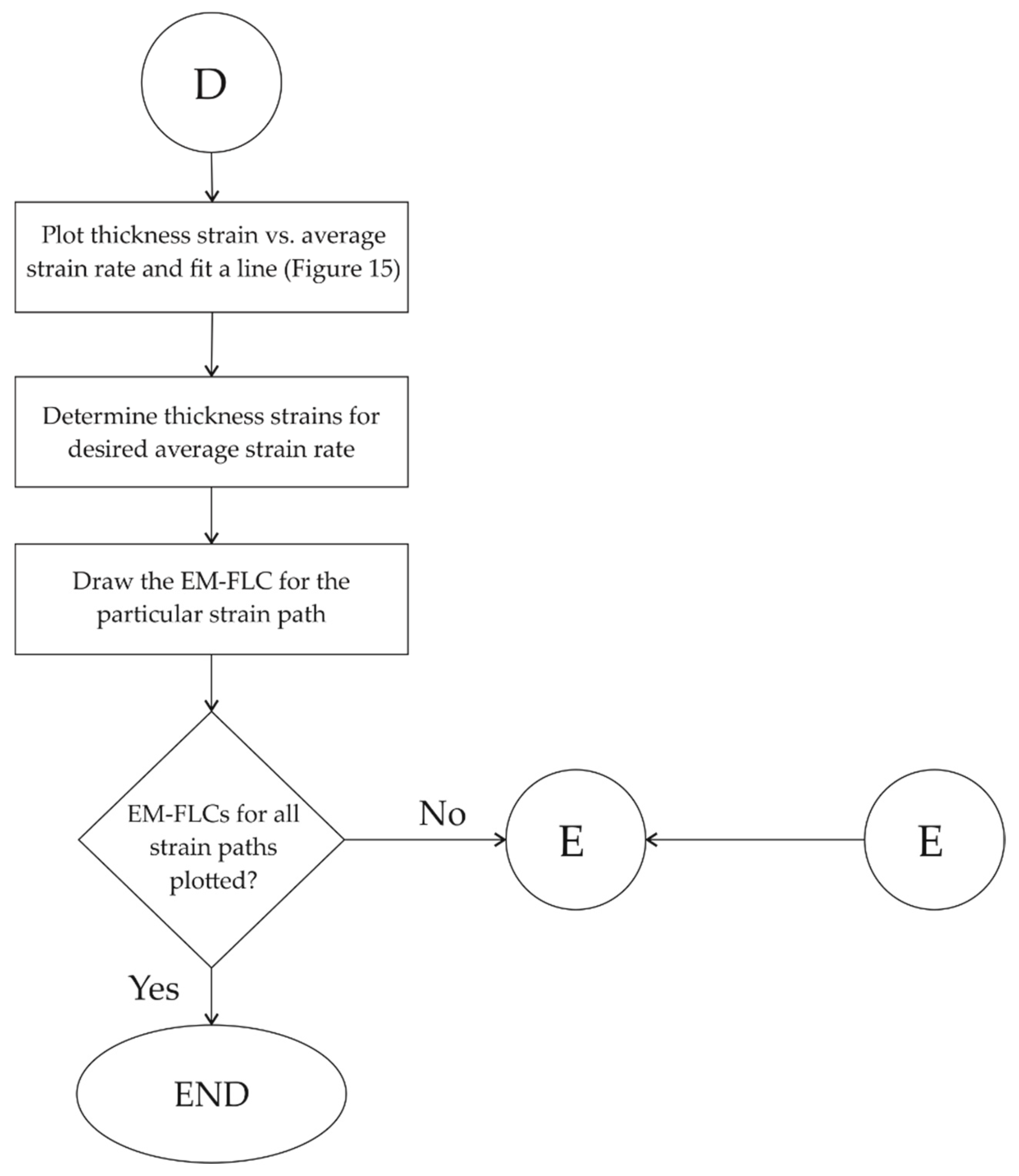
References
- Oliveira, D.A.; Worswick, M.J.; Finn, M.; Newman, D. Electromagnetic forming of aluminum alloy sheet: Free-form and cavity fill experiments and model. J. Mater. Process. Technol. 2005, 170, 350–362. [Google Scholar] [CrossRef]
- Imbert, J.M. Increased Formability and the Effects of the Tool/Sheet Interaction in Electromagnetic Forming of Aluminum Alloy Sheet; University of Waterloo: Waterloo, ON, Canda, 2005. [Google Scholar]
- Golovashchenko, S.F. Material Formability and Coil Design in Electromagnetic Forming. J. Mater. Eng. Perform. 2007, 16, 314–320. [Google Scholar] [CrossRef]
- Kamal, M. A Uniform Pressure Electromagnetic Actuator for Forming Flat Sheets; The Ohio State University: Columbus, OH, USA, 2005; p. 261. [Google Scholar]
- Jimbert, P.; Arroyo, A.; Eguia, I.; Fernandez, J.I.; Silveira, E.; Garuz, I.; Daehn, G.S. Efficiency improvement and analysis of changes in microstructure associated to a uniform pressure actuator. In Proceedings of the 2nd International Conference on High Speed Forming, Dortmund, Germany, 20–21 March 2006; pp. 175–186. [Google Scholar]
- Balanethiram, V.S.; Daehn, G.S. Enhanced formability of interstitial free iron at high strain rates. Scr. Metall. Mater. 1992, 27, 1783–1788. [Google Scholar] [CrossRef]
- Balanethiram, V.S.; Daehn, G.S. Hyperplasticity Increased forming limits at high workpice velocity. Scr. Metall. Mater. 1994, 30, 515–520. [Google Scholar] [CrossRef]
- Maris, C. Experimental Determination of the Forming Limits of DP600 and AA5182 Sheets in Electrohydraulic Forming, Department of Mechanical, Automotive & Materials Engineering; University of Windsor: Windsor, ON, Canada, 2014. [Google Scholar]
- Wood, W.W. Experimental mechanics at velocity extremes—Very high strain rates. Exp. Mech. 1967, 19, 441–446. [Google Scholar] [CrossRef]
- Li, F.; Mo, J.; Li, J.; Zhao, J. Formability evaluation for low conductive sheet metal by novel specimen design in electromagnetic forming. Int. J. Adv. Manuf. Technol. 2016, 88, 1677–1685. [Google Scholar] [CrossRef]
- Rohatgi, A.; Soulami, A.; Stephens, E.V.; Davies, R.W.; Smith, M.T. An investigation of enhanced formability in AA5182-O Al during high-rate free-forming at room-temperature: Quantification of deformation history. J. Mater. Process. Technol. 2014, 214, 722–732. [Google Scholar] [CrossRef]
- Maris, C.; Hassannejadasl, A.; Green, D.E.; Cheng, J.; Golovashchenko, S.F.; Gillard, A.J.; Liang, Y. Comparison of quasi-static and electrohydraulic free forming limits for DP600 and AA5182 sheets. J. Mater. Process. Technol. 2016, 235, 206–219. [Google Scholar] [CrossRef]
- Rohatgi, A.; Stephens, E.V.; Davies, R.W.; Smith, M.T.; Soulami, A.; Ahzi, S. Electro-hydraulic forming of sheet metals: Free-forming vs. Conical-die forming. J. Mater. Process. Technol. 2012, 212, 1070–1079. [Google Scholar] [CrossRef]
- Jenab, A.; Green, D.E.; Alpas, A.T. Microscopic investigation of failure mechanisms in AA5182-O sheets subjected to electro-hydraulic forming. Mater. Sci. Eng. A 2017, 691, 31–41. [Google Scholar] [CrossRef]
- Jenab, A.; Green, D.E.; Alpas, A.T.; Golovashchenko, S.F. Experimental and numerical analyses of formability improvement of AA5182-O sheet during electro-hydraulic forming. J. Mater. Process. Technol. 2018, 255, 914–926. [Google Scholar] [CrossRef]
- Hu, X.; Daehn, G.S. Effect of velocity on flow localization in tension. Acta Mater. 1995, 44, 1021–1033. [Google Scholar] [CrossRef]
- Altynova, M.M.; Hu, X.; Daehn, G.S. Increased ductility in high velocity electromagnetic ring expansion. Metall. Mater. Trans. A 1996, 27, 1837–1844. [Google Scholar] [CrossRef]
- Regazzoni, G.; Johnson, J.N.; Follansbee, P.S. Theoretical study of the dynamic in tensile test. J. Appl. Mech. 1986, 53, 519–528. [Google Scholar] [CrossRef]
- Thomas, J.D.; Triantafyllidis, N. Theory of necking localization in unconstrained electromagnetic expansion of thin sheets. Int. J. Sol. Struct. 2007, 44, 6744–6767. [Google Scholar] [CrossRef]
- Marciniak, Z.; Duncan, J.L.; Hu, S.J. Mechanics of Sheet Metal Forming; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Hadianfard, M.J.; Smerd, R.; Winkler, S.; Worswick, M. Effects of strain rate on mechanical properties and failure mechanism of structural Al–Mg alloys. Mater. Sci. Eng. A 2008, 492, 283–292. [Google Scholar] [CrossRef]
- Ferreira, P.J.; Vander Sande, J.B.; Amaral Fortes, M.; Kyrolainen, A. Microstructure development during high-velocity deformation. Metall. Mater. Trans. A 2004, 35A, 3091–3101. [Google Scholar] [CrossRef]
- Ulacia, I.; Dudamell, N.V.; Gálvez, F.; Yi, S.; Pérez-Prado, M.T.; Hurtado, I. Mechanical behavior and microstructural evolution of a Mg AZ31 sheet at dynamic strain rates. Acta Mater. 2010, 58, 2988–2998. [Google Scholar] [CrossRef]
- Li, L.; Muránsky, O.; Flores-Johnson, E.A.; Kabra, S.; Shen, L.; Proust, G. Effects of strain rate on the microstructure evolution and mechanical response of magnesium alloy AZ31. Mater. Sci. Eng. A 2017, 684, 37–46. [Google Scholar] [CrossRef]
- ISO/DIS 12004-2:2008, Metallic Materials—Sheet and Strip—Determination of Forming-Limit Curves—Part 2: Determination of forming-limit curves in the laboratory. Available online: https://www.iso.org/standard/43621.html (accessed on 21 December 2019).
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Dolan, D.H. Accuracy and precision in photonic Doppler Velocimetry. Rev. Sci. Instrum. 2010, 81, 053905. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.R.; Yu, H.P.; Cui, J.; Feng Li, C. Formability of AZ31 magnesium alloy sheets during magnetic pulse bulging. Mater. Sci. Eng. A 2013, 569, 150–158. [Google Scholar]
- Prasol, L. Steigerung des Formänderungsvermögens der Magnesiumlegierung AZ31 bei Raumtemperatur unter Nutzung der Elektromagnetischen Umformung; Technise Universität Berlin: Berlin, Germany, 2016. [Google Scholar]
- Shih-Chieh, L.; Duffy, J. Adiabatic shear bands in a TI-6AI-4V titanium alloy. J. Mech. Phys. Sol. 1998, 46, 2201–2231. [Google Scholar]
- Eyckens, P.; Van Bael, A.; Van Houtte, P. Marciniak–Kuczynski type modelling of the effect of Through-Thickness Shear on the forming limits of sheet metal. Int. J. Plast. 2009, 25, 2249–2268. [Google Scholar] [CrossRef]
- Allwood, J.M.; Shouler, D.R. Generalised forming limit diagrams showing increased forming limits with non-planar stress states. Int. J. Plast. 2009, 25, 1207–1230. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demir, K.; Goyal, S.; Hahn, M.; Tekkaya, E. Novel Approach and Interpretation for the Determination of Electromagnetic Forming Limits. Materials 2020, 13, 4175. https://doi.org/10.3390/ma13184175
Demir K, Goyal S, Hahn M, Tekkaya E. Novel Approach and Interpretation for the Determination of Electromagnetic Forming Limits. Materials. 2020; 13(18):4175. https://doi.org/10.3390/ma13184175
Chicago/Turabian StyleDemir, Koray, Siddhant Goyal, Marlon Hahn, and Erman Tekkaya. 2020. "Novel Approach and Interpretation for the Determination of Electromagnetic Forming Limits" Materials 13, no. 18: 4175. https://doi.org/10.3390/ma13184175
APA StyleDemir, K., Goyal, S., Hahn, M., & Tekkaya, E. (2020). Novel Approach and Interpretation for the Determination of Electromagnetic Forming Limits. Materials, 13(18), 4175. https://doi.org/10.3390/ma13184175




