On the Use of Strain Path Independent Metrics and Critical Distance Rule for Predicting Failure of AA7075-O Stretch-Bend Sheets
Abstract
1. Introduction
2. Experimentation
2.1. Tensile Tests
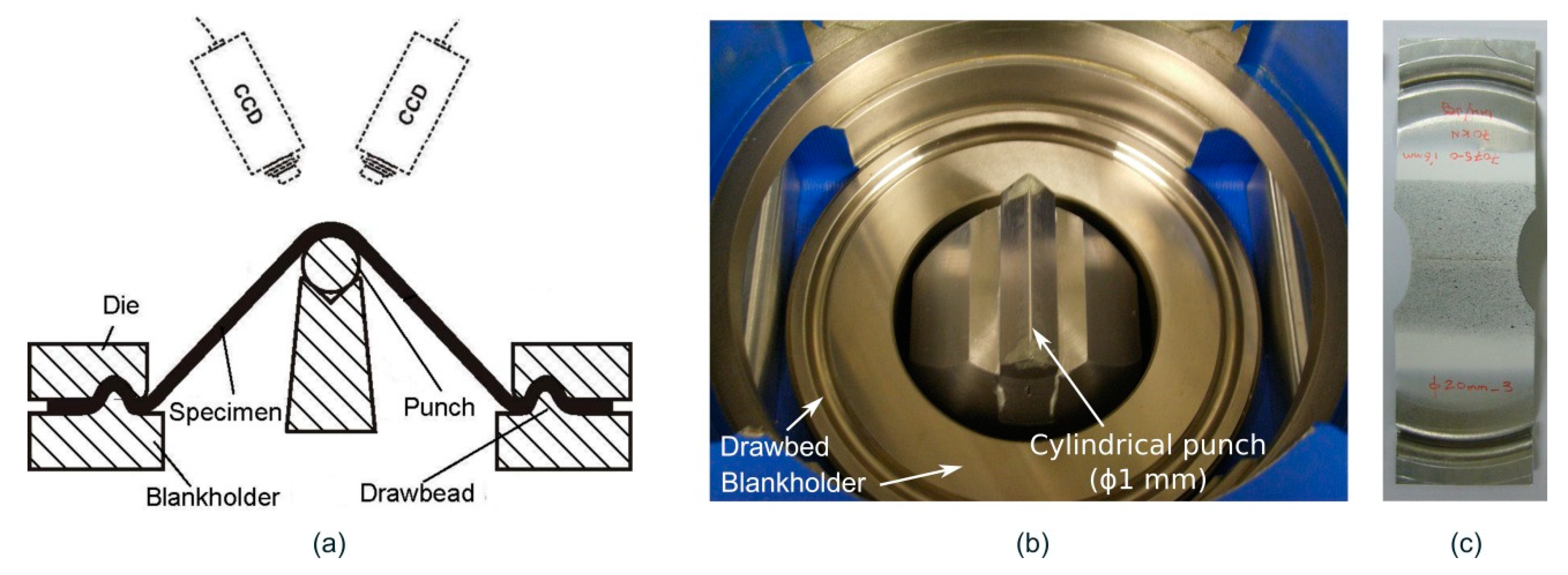
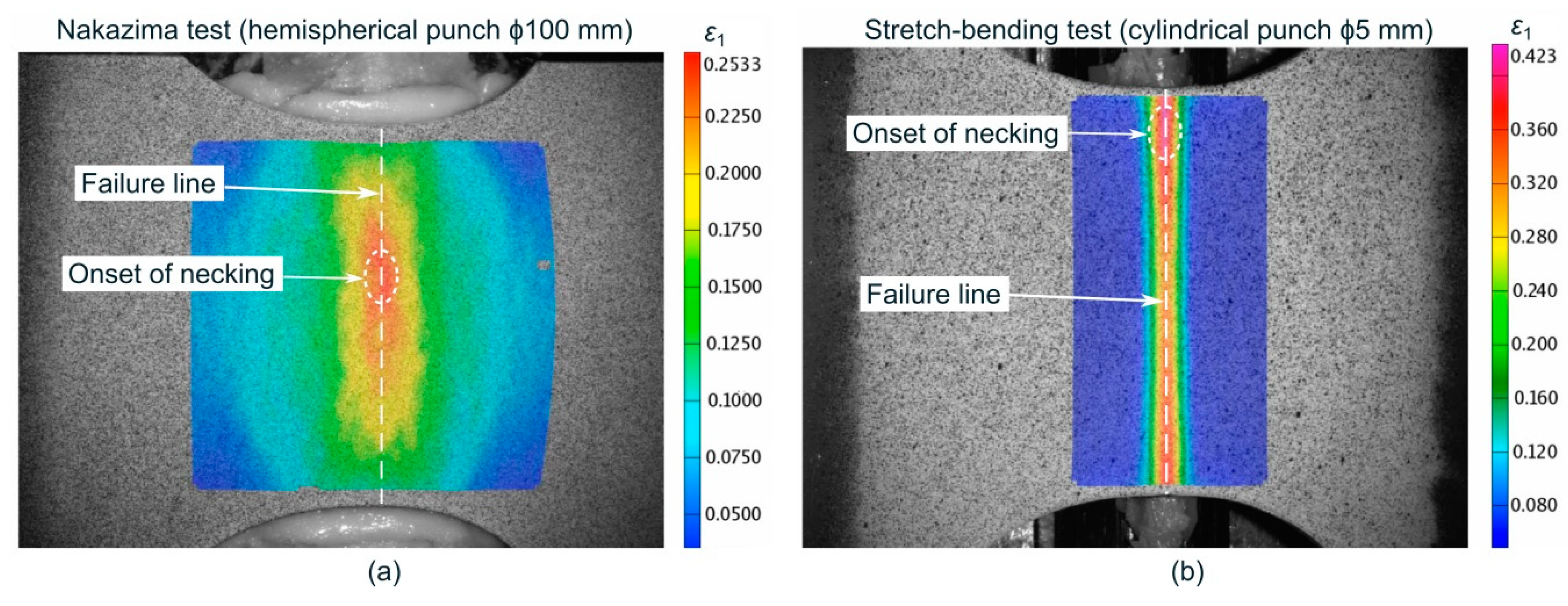
2.2. Nakazima Tests
2.3. Stretch-Bending Tests
3. Numerical Modelling
3.1. Accuracy of the Numerical Simulations
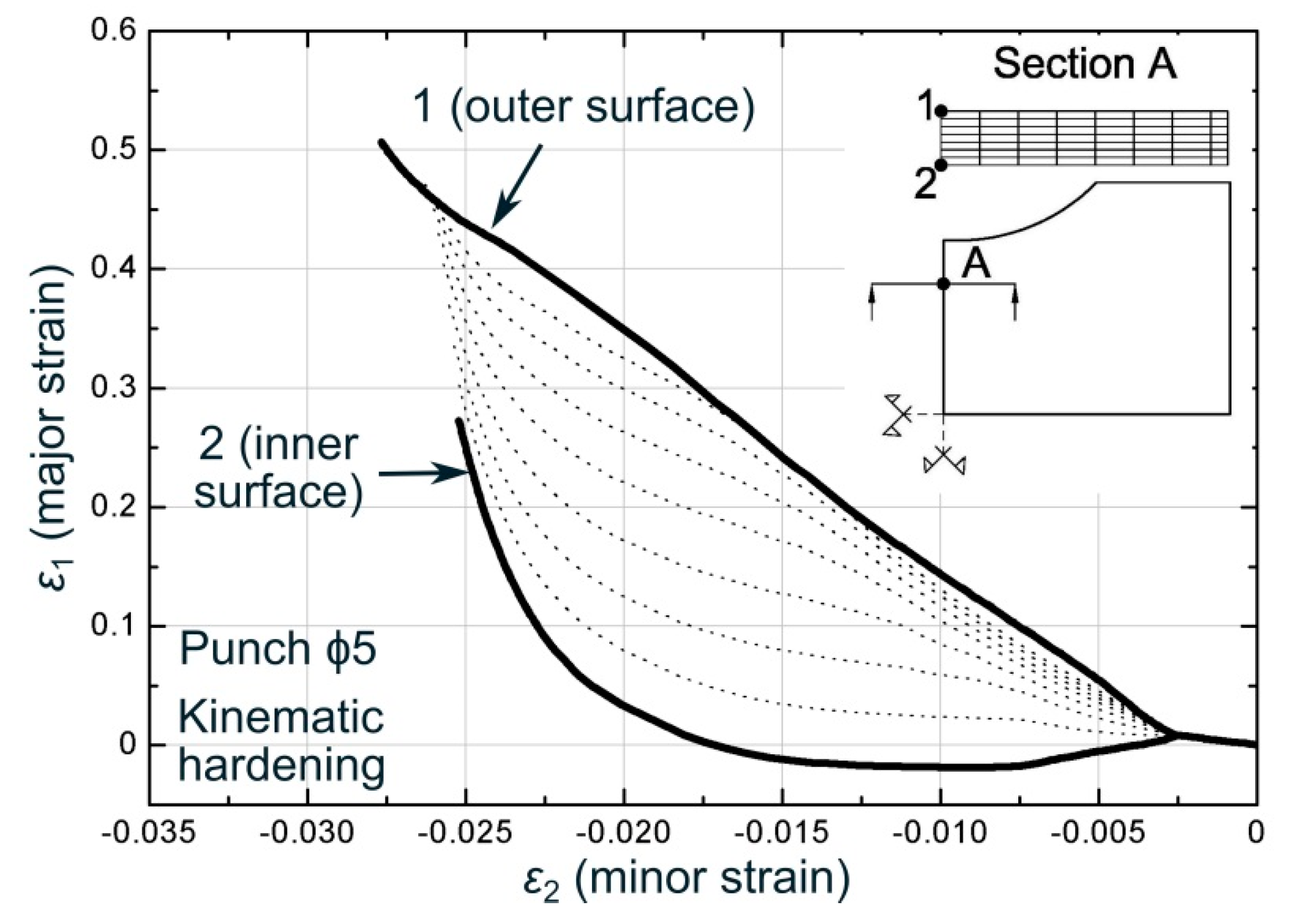
4. Strain Analysis and Failure Model in Stretch-Bending
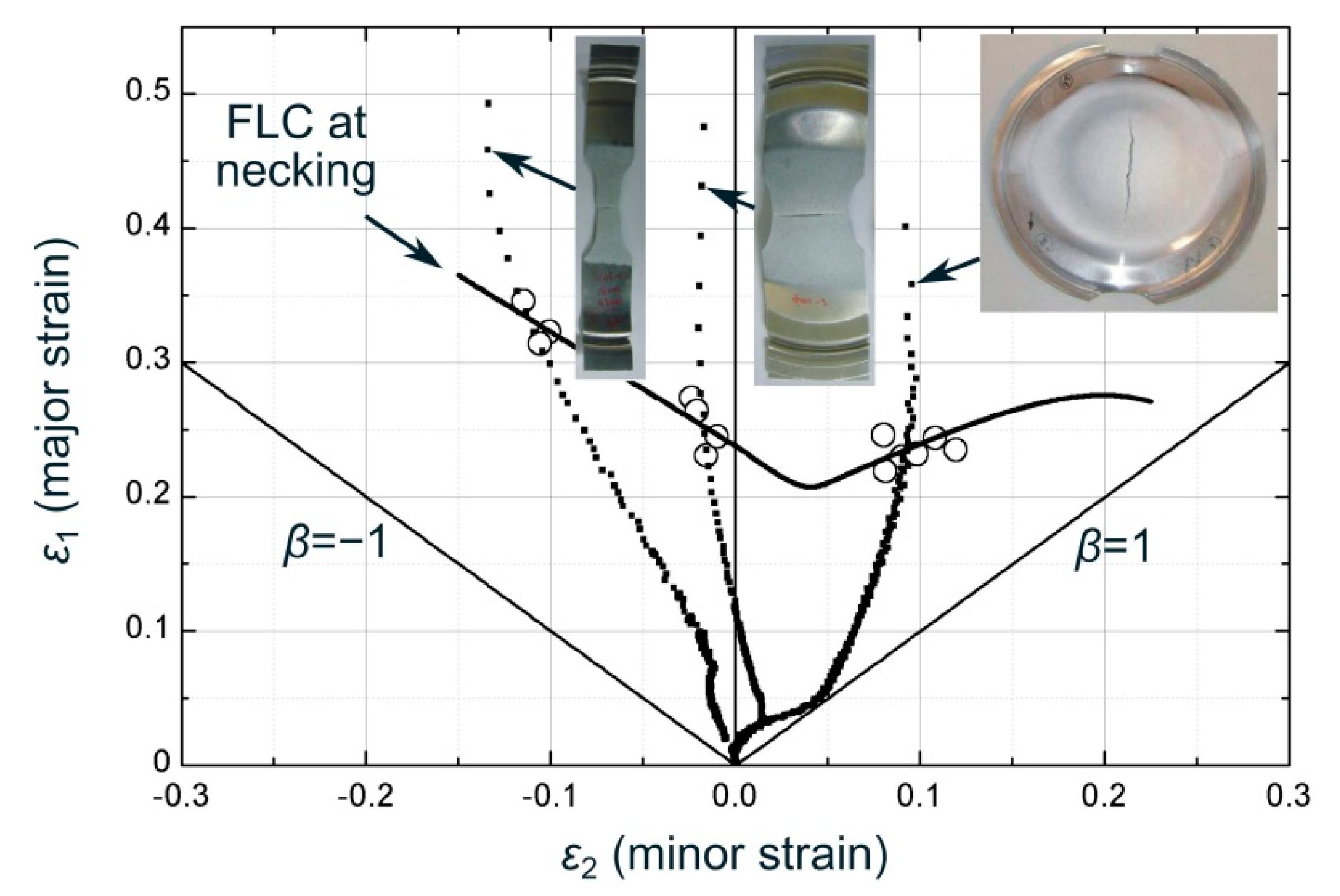
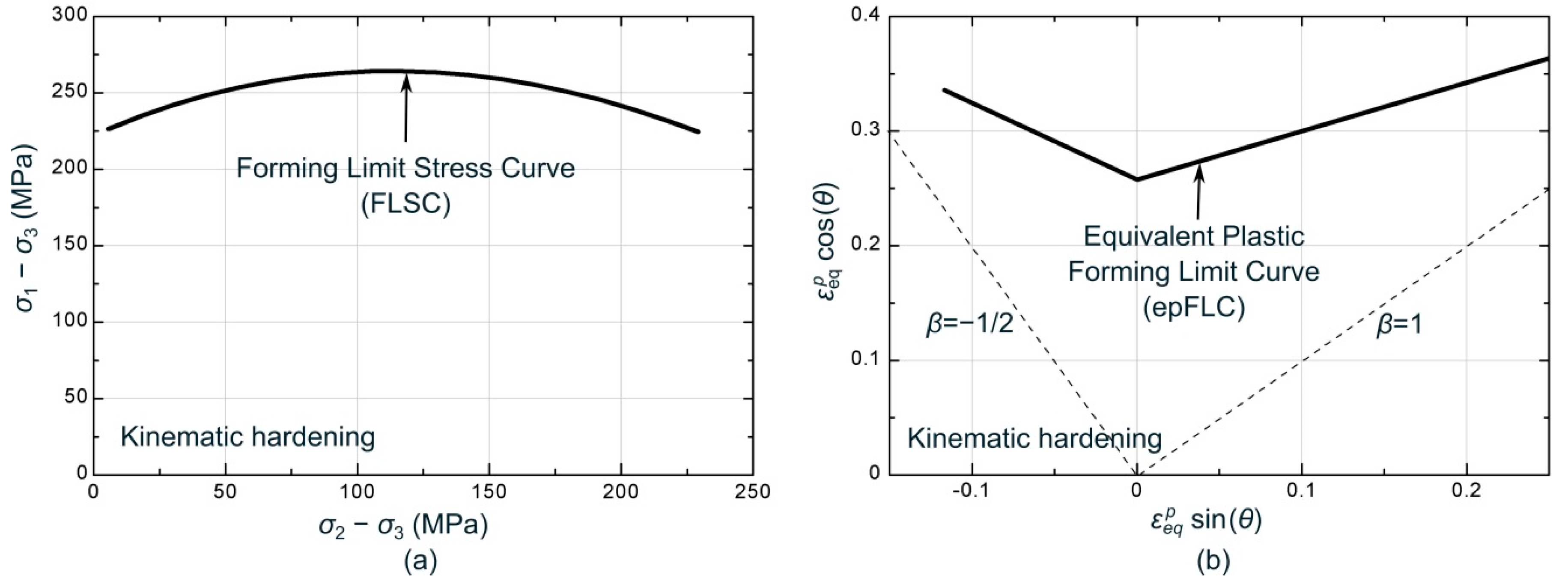
4.1. Construction of the FLSC and epFLC
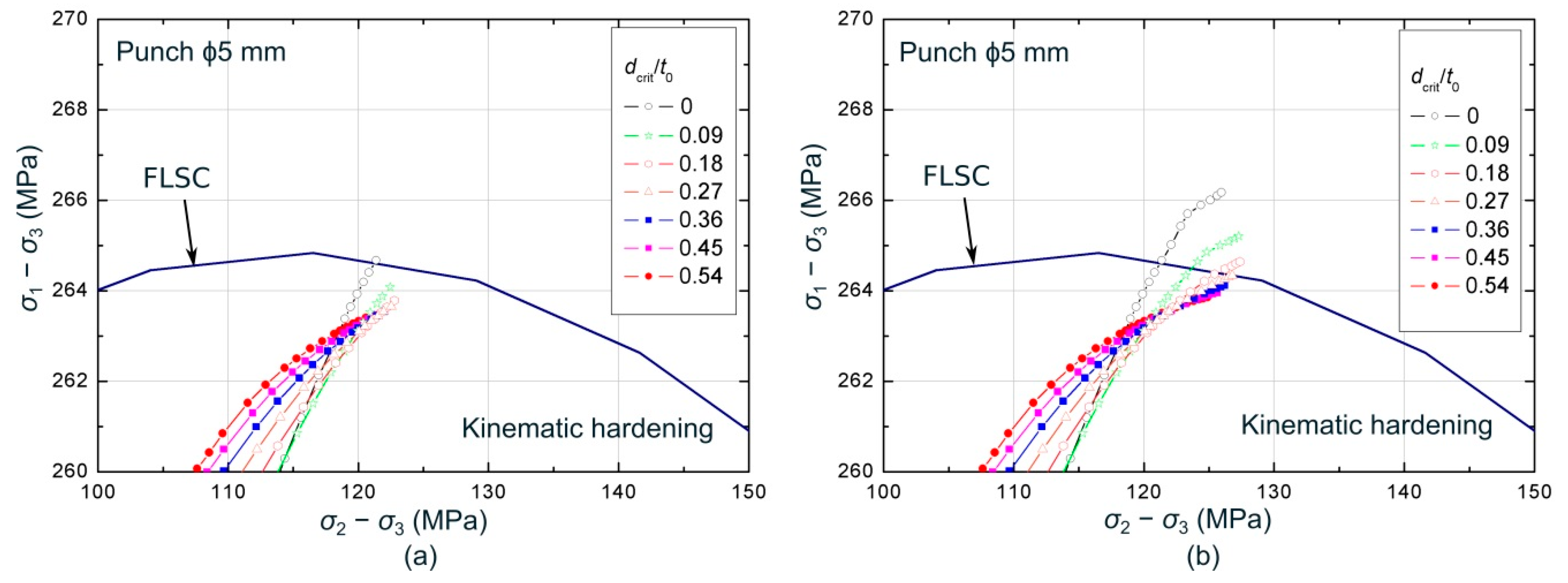
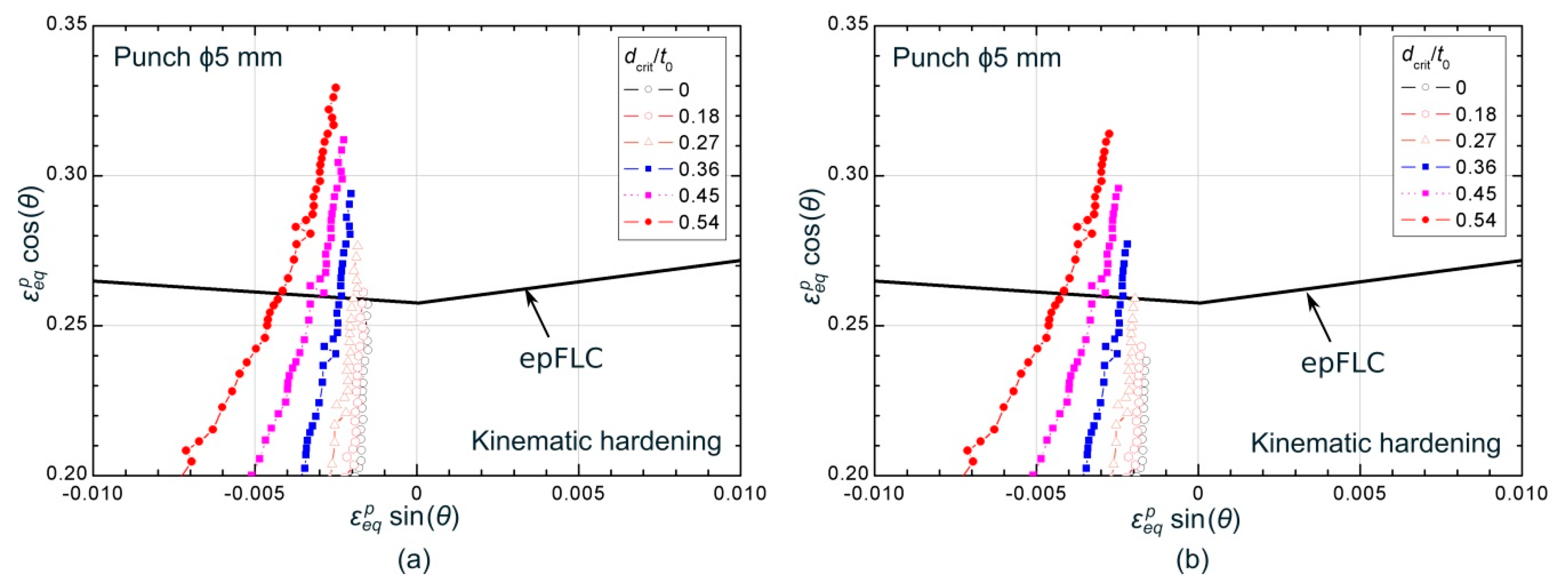
4.2. Failure Prediction Based on the Critical Distance Rule (CDR)
- The first alternative uses the principal stresses, particularly and , as key variables for the sheet failure. Thus, it is postulated that the onset of localized necking begins when the average values of vs. at a certain critical distance (dcrit) intersects the forming limit stress curve, FLSC. Hereafter, this failure model is referred as CDR-FLSC.
- The second variant makes use of the equivalent plastic strain () and the angle of the local strain ratio within the polar diagram, defined by , as key variables. Failure by necking begins when the average values of the equivalent plastic strain within the polar diagram, at a predetermined dcrit, reaches the polar epFLC. In the following, this failure model is named as CDR-epFLC.
5. Results and Discussion
5.1. Analysis of the Averaged Variables at Different Critical Distances within the Path-Independent Spaces
5.2. Failure Prediction under Complex Deformation Histories
6. Conclusions
- The experimental major strains of necking increased with increasing t0/R, up to the ϕ3 mm punch, due to the beneficial effect of bending in the sheet failure. The enhancement of formability was around a 72% when using a ϕ3 mm punch compared to a Nakazima punch.
- The material in a stretch-bending process evolved under a complex deformation history, showing a reversal loading around the inner layers and non-uniform strain/stress distribution across the sheet thickness.
- A little influence of the critical distance into the predictions was observed for the CDR-FLSC model, due to the smooth stress gradient observed as consequence of the Voce-type hardening response exhibited for the AA7075-O sheets. In general, the model provided reasonably good results by using a value of critical distance of half thickness (), i.e., 800 µm.
- The CDR-epFLC approach yielded the best predictions of the sheet formability at a critical distance of around , i.e., 672–800 µm. The beneficial effect of increasing critical distance became crucial for obtaining accurate predictions as the bending effect increased, that is, for the smaller punch radii.
- The results by CDR-epFLC were in better agreement with experimental data than the CDR-FLSC model for the whole range of bending ratio t0/R, except for the ϕ1 mm punch due to indentation issues.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Uko, D.K.; Sowerby, R.; Duncan, J.L. Strain distribution in the bending-under-tension test. CIM Bull. 1977, 70, 127–134. [Google Scholar]
- Keeler, S.P.; Backhofen, W.A. Plastic instability and fracture in sheet stretched over rigid punches. Trans. ASM 1963, 56, 25–48. [Google Scholar]
- ISO 12004-2:2008. Metallic Materials—Sheet and Strip—Determination of Forming-Limit Curves—Part 2: Determination of Forming-Limit curves in the Laboratory; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Dicecco, S.; Butcher, C.; Worswick, M.; Boettcher, E.; Chu, E.; Shi, C. Determination of forming limit diagrams of AA6013-T6 aluminum alloy sheet using a time and position dependent localized necking criterion. IOP Conf. Ser. Mater. Sci. Eng. 2016, 159, 012009. [Google Scholar] [CrossRef]
- Min, J.; Stoughton, T.B.; Carsley, J.E.; Lin, J. Comparison of DIC methods of determining forming limit strains. Procedia Manuf. 2017, 7, 668–674. [Google Scholar] [CrossRef]
- Song, Y.; Green, D.E.; Rose, A. Investigation of various necking criteria for sheet metal formability analysis using digital image strain data. Int. J. Mater. Form. 2019. [Google Scholar] [CrossRef]
- Sun, L.; Cai, Z.; He, D.; Li, L. Aluminum alloy sheet-forming limit curve prediction based on original measured stress-strain data and its application in stretch-forming process. Metals 2019, 9, 1129. [Google Scholar] [CrossRef]
- Jaremenko, C.; Ravikumar, N.; Affronti, E.; Merklein, M.; Maier, A. Determination of forming limits in sheet metal forming using deep learning. Materials 2019, 12, 1051. [Google Scholar] [CrossRef]
- Affronti, E.; Jaremenko, C.; Merklein, M.; Maier, A. Analysis of forming limits in sheet metal forming with pattern recognition methods. Part 1: Characterization of onset of necking and expert evaluation. Materials 2018, 11, 1495. [Google Scholar] [CrossRef] [PubMed]
- Jaremenko, C.; Affronti, E.; Maier, A.; Merklein, M. Analysis of forming limits in sheet metal forming with pattern recognition methods. Part 2: Unsupervised methodology and application. Materials 2018, 11, 1892. [Google Scholar] [CrossRef] [PubMed]
- Kleemola, H.J.; Pelkkikangas, M.T. Effect of predeformation and strain path on the forming limits of steel, copper and brass. Sheet Metal. Ind. 1977, 63, 591–599. [Google Scholar]
- Borrego, M.; Morales-Palma, D.; Martínez-Donaire, A.J.; Centeno, G.; Vallellano, C. Analysis of formability in conventional hole flanging of AA7075-O sheets: Punch edge radius effect and limitations of the FLC. Int. J. Mater. Form. 2019, 13, 303–316. [Google Scholar] [CrossRef]
- Charpentier, P. Influence of punch curvature on the stretching limits of sheet steel. Met. Mater. Trans. A 1975, 6, 1665–1669. [Google Scholar] [CrossRef]
- Raghavan, K.S. A simple technique to generate in-plane forming limit curves and selected applications. Met. Mater. Trans. A 1995, 26, 2075–2084. [Google Scholar] [CrossRef]
- Moshksar, M.M.; Mansorzadeh, S. Determination of the forming limit diagram for Al 31055 sheet. J. Mater. Process. Tech. 2003, 141, 138–142. [Google Scholar] [CrossRef]
- Fictorie, E.; Van den Boogaard, A.H.; Atzema, E.H. Influence of punch radius in a Nakazima test for mild steel and aluminium. Int. J. Mater. Form. 2010, 3, 1179–1182. [Google Scholar] [CrossRef]
- Affronti, E.; Merklein, M. Analysis of the bending effects and the biaxial pre-straining in sheet metal stretch forming processes for the determination of the forming limits. Int. J. Mech. Sci. 2018, 138, 295–309. [Google Scholar] [CrossRef]
- Neuhauser, F.M.; Terrazas, O.R.; Manopulo, N.; Hora, P.; Van Tyne, C.J. Stretch bending—The plane within the sheet where strains reach the forming limit curve. IOP Conf. Ser. Mater. Sci. Eng. 2016, 159, 012011. [Google Scholar] [CrossRef]
- Neuhauser, F.M.; Terrazas, O.; Manopulo, N.; Hora, P.; Van Tyne, C. The bending dependency of forming limit diagrams. Int. J. Mater. Form. 2019, 12, 815–825. [Google Scholar] [CrossRef]
- Tharrett, M.R.; Stoughton, T.B. Stretch-Bend Forming Limits of 1008 AK Steel; No. 2003-01-1157; SAE Paper: New York, NY, USA, 2003. [Google Scholar]
- Kitting, D.; Koplenig, M.; Ofenheimer, A.; Pauli, H.; Till, E.T. Application of a “concave-side rule” approach for assessing formability of stretch-bent steel sheets. Int. J. Mater. Form. 2009, 2, 427–430. [Google Scholar] [CrossRef]
- Martínez-Donaire, A.J.; Vallellano, C.; Morales-Palma, D.; García-Lomas, F.J. Experimental and numerical analysis of the failure of AA7075-O stretch-bend sheets. Steel Res. Int. 2012, 251–254. [Google Scholar]
- Martínez-Donaire, A.J.; Martínez-Palmeth, L.H.; Borrego, M.; Morales-Palma, D.; Vallellano, C. Analysis of the failure of H240LA steel sheets subjected to strecth-bending conditions. Proc. Manuf. 2019, 41, 626–633. [Google Scholar]
- Wu, J.; Zhou, D.; Zhang, L.; Zhou, Y.J.; Du, C.Q.; Shi, M.F. A failure criterion for stretch bendability of advanced high-strength steels. SAE Trans. 2006, 115, 311–319. [Google Scholar]
- Sadagopan, S.; Wong, C.; Huang, M.; Yan, B. Stretch bendability of advanced high-strength steels. SAE Paper 2003. [Google Scholar] [CrossRef]
- Vallellano, C.; Morales-Palma, D.; Martínez-Donaire, A.J.; García-Lomas, F.J. On the use of Concave-Side Rule and Critical-Distance Methods to predict the influence of bending on sheet-metal formability. Int. J. Mater. Form. 2010, 3, 1167–1170. [Google Scholar] [CrossRef]
- Taylor, D. The Theory of Critical Distances: A New Perspective in Fracture Mechanics; Elsevier Science: Oxford, UK, 2007. [Google Scholar]
- Morales-Palma, D.; Vallellano, C.; García-Lomas, F.J. Assessment of the effect of the through-thickness strain/stress gradient on the formability of stretch-bend metal sheets. Mater. Des. 2013, 50, 798–809. [Google Scholar] [CrossRef]
- Morales-Palma, D.; Martínez-Donaire, A.J.; Vallellano, C. On the use of maximum force criteria to predict localised necking in metal sheets under stretch-bending. Metals 2017, 7, 469. [Google Scholar] [CrossRef]
- Martínez-Palmeth, L.H.; Martínez-Donaire, A.J.; Vallellano, C. Formability limits of high-strength H240LA steel sheets under stress/strain gradients. Mech. Mater. 2019, 132, 47–56. [Google Scholar] [CrossRef]
- Graf, A.F.; Hosford, W.F. Effect of changing strain paths on forming limit diagrams of Al 2008-T4. Met. Trans. A 1993, 24, 2503–2512. [Google Scholar] [CrossRef]
- Arrieux, R. Determination of the forming limit stress curve for anisotropic sheets. Ann. CIRP 1987, 36, 195–198. [Google Scholar] [CrossRef]
- Arrieux, R. Determination and use of the forming limit stress diagrams in sheet metal forming. J. Mater. Process. Technol. 1995, 53, 47–56. [Google Scholar] [CrossRef]
- Stoughton, T.B. A general forming limit criterion for sheet metal forming. Int. J. Mech. Sci. 2000, 42, 1–27. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. A new approach for failure criterion for sheet metals. Int. J. Plast. 2011, 27, 440–459. [Google Scholar] [CrossRef]
- Bandyopadhyay, K.; Basak, S.; Panda, S.K.; Saha, P. Use of stress based forming limit diagram to predict formability in two-stage forming of tailor welded blanks. Mater. Des. 2015, 67, 558–570. [Google Scholar] [CrossRef]
- Panich, S.; Liewald, M.; Uthaisangsuk, V. Stress and strain based fracture forming limit curves for advanced high strength steel sheet. Int. J. Mater. Form. 2018, 11, 643–661. [Google Scholar] [CrossRef]
- Hakoyama, C.S.; Hakoyama, T.; Fukiharu, H.; Kuwabara, T. Fracture prediction for mild steel sheet and high-strength steel sheet subjected to draw bending using forming limit stress criterion. J. Mater. Process. Technol. 2019, 116313. [Google Scholar] [CrossRef]
- Huang, T.; Zhan, M.; Wang, K.; Chen, F.; Guo, J.; Li, Y.; Song, Z.; Bai, L. Forming limit stress diagram prediction of pure titanium sheet based on GTN model. Materials 2019, 12, 1783. [Google Scholar] [CrossRef]
- Yoshida, K.; Kuwabara, T. Effect of strain hardening behaviour on forming limit stresses of steel tube subjected to non proportional loading paths. Int. J. Plast. 2007, 23, 1260–1284. [Google Scholar] [CrossRef]
- Simha, C.H.M.; Gholipour, J.; Bardelcik, A.; Worswick, M.J. Prediction of necking in tubular hydroforming using an extended stress-based forming limit curve. J. Eng. Mater. Technol. 2007, 129, 36–47. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. Path independent forming limits in strain and stress spaces. Int. J. Solids Struct. 2012, 49, 3616–3625. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Lee, E.; Lee, M.G.; Kim, H.J.; Kim, H.Y. Hydroformability assessment of AA6063 tubes using the polar effective plastic strain diagram. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 647–653. [Google Scholar] [CrossRef]
- ASTM E8/E8M-08. Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM E132-04. Standard Test Method for Poisson’s Ratio at Room Temperature; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- ASTM E517-00. Standard Test Method for Plastic Strain Ratio r for Sheet Metal; ASTM International: West Conshohocken, PA, USA, 2000. [Google Scholar]
- Vacher, P.; Haddad, A.; Arrieux, R. Determination of the forming limit diagrams using image analysis by the correlation method. CIRP Ann. Manuf. Tech. 1999, 48, 227–230. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 1–17. [Google Scholar] [CrossRef]
- Orteu, J.J. 3-D computer vision in experimental mechanics. Opt. Lasers Eng. 2009, 47, 282–291. [Google Scholar] [CrossRef]
- Jin, T.L.; Ha, N.S.; Goo, N.S. A study of the thermal buckling behavior of a circular aluminum plate using the digital image correlation technique and finite element analysis. Thin-Walled Struct. 2014, 77, 187–197. [Google Scholar] [CrossRef]
- Martínez-Palmeth, L.H.; Martínez-Donaire, A.J.; Centeno, G.; García-Lomas, F.J.; Vallellano, C. Formability of automotive H240LA steel sheets in stretch-bending processes. Procedia Eng. 2013, 63, 669–677. [Google Scholar] [CrossRef][Green Version]
- Gorszczyk, J.; Malicki, K.; Zych, T. Application of digital image correlation (DIC) method for road material testing. Materials 2019, 12, 2349. [Google Scholar] [CrossRef]
- Mora-Macías, J.; Ayensa-Jiménez, J.; Reina-Romo, E.; Doweidar, M.H.; Domínguez, J.; Doblaré, M.; Sanz-Herrera, J.A. A multiscale data-driven approach for bone tissue biomechanics. Comput. Methods Appl. Mech. Eng. 2020, 368, 113136. [Google Scholar] [CrossRef]
- Jain, M.; Lloyd, D.J.; MacEwen, S.R. Hardening laws, surface roughness and biaxial tensile limit strains of sheet aluminium alloys. Int. J. Mech. Sci. 1996, 38, 219–232. [Google Scholar] [CrossRef]
- Butuc, M.C.; Gracio, J.J.; Barata da Rocha, A. Theoretical study on forming limit diagrams prediction. J. Mater. Process. Technol. 2003, 142, 714–724. [Google Scholar] [CrossRef]
- Li, J.; Carsley, J.E.; Stoughton, T.B.; Hector, L.G.; Hu, S.J. Forming limit analysis for two-stage forming of 5182-O aluminum sheet with intermediate annealing. Int. J. Plast. 2013, 45, 21–43. [Google Scholar] [CrossRef]
- Martínez-Donaire, A.J.; Vallellano, C.; Morales, D.; García-Lomas, F.J. Experimental detection of necking in stretch-bending conditions, a critical review and new methodology. Steel Res. Int. 2010, 81, 785–788. [Google Scholar]
- Martínez-Donaire, A.J.; García-Lomas, F.J.; Vallellano, C. New approaches to detect the onset of localised necking in sheets under through-thickness strain gradients. Mater. Des. 2014, 57, 135–145. [Google Scholar] [CrossRef]
- Silva, M.B.; Martínez-Donaire, A.J.; Centeno, G.; Morales-Palma, D.; Vallellano, C.; Martins, P.A.F. Recent approaches for the determination of forming limits by necking and fracture in sheet metal forming. Procedia Eng. 2015, 132, 342–349. [Google Scholar] [CrossRef]
- Centeno, G.; Martínez-Donaire, A.J.; Morales-Palma, D.; Vallellano, C.; Silva, M.B.; Martins, P.A.F. Novel experimental techniques for the determination of the forming limits at necking and fracture. In Materials Forming and Machining: Research and Development, 1st ed.; Davim, J.P., Ed.; Woodhead Publishing: Cambridge, UK, 2016; pp. 1–24. [Google Scholar]
- Martínez-Donaire, A.J. Análisis del Efecto del Gradiente de Deformaciones en el Conformado de Chapas Metálica. Ph.D. Thesis, University of Seville, Seville, Spain, August 2012. [Google Scholar]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic metals. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Habraken, F.A.C.M.; Dautzenberg, J.H. Some applications of the Barlat 1991 yield criterion. CIRP Ann. Manuf. Technol. 1995, 44, 185–188. [Google Scholar] [CrossRef]
- Barlat, F.; Becker, R.C.; Hayashida, Y.; Maeda, Y.; Yanagawa, M.; Chung, K.; Brem, J.C.; Lege, D.J.; Matsui, K.; Murtha, S.J.; et al. Yielding description for solution strengthened aluminum alloys. Int. J. Plast. 1997, 13, 385–401. [Google Scholar] [CrossRef]
- Wu, P.D.; Jain, M.; Savoie, J.; MacEwen, S.R.; Tuğcu, P.; Neale, K.W. Evaluation of anisotropic yield functions for aluminum sheets. Int. J. Plast. 2003, 19, 121–138. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, J.; Chen, J.; Zhu, X. Forming limits model evaluation for anisotropic sheet metals under through-thickness normal stress. Int. J. Mech. Sci. 2014, 89, 40–46. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G.; Xiang, X. High energy absorption efficiency of thin-walled conical corrugation tubes mimicking coconut tree configuration. Int. J. Mech. Sci. 2018, 148, 409–421. [Google Scholar] [CrossRef]
- Vallellano, C.; Morales-Palma, D.; García-Lomas, F.J. A study to predict failure in biaxially stretched sheets of aluminum alloy 2024-T3. Mater. Manuf. Process. 2008, 23, 303–310. [Google Scholar] [CrossRef]
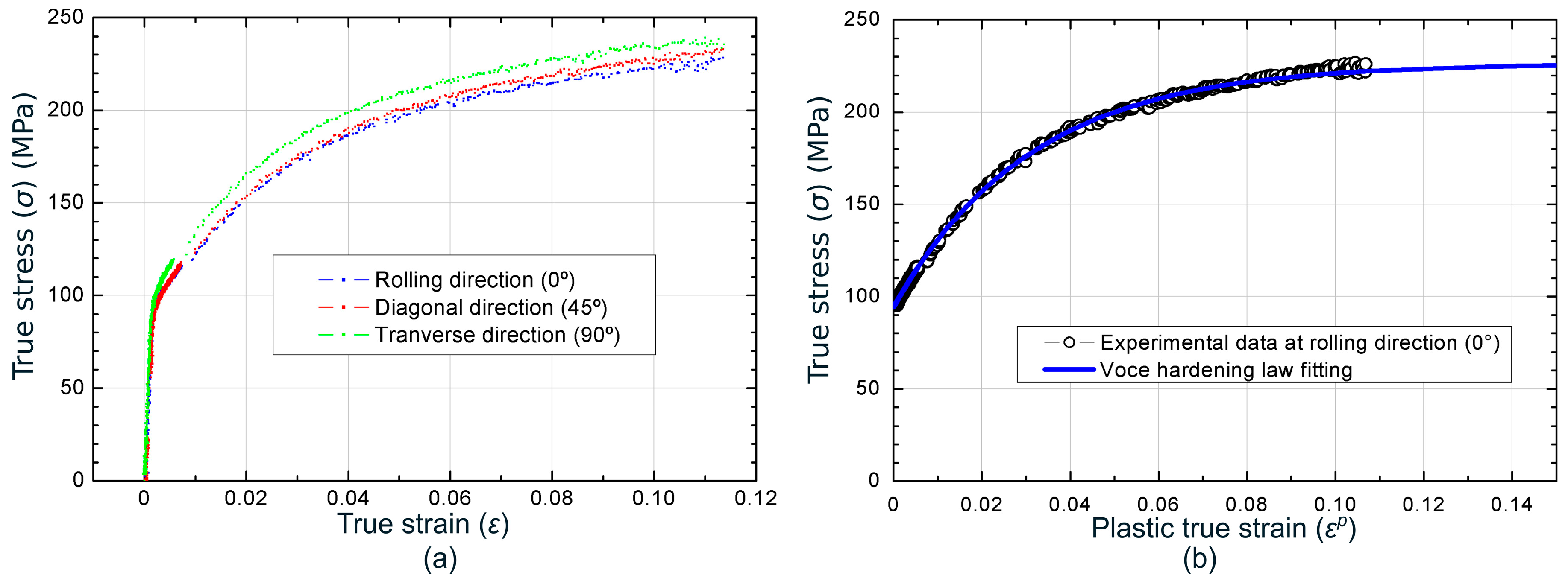
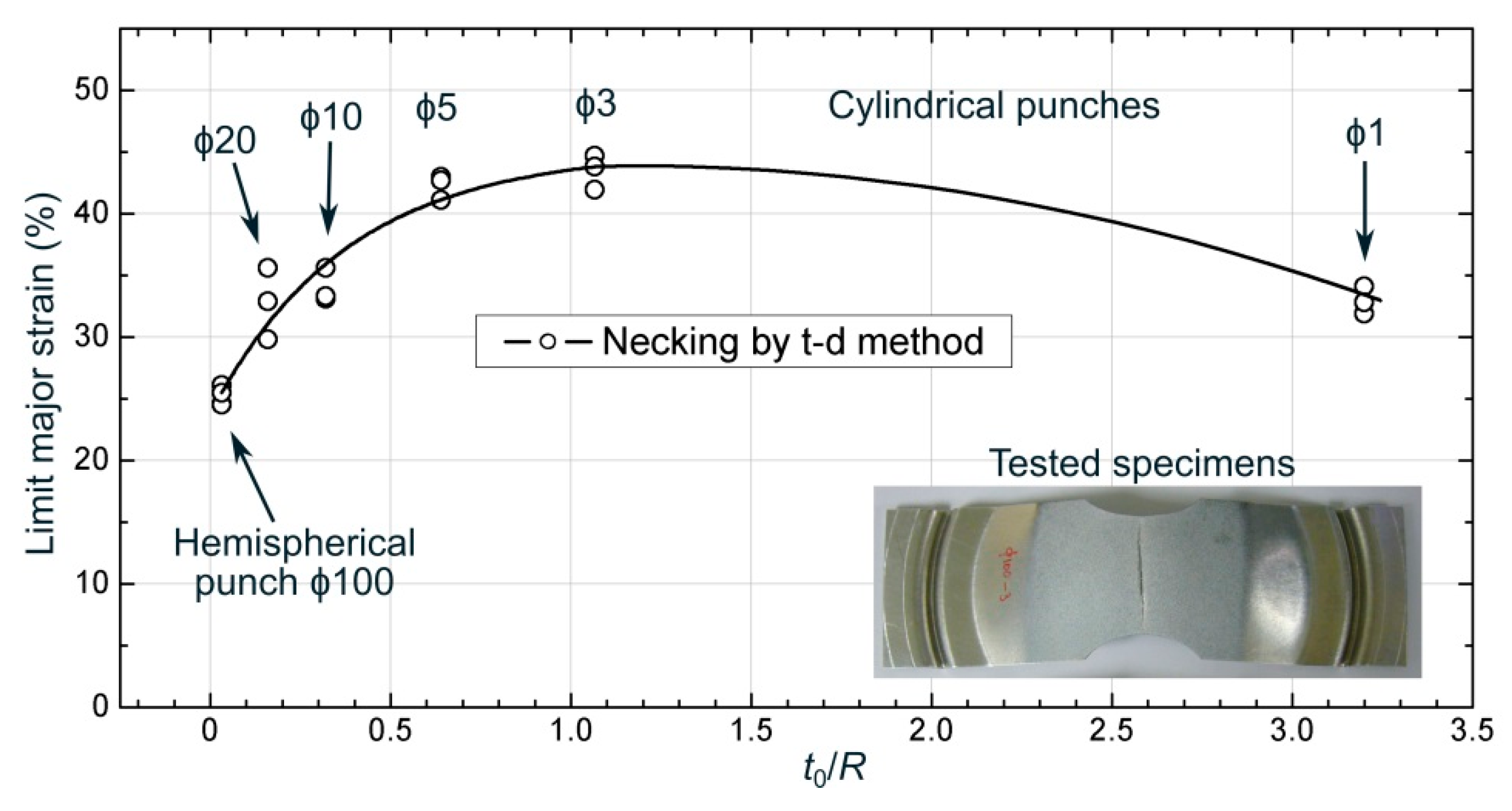

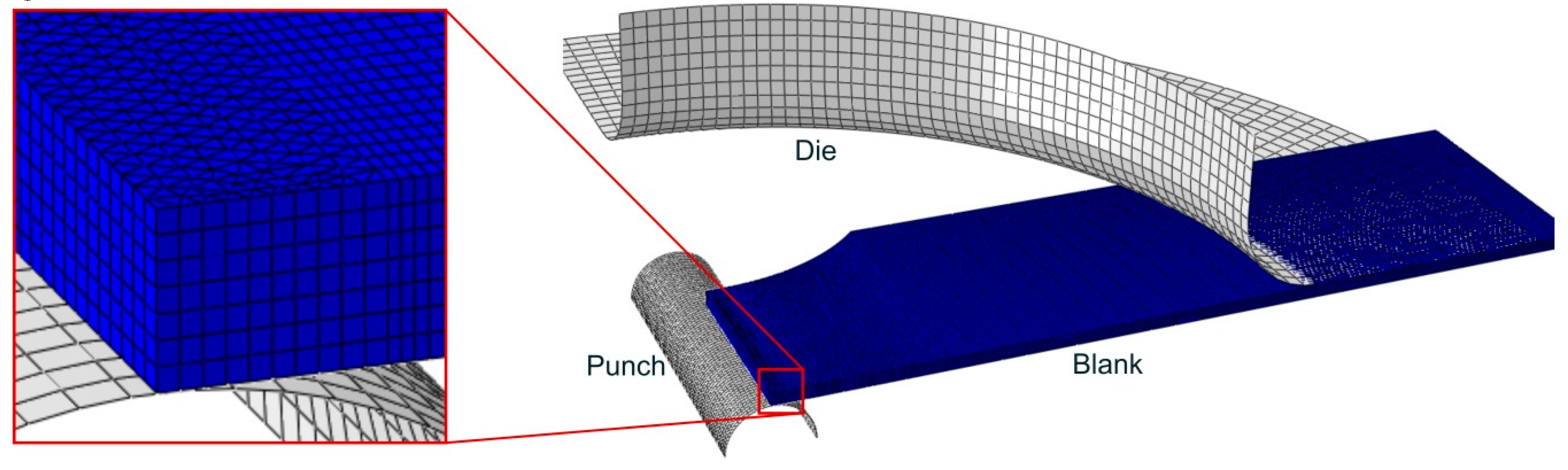
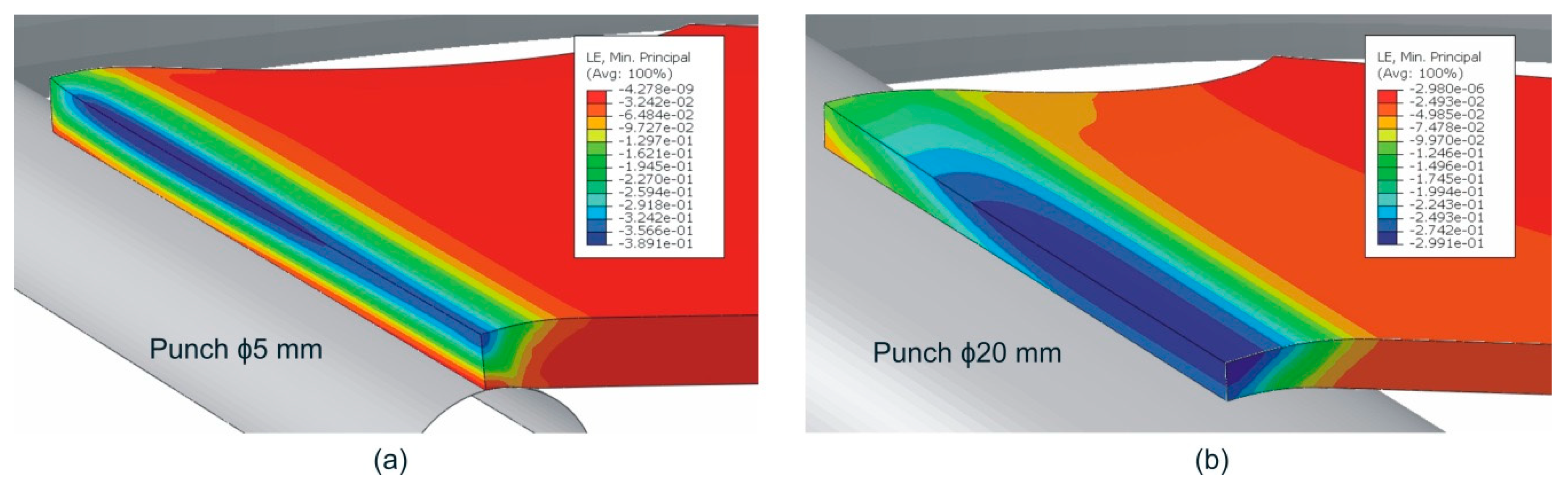
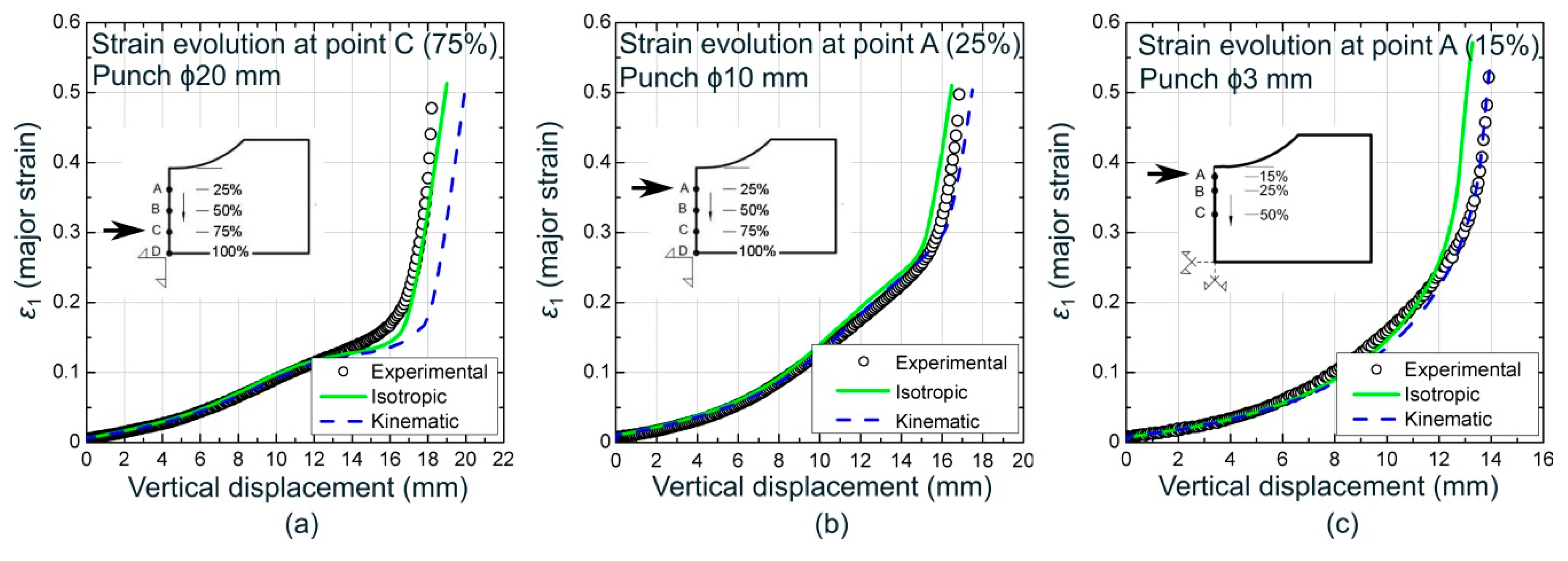


| Orientation | E (GPa) | ν | σY, 0.2% (MPa) | UTS (MPa) | eu | r |
|---|---|---|---|---|---|---|
| Rolling (0°) | 68.1 | 0.3 | 102.3 | 203.0 | 0.149 | 0.812 |
| Diagonal (45°) | 68.1 | 0.3 | 102.4 | 208.0 | 0.178 | 1.394 |
| Transverse (90°) | 69.4 | 0.3 | 107.4 | 213.0 | 0.163 | 1.317 |
| C1 | C2 | C3 | C4 | C5 | C6 | m |
|---|---|---|---|---|---|---|
| 0.926 | 1.021 | 0.978 | 1 | 1 | 1.007 | 8 |
| (a) | ||||||||
| Experimental Data (mean) | ||||||||
| ϕ (mm) | t0/R | % Error* | % Error* | |||||
| 20 | 0.16 | 0.328 | 0.211 | −35.67 | 0.232 | −29.27 | ||
| 10 | 0.32 | 0.340 | 0.313 | −7.94 | 0.365 | 7.35 | ||
| 5 | 0.64 | 0.423 | 0.442 | 4.49 | 0.471 | 11.35 | ||
| 3 | 1.07 | 0.435 | 0.474 | 8.97 | 0.486 | 11.72 | ||
| 1 | 3.2 | 0.329 | 0.330 | 0.30 | 0.303 | −7.90 | ||
| (b) | ||||||||
| Experim. Data (mean) | Numerical CDR-epFLC | Numerical CDR-epFLC | Numerical CDR-epFLC | |||||
| ϕ (mm) | t0/R | % Error* | % Error* | % Error* | ||||
| 20 | 0.16 | 0.328 | 0.291 | −11.28 | 0.286 | −12.80 | 0.286 | −12.80 |
| 10 | 0.32 | 0.340 | 0.369 | 8.53 | 0.357 | 5.00 | 0.353 | 3.82 |
| 5 | 0.64 | 0.423 | 0.471 | 11.35 | 0.450 | 6.38 | 0.443 | 4.73 |
| 3 | 1.07 | 0.435 | 0.532 | 22.30 | 0.445 | 2.30 | 0.413 | −5.06 |
| 1 | 3.2 | 0.329 | 0.314 | −4.56 | 0.258 | −21.58 | 0.249 | −24.32 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Donaire, A.J.; Morales-Palma, D.; Vallellano, C. On the Use of Strain Path Independent Metrics and Critical Distance Rule for Predicting Failure of AA7075-O Stretch-Bend Sheets. Materials 2020, 13, 3660. https://doi.org/10.3390/ma13173660
Martínez-Donaire AJ, Morales-Palma D, Vallellano C. On the Use of Strain Path Independent Metrics and Critical Distance Rule for Predicting Failure of AA7075-O Stretch-Bend Sheets. Materials. 2020; 13(17):3660. https://doi.org/10.3390/ma13173660
Chicago/Turabian StyleMartínez-Donaire, Andrés Jesús, Domingo Morales-Palma, and Carpóforo Vallellano. 2020. "On the Use of Strain Path Independent Metrics and Critical Distance Rule for Predicting Failure of AA7075-O Stretch-Bend Sheets" Materials 13, no. 17: 3660. https://doi.org/10.3390/ma13173660
APA StyleMartínez-Donaire, A. J., Morales-Palma, D., & Vallellano, C. (2020). On the Use of Strain Path Independent Metrics and Critical Distance Rule for Predicting Failure of AA7075-O Stretch-Bend Sheets. Materials, 13(17), 3660. https://doi.org/10.3390/ma13173660







