Plasticity and Formability of Annealed, Commercially-Pure Aluminum: Experiments and Modeling
Abstract
1. Introduction
2. Plastic Anisotropy
2.1. Material
2.2. Experiments
2.2.1. Uniaxial Tension
2.2.2. Plane-Strain Tension
2.2.3. Disk Compression
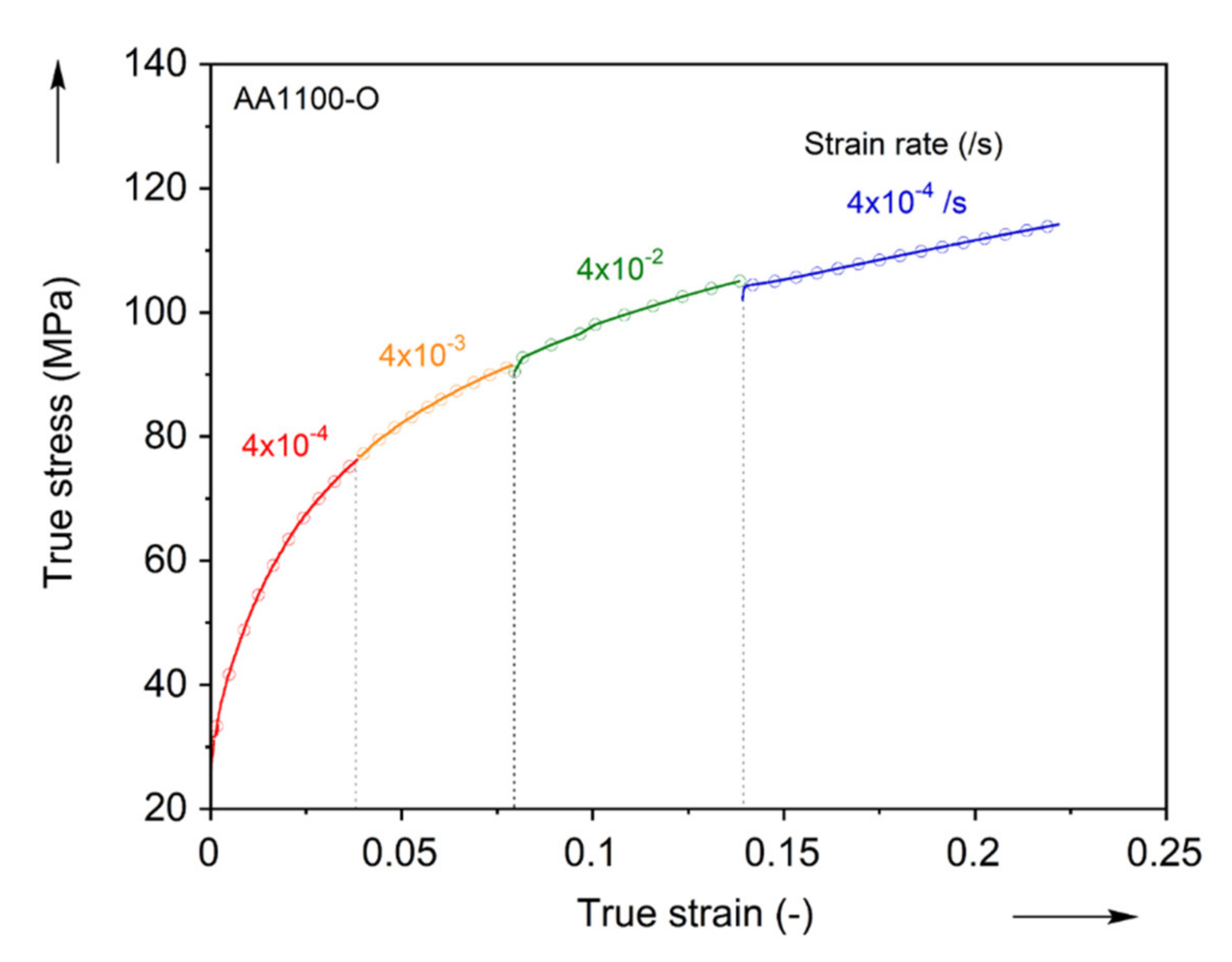
2.2.4. Strain-Rate Sensitivity
2.3. Material Modeling for Plasticity
2.3.1. Anisotropic Yield Function
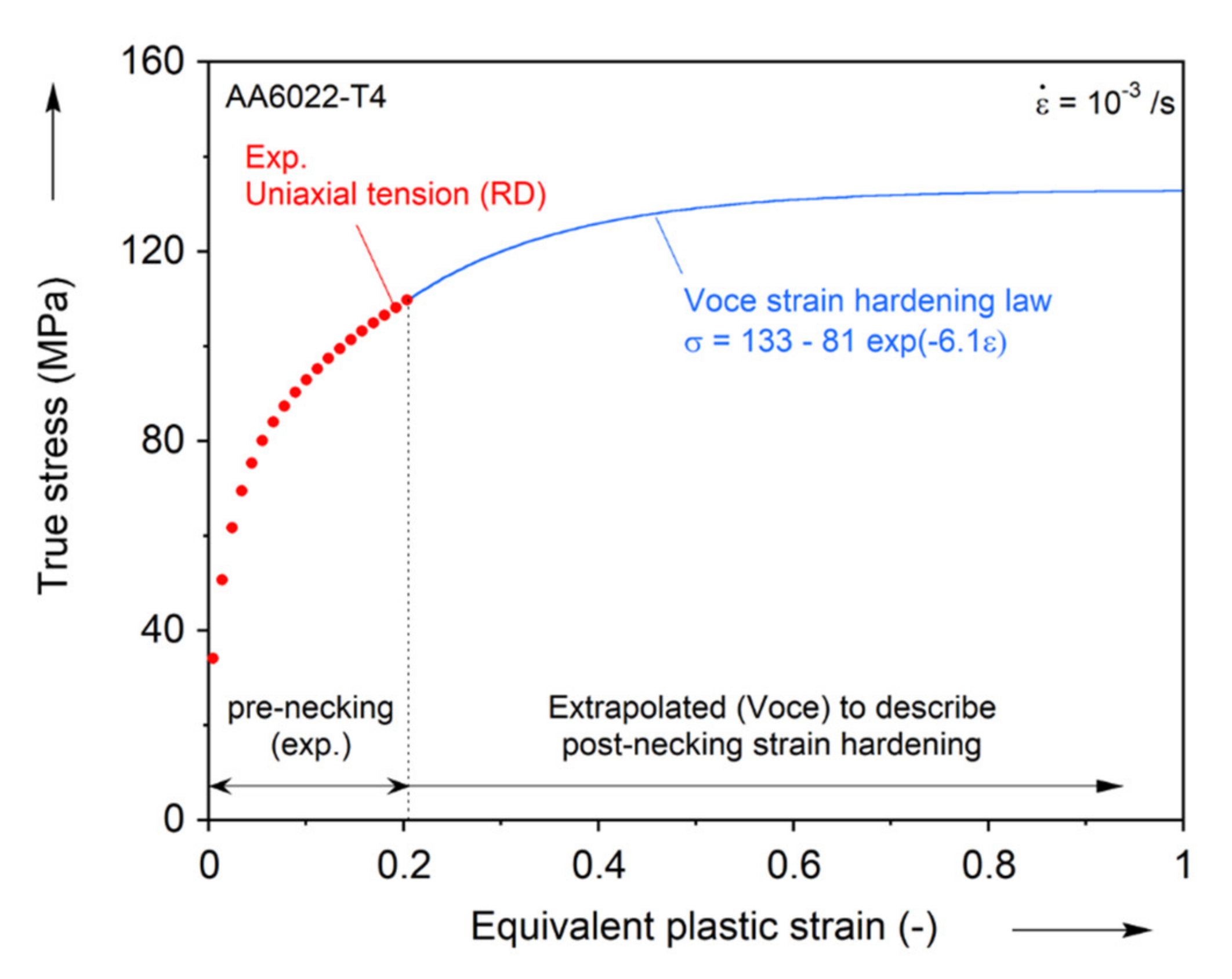
2.3.2. Strain Hardening Law
3. Formability
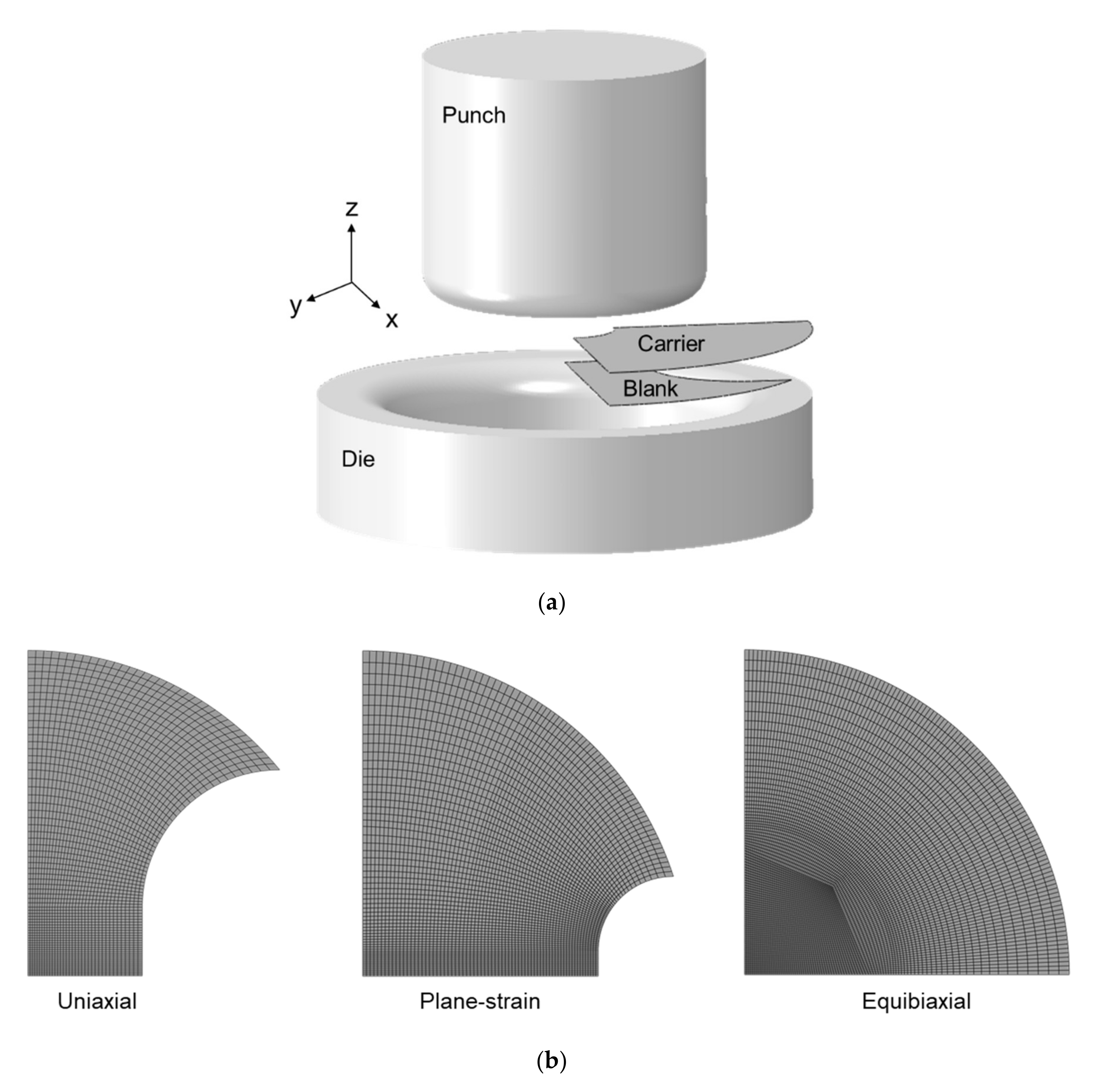
3.1. Experimental Set-Up
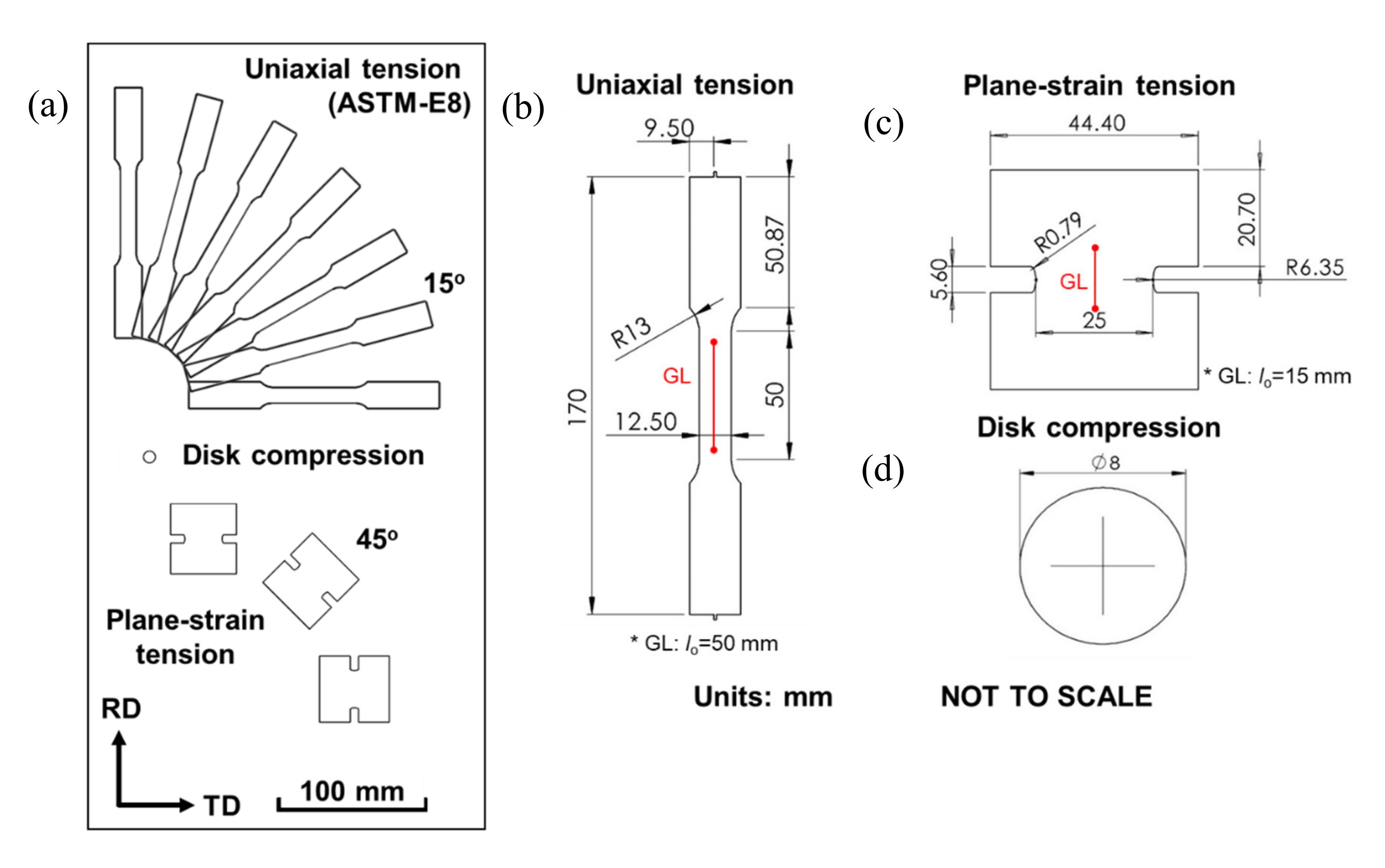
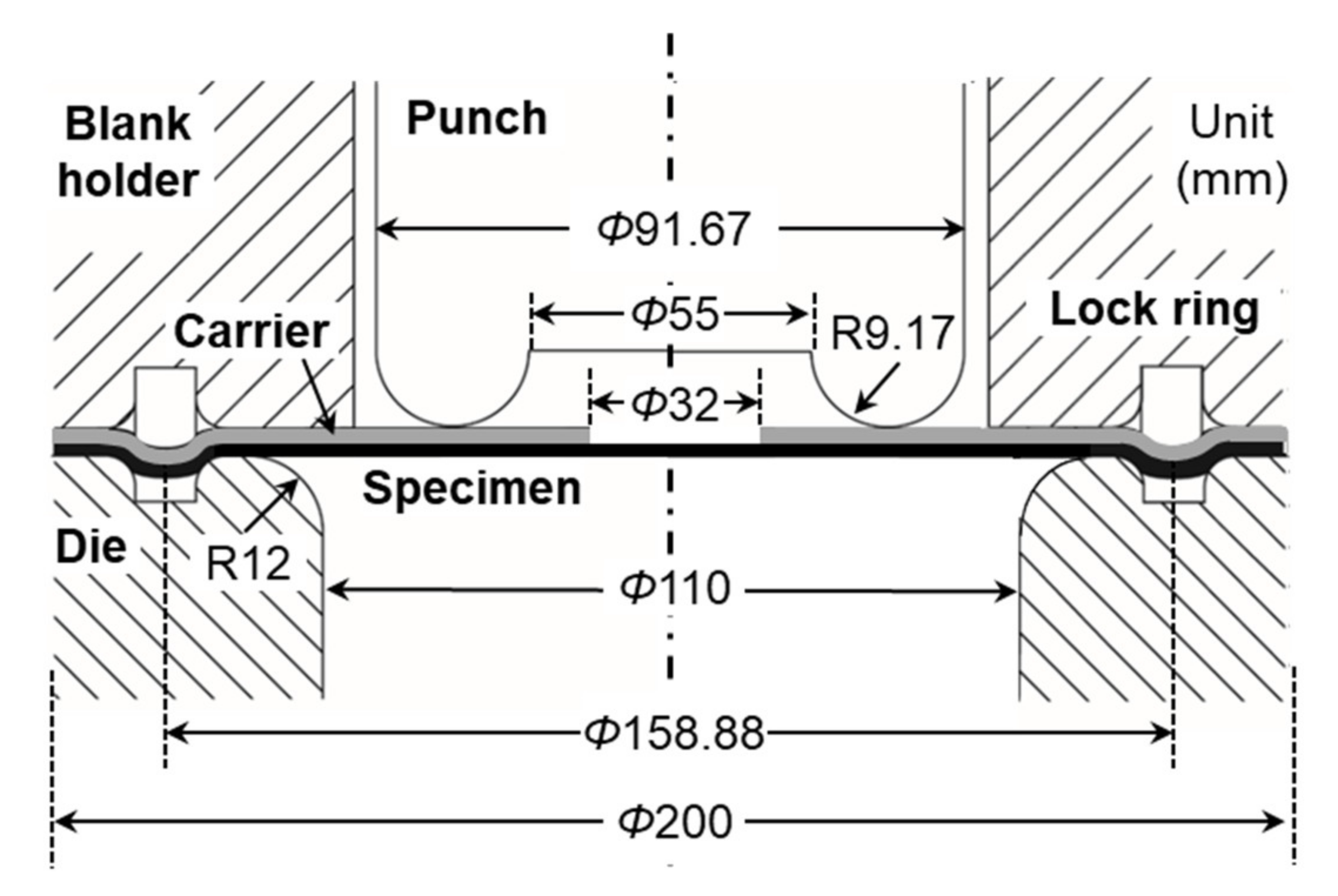
3.1.1. Specimens
3.1.2. Equipment and Testing Procedure
3.2. Experiments
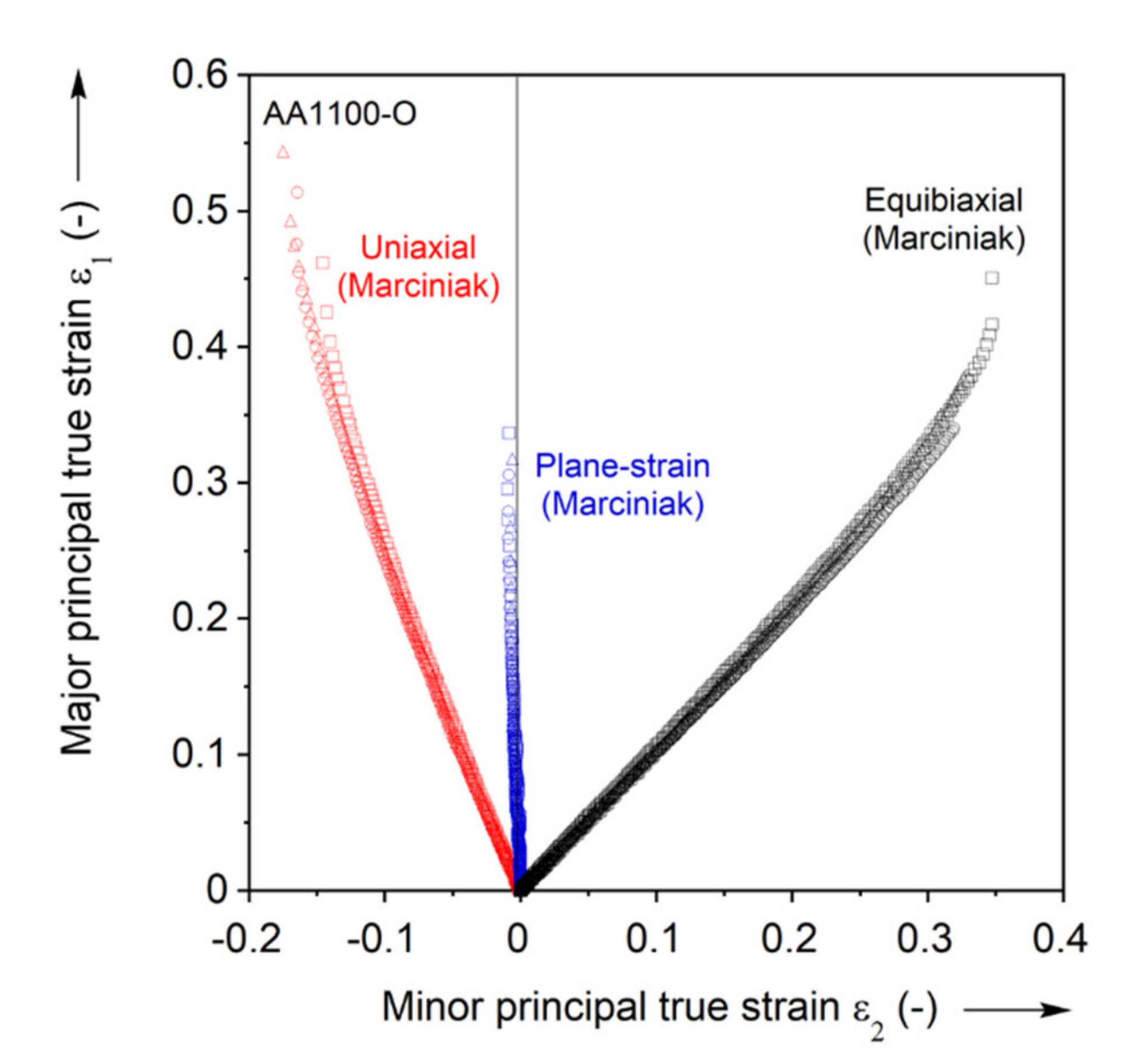
3.2.1. Strain Paths
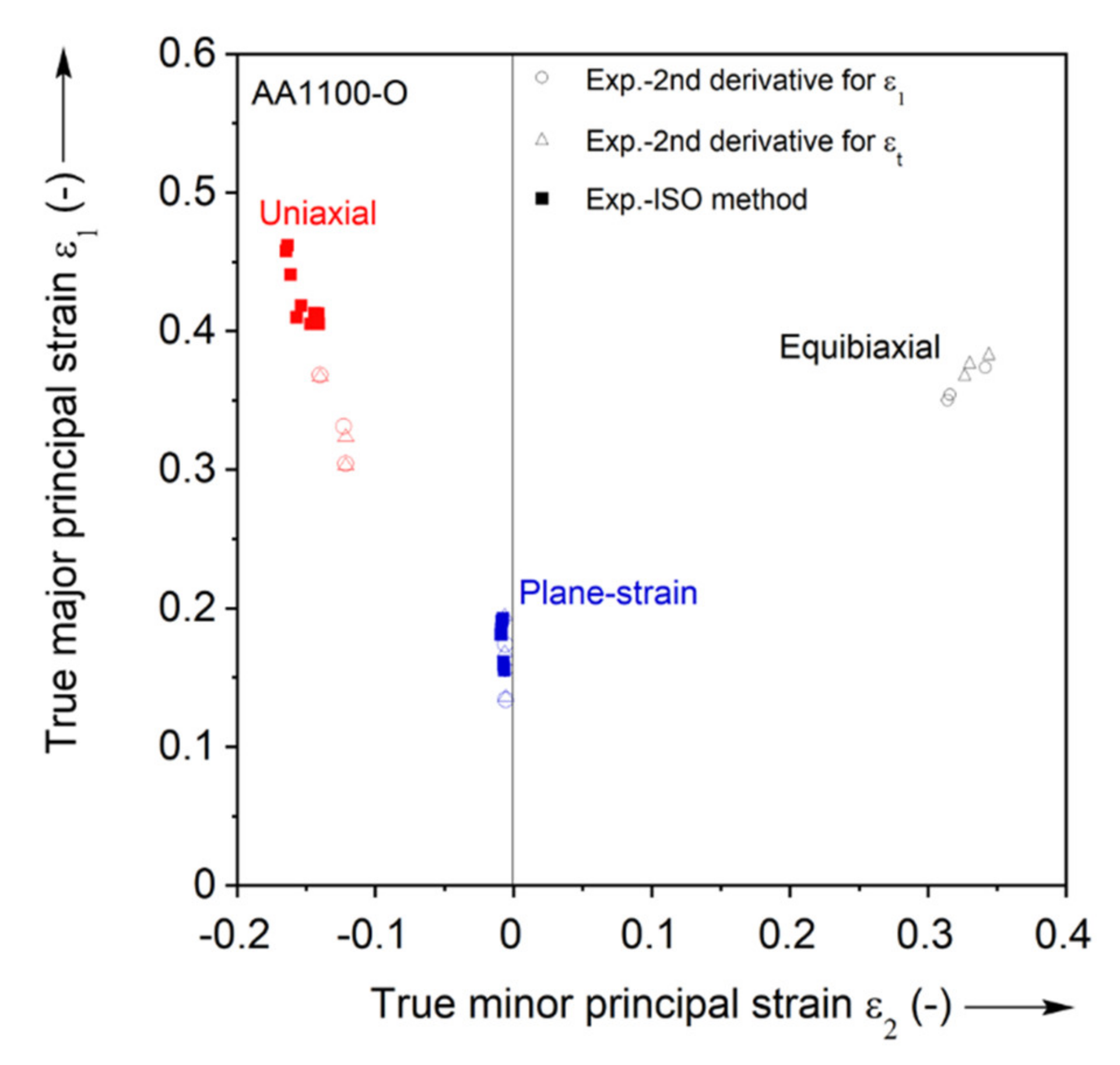
3.2.2. Detection of Necking
ISO Method
Second Derivative Methods
4. Finite Element Validation of Material Model
5. Conclusions
- (1)
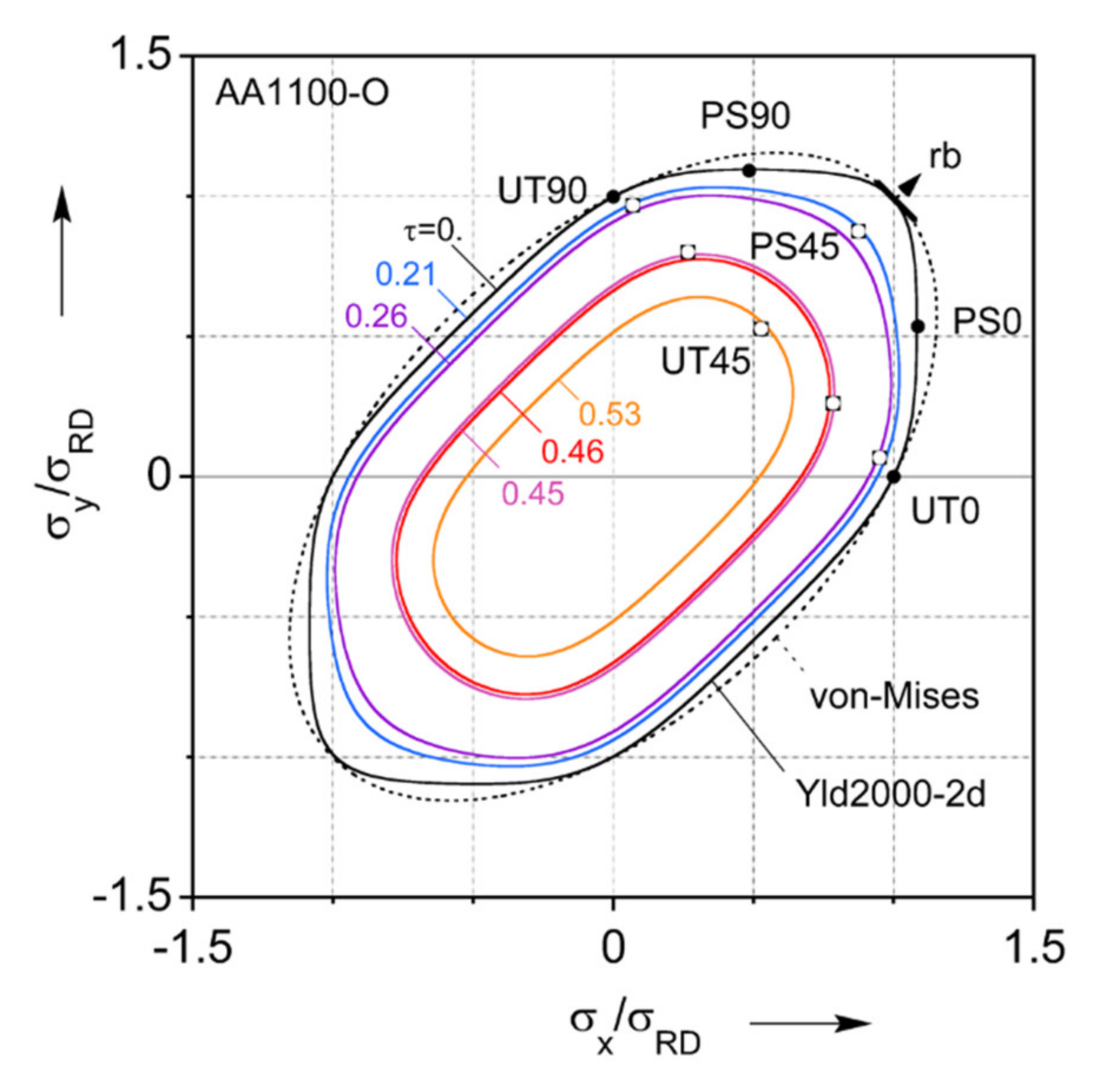
- The material is clearly plastically anisotropic: The flow curves in uniaxial tension vary by about 7% between different orientations, and the r-values range from 0.45 to 1.18.
- (2)
- The strain-rate sensitivity of AA1100-O is negligible in the quasistatic rates examined here.
- (3)
- The Yld2000-2d anisotropic yield criterion captures the material characterization experiments very well, and much better than von Mises with respect to the final yield loci. This provided a contrast in the modeling with and without the consideration of anisotropy.
- (4)
- Fracture in the FLC experiments always occurs well inside the test-section. However, accomplishing this for the plane-strain specimen requires significant iterations on the specimen geometry.
- (5)
- The strain paths recorded are linear, and the AA1100-O material is seen to possess good formability.
- (6)
- The FE model with the Yld2000-2d anisotropic yield criterion captures the experimental strain contour plots well for the uniaxial and equibiaxial cases and much better than the von Mises. The experimental plane-strain case is not predicted well by the FE simulations using either yield criteria for the onset of necking. On the other hand, the agreement is good for the majority of pre-necking deformation.
- (7)
- The final strain state values for both experiments and FE simulations at the same punch displacement, which is set by the experimental second derivative method, are reasonably accurate for FE models with both yield criteria, but the Yld2000-2d model is better.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | Disk compression |
| DIC | Digital Image Correlation |
| GL | Gauge length |
| FCC | Face-centered cubic |
| FLC | Forming Limit Curve |
| FE | Finite elements |
| ND | Normal direction |
| PST | Plane-strain tension |
| RD | Rolling direction |
| TD | Transverse direction |
| UMAT | User-material (subroutine) |
| UT | Uniaxial tension |
Appendix A
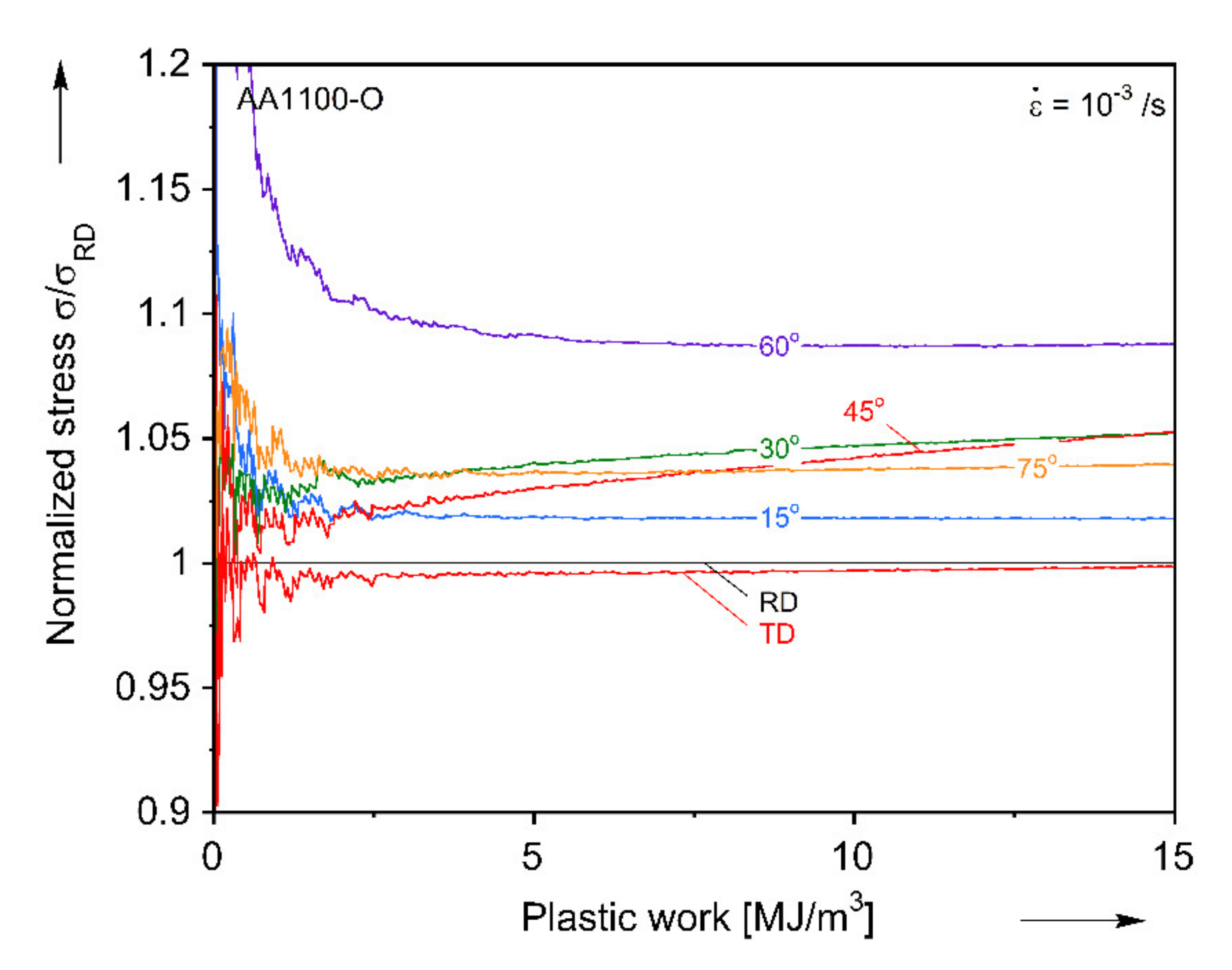
Appendix B

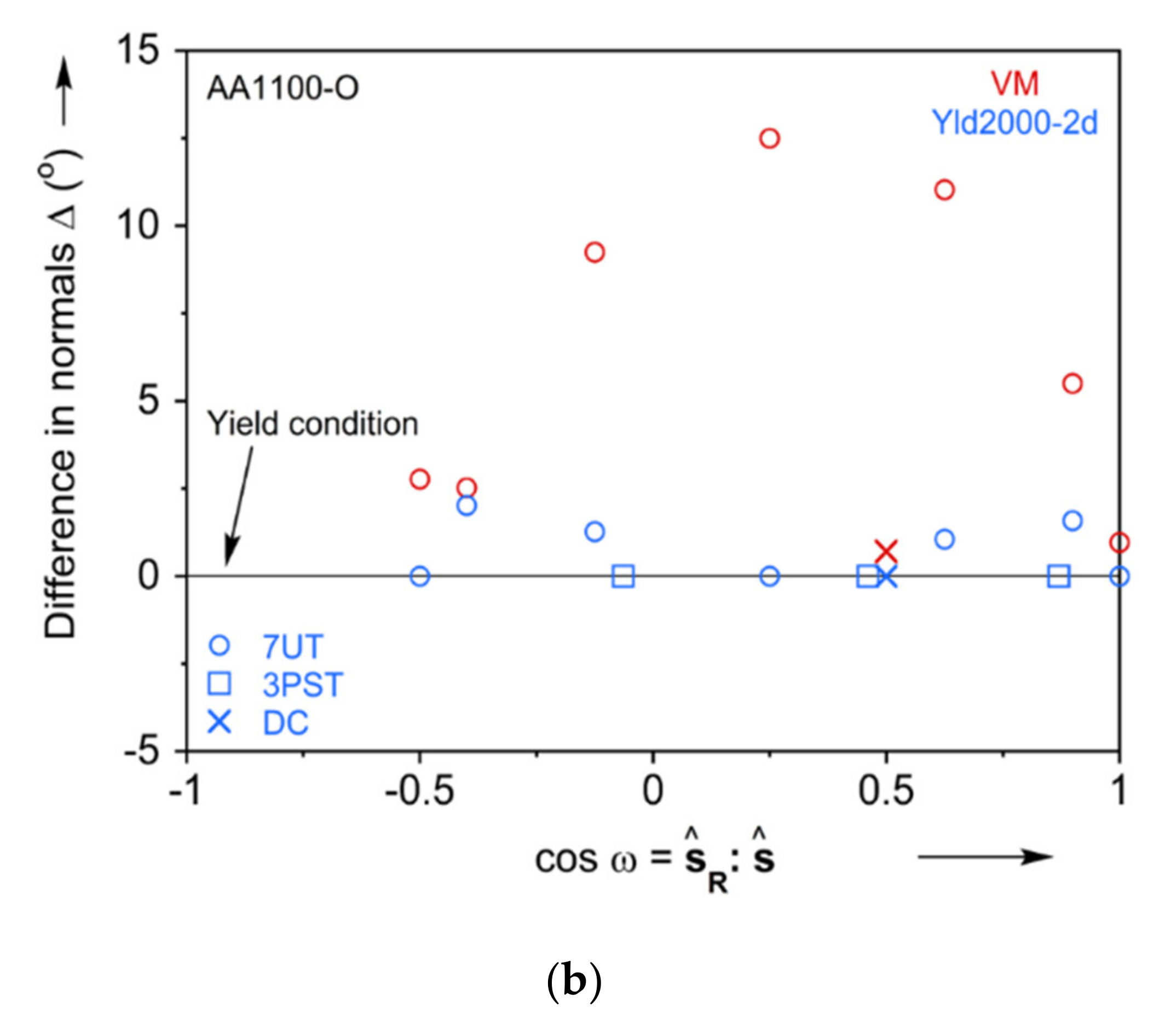
Appendix C

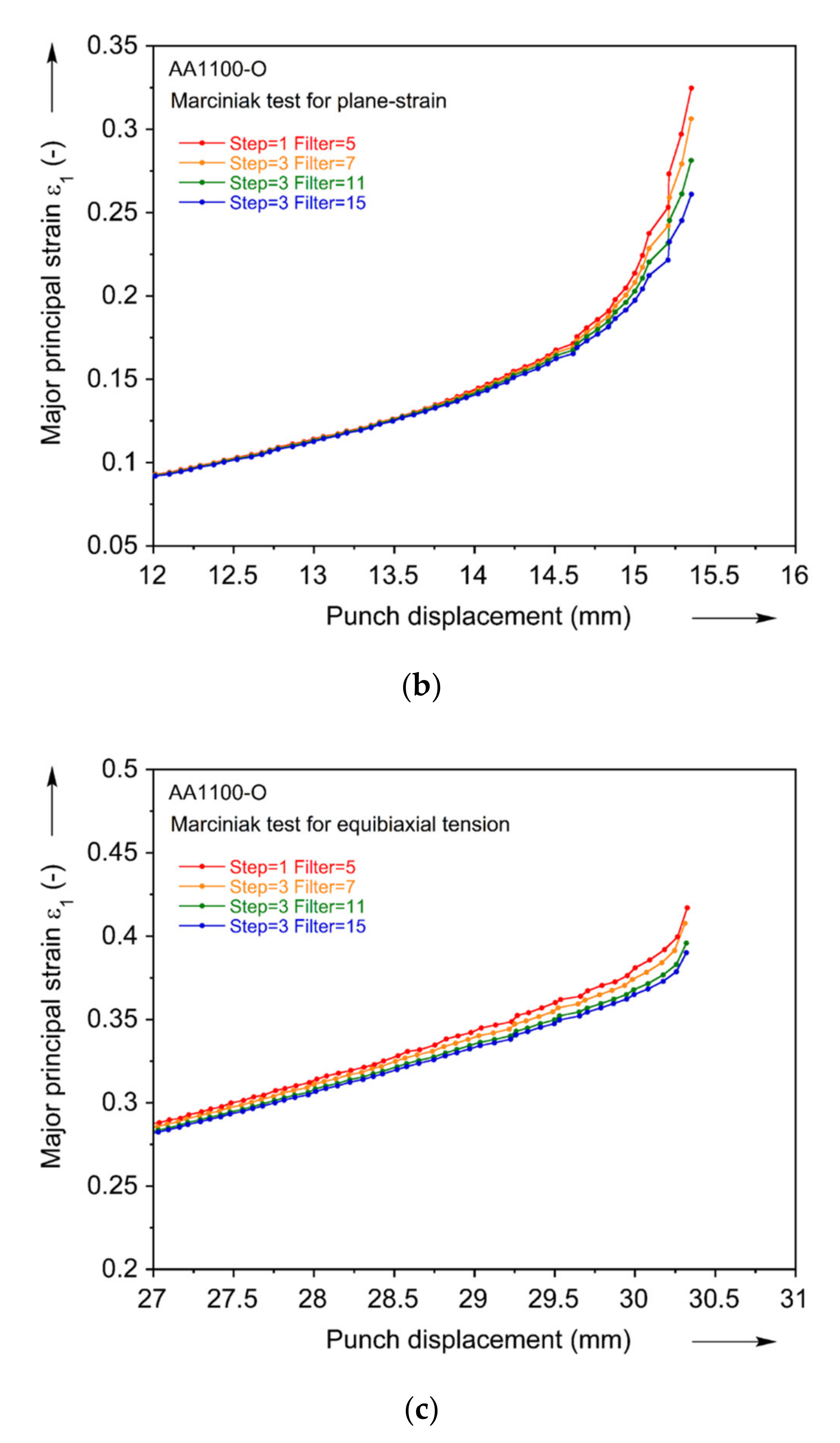
References
- Keeler, S.P.; Backofen, W.A. Forming Limit Diagrams. Trans. ASM 1963, 56, 25–28. [Google Scholar]
- Keeler, S.P. Plastic Instability and Fracture in Sheets Stretched over Rigid Punches. Ph.D. Thesis, Department of Metallurgy, Massachusetts Institute of Technology, Cambridge, MA, USA, 1961. [Google Scholar]
- Keeler, S.P. Determination of Forming Limits in Automotive Stampings. SAE Trans. 1966, 74, 1–9. [Google Scholar]
- Goodwin, G.M. Application of Strain Analysis to Sheet Metal Forming Problems in the Press Shop. SAE Trans. 1968, 77, 380–387. [Google Scholar]
- Hill, R. On Discontinuous Plastic States, with Special Reference to Localized Necking in Thin Sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic Instability under Plane Stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Hora, P. Prediction Methods for Ductile Sheet Metal Failure Using FE-Simulation. In Proceedings of the 18th IDDRG Biennial Congress, Lisbon, Portugal, 16–17 May 1994; pp. 363–375. [Google Scholar]
- Hora, P.; Tong, L.; Reissner, J. A prediction method for ductile sheet metal failure in FE-simulation. Proc. NUMISHEET 1996, 96, 252–256. [Google Scholar]
- Hou, Z.; Liu, Z.; Wan, M.; Wu, X.; Yang, B.; Lu, X. An Investigation on Anisotropy Behavior and Forming Limit of 5182-H111 Aluminum Alloy. J. Mater. Eng. Perform. 2020, 29, 3745–3756. [Google Scholar] [CrossRef]
- Lian, J.; Shen, F.; Jia, X.; Ahn, D.-C.; Chae, D.-C.; Münstermann, S.; Bleck, W. An Evolving Non-Associated Hill48 Plasticity Model Accounting for Anisotropic Hardening and r-Value Evolution and Its Application to Forming Limit Prediction. Int. J. Solids Struct. 2018, 151, 20–44. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit Strains in the Processes of Stretch-Forming Sheet Metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K.; Pokora, T. Influence of the Plastic Properties of a Material on the Forming Limit Diagram for Sheet Metal in Tension. Int. J. Mech. Sci. 1973, 15, 789–800. [Google Scholar] [CrossRef]
- Cao, J.; Yao, H.; Karafillis, A.; Boyce, M.C. Prediction of Localized Thinning in Sheet Metal Using a General Anisotropic Yield Criterion. Int. J. Plast. 2000, 16, 1105–1129. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Neale, K.W. Sheet Necking-II. Time-Independent Behavior. In Mechanics of Sheet Metal Forming; Springer: Boston, MA, USA, 1978; pp. 127–153. [Google Scholar]
- Hutchinson, J.W.; Neale, K.W. Sheet Necking-III. Strain-Rate Effects. In Mechanics of Sheet Metal Forming; Springer: Boston, MA, USA, 1978; pp. 269–285. [Google Scholar]
- Da Rocha, A.B.; Barlat, F.; Jalinier, J.M. Prediction of the Forming Limit Diagrams of Anisotropic Sheets in Linear and Non-Linear Loading. Mater. Sci. Eng. 1985, 68, 151–164. [Google Scholar] [CrossRef]
- Barlat, F. Crystallographic Texture, Anisotropic Yield Surfaces and Forming Limits of Sheet Metals. Mater. Sci. Eng. 1987, 91, 55–72. [Google Scholar] [CrossRef]
- Banabic, D.; Dannenmann, E. The Influence of the Yield Locus Shape on the Limits Strains. J. Mater. Process. Technol. 2001, 109, 9–12. [Google Scholar] [CrossRef]
- Hill, R. A User-Friendly Theory of Orthotropic Plasticity in Sheet Metals. Int. J. Mech. Sci. 1993, 35, 19–25. [Google Scholar] [CrossRef]
- Banabic, D.; Comsa, S.; Jurco, P.; Cosovici, G.; Paraianu, L.; Julean, D. FLD Theoretical Model Using a New Anisotropic Yield Criterion. J. Mater. Process. Technol. 2004, 157, 23–27. [Google Scholar] [CrossRef]
- Banabic, D.; Siegert, K. Anisotropy and Formability of AA5182-0 Aluminium Alloy Sheets. CIRP Ann. 2004, 53, 219–222. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. A Criterion for Description of Anisotropy and Yield Differential Effects in Pressure-Insensitive Metals. Int. J. Plast. 2004, 20, 2027–2045. [Google Scholar] [CrossRef]
- Paraianu, L.; Comsa, D.S.; Gracio, J.J.; Banabic, D. Influence of Yield Locus and Strain-Rate Sensitivity on the Forming Limit Diagrams. In Proceedings of the 9th ESAFORM Conference on Material Forming, Glasgow, UK, 26–28 April 2006; pp. 343–346. [Google Scholar]
- Paraianu, L.; Banabic, D. Calculation of Forming Limit Diagrams Using a Finite Element Model. In Proceedings of the 8th ESAFORM Conference on Material Forming, Cluj-Napoca, Romania, 27–29 April 2005; pp. 419–423. [Google Scholar]
- Yao, H.; Cao, J. Prediction of Forming Limit Curves Using an Anisotropic Yield Function with Prestrain Induced Backstress. Int. J. Plast. 2002, 18, 1013–1038. [Google Scholar] [CrossRef]
- Karafillis, A.P.; Boyce, M.C. A General Anisotropic Yield Criterion Using Bounds and a Transformation Weighting Tensor. J. Mech. Phys. Solids 1993, 41, 1859–1886. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.E.; Lege, D.J.; Pourboghrat, F.; Choi, S.-H.; Chu, E. Plane Stress Yield Function for Aluminum Alloy Sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Aretz, H. Impact of the Equibiaxial Plastic Strain Ratio on the FLD Prediction. In Proceedings of the 9th ESAFORM Conference on Material Forming, Glasgow, UK, 26–28 April 2006; pp. 311–314. [Google Scholar]
- Kim, K.J.; Kim, D.; Choi, S.H.; Chung, K.; Shin, K.S.; Barlat, F.; Oh, K.H.; Youn, J.R. Formability of AA5182/Polypropylene/AA5182 Sandwich Sheets. J. Mater. Process. Technol. 2003, 139, 1–7. [Google Scholar] [CrossRef]
- Yoshida, K.; Kuwabara, T. Effect of Strain Hardening Behavior on Forming Limit Stresses of Steel Tube Subjected to Nonproportional Loading Paths. Int. J. Plast. 2007, 23, 1260–1284. [Google Scholar] [CrossRef]
- Panich, S.; Barlat, F.; Uthaisangsuk, V.; Suranuntchai, S.; Jirathearanat, S. Experimental and Theoretical Formability Analysis Using Strain and Stress Based Forming Limit Diagram for Advanced High Strength Steels. Mater. Des. 2013, 51, 756–766. [Google Scholar] [CrossRef]
- Bong, H.J.; Barlat, F.; Lee, M.-G.; Ahn, D.C. The Forming Limit Diagram of Ferritic Stainless Steel Sheets: Experiments and Modeling. Int. J. Mech. Sci. 2012, 64, 1–10. [Google Scholar] [CrossRef]
- Basak, S.; Panda, S.K. Necking and Fracture Limit Analyses of Different Pre-Strained Sheet Materials in Polar Effective Plastic Strain Locus Using Yld2000-2d Yield Model. J. Mater. Process. Technol. 2019, 267, 289–307. [Google Scholar] [CrossRef]
- Chiba, R.; Takeuchi, H.; Kuroda, M.; Hakoyama, T.; Kuwabara, T. Theoretical and Experimental Study of Forming-Limit Strain of Half-Hard AA1100 Aluminium Alloy Sheet. Comput. Mater. Sci. 2013, 77, 61–71. [Google Scholar] [CrossRef]
- Butuc, M.C.; Barlat, F.; Gracio, J.J.; Barata da Rocha, A. A New Model for FLD Prediction Based on Advanced Constitutive Equations. Int. J. Mater. Form. 2010, 3, 191–204. [Google Scholar] [CrossRef]
- He, J.; Zeng, D.; Zhu, X.; Cedric Xia, Z.; Li, S. Effect of Nonlinear Strain Paths on Forming Limits under Isotropic and Anisotropic Hardening. Int. J. Solids Struct. 2014, 51, 402–415. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Yan, Y.; Han, F.; Wan, M. Experimental and Theoretical Investigations of the Forming Limit of 5754O Aluminum Alloy Sheet under Different Combined Loading Paths. Int. J. Mech. Sci. 2017, 133, 147–166. [Google Scholar] [CrossRef]
- Yue, Z.M.; Badreddine, H.; Dang, T.; Saanouni, K.; Tekkaya, A.E. Formability Prediction of AL7020 with Experimental and Numerical Failure Criteria. J. Mater. Process. Technol. 2015, 218, 80–88. [Google Scholar] [CrossRef]
- Chung, K.; Kim, H.; Lee, C. Forming Limit Criterion for Ductile Anisotropic Sheets as a Material Property and Its Deformation Path Insensitivity. Part I: Deformation Path Insensitive Formula Based on Theoretical Models. Int. J. Plast. 2014, 58, 3–34. [Google Scholar] [CrossRef]
- Keeler, S.P. Circular Grid System—A Valuable Aid for Evaluating Sheet Metal Formability. SAE Trans. 1968, 77, 371–379. [Google Scholar]
- Takashina, K.; Herai, T.; Komorida, H.; Horita, T. Relation between the Manufacturing Conditions and the Average Strain According to the Scribed Circle Tests in Steel Sheets. MET ITAL 1968, 60, 757–765. [Google Scholar]
- Hecker, S.S. A Simple Forming-Limit Curve Technique and Results on Aluminum Alloys. In Proceedings of the 7th Biennial Congress of the International Deep Drawing Research Group, Amsterdam, The Netherlands, 9–13 October 1972; Volume 35. [Google Scholar]
- Bragard, A.; JC, B. A Simplified Technique to Determine the FLD at the Onset of Necking; Rapport Centre de Recherche de la metallurgie: Paris, France, 1972; Volume 35. [Google Scholar]
- Anon. ISO 12004-2:2008 Metallic Materials—Sheet and Strip—Determination of Forming-Limit Curves—Part 2: Determination of Forming-Limit Curves in the Laboratory; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Marron, G.; Moinier, L.; Patou, P.; Celeski, J.C. A New Necking Criterion for the Forming Limit Diagrams. Rev. Metall. Cah. d’Informations Tech. 1997, 94, 837–845. [Google Scholar]
- Hora, P.; Krauer, J. Numerical and Experimental Methods in Prediction of Forming Limits in Sheet Metal Forming and Tube Hydroforming Processes. In Proceedings of the FLC-Zürich 06 Conference, Zürich, Germany, 15–16 March 2006. [Google Scholar]
- Leppin, C.; Li, J.; Daniel, D. Application of a Method to Correct the Effect of Non-Proportional Strain Paths on Nakajima Test Based Forming Limit Curves. In Proceedings of the NUMISHEET 2008 Conference, Interlaken, Switzerland, 1–5 September 2008; pp. 217–221. [Google Scholar]
- Volk, W.; Hora, P. New Algorithm for a Robust User-Independent Evaluation of Beginning Instability for the Experimental FLC Determination. Int. J. Mater. Form. 2011, 4, 339–346. [Google Scholar] [CrossRef]
- Geiger, M.; Merklein, M. Determination of Forming Limit Diagrams—A New Analysis Method for Characterization of Materials’ Formability. CIRP Ann. 2003, 52, 213–216. [Google Scholar] [CrossRef]
- Merklein, M.; Kuppert, A.; Geiger, M. Time Dependent Determination of Forming Limit Diagrams. CIRP Ann. 2010, 59, 295–298. [Google Scholar] [CrossRef]
- Huang, G.; Sadagopan, S.; Schreier, H. Determination of Forming Limit and Fracture Limit Curves Using Digital Image Correlation. SAE Int. J. Mater. Manuf. 2014, 7, 574–582. [Google Scholar] [CrossRef]
- Lumelskyj, D.; Rojek, J.; Lazarescu, L.; Banabic, D. Determination of Forming Limit Curve by Finite Element Method Simulations. Procedia Manuf. 2019, 27, 78–82. [Google Scholar] [CrossRef]
- Situ, Q.; Jain, M.K.; Bruhis, M. A Suitable Criterion for Precise Determination of Incipient Necking in Sheet Materials. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2006; pp. 111–116. [Google Scholar]
- Situ, Q.; Jain, M.K.; Metzger, D.R. Determination of Forming Limit Diagrams of Sheet Materials with a Hybrid Experimental–Numerical Approach. Int. J. Mech. Sci. 2011, 53, 707–719. [Google Scholar] [CrossRef]
- Safdarian, R.; Jorge, R.M.N.; Santos, A.D.; Naeini, H.M.; Parente, M.P.L. A Comparative Study of Forming Limit Diagram Prediction of Tailor Welded Blanks. Int. J. Mater. Form. 2015, 8, 293–304. [Google Scholar] [CrossRef]
- Ju, L.; Mao, T.; Li, H. An Experimental and Numerical Study of Forming Limits of AA5182-O. Int. J. Adv. Manuf. Technol. 2015, 79, 221–228. [Google Scholar] [CrossRef]
- Bagheriasl, R.; Worswick, M.J. Formability of AA3003 Brazing Sheet at Elevated Temperatures: Limiting Dome Height Experiments and Determination of Forming Limit Diagrams. Int. J. Mater. Form. 2015, 8, 229–244. [Google Scholar] [CrossRef]
- Magrinho, J.P.; Silva, M.B.; Centeno, G.; Moedas, F.; Vallellano, C.; Martins, P.A.F. On the Determination of Forming Limits in Thin-Walled Tubes. Int. J. Mech. Sci. 2019, 155, 381–391. [Google Scholar] [CrossRef]
- Iadicola, M.A. Augmented Use of Standard Mechanical Testing Measurements for Sheet Metal Forming: Digital Image Correlation for Localized Necking. AIP Conf. Proc. 2013, 1567, 614–619. [Google Scholar]
- Durán, A.I.; Signorelli, J.W.; Celentano, D.J.; Cruchaga, M.A.; François, M. Experimental and Numerical Analysis on the Formability of a Heat-Treated AA1100 Aluminum Alloy Sheet. J. Mater. Eng. Perform. 2015, 24, 4156–4170. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Qin, N. Development of Through-Thickness Texture Gradient and Persistence of Shear-Type Textures during Annealing of Commercial Purity Aluminium Sheet Processed by Accumulative Roll-Bonding. J. Mater. Sci. Technol. 2018, 34, 821–831. [Google Scholar] [CrossRef]
- Anderson, K.; Weritz, J.; Kaufman, J.G. ASM Handbook, Volume 2B, Properties and Selection of Aluminum Alloys; ASM International: Materials Park, OH, USA, 2019. [Google Scholar]
- Tardif, N.; Kyriakides, S. Determination of Anisotropy and Material Hardening for Aluminum Sheet Metal. Int. J. Solids Struct. 2012, 49, 3496–3506. [Google Scholar] [CrossRef]
- Tian, H.; Brownell, B.; Baral, M.; Korkolis, Y.P. Earing in Cup-Drawing of Anisotropic Al-6022-T4 Sheets. Int. J. Mater. Form. 2017, 10, 329–343. [Google Scholar] [CrossRef]
- Ha, J.; Baral, M.; Korkolis, Y.P. Plastic Anisotropy and Ductile Fracture of Bake-Hardened AA6013 Aluminum Sheet. Int. J. Solids Struct. 2018, 155, 123–139. [Google Scholar] [CrossRef]
- Baral, M.; Ha, J.; Korkolis, Y.P. Plasticity and Ductile Fracture Modeling of an Al–Si–Mg Die-Cast Alloy. Int. J. Fract. 2019, 216, 101–121. [Google Scholar] [CrossRef]
- Baral, M.; Hama, T.; Knudsen, E.; Korkolis, Y.P. Plastic Deformation of Commercially-Pure Titanium: Experiments and Modeling. Int. J. Plast. 2018, 105, 164–194. [Google Scholar] [CrossRef]
- Dick, C.P.; Korkolis, Y.P. Anisotropy of Thin-Walled Tubes by a New Method of Combined Tension and Shear Loading. Int. J. Plast. 2015, 71, 87–112. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.E.; Brem, J.C.; Dick, R.E. Linear Transformation-Based Anisotropic Yield Functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Ha, J.; Dirian, M.; Dunn, C.; Korkolis, Y.P. Failure of AA6022-T4 Sheets in Hole-Expansion after Uniaxial Prestrain. AIP Conf. Proc. 2019, 2113, 180005. [Google Scholar]
- Ha, J.; Coppieters, S.; Korkolis, Y.P. On the Expansion of a Circular Hole in an Orthotropic Elastoplastic Thin Sheet. Int. J. Mech. Sci. 2020, 182, 105706. [Google Scholar] [CrossRef]
- Ha, J.; Baral, M.; Korkolis, Y.P. Ductile Fracture of an Aluminum Sheet under Proportional Loading. J. Mech. Phys. Solids 2019, 132, 103685. [Google Scholar] [CrossRef]
- Chawla, K.; Meyers, M.A. Mechanical Behavior of Materials; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Banabic, D. Sheet Metal Forming Processes: Constitutive Modelling and Numerical Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Deng, N.; Kuwabara, T.; Korkolis, Y.P. On the Non-Linear Unloading Behavior of a Biaxially Loaded Dual-Phase Steel Sheet. Int. J. Mech. Sci. 2018, 138–139, 383–397. [Google Scholar] [CrossRef]
- Roemer, T.J.; Barrett, T.J.; Knezevic, M.; Kinsey, B.L.; Korkolis, Y.P. Experimental Study of Continuous-Bending-under-Tension of AA6022-T4. J. Mater. Process. Technol. 2019, 266, 707–714. [Google Scholar] [CrossRef]
- Kurokawa, T.; Tanaka, K. Strength of aluminum under high velocity deformation. In Mechanical Behaviour of Materials VI; Pergamon: Oxford, UK, 1992; pp. 313–318. [Google Scholar]
- Hosford, W.F. A Generalized Isotropic Yield Criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Hershey, A.V. The Plasticity of an Isotropic Aggregate of Anisotropic Face-Centered Cubic Crystals. J. Appl. Mech. ASME 1954, 21, 241–249. [Google Scholar]
- Logan, R.W.; Hosford, W.F. Upper-Bound Anisotropic Yield Locus Calculations Assuming 〈111〉-Pencil Glide. Int. J. Mech. Sci. 1980, 22, 419–430. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Determination of the Fraction of Plastic Work Converted into Heat in Metals. Mech. Mater. 2015, 86, 71–80. [Google Scholar] [CrossRef]
- Cullen, G.W.; Korkolis, Y.P. Ductility of 304 Stainless Steel under Pulsed Uniaxial Loading. Int. J. Solids Struct. 2013, 50, 1621–1633. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Identification of the Post-Necking Hardening Response of Rate- and Temperature-Dependent Metals. Int. J. Solids Struct. 2017, 115, 149–160. [Google Scholar] [CrossRef]
- Voce, E. The Relationship between Stress and Strain for Homogeneous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Hasan, R.Z.; Kinsey, B.L.; Tsukrov, I. Effect of Element Types on Failure Prediction Using a Stress-Based Forming Limit Curve. J. Manuf. Sci. Eng. 2011, 133, 061002. [Google Scholar] [CrossRef]
- Hasan, R.; Kasikci, T.; Tsukrov, I.; Kinsey, B.L. Numerical and Experimental Investigations of Key Assumptions in Analytical Failure Models for Sheet Metal Forming. J. Manuf. Sci. Eng. 2013, 136, 011013. [Google Scholar] [CrossRef]
- Booser, E.R. CRC Handbook of Lubrication: Application and Maintenance; CRC Pr I LLC: Boca Raton, FL, USA, 1983. [Google Scholar]
- Korkolis, Y.P.; Barlat, F.; Kuwabara, T. Simplified Representations of Multiaxial Test Results in Plasticity. In Proceedings of the 5th International Conference on Material Modeling (ICMM5), Rome, Italy, 13–16 June 2017. [Google Scholar]

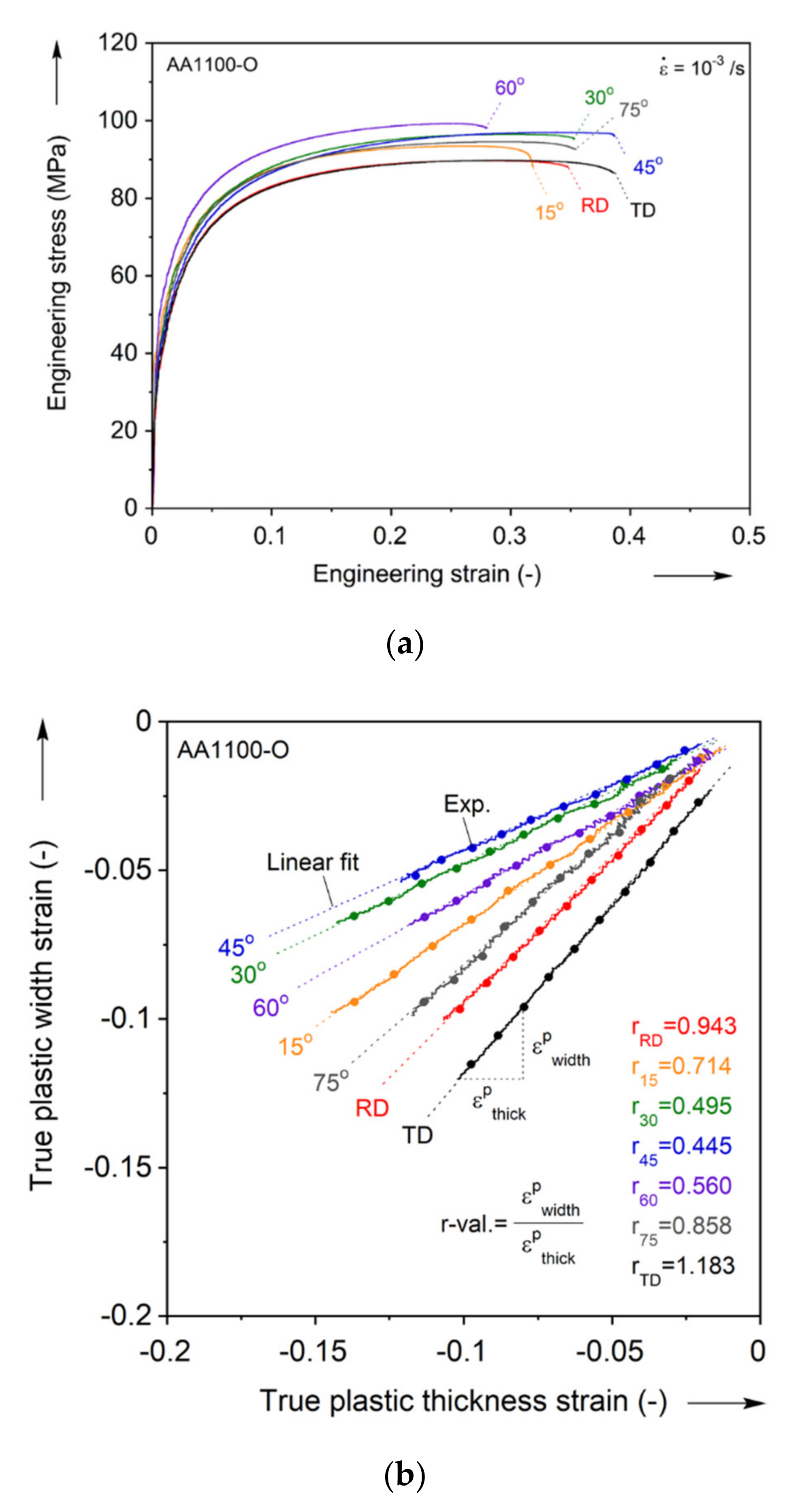
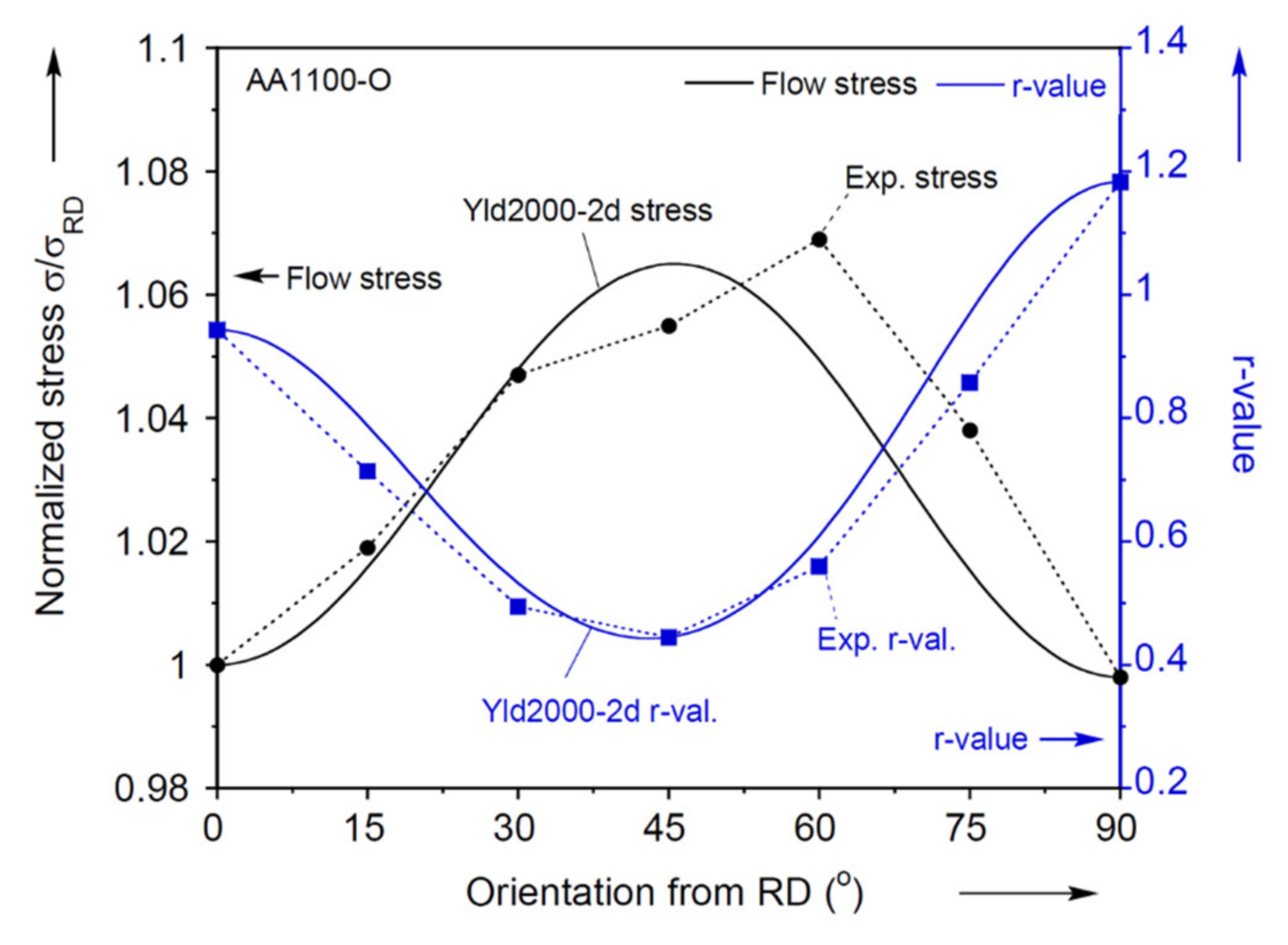
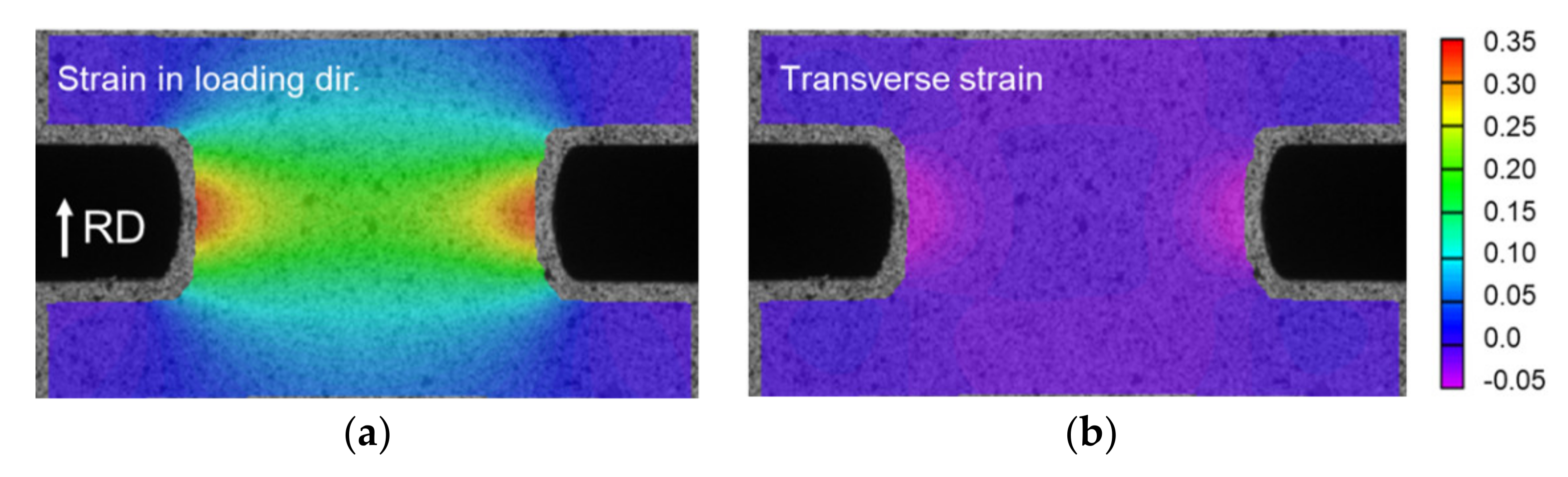
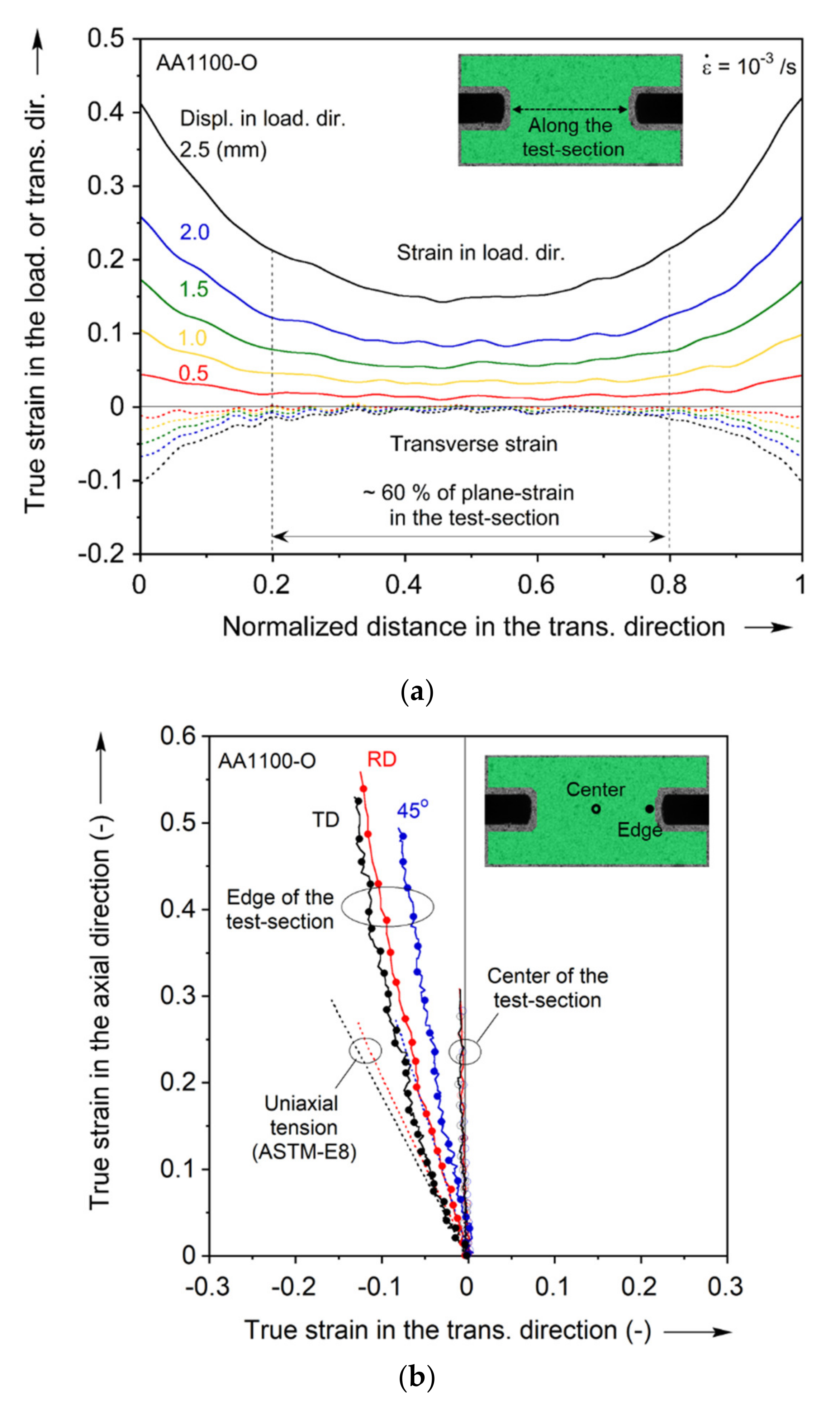









| Young’s Modulus | E = 70 GPa | Poisson’s Ratio | ν = 0.3 | |||||
|---|---|---|---|---|---|---|---|---|
| RD | 15° | 30° | 45° | 60° | 75° | 90° | ||
| UT | [MPa] 0.2 % offset | 23 | 27 | 28 | 30 | 32 | 30 | 26 |
| [MPa] | 90 | 93 | 97 | 97 | 99 | 95 | 90 | |
| (Standard deviation) | 1.000 | 1.019 (0.006) | 1.047 (0.002) | 1.055 (0.007) | 1.069 (0.01) | 1.038 (0.009) | 0.998 (0.007) | |
| r-value | 0.943 | 0.714 | 0.495 | 0.445 | 0.560 | 0.858 | 1.183 | |
| PST | RD | 45° | 90° | |||||
| 1.087 | 1.089 | 1.091 | ||||||
| DC | rb | 0.958 | ||||||
| Jump | m | 0.003–0.008 | ||||||
| Mat. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| AA1100-O | 8 | 0.969 | 1.041 | 1.025 | 0.995 | 1.006 | 1.003 | 0.891 | 0.943 |
| EDDQ | 6 | 0.962 | 1.119 | 0.891 | 0.912 | 0.929 | 0.762 | 0.999 | 1.011 |
| 133 MPa | 81 MPa | 6.1 |
| Specimen | W | L | B | T | Rs | ϕc |
|---|---|---|---|---|---|---|
| Uniaxial | 200 | 200 | 50 | 30 | 30 | - |
| Plane-strain | 200 | 200 | 95 | 10 | 15 | - |
| Equibiaxial | 200 | 200 | - | - | - | - |
| Carrier | 200 | 200 | - | - | - | 32 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, J.; Fones, J.; Kinsey, B.L.; Korkolis, Y.P. Plasticity and Formability of Annealed, Commercially-Pure Aluminum: Experiments and Modeling. Materials 2020, 13, 4285. https://doi.org/10.3390/ma13194285
Ha J, Fones J, Kinsey BL, Korkolis YP. Plasticity and Formability of Annealed, Commercially-Pure Aluminum: Experiments and Modeling. Materials. 2020; 13(19):4285. https://doi.org/10.3390/ma13194285
Chicago/Turabian StyleHa, Jinjin, Johnathon Fones, Brad L. Kinsey, and Yannis P. Korkolis. 2020. "Plasticity and Formability of Annealed, Commercially-Pure Aluminum: Experiments and Modeling" Materials 13, no. 19: 4285. https://doi.org/10.3390/ma13194285
APA StyleHa, J., Fones, J., Kinsey, B. L., & Korkolis, Y. P. (2020). Plasticity and Formability of Annealed, Commercially-Pure Aluminum: Experiments and Modeling. Materials, 13(19), 4285. https://doi.org/10.3390/ma13194285






