Writing 3D Nanomagnets Using Focused Electron Beams
Abstract
1. Introduction
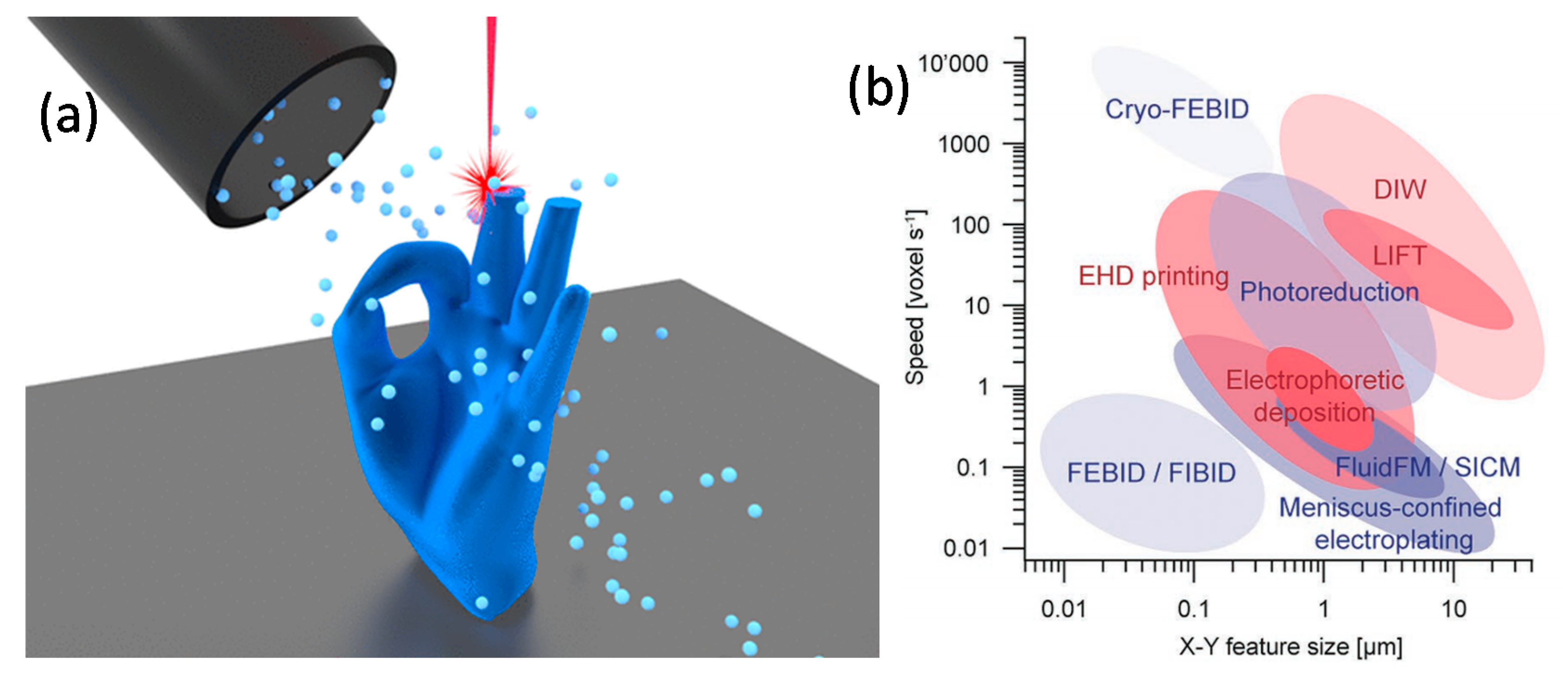
2. Writing Nanomagnets Using FEBID
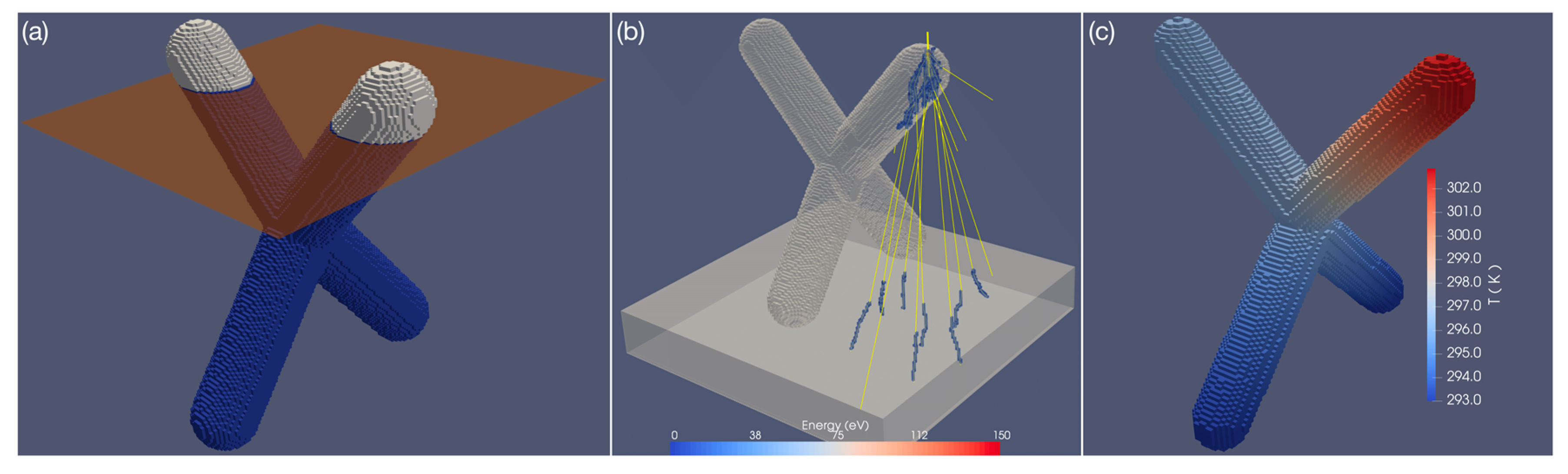
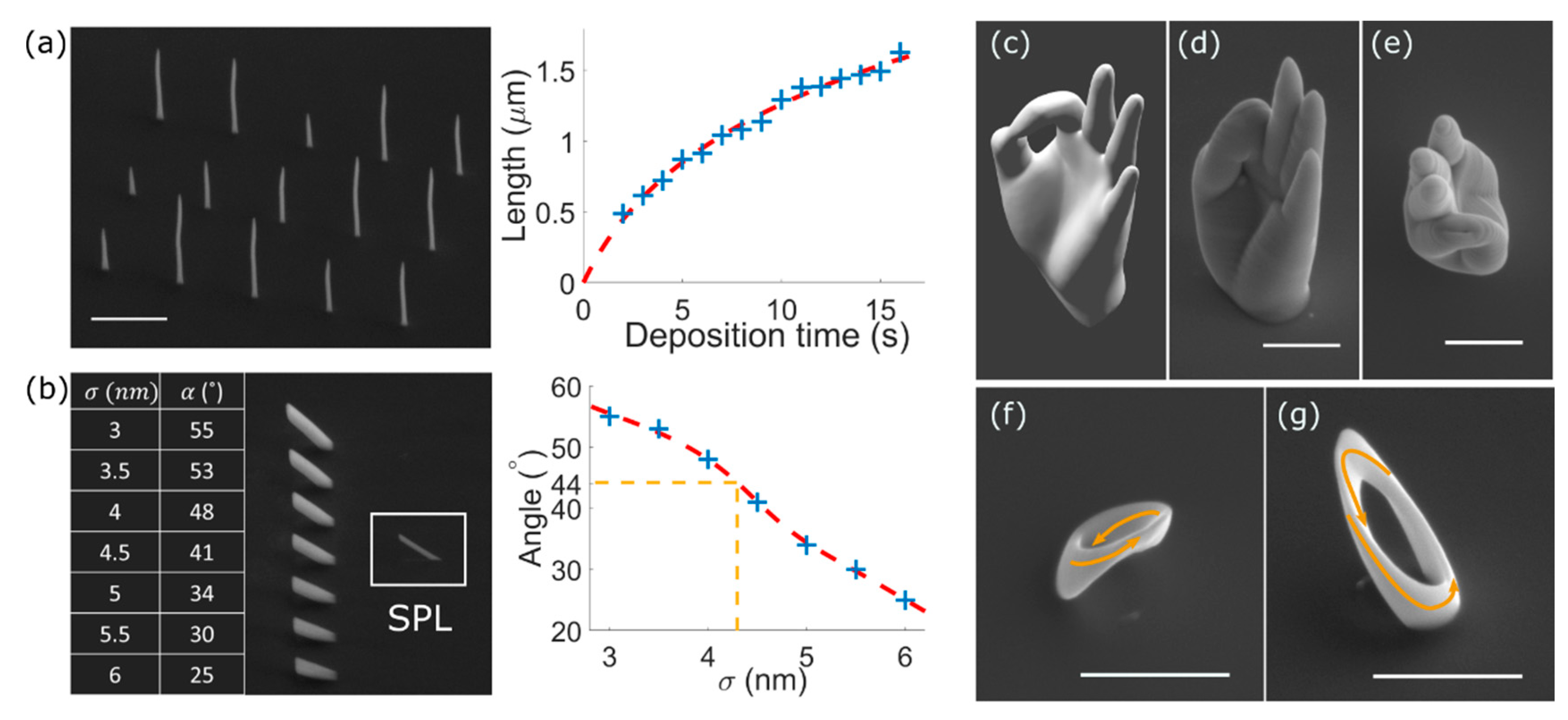
2.1. 3D Printing via FEBID
2.2. 3D Printing of Arbitrary-Shaped Nanomagnets
3. Ferromagnetic 3D Nanostructured FEBID Materials
3.1. Tuning of Cobalt and Iron FEBID Materials by Post-Growth Annealing

3.2. Ferromagnetic Alloys
3.3. 3D FEBID Scaffolds and Magnetic Thin Films
4. FEBID Nanostructures for 3D Nanomagnetism
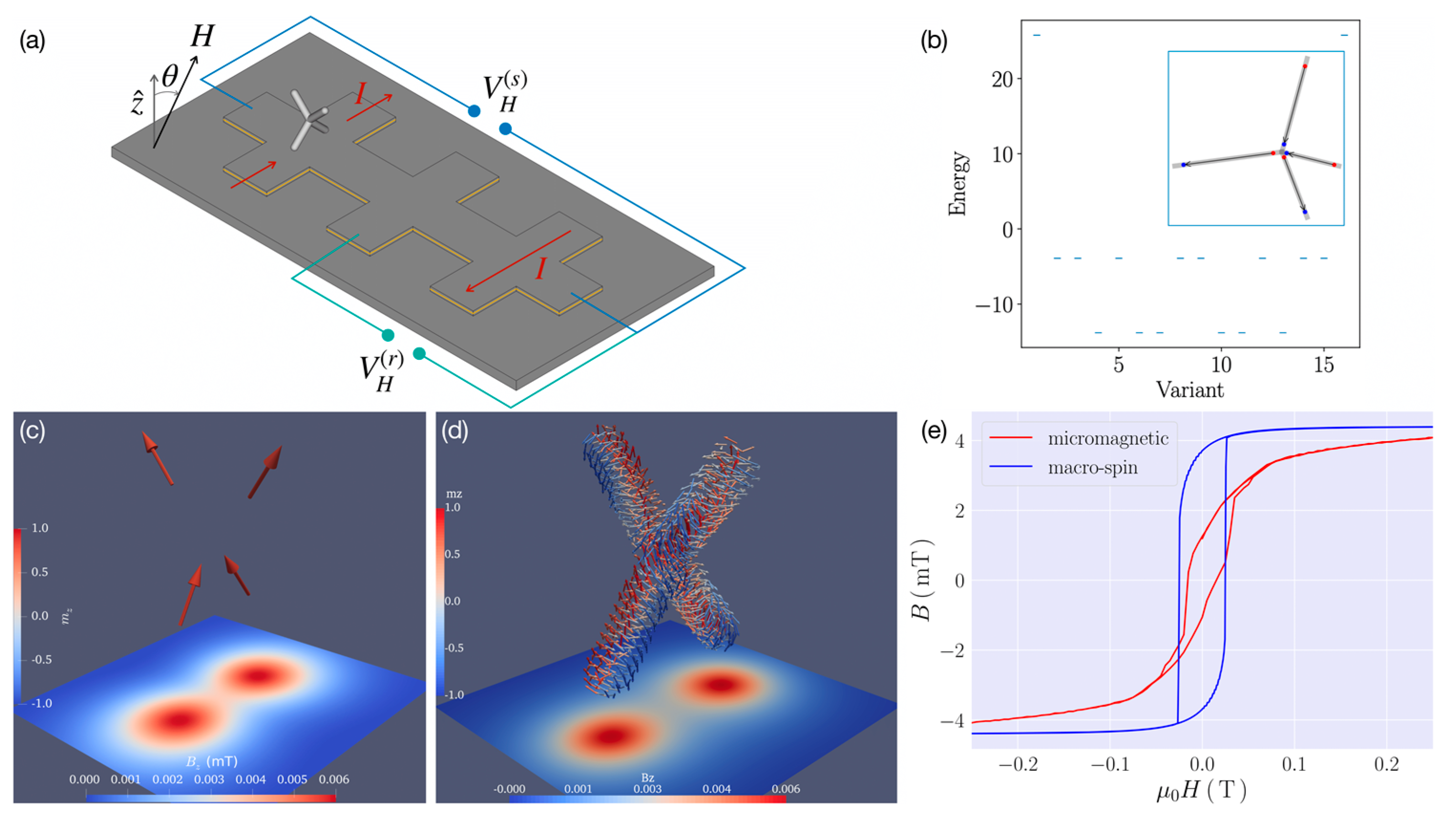
4.1. Scanning Probe Microscopy Magnetic Sensing
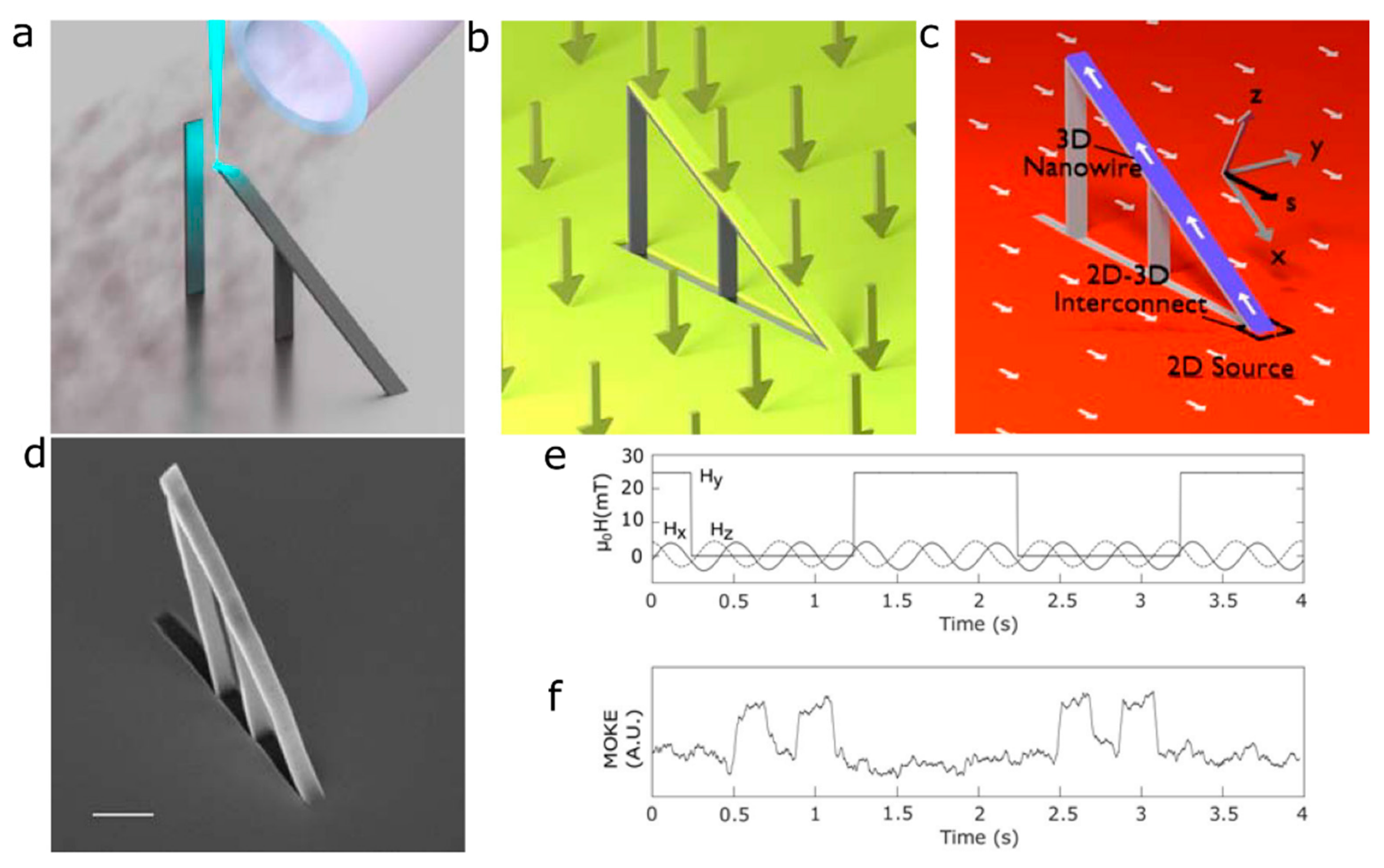
4.2. Magnetic Nanowires and Nanowire Networks
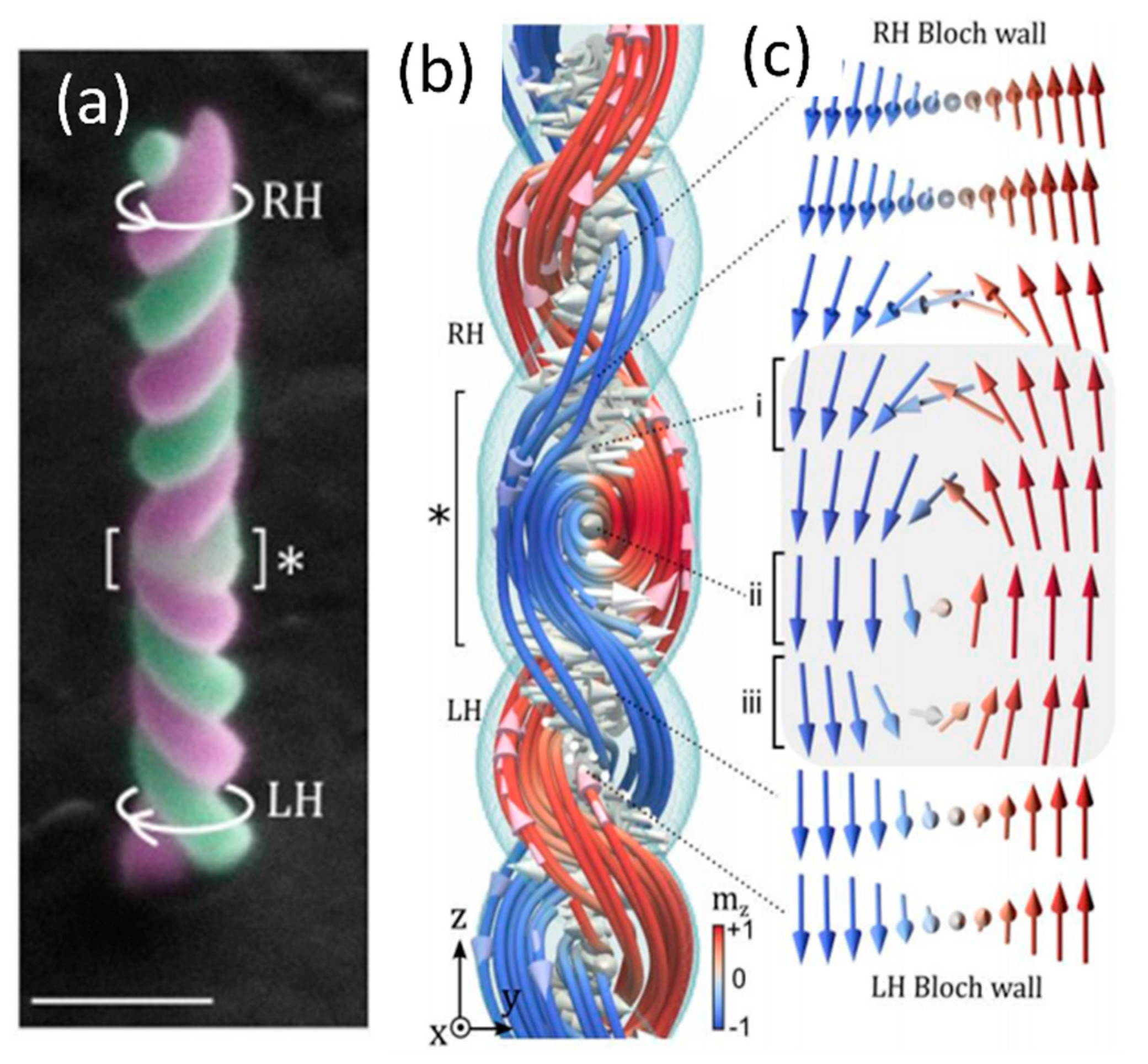
4.3. Curvilinear Nanomagnetism
4.4. Superconducting Spintronics and Fluxonics
4.5. Magnonics
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baibich, M.N.; Broto, J.M.; Fert, A.; Van Dau, F.N.; Petroff, F.; Eitenne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef]
- Fert, A.; Campbell, I.A. Transport Properties of Ferromagnetic Transition Metals. J. Phys. Colloq. 1971, 32, C1-46–C1-50. [Google Scholar] [CrossRef]
- Beach, G.S.D.; Tsoi, M.; Erskine, J.L. Current-induced domain wall motion. J. Magn. Magn. Mater. 2008, 320, 1272–1281. [Google Scholar] [CrossRef]
- Emori, S.; Bauer, U.; Ahn, S.-M.; Martinez, E.; Beach, G.S.D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 2013, 12, 611–616. [Google Scholar] [CrossRef]
- Fernández-Pacheco, A.; Streubel, R.; Fruchart, O.; Hertel, R.; Fischer, P.; Cowburn, R.P. Three-dimensional nanomagnetism. Nat. Commun. 2017, 8, 15756. [Google Scholar] [CrossRef]
- Streubel, R.; Fischer, P.; Kronast, F.; Kravchuk, V.P.; Sheka, D.D.; Gaididei, Y.; Schmidt, O.G.; Makarov, D. Magnetism in curved geometries. J. Phys. D Appl. Phys. 2016, 49, 363001. [Google Scholar] [CrossRef]
- Hertel, R. Ultrafast domain wall dynamics in magnetic nanotubes and nanowires. J. Phys. Condens. Matter 2016, 28, 483002. [Google Scholar] [CrossRef]
- Fischer, P.; Sanz-Hernández, D.; Streubel, R.; Fernández-Pacheco, A. Launching a new dimension with 3D magnetic nanostructures. APL Mater. 2020, 8, 010701. [Google Scholar] [CrossRef]
- Hunt, M.; Taverne, M.; Askey, J.; May, A.; Van Den Berg, A.; Ho, Y.L.D.; Rarity, J.; Ladak, S. Harnessing multi-photon absorption to produce three-dimensional magnetic structures at the nanoscale. Materials 2020, 13, 761. [Google Scholar] [CrossRef]
- Seniutinas, G.; Weber, A.; Padeste, C.; Sakellari, I.; Farsari, M.; David, C. Beyond 100 nm resolution in 3D laser lithography—Post processing solutions. Microelectron. Eng. 2018, 191, 25–31. [Google Scholar] [CrossRef]
- Donnelly, C.; Guizar-Sicairos, M.; Scagnoli, V.; Holler, M.; Huthwelker, T.; Menzel, A.; Vartiainen, I.; Müller, E.; Kirk, E.; Gliga, S.; et al. Element-Specific X-Ray Phase Tomography of 3D Structures at the Nanoscale. Phys. Rev. Lett. 2015, 114, 115501. [Google Scholar] [CrossRef] [PubMed]
- Bochmann, S.; Döhler, D.; Trapp, B.; Staňo, M.; Fruchart, O.; Bachmann, J. Preparation and physical properties of soft magnetic nickel-cobalt three-segmented nanowires. J. Appl. Phys. 2018, 124, 163907. [Google Scholar] [CrossRef]
- Andersen, I.M.; Rodríguez, L.A.; Bran, C.; Marcelot, C.; Joulie, S.; Hungria, T.; Vazquez, M.; Gatel, C.; Snoeck, E. Exotic Transverse-Vortex Magnetic Configurations in CoNi Nanowires. ACS Nano 2019, 14, 1399–1405. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Gómez, S.; Foerster, M.; Aballe, L.; Proenca, M.P.; Lucas, I.; Prieto, J.L.; Mascaraque, A.; de la Figuera, J.; Quesada, A.; Pérez, L. Observation of a topologically protected state in a magnetic domain wall stabilized by a ferromagnetic chemical barrier. Sci. Rep. 2018, 8, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Lewis, B.B.; Fowlkes, J.D.; Rack, P.D.; Plank, H. High-Fidelity 3D-Nanoprinting via Focused Electron Beams: Growth Fundamentals. ACS Appl. Nano Mater. 2018, 1, 1014–1027. [Google Scholar] [CrossRef]
- Skoric, L.; Sanz-Hernández, D.; Meng, F.; Donnelly, C.; Merino-Aceituno, S.; Fernández-Pacheco, A. Layer-by-layer growth of complex-shaped three-dimensional nanostructures with focused electron beams. Nano Lett. 2019, 20, 184–191. [Google Scholar] [CrossRef]
- Bresin, M.; Toth, M.; Dunn, K.A. Direct-write 3D nanolithography at cryogenic temperatures. Nanotechnology 2013, 24, 035301. [Google Scholar] [CrossRef]
- Sanz-Hernández, D.; Fernández-Pacheco, A. Modelling focused electron beam induced deposition beyond Langmuir adsorption. Beilstein J. Nanotechnol. 2017, 8, 2151–2161. [Google Scholar] [CrossRef]
- Córdoba, R.; Orús, P.; Strohauer, S.; Torres, T.E.; De Teresa, J.M. Ultra-fast direct growth of metallic micro- and nano-structures by focused ion beam irradiation. Sci. Rep. 2019, 9, 14076. [Google Scholar] [CrossRef]
- De Teresa, J.; Orús, P.; Córdoba, R.; Philipp, P. Comparison between Focused Electron/Ion Beam-Induced Deposition at Room Temperature and under Cryogenic Conditions. Micromachines 2019, 10, 799. [Google Scholar] [CrossRef]
- Hirt, L.; Reiser, A.; Spolenak, R.; Zambelli, T. Additive Manufacturing of Metal Structures at the Micrometer Scale. Adv. Mater. 2017, 29, 1604211. [Google Scholar] [CrossRef] [PubMed]
- Fowlkes, J.D.; Winkler, R.; Lewis, B.B.; Stanford, M.G.; Plank, H.; Rack, P.D. Simulation-Guided 3D Nanomanufacturing via Focused Electron Beam Induced Deposition. ACS Nano 2016, 10, 6163–6172. [Google Scholar] [CrossRef] [PubMed]
- Matsui, S. Three-Dimensional Nanostructure Fabrication by Focused Ion Beam Chemical Vapor Deposition. In Springer Handbook of Nanotechnology; Springer: Berlin/Heidelberg, Germany, 2010; pp. 211–229. [Google Scholar]
- Niessen, F.; Nancarrow, M.J.B. Computer-aided manufacturing and focused ion beam technology enable machining of complex micro- and nano-structures. Nanotechnology 2019, 30, 435301. [Google Scholar] [CrossRef]
- Fowlkes, J.D.; Winkler, R.; Lewis, B.B.; Fernández-Pacheco, A.; Skoric, L.; Sanz-Hernández, D.; Stanford, M.G.; Mutunga, E.; Rack, P.D.; Plank, H. High-Fidelity 3D-Nanoprinting via Focused Electron Beams: Computer-Aided Design (3BID). ACS Appl. Nano Mater. 2018, 1, 1028–1041. [Google Scholar] [CrossRef]
- Keller, L.; Huth, M. Pattern generation for direct-write three-dimensional nanoscale structures via focused electron beam induced deposition. Beilstein J. Nanotechnol. 2018, 9, 2581–2598. [Google Scholar] [CrossRef]
- Al Mamoori, M.; Keller, L.; Pieper, J.; Barth, S.; Winkler, R.; Plank, H.; Müller, J.; Huth, M. Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices. Materials 2018, 11, 289. [Google Scholar] [CrossRef]
- Al Mamoori, M.; Schröder, C.; Keller, L.; Huth, M.; Müller, J. First-order reversal curves (FORCs) of nano-engineered 3D Co-Fe structures. AIP Adv. 2020, 10, 015319. [Google Scholar] [CrossRef]
- Mutunga, E.; Winkler, R.; Sattelkow, J.; Rack, P.D.; Plank, H.; Fowlkes, J.D. Impact of Electron-Beam Heating during 3D Nanoprinting. ACS Nano 2019, 13, 5198–5213. [Google Scholar] [CrossRef]
- Vázquez, M. Magnetic Nano-and Microwires: Design, Synthesis, Properties and Applications; Woodhead Publishing: Cambridge, UK, 2020; ISBN 9780081028322. [Google Scholar]
- Winkler, R.; Fowlkes, J.D.; Rack, P.D.; Plank, H. 3D nanoprinting via focused electron beams. J. Appl. Phys. 2019, 125, 210901. [Google Scholar] [CrossRef]
- Toth, M.; Lobo, C.; Friedli, V.; Szkudlarek, A.; Utke, I. Continuum models of focused electron beam induced processing. Beilstein J. Nanotechnol. 2015, 6, 1518–1540. [Google Scholar] [CrossRef]
- Utke, I.; Hoffmann, P.; Melngailis, J. Gas-assisted focused electron beam and ion beam processing and fabrication. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2008, 26, 1197. [Google Scholar] [CrossRef]
- De Teresa, J.M.; Fernández-Pacheco, A.; Córdoba, R.; Serrano-Ramón, L.; Sangiao, S.; Ibarra, M.R. Review of magnetic nanostructures grown by focused electron beam induced deposition (FEBID). J. Phys. D Appl. Phys. 2016, 49, 243003. [Google Scholar] [CrossRef]
- De Teresa, J.M.; Fernández-Pacheco, A. Present and future applications of magnetic nanostructures grown by FEBID. Appl. Phys. A 2014, 117, 1645–1658. [Google Scholar] [CrossRef]
- Fernández-Pacheco, A.; Serrano-Ramón, L.; Michalik, J.M.; Ibarra, M.R.; De Teresa, J.M.; O’Brien, L.; Petit, D.; Lee, J.; Cowburn, R.P. Three dimensional magnetic nanowires grown by focused electron-beam induced deposition. Sci. Rep. 2013, 3, 1492. [Google Scholar] [CrossRef] [PubMed]
- Gavagnin, M.; Wanzenboeck, H.D.; Wachter, S.; Shawrav, M.M.; Persson, A.; Gunnarsson, K.; Svedlindh, P.; Stöger-Pollach, M.; Bertagnolli, E. Free-Standing Magnetic Nanopillars for 3D Nanomagnet Logic. ACS Appl. Mater. Interfaces 2014, 6, 20254–20260. [Google Scholar] [CrossRef] [PubMed]
- Córdoba, R.; Sharma, N.; Kölling, S.; Koenraad, P.M.; Koopmans, B. High-purity 3D nano-objects grown by focused-electron-beam induced deposition. Nanotechnology 2016, 27, 355301. [Google Scholar] [CrossRef] [PubMed]
- Botman, A.; Mulders, J.J.L.; Hagen, C.W. Creating pure nanostructures from electron-beam-induced deposition using purification techniques: A technology perspective. Nanotechnology 2009, 20, 372001. [Google Scholar] [CrossRef]
- Mulders, J.J.L. Practical precursor aspects for electron beam induced deposition. Nanofabrication 2014, 1. [Google Scholar] [CrossRef]
- Shimojo, M.; Takeguchi, M.; Tanaka, M.; Mitsuishi, K.; Furuya, K. Electron beam-induced deposition using iron carbonyl and the effects of heat treatment on nanostructure. Appl. Phys. A 2004, 79, 1869–1872. [Google Scholar] [CrossRef]
- Puydinger Dos Santos, M.V.; Velo, M.F.; Domingos, R.D.; Zhang, Y.; Maeder, X.; Guerra-Nuñez, C.; Best, J.P.; Béron, F.; Pirota, K.R.; Moshkalev, S.; et al. Annealing-Based Electrical Tuning of Cobalt-Carbon Deposits Grown by Focused-Electron-Beam-Induced Deposition. ACS Appl. Mater. Interfaces 2016, 8, 32496–32503. [Google Scholar] [CrossRef]
- Begun, E.; Dobrovolskiy, O.V.; Kompaniiets, M.; Sachser, R.; Gspan, C.; Plank, H.; Huth, M. Post-growth purification of Co nanostructures prepared by focused electron beam induced deposition. Nanotechnology 2015, 26, 075301. [Google Scholar] [CrossRef] [PubMed]
- Dobrovolskiy, O.V.; Kompaniiets, M.; Sachser, R.; Porrati, F.; Gspan, C.; Plank, H.; Huth, M. Tunable magnetism on the lateral mesoscale by post-processing of Co/Pt heterostructures. Beilstein J. Nanotechnol. 2015, 6, 1082–1090. [Google Scholar] [CrossRef] [PubMed]
- Córdoba, R.; Sesé, J.; De Teresa, J.M.; Ibarra, M.R. High-purity cobalt nanostructures grown by focused-electron-beam-induced deposition at low current. Microelectron. Eng. 2010, 87, 1550–1553. [Google Scholar] [CrossRef]
- Mulders, J.J.L.; Belova, L.M.; Riazanova, A. Electron beam induced deposition at elevated temperatures: Compositional changes and purity improvement. Nanotechnology 2011, 22, 055302. [Google Scholar] [CrossRef]
- Gazzadi, G.C.; Frabboni, S. Structural transitions in electron beam deposited Co-carbonyl suspended nanowires at high electrical current densities. Beilstein J. Nanotechnol. 2015, 6, 1298–1305. [Google Scholar] [CrossRef] [PubMed]
- Pablo-Navarro, J.; Sanz-Hernández, D.; Magén, C.; Fernández-Pacheco, A.; De Teresa, J.M. Tuning shape, composition and magnetization of 3D cobalt nanowires grown by focused electron beam induced deposition (FEBID). J. Phys. D Appl. Phys. 2017, 50, 18LT01. [Google Scholar] [CrossRef]
- Rodríguez, L.A.; Deen, L.; Córdoba, R.; Magén, C.; Snoeck, E.; Koopmans, B.; De Teresa, J.M. Influence of the shape and surface oxidation in the magnetization reversal of thin iron nanowires grown by focused electron beam induced deposition. Beilstein J. Nanotechnol. 2015, 6, 1319–1331. [Google Scholar] [CrossRef]
- Pablo-Navarro, J.; Magén, C.; De Teresa, J.M. Three-dimensional core-shell ferromagnetic nanowires grown by focused electron beam induced deposition. Nanotechnology 2016, 27, 285302. [Google Scholar] [CrossRef]
- Wartelle, A.; Pablo-Navarro, J.; Staňo, M.; Bochmann, S.; Pairis, S.; Rioult, M.; Thirion, C.; Belkhou, R.; De Teresa, J.M.; Magén, C.; et al. Transmission XMCD-PEEM imaging of an engineered vertical FEBID cobalt nanowire with a domain wall. Nanotechnology 2018, 29, 045704. [Google Scholar] [CrossRef]
- Pablo-Navarro, J.; Magén, C.; de Teresa, J.M. Purified and Crystalline Three-Dimensional Electron-Beam-Induced Deposits: The Successful Case of Cobalt for High-Performance Magnetic Nanowires. ACS Appl. Nano Mater. 2018, 1, 38–46. [Google Scholar] [CrossRef]
- Pablo-Navarro, J.; Winkler, R.; Haberfehlner, G.; Magén, C.; Plank, H.; De Teresa, J.M. In situ real-time annealing of ultrathin vertical Fe nanowires grown by focused electron beam induced deposition. Acta Mater. 2019, 174, 379–386. [Google Scholar] [CrossRef]
- Puydinger, M.V.; Szkudlarek, A.; Rydosz, A.; Guerra-nuñez, C.; Béron, F.; Pirota, K.R.; Moshkalev, S.; Diniz, J.A.; Utke, I. Comparative study of post-growth annealing of Cu(hfac)2, Co2(CO)8 and Me2Au (acac) metal precursors deposited by FEBID. Beilstein J. Nanotechnol. 2018, 9, 91–101. [Google Scholar] [CrossRef]
- Martínez-Pérez, M.J.; Pablo-Navarro, J.; Müller, B.; Kleiner, R.; Magén, C.; Koelle, D.; De Teresa, J.M.; Sesé, J. NanoSQUID Magnetometry on Individual As-grown and Annealed Co Nanowires at Variable Temperature. Nano Lett. 2018, 18, 7674–7682. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780511845000. [Google Scholar]
- Huth, M.; Porrati, F.; Dobrovolskiy, O.V. Focused electron beam induced deposition meets materials science. Microelectron. Eng. 2018, 185–186, 9–28. [Google Scholar] [CrossRef]
- Porrati, F.; Kämpken, B.; Terfort, A.; Huth, M. Fabrication and electrical transport properties of binary Co-Si nanostructures prepared by focused electron beam-induced deposition. J. Appl. Phys. 2013, 113, 053707. [Google Scholar] [CrossRef]
- Porrati, F.; Barth, S.; Sachser, R.; Jungwirth, F.; Eltsov, M.; Frangakis, A.S.; Huth, M. Binary Mn-Si nanostructures prepared by focused electron beam induced deposition from the precursor SiH3Mn(CO)5. J. Phys. D Appl. Phys. 2018, 51, 455301. [Google Scholar] [CrossRef]
- Porrati, F.; Sachser, R.; Gazzadi, G.C.; Frabboni, S.; Huth, M. Fabrication of FeSi and Fe3Si compounds by electron beam induced mixing of [Fe/Si]2 and [Fe3/Si]2 multilayers grown by focused electron beam induced deposition. J. Appl. Phys. 2016, 119, 234306. [Google Scholar] [CrossRef]
- Porrati, F.; Sachser, R.; Gazzadi, G.C.; Frabboni, S.; Terfort, A.; Huth, M. Alloy multilayers and ternary nanostructures by direct-write approach. Nanotechnology 2017, 28, 415302. [Google Scholar] [CrossRef]
- Porrati, F.; Pohlit, M.; Uller, J.; Barth, S.; Biegger, F.; Gspan, C.; Plank, H.; Huth, M. Direct writing of CoFe alloy nanostructures by focused electron beam induced deposition from a heteronuclear precursor. Nanotechnology 2015, 26, 475701. [Google Scholar] [CrossRef]
- Kumar, T.P.R.; Weirich, P.; Hrachowina, L.; Hanefeld, M.; Bjornsson, R.; Hrodmarsson, H.R.; Barth, S.; Fairbrother, D.H.; Huth, M.; Ingólfsson, O. Electron interactions with the heteronuclear carbonyl precursor H2FeRu3(CO)13 and comparison with HFeCo3(CO)12: From fundamental gas phase and surface science studies to focused electron beam induced deposition. Beilstein J. Nanotechnol. 2018, 9, 555–579. [Google Scholar] [CrossRef]
- Barth, S.; Huth, M.; Jungwirth, F. Precursors for Focused Electron Beam Deposition: A Review Highlighting the Chemical Characteristics and State-of-the-Art. Chem. Rev. 2020. submitted. [Google Scholar]
- Sanz-Hernández, D.; Hamans, R.F.; Liao, J.W.; Welbourne, A.; Lavrijsen, R.; Fernández-Pacheco, A. Fabrication, Detection, and Operation of a Three-Dimensional Nanomagnetic Conduit. ACS Nano 2017, 11, 11066–11073. [Google Scholar] [CrossRef]
- Sanz-Hernández, D.; Hamans, R.; Osterrieth, J.; Liao, J.-W.; Skoric, L.; Fowlkes, J.; Rack, P.; Lippert, A.; Lee, S.; Lavrijsen, R.; et al. Fabrication of Scaffold-Based 3D Magnetic Nanowires for Domain Wall Applications. Nanomaterials 2018, 8, 483. [Google Scholar] [CrossRef]
- Plank, H.; Winkler, R.; Schwalb, C.H.; Hütner, J.; Fowlkes, J.D.; Rack, P.D.; Utke, I.; Huth, M. Focused Electron Beam-Based 3D Nanoprinting for Scanning Probe Microscopy: A Review. Micromachines 2019, 11, 48. [Google Scholar] [CrossRef]
- Guo, F.; Belova, L.M.; McMichael, R.D. Spectroscopy and Imaging of Edge Modes in Permalloy Nanodisks. Phys. Rev. Lett. 2013, 110, 017601. [Google Scholar] [CrossRef]
- Belova, L.M.; Hellwig, O.; Dobisz, E.; Dan Dahlberg, E. Rapid preparation of electron beam induced deposition Co magnetic force microscopy tips with 10 nm spatial resolution. Rev. Sci. Instrum. 2012, 83, 093711. [Google Scholar] [CrossRef]
- Chia, H.J.; Guo, F.; Belova, L.M.; McMichael, R.D. Nanoscale spin wave localization using ferromagnetic resonance force microscopy. Phys. Rev. Lett. 2012, 108, 087206. [Google Scholar] [CrossRef]
- Sangiao, S.; Magén, C.; Mofakhami, D.; de Loubens, G.; De Teresa, J.M. Magnetic properties of optimized cobalt nanospheres grown by focused electron beam induced deposition (FEBID) on cantilever tips. Beilstein J. Nanotechnol. 2017, 8, 2106–2115. [Google Scholar] [CrossRef]
- Lavenant, H.; Naletov, V.; Klein, O.; de Loubens, G.; Casado, L.; De Teresa, J.M. Mechanical magnetometry of Cobalt nanospheres deposited by focused electron beam at the tip of ultra-soft cantilevers. Nanofabrication 2014, 1, 65–73. [Google Scholar] [CrossRef]
- Mattiat, H.; Rossi, N.; Gross, B.; Pablo-Navarro, J.; Magén, C.; Badea, R.; Berezovsky, J.; De Teresa, J.M.; Poggio, M. Nanowire Magnetic Force Sensors Fabricated by Focused-Electron-Beam-Induced Deposition. Phys. Rev. Appl. 2020, 13, 044043. [Google Scholar] [CrossRef]
- Lau, Y.M.; Chee, P.C.; Thong, J.T.L.; Ng, V. Properties and applications of cobalt-based material produced by electron-beam-induced deposition. J. Vac. Sci. Technol. A Vac. Surf. Film. 2002, 20, 1295. [Google Scholar] [CrossRef][Green Version]
- Utke, I.; Hoffmann, P.; Berger, R.; Scandella, L. High-resolution magnetic Co supertips grown by a focused electron beam. Appl. Phys. Lett. 2002, 80, 4792. [Google Scholar] [CrossRef]
- Stiller, M.; Barzola-Quiquia, J.; Esquinazi, P.D.; Sangiao, S.; De Teresa, J.M.; Meijer, J.; Abel, B. Functionalized Akiyama tips for magnetic force microscopy measurements. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Jaafar, M.; Pablo-Navarro, J.; Berganza, E.; Ares, P.; Magén, C.; Masseboeuf, A.; Gatel, C.; Snoeck, E.; Gómez-Herrero, J.; de Teresa, J.M.; et al. Customized MFM probes based on magnetic nanorods. Nanoscale 2020, 12, 10090–10097. [Google Scholar] [CrossRef]
- Berganza Eguiarte, E.; Jaafar, M.; Fernández-Roldán, J.Á.; Goiriena-Goikoetxea, M.; Pablo-Navarro, J.; García Arribas, A.; Guslienko, K.; Magen, C.; De Teresa, J.M.; Chubykalo-Fesenko, O.; et al. Half-hedgehog spin textures in sub-100 nm soft magnetic nanodots. Nanoscale 2020. [Google Scholar] [CrossRef]
- Jaafar, M.; De Teresa, J.M.; Asenjo, A.; Pablo-Navarro, J.; Ares, P.; Magén, C.; Gómez-Herrero, J. System for an Atomic Force Microscope. Patent PCT/ES2018/070709 and WO19086745, 11 May 2018. [Google Scholar]
- Braakman, F.R.; Poggio, M. Force sensing with nanowire cantilevers. Nanotechnology 2019, 30, 332001. [Google Scholar] [CrossRef]
- Che, R.C.; Takeguchi, M.; Shimojo, M.; Zhang, W.; Furuya, K. Fabrication and electron holography characterization of FePt alloy nanorods. Appl. Phys. Lett. 2005, 87, 223109. [Google Scholar] [CrossRef]
- Porrati, F.; Begun, E.; Sachser, R.; Huth, M. Spin-dependent transport between magnetic nanopillars through a nano-granular metal matrix. J. Phys. D Appl. Phys. 2014, 47, 495001. [Google Scholar] [CrossRef]
- Vavassori, P.; Pancaldi, M.; Perez-Roldan, M.J.; Chuvilin, A.; Berger, A. Remote Magnetomechanical Nanoactuation. Small 2016, 12, 1013–1023. [Google Scholar] [CrossRef]
- Keller, L.; Al Mamoori, M.K.I.; Pieper, J.; Gspan, C.; Stockem, I.; Schröder, C.; Barth, S.; Winkler, R.; Plank, H.; Pohlit, M.; et al. Direct-write of free-form building blocks for artificial magnetic 3D lattices. Sci. Rep. 2018, 8, 6160. [Google Scholar] [CrossRef]
- Castelnovo, C.; Moessner, R.; Sondhi, S.L. Magnetic monopoles in spin ice. Nature 2008, 451, 42–45. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, C.; Moessner, R.; Schiffer, P. Colloquium: Artificial spin ice: Designing and imaging magnetic frustration. Rev. Mod. Phys. 2013, 85, 1473–1490. [Google Scholar] [CrossRef]
- Volkov, O.M.; Kákay, A.; Kronast, F.; Mönch, I.; Mawass, M.-A.; Fassbender, J.; Makarov, D. Experimental Observation of Exchange-Driven Chiral Effects in Curvilinear Magnetism. Phys. Rev. Lett. 2019, 123, 077201. [Google Scholar] [CrossRef] [PubMed]
- Sheka, D.D.; Pylypovskyi, O.V.; Landeros, P.; Gaididei, Y.; Kákay, A.; Makarov, D. Nonlocal chiral symmetry breaking in curvilinear magnetic shells. Commun. Phys. 2020, 3, 1–7. [Google Scholar] [CrossRef]
- Pylypovskyi, O.V.; Kravchuk, V.P.; Sheka, D.D.; Makarov, D.; Schmidt, O.G.; Gaididei, Y. Coupling of Chiralities in Spin and Physical Spaces: The Möbius Ring as a Case Study. Phys. Rev. Lett. 2015, 114, 197204. [Google Scholar] [CrossRef]
- Kravchuk, V.P.; Sheka, D.D.; Kákay, A.; Volkov, O.M.; Rößler, U.K.; Van Den Brink, J.; Makarov, D.; Gaididei, Y. Multiplet of skyrmion states on a curvilinear defect: Reconfigurable skyrmion lattices. Phys. Rev. Lett. 2018, 120, 067201. [Google Scholar] [CrossRef]
- Yan, M.; Kákay, A.; Gliga, S.; Hertel, R. Beating the Walker Limit with Massless Domain Walls in Cylindrical Nanowires. Phys. Rev. Lett. 2010, 104, 057201. [Google Scholar] [CrossRef]
- Otálora, J.A.; Yan, M.; Schultheiss, H.; Hertel, R.; Kákay, A. Curvature-Induced Asymmetric Spin-Wave Dispersion. Phys. Rev. Lett. 2016, 117, 227203. [Google Scholar] [CrossRef]
- Yan, M.; Kákay, A.; Andreas, C.; Hertel, R. Spin-Cherenkov effect and magnonic Mach cones. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 220412. [Google Scholar] [CrossRef]
- Staňo, M.; Fruchart, O. Magnetic Nanowires and Nanotubes. Handb. Magn. Mater. 2018, 27, 155–267. [Google Scholar] [CrossRef]
- Volkov, O.M.; Sheka, D.D.; Gaididei, Y.; Kravchuk, V.P.; Rößler, U.K.; Fassbender, J.; Makarov, D. Mesoscale Dzyaloshinskii-Moriya interaction: Geometrical tailoring of the magnetochirality. Sci. Rep. 2018, 8, 866. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Cuscunà, M.; Todisco, F.; Benedetti, A.; Tarantini, I.; De Giorgi, M.; Sanvitto, D.; Passaseo, A. Nanoscale 3D Chiral Plasmonic Helices with Circular Dichroism at Visible Frequencies. ACS Photonics 2015, 2, 105–114. [Google Scholar] [CrossRef]
- Phatak, C.; Miller, C.S.; Thompson, Z.; Gulsoy, E.B.; Petford-Long, A. Curved Three-Dimensional Cobalt Nanohelices for Use in Domain Wall Device Applications. ACS Appl. Nano Mater. 2020, 3, 6009–6016. [Google Scholar] [CrossRef]
- Sanz-Hernández, D.; Hierro-Rodriguez, A.; Donnelly, C.; Pablo-Navarro, J.; Sorrentino, A.; Pereiro, E.; Magén, C.; McVitie, S.; De Teresa, J.M.; Ferrer, S.; et al. Artificial Double-Helix for Geometrical Control of Magnetic Chirality. ACS Nano 2020, 14, 8092. [Google Scholar] [CrossRef] [PubMed]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nat. Phys. 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Kim, S.K.; Myers, R.; Tserkovnyak, Y. Nonlocal Spin Transport Mediated by a Vortex Liquid in Superconductors. Phys. Rev. Lett. 2018, 121, 187203. [Google Scholar] [CrossRef]
- Jeon, K.R.; Ciccarelli, C.; Ferguson, A.J.; Kurebayashi, H.; Cohen, L.F.; Montiel, X.; Eschrig, M.; Robinson, J.W.A.; Blamire, M.G. Enhanced spin pumping into superconductors provides evidence for superconducting pure spin currents. Nat. Mater. 2018, 17, 499–503. [Google Scholar] [CrossRef]
- Wang, J.; Singh, M.; Tian, M.; Kumar, N.; Liu, B.; Shi, C.; Jain, J.K.; Samarth, N.; Mallouk, T.E.; Chan, M.H.W. Interplay between superconductivity and ferromagnetism in crystalline nanowires. Nat. Phys. 2010, 6, 389–394. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Volkov, A.F.; Efetov, K.B. Odd triplet superconductivity and related phenomena in superconductor- ferromagnet structures. Rev. Mod. Phys. 2005, 77, 1321–1373. [Google Scholar] [CrossRef]
- Kompaniiets, M.; Dobrovolskiy, O.V.; Neetzel, C.; Porrati, F.; Brötz, J.; Ensinger, W.; Huth, M. Long-range superconducting proximity effect in polycrystalline Co nanowires. Appl. Phys. Lett. 2014, 104, 052603. [Google Scholar] [CrossRef]
- Mel’nikov, A.S.; Buzdin, A.I. Giant Mesoscopic Fluctuations and Long-Range Superconducting Correlations in Superconductor-Ferromagnet Structures. Phys. Rev. Lett. 2016, 117, 077001. [Google Scholar] [CrossRef] [PubMed]
- MacHon, P.; Eschrig, M.; Belzig, W. Nonlocal thermoelectric effects and nonlocal onsager relations in a three-terminal proximity-coupled superconductor-ferromagnet device. Phys. Rev. Lett. 2013, 110, 047002. [Google Scholar] [CrossRef] [PubMed]
- Linder, J.; Bathen, M.E. Spin caloritronics with superconductors: Enhanced thermoelectric effects, generalized Onsager response-matrix, and thermal spin currents. Phys. Rev. B 2016, 93, 224509. [Google Scholar] [CrossRef]
- Shaw, G.; Blanco Alvarez, S.B.; Brisbois, J.; Burger, L.; Pinheiro, L.B.L.G.; Kramer, R.B.G.; Motta, M.; Fleury-Frenette, K.; Ortiz, W.A.; Vanderheyden, B.; et al. Magnetic Recording of Superconducting States. Metals 2019, 9, 1022. [Google Scholar] [CrossRef]
- Jafri, H.M.; Ma, X.; Huang, H.; Zhao, C.; Qazi, H.I.A.; Kazmi, S.B.F.; Liu, Z.; Liu, L.; Shi, S.-Q.; Li, Y.; et al. Current assisted memory effect in superconductor–ferromagnet bilayers: A potential candidate for memristors. Supercond. Sci. Technol. 2019, 32, 095002. [Google Scholar] [CrossRef]
- Gömöry, F.; Solovyov, M.; Šouc, J.; Navau, C.; Prat-Camps, J.; Sanchez, A. Experimental realization of a magnetic cloak. Science 2012, 335, 1466–1468. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Huth, M.; Shklovskij, V.A. Anisotropic magnetoresistive response in thin Nb films decorated by an array of Co stripes. Supercond. Sci. Technol. 2010, 23, 125014. [Google Scholar] [CrossRef]
- Rouco, V.; Córdoba, R.; De Teresa, J.M.; Rodríguez, L.A.; Navau, C.; Del-Valle, N.; Via, G.; Sánchez, A.; Monton, C.; Kronast, F.; et al. Competition between Superconductor-Ferromagnetic stray magnetic fields in YBa2Cu3O7-x films pierced with Co nano-rods. Sci. Rep. 2017, 7, 5663. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Begun, E.; Huth, M.; Shklovskij, V.A.; Tsindlekht, M.I. Vortex lattice matching effects in a washboard pinning potential induced by Co nanostripe arrays. Phys. C Supercond. Appl. 2011, 471, 449–452. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V. Abrikosov fluxonics in washboard nanolandscapes. Phys. C Supercond. Appl. 2017, 533, 80–90. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Begun, E.; Bevz, V.M.; Sachser, R.; Huth, M. Upper Frequency Limits for Vortex Guiding and Ratchet Effects. Phys. Rev. Appl. 2020, 13, 024012. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Bevz, V.M.; Begun, E.; Sachser, R.; Vovk, R.V.; Huth, M. Fast Dynamics of Guided Magnetic Flux Quanta. Phys. Rev. Appl. 2019, 11, 054064. [Google Scholar] [CrossRef]
- Bulaevskii, L.N.; Chudnovsky, E.M. Sound generation by the vortex flow in type-II superconductors. Phys. Rev. B 2005, 72, 094518. [Google Scholar] [CrossRef]
- Bespalov, A.A.; Mel’Nikov, A.S.; Buzdin, A.I. Magnon radiation by moving Abrikosov vortices in ferromagnetic superconductors and superconductor-ferromagnet multilayers. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Golovchanskiy, I.A.; Abramov, N.N.; Pfirrmann, M.; Piskor, T.; Voss, J.N.; Baranov, D.S.; Hovhannisyan, R.A.; Stolyarov, V.S.; Dubs, C.; Golubov, A.A.; et al. Interplay of Magnetization Dynamics with a Microwave Waveguide at Cryogenic Temperatures. Phys. Rev. Appl. 2019, 11, 044076. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Sachser, R.; Brächer, T.; Böttcher, T.; Kruglyak, V.V.; Vovk, R.V.; Shklovskij, V.A.; Huth, M.; Hillebrands, B.; Chumak, A.V. Magnon–fluxon interaction in a ferromagnet/superconductor heterostructure. Nat. Phys. 2019, 15, 477–482. [Google Scholar] [CrossRef]
- Golovchanskiy, I.A.; Abramov, N.N.; Stolyarov, V.S.; Bolginov, V.V.; Ryazanov, V.V.; Golubov, A.A.; Ustinov, A.V. Ferromagnet/Superconductor Hybridization for Magnonic Applications. Adv. Funct. Mater. 2018, 28, 1802375. [Google Scholar] [CrossRef]
- Moll, P.J.W.; Balicas, L.; Geshkenbein, V.; Blatter, G.; Karpinski, J.; Zhigadlo, N.D.; Batlogg, B. Transition from slow Abrikosov to fast moving Josephson vortices in iron pnictide superconductors. Nat. Mater. 2013, 12, 134–138. [Google Scholar] [CrossRef]
- Golod, T.; Iovan, A.; Krasnov, V.M. Single Abrikosov vortices as quantized information bits. Nat. Commun. 2015, 6, 8628. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Bevz, V.M.; Mikhailov, M.Y.; Yuzephovich, O.I.; Shklovskij, V.A.; Vovk, R.V.; Tsindlekht, M.I.; Sachser, R.; Huth, M. Microwave emission from superconducting vortices in Mo/Si superlattices. Nat. Commun. 2018, 9, 4927. [Google Scholar] [CrossRef]
- Rouco, V.; Massarotti, D.; Stornaiuolo, D.; Papari, G.; Obradors, X.; Puig, T.; Tafuri, F.; Palau, A. Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires. Materials 2018, 11, 211. [Google Scholar] [CrossRef] [PubMed]
- Lösch, S.; Alfonsov, A.; Dobrovolskiy, O.V.; Keil, R.; Engemaier, V.; Baunack, S.; Li, G.; Schmidt, O.G.; Bürger, D. Microwave Radiation Detection with an Ultrathin Free-Standing Superconducting Niobium Nanohelix. ACS Nano 2019, 13, 2948–2955. [Google Scholar] [CrossRef]
- Makise, K.; Mitsuishi, K.; Shimojo, M.; Shinozaki, B. Microstructural analysis and transport properties of MoO and MoC nanostructures prepared by focused electron beam-induced deposition. Sci. Rep. 2014, 4, 5740. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Li, C.; Baumier, C.; Kasumov, A.; Guéron, S.; Bouchiat, H.; Fortuna, F. Superconducting nanowires by electron-beam-induced deposition. Appl. Phys. Lett. 2015, 106, 042601. [Google Scholar] [CrossRef]
- Winhold, M.; Weirich, P.M.; Schwalb, C.H.; Huth, M. Superconductivity and metallic behavior in PbxCyOδ structures prepared by focused electron beam induced deposition. Appl. Phys. Lett. 2014, 105, 162603. [Google Scholar] [CrossRef]
- Córdoba, R.; Ibarra, A.; Mailly, D.; De Teresa, J.M. Vertical Growth of Superconducting Crystalline Hollow Nanowires by He+ Focused Ion Beam Induced Deposition. Nano Lett. 2018, 18, 1379–1386. [Google Scholar] [CrossRef]
- Córdoba, R.; Mailly, D.; Rezaev, R.O.; Smirnova, E.I.; Schmidt, O.G.; Fomin, V.M.; Zeitler, U.; Guillamón, I.; Suderow, H.; De Teresa, J.M. Three-Dimensional Superconducting Nanohelices Grown by He+-Focused-Ion-Beam Direct Writing. Nano Lett. 2019, 19, 8597–8604. [Google Scholar] [CrossRef]
- Gladilin, V.N.; Tempere, J.; Devreese, J.T.; Moshchalkov, V.V. Aharonov-Bohm oscillations in the vortex dynamics in superconducting hollow cylinders. Phys. Rev. B 2012, 86, 104508. [Google Scholar] [CrossRef]
- Rezaev, R.O.; Levchenko, E.A.; Fomin, V.M. Branching of the vortex nucleation period in superconductor Nb microtubes due to an inhomogeneous transport current. Supercond. Sci. Technol. 2016, 29, 045014. [Google Scholar] [CrossRef][Green Version]
- Porrati, F.; Barth, S.; Sachser, R.; Dobrovolskiy, O.V.; Seybert, A.; Frangakis, A.S.; Huth, M. Crystalline Niobium Carbide Superconducting Nanowires Prepared by Focused Ion Beam Direct Writing. ACS Nano 2019, 13, 6287–6296. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Vodolazov, D.Y.; Porrati, F.; Sachser, R.; Bevz, V.M.; Mikhailov, M.Y.; Chumak, A.V.; Huth, M. Ultra-fast vortex motion in a direct-write Nb-C superconductor. Nat. Commun. 2020, 11, 3291. [Google Scholar] [CrossRef] [PubMed]
- Sidorova, M.; Semenov, A.; Hübers, H.-W.; Ilin, K.; Siegel, M.; Charaev, I.; Moshkova, M.; Kaurova, N.; Goltsman, G.N.; Zhang, X.; et al. Electron energy relaxation in disordered superconducting NbN films. Phys. Rev. B 2019, 102, 054501. [Google Scholar] [CrossRef]
- Korneeva, Y.P.; Manova, N.N.; Florya, I.N.; Mikhailov, M.Y.; Dobrovolskiy, O.V.; Korneev, A.A.; Vodolazov, D.Y. Different Single-Photon Response of Wide and Narrow Superconducting MoxSi1-x Strips. Phys. Rev. Appl. 2020, 13, 024011. [Google Scholar] [CrossRef]
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453–461. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnonic crystals for data processing. J. Phys. D Appl. Phys. 2017, 50, 244001. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Sachser, R.; Bunyaev, S.A.; Navas, D.; Bevz, V.M.; Zelent, M.; Śmigaj, W.; Rychły, J.; Krawczyk, M.; Vovk, R.V.; et al. Spin-Wave Phase Inverter upon a Single Nanodefect. ACS Appl. Mater. Interfaces 2019, 11, 17654–17662. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Bunyaev, S.A.; Vovk, N.R.; Navas, D.; Gruszecki, P.; Krawczyk, M.; Sachser, R.; Huth, M.; Chumak, A.V.; Guslienko, K.Y.; et al. Spin-wave spectroscopy of individual ferromagnetic nanodisks. arXiv 2020, arXiv:2006.00763. [Google Scholar]
- Krawczyk, M.; Grundler, D. Review and prospects of magnonic crystals and devices with reprogrammable band structure. J. Phys. Condens. Matter. 2014, 26, 123202. [Google Scholar] [CrossRef]
- Vogel, M.; Aßmann, R.; Pirro, P.; Chumak, A.V.; Hillebrands, B.; von Freymann, G. Control of Spin-Wave Propagation using Magnetisation Gradients. Sci. Rep. 2018, 8, 11099. [Google Scholar] [CrossRef]
- Gruszecki, P.; Krawczyk, M. Spin-wave beam propagation in ferromagnetic thin films with graded refractive index: Mirage effect and prospective applications. Phys. Rev. B 2018, 97, 094424. [Google Scholar] [CrossRef]
- Lara, A.; Dobrovolskiy, O.V.; Prieto, J.L.; Huth, M.; Aliev, F.G. Magnetization reversal assisted by half antivortex states in nanostructured circular cobalt disks. Appl. Phys. Lett. 2014, 105, 182402. [Google Scholar] [CrossRef]
- Gubbiotti, G. Three-Dimensional Magnonics: Layered, Micro-and Nanostructures, 1st ed.; Jenny Stanford Publishing: Delhi, India, 2019; ISBN 9789814800730. [Google Scholar]
- Heyroth, F.; Hauser, C.; Trempler, P.; Geyer, P.; Syrowatka, F.; Dreyer, R.; Ebbinghaus, S.G.; Woltersdorf, G.; Schmidt, G. Monocrystalline Freestanding Three-Dimensional Yttrium-Iron-Garnet Magnon Nanoresonators. Phys. Rev. Appl. 2019, 12, 054031. [Google Scholar] [CrossRef]
- Wang, Q.; Kewenig, M.; Schneider, M.; Verba, R.; Kohl, F.; Heinz, B.; Geilen, M.; Mohseni, M.; Lägel, B.; Ciubotaru, F.; et al. A magnonic directional coupler for integrated magnonic half-adders, A magnonic directional coupler for integrated magnonic half-adders. Nat. Electron. 2020. accepted. [Google Scholar]
- Gliga, S.; Kákay, A.; Hertel, R.; Heinonen, O.G. Spectral analysis of topological defects in an artificial spin-ice lattice. Phys. Rev. Lett. 2013, 110, 117205. [Google Scholar] [CrossRef]
- Dubowik, J.; Kuświk, P.; Matczak, M.; Bednarski, W.; Stobiecki, F.; Aleshkevych, P.; Szymczak, H.; Kisielewski, M.; Kisielewski, J. Ferromagnetic resonance and resonance modes in kagome lattices: From an open to a closed kagome structure. Phys. Rev. B 2016, 93, 224423. [Google Scholar] [CrossRef]
- Bhat, V.S.; Heimbach, F.; Stasinopoulos, I.; Grundler, D. Angular-dependent magnetization dynamics of kagome artificial spin ice incorporating topological defects. Phys. Rev. B 2017, 96, 014426. [Google Scholar] [CrossRef]
- Jungfleisch, M.B.; Sklenar, J.; Ding, J.; Park, J.; Pearson, J.E.; Novosad, V.; Schiffer, P.; Hoffmann, A. High-Frequency Dynamics Modulated by Collective Magnetization Reversal in Artificial Spin Ice. Phys. Rev. Appl. 2017, 8, 064026. [Google Scholar] [CrossRef]
- May, A.; Hunt, M.; Van Den Berg, A.; Hejazi, A.; Ladak, S. Realisation of a frustrated 3D magnetic nanowire lattice. Commun. Phys. 2019, 2, 13. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Pacheco, A.; Skoric, L.; De Teresa, J.M.; Pablo-Navarro, J.; Huth, M.; Dobrovolskiy, O.V. Writing 3D Nanomagnets Using Focused Electron Beams. Materials 2020, 13, 3774. https://doi.org/10.3390/ma13173774
Fernández-Pacheco A, Skoric L, De Teresa JM, Pablo-Navarro J, Huth M, Dobrovolskiy OV. Writing 3D Nanomagnets Using Focused Electron Beams. Materials. 2020; 13(17):3774. https://doi.org/10.3390/ma13173774
Chicago/Turabian StyleFernández-Pacheco, Amalio, Luka Skoric, José María De Teresa, Javier Pablo-Navarro, Michael Huth, and Oleksandr V. Dobrovolskiy. 2020. "Writing 3D Nanomagnets Using Focused Electron Beams" Materials 13, no. 17: 3774. https://doi.org/10.3390/ma13173774
APA StyleFernández-Pacheco, A., Skoric, L., De Teresa, J. M., Pablo-Navarro, J., Huth, M., & Dobrovolskiy, O. V. (2020). Writing 3D Nanomagnets Using Focused Electron Beams. Materials, 13(17), 3774. https://doi.org/10.3390/ma13173774









