A Particle-Based Cohesive Crack Model for Brittle Fracture Problems
Abstract
1. Introduction
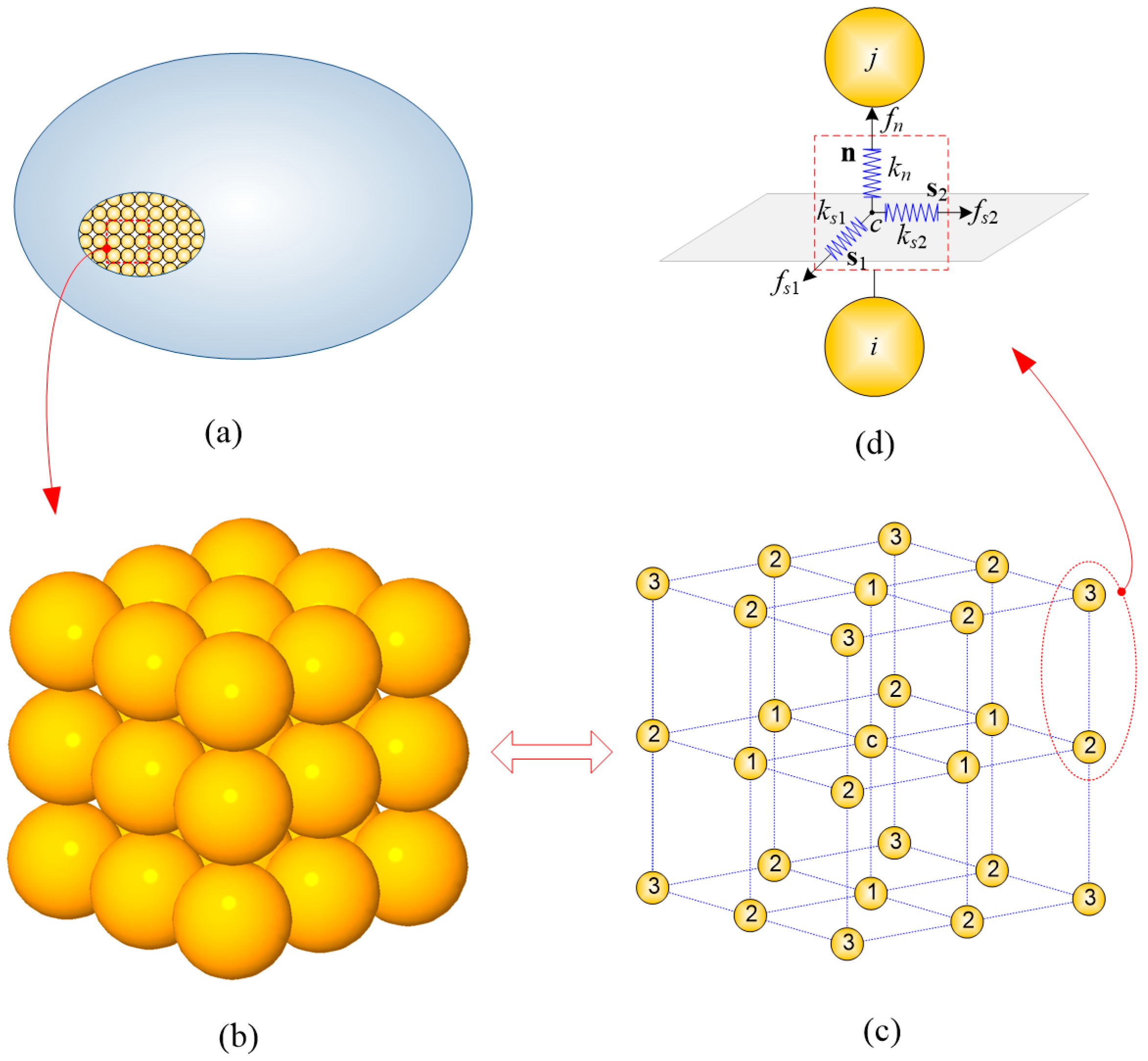
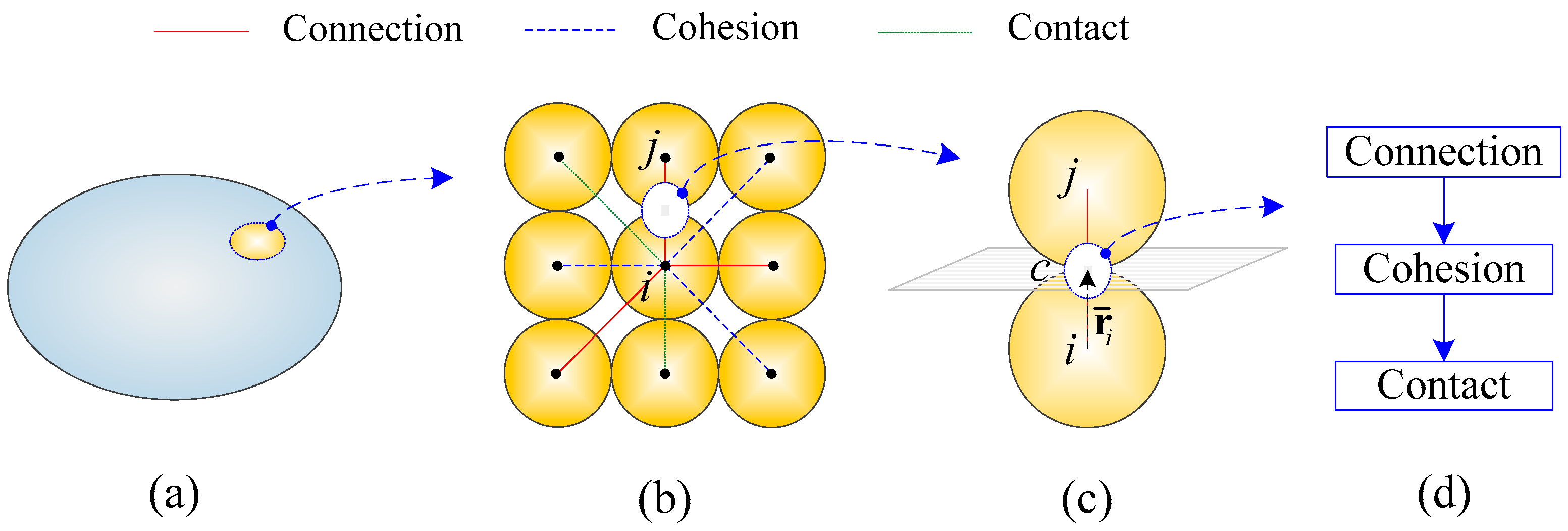
2. Connective Model: Representation of Isotropic Elastic Solid
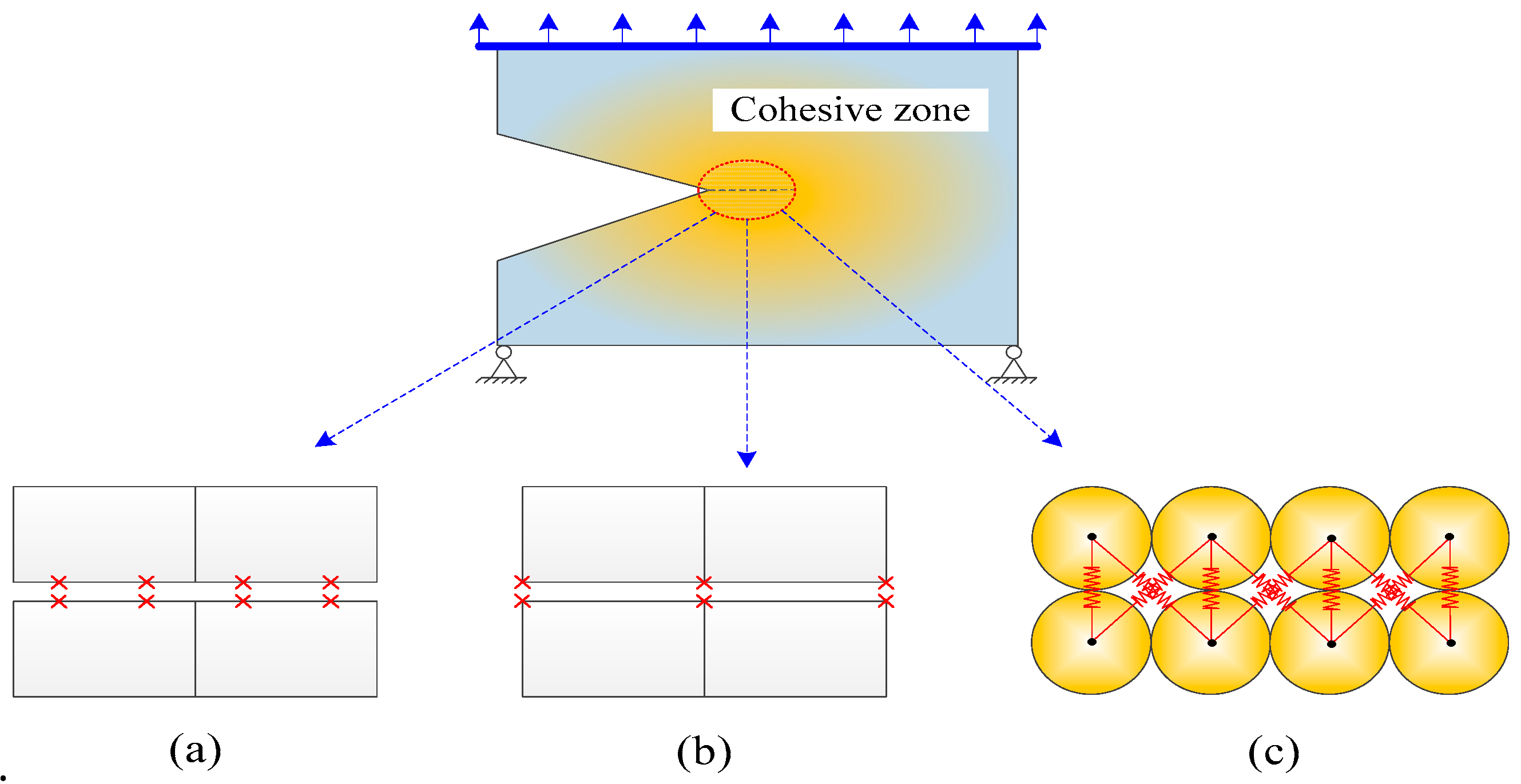
3. Cohesive Crack Model: Formulation of Fracture Process
3.1. General Description
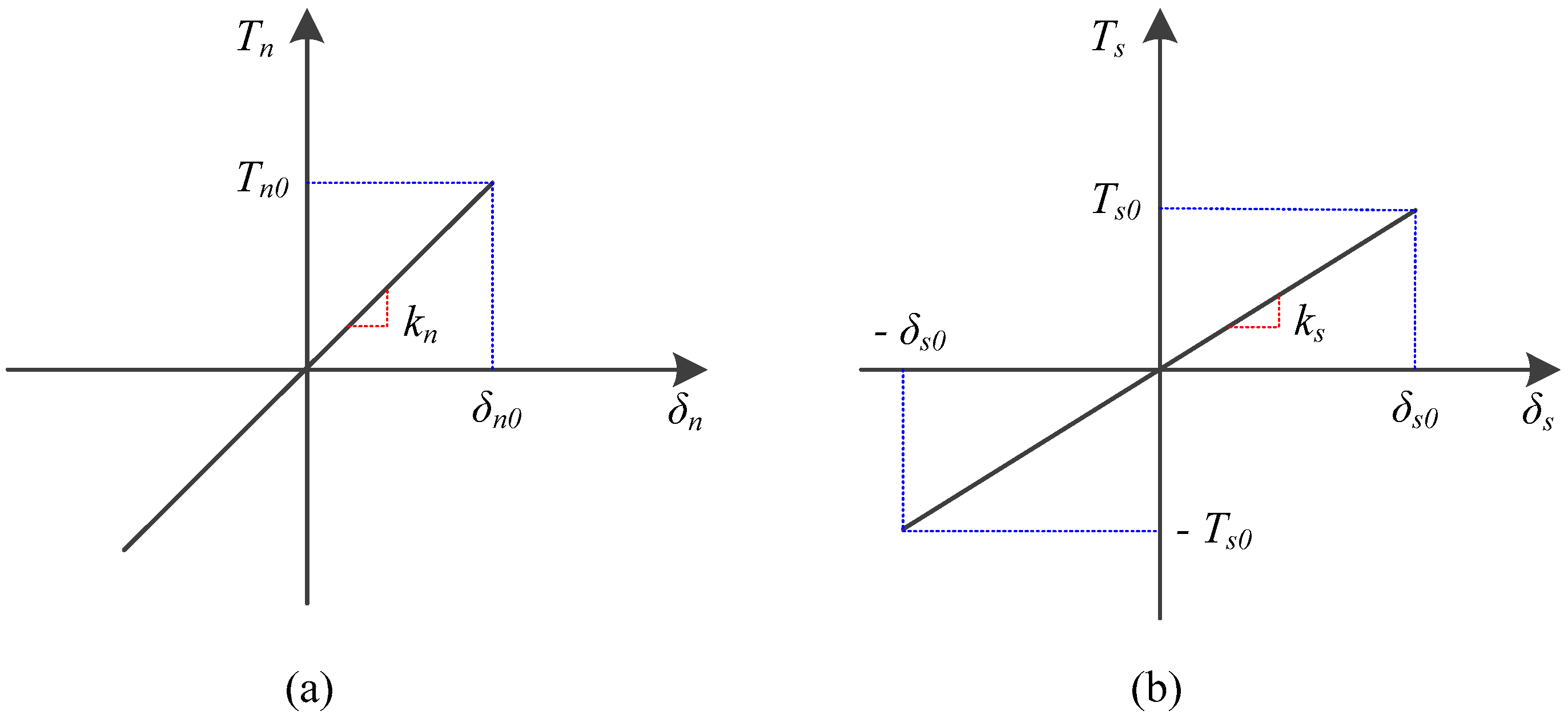
3.2. Mixed-Mode Fracture Propagation Criterion
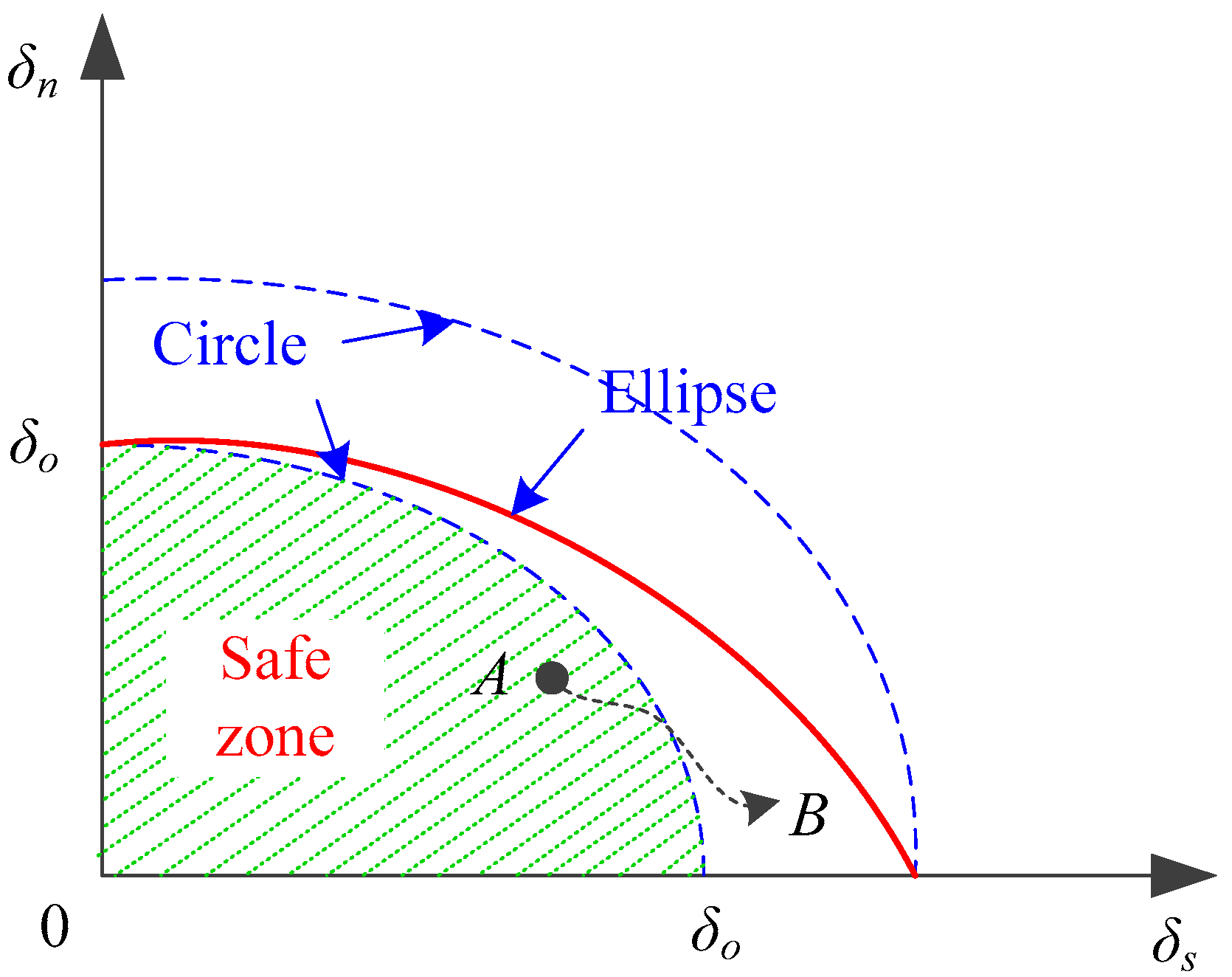
3.3. Mixed-Mode Fracture Initiation Criterion
4. Contact Model: Representation of Particulate Materials
5. Model Transition: Monotonically from Connection to Contact
6. Implementation: Explicit Update of Kinematics
7. Numerical Simulations
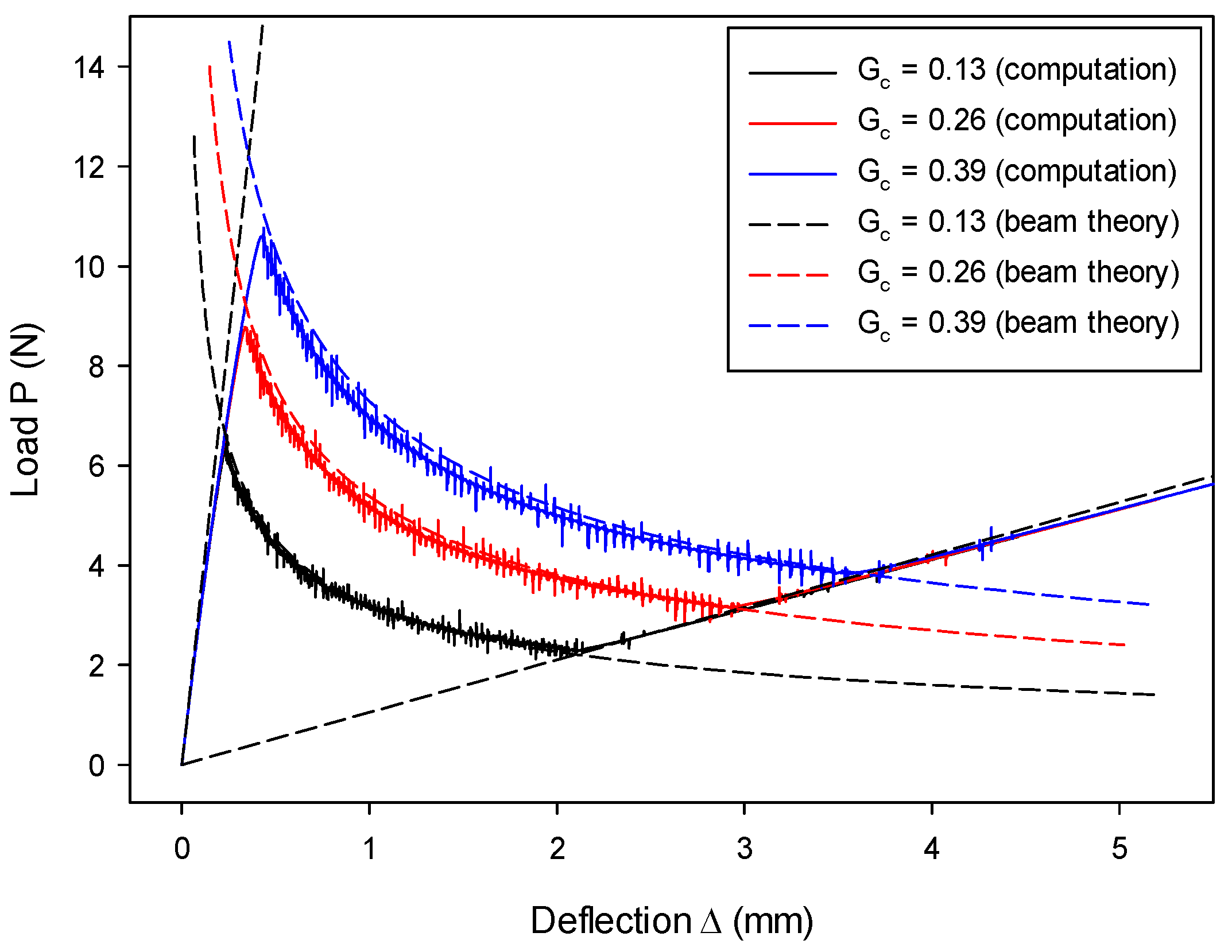
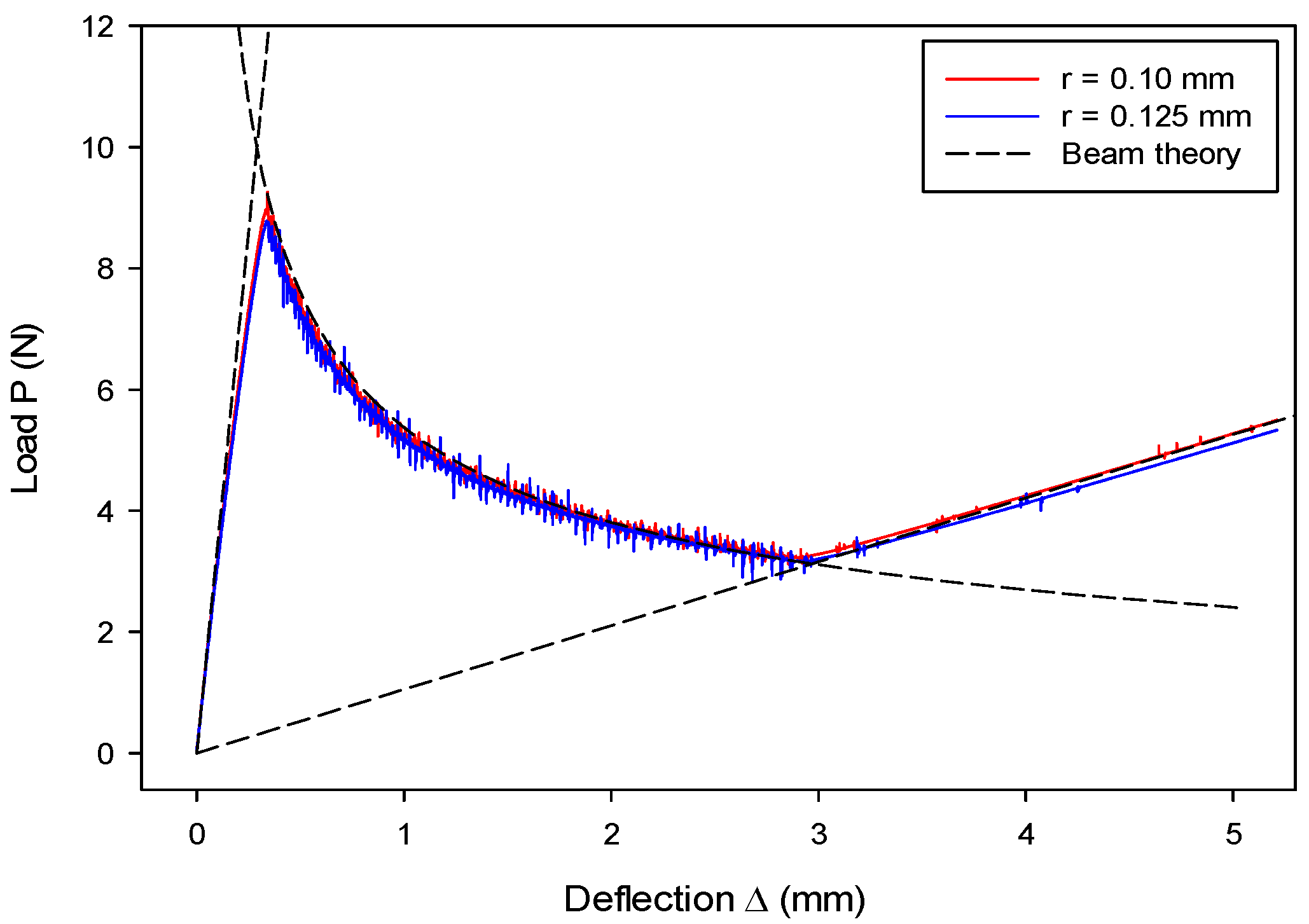
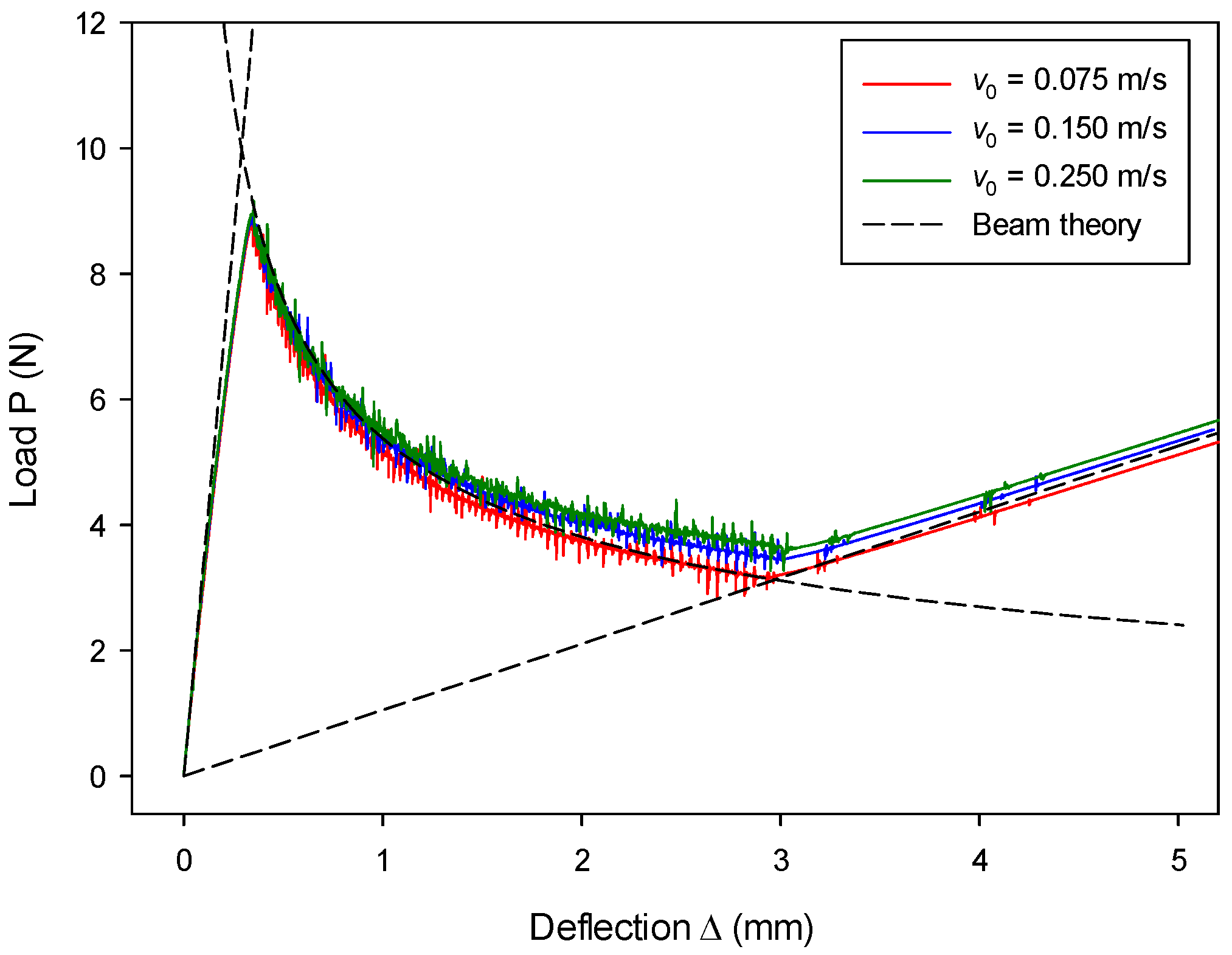
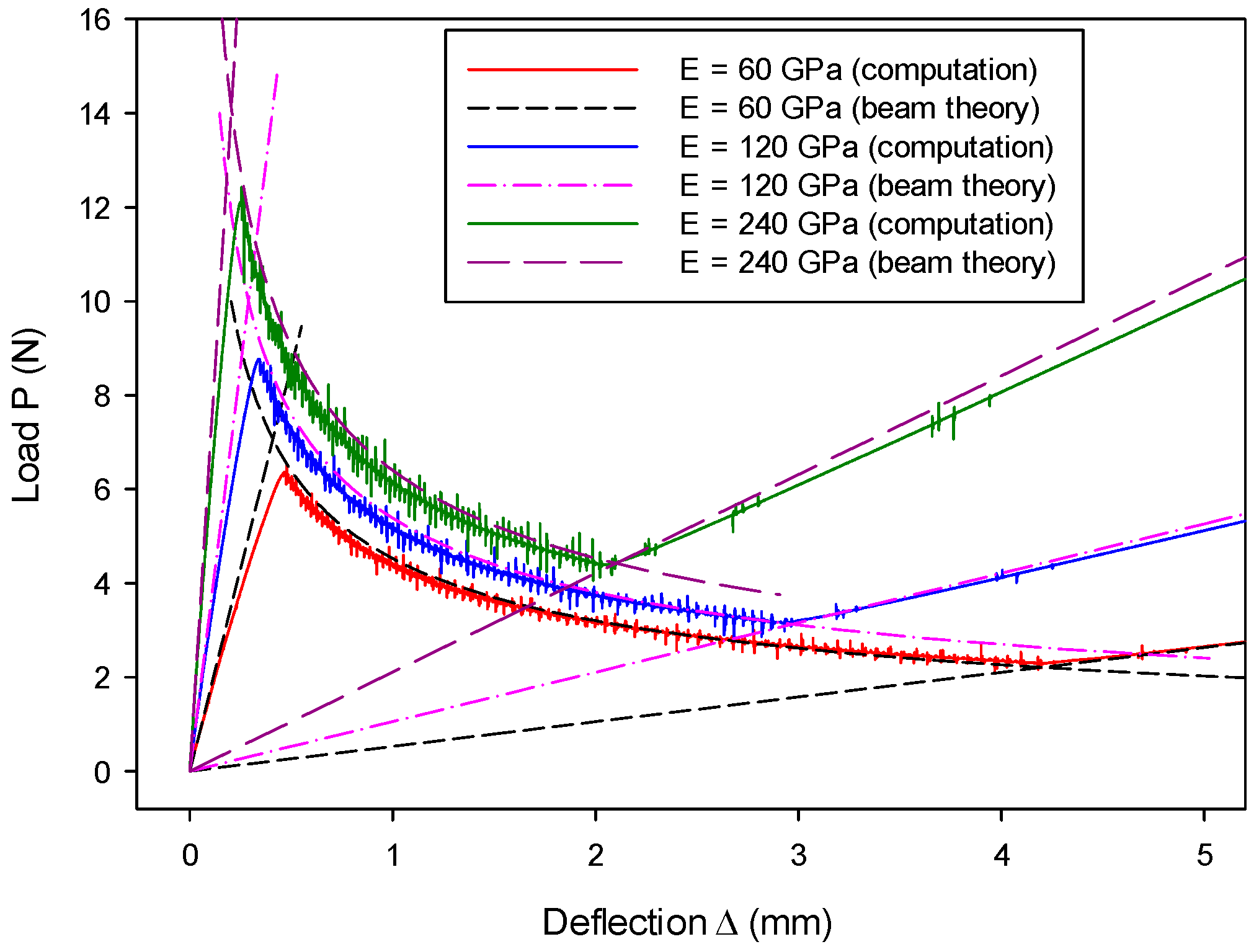
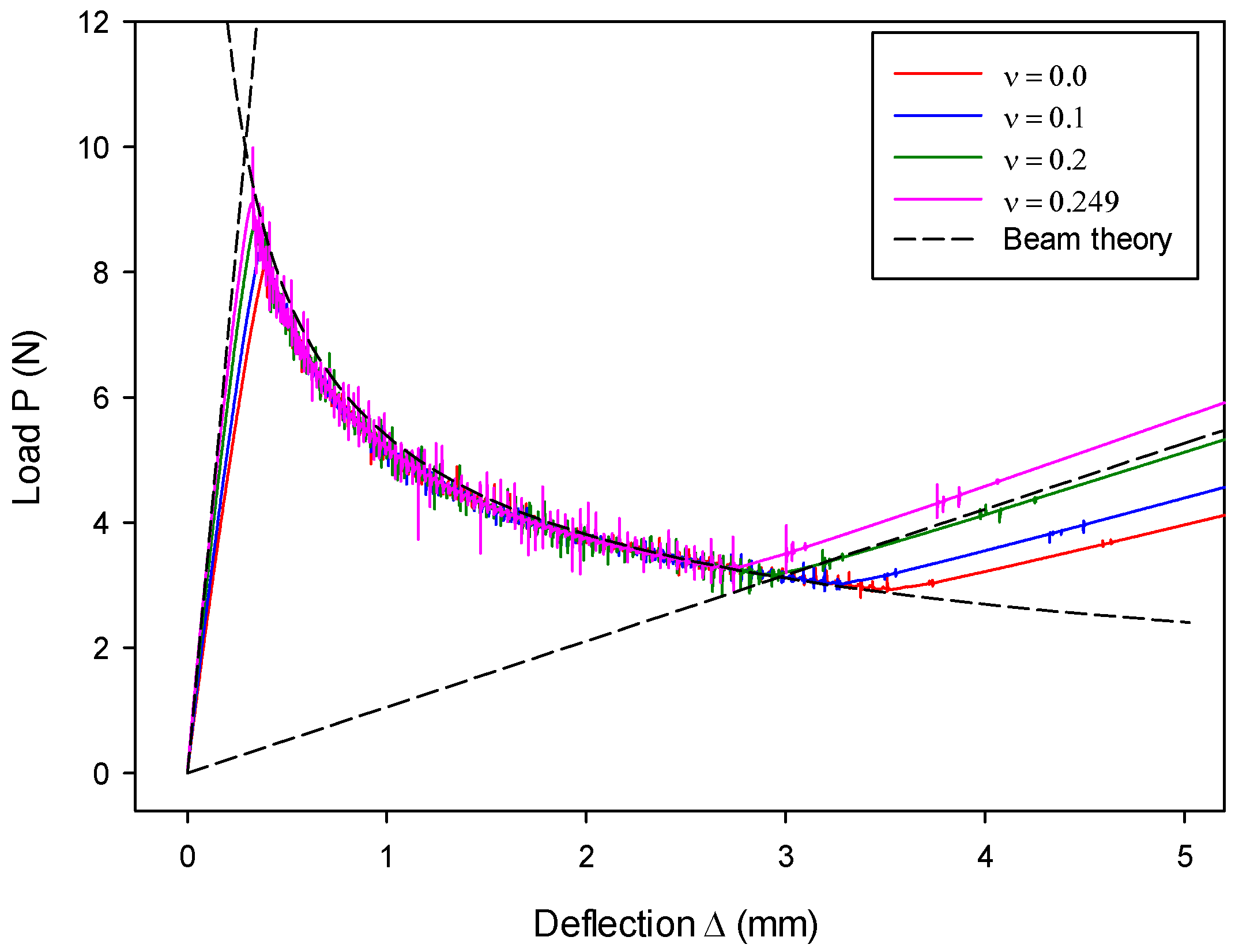
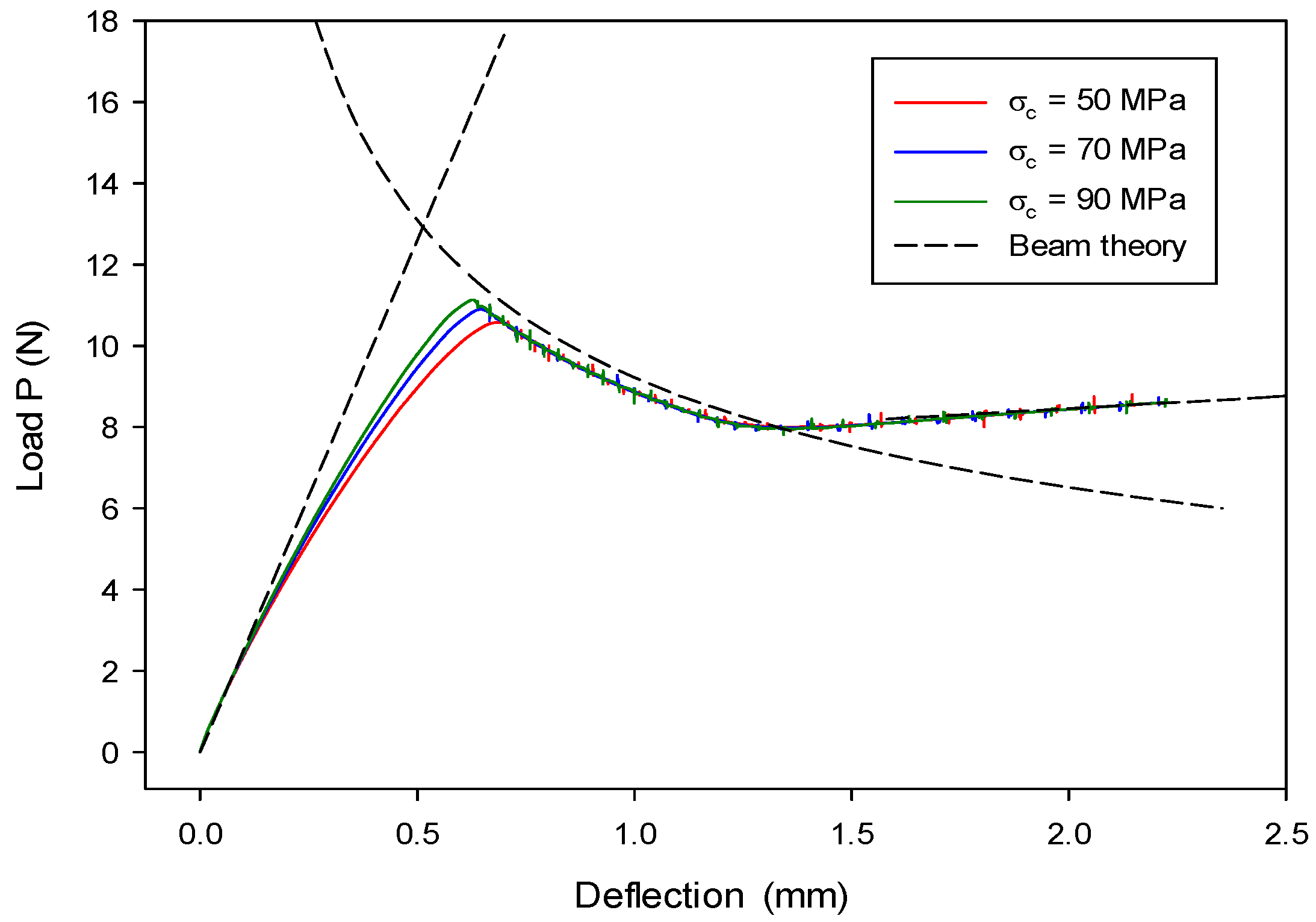
7.1. Mode-I Validation: Numerical Analysis of a DCB Model
7.2. Mode-II Validation: Numerical Analysis of an ENF Model
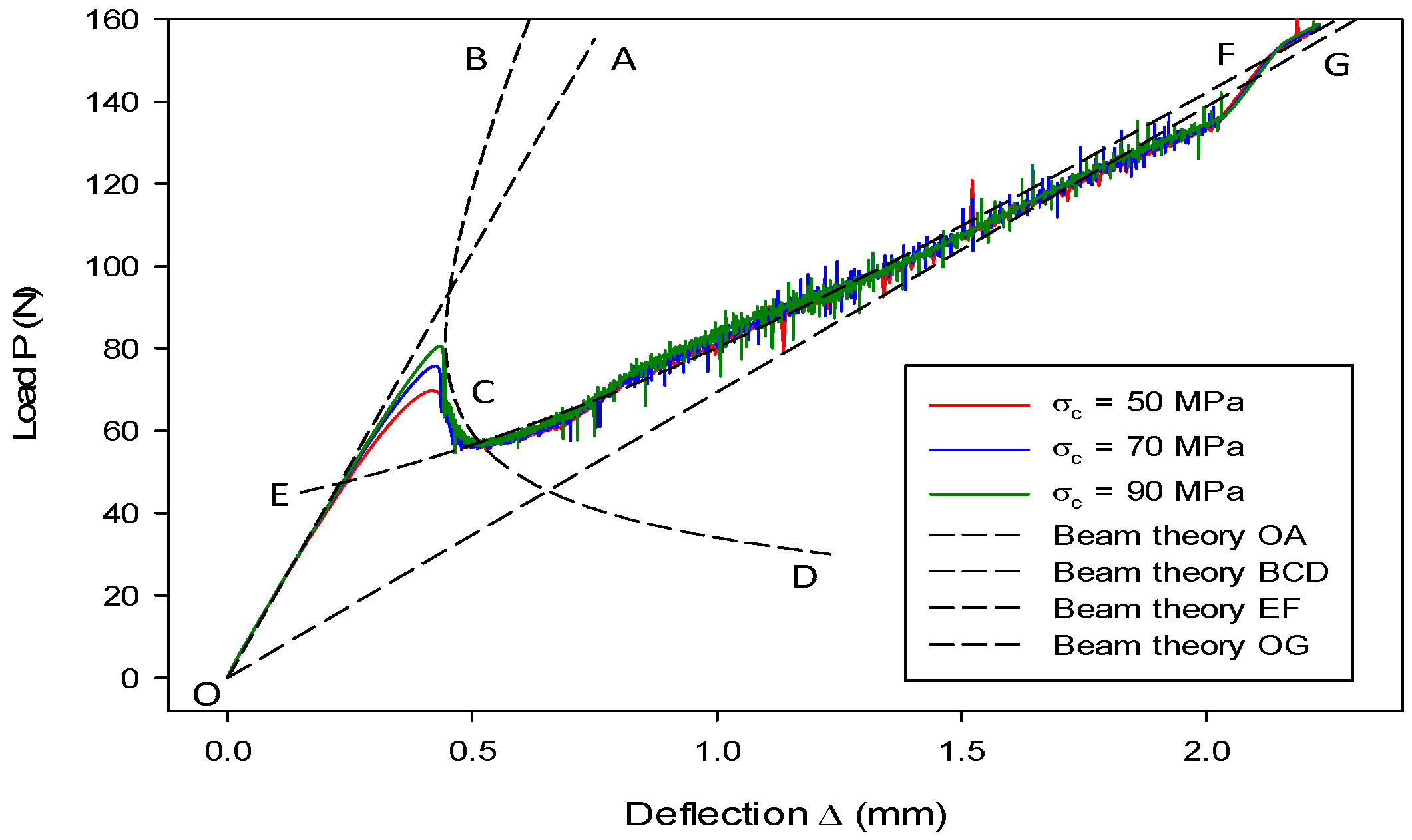
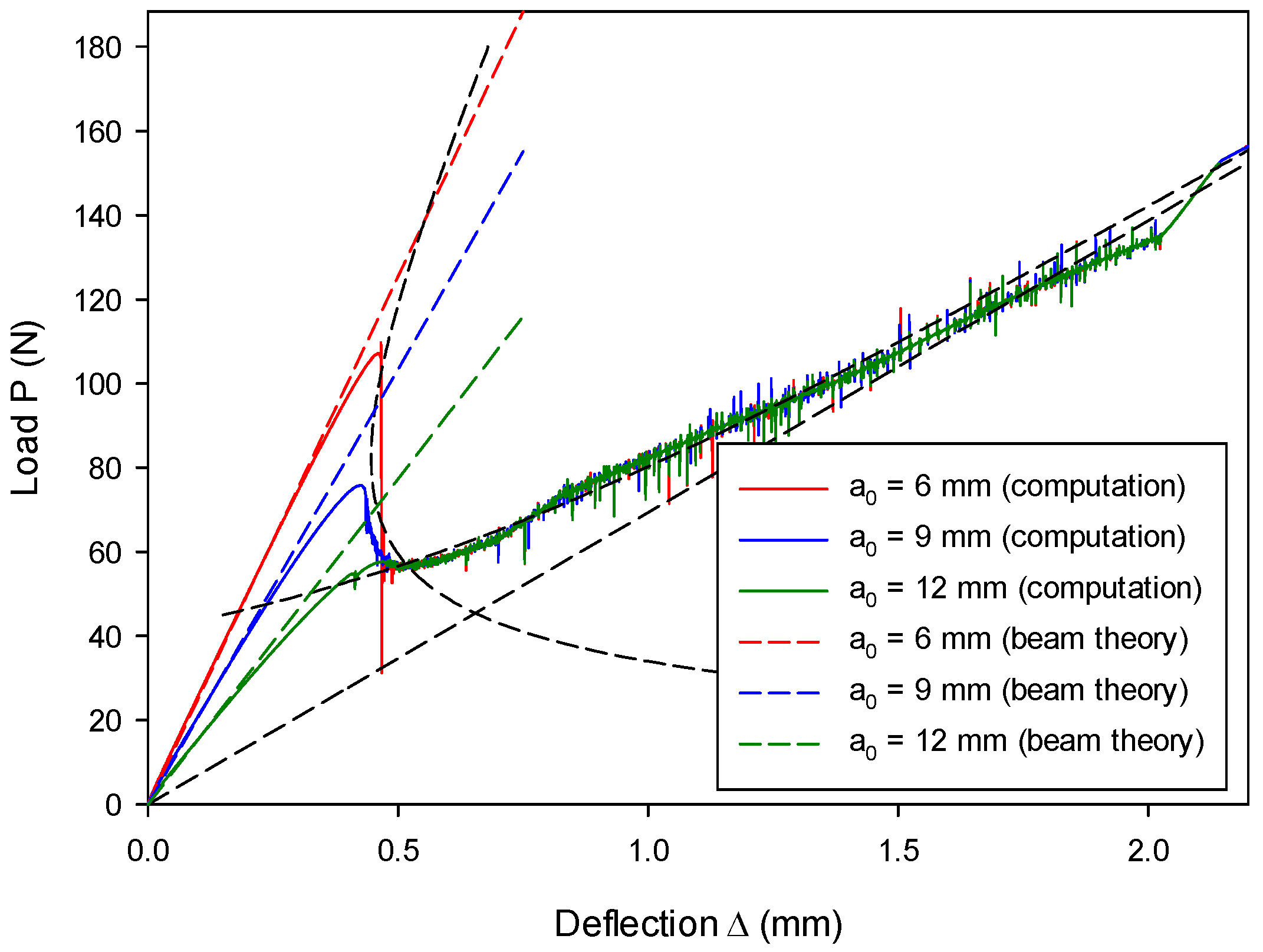
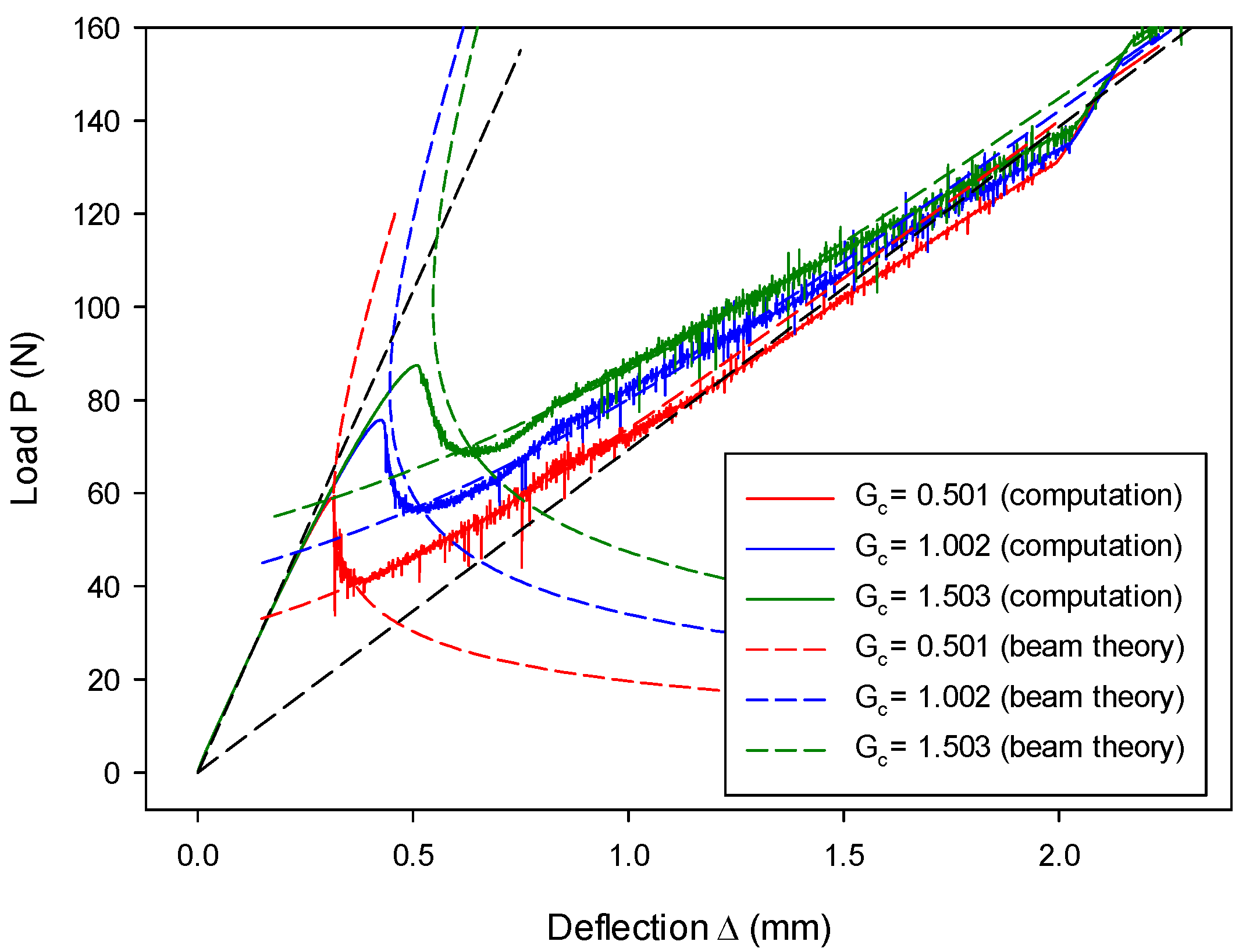
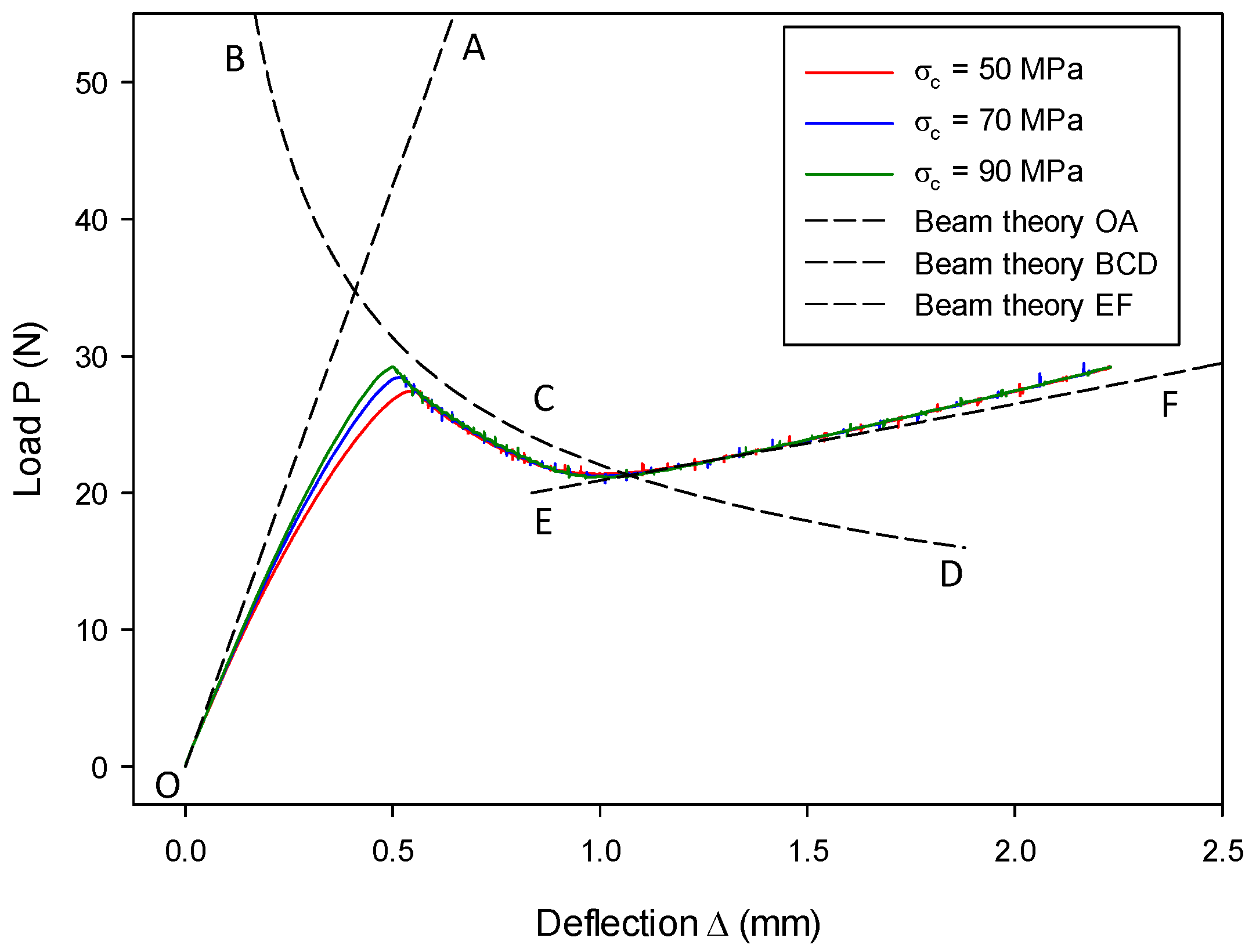
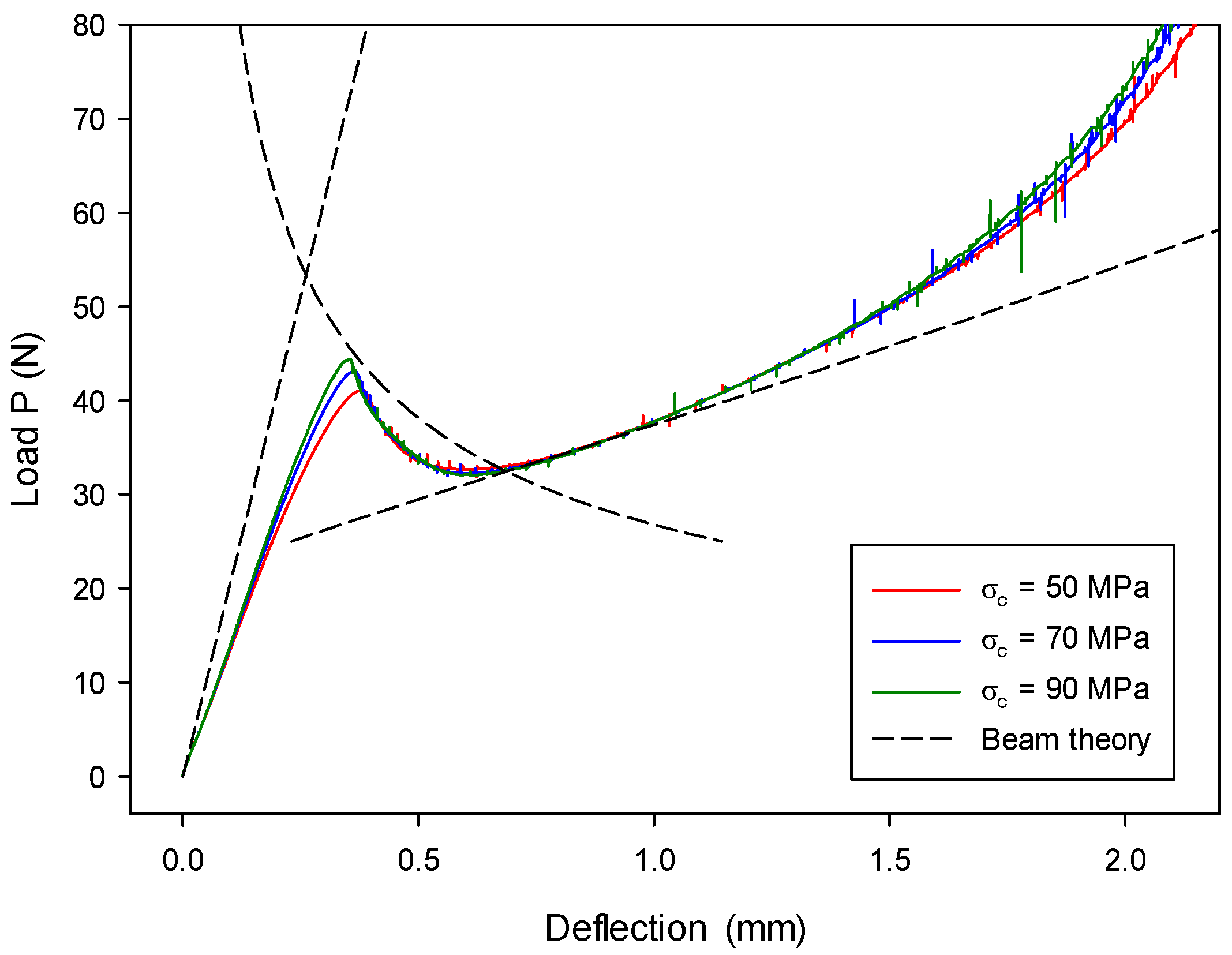
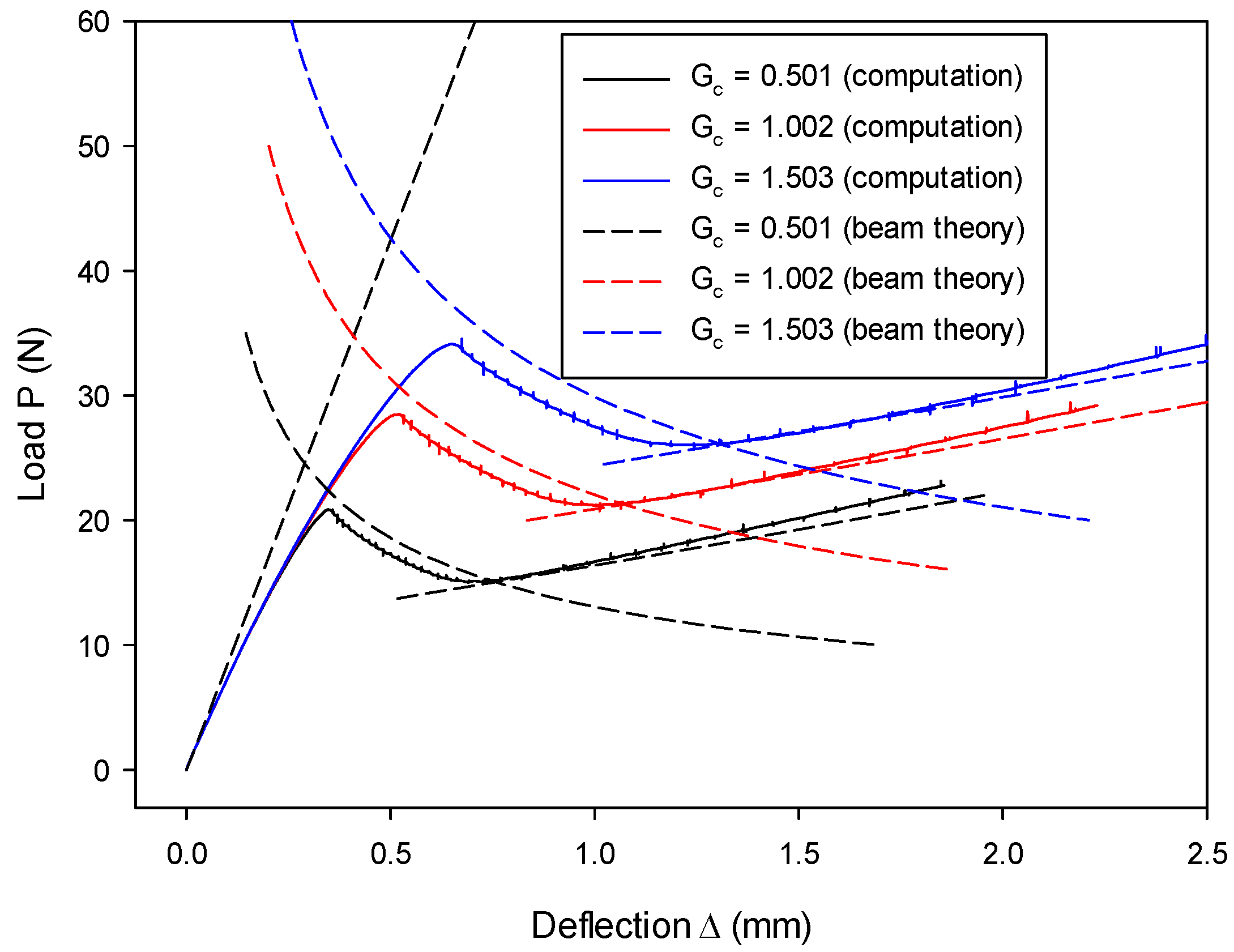
7.3. Mixed-Mode I & II Validation: Numerical Analysis of an MMB Model
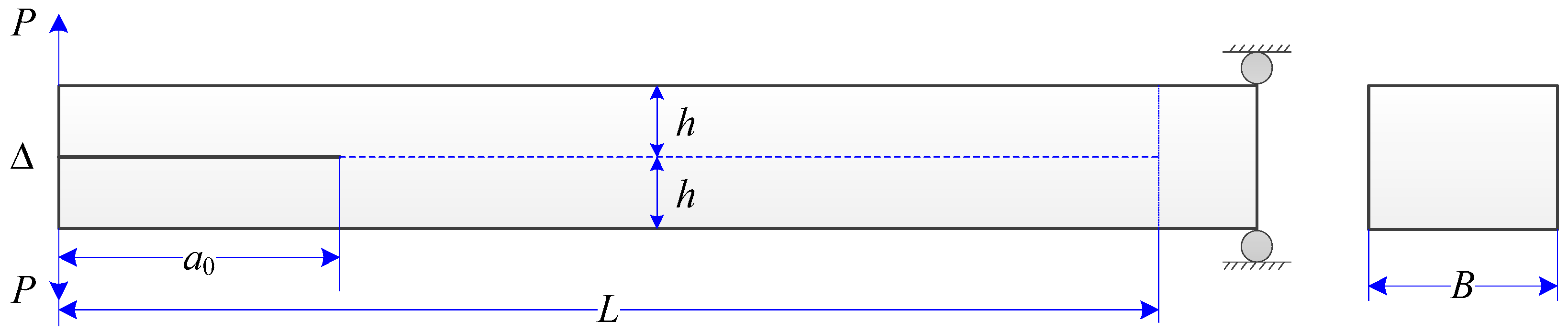
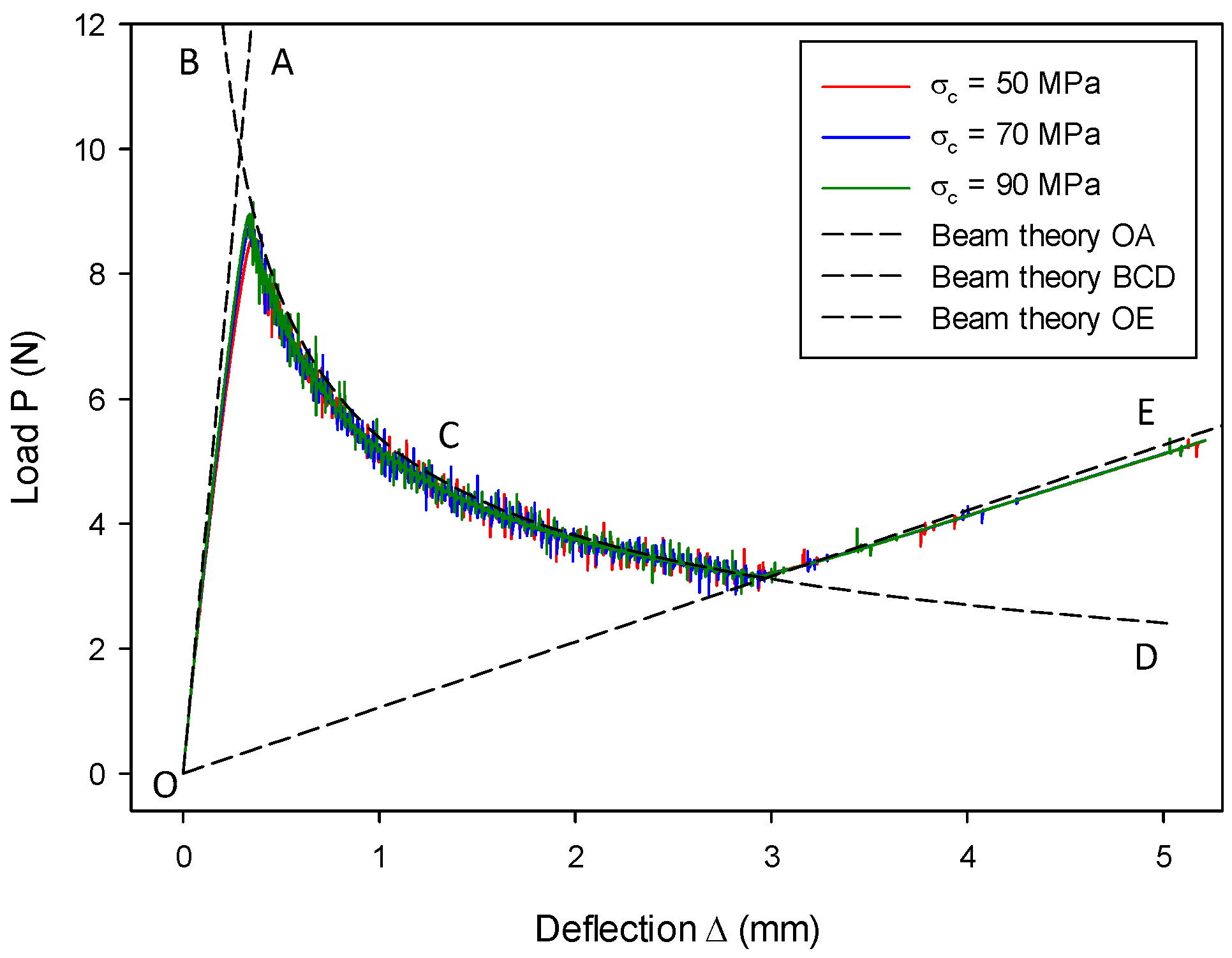
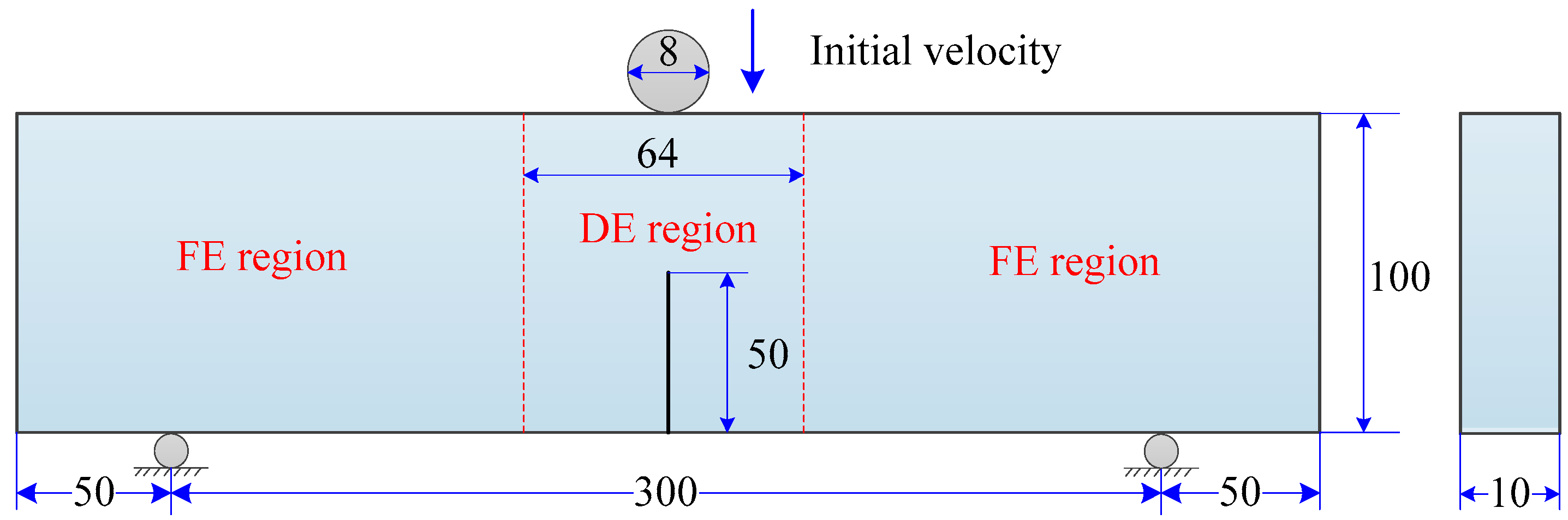
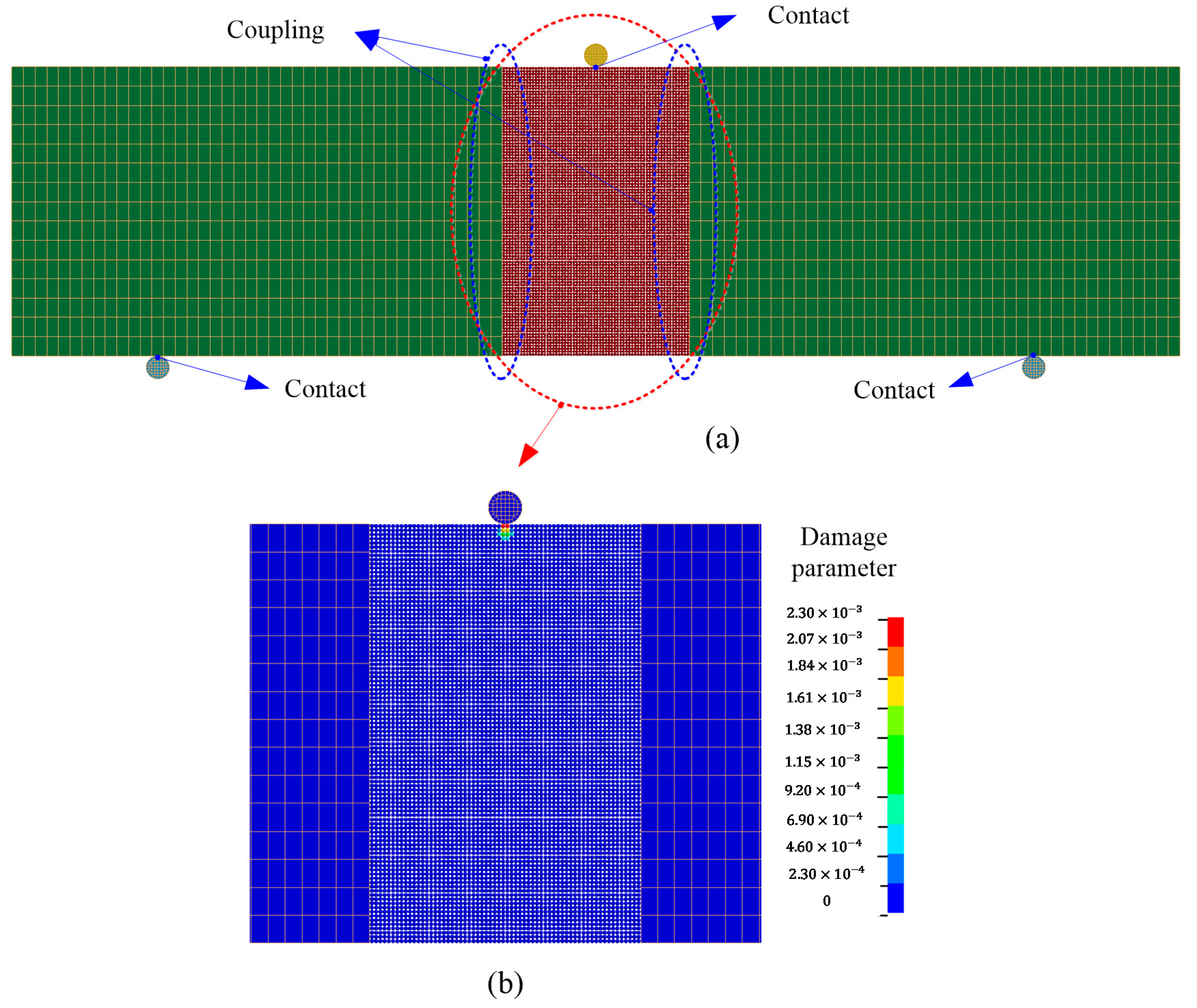
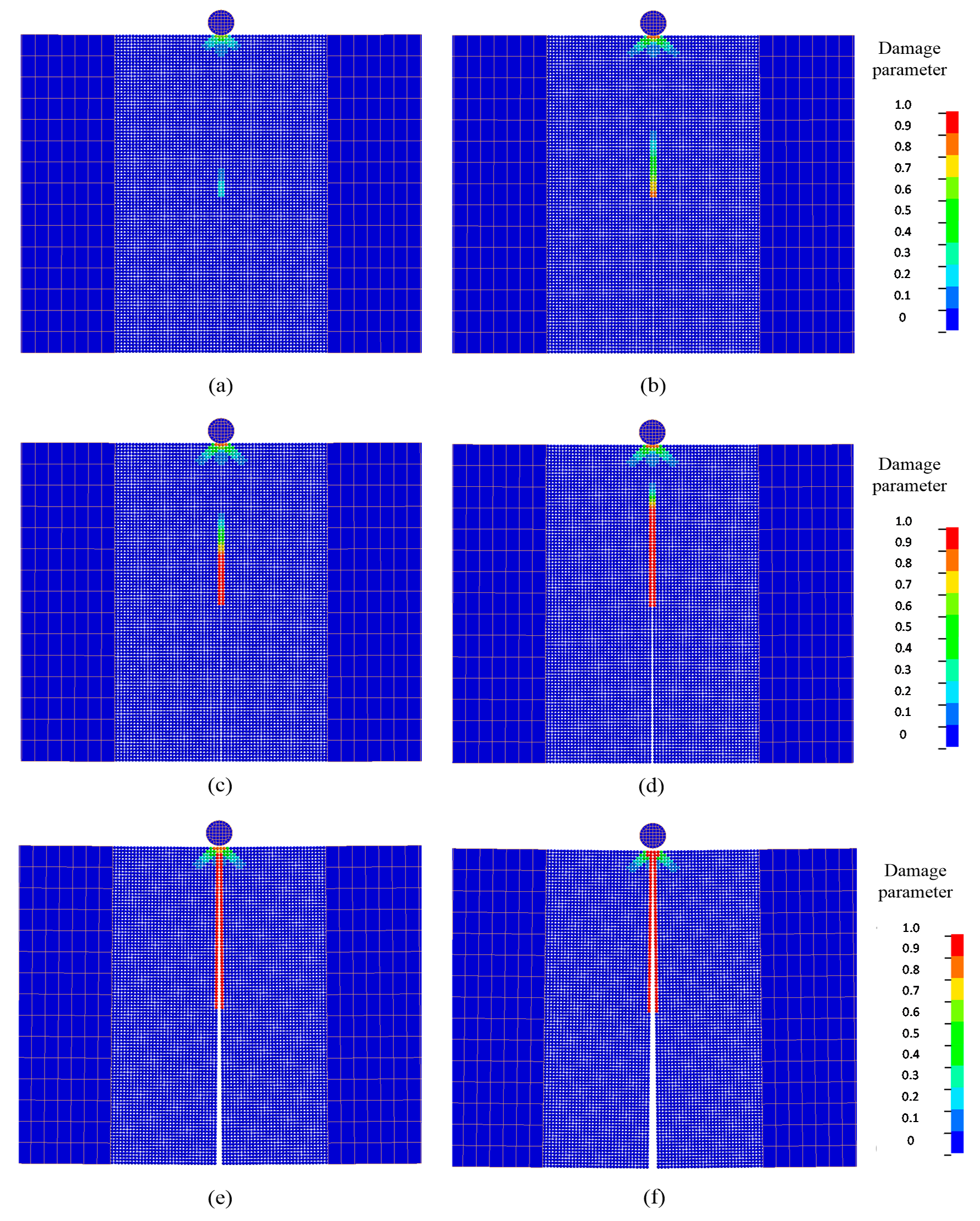
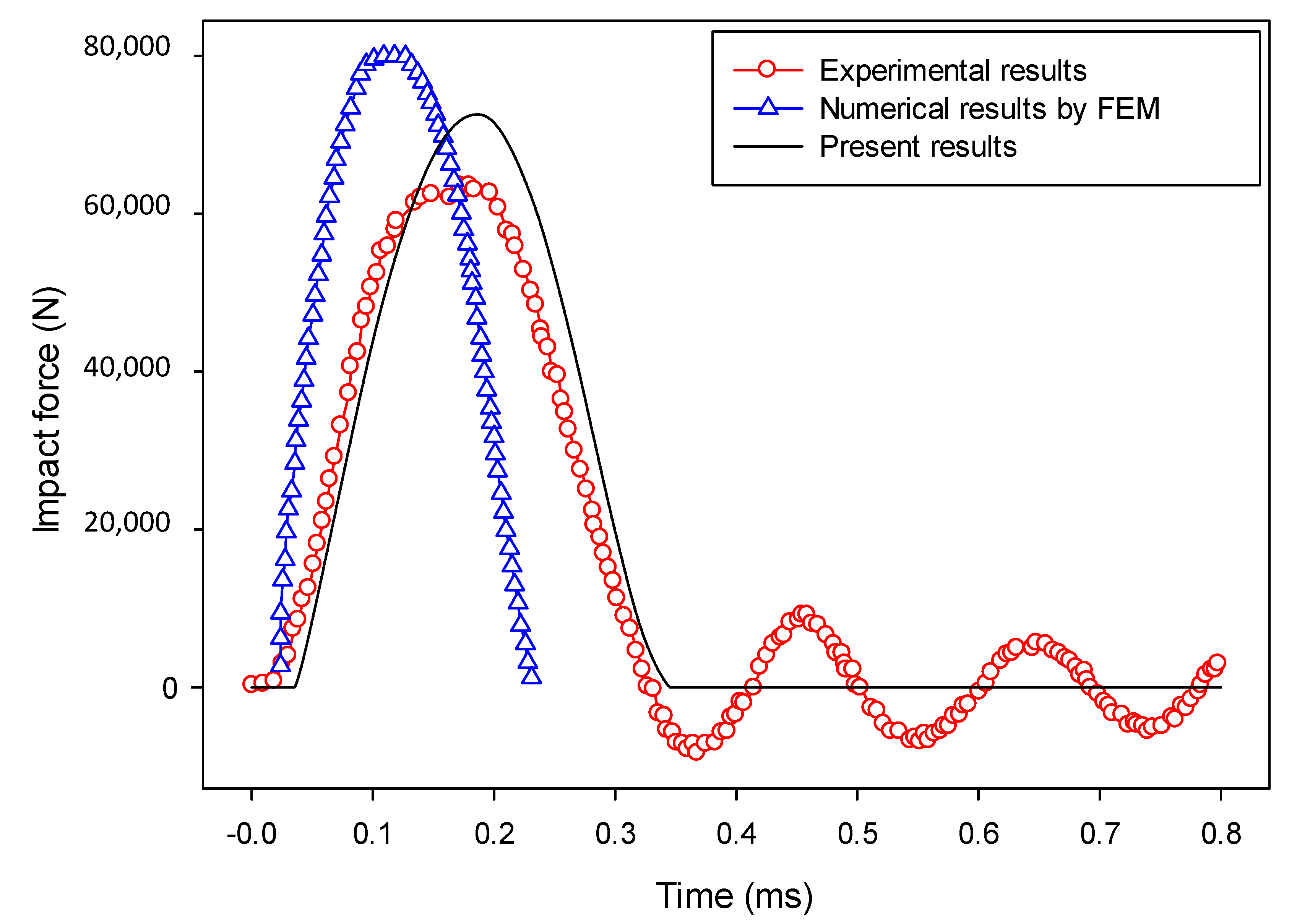
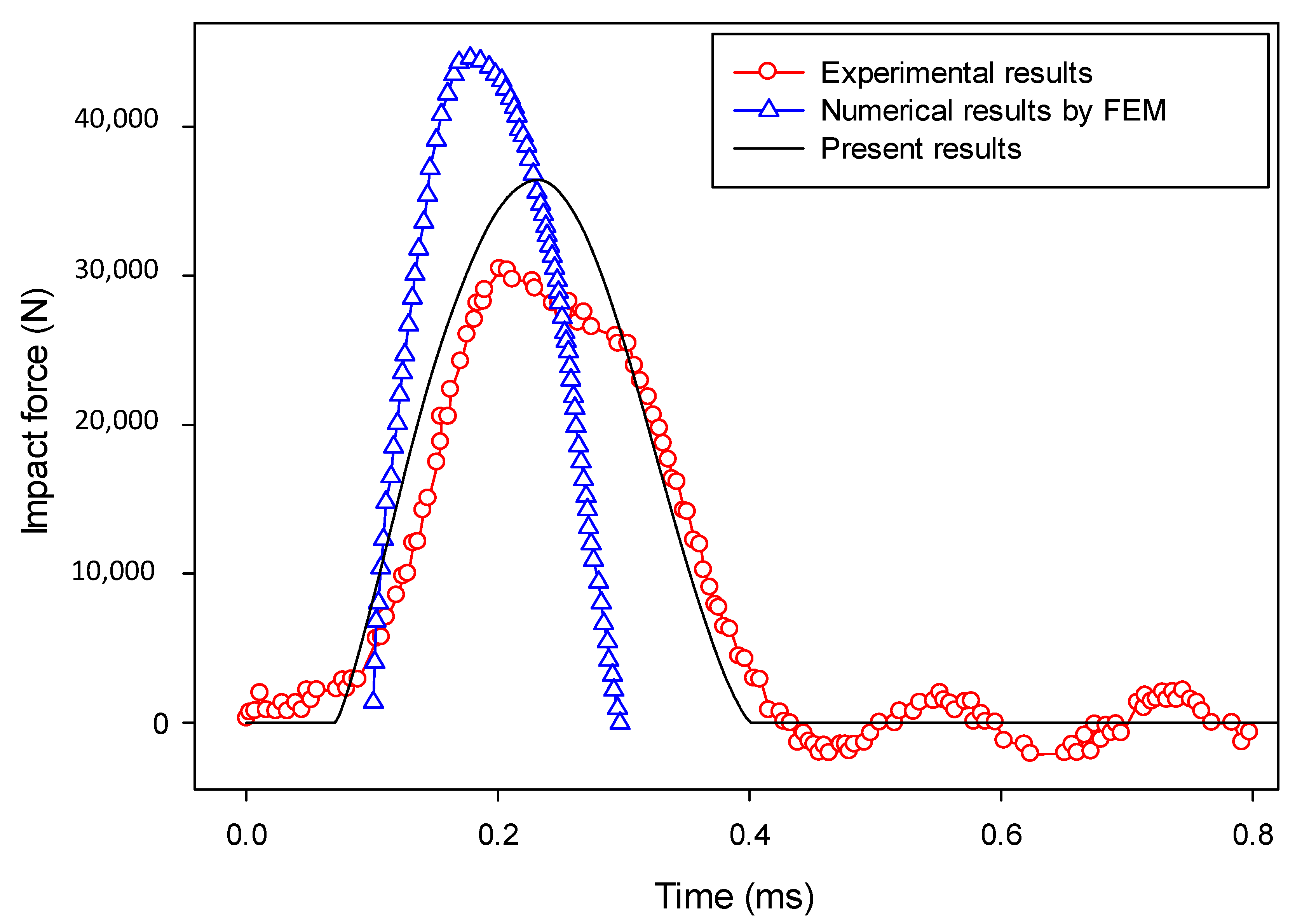
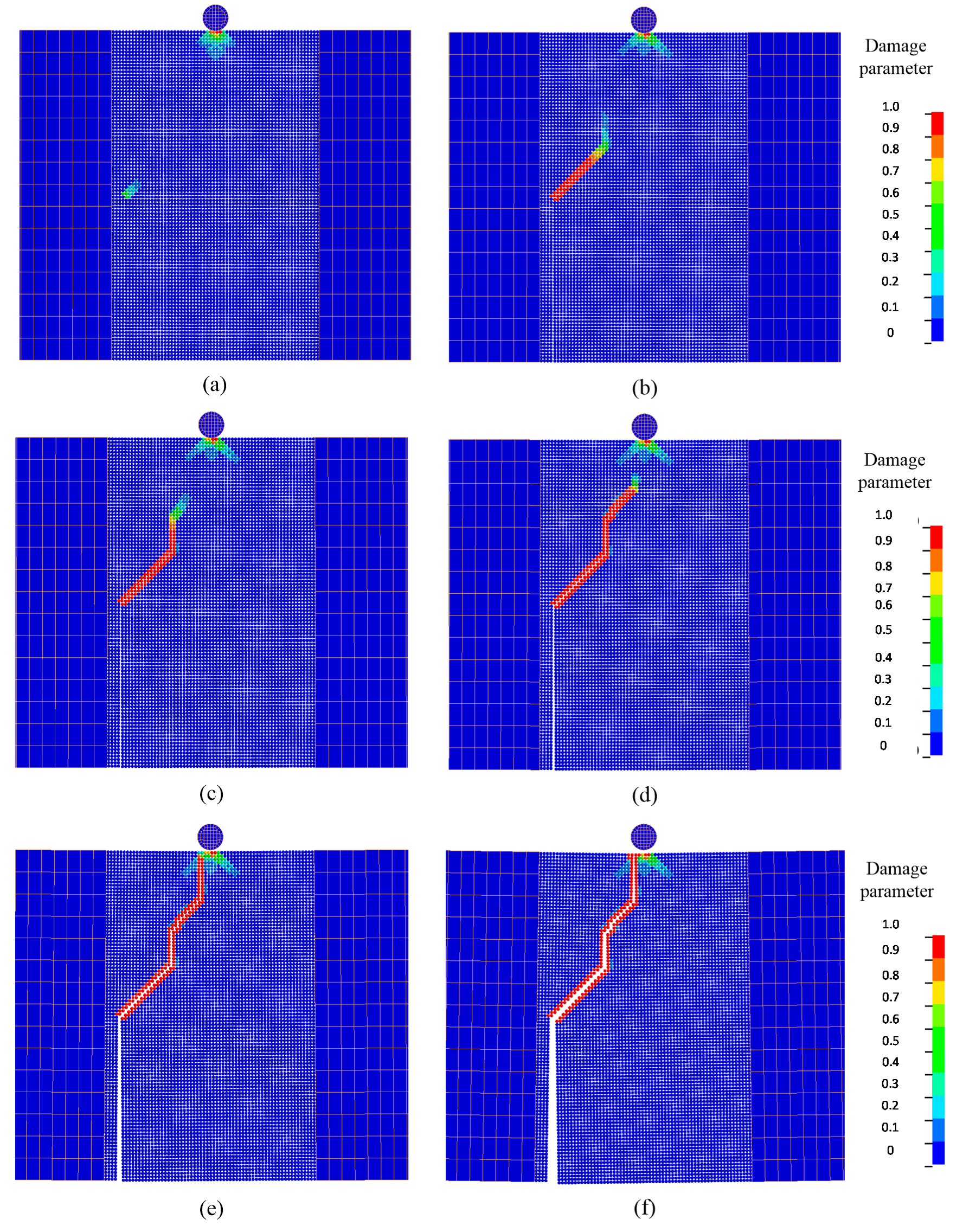
7.4. Application to the Impact Fracture of a Notched Concrete Beam
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| : (, , ) | Interaction force vector and its components in local coordinates. |
| : () | Relative displacement vector and its components in local coordinates. |
| : (, , ) | Spring stiffness and its components of the normal and two shear spring stiffness. |
| , | Young’s modulus and equivalent Young’s modulus. |
| Equivalent shear modulus. | |
| Poisson’s ratio. | |
| , | Particle radius and equivalent radius. |
| , , | The unit base vectors of the local coordinate system to be expressed in global coordinates. |
| , , | Components of . |
| , , | Components of . |
| Transformation matrix from the global frame to the local frame. | |
| , | Internal force and associated moment. |
| The effective radius vector. | |
| Position vector of particle i. | |
| : (,,) | Traction vector and its components in local coordinates. |
| Effective area. | |
| , | Critical values of the relative displacement in the normal and shear directions at the elastic limit. |
| , | Material strengths in the normal and shear directions. |
| Material tensile strength. | |
| Non-dimensional scalar of the effective displacement jump. | |
| , | Opening and shear separation components. |
| , | Critical values for opening mode and shear mode at complete cracking points. |
| Critical value of the scalar at the fracture initiation point. | |
| Potential function. | |
| Critical energy release rate. | |
| Damage index. | |
| Loading ratio. | |
| , | Cohesive force vectors in local and global coordinates. |
| Moment due to cohesive force in global coordinates. | |
| , | Critical energy release rates of the opening mode and shear mode. |
| Non-dimensional scalar. | |
| Contact force vector. | |
| A user-defined penalty factor. | |
| The period of persistent contact. | |
| Relative velocity at contact point . | |
| , | Translational and angular velocities. |
| , | Particle mass and moment of inertia. |
| External force. | |
| Moment induced from all forces. | |
| The number of surrounding particles. | |
| ,, | Length, breadth, and half height of the beam. |
| , | Initial and current crack lengths. |
| Second moment of area. | |
| , | Correction factors for mode-I and mode-II fracture problems. |
| Elastic modulus correction parameter. | |
| Deflection. | |
| Load. | |
| Loading arm. | |
| Mixed-mode ratio. |
References
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Belytschko, T.; Gu, L.; Lu, Y.Y. Fracture and crack growth by element free Galerkin methods. Model. Simul. Mater. Sci. Eng. 1994, 2, 519–534. [Google Scholar] [CrossRef]
- Onate, E.; Owen, D. Particle-Based Methods: Fundamentals and Applications; Springer Science & Business Media: Wales, UK, 2011. [Google Scholar]
- Krivtsov, A.M. Molecular Dynamics Simulation of Impact Fracture in Polycrystalline Materials. Mecanica 2003, 38, 61–70. [Google Scholar] [CrossRef]
- Brighenti, R.; Corbari, N. Dynamic behaviour of solids and granular materials: A force potential-based particle method. Int. J. Numer. Methods Eng. 2015, 105, 936–959. [Google Scholar] [CrossRef]
- Skogsrud, J.; Thaulow, C. Application of CTOD in atomistic modeling of fracture. Eng. Fract. Mech. 2015, 150, 153–160. [Google Scholar] [CrossRef]
- Shiari, B.; Miller, R. Multiscale modeling of crack initiation and propagation at the nanoscale. J. Mech. Phys. Solids 2016, 88, 35–49. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Buehler, M.J. Atomistic Modeling of Materials Failure; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Stein, E.; de Borst, R.; Hughes, T.J. Encyclopedia of Computational Mechanics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zang, M.; Lei, Z.; Wang, S. Investigation of impact fracture behavior of automobile laminated glass by 3D discrete element method. Comput. Mech. 2007, 41, 73–83. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Gao, W.; Chen, S.; Wang, C. Numerical investigation of impact injury of a human head during contact interaction with a windshield glazing considering mechanical failure. Int. J. Impact Eng. 2020, 141, 103577. [Google Scholar] [CrossRef]
- Tan, Y.; Yang, D.; Sheng, Y. Discrete element method (DEM) modeling of fracture and damage in the machining process of polycrystalline SiC. J. Eur. Ceram. Soc. 2009, 29, 1029–1037. [Google Scholar] [CrossRef]
- Martin, C.L.; Bouvard, D.; Delette, G. Discrete Element Simulations of the Compaction of Aggregated Ceramic Powders. J. Am. Ceram. Soc. 2006, 89, 3379–3387. [Google Scholar] [CrossRef]
- Oñate, E.; Zárate, F.; Miquel, J.; Santasusana, M.; Celigueta, M.A.; Arrufat, F.; Gandikota, R.; Valiullin, K.; Ring, L. A local constitutive model for the discrete element method. Application to geomaterials and concrete. Comput. Part. Mech. 2015, 2, 139–160. [Google Scholar] [CrossRef]
- Tavarez, F.A.; Plesha, M.E. Discrete element method for modelling solid and particulate materials. Int. J. Numer. Methods Eng. 2007, 70, 379–404. [Google Scholar] [CrossRef]
- Griffiths, D.; Mustoe, G.G.W. Modelling of elastic continua using a grillage of structural elements based on discrete element concepts. Int. J. Numer. Methods Eng. 2001, 50, 1759–1775. [Google Scholar] [CrossRef]
- Yu, J. Analysis and Application of the Algorithm by Combining Discrete and Finite Element Method in Plane. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2011. [Google Scholar]
- Gao, W.; Wang, J.; Yin, S.; Feng, Y.; Wang, J. A coupled 3D isogeometric and discrete element approach for modeling interactions between structures and granular matters. Comput. Methods Appl. Mech. Eng. 2019, 354, 441–463. [Google Scholar] [CrossRef]
- De Borst, R. Numerical aspects of cohesive-zone models. Eng. Fract. Mech. 2003, 70, 1743–1757. [Google Scholar] [CrossRef]
- Dugdale, D. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. Adv. Cryst. Elast. Metamater. Part 1 1962, 7, 55–129. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Camacho, G.; Ortiz, M. Computational modelling of impact damage in brittle materials. Int. J. Solids Struct. 1996, 33, 2899–2938. [Google Scholar] [CrossRef]
- Woelke, P.; Shields, M.D.; Hutchinson, J. Cohesive zone modeling and calibration for mode I tearing of large ductile plates. Eng. Fract. Mech. 2015, 147, 293–305. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H.; Roesler, J.R. A unified potential-based cohesive model of mixed-mode fracture. J. Mech. Phys. Solids 2009, 57, 891–908. [Google Scholar] [CrossRef]
- Gao, W.; Wang, R.; Chen, S.; Zang, M. An intrinsic cohesive zone approach for impact failure of windshield laminated glass subjected to a pedestrian headform. Int. J. Impact Eng. 2019, 126, 147–159. [Google Scholar] [CrossRef]
- Gao, W.; Liu, X.; Chen, S.; Bui, T.Q.; Yoshimura, S. A cohesive zone based DE/FE coupling approach for interfacial debonding analysis of laminated glass. Theor. Appl. Fract. Mech. 2020, 108, 102668. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Numer. Methods Eng. 1999, 44, 1267–1282. [Google Scholar] [CrossRef]
- Chen, S.; Zang, M.; Xu, W. A three-dimensional computational framework for impact fracture analysis of automotive laminated glass. Comput. Methods Appl. Mech. Eng. 2015, 294, 72–99. [Google Scholar] [CrossRef]
- Chen, S.; Mitsume, N.; Gao, W.; Yamada, T.; Zang, M.; Yoshimura, S. A nodal-based extrinsic cohesive/contact model for interfacial debonding analyses in composite structures. Comput. Struct. 2019, 215, 80–97. [Google Scholar] [CrossRef]
- Gao, W.; Zang, M. The simulation of laminated glass beam impact problem by developing fracture model of spherical DEM. Eng. Anal. Bound. Elem. 2014, 42, 2–7. [Google Scholar] [CrossRef]
- Kim, H.; Wagoner, M.P.; Buttlar, W.G. Simulation of Fracture Behavior in Asphalt Concrete Using a Heterogeneous Cohesive Zone Discrete Element Model. J. Mater. Civ. Eng. 2008, 20, 552–563. [Google Scholar] [CrossRef]
- Xu, W.; Zang, M.; Sakamoto, J. Modeling Mixed Mode Fracture of Concrete by Using the Combined Discrete and Finite Elements Method. Int. J. Comput. Methods 2016, 13, 1650007. [Google Scholar] [CrossRef]
- Le, B.; Dau, F.; Charles, J.; Iordanoff, I. Modeling damages and cracks growth in composite with a 3D discrete element method. Compos. Part B: Eng. 2016, 91, 615–630. [Google Scholar] [CrossRef]
- Yang, D.; Ye, J.; Tan, Y.; Sheng, Y. Modeling progressive delamination of laminated composites by discrete element method. Comput. Mater. Sci. 2011, 50, 858–864. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Miller, R.E. Modeling Materials: Continuum, Atomistic and Multiscale Techniques; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Chen, H. Developments of a Combined Finite-Discrete Element Model for Multiscale Modelling of Impact Fracture. Ph.D. Thesis, The University of New South Wales, Canberra, Australia, 2016. [Google Scholar]
- Liu, K.X.; Liu, W. Application of Discrete Element Method for Continuum Dynamic Problems. Arch. Appl. Mech. 2006, 76, 229–243. [Google Scholar] [CrossRef]
- Li, S.; Ming, C.; Kai-Xin, L.; Wei-Fu, L.; Shi-Yang, C. New Discrete Element Models for Three-Dimensional Impact Problems. Chin. Phys. Lett. 2009, 26, 120202. [Google Scholar] [CrossRef]
- Chen, H.; Zang, M.; Zhang, Y. A ghost particle-based coupling approach for the combined finite-discrete element method. Finite Elem. Anal. Des. 2016, 114, 68–77. [Google Scholar] [CrossRef]
- Remmers, J.J.C.; Deborst, R.; Needleman, A. The simulation of dynamic crack propagation using the cohesive segments method. J. Mech. Phys. Solids 2008, 56, 70–92. [Google Scholar] [CrossRef]
- Xie, D.; Salvi, A.G.; Sun, C.; Waas, A.M.; Caliskan, A. Discrete Cohesive Zone Model to Simulate Static Fracture in 2D Triaxially Braided Carbon Fiber Composites. J. Compos. Mater. 2006, 40, 2025–2046. [Google Scholar] [CrossRef]
- Borg, R.; Nilsson, L.; Simonsson, K. Simulation of delamination in fiber composites with a discrete cohesive failure model. Compos. Sci. Technol. 2001, 61, 667–677. [Google Scholar] [CrossRef]
- Cui, W.; Wisnom, M. A combined stress-based and fracture-mechanics-based model for predicting delamination in composites. Composites 1993, 24, 467–474. [Google Scholar] [CrossRef]
- Xie, D.; Waas, A.M. Discrete cohesive zone model for mixed-mode fracture using finite element analysis. Eng. Fract. Mech. 2006, 73, 1783–1796. [Google Scholar] [CrossRef]
- Schellekens, J.C.J.; De Borst, R. On the numerical integration of interface elements. Int. J. Numer. Methods Eng. 1993, 36, 43–66. [Google Scholar] [CrossRef]
- Vignollet, J.; May, S.; De Borst, R. On the numerical integration of isogeometric interface elements. Int. J. Numer. Methods Eng. 2015, 102, 1733–1749. [Google Scholar] [CrossRef]
- Gao, H.; Klein, P. Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bonds. J. Mech. Phys. Solids 1998, 46, 187–218. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The influence of plasticity on mixed mode interface toughness. J. Mech. Phys. Solids 1993, 41, 1119–1135. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Zavattieri, P.D. A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part I: Theory and numerical implementation. Mech. Mater. 2003, 35, 333–364. [Google Scholar] [CrossRef]
- Song, S.H.; Paulino, G.H.; Buttlar, W.G. A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material. Eng. Fract. Mech. 2006, 73, 2829–2848. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Jiang, W.-G.; Hallett, S.R.; Green, B.G.; Wisnom, M.R. A concise interface constitutive law for analysis of delamination and splitting in composite materials and its application to scaled notched tensile specimens. Int. J. Numer. Methods Eng. 2007, 69, 1982–1995. [Google Scholar] [CrossRef]
- Mi, Y.; Crisfield, M.A.; Davies, G.A.O.; Hellweg, H.B. Progressive Delamination Using Interface Elements. J. Compos. Mater. 1998, 32, 1246–1272. [Google Scholar] [CrossRef]
- Liu, X.; Duddu, R.; Waisman, H. Discrete damage zone model for fracture initiation and propagation. Eng. Fract. Mech. 2012, 92, 1–18. [Google Scholar] [CrossRef]
- Qiu, Y.; Crisfield, M.; Alfano, G. An interface element formulation for the simulation of delamination with buckling. Eng. Fract. Mech. 2001, 68, 1755–1776. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; De Moura, M.F.; De Moura, M. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Balzani, C.; Wagner, W. An interface element for the simulation of delamination in unidirectional fiber-reinforced composite laminates. Eng. Fract. Mech. 2008, 75, 2597–2615. [Google Scholar] [CrossRef]
- Harper, P.W.; Sun, L.; Hallett, S. A study on the influence of cohesive zone interface element strength parameters on mixed mode behaviour. Compos. Part A: Appl. Sci. Manuf. 2012, 43, 722–734. [Google Scholar] [CrossRef]
- Wu, E.M.; Reuter, R.C. Crack Extension in Fiberglass Reinforced Plastics; Defense Technical Information Center (DTIC): Champaign, IL, USA, 1965. [Google Scholar]
- Reeder, J. An evaluation of Mixed-Mode Delamination Failure Criteria; NASA Langley Technical Report Server: Hampton, VA, USA, 1992.
- Benzeggagh, M.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Pinho, S.; Iannucci, L.; Robinson, P. Formulation and implementation of decohesion elements in an explicit finite element code. Compos. Part A: Appl. Sci. Manuf. 2006, 37, 778–789. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J.; Renart, J. Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: Definition of interlaminar strengths and elastic stiffness. Compos. Struct. 2010, 92, 1857–1864. [Google Scholar] [CrossRef]
- Iannucci, L. Dynamic delamination modelling using interface elements. Comput. Struct. 2006, 84, 1029–1048. [Google Scholar] [CrossRef]
- Zhang, Z.; Paulino, G.H.; Celes, W. Extrinsic cohesive modelling of dynamic fracture and microbranching instability in brittle materials. Int. J. Numer. Methods Eng. 2007, 72, 893–923. [Google Scholar] [CrossRef]
- Dziugys, A.; Peters, B. An approach to simulate the motion of spherical and non-spherical fuel particles in combustion chambers. Granul. Matter 2001, 3, 231–266. [Google Scholar] [CrossRef]
- Balevičius, R.; Džiugys, A.; Kačianauskas, R. Discrete element method and its application to the analysis of penetration into granular media. J. Civ. Eng. Manag. 2004, 10, 3–14. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Zang, M.; Hazell, P.J. An accurate and robust contact detection algorithm for particle-solid interaction in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 2015, 103, 598–624. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact Under Varying Oblique Forces. Collect. Papers Raymond D. Mindlin Volume I 1989, 20, 269–286. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Bray, J.D. Selecting a suitable time step for discrete element simulations that use the central difference time integration scheme. Eng. Comput. 2004, 21, 278–303. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Irwin, G. Onset of Fast Crack Propagation in High Strength Steel and Aluminum Alloys; Naval Research Laboratory: Washington, DC, USA, 1956; pp. 289–305. [Google Scholar] [CrossRef]
- Williams, J. End corrections for orthotropic DCB specimens. Compos. Sci. Technol. 1989, 35, 367–376. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.; Williams, J.G. The analysis of interlaminar fracture in uniaxial fibre-polymer composites. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1990, 427, 173–199. [Google Scholar] [CrossRef]
- Kinloch, A.; Wang, Y.; Williams, J.; Yayla, P. The mixed-mode delamination of fibre composite materials. Compos. Sci. Technol. 1993, 47, 225–237. [Google Scholar] [CrossRef]
- Chen, J.; Crisfield, M.; Kinloch, A.J.; Busso, E.P.; Matthews, F.L.; Qiu, Y. Predicting Progressive Delamination of Composite Material Specimens via Interface Elements. Mech. Adv. Mater. Struct. 1999, 6, 301–317. [Google Scholar] [CrossRef]
- Goyal, V.K. Analytical modeling of the mechanics of nucleation and growth of cracks. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2002. [Google Scholar]
- Wang, Y.; Williams, J. Corrections for mode II fracture toughness specimens of composites materials. Compos. Sci. Technol. 1992, 43, 251–256. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.J.; Williams, J. The Effects of Geometry, Rate and Temperature on the Mode I, Mode II and Mixed-Mode I/II Interlaminar Fracture of Carbon-Fibre/Poly(ether-ether ketone) Composites. J. Compos. Mater. 1990, 24, 918–956. [Google Scholar] [CrossRef]
- Reeder, J.R.; Crews, J.H.; Rews, J.H. Mixed-mode bending method for delamination testing. AIAA J. 1990, 28, 1270–1276. [Google Scholar] [CrossRef]
- John, R.; Shah, S.P. Mixed?Mode Fracture of Concrete Subjected to Impact Loading. J. Struct. Eng. 1990, 116, 585–602. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Yu, R.C.; Ruiz, G.; Tarifa, M.; Camara, M.A. Effect of loading rate on crack velocities in HSC. Int. J. Impact Eng. 2010, 37, 359–370. [Google Scholar] [CrossRef]
- Yu, R.C.; Ruiz, G.; Chaves, E.W. A comparative study between discrete and continuum models to simulate concrete fracture. Eng. Fract. Mech. 2008, 75, 117–127. [Google Scholar] [CrossRef]
- Bede, N.; Ožbolt, J.; Sharma, A.; Irhan, B. Dynamic fracture of notched plain concrete beams: 3D finite element study. Int. J. Impact Eng. 2015, 77, 176–188. [Google Scholar] [CrossRef]
- Guo, Z.; Kobayashi, A.; Hawkins, N. Dynamic mixed mode fracture of concrete. Int. J. Solids Struct. 1995, 32, 2591–2607. [Google Scholar] [CrossRef]

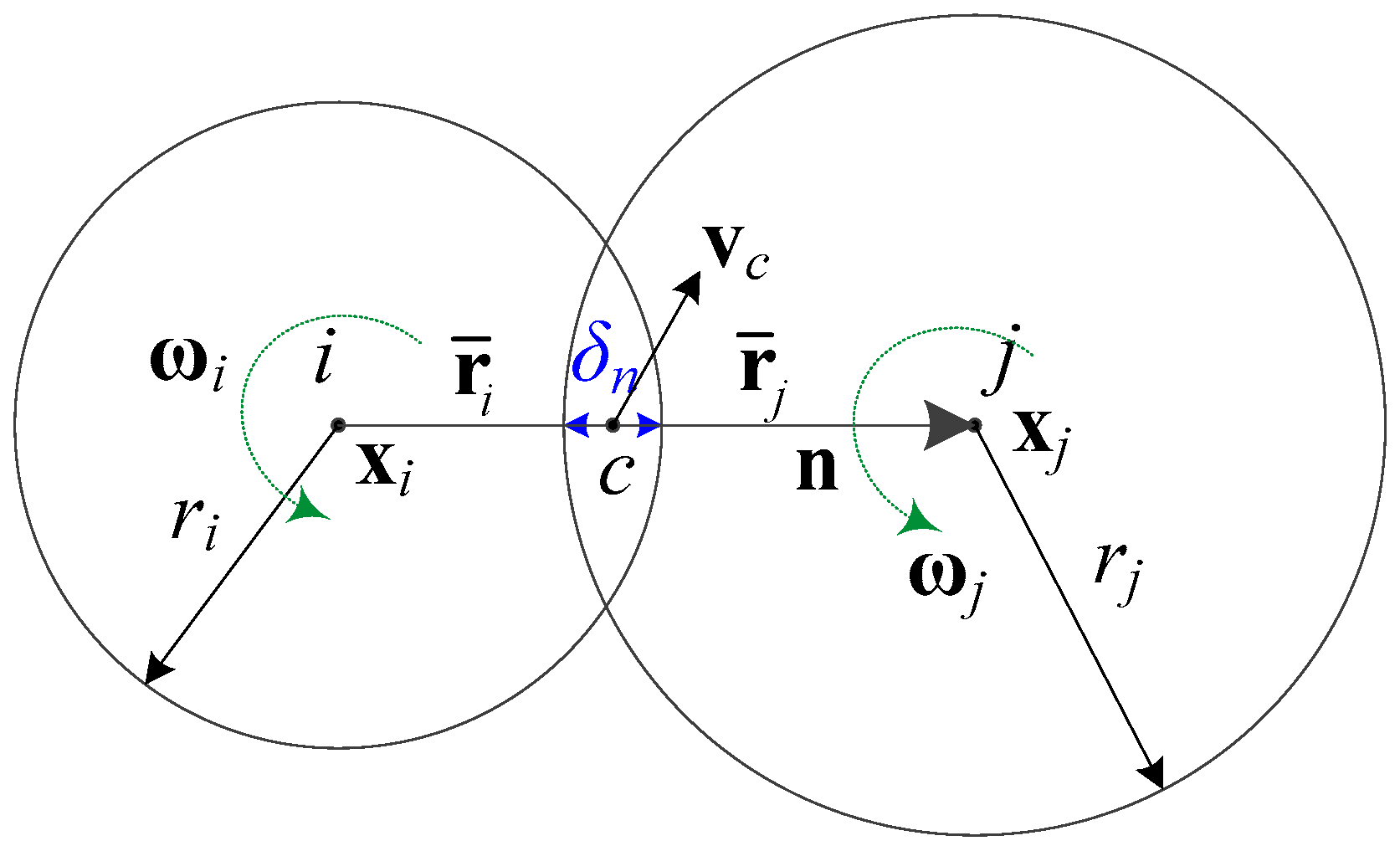



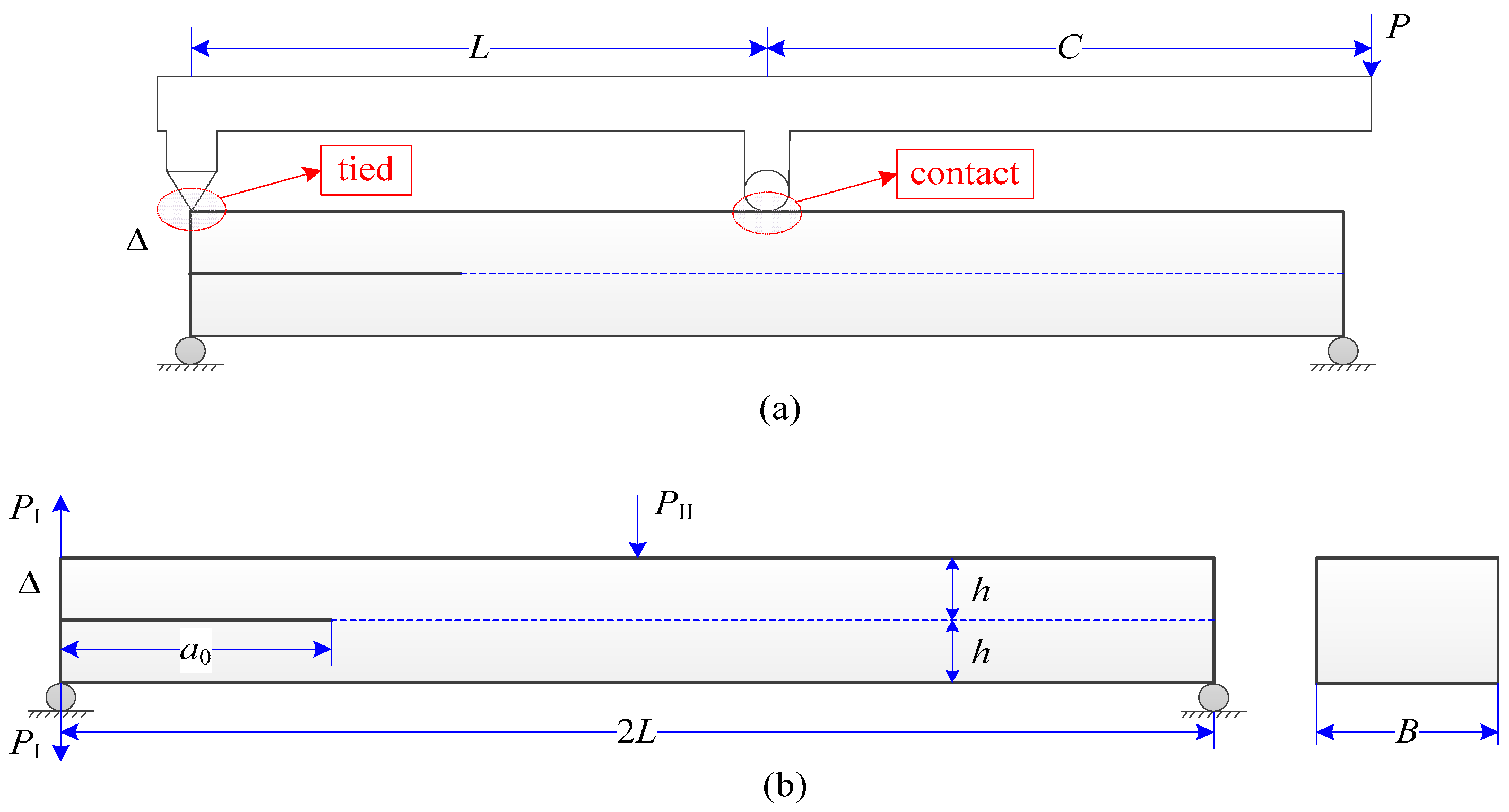

| Initial: All Pairs Being Connective |
|---|
| If (connective and ) then connective  cohesive cohesiveelse if (cohesive and ) then cohesive 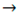 contact contactend if |
| If (Connective) then |
|---|
| Use Equations (1) and (5) to calculate internal force else if (cohesive) then |
| Use Equations (25), (26) and (29) to calculate cohesive force else if (contact) then |
| Use Equations (34) and (39) to calculate contact force end if |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Zhang, Y.X.; Zhu, L.; Xiong, F.; Liu, J.; Gao, W. A Particle-Based Cohesive Crack Model for Brittle Fracture Problems. Materials 2020, 13, 3573. https://doi.org/10.3390/ma13163573
Chen H, Zhang YX, Zhu L, Xiong F, Liu J, Gao W. A Particle-Based Cohesive Crack Model for Brittle Fracture Problems. Materials. 2020; 13(16):3573. https://doi.org/10.3390/ma13163573
Chicago/Turabian StyleChen, Hu, Y. X. Zhang, Linpei Zhu, Fei Xiong, Jing Liu, and Wei Gao. 2020. "A Particle-Based Cohesive Crack Model for Brittle Fracture Problems" Materials 13, no. 16: 3573. https://doi.org/10.3390/ma13163573
APA StyleChen, H., Zhang, Y. X., Zhu, L., Xiong, F., Liu, J., & Gao, W. (2020). A Particle-Based Cohesive Crack Model for Brittle Fracture Problems. Materials, 13(16), 3573. https://doi.org/10.3390/ma13163573







