Experimental Investigation and Micromechanical Modeling of Elastoplastic Damage Behavior of Sandstone
Abstract
:1. Introduction
2. Experimental Investigations
2.1. Description of Sandstone
2.2. Experimental Method
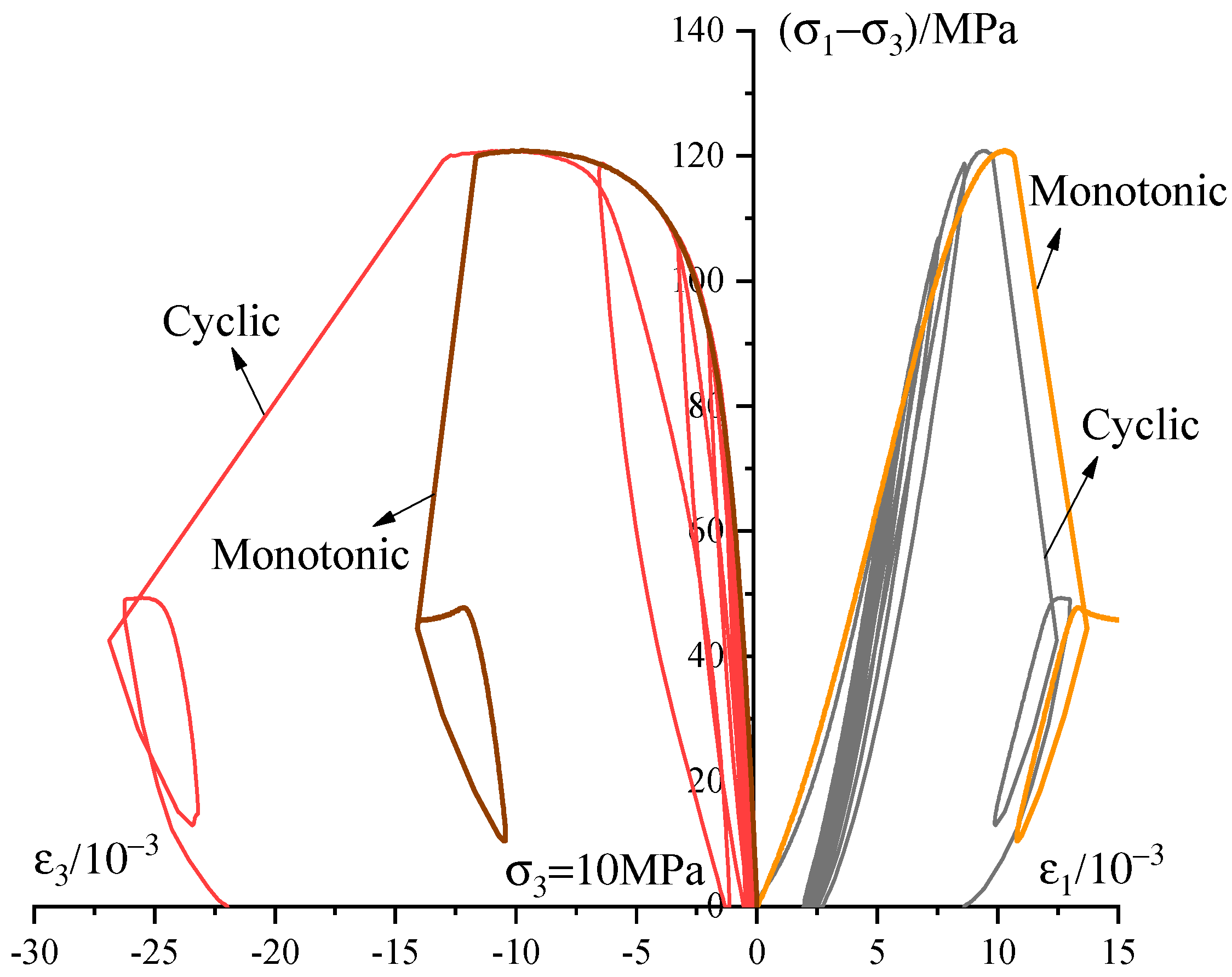
2.3. Experimental Results and Discussions
3. Thermodynamic Framework
4. Microscopic Prediction
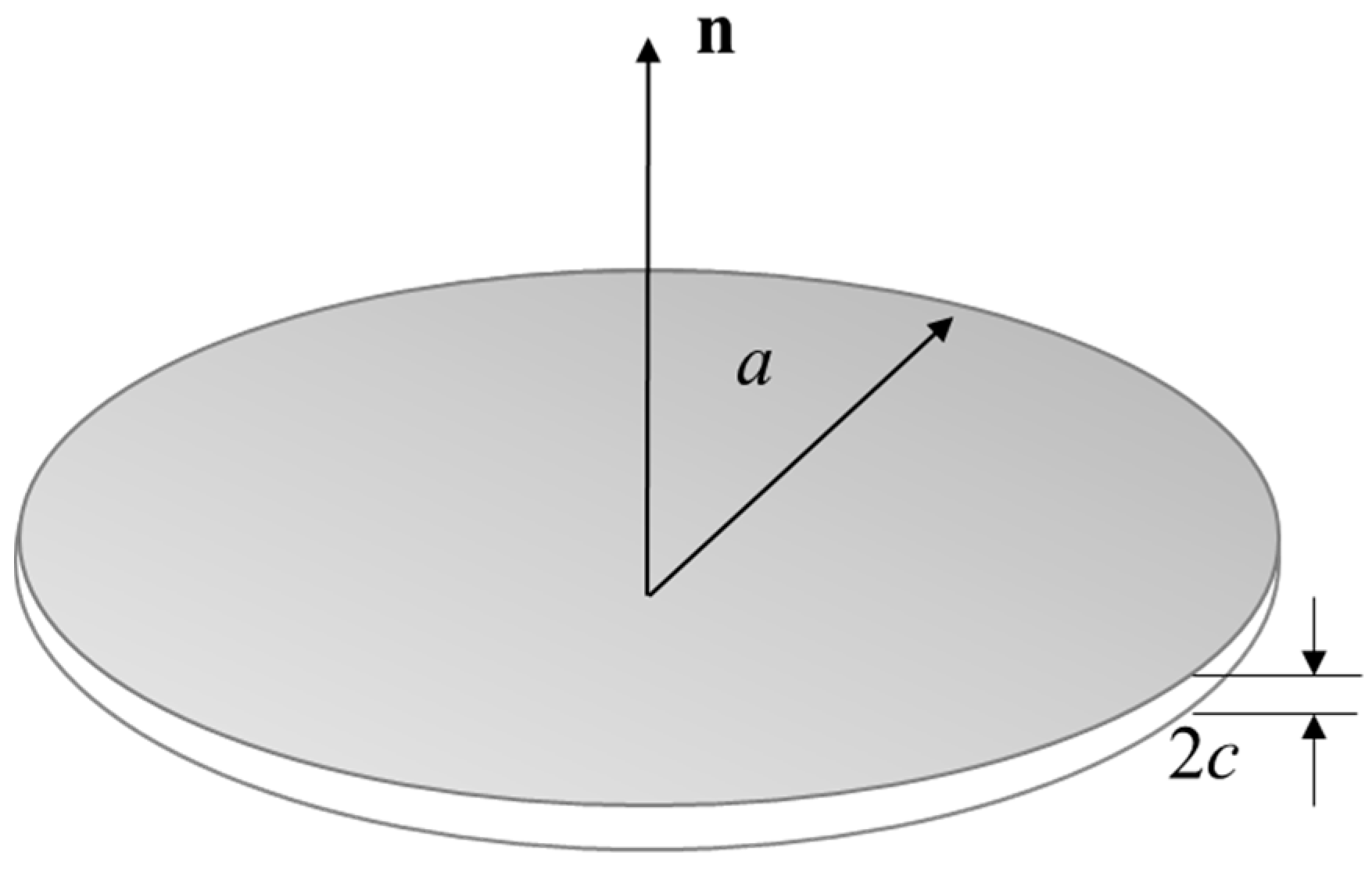
4.1. Effective Elastic Properties of Cracked Materials
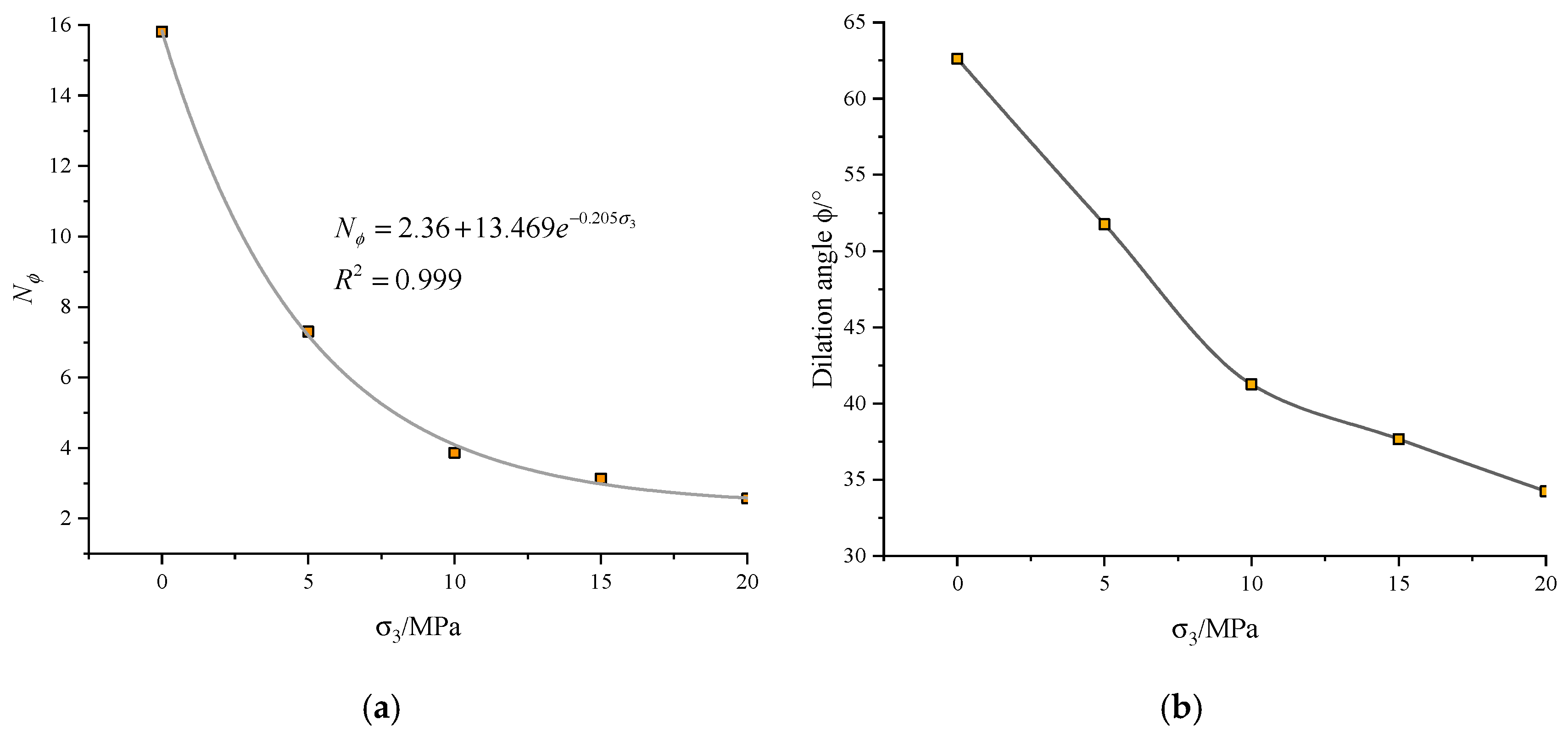
4.2. Plastic Characterization
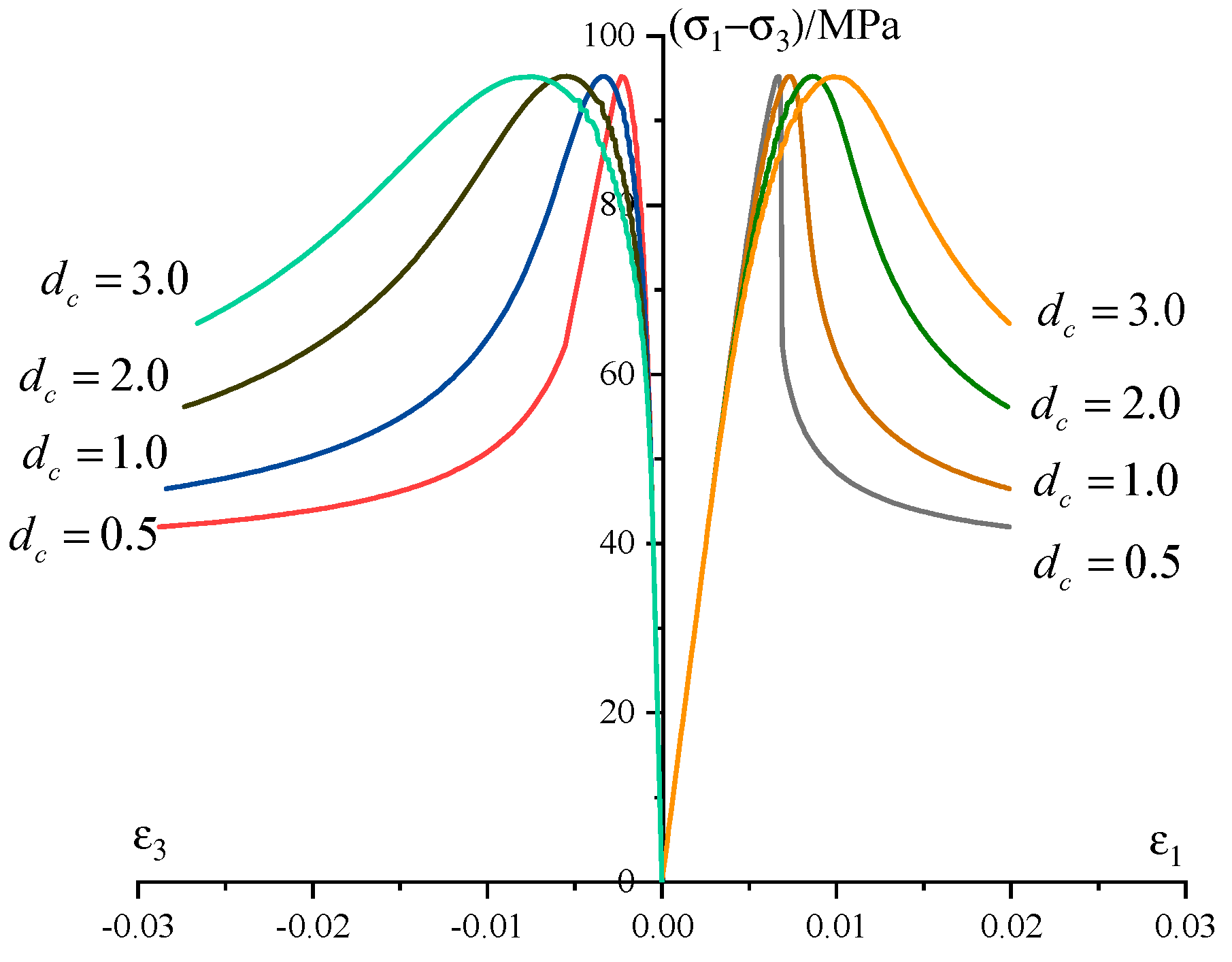
4.3. Damage Characterization
5. Elastoplastic Damage Coupling Correction Algorithm
5.1. Integration by Return Mapping Algorithm
5.2. Implementation Procedure
6. Numerical Simulations
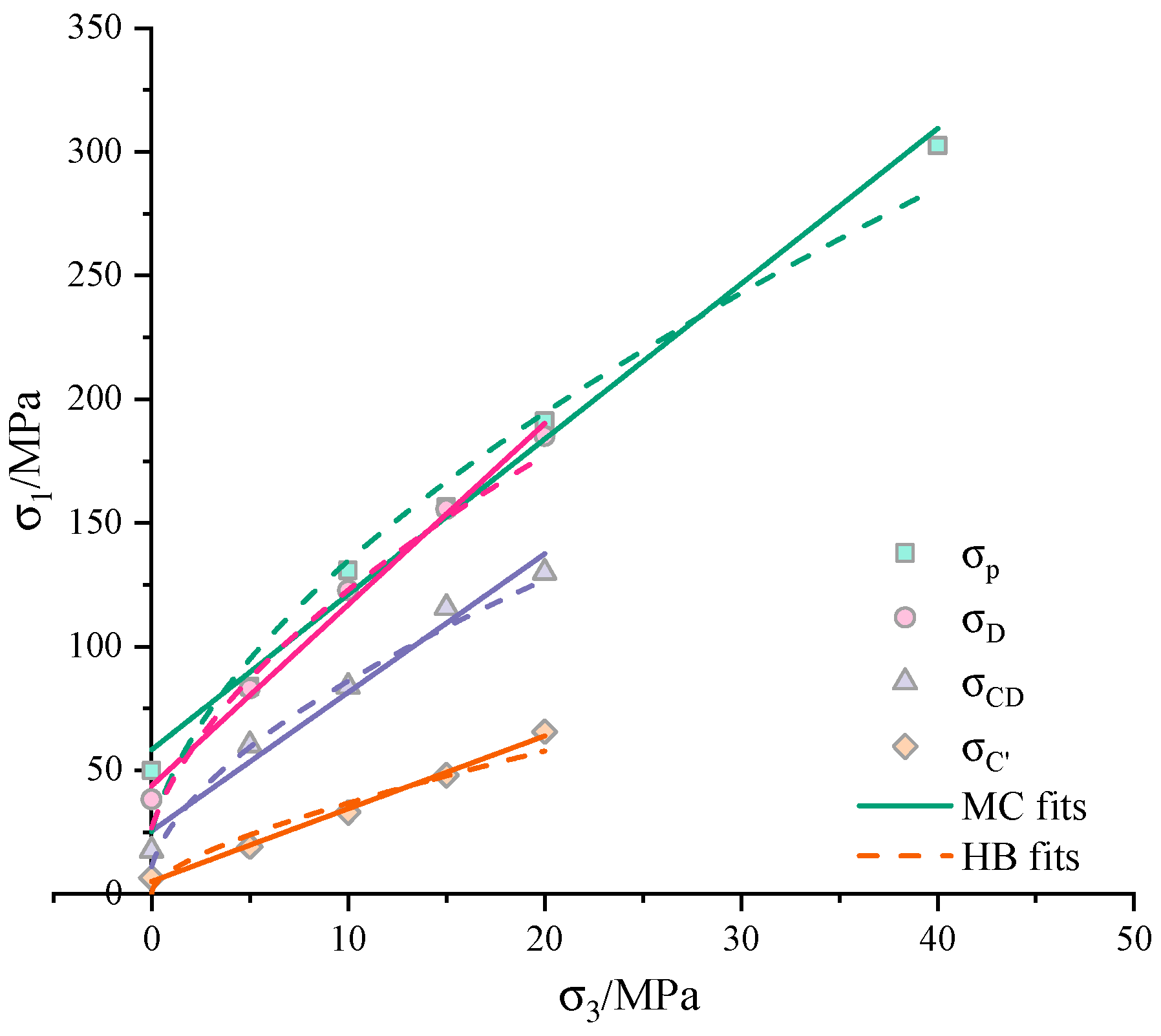
6.1. Identification of Model Parameters
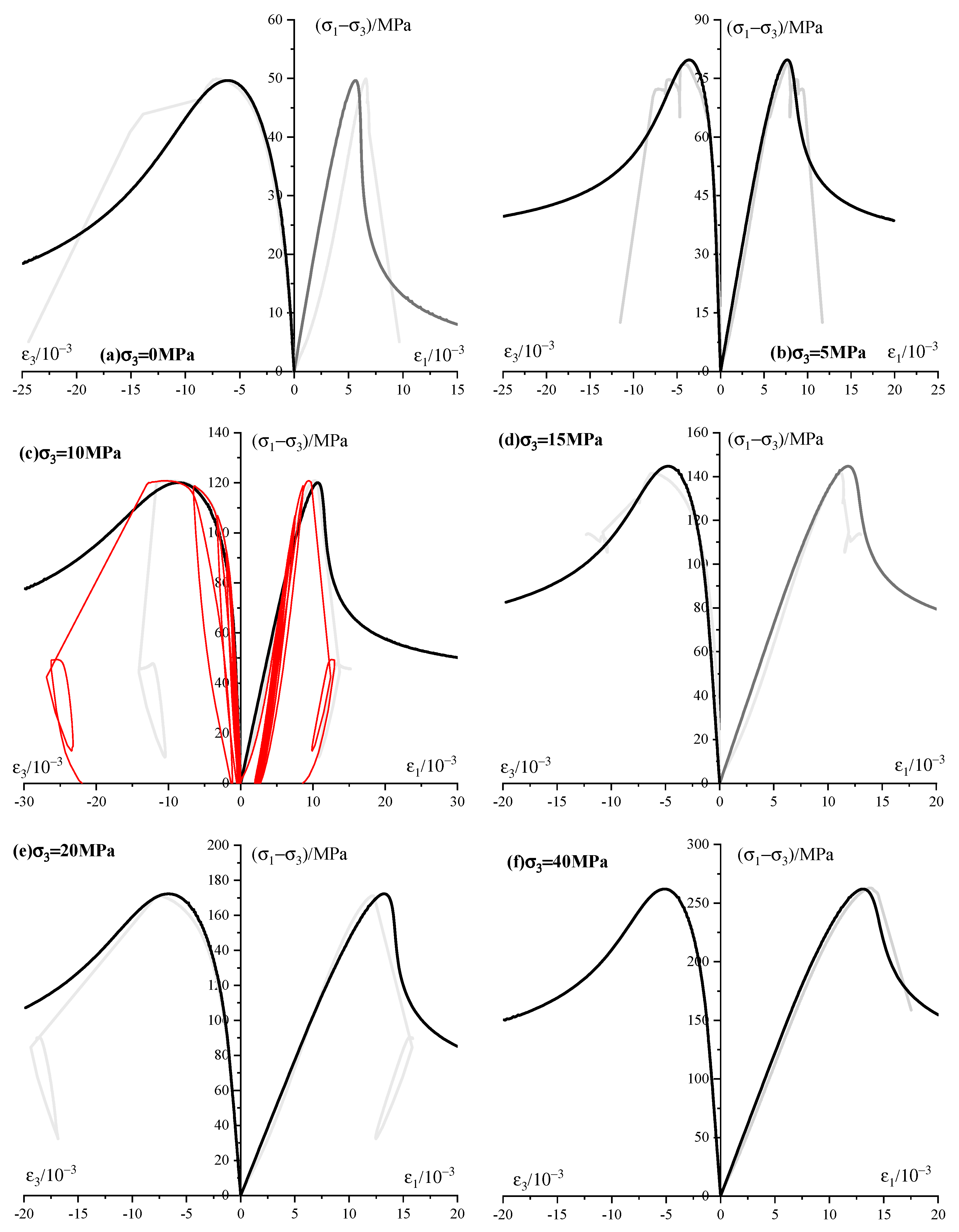
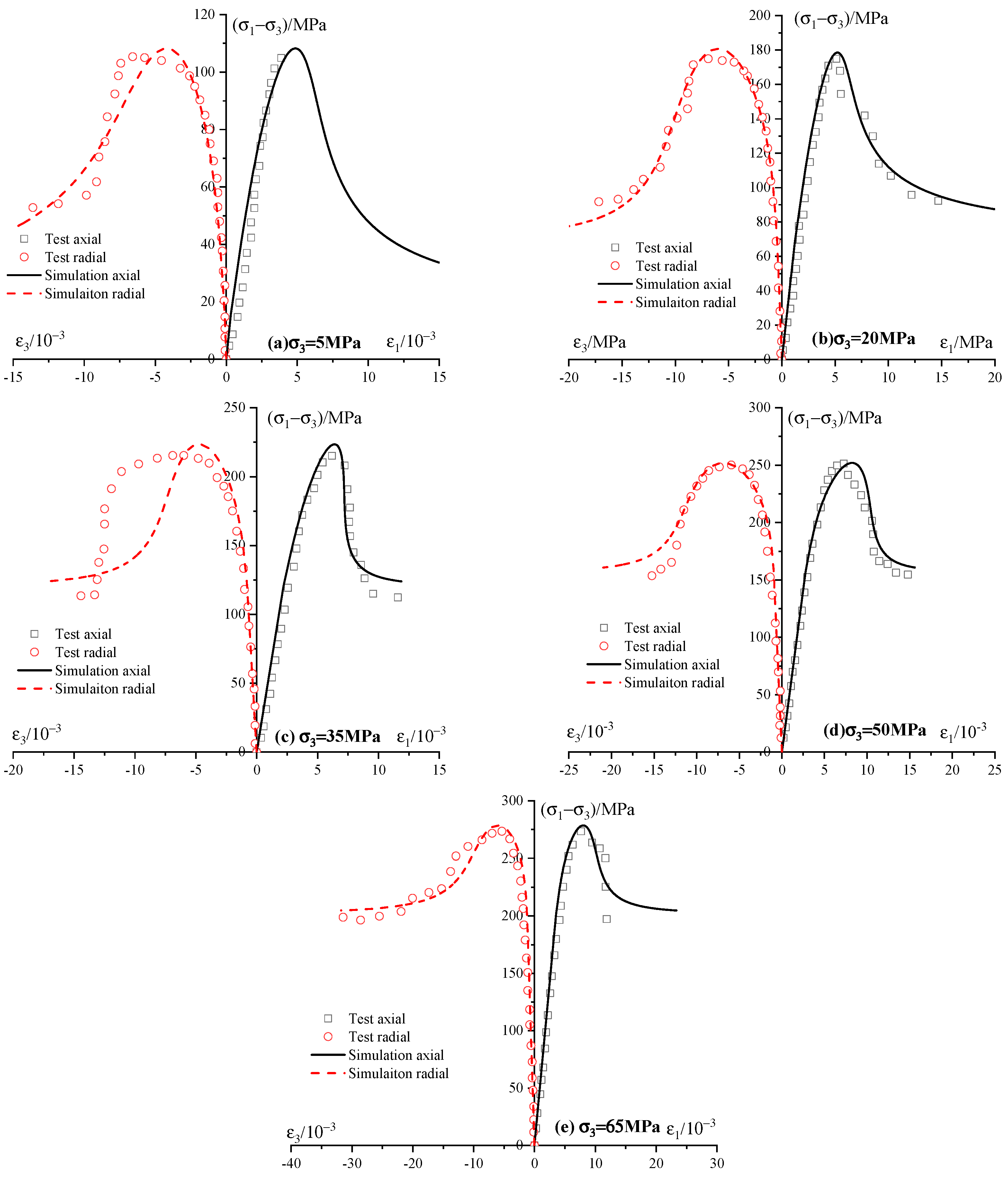
6.2. Simulation of Experimental Results of Test Sandstone
6.3. Simulation of Experimental Results of Shandong Red Sandstone
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, S.Q. Experimental study on deformation, peak strength and crack damage behavior of hollow sandstone under conventional triaxial compression. Eng. Geol. 2016, 213, 11–24. [Google Scholar] [CrossRef]
- Wong, T.F.; David, C.; Zhu, W. The transition from brittle faulting to cataclastic flow in porous sandstones: Mechanical deformation. J. Geophys. Res. Solid Earth 1997, 102, 3009–3025. [Google Scholar] [CrossRef]
- Wasantha, P.L.P.; Ranjith, P.G.; Zhao, J.; Shao, S.S.; Permata, G. Strain Rate Effect on the Mechanical Behaviour of Sandstones with Different Grain Sizes. Rock Mech. Rock Eng. 2015, 48, 1883–1895. [Google Scholar] [CrossRef]
- Heap, M.J.; Baud, P.; Meredith, P.G. Influence of temperature on brittle creep in sandstones. Geophys. Res. Lett. 2009, 36, 6. [Google Scholar] [CrossRef] [Green Version]
- Benson, P.M.; Meredith, P.G.; Platzman, E.S.; White, R.E. Pore fabric shape anisotropy in porous sandstones and its relation to elastic wave velocity and permeability anisotropy under hydrostatic pressure. Int. J. Rock Mech. Min. 2005, 42, 890–899. [Google Scholar] [CrossRef]
- Hu, S.C.; Tan, Y.L.; Zhou, H.; Guo, W.Y.; Hu, D.W.; Meng, F.Z.; Liu, Z.G. Impact of Bedding Planes on Mechanical Properties of Sandstone. Rock Mech. Rock Eng. 2017, 50, 2243–2251. [Google Scholar] [CrossRef]
- Baud, P.; Zhu, W.L.; Wong, T.F. Failure mode and weakening effect of water on sandstone. J. Geophys. Res. Solid Earth 2000, 105, 16371–16389. [Google Scholar] [CrossRef]
- Feng, X.T.; Chen, S.L.; Zhou, H. Real-time computerized tomography (CT) experiments on sandstone damage evolution during triaxial compression with chemical corrosion. Int. J. Rock Mech. Min. 2004, 41, 181–192. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Li, Y.B.; Huang, Y.H. Experimental investigation on triaxial mechanical and permeability behavior of sandstone after exposure to different high temperature treatments. Geothermics 2017, 69, 93–109. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.; Yan, L.; Feng, X.T.; Xie, W.C.; Chen, H. Experimental investigation and failure mechanism analysis for dacite under true triaxial unloading conditions. Eng. Geol. 2020, 264, 105407. [Google Scholar] [CrossRef]
- Menéndez, B.; Zhu, W.; Wong, T.F. Micromechanics of brittle faulting and cataclastic flow in Berea sandstone. J. Struct. Geol. 1996, 18, 1–16. [Google Scholar] [CrossRef]
- Dahou, A.; Shao, J.F.; Bederiat, M. Experimental and numerical investigations on transient creep of porous chalk. Mech. Mater. 1995, 21, 147–158. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.; Jia, C.; Wang, W. Mechanical behavior of fine-grained sandstone in triaxial compression and elastoplastic modeling by return mapping algorithms. Bull. Eng. Geol. Environ. 2017, 77, 1689–1699. [Google Scholar] [CrossRef]
- Bruning, T.; Karakus, M.; Nguyen, G.D.; Goodchild, D. An experimental and theoretical stress-strain-damage correlation procedure for constitutive modelling of granite. Int. J. Rock Mech. Min. 2019, 116, 1–12. [Google Scholar] [CrossRef]
- Kranz, R.L. Microcracks in rocks: A review. Tectonophysics 1983, 100, 449–480. [Google Scholar] [CrossRef]
- Huang, Y.H.; Yang, S.Q. Mechanical and cracking behavior of granite containing two coplanar flaws under conventional triaxial compression. Int. J. Damage Mech. 2019, 28, 590–610. [Google Scholar] [CrossRef]
- Hansen, N.R.; Schreyer, H.L. A thermodynamically consistent framework for theories of elastoplasticity coupled with damage. Int. J. Solids Struct. 1994, 31, 359–389. [Google Scholar] [CrossRef]
- Basista, M.; Gross, D. The sliding crack model of brittle deformation: An internal variable approach. Int. J. Solids Struct. 1998, 35, 487–509. [Google Scholar] [CrossRef]
- Murakami, S. Continuum Damage Mechanics: A Continuum Mechanics Approach to the Analysis of Damage and Fracture; Springer Science & Business Media: Nagoya, Japan, 2012; Volume 185. [Google Scholar]
- Zhang, J.C.; Xu, W.Y.; Wang, H.L.; Wang, R.B.; Meng, Q.X.; Du, S.W. A coupled elastoplastic damage model for brittle rocks and its application in modelling underground excavation. Int. J. Rock Mech. Min. 2016, 84, 130–141. [Google Scholar] [CrossRef]
- Jia, C.; Xu, W.; Wang, S.; Wang, R.; Yu, J. Experimental analysis and modeling of the mechanical behavior of breccia lava in the dam foundation of the Baihetan Hydropower Project. Bull. Eng. Geol. Environ. 2018, 78, 2681–2695. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, J.; Wang, J.; Jia, Y.; Shao, J.F. Damage and Plastic Deformation Modeling of Beishan Granite Under Compressive Stress Conditions. Rock Mech. Rock Eng. 2014, 48, 1623–1633. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, D.Q.; Jiang, Q.H.; Zhou, C.B. Micromechanical analysis of anisotropic damage and its influence on effective thermal conductivity in brittle rocks. Int. J. Rock Mech. Min. 2012, 50, 102–116. [Google Scholar] [CrossRef]
- Bary, B. Estimation of poromechanical and thermal conductivity properties of unsaturated isotropically microcracked cement pastes. Int. J. Numer. Anal. Met. 2011, 35, 1560–1586. [Google Scholar] [CrossRef]
- Hashin, Z. The differential scheme and its application to cracked materials. J. Mech. Phys. Solids 1988, 36, 719–734. [Google Scholar] [CrossRef]
- Guery, A.A.C.; Cormery, F.; Shao, J.F.; Kondo, D. A micromechanical model of elastoplastic and damage behavior of a cohesive geomaterial. Int. J. Solids Struct. 2008, 45, 1406–1429. [Google Scholar] [CrossRef]
- Zhu, Q.Z.; Kondo, D.; Shao, J.F. Micromechanical analysis of coupling between anisotropic damage and friction in quasi brittle materials: Role of the homogenization scheme. Int. J. Solids Struct. 2008, 45, 1385–1405. [Google Scholar] [CrossRef]
- Zhu, Q.Z.; Shao, J.F. Micromechanics of rock damage: Advances in the quasi-brittle field. J. Rock Mech. Geotech. Eng. 2017, 9, 29–40. [Google Scholar] [CrossRef]
- Wang, H.L.; Xu, W.Y.; Jia, C.J.; Cai, M.; Meng, Q.X. Experimental Research on Permeability Evolution with Microcrack Development in Sandstone under Different Fluid Pressures. J. Geotech. Geoenviron. 2016, 142, 04016014. [Google Scholar] [CrossRef]
- Yu, J.; Xu, W.; Jia, C.; Wang, R.; Wang, H. Experimental measurement of permeability evolution in sandstone during hydrostatic compaction and triaxial deformation. Bull. Eng. Geol. Environ. 2018, 78, 5269–5280. [Google Scholar] [CrossRef]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. 1999, 36, 281–289. [Google Scholar]
- Brace, W.; Paulding, B.; Scholz, C. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Grindrod, P.M.; Heap, M.J.; Fortes, A.D.; Meredith, P.G.; Wood, I.G.; Trippetta, F.; Sammonds, P.R. Experimental investigation of the mechanical properties of synthetic magnesium sulfate hydrates: Implications for the strength of hydrated deposits on Mars. J. Geophys. Res. Planets 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Vermeer, P.A.; De Borst, R. Non-associated plasticity for soils, concrete and rock. Heron 1984, 29, 3–64. [Google Scholar]
- Cai, W.; Dou, L.M.; Ju, Y.; Cao, W.Z.; Yuan, S.S.; Si, G.Y. A plastic strain-based damage model for heterogeneous coal using cohesion and dilation angle. Int. J. Rock Mech. Min. 2018, 110, 151–160. [Google Scholar] [CrossRef]
- Walton, G.; Arzúa, J.; Alejano, L.R.; Diederichs, M.S. A Laboratory-Testing-Based Study on the Strength, Deformability, and Dilatancy of Carbonate Rocks at Low Confinement. Rock Mech. Rock Eng. 2014, 48, 941–958. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The non-linear field theories of mechanics. In The Non-Linear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–579. [Google Scholar]
- Dormieux, L.; Kondo, D. Micromechanics of damage propagation in fluid-saturated cracked media. Rev. Eur. Génie Civ. 2011, 11, 945–962. [Google Scholar] [CrossRef]
- Zaoui, A. Continuum micromechanics: Survey. J. Eng. Mech. 2002, 128, 808–816. [Google Scholar] [CrossRef] [Green Version]
- Budiansky, B.; O’Connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Zhu, Q.Z. Strength prediction of dry and saturated brittle rocks by unilateral damage-friction coupling, analyses. Comput. Geotech. 2016, 73, 16–23. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.; Wang, W.; Jia, C. Experimental and numerical investigations on the mechanical behavior of fine-grained sandstone. Int. J. Geomech. 2017, 18, 04017150. [Google Scholar] [CrossRef]
- Zhu, Q.Z.; Shao, J.F. A refined micromechanical damage-friction model with strength prediction for rock-like materials under compression. Int. J. Solids Struct. 2015, 60, 75–83. [Google Scholar] [CrossRef]
- Hu, K.; Zhu, Q.Z.; Chen, L.; Shao, J.F.; Liu, J. A Micromechanics-Based Elastoplastic Damage Model for Rocks with a Brittle-Ductile Transition in Mechanical Response. Rock Mech. Rock Eng. 2018, 51, 1729–1737. [Google Scholar] [CrossRef]
- Pensee, V.; Kondo, D.; Dormieux, L. Micromechanical analysis of anisotropic damage in brittle materials. J. Eng. Mech. 2002, 128, 889–897. [Google Scholar] [CrossRef]
- Xu, H.; Prevost, J.H. Integration of a continuum damage model for shale with the cutting plane algorithm. Int. J. Numer. Anal. Met. 2017, 41, 471–487. [Google Scholar] [CrossRef] [Green Version]
- Simo, J.C.; Ortiz, M. A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations. Comput. Methods Appl. Mech. Eng. 1985, 49, 221–245. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. Consistent tangent operators for rate-independent elastoplasticity. Comput. Methods Appl. Mech. Eng. 1985, 48, 101–118. [Google Scholar] [CrossRef]
- Lockner, D.A. A generalized law for brittle deformation of Westerly granite. J. Geophys. Res. Solid Earth 1998, 103, 5107–5123. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jing, H.W.; Wang, S.Y. Experimental Investigation on the Strength, Deformability, Failure Behavior and Acoustic Emission Locations of Red Sandstone Under Triaxial Compression. Rock Mech. Rock Eng. 2012, 45, 583–606. [Google Scholar] [CrossRef]


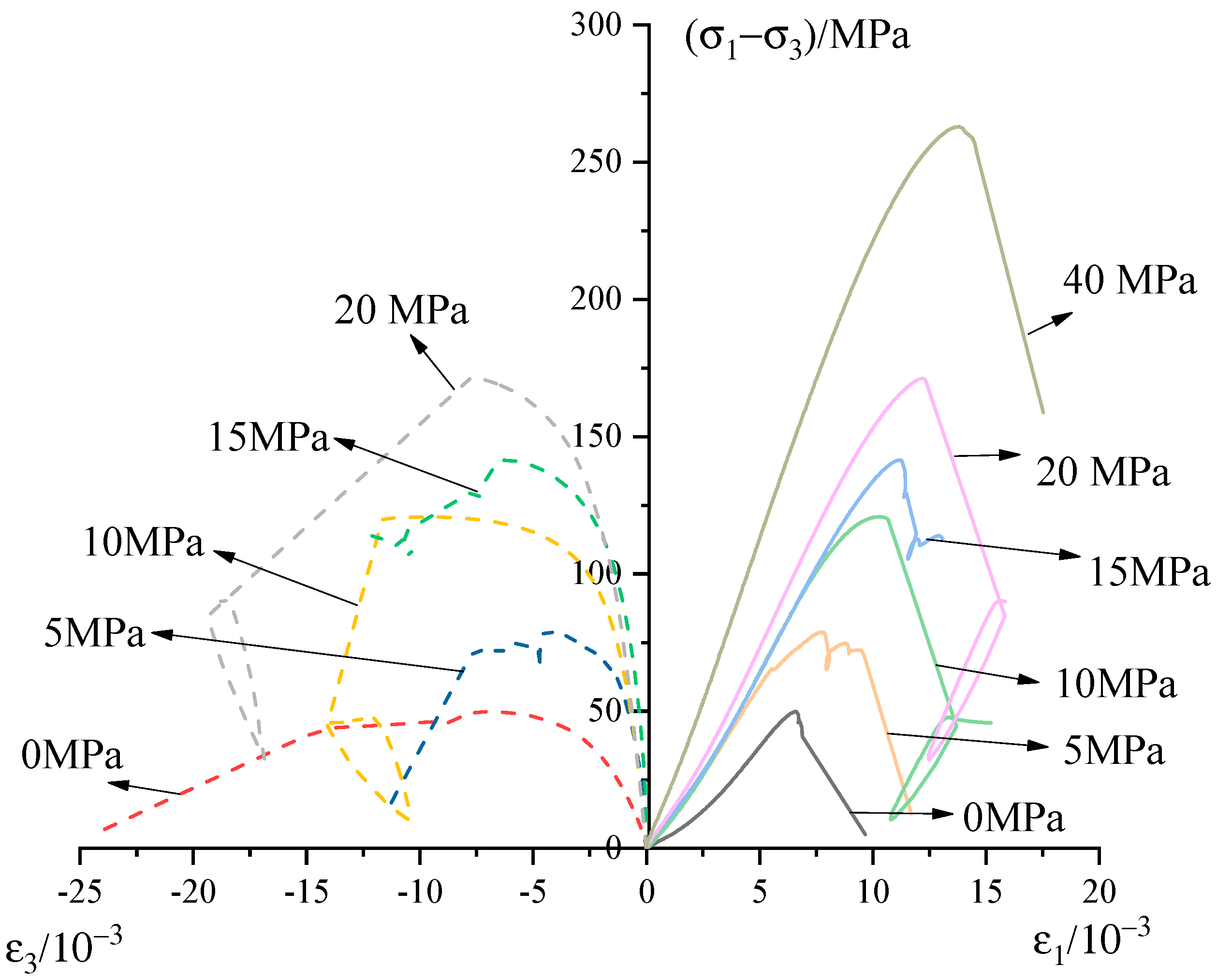
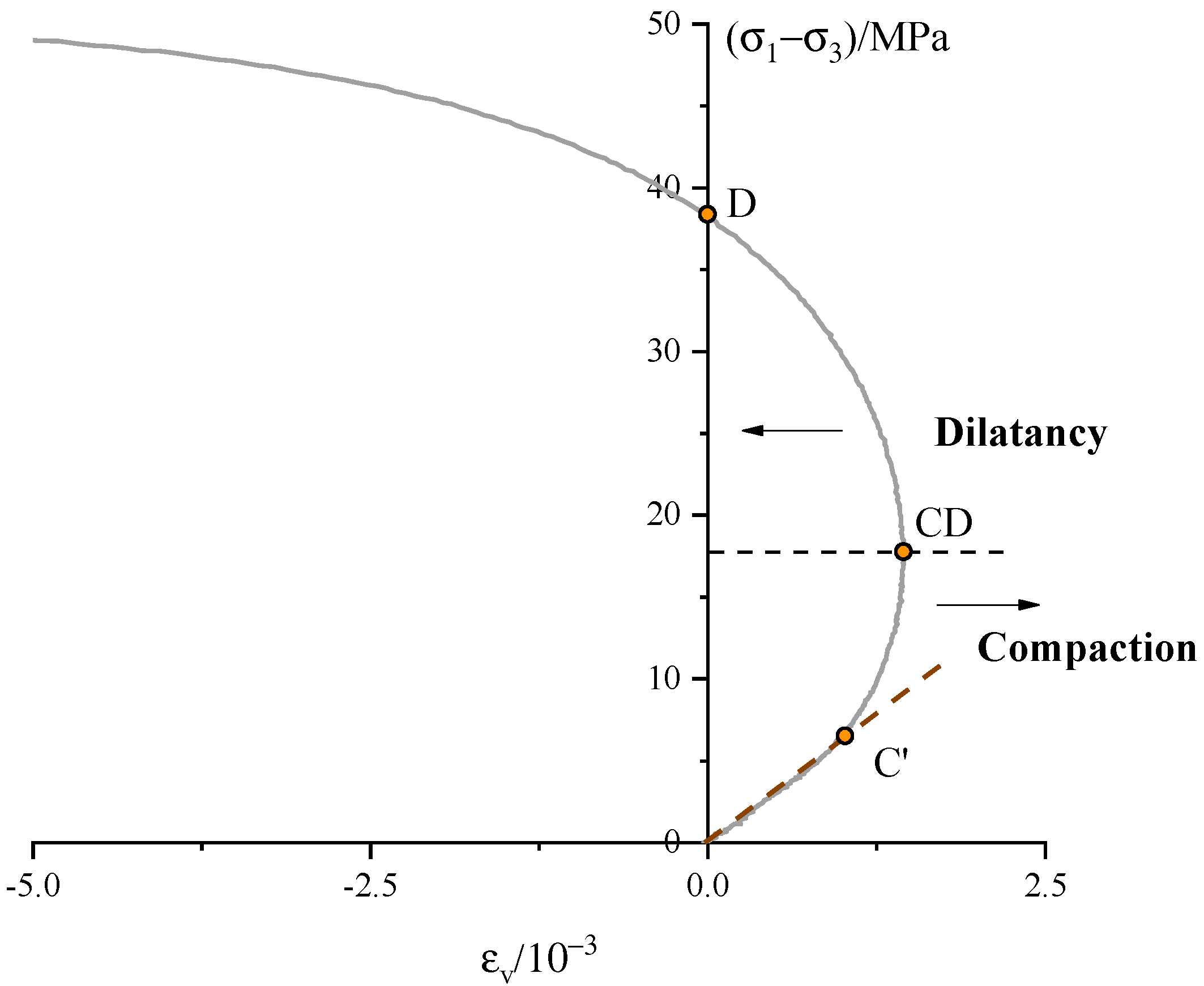


| 0 | 6.558 | 17.658 | 38.259 | 49.933 |
| 5 | 14.093 | 55.263 | 78.135 | 78.797 |
| 10 | 22.967 | 73.777 | 112.724 | 120.904 |
| 15 | 33.081 | 100.74 | 140.601 | 141.510 |
| 20 | 45.604 | 109.955 | 165.122 | 171.250 |
| 40 | - | - | - | 262.597 |
| Points | UCS/MPa | m | s | a | c/MPa | R2(HB) | R2(MC) | |
|---|---|---|---|---|---|---|---|---|
| 0.096 | 746.694 | 1.0 | 0.5 | 29.511 | 1.471 | 0.966 | 0.996 | |
| CD | 11.102 | 51.033 | 1.0 | 0.5 | 44.190 | 5.380 | 0.974 | 0.974 |
| D | 26.738 | 44.963 | 1.0 | 0.5 | 49.440 | 8.079 | 0.977 | 0.992 |
| peak | 25.295 | 58.911 | 1.0 | 0.5 | 46.491 | 11.633 | 0.973 | 0.992 |
| Load to next step , ; , , ; |
| Plastic correction Determine the plastic multiplier with Equation (47) while . Update the variables: , , ; Update the macroscopic stress and strain: |
| Elastoplastic damage coupling correction Calculate the multipliers {, } using the Equation (48) Update the variables: , , ; Update the macroscopic stress and strain: |
| Parameters | Es (GPa) | ||||
|---|---|---|---|---|---|
| Values | 15.86 | 0.198 | 1.56 | 0.009 | 1.0 |
| Parameters | Es (GPa) | ||||
|---|---|---|---|---|---|
| Values | 46.0 | 0.33 | 1.16 | 0.034 | 2.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Zhang, Q.; Wang, S. Experimental Investigation and Micromechanical Modeling of Elastoplastic Damage Behavior of Sandstone. Materials 2020, 13, 3414. https://doi.org/10.3390/ma13153414
Jia C, Zhang Q, Wang S. Experimental Investigation and Micromechanical Modeling of Elastoplastic Damage Behavior of Sandstone. Materials. 2020; 13(15):3414. https://doi.org/10.3390/ma13153414
Chicago/Turabian StyleJia, Chaojun, Qiang Zhang, and Susheng Wang. 2020. "Experimental Investigation and Micromechanical Modeling of Elastoplastic Damage Behavior of Sandstone" Materials 13, no. 15: 3414. https://doi.org/10.3390/ma13153414





