Molecular Dynamics as a Means to Investigate Grain Size and Strain Rate Effect on Plastic Deformation of 316 L Nanocrystalline Stainless-Steel
Abstract
1. Introduction
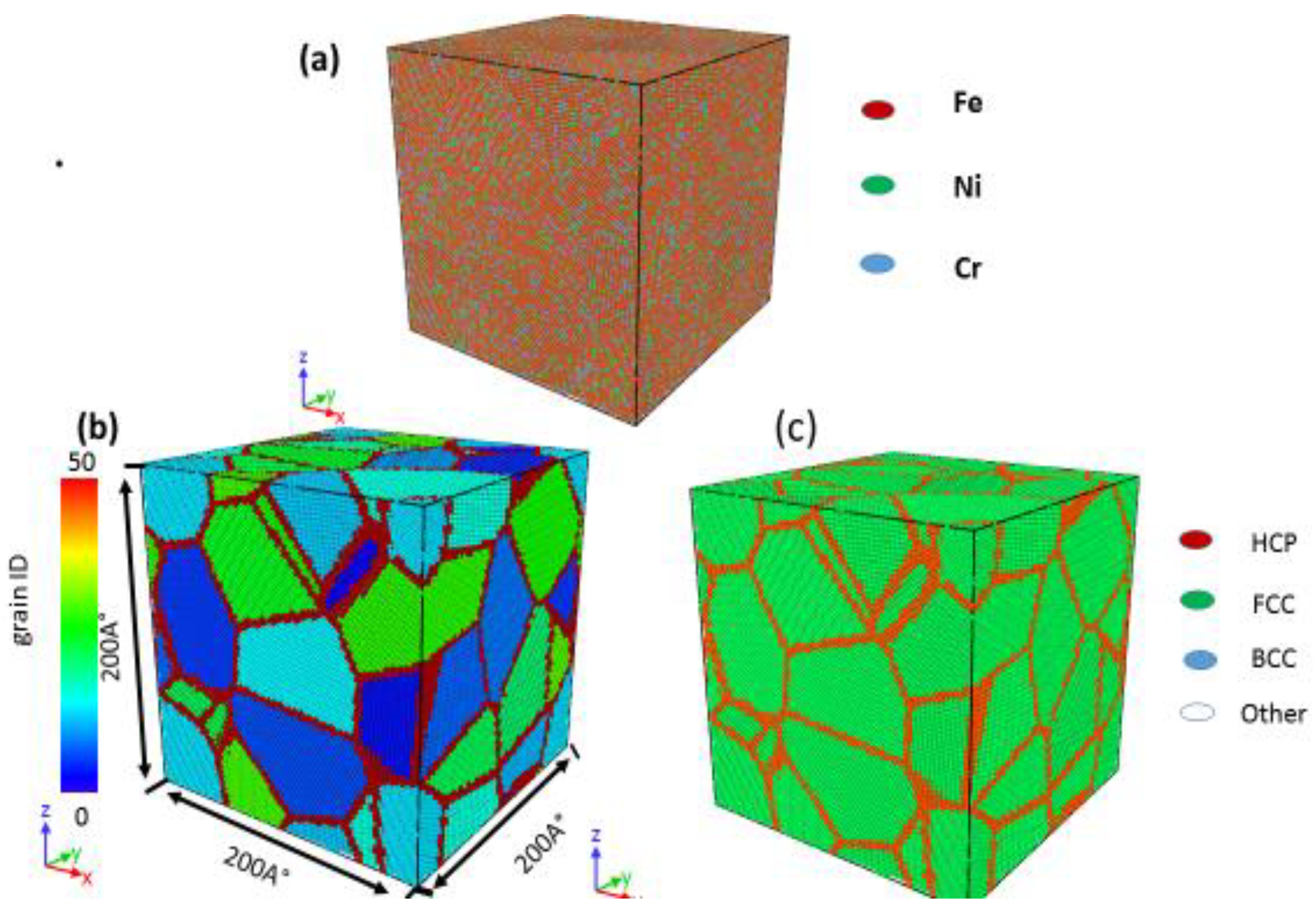
2. Simulation Methods
3. Results and Discussion
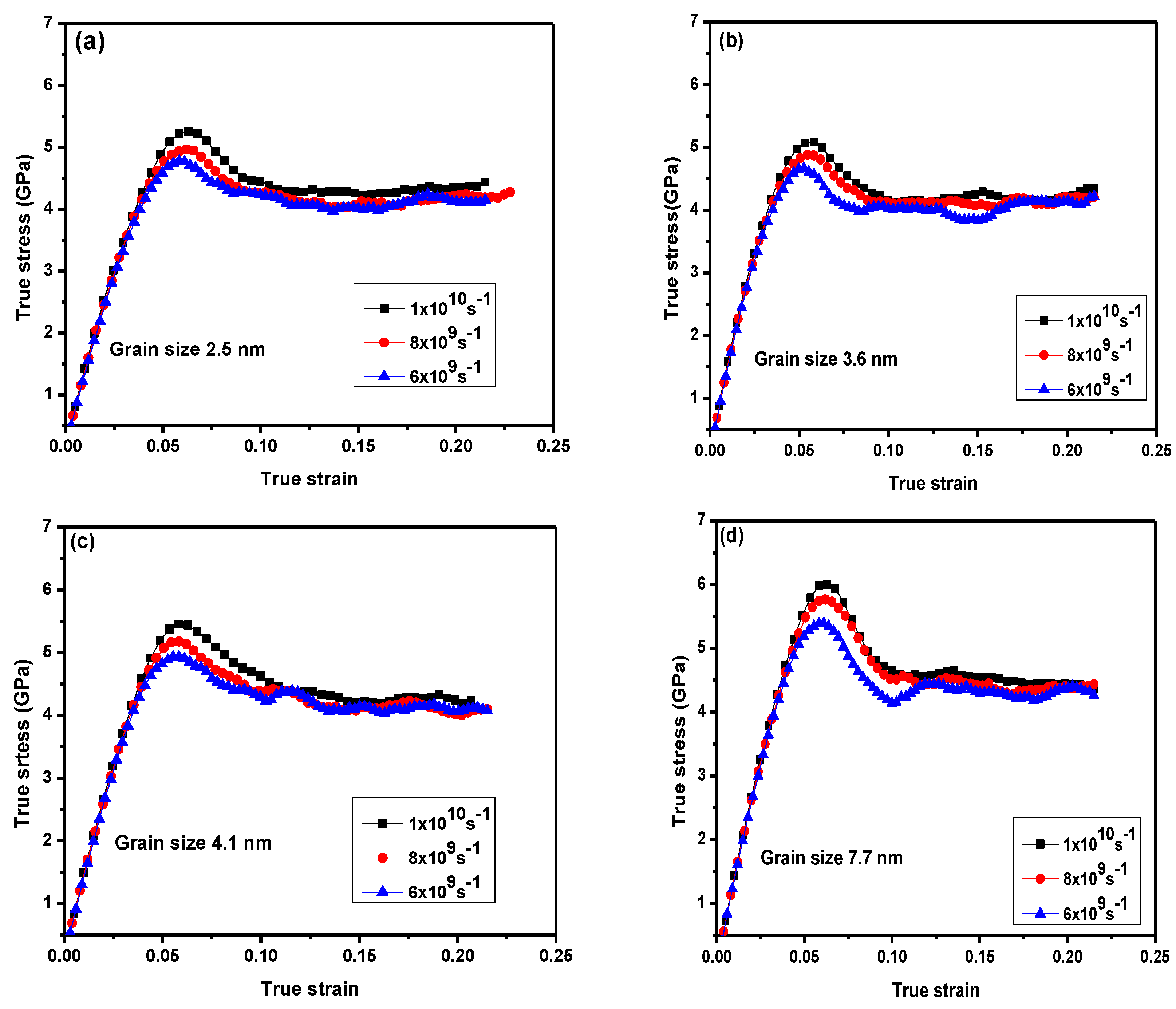
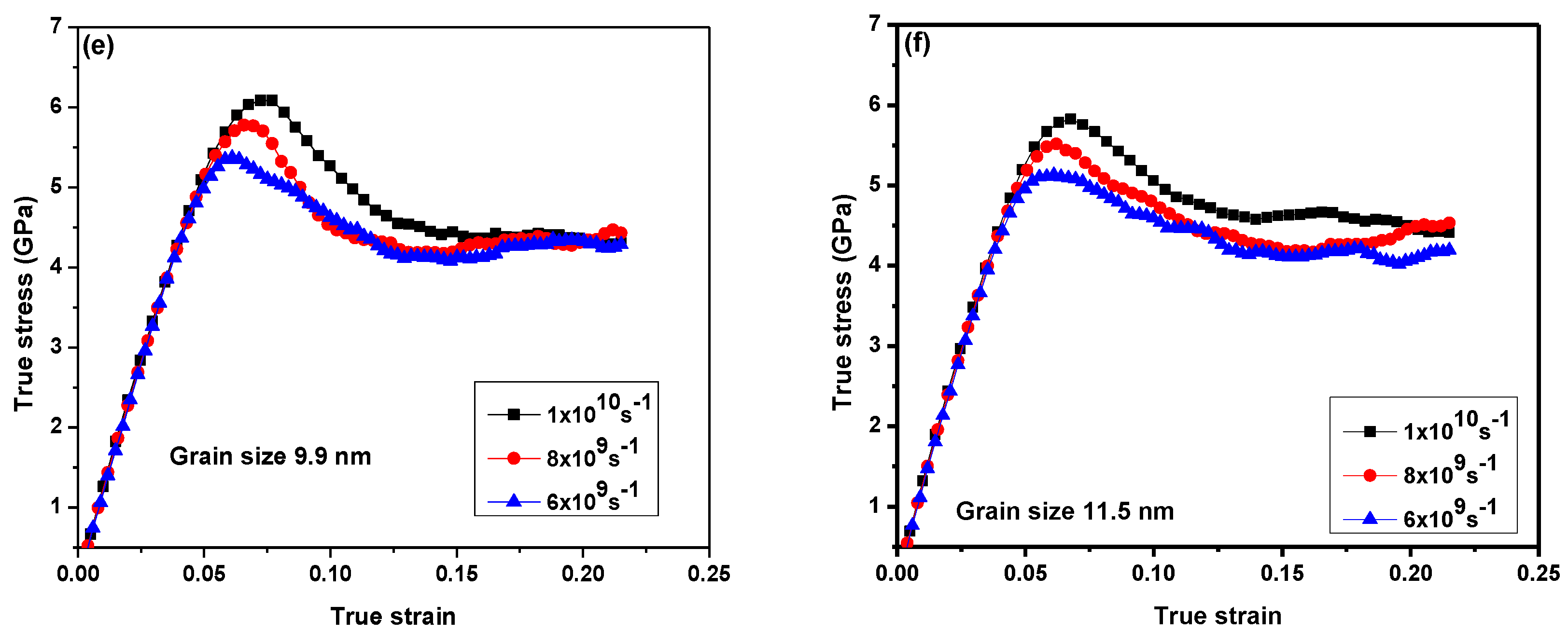
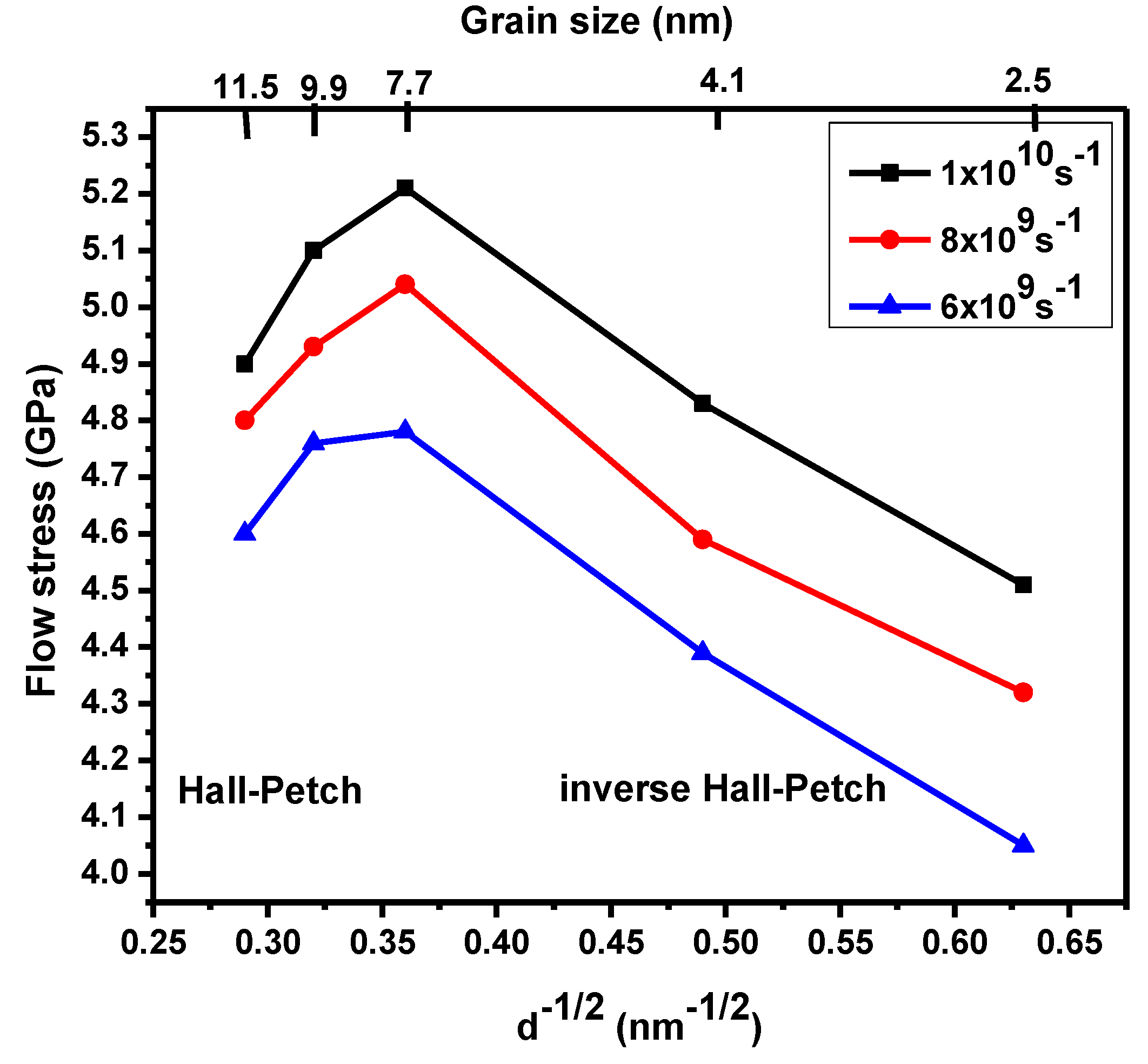
3.1. Tensile Deformation
3.2. Deformation Mechanism
4. Conclusions
- The result showed that grain sliding and grain rotation dominated in small grain sizes. Additionally, dislocation activities and twins were observed for large grain sizes.
- Transitioning between plastic deformation mechanisms and dislocation-based plasticity to grain boundaries was observed.
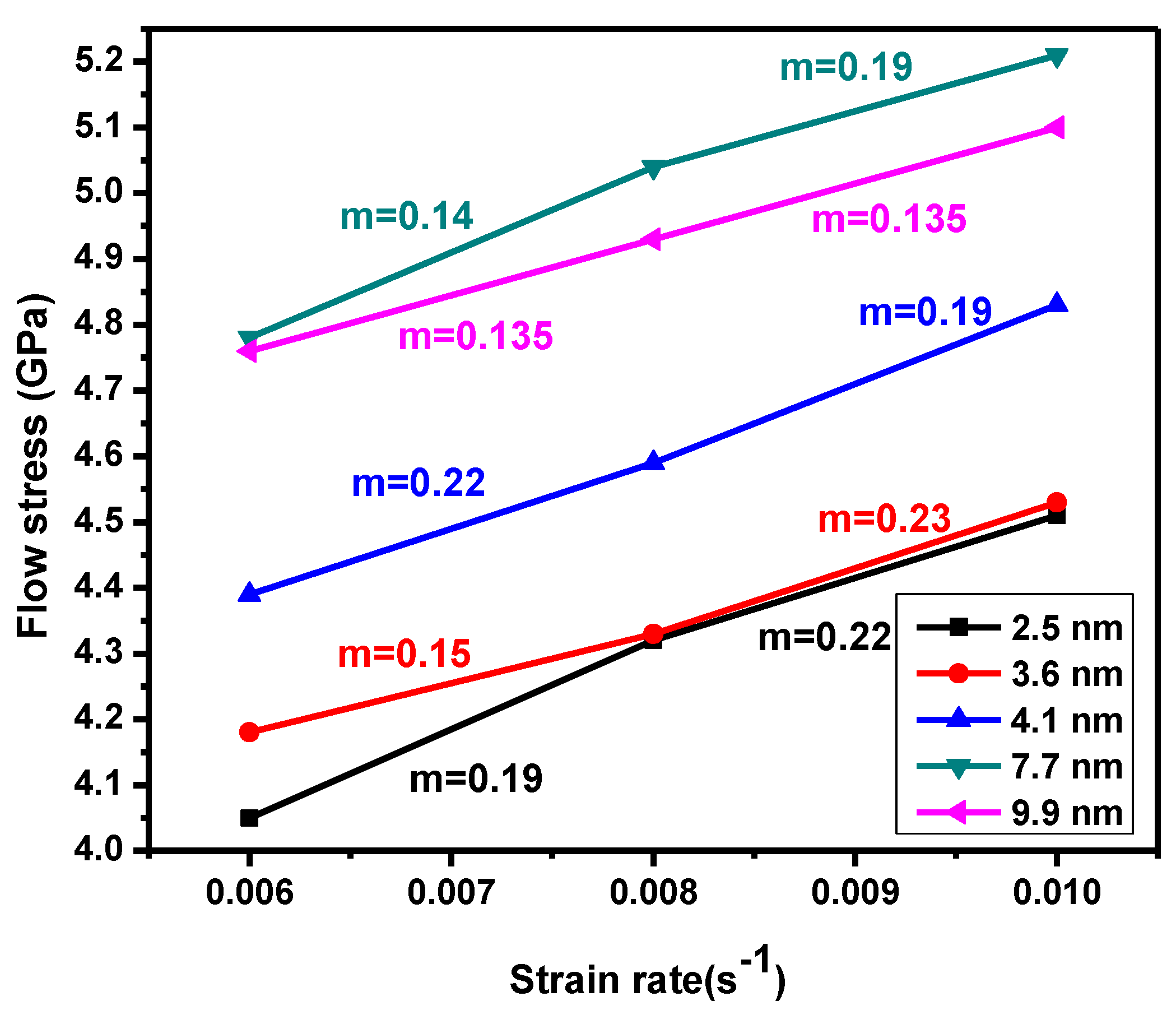
- The influence of strain rates on small grain sizes was greater than on large grain sizes. Therefore, strain rate sensitivity increased when the grain size decreased. The stacking fault created by partial dislocation was observed in every sample.
- For small grain sizes or lower strain rates, the stacking fault had a partial dislocation emission. Therefore, the grain boundary movement was the most active in the small grain.
- For large grain sizes or high strain rates, the stacking fault did not represent any impediment to the movement of partial dislocations. Therefore, the twin was formed through the stacking fault and was spread inside the grains.
- Partial dislocation was observed at a lower strain rate, before it was observed at a higher strain rate, at the same applied strain.
- As the strain rate was increased, mechanical properties such as the yield stress and flow stress increased.
Author Contributions
Funding
Conflicts of Interest
References
- Eskandari, M.; Zarei-Hanzaki, A.; Abedi, H. An investigation into the room temperature mechanical properties of nanocrystalline austenitic stainless steels. Mater. Des. 2013, 45, 674–681. [Google Scholar] [CrossRef]
- Chen, X.; Lu, J.; Lu, L.; Lu, K. Tensile properties of a nanocrystalline 316L austenitic stainless steel. Scr. Mater. 2005, 52, 1039–1044. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Gong, S.K.; Mao, S.X. High resolution transmission electron microscope observation of zero-strain deformation twinning mechanisms in Ag. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef]
- Li, J.; Cao, Y.; Gao, B.; Li, Y.; Zhu, Y. Superior strength and ductility of 316L stainless steel with heterogeneous lamella structure. Mater. Sci. 2018, 53, 10442–10456. [Google Scholar] [CrossRef]
- Li, J.; Gao, W.-D.; Cao, Y.; Huang, Z.-W.; Gao, B.; Mao, Q.; Li, Y.-S. Microstructures and mechanical properties of a gradient nanostructured 316L stainless steel processed by rotationally accelerated shot peening. Adv. Eng. Mater. 2018, 20. [Google Scholar] [CrossRef]
- Koch, C.C. Bulk behavior of nanostructured materials. In Siegel RW; Hu, E., Roco, M.C., Eds.; Springer Science and Business Media: Dordrecht, The Netherlands, 1999; pp. 93–111. [Google Scholar]
- Koch, C.C. Optimization of strength and ductility in nanocrystalline and ultrafine grained metals. Scr. Mater. 2003, 49, 657–662. [Google Scholar] [CrossRef]
- Kumar, S.; Suresh, S.; Chisholm, M.; Horton, J.; Wang, P. Deformation of electrodeposited nanocrystalline nickel. Acta Mater. 2003, 51, 387–405. [Google Scholar] [CrossRef]
- Asaro, R.J.; Suresh, S. Mechanistic models for the activation volume and rate sensitivity in metals with nanocrystalline grains and nano-scale twins. Acta Mater. 2005, 53, 3369–3382. [Google Scholar] [CrossRef]
- El-Danaf, E.A.; Kalidindi, S.R.; Doherty, R.D. Influence of grain size and stacking-fault energy on deformation twinning in fcc metals. Metall. Mater. Trans. A 1999, 30, 1223–1233. [Google Scholar] [CrossRef]
- Rice, J.R. Dislocation nucleation from a crack tip: An analysis based on the Peierls concept. J. Mech. Phys. Solids 1992, 40, 239–271. [Google Scholar] [CrossRef]
- Tao, N.; Lu, K. Nanoscale structural refinement via deformation twinning in face-centered cubic metals. Scr. Mater. 2009, 60, 1039–1043. [Google Scholar] [CrossRef]
- Huang, C.; Wang, K.; Wu, S.; Zhang, Z.; Li, G.; Li, S. Deformation twinning in polycrystalline copper at room temperature and low strain rate. Acta Mater. 2006, 54, 655–665. [Google Scholar] [CrossRef]
- Schiøtz, J.; Di Tolla, F.D.; Jacobsen, K.W. Softening of nanocrystalline metals at very small grain sizes. Nature 1998, 391, 561–563. [Google Scholar] [CrossRef]
- Ke, M.; Hackney, S.; Milligan, W.; Aifantis, E. Observation and measurement of grain rotation and plastic strain in nanostructured metal thin films. Nanostruct. Mater. 1995, 5, 689–697. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.A. Grain-boundary sliding in nanocrystalline fcc metals. Phys. Rev. B 2001, 64, 224105. [Google Scholar] [CrossRef]
- Lecroisey, F.; Pineau, A. Martensitic transformations induced by plastic deformation in the Fe-Ni-Cr-C system. Met. Mater. Trans. A 1972, 3, 391–400. [Google Scholar] [CrossRef]
- De, A.K.; Speer, J.G.; Matlock, D.K.; Murdock, D.C.; Mataya, M.C.; Comstock, R.J. Deformation-induced phase transformation and strain hardening in type 304 austenitic stainless steel. Met. Mater. Trans. A 2006, 37, 1875–1886. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Y.; Chen, M.; Ma, E. Twinning and stacking fault formation during tensile deformation of nanocrystalline Ni. Scr. Mater. 2006, 54, 1685–1690. [Google Scholar] [CrossRef]
- Wang, Y.B.; Ho, J.C.; Liao, X.; Li, H.Q.; Ringer, S.P.; Zhu, Y. Mechanism of grain growth during severe plastic deformation of a nanocrystalline Ni–Fe alloy. Appl. Phys. Lett. 2009, 94, 11908. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, H.; Chen, Z.; Lu, C.; Mai, Y.-W. Roles of grain boundary and dislocations at different deformation stages of nanocrystalline copper under tension. Phys. Lett. A 2009, 373, 570–574. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, B.; Yao, Y.J.; Zhong, K. Inverse problem for 2D unsteady pollutant transport. Mater. Sci. Eng. A 2014, 595, 118–125. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, B.; Yao, Y.; Zhong, K. Effects of grain size and shape on mechanical properties of nanocrystalline copper investigated by molecular dynamics. Mater. Sci. Eng. A 2014, 615, 92–97. [Google Scholar] [CrossRef]
- Schiøtz, J. Atomic-scale modeling of plastic deformation of nanocrystalline copper. Scr. Mater. 2004, 51, 837–841. [Google Scholar] [CrossRef]
- Finney, J.L. A procedure for the construction of voronoipolyhedra. J. Comput. Phys. 1979, 32, 137–143. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Zhou, X.W.; Foster, M.E.; Sills, R.B. An Fe-Ni-Cr embedded atom method potential for austenitic and ferritic systems. J. Comput. Chem. 2018, 39, 2420–2431. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nose–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Ray, J.R.; Rahman, A. Statistical ensembles and molecular dynamics studies of anisotropic solids. J. Chem. Phys. 1984, 80, 4423–4428. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 15012. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 45021. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Husain, A.; La, P.; Hongzheng, Y.; Jie, S. Molecular Dynamics as a Means to Investigate Grain Size and Strain Rate Effect on Plastic Deformation of 316 L Nanocrystalline Stainless-Steel. Materials 2020, 13, 3223. https://doi.org/10.3390/ma13143223
Husain A, La P, Hongzheng Y, Jie S. Molecular Dynamics as a Means to Investigate Grain Size and Strain Rate Effect on Plastic Deformation of 316 L Nanocrystalline Stainless-Steel. Materials. 2020; 13(14):3223. https://doi.org/10.3390/ma13143223
Chicago/Turabian StyleHusain, Abdelrahim, Peiqing La, Yue Hongzheng, and Sheng Jie. 2020. "Molecular Dynamics as a Means to Investigate Grain Size and Strain Rate Effect on Plastic Deformation of 316 L Nanocrystalline Stainless-Steel" Materials 13, no. 14: 3223. https://doi.org/10.3390/ma13143223
APA StyleHusain, A., La, P., Hongzheng, Y., & Jie, S. (2020). Molecular Dynamics as a Means to Investigate Grain Size and Strain Rate Effect on Plastic Deformation of 316 L Nanocrystalline Stainless-Steel. Materials, 13(14), 3223. https://doi.org/10.3390/ma13143223




