Holography and Coherent Diffraction Imaging with Low-(30–250 eV) and High-(80–300 keV) Energy Electrons: History, Principles, and Recent Trends
Abstract
1. Introduction
2. Electron Waves
2.1. The Wavelength of an Electron
2.2. Electron Scattering in the First Born Approximation
2.2.1. The Schrödinger Equation
2.2.2. The Born Approximation
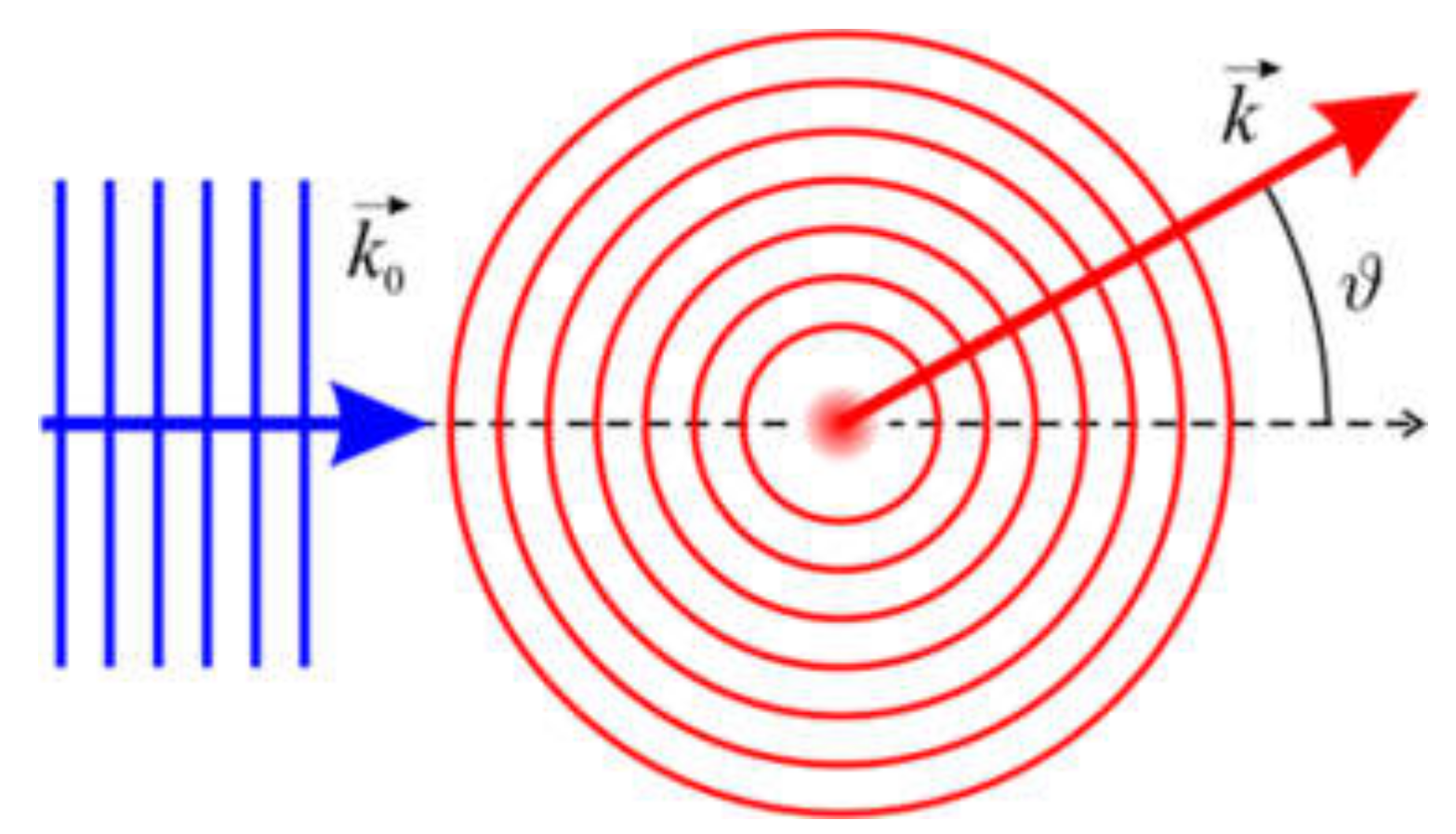
2.2.3. Scattering Amplitude
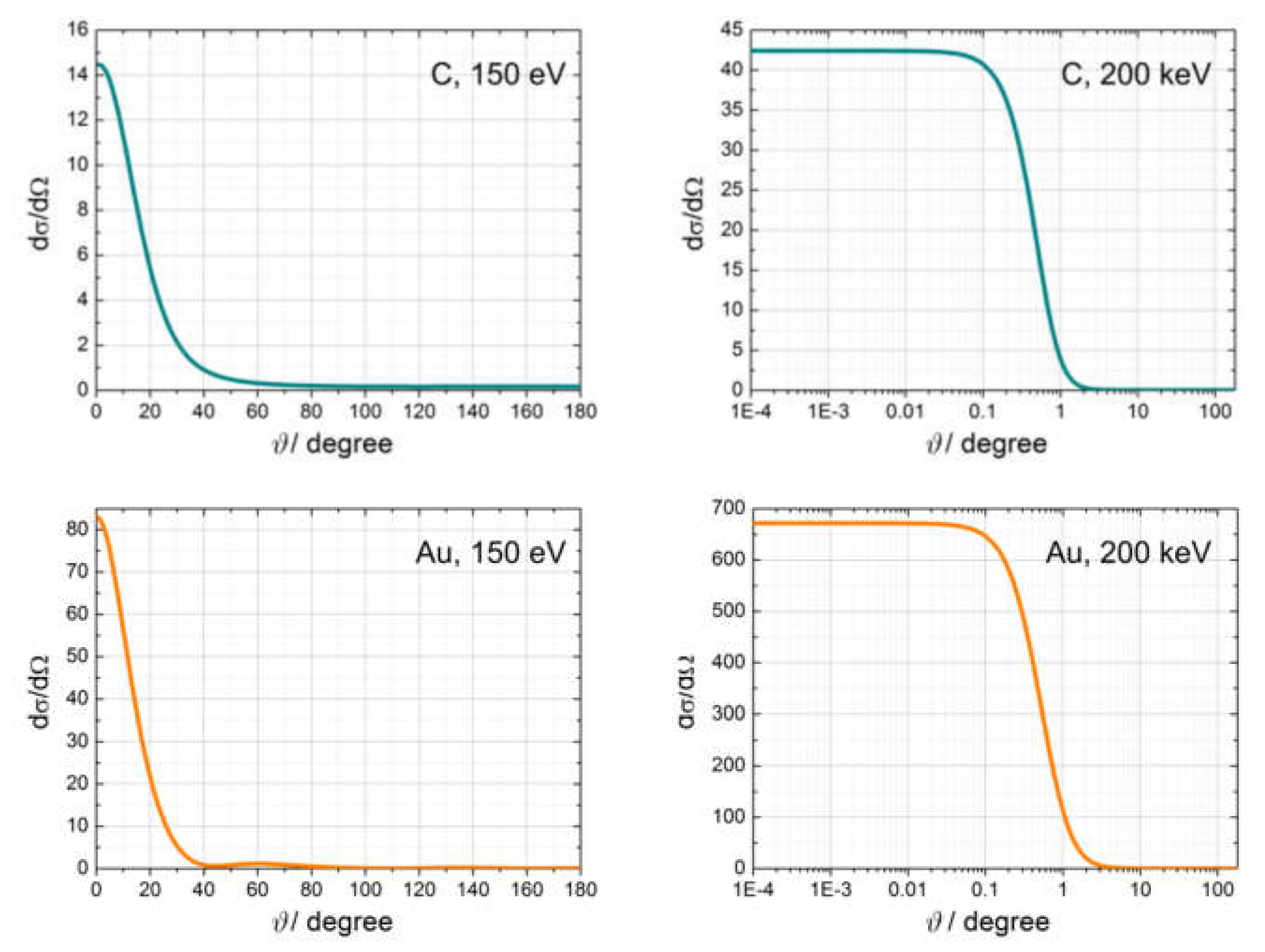
2.2.4. Examples of Scattering Amplitudes
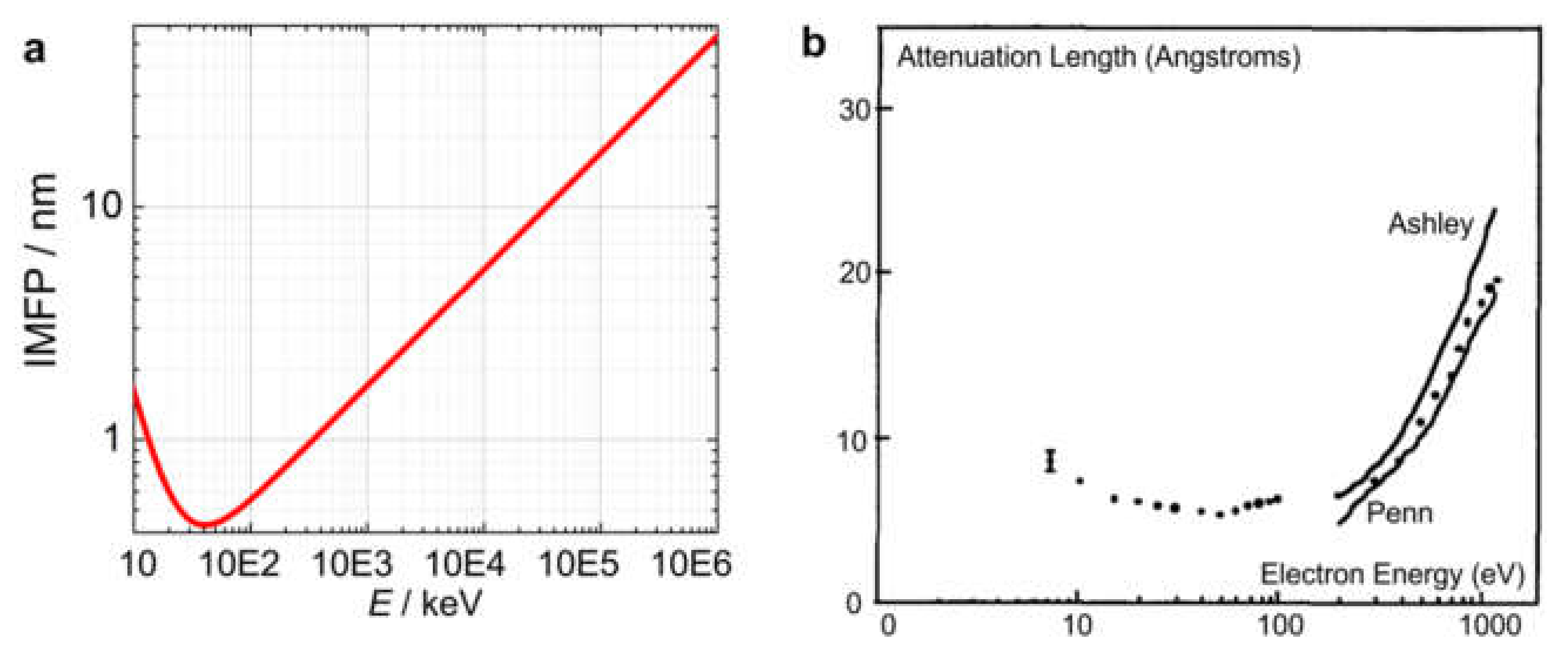
2.2.5. Inelastic Mean Free Path (IMFP) for High- and Low-Energy Electrons
2.3. Transmission Function, Object Phase, Exit Wave, and Phase Problem
2.4. Phase Shift of an Electron Wave in Electric and Magnetic Fields
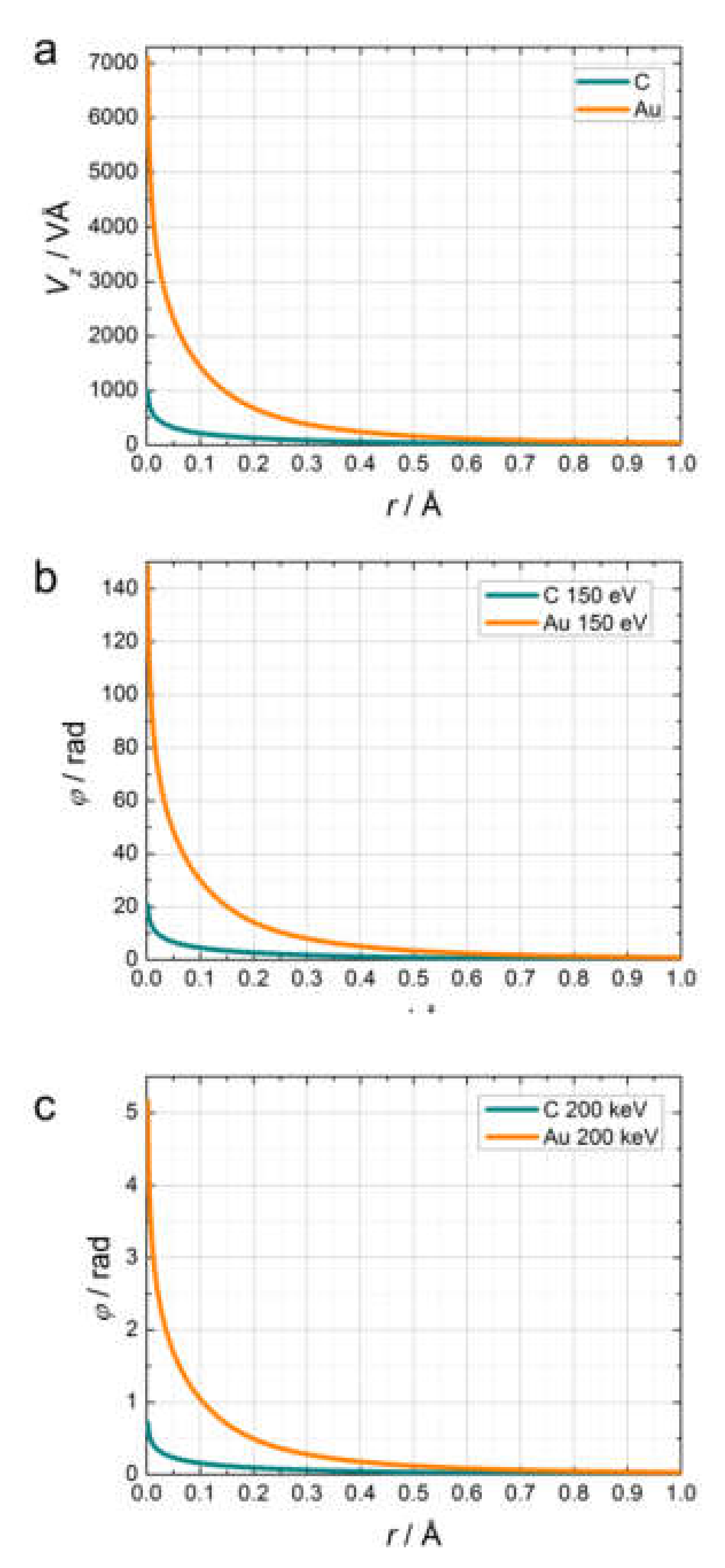
2.4.1. Phase Shift of an Electron Wave in an Electric Potential
2.4.2. Transmission Functions
2.4.3. Phase Shift of an Electron Wave in a Magnetic Potential
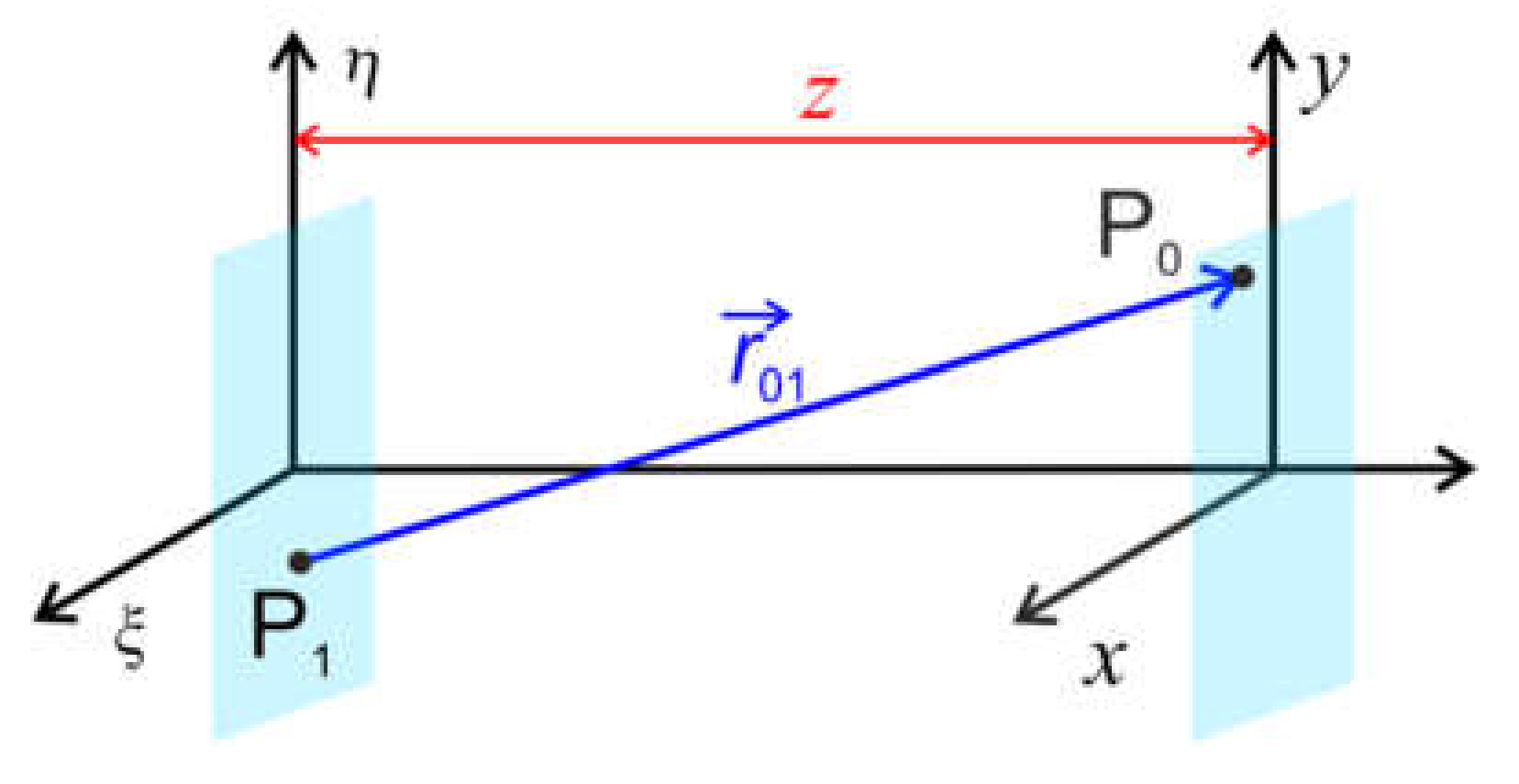
2.5. Wavefront Propagation: Fresnel and Fraunhofer Diffraction
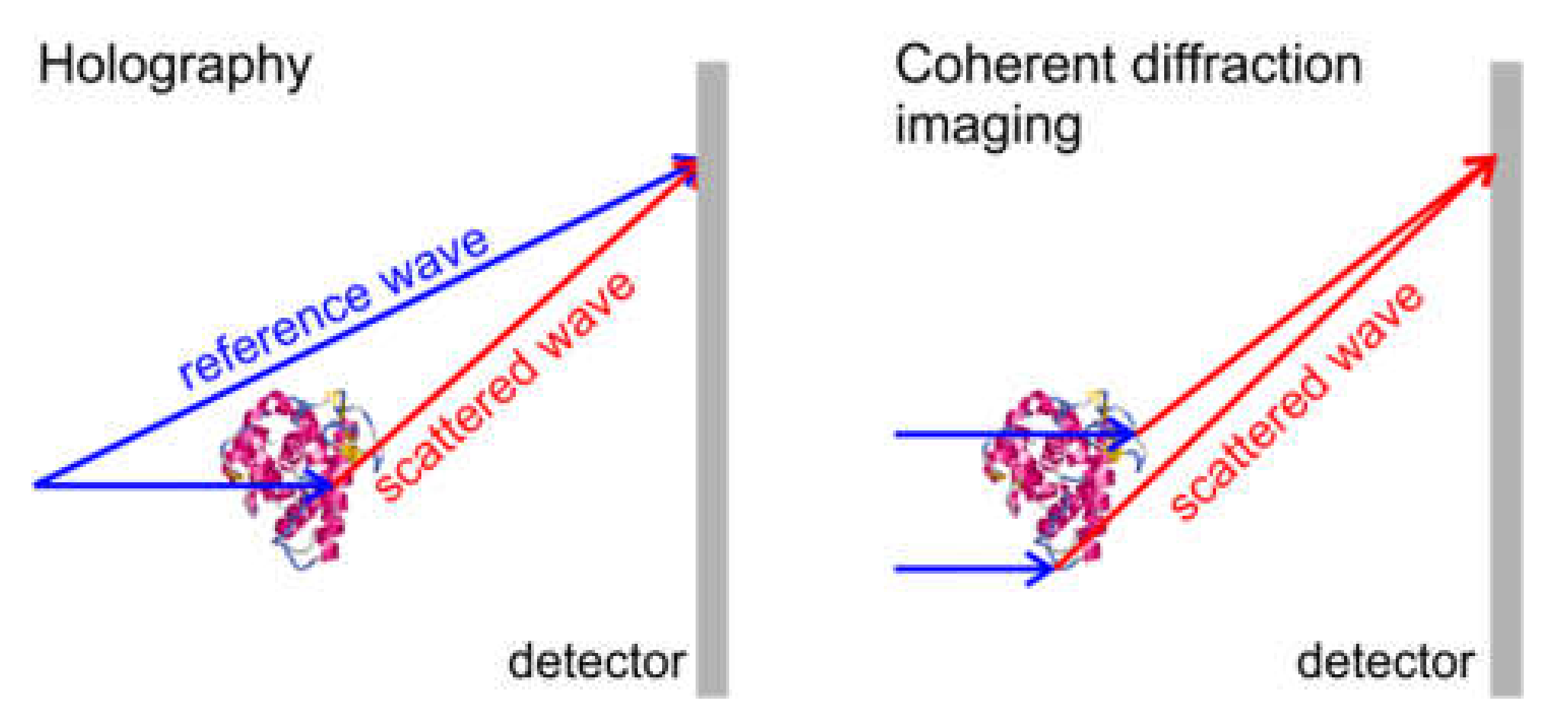
3. Holography Principle
4. Coherence
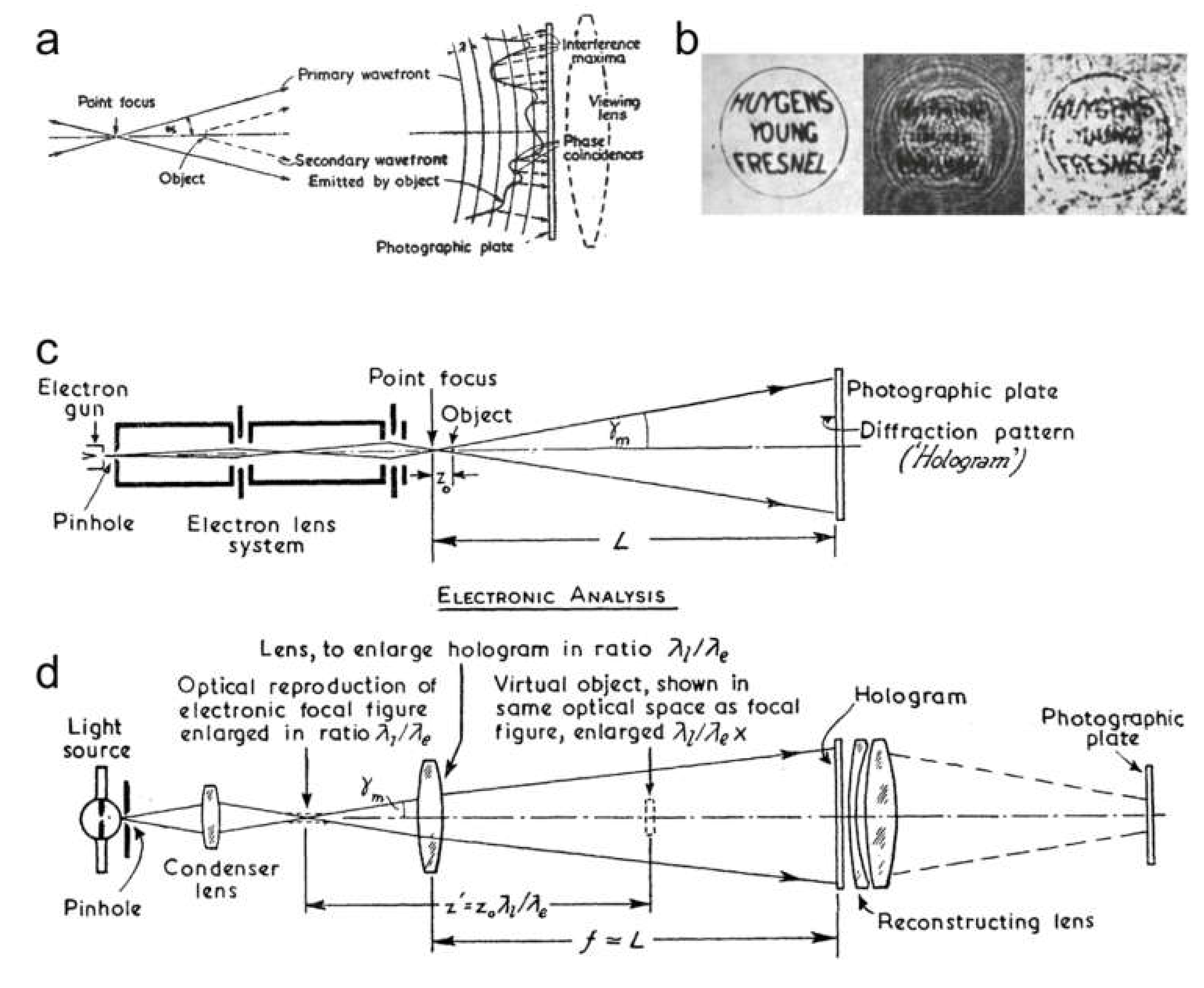
5. Principle of Gabor Holography
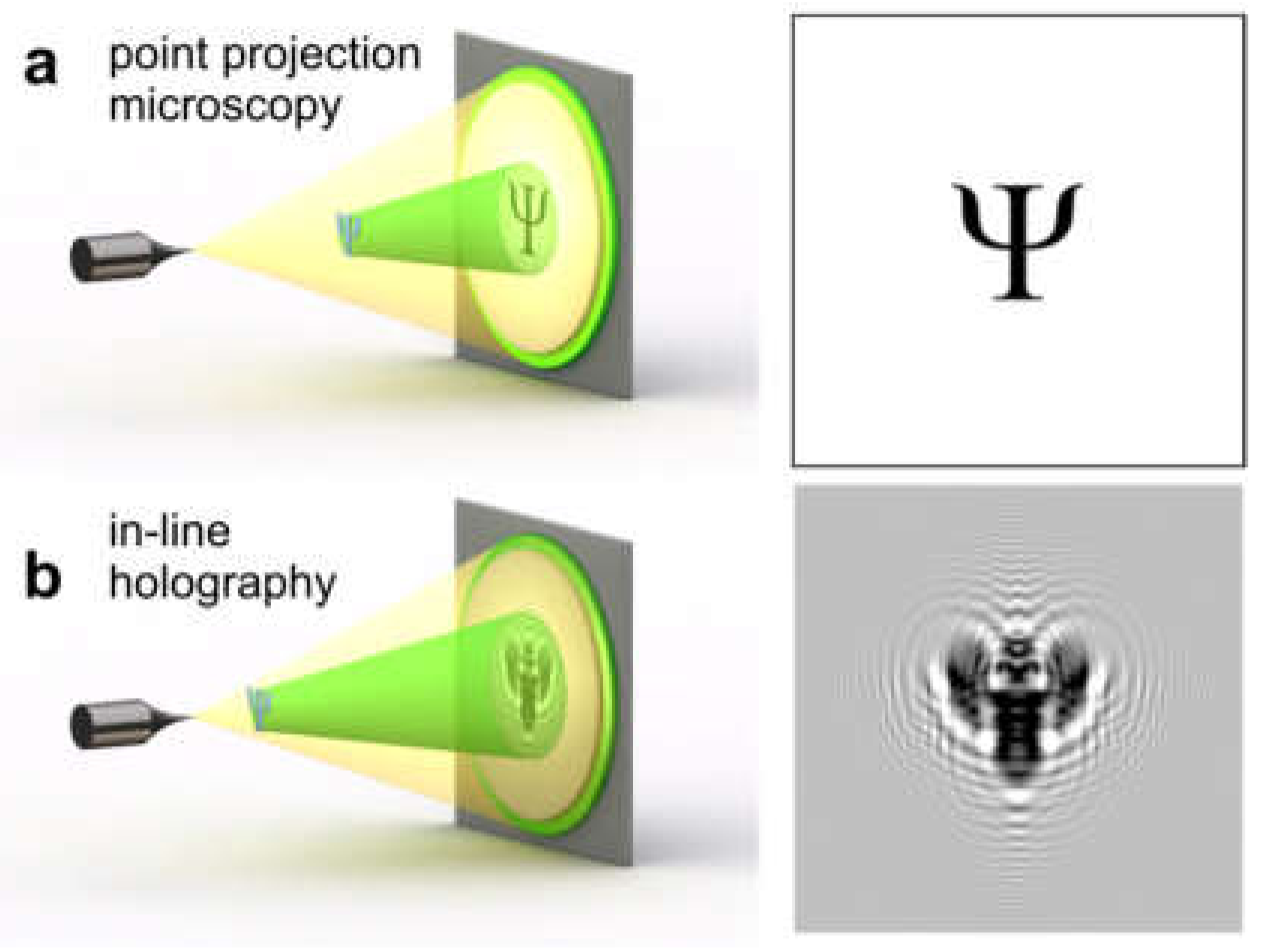
6. Point Projection Microscopy (PPM)
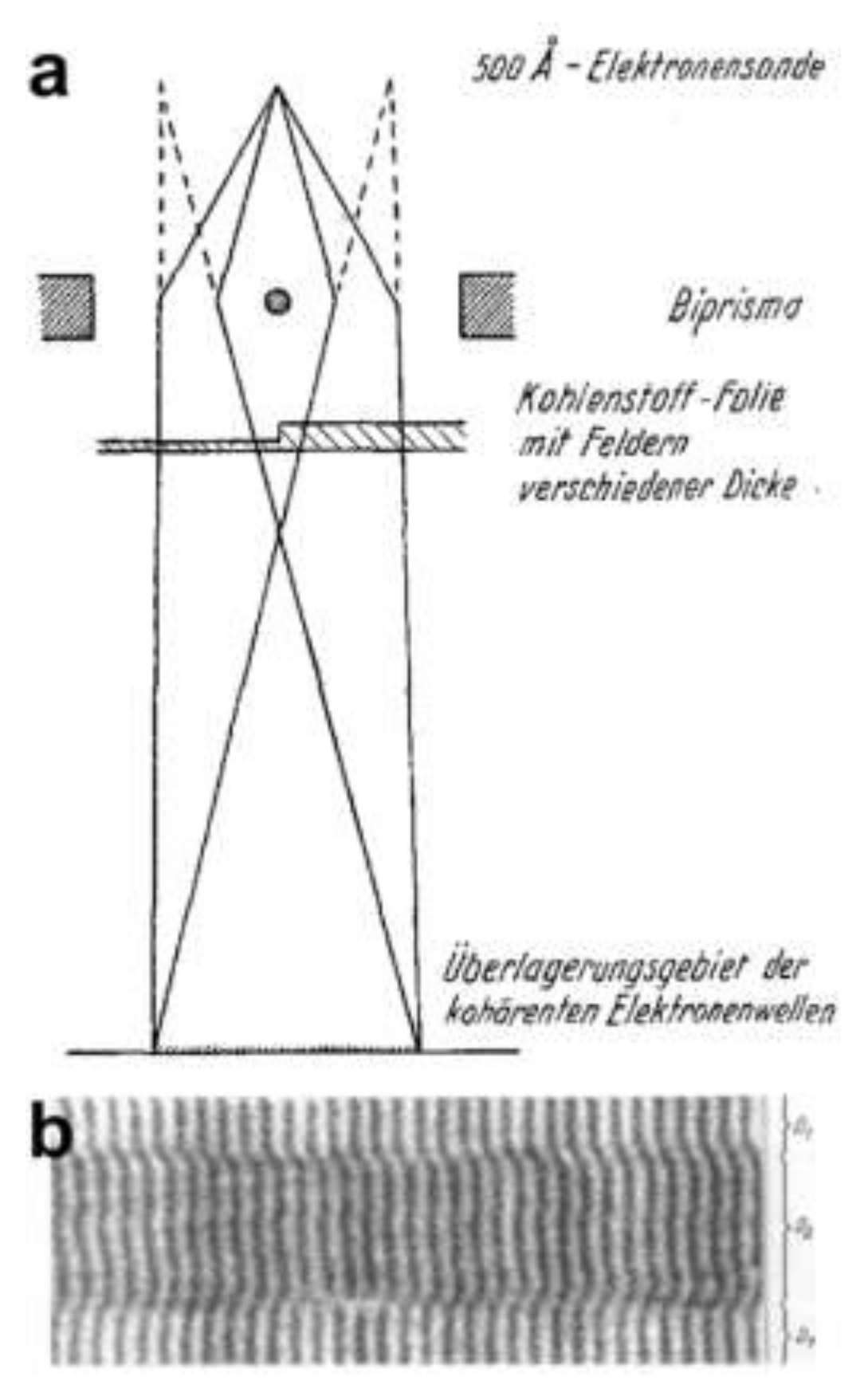
7. Off-Axis Holography
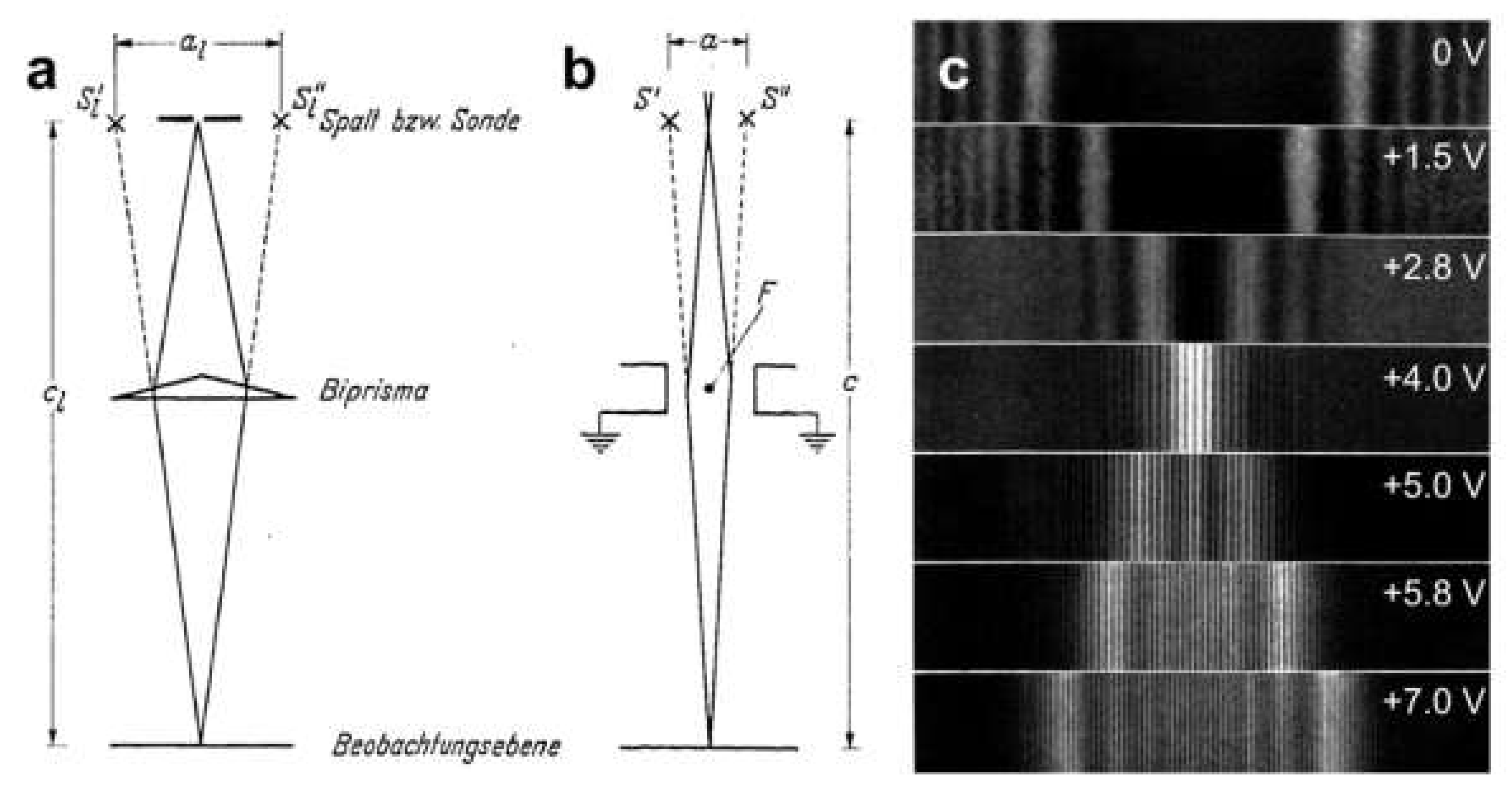
7.1. The Electron Biprism
7.2. Measuring Potentials Using Off-Axis Holography
7.2.1. Electrostatic Potential
7.2.2. Magnetic Potential
7.3. Reconstruction of an Off-Axis Hologram
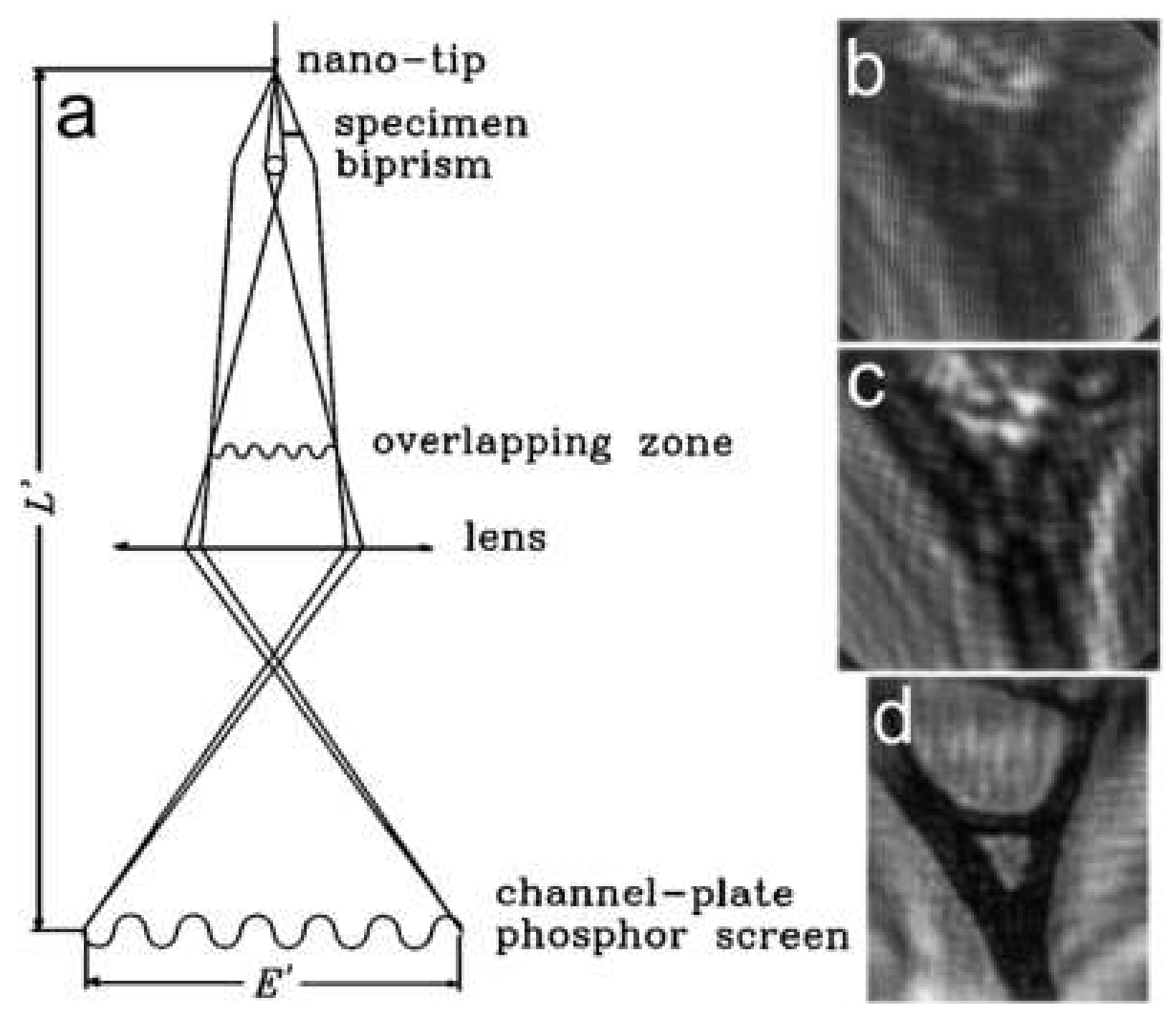
7.4. Low-Energy Electron Off-Axis Holography
7.5. Further Reading about Off-Axis Holography
8. In-Line Holography
8.1. In-Line Holography in TEM
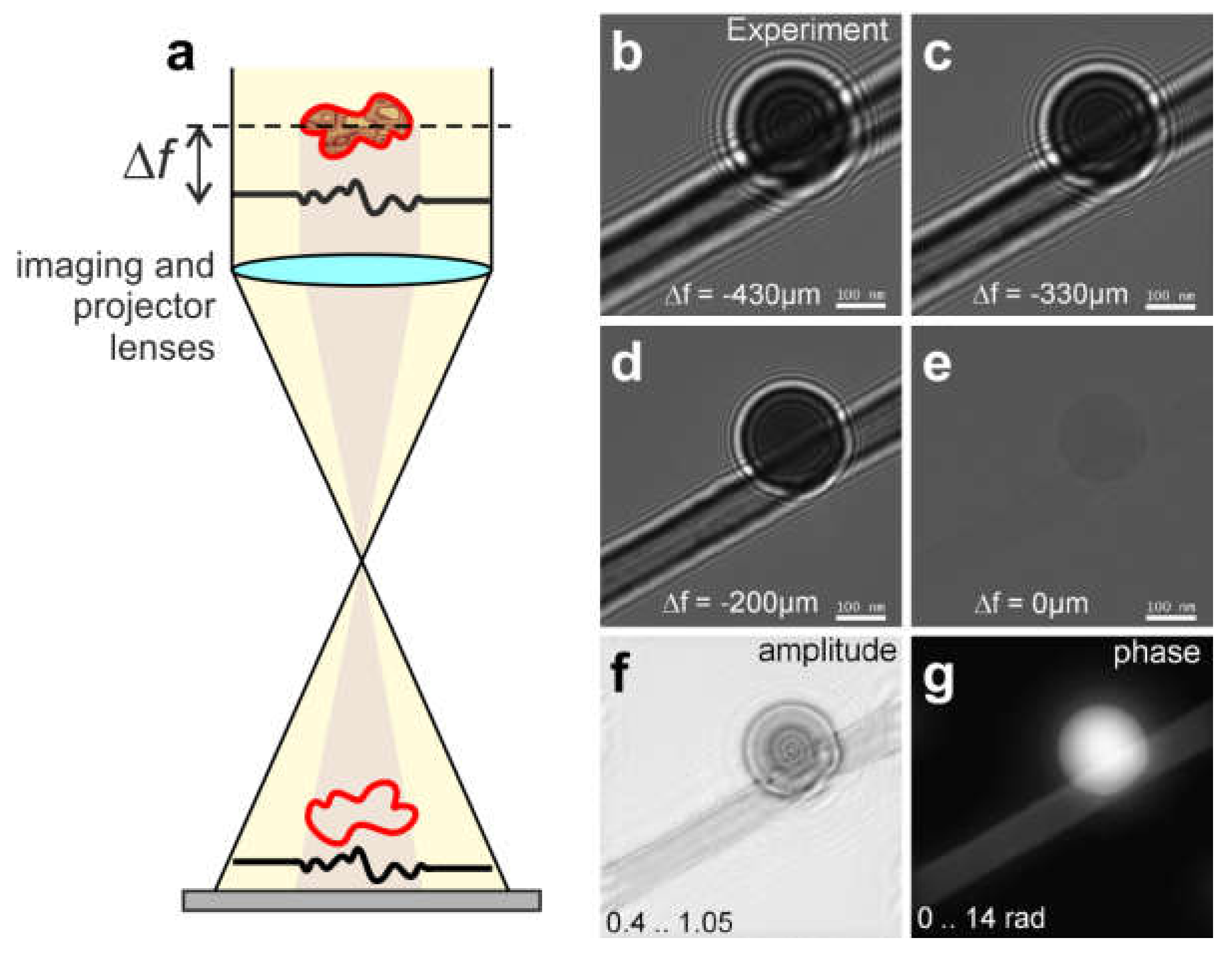
8.1.1. Defocused, Over-Focused, and Under-Focused Imaging
8.1.2. Focal (Defocus) Series
8.1.3. Single In-Line Hologram and Its Reconstruction
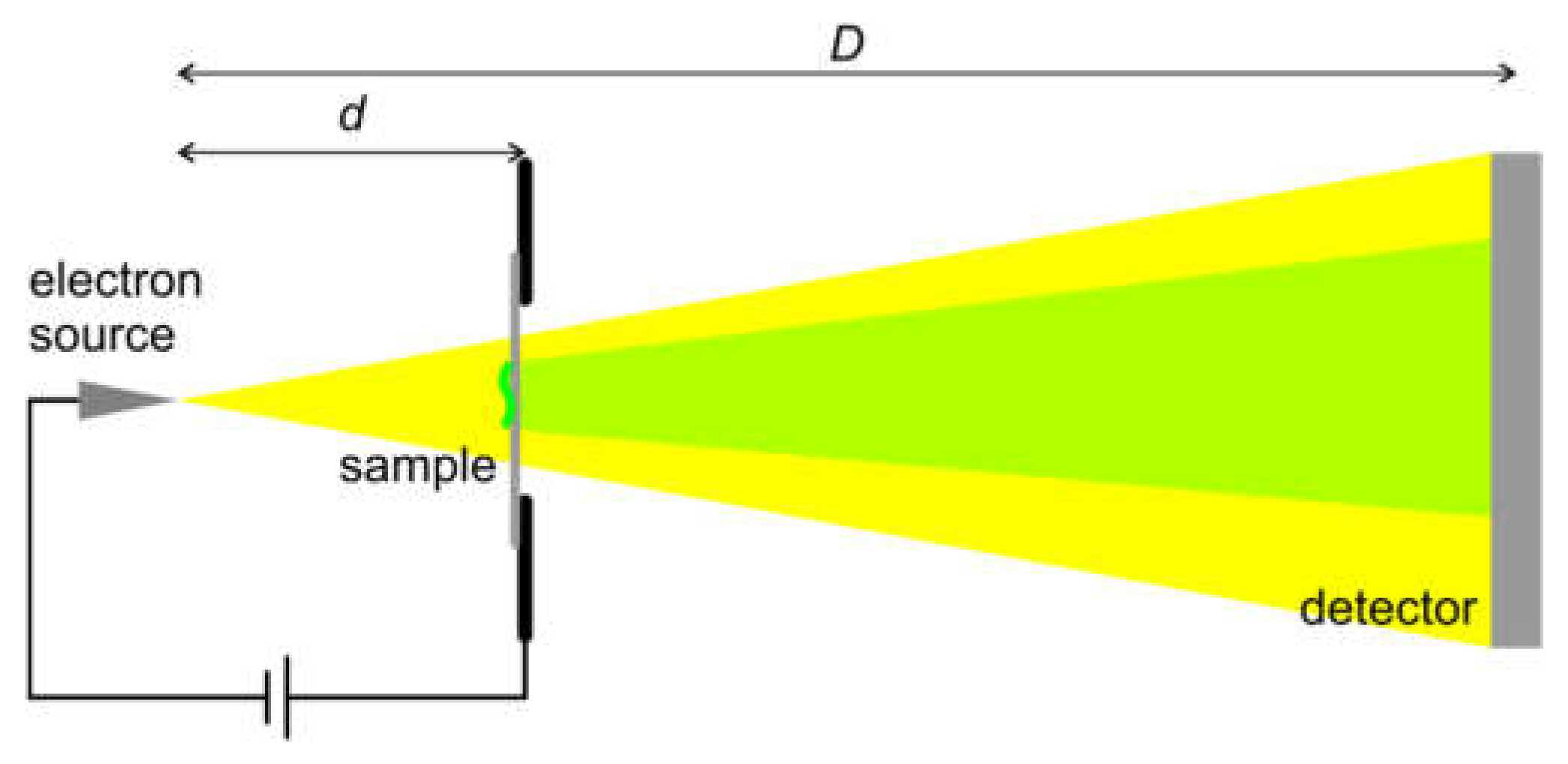
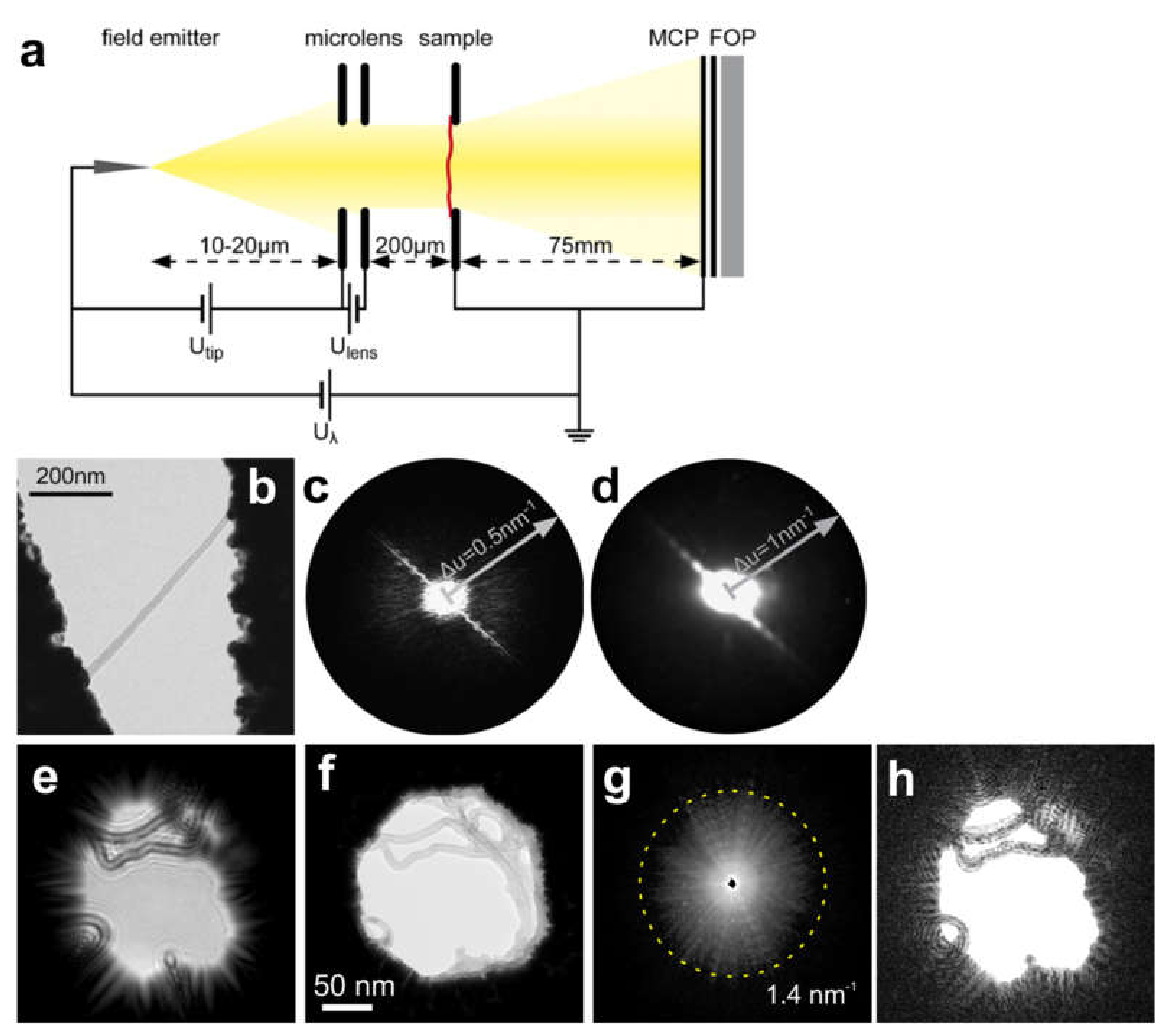
8.2. Low-Energy Electron Holography
8.2.1. Experimental Arrangement
8.2.2. Reconstruction of In-Line Holograms
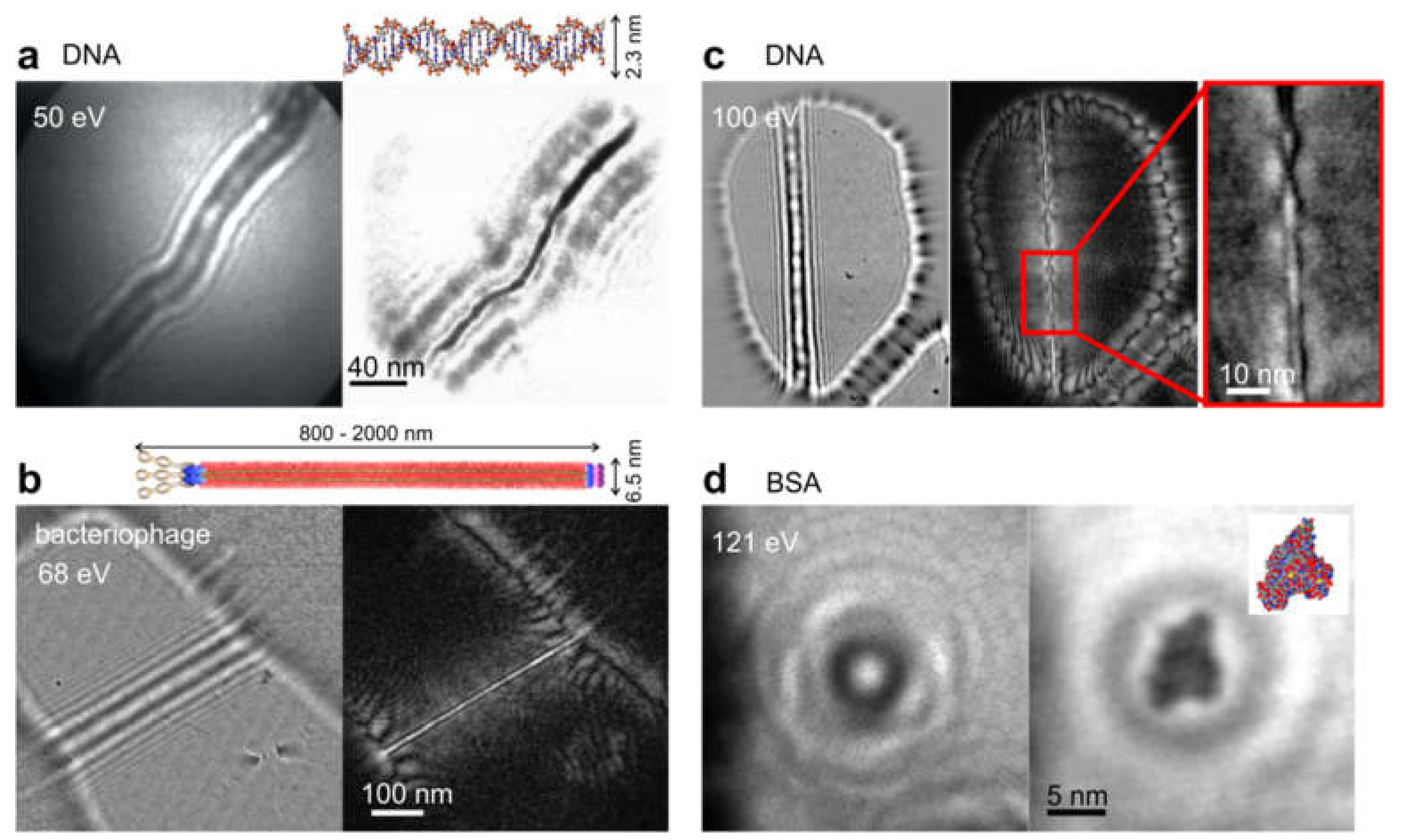
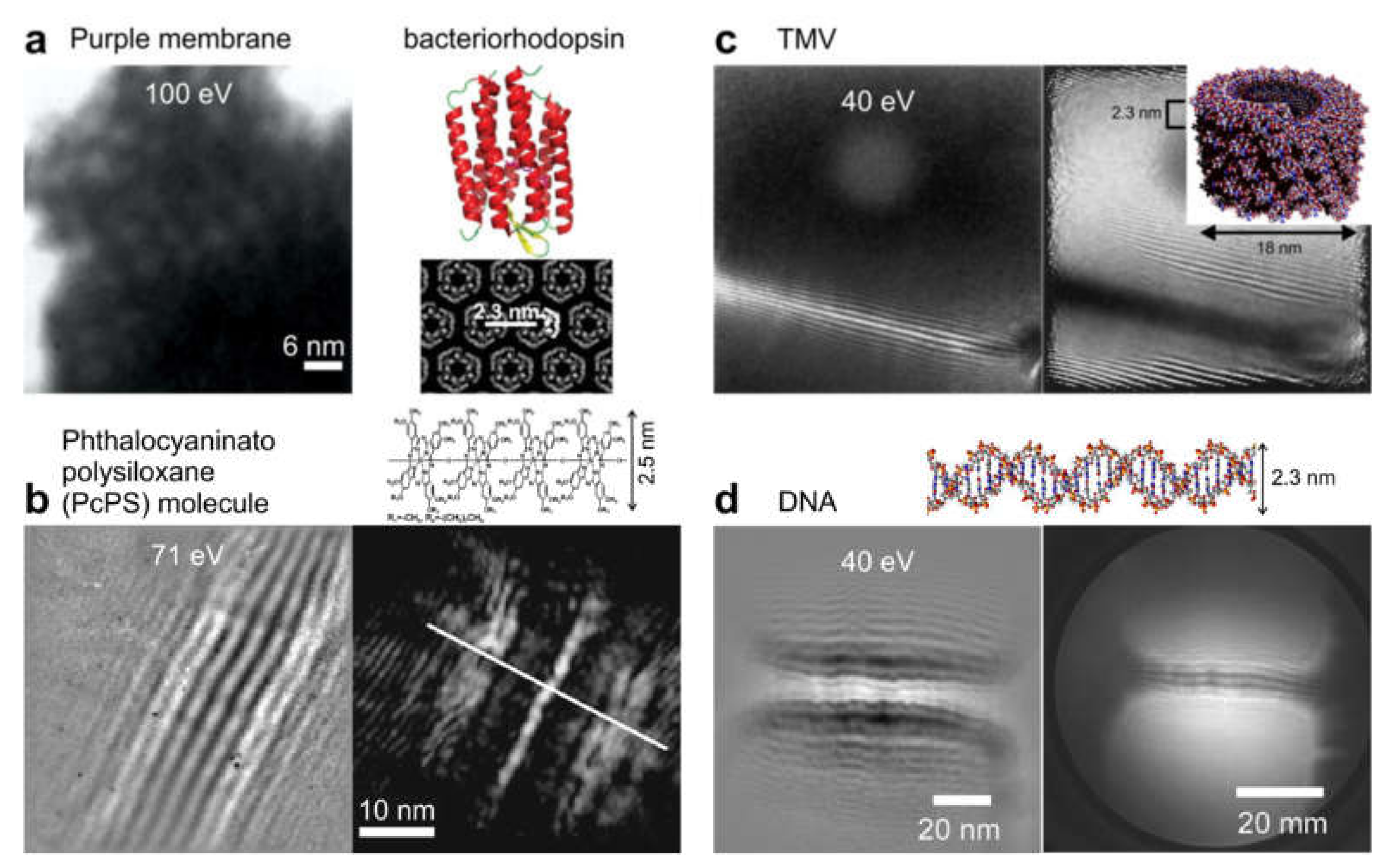
8.2.3. Imaging Biological Samples and Individual Macromolecules
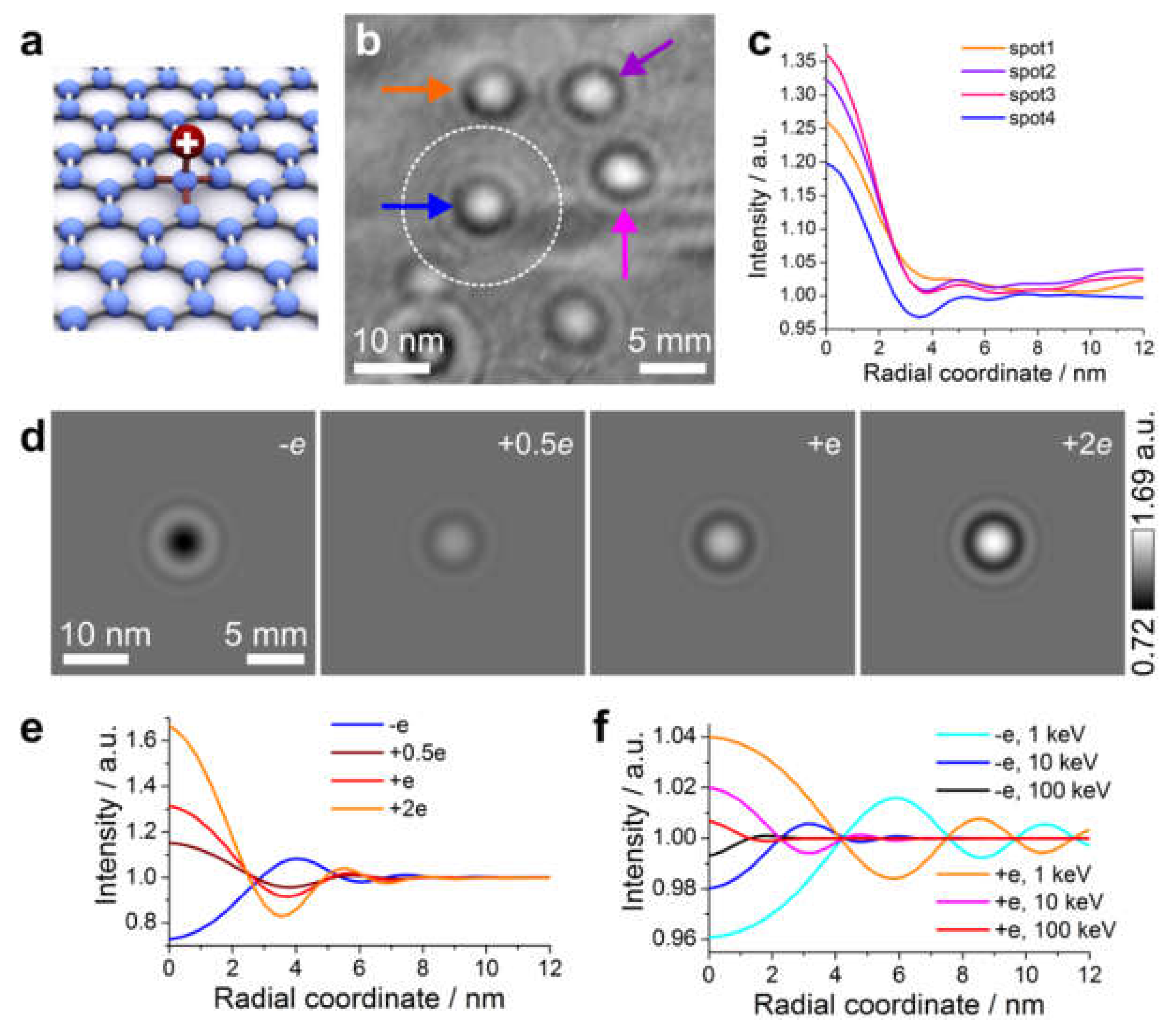
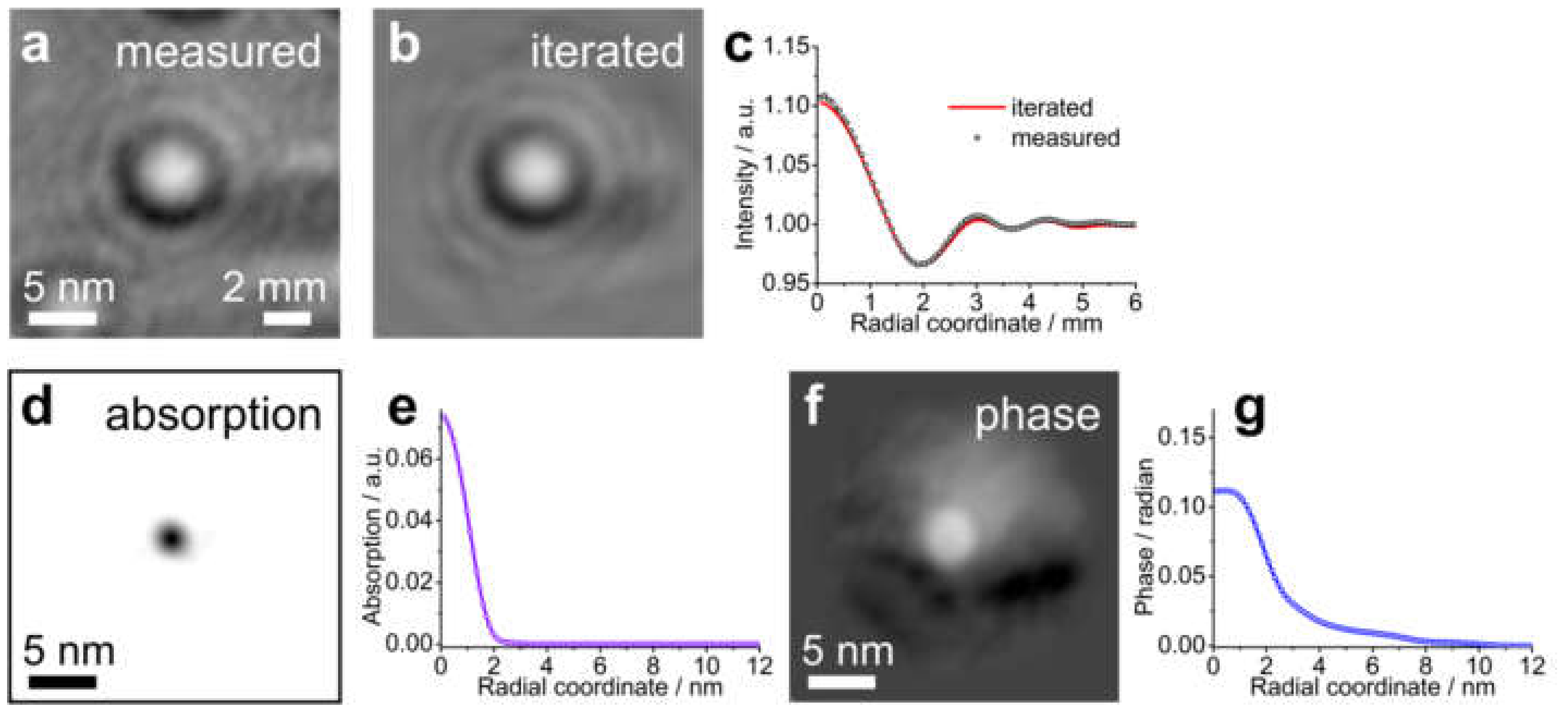
8.2.4. Imaging Electric Potentials
8.3. 3D Sample Reconstruction from Two or More In-Line Holograms
9. Coherent Diffraction Imaging (CDI) with Electrons
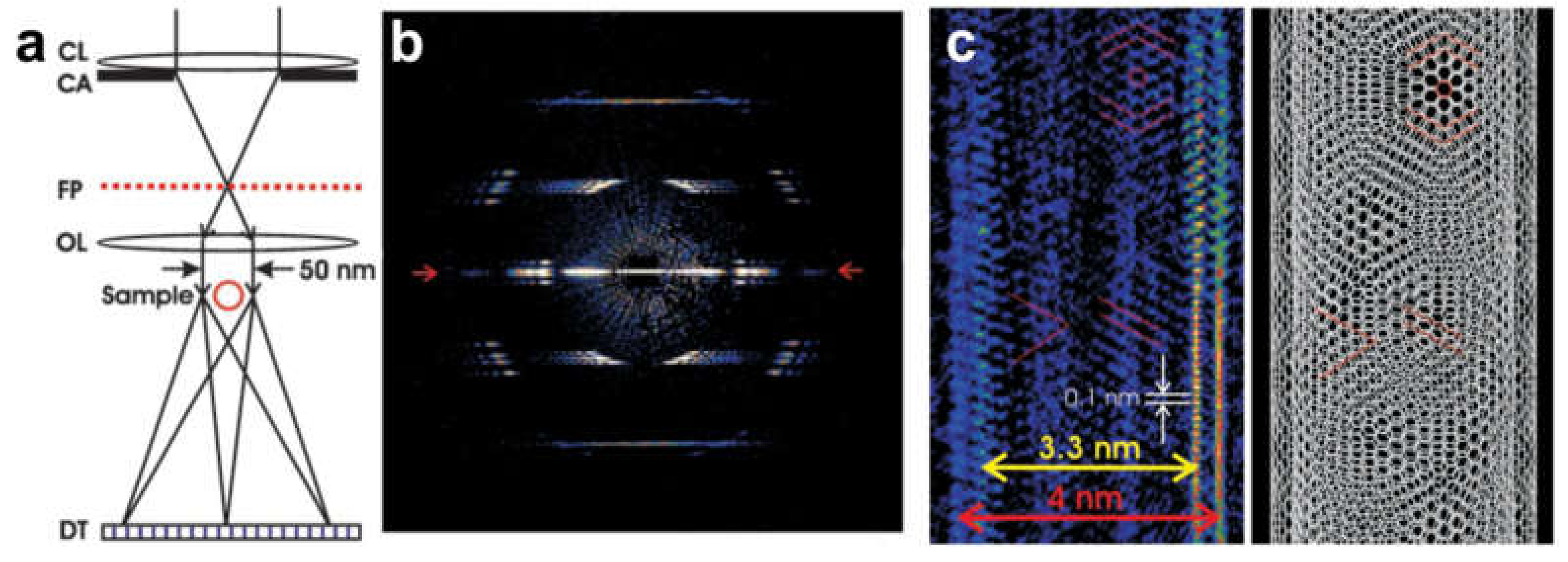
9.1. CDI with High-Energy Electrons
9.2. CDI with Low-Energy Electrons
10. Discussion
10.1. In-Line Holography (Defocus Imaging) vs. CDI
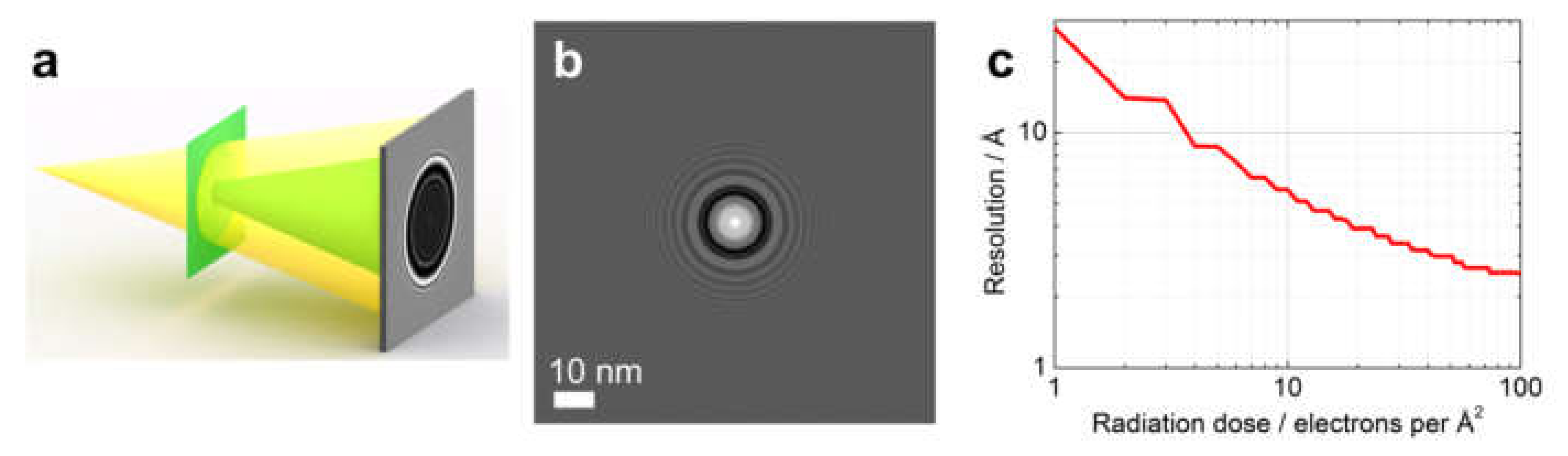
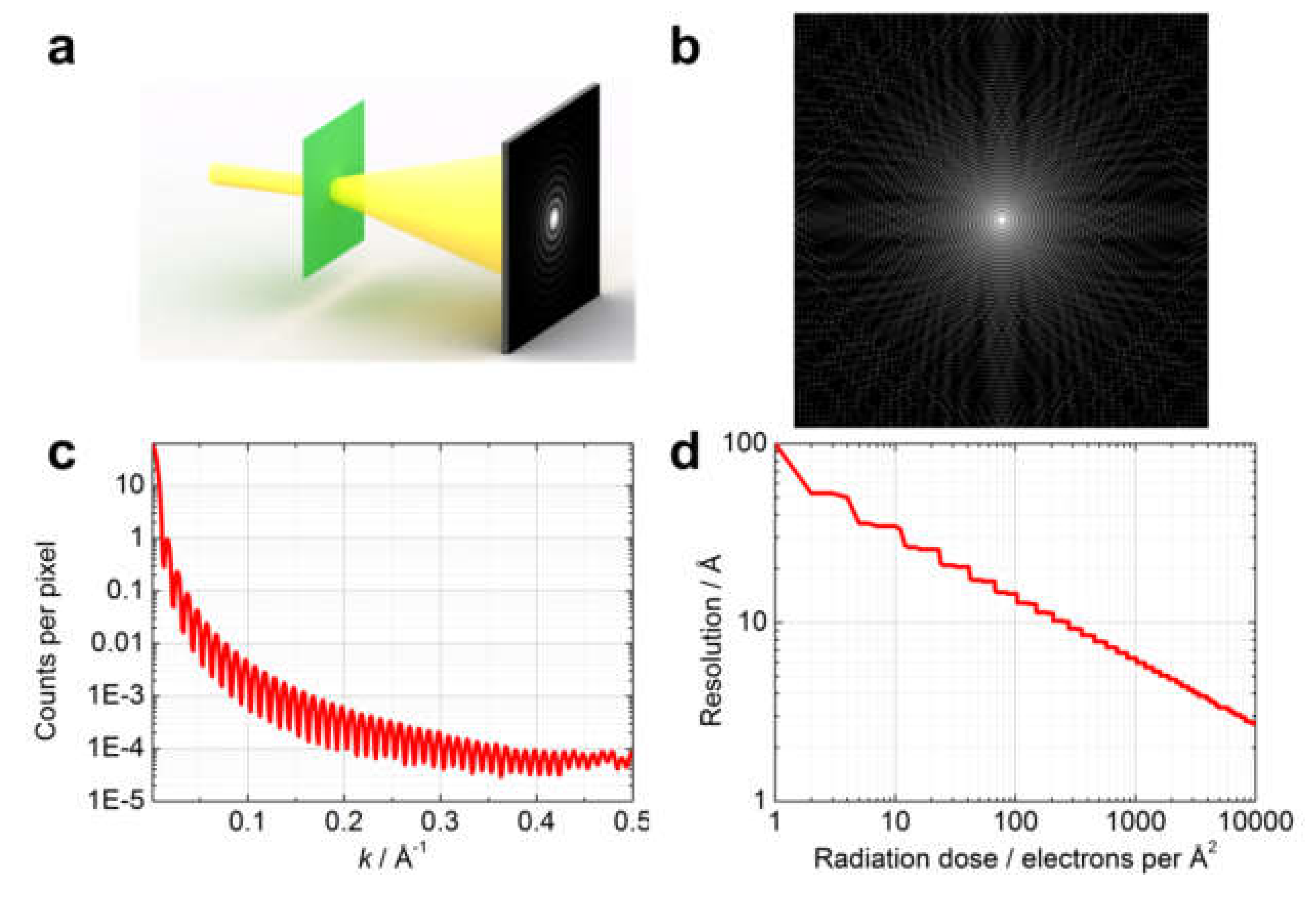
Radiation Dose
10.2. Low vs. High-Energy Electrons
Funding
Conflicts of Interest
Appendix A
- Lysozyme atomic coordinates were downloaded from PDB 253L [134], and hydrogen atoms were added using Chimera software.
- The sequence of atoms was re-arranged in order of increasing -coordinate, and atoms were numbered as a1, a2 etc.
- An incident plane wave with unit amplitude was assumed,
- The coordinates of the first atom a1 were read from the text file as .
- The transmission function in plane at was calculated as , where is the interaction parameter at 200 keV and is the projected potential of atom a1, calculated from the tabulated parameters corresponding to the chemical elements as described in reference [8].
- The exit wave in the plane was calculated as
- The -coordinate of the next atom a2 was read as , and the distance was calculated.
- The wave function was propagated for using the angular spectrum method [77]. The resulting wavefront was .
References
- Broglie, L.D. Recherches sur la Théorie des Quanta. Ph.D. Thesis, Sorbonne Université, Paris, France, 1924. [Google Scholar]
- Davisson, C.; Germer, L.H. The scattering of electrons by a single crystal of nickel. Nature 1927, 119, 558–560. [Google Scholar] [CrossRef]
- NIST. NIST Electron Elastic-Scattering Cross-Section Database; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2000.
- Seah, M.P.; Dench, W.A. Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids. Surf. Interface Anal. 1979, 1, 2–11. [Google Scholar] [CrossRef]
- Spence, J.C.H. STEM and shadow-imaging of biomolecules at 6 eV beam energy. Micron 1997, 28, 101–116. [Google Scholar] [CrossRef]
- Ashley, J.C. Energy-loss rate and inelastic mean free-path of low-energy electrons and positrons in condensed matter. J. Electron Spectrosc. Relat. Phenom. 1990, 50, 323–334. [Google Scholar] [CrossRef]
- Penn, D.R. Electron mean-free-path calculations using a model dielectric function. Phys. Rev. B 1987, 35, 482–486. [Google Scholar] [CrossRef]
- Kirkland, E.J. Advanced Computing in Electron Microscopy; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Latychevskaia, T.; Escher, C.; Fink, H.-W. Moiré structures in twisted bilayer graphene studied by transmission electron microscopy. Ultramicroscopy 2019, 197, 46–52. [Google Scholar] [CrossRef]
- Kasama, T.; Dunin-Borkowski, R.E.; Beleggia, M. Electron Holography of Magnetic Materials. In Holography; Ramirez, F.A.M., Ed.; IntechOpen: London, UK, 2011. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Company Publishers: Greenwood Village, CO, USA, 2004. [Google Scholar]
- Thompson, B.J.; Wolf, E. Two-beam interference with partially coherent light. J. Opt. Soc. Am. A 1957, 47, 895–902. [Google Scholar] [CrossRef]
- Lichte, H.; Lehmann, M. Electron holography—Basics and applications. Rep. Prog. Phys. 2008, 71, 1–46. [Google Scholar] [CrossRef]
- Van Cittert, P.H. Die wahrscheinliche Schwingungsverteilung in einer von einer Lichtquelle direkt oder mittels einer Linse beleuchteten Ebene. Physica 1934, 1, 201–210. [Google Scholar] [CrossRef]
- Zernike, F. The concept of degree of coherence and its application to optical problems. Physica 1938, 5, 785–795. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics; Wiley Classics Library: Hoboken, NJ, USA, 1985. [Google Scholar]
- Latychevskaia, T. Spatial coherence of electron beams from field emitters and its effect on the resolution of imaged objects. Ultramicroscopy 2017, 175, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Pozzi, G. Theoretical considerations on the spatial coherence in field-emission electron microscopes. Optik 1987, 77, 69–73. [Google Scholar]
- Knoll, M.; Ruska, E. The electron microscope. Z. Phys. 1932, 78, 318–339. [Google Scholar] [CrossRef]
- Iwanowski, D. Ueber die Mosaikkrankheit der Tabakspflanze. In Bulletin Scientifique Publié Par l’Académie Impériale des Sciences de Saint-Pétersbourg/Nouvelle Serie III; Imperial Academy of Arts: St.-Petersburg, Russia, 1892. [Google Scholar]
- Beijerinck, M.W. Ueber ein Contagium vivurn fluidum als Ursaehe der Fleekenkrankheit der Tabaksblätter. Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam, Müller, Amsterdam; KNAW: Amsterdam, The Netherlands, 1898. [Google Scholar]
- Kausche, G.A.; Pfankuch, E.; Ruska, H. The visualisation of herbal viruses in surface microscopes. Naturwissenschaften 1939, 27, 292–299. [Google Scholar] [CrossRef]
- Scherzer, O. Über einige Fehler von Elektronenlinsen. Z. Phys. 1936, 101, 593–603. [Google Scholar] [CrossRef]
- Gabor, D. Improvements in and Relating to Microscopy. Patent GB685286, 17 December 1947. [Google Scholar]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Gabor, D. Microscopy by reconstructed wave-fronts. Proc. R. Soc. Lond. A 1949, 197, 454–487. [Google Scholar] [CrossRef]
- Morton, G.A.; Ramberg, E.G. Point projector electron microscope. Phys. Rev. 1939, 56, 705. [Google Scholar] [CrossRef]
- Golzhauser, A.; Volkel, B.; Jager, B.; Zharnikov, M.; Kreuzer, H.J.; Grunze, M. Holographic imaging of macromolecules. J. Vac. Sci. Technol. A 1998, 16, 3025–3028. [Google Scholar] [CrossRef]
- Golzhauser, A.; Volkel, B.; Grunze, M.; Kreuzer, H.J. Optimization of the low energy electron point source microscope: Imaging of macromolecules. Micron 2002, 33, 241–255. [Google Scholar] [CrossRef]
- Eisele, A.; Voelkel, B.; Grunze, M.; Golzhauser, A. Nanometer resolution holography with the low energy electron point source microscope. Z. Phys. Chem. 2008, 222, 779–787. [Google Scholar] [CrossRef]
- Beyer, A.; Golzhauser, A. Low energy electron point source microscopy: Beyond imaging. J. Phys. Condes. Matter 2010, 22, 343001. [Google Scholar] [CrossRef] [PubMed]
- Beyer, A.; Weber, D.H.; Volkel, B.; Golzhauser, A. Characterization of nanowires with the low energy electron point source (LEEPS) microscope. Phys. Status Solidi B 2010, 247, 2550–2556. [Google Scholar] [CrossRef]
- Vieker, H.; Beyer, A.; Blank, H.; Weber, D.H.; Gerthsen, D.; Golzhauser, A. Low energy electron point source microscopy of two-dimensional carbon nanostructures. Z. Phys. Chem. 2011, 225, 1433–1445. [Google Scholar] [CrossRef]
- Hwang, I.-S.; Chang, C.-C.; Lu, C.-H.; Liu, S.-C.; Chang, Y.-C.; Lee, T.-K.; Jeng, H.-T.; Kuo, H.-S.; Lin, C.-Y.; Chang, C.-S.; et al. Investigation of single-walled carbon nanotubes with a low-energy electron point projection microscope. New J. Phys. 2013, 15, 043015. [Google Scholar] [CrossRef][Green Version]
- Muller, M.; Paarmann, A.; Ernstorfer, R. Visualization of photocurrents in nanoobjects by ultrafast low-energy electron point-projection imaging. In Ultrafast Phenomena Xix; Yamanouchi, I., Cundiff, S., De Vivie Riedle, R., Kuwata Gonokami, M., Di Mauro, L., Eds.; Springer-Verlag Berlin: Berlin, Germany, 2015; Volume 162, pp. 667–670. [Google Scholar]
- Schmid, H.; Fink, H.-W. Combined electron and ion projection microscopy. Appl. Surf. Sci. 1993, 67, 436–443. [Google Scholar] [CrossRef]
- Fink, H.-W.; Stocker, W.; Schmid, H. Holography with low-energy electrons. Phys. Rev. Lett. 1990, 65, 1204–1206. [Google Scholar] [CrossRef]
- Fink, H.-W.; Schmid, H.; Ermantraut, E.; Schulz, T. Electron holography of individual DNA molecules. J. Opt. Soc. Am. A 1997, 14, 2168–2172. [Google Scholar] [CrossRef]
- Mollenstedt, G.; Duker, H. Beobachtungen und Messungen an Biprisma-Interferenzen mit Elektronenwellen. Z. Phys. 1956, 145, 377–397. [Google Scholar] [CrossRef]
- Mollenstedt, G.; Keller, M. Elektroneninterferometrisehe Messung des inneren Potentials. Z. Phys. 1957, 148, 34–37. [Google Scholar] [CrossRef]
- Twitchett, A.C.; Dunin-Borkowski, R.E.; Midgley, P.A. Quantitative electron holography of biased semiconductor devices. Phys. Rev. Lett. 2002, 88, 238302. [Google Scholar] [CrossRef] [PubMed]
- Twitchett, A.C.; Dunin-Borkowski, R.E.; Midgley, P.A. Comparison of off-axis and in-line electron holography as quantitative dopant-profiling techniques. Philos. Mag. 2006, 86, 5805–5823. [Google Scholar] [CrossRef]
- Harscher, A.; Lichte, H. Determination of mean internal potential and mean free wavelength for inelastic scattering of vitrified iron by electron holography. Eur. J. Cell Biol. 1997, 74, 7. [Google Scholar]
- Gatel, C.; Lubk, A.; Pozzi, G.; Snoeck, E.; Hytch, M. Counting elementary charges on nanoparticles by electron holography. Phys. Rev. Lett. 2013, 111, 025501. [Google Scholar] [CrossRef]
- Vicarelli, L.; Migunov, V.; Malladi, S.K.; Zandbergen, H.W.; Dunin-Borkowski, R.E. Single electron precision in the measurement of charge distributions on electrically biased graphene nanotips using electron holography. Nano Lett. 2019, 19, 4091–4096. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Chambers, R.G. Shift of an electron interfreence pattern by enclosed magnetic flux. Phys. Rev. Lett. 1960, 5, 3–5. [Google Scholar] [CrossRef]
- Dunin-Borkowski, R.E.; McCartney, M.R.; Frankel, R.B.; Bazylinski, D.A.; Posfai, M.; Buseck, P.R. Magnetic microstructure of magnetotactic bacteria by electron holography. Science 1998, 282, 1868–1870. [Google Scholar] [CrossRef]
- de Graef, M.; Nuhfer, N.T.; McCartney, M.R. Phase contrast of spherical magnetic particles. J. Microsc. Oxf. 1999, 194, 84–94. [Google Scholar] [CrossRef]
- Thomas, J.M.; Simpson, E.T.; Kasama, T.; Dunin-Borkowski, R.E. Electron holography for the study of magnetic nanomaterials. Acc. Chem. Res. 2008, 41, 665–674. [Google Scholar] [CrossRef]
- Midgley, P.A.; Dunin-Borkowski, R.E. Electron tomography and holography in materials science. Nat. Mater. 2009, 8, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Dunin-Borkowski, R.E.; Kasama, T.; Harrison, R.J. Chapter 5 Electron Holography of Nanostructured Materials. In Nanocharacterisation (2); The Royal Society of Chemistry: London, UK, 2015; pp. 158–210. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Formanek, P.; Koch, C.T.; Lubk, A. Off-axis and inline electron holography: Experimental comparison. Ultramicroscopy 2010, 110, 472–482. [Google Scholar] [CrossRef]
- Degiovanni, A.; Morin, R. Low Energy Electron Interferences Using A Biprism-Projection Microscope Combination. In Electron Microscopy 1994, Vol 1—Interdisciplinary Developments and Tools; Les Editions de Physique: Paris, France, 1994; pp. 331–332. [Google Scholar]
- Morin, R. Point source physics: Application to electron projection microscopy and holography. Microsc. Microanal. Microstruct. 1994, 5, 501–508. [Google Scholar] [CrossRef][Green Version]
- Morin, P.; Pitaval, M.; Vicario, E. Low energy off-axis holography in electron microscopy. Phys. Rev. Lett. 1996, 76, 3979–3982. [Google Scholar] [CrossRef]
- Morin, P. Computer simulation and object reconstruction in low-energy off-axis electron holography. Ultramicroscopy 1999, 76, 1–12. [Google Scholar] [CrossRef]
- Degiovanni, A.; Bardon, J.; Georges, V.; Morin, R. Magnetic fields and fluxes probed by coherent low-energy electron beams. Appl. Phys. Lett. 2004, 85, 2938–2940. [Google Scholar] [CrossRef]
- Lehmann, M.; Lichte, H. Tutorial on off-axis electron holography. Microsc. Microanal. 2002, 8, 447–466. [Google Scholar] [CrossRef]
- Lichte, H. Electron interference: Mystery and reality. Philos. Trans. R. Soc. A 2002, 360, 897–920. [Google Scholar] [CrossRef]
- Lichte, H.; Lehmann, H.W. Electron holography—A powerful tool for the analysis of nanostructures. Adv. Imaging Elect. Phys. 2002, 123, 225–255. [Google Scholar] [CrossRef]
- Lichte, H.; Formanek, P.; Lenk, A.; Linck, M.; Matzeck, C.; Lehmann, M.; Simon, P. Electron holography: Applications to materials questions. Annu. Rev. Mater. Res. 2007, 37, 539–588. [Google Scholar] [CrossRef]
- Simon, P.; Lichte, H.; Drechsel, J.; Formanek, P.; Graff, A.; Wahl, R.; Mertig, M.; Adhikari, R.; Michler, G.H. Electron holography of organic and biological materials. Adv. Mater. 2003, 15, 1475–1481. [Google Scholar] [CrossRef]
- Simon, P.; Lichte, H.; Formanek, P.; Lehmann, M.; Huhle, R.; Carrillo-Cabrera, W.; Harscher, A.; Ehrlich, H. Electron holography of biological samples. Micron 2008, 39, 229–256. [Google Scholar] [CrossRef] [PubMed]
- Lichte, H. Performance limits of electron holography. Ultramicroscopy 2008, 108, 256–262. [Google Scholar] [CrossRef] [PubMed]
- Teague, M.R. Deterministic phase retrieval—A Green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Schiske, P. Image reconstruction by means of focus series (Reprint of the original 1968 paper). J. Microsc. 2002, 207, 154. [Google Scholar] [CrossRef]
- Coene, W.; Janssen, G.; Debeeck, M.O.; Vandyck, D. Phase retrieval through focus variation for ultra-resolution in field-emission transmission electron microscopy. Phys. Rev. Lett. 1992, 69, 3743–3746. [Google Scholar] [CrossRef]
- Allen, L.J.; McBride, W.; O’Leary, N.L.; Oxley, M.P. Exit wave reconstruction at atomic resolution. Ultramicroscopy 2004, 100, 91–104. [Google Scholar] [CrossRef]
- Allen, L.J.; Oxley, M.P. Phase retrieval from series of images obtained by defocus variation. Opt. Commun. 2001, 199, 65–75. [Google Scholar] [CrossRef]
- Koch, C.T. A flux-preserving non-linear inline holography reconstruction algorithm for partially coherent electrons. Ultramicroscopy 2008, 108, 141–150. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H.-W. Solution to the twin image problem in holography. Phys. Rev. Lett. 2007, 98, 233901. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H.-W. Reconstruction of purely absorbing, absorbing and phase-shifting, and strong phase-shifting objects from their single-shot in-line holograms. Appl. Opt. 2015, 54, 3925–3932. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Wicki, F.; Escher, C.; Fink, H.-W. Imaging the potential distribution of individual charged impurities on graphene by low-energy electron holography. Ultramicroscopy 2017, 182, 276–282. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Latychevskaia, T. Iterative phase retrieval for digital holography. J. Opt. Soc. Am. A 2019, 36, D31–D40. [Google Scholar] [CrossRef]
- Latychevskaia, T. Reconstruction of missing information in diffraction patterns and holograms by iterative phase retrieval. Opt. Commun. 2019, 452, 56–67. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H.-W. Practical algorithms for simulation and reconstruction of digital in-line holograms. Appl. Opt. 2015, 54, 2424–2434. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H.-W. Simultaneous reconstruction of phase and amplitude contrast from a single holographic record. Opt. Express 2009, 17, 10697–10705. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. Phase determination from image and diffraction plane pictures in electron microscope. Optik 1971, 34, 275–284. [Google Scholar]
- Koren, G.; Joyeux, D.; Polack, F. Twin-image elimination in in-line holography of finite-support complex objects. Opt. Lett. 1991, 16, 1979–1981. [Google Scholar] [CrossRef]
- Koren, G.; Polack, F.; Joyeux, D. Iterative algorithms for twin-image elimination in in-line holography using finite-support constraints. J. Opt. Soc. Am. A 1993, 10, 423–433. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Longchamp, J.-N.; Escher, C.; Fink, H.-W. Holography and coherent diffraction with low-energy electrons: A route towards structural biology at the single molecule level. Ultramicroscopy 2015, 159, 395–402. [Google Scholar] [CrossRef]
- Spence, J.C.H.; Qian, W.; Melmed, A.J. Experimental low-voltage point-projection microscopy and its possibilities. Ultramicroscopy 1993, 52, 473–477. [Google Scholar] [CrossRef]
- Spence, J.; Qian, W.; Zhang, X. Contrast and radiation-damage in point-projection electron imaging of purple membrane at 100-V. Ultramicroscopy 1994, 55, 19–23. [Google Scholar] [CrossRef]
- Germann, M.; Latychevskaia, T.; Escher, C.; Fink, H.-W. Nondestructive imaging of individual biomolecules. Phys. Rev. Lett. 2010, 104, 095501. [Google Scholar] [CrossRef] [PubMed]
- Latychevskaia, T.; Escher, C.; Andregg, W.; Andregg, M.; Fink, H.W. Direct visualization of charge transport in suspended (or free-standing) DNA strands by low-energy electron microscopy. Sci. Rep. 2019, 9, 8889. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Longchamp, J.-N.; Escher, C.; Fink, H.-W. Coherent Diffraction and Holographic Imaging of Individual Biomolecules Using Low-Energy Electrons. In Advancing Methods for Biomolecular Crystallography; Springer: Berlin/Heidelberg, Germany, 2013; pp. 331–342. [Google Scholar] [CrossRef]
- Weierstall, U.; Spence, J.C.H.; Stevens, M.; Downing, K.H. Point-projection electron imaging of tobacco mosaic virus at 40 eV electron energy. Micron 1999, 30, 335–338. [Google Scholar] [CrossRef]
- Longchamp, J.-N.; Latychevskaia, T.; Escher, C.; Fink, H.-W. Low-energy electron holographic imaging of individual tobacco mosaic virions. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
- Stevens, G.B.; Krüger, M.; Latychevskaia, T.; Lindner, P.; Plückthun, A.; Fink, H.-W. Individual filamentous phage imaged by electron holography. Eur. Biophys. J. 2011, 40, 1197–1201. [Google Scholar] [CrossRef]
- Longchamp, J.-N.; Latychevskaia, T.; Escher, C.; Fink, H.-W. Non-destructive imaging of an individual protein. Appl. Phys. Lett. 2012, 101, 093701. [Google Scholar] [CrossRef]
- Longchamp, J.-N.; Rauschenbach, S.; Abb, S.; Escher, C.; Latychevskaia, T.; Kern, K.; Fink, H.-W. Imaging proteins at the single-molecule level. Proc. Natl. Acad. Sci. USA 2017, 114, 1474–1479. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Blake, J.R.; Zan, R.; Anissimova, S.; Bangert, U.; Golovanov, A.P.; Morozov, S.V.; Geim, A.K.; Novoselov, K.S.; et al. Graphene as a transparent conductive support for studying biological molecules by transmission electron microscopy. Appl. Phys. Lett. 2010, 97, 153102. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Wicki, F.; Longchamp, J.-N.; Escher, C.; Fink, H.-W. Direct observation of individual charges and their dynamics on graphene by low-energy electron holography. Nano Lett. 2016, 16, 5469–5474. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Pedrini, G.; Osten, W.; Tiziani, H.J. Whole optical wave field reconstruction from double or multi in-line holograms by phase retrieval algorithm. Opt. Express 2003, 11, 3234–3241. [Google Scholar] [CrossRef] [PubMed]
- Pedrini, G.; Osten, W.; Zhang, Y. Wave-front reconstruction from a sequence of interferograms recorded at different planes. Opt. Lett. 2005, 30, 833–835. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.; Pedrini, G.; Osten, W. Complete wavefront reconstruction using sequential intensity measurements of a volume speckle field. Appl. Opt. 2006, 45, 8596–8605. [Google Scholar] [CrossRef]
- Li, Z.Y.; Li, L.; Qin, Y.; Li, G.B.; Wang, D.; Zhou, X. Resolution and quality enhancement in terahertz in-line holography by sub-pixel sampling with double-distance reconstruction. Opt. Express 2016, 24, 21134–21146. [Google Scholar] [CrossRef]
- Guo, C.; Shen, C.; Li, Q.; Tan, J.B.; Liu, S.T.; Kan, X.C.; Liu, Z.J. A fast-converging iterative method based on weighted feedback for multi-distance phase retrieval. Sci. Rep. 2018, 8, 6436. [Google Scholar] [CrossRef]
- Miao, J.W.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Miao, J.W.; Hodgson, K.O.; Ishikawa, T.; Larabell, C.A.; LeGros, M.A.; Nishino, Y. Imaging whole Escherichia coli bacteria by using single-particle X-ray diffraction. Proc. Natl. Acad. Sci. USA 2003, 100, 110–112. [Google Scholar] [CrossRef]
- Shapiro, D.; Thibault, P.; Beetz, T.; Elser, V.; Howells, M.; Jacobsen, C.; Kirz, J.; Lima, E.; Miao, H.; Neiman, A.M.; et al. Biological imaging by soft X-ray diffraction microscopy. Proc. Natl. Acad. Sci. USA 2005, 102, 15343–15346. [Google Scholar] [CrossRef]
- Song, C.Y.; Jiang, H.D.; Mancuso, A.; Amirbekian, B.; Peng, L.; Sun, R.; Shah, S.S.; Zhou, Z.H.; Ishikawa, T.; Miao, J.W. Quantitative imaging of single, unstained viruses with coherent X-rays. Phys. Rev. Lett. 2008, 101, 158101. [Google Scholar] [CrossRef]
- Williams, G.J.; Hanssen, E.; Peele, A.G.; Pfeifer, M.A.; Clark, J.; Abbey, B.; Cadenazzi, G.; de Jonge, M.D.; Vogt, S.; Tilley, L.; et al. High-resolution X-ray imaging of plasmodium falciparum-infected red blood cells. Cytom. Part A 2008, 73A, 949–957. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Nelson, J.; Kirz, J.; Lima, E.; Marchesini, S.; Miao, H.; Neiman, A.M.; Shapiro, D.; Steinbrener, J.; Stewart, A.; et al. Soft X-ray diffraction microscopy of a frozen hydrated yeast cell. Phys. Rev. Lett. 2009, 103, 198101. [Google Scholar] [CrossRef] [PubMed]
- Nishino, Y.; Takahashi, Y.; Imamoto, N.; Ishikawa, T.; Maeshima, K. Three-dimensional visualization of a human chromosome using coherent X-ray diffraction. Phys. Rev. Lett. 2009, 102, 018101. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J.; Huang, X.J.; Steinbrener, J.; Shapiro, D.; Kirz, J.; Marchesini, S.; Neiman, A.M.; Turner, J.J.; Jacobsen, C. High-resolution X-ray diffraction microscopy of specifically labeled yeast cells. Proc. Natl. Acad. Sci. USA 2010, 107, 7235–7239. [Google Scholar] [CrossRef]
- Wilke, R.N.; Priebe, M.; Bartels, M.; Giewekemeyer, K.; Diaz, A.; Karvinen, P.; Salditt, T. Hard X-ray imaging of bacterial cells: Nano-diffraction and ptychographic reconstruction. Opt. Express 2012, 20, 19232–19254. [Google Scholar] [CrossRef]
- Seibert, M.M.; Ekeberg, T.; Maia, F.R.N.C.; Svenda, M.; Andreasson, J.; Jonsson, O.; Odic, D.; Iwan, B.; Rocker, A.; Westphal, D.; et al. Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 2011, 470, 78–81. [Google Scholar] [CrossRef]
- Ekeberg, T.; Svenda, M.; Abergel, C.; Maia, F.R.N.C.; Seltzer, V.; Claverie, J.-M.; Hantke, M.; Jönsson, O.; Nettelblad, C.; van der Schot, G.; et al. Three-dimensional reconstruction of the giant mimivirus particle with an X-ray free-electron laser. Phys. Rev. Lett. 2015, 114, 098102. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms—A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Latychevskaia, T. Iterative phase retrieval in coherent diffractive imaging: Practical issues. Appl. Opt. 2018, 57, 7187–7197. [Google Scholar] [CrossRef]
- Whitehead, L.W.; Williams, G.J.; Quiney, H.M.; Vine, D.J.; Dilanian, R.A.; Flewett, S.; Nugent, K.A.; Peele, A.G.; Balaur, E.; McNulty, I. Diffractive imaging using partially coherent X-rays. Phys. Rev. Lett. 2009, 103, 243902. [Google Scholar] [CrossRef] [PubMed]
- Zuo, J.M.; Vartanyants, I.; Gao, M.; Zhang, R.; Nagahara, L.A. Atomic resolution imaging of a carbon nanotube from diffraction intensities. Science 2003, 300, 1419–1421. [Google Scholar] [CrossRef] [PubMed]
- Latychevskaia, T.; Fink, H.-W. Three-dimensional double helical DNA structure directly revealed from its X-ray fiber diffraction pattern by iterative phase retrieval. Opt. Express 2018, 26, 30991–31017. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.S.; Weierstall, U.; Spence, J.C.H. RETRACTED: Diffractive electron imaging of nanoparticles on a substrate (Retracted Article. See vol 5, pg 837, 2006). Nat. Mater. 2005, 4, 912–916. [Google Scholar] [CrossRef] [PubMed]
- De Caro, L.; Carlino, E.; Caputo, G.; Cozzoli, P.D.; Giannini, C. Electron diffractive imaging of oxygen atoms in nanocrystals at sub-angstrom resolution. Nat. Nanotechnol. 2010, 5, 360–365. [Google Scholar] [CrossRef] [PubMed]
- De Caro, L.; Carlino, E.; Vittoria, F.A.; Siliqi, D.; Giannini, C. Keyhole electron diffractive imaging (KEDI). Acta Cryst. A 2012, 68, 687–702. [Google Scholar] [CrossRef]
- Steinwand, E.; Longchamp, J.-N.; Fink, H.-W. Fabrication and characterization of low aberration micrometer-sized electron lenses. Ultramicroscopy 2010, 110, 1148–1153. [Google Scholar] [CrossRef] [PubMed]
- Steinwand, E.; Longchamp, J.-N.; Fink, H.-W. Coherent low-energy electron diffraction on individual nanometer sized objects. Ultramicroscopy 2011, 111, 282–284. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Longchamp, J.-N.; Fink, H.-W. When holography meets coherent diffraction imaging. Opt. Express 2012, 20, 28871–28892. [Google Scholar] [CrossRef]
- Longchamp, J.-N.; Latychevskaia, T.; Escher, C.; Fink, H.-W. Graphene unit cell imaging by holographic coherent diffraction. Phys. Rev. Lett. 2013, 110, 255501. [Google Scholar] [CrossRef]
- Adaniya, H.; Cheung, M.; Cassidy, C.; Yamashita, M.; Shintake, T. Development of a SEM-based low-energy in-line electron holography microscope for individual particle imaging. Ultramicroscopy 2018, 188, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Cheung, M.; Adaniya, H.; Cassidy, C.; Yamashita, M.; Shintake, T. Low-energy in-line electron holographic imaging of vitreous ice-embedded small biomolecules using a modified scanning electron microscope. Ultramicroscopy 2020, 209, 112883. [Google Scholar] [CrossRef] [PubMed]
- Carlino, E. In-line holography in transmission electron microscopy for the atomic resolution imaging of single particle of radiation-sensitive matter. Materials 2020, 13, 1413. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Song, J.; Kim, J.S.; Pei, X.; Huang, C.; Boyce, M.; Mendonça, L.; Clare, D.; Siebert, A.; Allen, C.S.; et al. Low-dose phase retrieval of biological specimens using cryo-electron ptychography. Nat. Commun. 2020, 11, 2773. [Google Scholar] [CrossRef] [PubMed]
- Latychevskaia, T. Lateral and axial resolution criteria in incoherent and coherent optics and holography, near- and far-field regimes. Appl. Opt. 2019, 58, 3597–3603. [Google Scholar] [CrossRef] [PubMed]
- Neutze, R.; Wouts, R.; van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef]
- Branden, G.; Hammarin, G.; Harimoorthy, R.; Johansson, A.; Arnlund, D.; Malmerberg, E.; Barty, A.; Tangefjord, S.; Berntsen, P.; DePonte, D.P.; et al. Coherent diffractive imaging of microtubules using an X-ray laser. Nat. Commun. 2019, 10, 2589. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Longchamp, J.-N.; Escher, C.; Fink, H.-W. On artefact-free reconstruction of low-energy (30–250 eV) electron holograms. Ultramicroscopy 2014, 145, 22–27. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Hsu, W.-H.; Chang, W.-T.; Lin, C.-Y.; Hwang, I.-S. Three-dimensional surface topography of graphene by divergent beam electron diffraction. Nat. Commun. 2017, 8, 14440. [Google Scholar] [CrossRef]
- Wicki, F.; Longchamp, J.-N.; Latychevskaia, T.; Escher, C.; Fink, H.-W. Mapping unoccupied electronic states of freestanding graphene by angle-resolved low-energy electron transmission. Phys. Rev. B 2016, 94, 075424. [Google Scholar] [CrossRef]
- Shoichet, B.K.; Baase, W.A.; Kuroki, R.; Matthews, B.W. A relationship between protein stability and protein function. Proc. Natl. Acad. Sci. USA 1995, 92, 452–456. [Google Scholar] [CrossRef] [PubMed]









| In-Line Holography | CDI | |
|---|---|---|
| Finding the sample in the microscope when imaging | Easy when imaging with widely expanded spherical wave (+) | Difficult when imaging with narrow collimated beam (−) |
| Phase information | Available from the recorded intensity (+) | Lost from the recorded intensity (−) |
| Reconstruction procedure | “One-step” reconstruction by calculating back-propagation integral (+) | Iterative reconstruction |
| Reconstructed information | z-information is available and a "three-dimensional" reconstruction is possible (+) | Reconstructed distribution is always a projection of the sample onto one plane (−) |
| Stability of the recorded image | Any lateral shift of the sample results in a lateral shift of the entire hologram (−) | Invariant to lateral shifts of the sample (+) |
| Resolution | Low resolution due to lateral and axial vibrations (−) | High resolution (+) |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latychevskaia, T. Holography and Coherent Diffraction Imaging with Low-(30–250 eV) and High-(80–300 keV) Energy Electrons: History, Principles, and Recent Trends. Materials 2020, 13, 3089. https://doi.org/10.3390/ma13143089
Latychevskaia T. Holography and Coherent Diffraction Imaging with Low-(30–250 eV) and High-(80–300 keV) Energy Electrons: History, Principles, and Recent Trends. Materials. 2020; 13(14):3089. https://doi.org/10.3390/ma13143089
Chicago/Turabian StyleLatychevskaia, Tatiana. 2020. "Holography and Coherent Diffraction Imaging with Low-(30–250 eV) and High-(80–300 keV) Energy Electrons: History, Principles, and Recent Trends" Materials 13, no. 14: 3089. https://doi.org/10.3390/ma13143089
APA StyleLatychevskaia, T. (2020). Holography and Coherent Diffraction Imaging with Low-(30–250 eV) and High-(80–300 keV) Energy Electrons: History, Principles, and Recent Trends. Materials, 13(14), 3089. https://doi.org/10.3390/ma13143089





