Out-Of-Plane Permeability Evaluation of Carbon Fiber Preforms by Ultrasonic Wave Propagation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
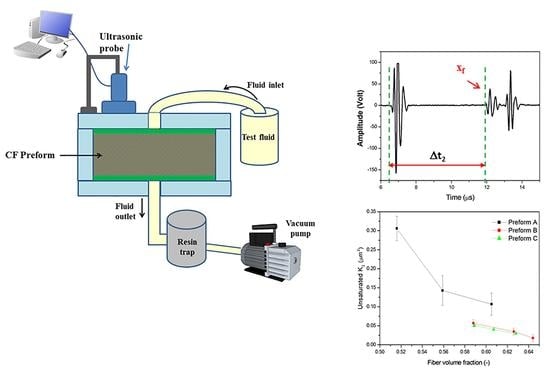
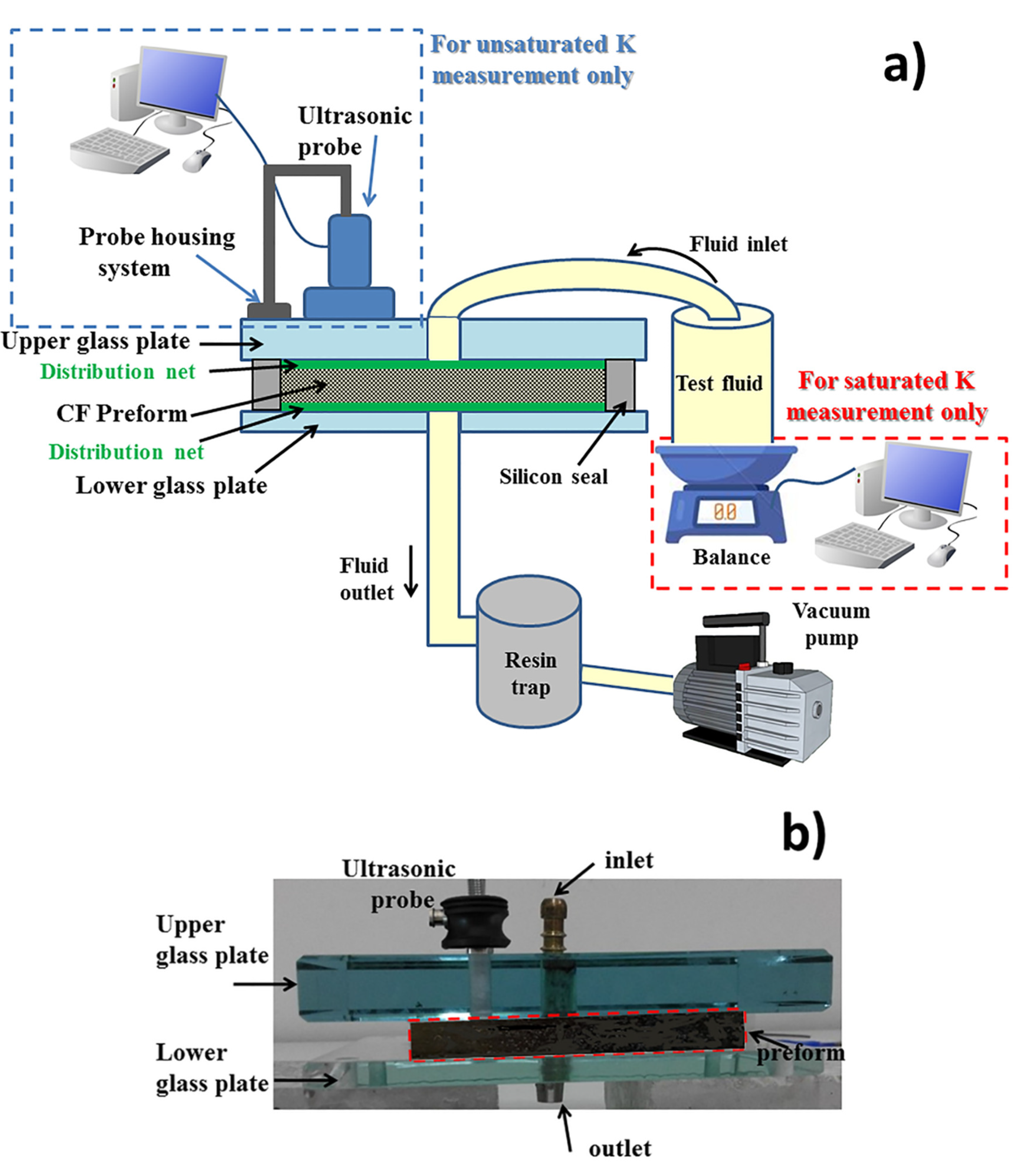
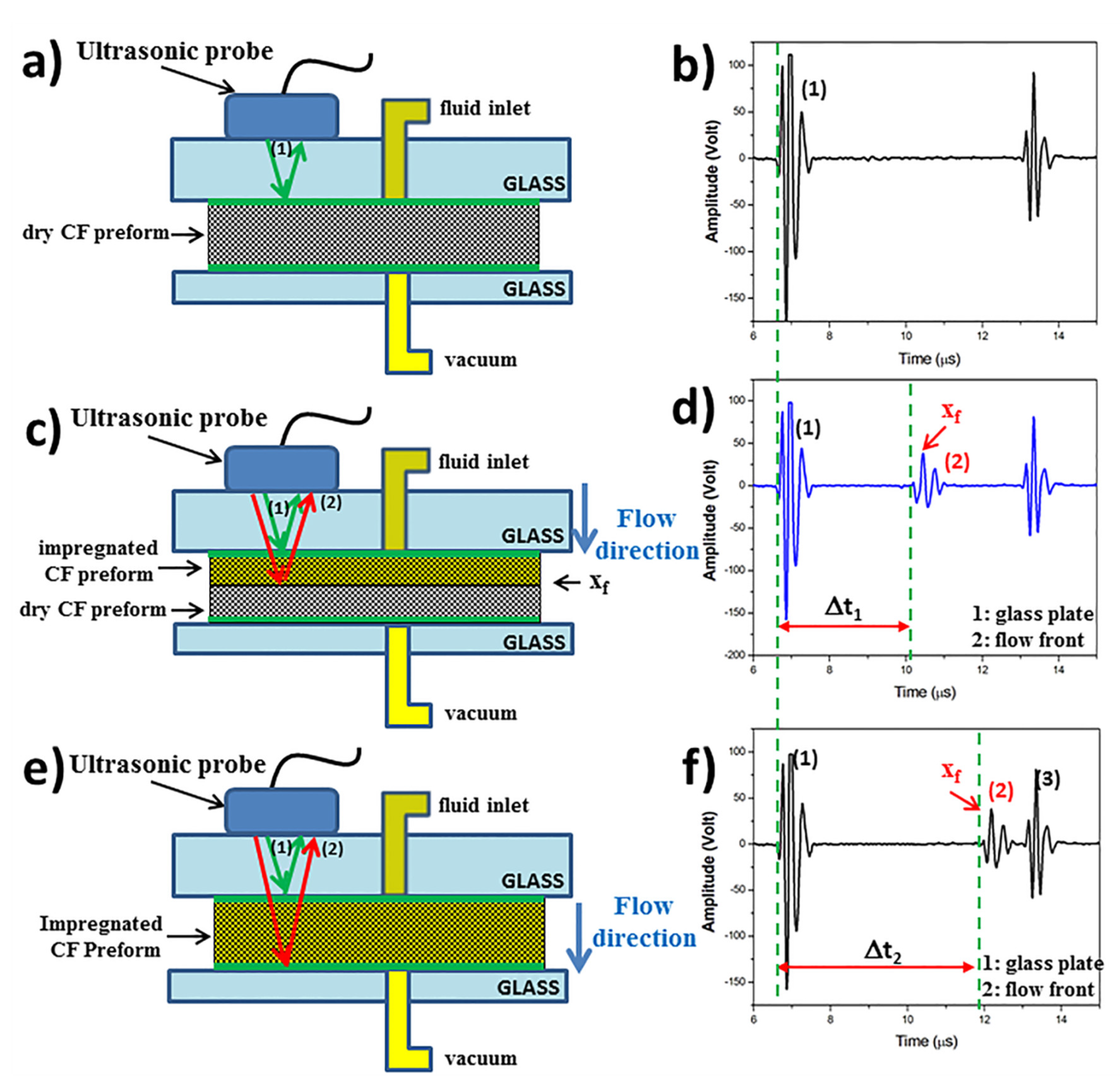
2.2. Experimental Set-Up for Permeability Measurements by Ultrasonic Wave Propagation
2.3. Experimental Set-Up for Measurement of Saturatedpermeability
3. Results
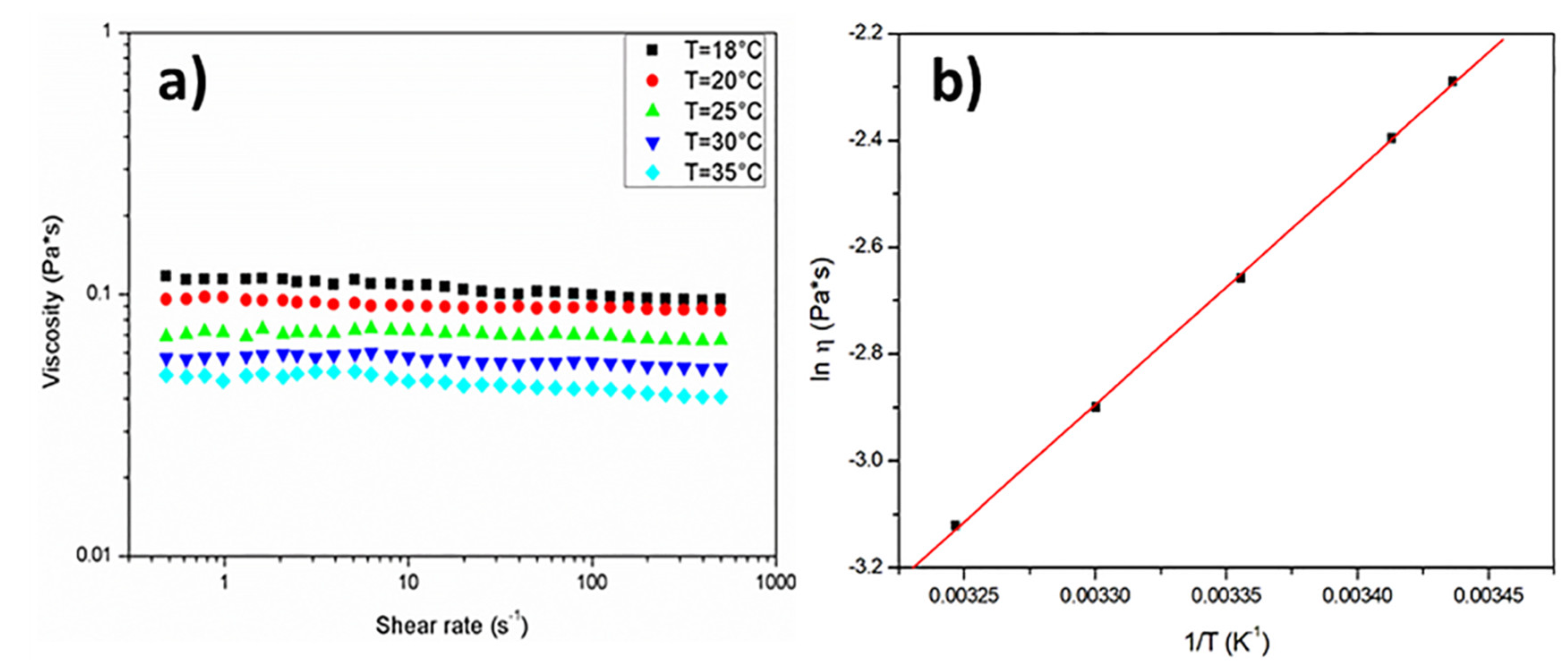
3.1. Rheological Analysis of the Model Fluid
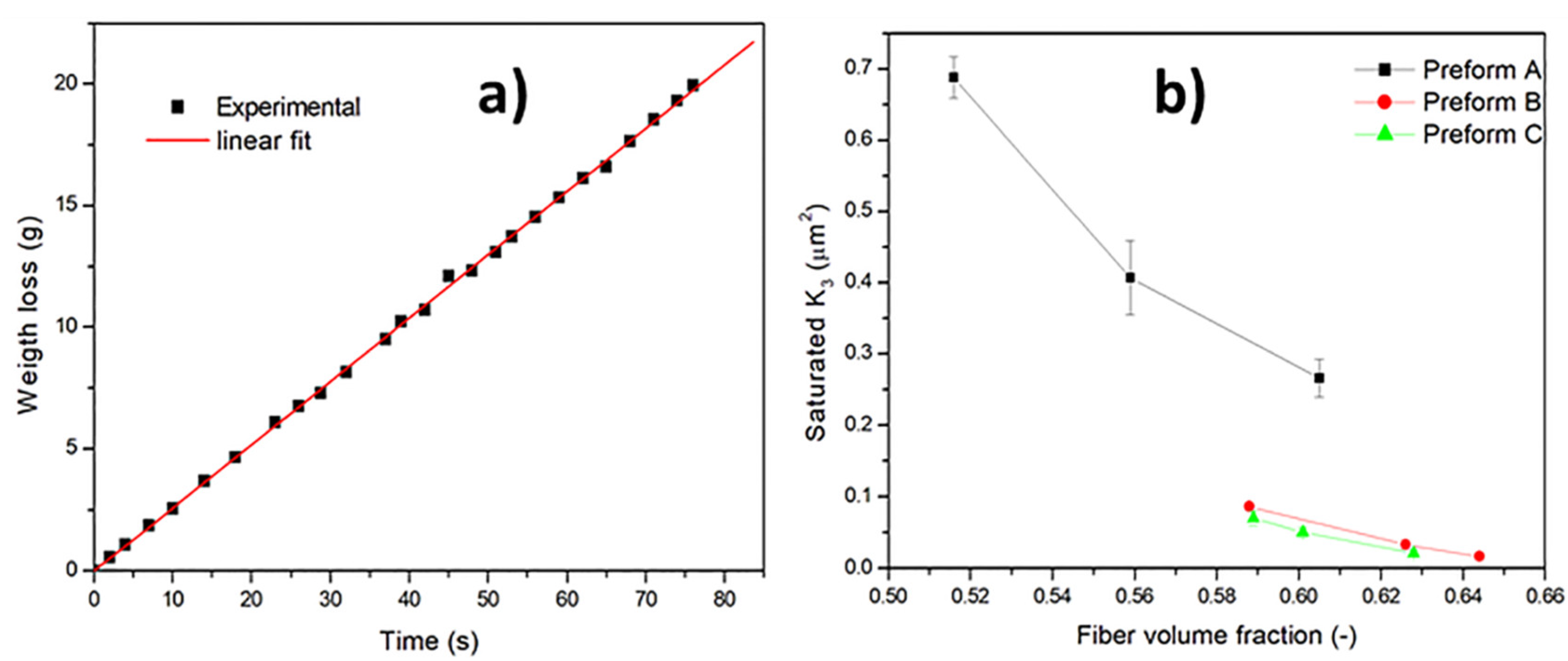
3.2. Saturated Out-Of-PlanePermeability Measurements by VARI Process
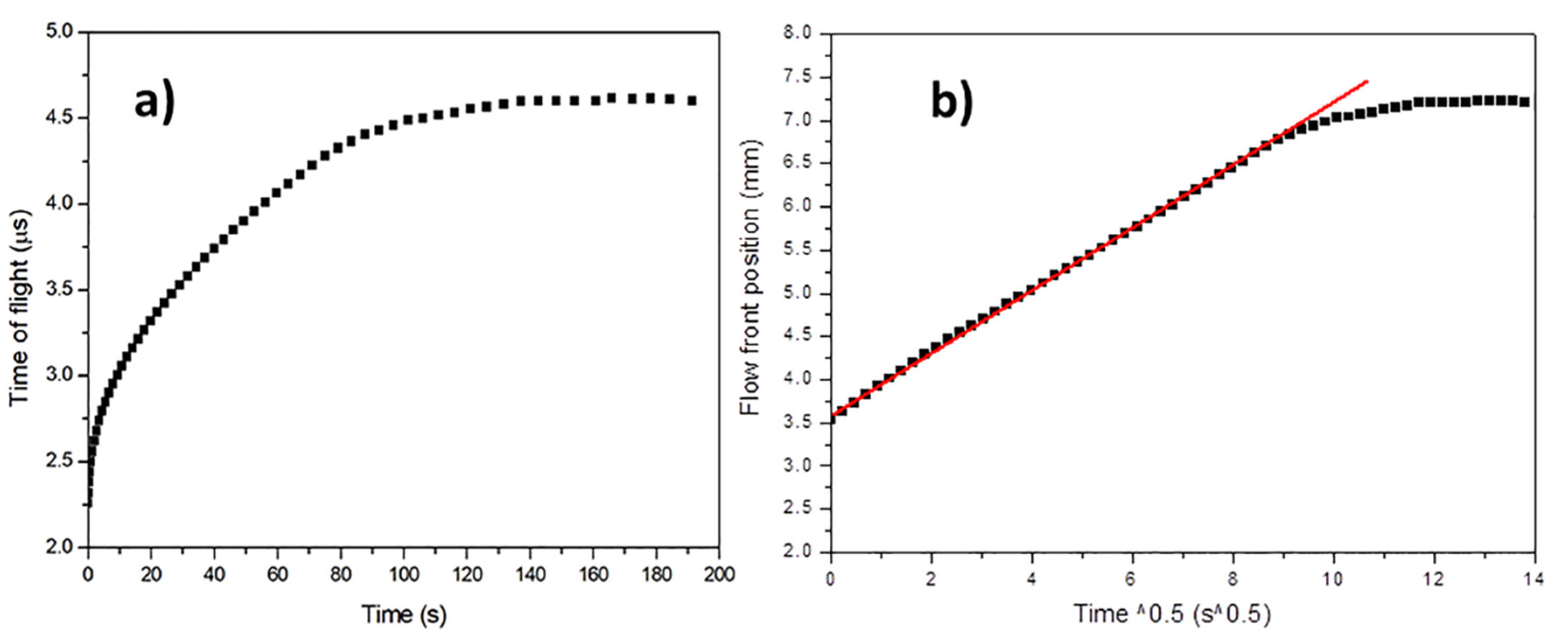
3.3. Out-Of-PlanePermeability Measurements by Ultrasonic Wave Propagation
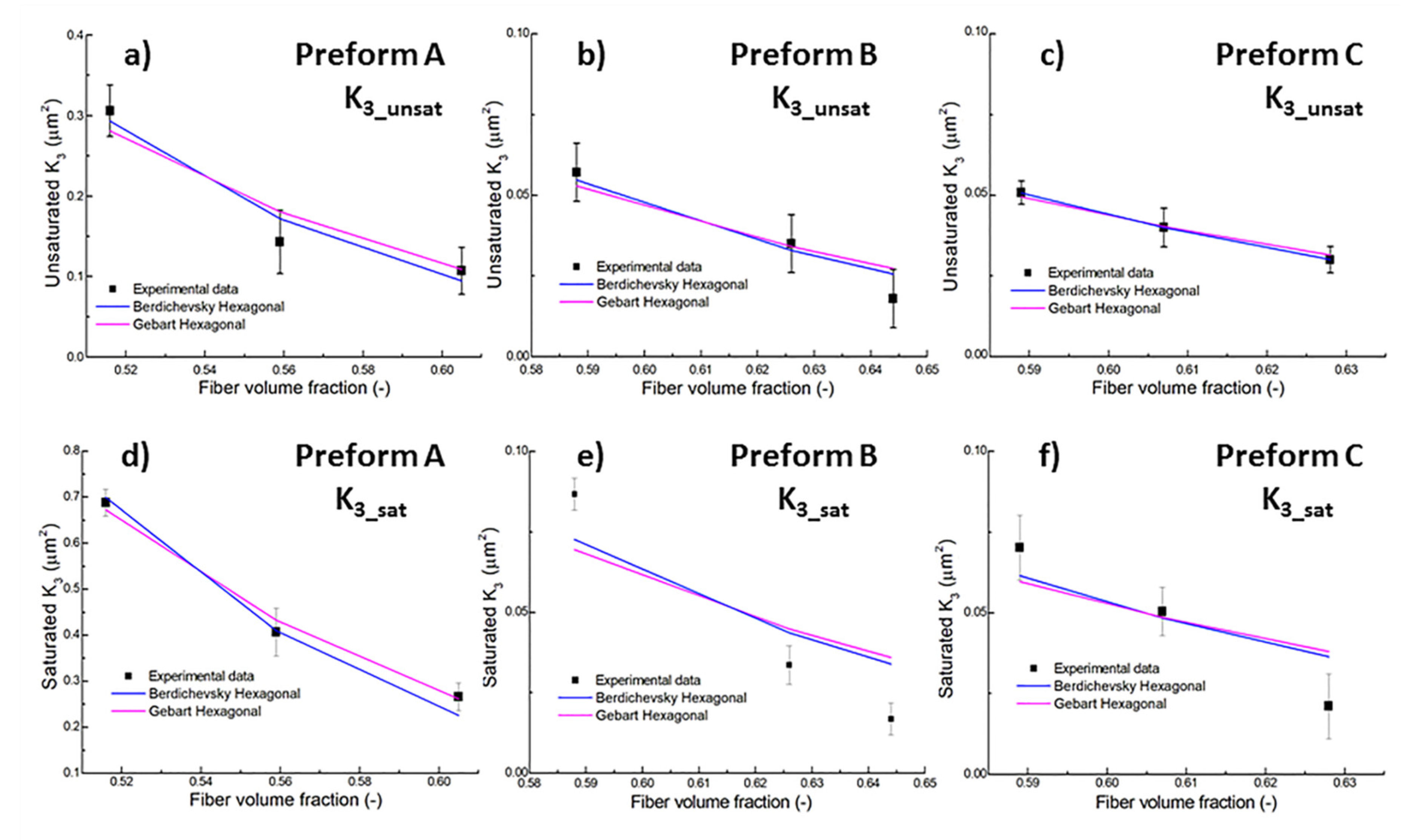
3.4. Mathematical Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Donadei, V.; Lionetto, F.; Wielandt, M.; Offringa, A.; Maffezzoli, A. Effects of Blank Quality on Press-Formed PEKK/Carbon Composite Parts. Materials 2018, 11, 1063. [Google Scholar] [CrossRef] [PubMed]
- De Bruijn, T.; Vincent, G.A.; Meuzelaar, J.; Nunes, J.P.; van Hattum, F. Design, manufacturing and testing of a rotorcraft access panel door from recycled carbon fiber reinforced polyphenylenesulfide. In Proceedings of the SAMPE North America Conference and Exhibition, Charlotte, NC, USA, 20–23 May 2019. [Google Scholar]
- Paleo, A.J.; Zille, A.; Van Hattum, F.W.; Ares-Pernas, A.; Moreira, J.A. Dielectric relaxation of near-percolated carbon nanofiber polypropylene composites. Phys. B Condens. Matter 2017, 516, 41–47. [Google Scholar] [CrossRef]
- Barra, G.; Guadagno, L.; Vertuccio, L.; Simonet, B.; Santos, B.; Zarrelli, M.; Arena, M.; Viscardi, M. Different Methods of Dispersing Carbon Nanotubes in Epoxy Resin and Initial Evaluation of the Obtained Nanocomposite as a Matrix of Carbon Fiber Reinforced Laminate in Terms of Vibroacoustic Performance and Flammability. Materials 2019, 12, 2998. [Google Scholar] [CrossRef] [PubMed]
- Arena, M.; Viscardi, M.; Barra, G.; Vertuccio, L.; Guadagno, L. Multifunctional performance of a nano-modified fiber reinforced composite aeronautical panel. Materials 2019, 12, 869. [Google Scholar] [CrossRef] [PubMed]
- Martulli, L.M.; Creemers, T.; Schöberl, E.; Hale, N.; Kerschbaum, M.; Lomov, S.V.; Swolfs, Y. A thick-walled sheet moulding compound automotive component: Manufacturing and performance. Compos. Part A Appl. Sci. Manuf. 2020, 128, 105688. [Google Scholar] [CrossRef]
- Schneeberger, C.; Wong, J.C.H.; Ermanni, P. Hybrid bicomponent fibres for thermoplastic composite preforms. Compos. Part A Appl. Sci. Manuf. 2017, 103, 69–73. [Google Scholar] [CrossRef]
- Luzi, F.; Torre, L.; Kenny, J.M.; Puglia, D. Bio-and fossil-based polymeric blends and nanocomposites for packaging: Structure–property relationship. Materials 2019, 12, 471. [Google Scholar] [CrossRef]
- Greco, A.; Lionetto, F.; Maffezzoli, A. Processing and characterization of amorphous polyethylene terephthalate fibers for the alignment of carbon nanofillers in thermosetting resins. Polym. Compos. 2015, 36, 1096–1103. [Google Scholar] [CrossRef]
- Becker, D.; Grössing, H.; Konstantopoulos, S.; Fauster, E.; Mitschang, P.; Schledjewski, R. An evaluation of the reproducibility of ultrasonic sensor-based out-of-plane permeability measurements: A benchmarking study. Adv. Manuf. Polym. Compos. Sci. 2016, 2, 34–45. [Google Scholar] [CrossRef]
- Semperger, O.V.; Suplicz, A. The Effect of the Parameters of T-RTM on the Properties of Polyamide 6 Prepared by in Situ Polymerization. Materials 2020, 13, 4. [Google Scholar] [CrossRef]
- Parnas, R.S. Liquid Composite Molding; Carl Hanser Verlag GmbH Co KG: Munich, Germany, 2014; ISBN 3446443029. [Google Scholar]
- Mallick, P.K. Thermoset-matrix composites for lightweight automotive structures. In Materials, Design and Manufacturing for Lightweight Vehicles; Elsevier: Amsterdam, The Netherlands, 2010; pp. 208–231. [Google Scholar]
- Seong, D.G.; Kim, S.; Lee, D.; Yi, J.W.; Kim, S.W.; Kim, S.Y. Prediction of Defect Formation during Resin Impregnation Process through a Multi-Layered Fiber Preform in Resin Transfer Molding by a Proposed Analytical Model. Materials 2018, 11, 2055. [Google Scholar] [CrossRef] [PubMed]
- Lionetto, F.; Moscatello, A.; Maffezzoli, A. Effect of binder powders added to carbon fiber reinforcements on the chemoreology of an epoxy resin for composites. Compos. Part B Eng. 2017, 112, 243–250. [Google Scholar] [CrossRef]
- Sun, Z.; Xiao, J.; Tao, L.; Wei, Y.; Wang, S.; Zhang, H.; Zhu, S.; Yu, M. Preparation of High-Performance Carbon Fiber-Reinforced Epoxy Composites by Compression Resin Transfer Molding. Materials 2019, 12, 13. [Google Scholar] [CrossRef] [PubMed]
- Geng, Z.; Yang, S.; Zhang, L.; Huang, Z.; Pan, Q.; Li, J.; Weng, J.; Bao, J.; You, Z.; He, Y. Self-Extinguishing Resin Transfer Molding Composites Using Non-Fire-Retardant Epoxy Resin. Materials 2018, 11, 2554. [Google Scholar] [CrossRef]
- Karaki, M.; Younes, R.; Trochu, F.; Lafon, P. Progress in Experimental and Theoretical Evaluation Methods for Textile Permeability. J. Compos. Sci. 2019, 3, 73. [Google Scholar] [CrossRef]
- Luo, Y.; Verpoest, I.; Hoes, K.; Vanheule, M.; Sol, H.; Cardon, A. Permeability measurement of textile reinforcements with several test fluids. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1497–1504. [Google Scholar] [CrossRef]
- Naik, N.K.; Sirisha, M.; Inani, A. Permeability characterization of polymer matrix composites by RTM/VARTM. Prog. Aerosp. Sci. 2014, 65, 22–40. [Google Scholar] [CrossRef]
- Sharma, S.; Siginer, D.A. Permeability measurement methods in porous media of fiber reinforced composites. Appl. Mech. Rev. 2010, 63. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Parnas, R.S.; Howard, J.G.; Luce, T.L.; Advani, S.G. Permeability characterization. Part 1: A proposed standard reference fabric for permeability. Polym. Compos. 1995, 16, 429–445. [Google Scholar] [CrossRef]
- Verheus, A.S.; Peeters, J.H.A. The role of reinforcement permeability in resin transfer moulding. Compos. Manuf. 1993, 4, 33–38. [Google Scholar] [CrossRef]
- Park, C.H.; Krawczak, P. Unsaturated and Saturated Permeabilities of Fiber Reinforcement: Critics and Suggestions. Front. Mater. 2015, 2, 38. [Google Scholar] [CrossRef][Green Version]
- Vernet, N.; Ruiz, E.; Advani, S.; Alms, J.B.; Aubert, M.; Barburski, M.; Barari, B.; Beraud, J.M.; Berg, D.C.; Correia, N. Experimental determination of the permeability of engineering textiles: Benchmark II. Compos. Part A Appl. Sci. Manuf. 2014, 61, 172–184. [Google Scholar] [CrossRef]
- Amico, S.; Lekakou, C. An experimental study of the permeability and capillary pressure in resin-transfer moulding. Compos. Sci. Technol. 2001, 61, 1945–1959. [Google Scholar] [CrossRef]
- Ding, L.; Shih, C.; Liang, Z.; Zhang, C.; Wang, B. In situ measurement and monitoring of whole-field permeability profile of fiber preform for liquid composite molding processes. Compos. Part A Appl. Sci. Manuf. 2003, 34, 779–789. [Google Scholar] [CrossRef]
- May, D.; Aktas, A.; Advani, S.G.; Berg, D.C.; Endruweit, A.; Fauster, E.; Lomov, S.V.; Long, A.; Mitschang, P.; Abaimov, S. In-plane permeability characterization of engineering textiles based on radial flow experiments: A benchmark exercise. Compos. Part A Appl. Sci. Manuf. 2019, 121, 100–114. [Google Scholar] [CrossRef]
- Agogue, R.; Chebil, N.; Deleglise-Lagardere, M.; Beauchene, P.; Park, C.H. Efficient permeability measurement and numerical simulation of the resin flow in low permeability preform fabricated by automated dry fiber placement. Appl. Compos. Mater. 2018, 25, 1169–1182. [Google Scholar] [CrossRef]
- Thomas, S.; Bongiovanni, C.; Nutt, S.R. In situ estimation of through-thickness resin flow using ultrasound. Compos. Sci. Technol. 2008, 68, 3093–3098. [Google Scholar] [CrossRef]
- Tuncol, G.; Danisman, M.; Kaynar, A.; Sozer, E.M. Constraints on monitoring resin flow in the resin transfer molding (RTM) process by using thermocouple sensors. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1363–1386. [Google Scholar] [CrossRef]
- Buchmann, C.; Filsinger, J.; Ladstätter, E. Investigation of Electrical Time Domain Reflectometry for infusion and cure monitoring in combination with electrically conductive fibers and tooling materials. Compos. Part B Eng. 2016, 94, 389–398. [Google Scholar] [CrossRef]
- Visvanathan, K.; Balasubramaniam, K. Ultrasonic torsional guided wave sensor for flow front monitoring inside molds. Rev. Sci. Instrum. 2007, 78, 15110. [Google Scholar] [CrossRef]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y.; Ade, B.; Khellil, K. Detection of the key steps during Liquid Resin Infusion manufacturing of a polymer-matrix composite using an in-situ piezoelectric sensor. Mater. Today Commun. 2020, 101077. [Google Scholar] [CrossRef]
- Carlone, P.; Rubino, F.; Paradiso, V.; Tucci, F. Multi-scale modeling and online monitoring of resin flow through dual-scale textiles in liquid composite molding processes. Int. J. Adv. Manuf. Technol. 2018, 96, 2215–2230. [Google Scholar] [CrossRef]
- Di Fratta, C.; Klunker, F.; Ermanni, P. A methodology for flow-front estimation in LCM processes based on pressure sensors. Compos. Part A Appl. Sci. Manuf. 2013, 47, 1–11. [Google Scholar] [CrossRef]
- Kahali Moghaddam, M.; Salas, M.; Ersöz, I.; Michels, I.; Lang, W. Study of resin flow in carbon fiber reinforced polymer composites by means of pressure sensors. J. Compos. Mater. 2017, 51, 3585–3594. [Google Scholar] [CrossRef]
- Liebers, N.; Bertling, D. Reducing NDT effort by coupled monitoring and simulation of liquid composite molding processes. In Proceedings of the 11th Symposium on NDT in Aerospace, Paris, France, 13–15 November 2019. [Google Scholar]
- Konstantopoulos, S.; Fauster, E.; Schledjewski, R. Monitoring the production of FRP composites: A review of in-line sensing methods. Express Polym. Lett. 2014, 8. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Collombet, F.; Torres, M.; Douchin, B.; Crouzeix, L.; Grunevald, Y.-H.; Lubin, J.; Camps, T.; Jacob, X.; Luyckx, G.; Wu, K.-T. Multi-instrumentation monitoring for the curing process of a composite structure. Measurement 2020, 157, 107635. [Google Scholar] [CrossRef]
- El-Sabbagh, A.; Steuernagel, L.; Ziegmann, G. Characterisation of flax polypropylene composites using ultrasonic longitudinal sound wave technique. Compos. Part B Eng. 2013, 45, 1164–1172. [Google Scholar] [CrossRef]
- Lionetto, F.; López-Muñoz, R.; Espinoza-González, C.; Mis-Fernández, R.; Rodríguez-Fernández, O.; Maffezzoli, A. A Study on Exfoliation of Expanded Graphite Stacks in Candelilla Wax. Materials 2019, 12, 2530. [Google Scholar] [CrossRef]
- Hanse Wampo, F.L.; Lemanle Sanga, R.P.; Maréchal, P.; Ntamack, G.E. Piezocomposite transducer design and performance for high resolution ultrasound imaging transducers. Int. J. Comput. Mater. Sci. Eng. 2019, 8. [Google Scholar] [CrossRef]
- Samet, N.; Marechal, P.; Duflo, H. Monitoring of an ascending air bubble in a viscous fluid/fiber matrix medium using a phased array transducer. Eur. J. Mech. B/Fluids 2015, 54, 45–52. [Google Scholar] [CrossRef]
- Maréchal, P.; Ghodhbani, N.; Duflo, H. High temperature polymerization monitoring of an epoxy resin using ultrasound. In Proceedings of the 5th Global Conference on Polymer and Composite Materials (PCM 2018), Kitakyushu, Japan, 10–13 April 2018. [Google Scholar]
- Dell’Anna, R.; Lionetto, F.; Montagna, F.; Maffezzoli, A. Lay-Up and Consolidation of a Composite Pipe by In Situ Ultrasonic Welding of a Thermoplastic Matrix Composite Tape. Materials 2018, 11, 786. [Google Scholar] [CrossRef] [PubMed]
- Cascardi, A.; Dell’Anna, R.; Micelli, F.; Lionetto, F.; Aiello, M.A.; Maffezzoli, A. Reversible techniques for FRP-confinement of masonry columns. Constr. Build. Mater. 2019, 225, 415–428. [Google Scholar] [CrossRef]
- Lionetto, F.; Morillas, M.N.; Pappadà, S.; Buccoliero, G.; Villegas, I.F.; Maffezzoli, A. Hybrid welding of carbon-fiber reinforced epoxy based composites. Compos. Part A Appl. Sci. Manuf. 2018, 104, 32–40. [Google Scholar] [CrossRef]
- Liu, H.L.; Tu, X.-C.; Lee, J.O.; Kim, H.-B.; Hwang, W.R. Visualization of resin impregnation through opaque reinforcement textiles during the vacuum-assisted resin transfer molding process using ultrasound. J. Compos. Mater. 2014, 48, 1113–1120. [Google Scholar] [CrossRef]
- Stöven, T.; Weyrauch, F.; Mitschang, P.; Neitzel, M. Continuous monitoring of three-dimensional resin flow through a fibre preform. Compos. Part A Appl. Sci. Manuf. 2003, 34, 475–480. [Google Scholar] [CrossRef]
- Konstantopoulos, S.; Grössing, H.; Hergan, P.; Weninger, M.; Schledjewski, R. Determination of the unsaturated through-thickness permeability of fibrous preforms based on flow front detection by ultrasound. Polym. Compos. 2018, 39, 360–367. [Google Scholar] [CrossRef]
- Zima, B.; Rafael, K. Numerical Study of Concrete Mesostructure Effect on Lamb Wave Propagation. Material 2020, 13, 2570. [Google Scholar] [CrossRef]
- Jeong, J.J.; Choi, H. An impedance measurement system for piezoelectric array element transducers. Measurement 2017, 97, 138–144. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J.J.; Kim, J. Development of an Estimation Instrument of Acoustic Lens Properties for Medical Ultrasound Transducers. J. Healthc. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Lionetto, F.; Maffezzoli, A. Relaxations during the postcure of unsaturated polyester networks by ultrasonic wave propagation, dynamic mechanical analysis, and dielectric analysis. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 596–602. [Google Scholar] [CrossRef]
- Aziz, A.R.; Ali, M.A.; Zeng, X.; Umer, R.; Schubel, P.; Cantwell, W.J. Transverse permeability of dry fiber preforms manufactured by automated fiber placement. Compos. Sci. Technol. 2017, 152, 57–67. [Google Scholar] [CrossRef]
- Lionetto, F.; Maffezzoli, A.; Ottenhof, M.A.; Farhat, I.A.; Mitchell, J.R. Ultrasonic investigation of wheat starch retrogradation. J. Food Eng. 2006, 75, 258–266. [Google Scholar] [CrossRef]
- Lionetto, F.; Dell’Anna, R.; Moscatello, A.; Totaro, G.S.; Pappadà, A.M. Permeability of stitched and hot-bonded preforms for resin infusion. In Proceedings of the SAMPE Europe Conference, Southampton, UK, 15–17 September 2018. [Google Scholar]
- Karaki, M.; Hallal, A.; Younes, R.; Trochu, F.; Lafon, P.; Hayek, A.; Kobeissy, A.; Fayad, A. A comparative analytical, numerical and experimental analysis of the microscopic permeability of fiber bundles in composite materials. Int. J. Compos. Mater 2017, 7, 82–102. [Google Scholar]
- Gebart, B.R. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Berdichevsky, A.L.; Cai, Z. Preform permeability predictions by self-consistent method and finite element simulation. Polym. Compos. 1993, 14, 132–143. [Google Scholar] [CrossRef]

| A Balanced Preform | B Stitched Preform | C AFP Preform | |
|---|---|---|---|
| Carbon fiber type | G0926 HS06K (Hexcel) | BNCF-24KIMS-(0)-196-600 (Cytec) | TX 1100 IMS65 24k(Cytec) |
| Fiber diameter (μm) | 6.9 | 5.0 | 5.0 |
| Fiber elastic modulus (GPa) | 231 | 290 | 290 |
| Fiber areal weight (g/m2) | 375 | 196 | 200 |
| Number of layers | 22 | 40 | 40 |
| Nominal preform size (mm3) | 80 × 50 × 8 | 80 × 50 × 8 | 80 × 50 × 8 |
| Preform manufacturing process | vacuum bagging | vacuum bagging | automated fiber placement |
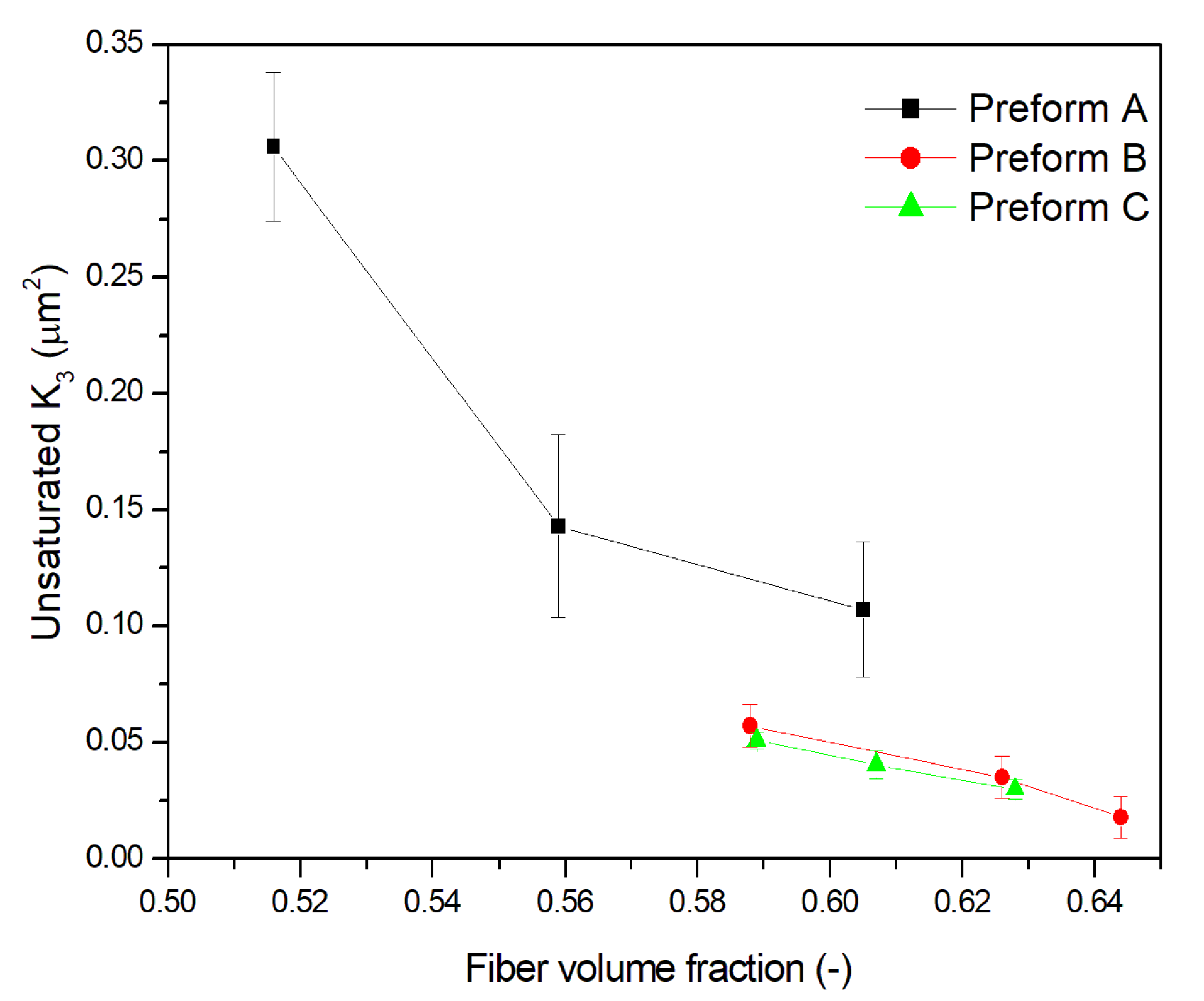
| Material | Vf (%) | Out-Of-Plane Saturated Permeability (µm2) | Out-Of-Plane Unsaturated Permeability (µm2) |
|---|---|---|---|
| Preform A | 51.6 | 0.688 ± 0.0290 | 0.306 ± 0.032 |
| 55.9 | 0.407 ± 0.0052 | 0.143 ± 0.039 | |
| 60.5 | 0.266 ± 0.0027 | 0.107 ±0.029 | |
| Preform B | 58.8 | 0.087 ± 0.005 | 0.057 ± 0.009 |
| 62.6 | 0.034 ± 0.006 | 0.035 ± 0.009 | |
| 64.4 | 0.017 ± 0.005 | 0.018 ± 0.009 | |
| Preform C | 58.9 | 0.070 ± 0.010 | 0.051 ± 0.003 |
| 60.1 | 0.050 ± 0.007 | 0.040 ± 0.006 | |
| 62.8 | 0.021 ± 0.005 | 0.029 ± 0.004 |
| Fiber Arrangement | C1 | Vfmax |
|---|---|---|
| Quadratic | ||
| Hexagonal |
| Material | Out-Of-Plane Permeability | Model | Fiber Radius from Model Best Fit, rf (µm) | Nominal Fiber Radius rfn (µm) | Difference [(rfn − rf)/rf] × 100 (%) |
|---|---|---|---|---|---|
| Preform A | Unsaturated | Gebart-hexagonal | 4.57 | 3.45 | +32 |
| Gebart-quadratic | 5.45 | 3.45 | +58 | ||
| Berdichevsky-hexagonal | 3.23 | 3.45 | −6.8 | ||
| Berdichevsky-quadratic | 4.80 | 3.45 | +39 | ||
| Saturated | Gebart-hexagonal | 7.09 | 3.45 | +105 | |
| Gebart-quadratic | 8.41 | 3.45 | +144 | ||
| Berdichevsky-hexagonal | 4.99 | 3.45 | +45 | ||
| Berdichevsky-quadratic | 7.39 | 3.45 | +114 | ||
| Preform B | Unsaturated | Gebart-hexagonal | 2.89 | 2.5 | +16 |
| Gebart-quadratic | 4.04 | 2.5 | +62 | ||
| Berdichevsky-hexagonal | 2.20 | 2.5 | −12 | ||
| Berdichevsky-quadratic | 3.73 | 2.5 | +49 | ||
| Saturated | Gebart-hexagonal | 3.32 | 2.5 | +33 | |
| Gebart-quadratic | 4.69 | 2.5 | +88 | ||
| Berdichevsky-hexagonal | 2.53 | 2.5 | +1.2 | ||
| Berdichevsky-quadratic | 4.43 | 2.5 | +77 | ||
| Preform C | Unsaturated | Gebart-hexagonal | 2.81 | 2.5 | +12 |
| Gebart-quadratic | 3.87 | 2.5 | +55 | ||
| Berdichevsky-hexagonal | 2.13 | 2.5 | −15 | ||
| Berdichevsky-quadratic | 3.65 | 2.5 | +46 | ||
| Saturated | Gebart-hexagonal | 3.09 | 2.5 | +24 | |
| Gebart-quadratic | 4.29 | 2.5 | +72 | ||
| Berdichevsky-hexagonal | 2.35 | 2.5 | −6 | ||
| Berdichevsky-quadratic | 4.05 | 2.5 | +62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lionetto, F.; Montagna, F.; Maffezzoli, A. Out-Of-Plane Permeability Evaluation of Carbon Fiber Preforms by Ultrasonic Wave Propagation. Materials 2020, 13, 2684. https://doi.org/10.3390/ma13122684
Lionetto F, Montagna F, Maffezzoli A. Out-Of-Plane Permeability Evaluation of Carbon Fiber Preforms by Ultrasonic Wave Propagation. Materials. 2020; 13(12):2684. https://doi.org/10.3390/ma13122684
Chicago/Turabian StyleLionetto, Francesca, Francesco Montagna, and Alfonso Maffezzoli. 2020. "Out-Of-Plane Permeability Evaluation of Carbon Fiber Preforms by Ultrasonic Wave Propagation" Materials 13, no. 12: 2684. https://doi.org/10.3390/ma13122684
APA StyleLionetto, F., Montagna, F., & Maffezzoli, A. (2020). Out-Of-Plane Permeability Evaluation of Carbon Fiber Preforms by Ultrasonic Wave Propagation. Materials, 13(12), 2684. https://doi.org/10.3390/ma13122684