Evaluation of Cracking Patterns in Cement Composites—From Basics to Advances: A Review
Abstract
1. Introduction
2. Causes of Cracks and Cracking Patterns in Cement Composites
- —the Young’s modulus of elasticity [N/m2],
- —the surface energy [N/m],
- —half the length of the crack [m].
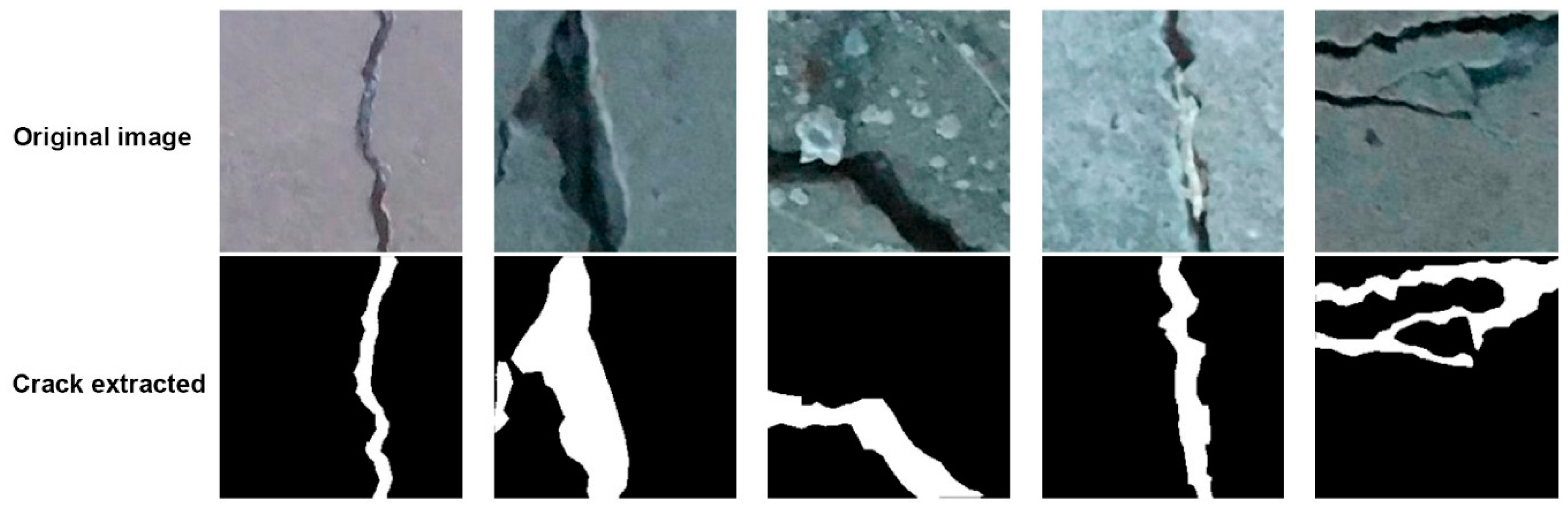
3. Techniques for the Detection of Individual Cracks and the Whole Cracking Pattern
3.1. Global Thresholding
3.2. Locally Adaptive Thresholding
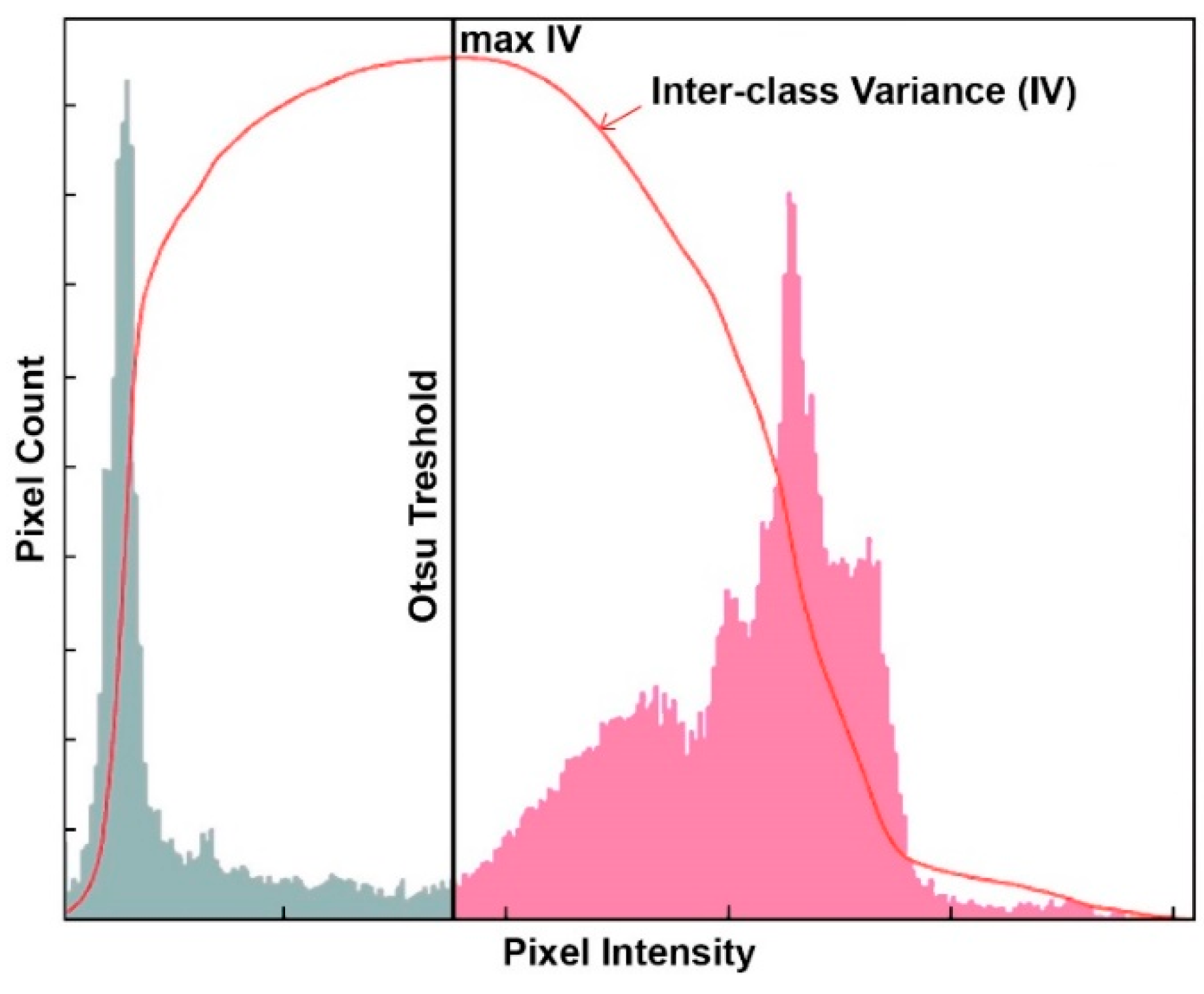
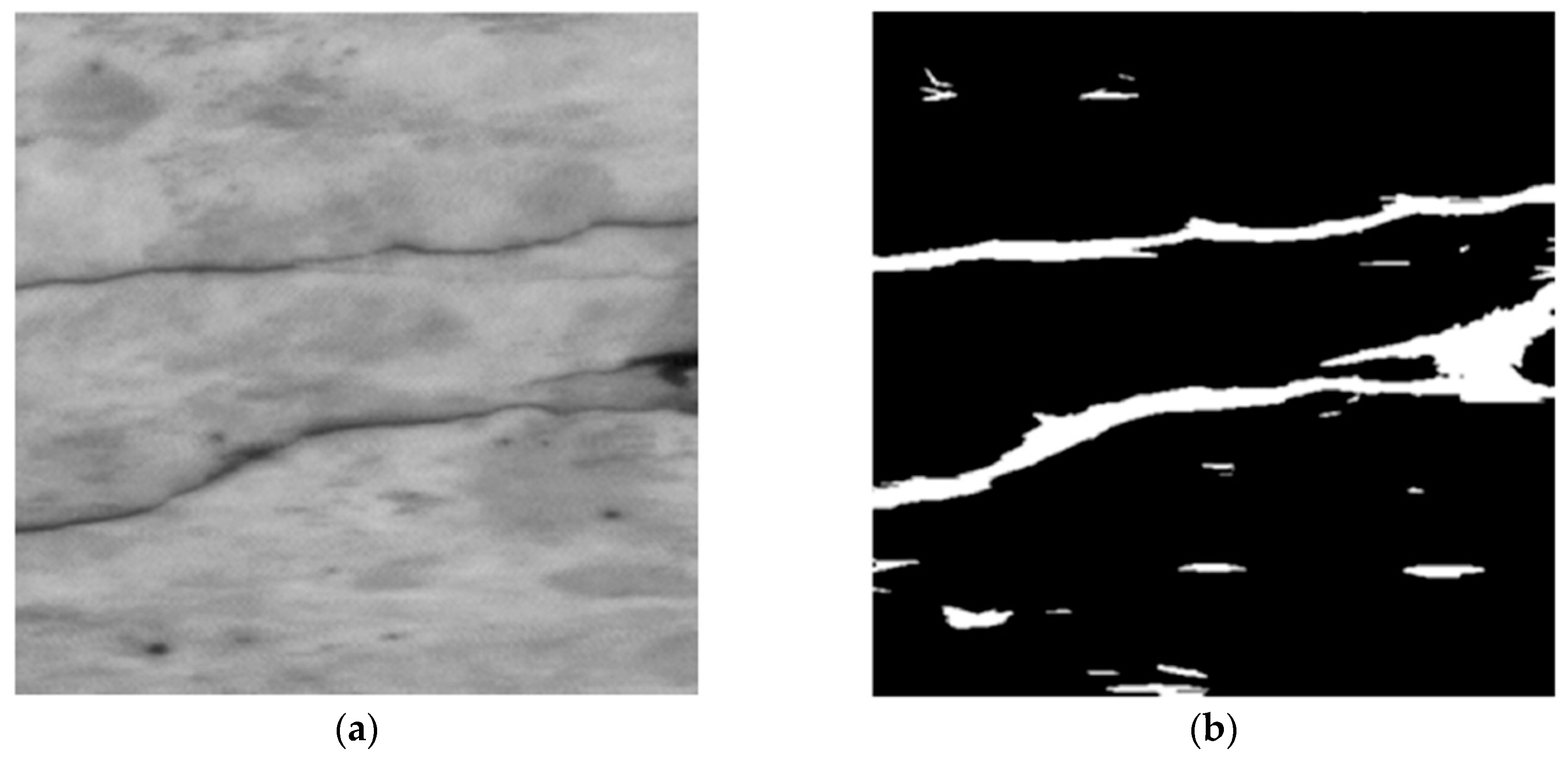
3.3. Otsu Thresholding
3.4. Genetic Algorithms
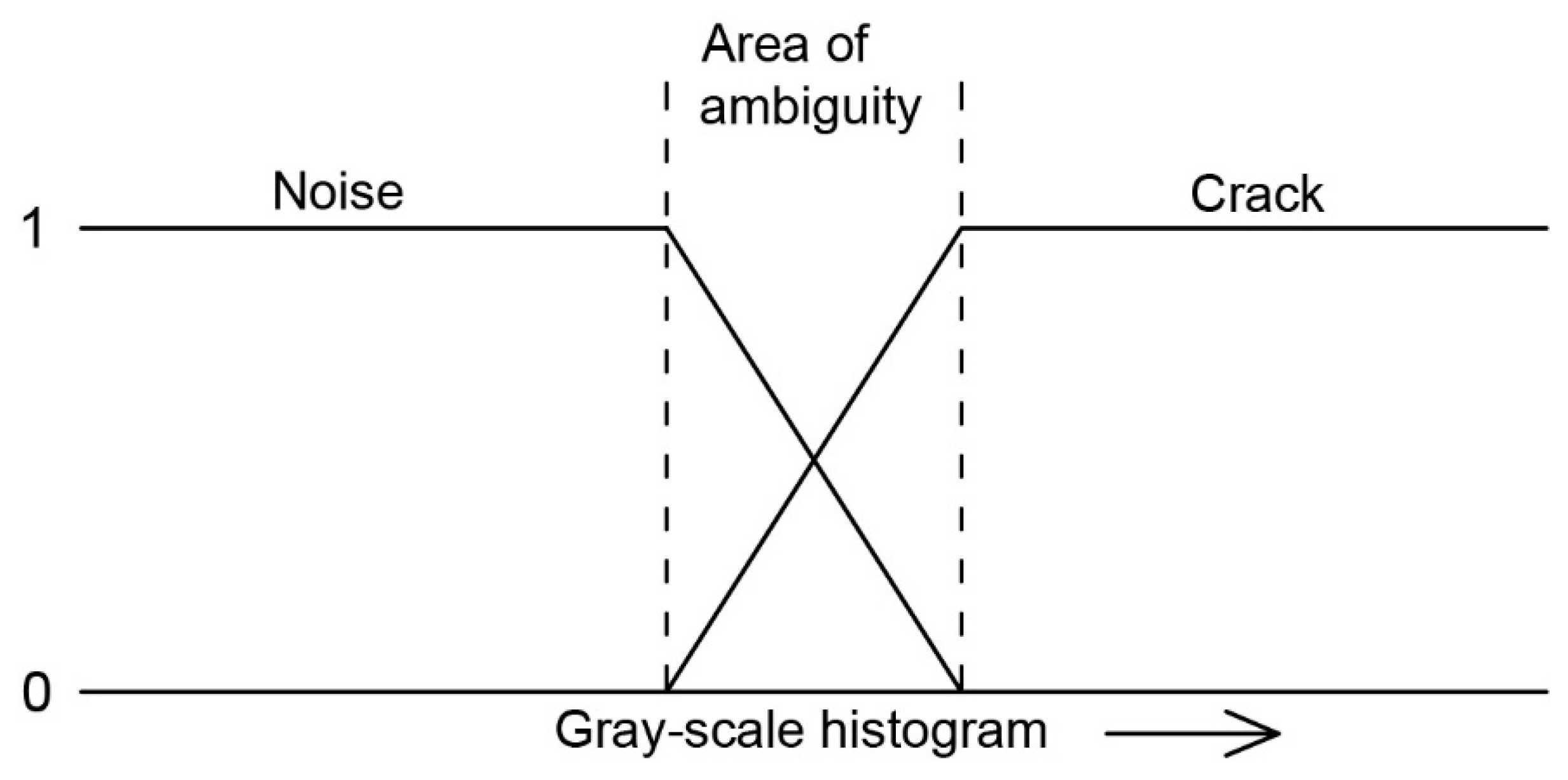
3.5. Fuzzy Logic Based Techniques
3.6. Artificial Neural Networks
3.7. Dijkstra Algorithm
3.8. The Bayesian Classifier
3.9. The AdaBoost Classifier
3.10. Summary of Techniques for Identifying Cracks and Their Accuracy in the Literature Review Works
4. Parameters to Describe the Morphology of the Cracking Patterns
4.1. Opening Width of the Cracks
4.2. Length and Orientation of the Cracks
4.3. The Crack Density
- —the crack density [mm−1],
- —the average crack length [mm],
- —the area of the test section [mm2].
4.4. The Crack Area
4.5. The Fractal Dimension
- formlessness—an unambiguous shape is impossible to determine,
- description by a recursive relationship, not a mathematical formula,
- self-similarity—an isolated fragment resembles its larger whole.
4.6. A Summary of the Use of Individual Parameters to Describe the Morphology of the Cracking Patterns
5. Influence of Morphology of the Cracking Patterns on the Properties of Cement Composites
5.1. Performance at Elevated Temperatures
5.2. Shrinkage and Drying
5.3. Water Permeability
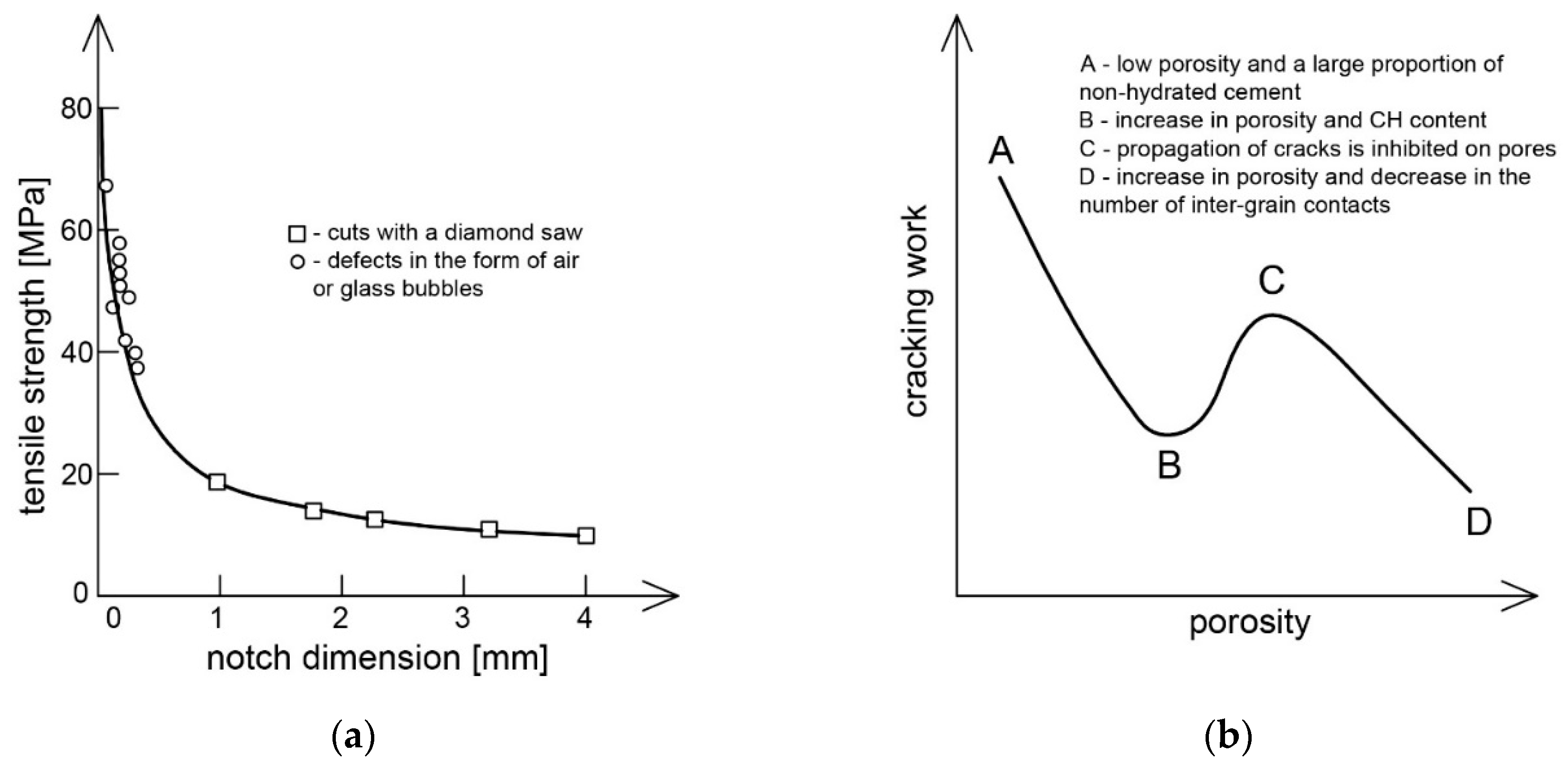
5.4. Mechanical Strength
- —the damage index; ,
- —the fractal dimension of the current status of the cracking pattern,
- —the fractal dimension of the cracking pattern computed during the first inspection.
5.5. Chemical Corrosion
6. Summary
- the process of cracks formation in brittle cement composites and their evolution into an extensive and complex system of cracks,
- methods and techniques of digital extraction of the cracking patterns for their further evaluation,
- quantitative parameters used to describe the complexity of the cracking patterns,
- evaluation of the influence of morphology of the cracking patterns on selected properties of cement composites.
Funding
Acknowledgments
Conflicts of Interest
References
- Neville, A.M. Properties of Concrete, 4th ed.; Arkady: Warsaw, Poland, 2000. [Google Scholar]
- Brandtzaeg, A. Failure of A Material Composed of Non-isotropic Elements; Trondhjem Bruns i Komm.: Trondheim, Norway, 1927. [Google Scholar]
- Yoshida, H. Über Das Elastische Verhalten Von Beton: mit Besonderer Berücksichtigung Der Querdehnung; Springer Verlag: Berlin, Germany, 1930. [Google Scholar]
- VanMier, J. Concrete Fracture: A Multiscale Approach; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Recho, N. Fracture Mechanics and Crack Growth; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kurumatani, M.; Terada, K.; Kato, J.; Kyoya, T.; Kashiyama, K. An isotropic damage model based on fracture mechanics for concrete. Eng. Fract. Mech. 2016, 155, 49–66. [Google Scholar] [CrossRef]
- Hlobil, M.; Smilauer, V.; Chanvillard, G. Micromechanical multiscale fracture model for compressive strength of blended cement pastes. Cem. Concr. Res. 2016, 83, 188–202. [Google Scholar] [CrossRef]
- Bisschop, J.; Wittel, F. Contraction gradient induced microcracking in hardened cement paste. Cem. Concr. Compos. 2011, 33, 466–473. [Google Scholar] [CrossRef]
- Xu, Y.; Wong, Y.; Poon, C.; Anson, M. Influence of PFA on cracking of concrete and cement paste after exposure to high temperatures. Cem. Concr. Res. 2003, 33, 2009–2016. [Google Scholar] [CrossRef]
- Tosun-Felekoglu, K.; Felekoglu, B. Effects of fibre hybridization on multiple cracking potential of cement-based composites under flexural loading. Constr. Build. Mater. 2013, 41, 15–20. [Google Scholar] [CrossRef]
- Banthia, N.; Azzabi, M.; Pigeon, M. Restrained shrinkage cracking in fiber-reinforced cementitious composites. Mater. Struct. 1993, 26, 405–413. [Google Scholar] [CrossRef]
- Szelag, M. Evaluation of cracking patterns of cement paste containing polypropylene fibers. Compos. Struct. 2019, 220, 402–411. [Google Scholar] [CrossRef]
- Szelag, M. Properties of cracking patterns of multi-walled carbon nanotube-reinforced cement matrix. Materials 2019, 12, 2942. [Google Scholar] [CrossRef]
- Szelag, M. Development of Cracking Patterns in Modified Cement Matrix with Microsilica. Materials 2018, 11, 1928. [Google Scholar] [CrossRef]
- Szelag, M. Influence of specimen’s shape and size on the thermal cracks’ geometry of cement paste. Constr. Build. Mater. 2018, 189, 1155–1172. [Google Scholar] [CrossRef]
- Szelag, M. The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials 2018, 11, 520. [Google Scholar] [CrossRef]
- Griffith, A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Sereis A 1921, 221, 163–198. [Google Scholar]
- Mindess, S.; Barnes, P. Structure and Performance of Cements; Applied Science Publishers: London, UK, 1983. [Google Scholar]
- Mindess, S. Fracture toughness testing of cement and concrete. In Fracture Mechanics of Concrete: Material Characterization and Testing; Springer: Dordrecht, Germany, 1984; pp. 67–110. [Google Scholar]
- Powers, T.C. Rheology of Freshly Mixed Concrete. The Properties of Fresh Concrete; John Wiley: New York, NY, USA, 1968. [Google Scholar]
- Oberholster, R.E. Pore structure, permeability and diffusivity of hardened cement paste and concrete in relation to durability: Status and prospects. In Proceedings of the 8th International congress on chemistry of cement, Rio de Janeiro, Brasil, 22–27 September 1986; pp. 323–335. [Google Scholar]
- Brown, J.H.; Pomeroy, C.D. Fracture toughness of cement paste and mortars. Cem. Concr. Res. 1973, 3, 475–480. [Google Scholar] [CrossRef]
- Hillemeier, B.; Hilsdorf, H. Fracture mechanics studies on concrete compounds. Cem. Concr. Res. 1977, 7, 523–535. [Google Scholar] [CrossRef]
- Beaudoin, J. Effect of humiidty and porosity on fracture of hardened Portland-cement. Cem. Concr. Res. 1982, 12, 705–716. [Google Scholar] [CrossRef]
- Shah, S. Determination of fracture parameters (KIcs and CTODc) of plain concrete using three-point bend tests. Mater. Struct. 1990, 23, 457–460. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Zhou, J. Influence of porosity on compressive and tensile strength of cement mortar. Constr. Build. Mater. 2013, 40, 869–874. [Google Scholar] [CrossRef]
- Kumar, R.; Bhattacharjee, B. Porosity, pore size distribution and in situ strength of concrete. Cem. Concr. Res. 2003, 33, 155–164. [Google Scholar] [CrossRef]
- Lian, C.; Zhuge, Y.; Beecham, S. The relationship between porosity and strength for porous concrete. Constr. Build. Mater. 2011, 25, 4294–4298. [Google Scholar] [CrossRef]
- Roy, D.; Gouda, G. Porosity-strength relation in cementitious materials with very high strengths. J. Am. Ceram. Soc. 1973, 56, 549–550. [Google Scholar] [CrossRef]
- Taylor, H. Discussion of the paper “Microstructure and strength of hydrated cements” by RF Feldman and JJ Beaudoin. Cem. Concr. Res. 1977, 7, 465–468. [Google Scholar] [CrossRef]
- Mindess, S. Relation between the compressive strength and porosity of autoclaved calcium silicate hydrates. J. Am. Ceram. Soc. 1970, 53, 621–624. [Google Scholar] [CrossRef]
- Nadeau, J.; Mindess, S.; Hay, J. Slow crack growth in cement paste. J. Am. Ceram. Soc. 1974, 57, 51–54. [Google Scholar] [CrossRef]
- Wittmann, F. Trends in research on creep and shrinkage of concrete. In Cement Production an Use; Engineering Foundation: New York, NY, USA, 1979; pp. 143–162. [Google Scholar]
- Birchall, J.; Howard, A.; Kendall, K. Flexural strength and porosity of cements. Nature 1981, 289, 388–390. [Google Scholar] [CrossRef]
- Alford, N.; Rahman, A. An assesment of porosity and pore sizes in hardened cement pastes. J. Mater. Sci. 1981, 16, 3105–3114. [Google Scholar] [CrossRef]
- Wittmann, F. Surface tension skrinkage and strength of hardened cement paste. Matériaux et Construction 1968, 1, 547–552. [Google Scholar] [CrossRef]
- Robertson, B.; Mills, R. Influence of sorbed fluids on compressive strength of cement paste. Cem. Concr. Res. 1985, 15, 225–232. [Google Scholar] [CrossRef]
- Costa, U.; Massazza, F. Rheological properties of fly ash cement pastes. Il Cemento 1986, 4, 397–414. [Google Scholar]
- Beaudoin, J. Calcium hydroxide in cement matrices: Physico-mechanical and physico-chemical contributions. In Calcium Hydroxide in Concrete in Materials Science of Concrete; American Ceramic Society: Westerville, OH, USA, 2000; pp. 131–132. [Google Scholar]
- Alford, N.; Groves, G.; Double, D. Physical properties of high-strength cement pastes. Cem. Concr. Res. 1982, 12, 349–358. [Google Scholar] [CrossRef]
- Neville, A. The influence of the direction of loading on the strength of concrete test cubes. ASTM Bull. 1959, 239, 63–65. [Google Scholar]
- Hsu, T.; Slate, F.; Sturman, G.; Winter, G. Microcracking of plain concrete and the shape of the stress-strain curve. J. Am. Concr. Inst. 1963, 60, 209–224. [Google Scholar]
- Akcaoglu, R.; Tokyay, M.; Celik, T. Assessing the ITZ microcracking via scanning electron microscope and its effect on the failure behavior of concrete. Cem. Concr. Res. 2005, 35, 358–363. [Google Scholar] [CrossRef]
- Golewski, G. An assessment of microcracks in the Interfacial Transition Zone of durable concrete composites with fly ash additives. Compos. Struct. 2018, 200, 515–520. [Google Scholar] [CrossRef]
- Jornet, A.; Guidali, E.; Muhlethaler, U. Microcracking in high-performance concrete. In Proceedings of the 4th euroseminar on microscopy applied to building materials, Boras, Sweden, 30 September 1993; Swedish National Testing and Research Institute: Stockholm, Sweden, 1993; p. 6. [Google Scholar]
- Slate, F.; Hover, K. Microcracking in concrete. In Fracture Mechanics of Concrete: Material Characterization and Testing; Springer: Dordrecht, Germany, 1984; pp. 137–159. [Google Scholar]
- Smadi, M.; Slate, F. Microcracking of high and normal strength concreters under short-term and long-term loadings. Mater. J. 1989, 86, 117–127. [Google Scholar]
- Solomatov, V.I. Polystructural theory development of composite building materials. In The Success of Modern Materials Science. Proceedings of the Anniversary Conference, RAASN; MGUPS: Moscow, Russia, 2001; pp. 56–66. [Google Scholar]
- Solomatov, V.I.; Vyrovoy, V.N.; Bobryshev, A.N. Polystructural Theory of Composite Building Materials; FAN: Tashkent, Uzbekistan, 1991. [Google Scholar]
- Sukhanov, V.; Vyrovoy, V.; Dorofeev, V. Crack’s role in structural development of the constructional composite materials. Mod. Ind. Civ. Constr. 2011, 7, 135–141. [Google Scholar]
- Vyrovoy, V.N.; Dorofeev, V.S.; Sukhanov, V.G. Composite Building Materials and Constructions. Structure, Self-Organization, Properties; TES: Odess, Ukraine, 2010. [Google Scholar]
- Report, C.S. Non-Structural Cracks in Concrete. Technical Report no. 22; Concrete Society: London, UK, 1992. [Google Scholar]
- Henrichsen, A.; Laugesen, P.; Diamond, S.; Mindess, S.; Glasser, F.; Roberts, L.; Skalny, J.; Wakeley, L. Monitoring of concrete quality in high performance civil engineering constructions. MRS Online Proceed. Library Arch. 1995, 370, 49–56. [Google Scholar]
- Acosta, J.A.; Figueroa, J.L.; Mullen, R.L. Low-cost video image processing system for evaluating pavement surface distress. Transp. Res. Rec. 1992, 1348, 63–72. [Google Scholar]
- Fujita, Y.; Hamamoto, Y. A robust automatic crack detection method from noisy concrete surfaces. Mach. Vis. Appl. 2011, 22, 245–254. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imag. 2004, 13, 146–168. [Google Scholar] [CrossRef]
- Tang, J.; Gu, Y. Automatic crack detection and segmentation using a hybrid algorithm for road distress analysis. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 3026–3030. [Google Scholar]
- Tong, X.; Guo, J.; Ling, Y.; Yin, Z. A new image-based method for concrete bridge bottom crack detection. In Proceedings of the International Conference on Image Analysis and Signal Processing, Wuhan, China, 21–23 October. 2011; IEEE: Piscataway, NJ, USA, 2001; pp. 568–571. [Google Scholar]
- Liu, X.; Ai, Y.; Scherer, S. Robust image-based crack detection in concrete structure using multi-scale enhancement and visual features. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 7–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2304–2308. [Google Scholar]
- Gavilan, M.; Balcones, D.; Marcos, O.; Llorca, D.; Sotelo, M.; Parra, I.; Ocana, M.; Aliseda, P.; Yarza, P.; Amirola, A. Adaptive Road Crack Detection System by Pavement Classification. Sensors 2011, 11, 9628–9657. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Talab, A.; Huang, Z.; Xi, F.; Liu, H. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Optik 2016, 127, 1030–1033. [Google Scholar] [CrossRef]
- Valenca, J.; Dias-da-Costa, D.; Julio, E. Characterisation of concrete cracking during laboratorial tests using image processing. Constr. Build. Mater. 2012, 28, 607–615. [Google Scholar] [CrossRef]
- Hoang, D. Detection of Surface Crack in Building Structures Using Image Processing Technique with an Improved Otsu Method for Image Thresholding. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Nishikawa, T.; Yoshida, J.; Sugiyama, T.; Saito, S.; Fujino, Y. Robust Image Procesing for detection of Concrete Cracks Using a Parallel Image-Filter. J. JSCE 2007, 63, 599–616. [Google Scholar]
- Aoki, S.; Nagao, T. Automatic construction of tree-structural image transformations using genetic programming. In Proceedings of the 10th International Conference on Image Analysis and Processing, Kobe, Japan, 24–28 October 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 136–141. [Google Scholar]
- Nishikawa, T.; Yoshida, J.; Sugiyama, T.; Fujino, Y. Concrete Crack Detection by Multiple Sequential Image Filtering. Comput. Aided Civ. Infrastruct. Eng. 2012, 27, 29–47. [Google Scholar] [CrossRef]
- Tomikawa, T. A study of road crack detection by the meta-genetic algorithm. In Proceedings of the 1999 IEEE Africon. 5th Africon Conference in Africa (Cat. No. 99CH36342), Cape Town, South Africa, 28 September–1 October 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 543–548. [Google Scholar]
- Medina, R.; Llamas, J.; Gomez-Garcia-Bermejo, J.; Zalama, E.; Segarra, M. Crack Detection in Concrete Tunnels Using a Gabor Filter Invariant to Rotation. Sensors 2017, 17. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy-logic. Computer 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Choudhary, G.; Dey, S. Crack Detection in Concrete Surfaces using Image Processing, Fuzzy Logic, and Neural Networks. In Proceedings of the 2012 IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 18–20 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 404–411. [Google Scholar]
- Cheng, H.; Chen, J.; Glazier, C.; Hu, Y. Novel approach to pavement cracking detection based on fuzzy set theory. J. Comput. Civ. Eng. 1999, 13, 270–280. [Google Scholar] [CrossRef]
- Maode, Y.; Shaobo, B.; Xue, L.; Yuyao, H. An adaptive fuzzy image enhancement algorithm for local regions. In Proceedings of the 2007 Chinese Control Conference, Hunan, China, 26–31 July 2007; IEEE: Piscataway, NJ, USA, 2007; Volume 5, pp. 308–311. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: New York, NY, USA, 1994. [Google Scholar]
- Lee, B.; Lee, H. Position-invariant neural network for digital pavement crack analysis. Comput. Aided Civ. Infrastruct. Eng. 2004, 19, 105–118. [Google Scholar] [CrossRef]
- Bray, J.; Verma, B.; Li, X.; He, W. A neural network based technique for automatic classification of road cracks. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2161–4393. [Google Scholar]
- Moon, H.; Kim, J. Intelligent crack detecting algorithm on the concrete crack image using neural network. In Proceedings of the 28th ISARC, Seoul, Korea, 9 June–2 July 2011; pp. 1461–1467. [Google Scholar]
- Dung, C.; Anh, L. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, C.; Wang, J.; Wang, L.; Yue, X. Concrete Cracks Detection Based on FCN with Dilated Convolution. Appl. Sci. 2019, 9. [Google Scholar] [CrossRef]
- Cha, Y.; Choi, W.; Caicedo, J.; Pakzad, S. Vision-Based Concrete Crack Detection Using a Convolutional Neural Network. Dyn. Civ. Struct. 2017, 2, 71–73. [Google Scholar] [CrossRef]
- Lee, B.; Kim, Y.; Yi, S.; Kim, J. Automated image processing technique for detecting and analysing concrete surface cracks. Struct. Infrastruct. Eng. 2013, 9, 567–577. [Google Scholar] [CrossRef]
- Dijkstra, E. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Amhaz, R.; Chambon, S.; Idier, J.; Baltazart, V. Automatic Crack Detection on Two-Dimensional Pavement Images: An Algorithm Based on Minimal Path Selection. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2718–2729. [Google Scholar] [CrossRef]
- Gunkel, C.; Stepper, A.; Muller, A.; Muller, C. Micro crack detection with Dijkstra’s shortest path algorithm. Mach. Vis. Appl. 2012, 23, 589–601. [Google Scholar] [CrossRef]
- Yu, S.; Jang, J.; Han, C. Auto inspection system using a mobile robot for detecting concrete cracks in a tunnel. Autom. Constr. 2007, 16, 255–261. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, S.; Shin, D.; Son, Y.; Han, C. Development of an inspection system for cracks in a concrete tunnel lining. Can. J. Civ. Eng. 2007, 34, 966–975. [Google Scholar] [CrossRef]
- Lindley, D. Kendall’s advanced theory of statistics, volume 2B, Bayesian inference, 2nd edition. J. R. Stat. Soc. Ser. A Stat. Soc. 2005, 168, 259–260. [Google Scholar] [CrossRef]
- Schmugge, S.; Nguyen, N.; Thao, C.; Lindberg, J.; Grizzi, R.; Joffe, C.; Shin, M. Automatic detection of cracks during power plant inspection. In Proceedings of the 3rd International Conference on Applied Robotics for the Power Industry, Iguassu, Brazil, 14–16 October 2014; pp. 1–5. [Google Scholar]
- Hutchinson, T.; Chen, Z. Improved image analysis for evaluating concrete damage. J. Comput. Civ. Eng. 2006, 20, 210–216. [Google Scholar] [CrossRef]
- Valenca, J.; Goncalves, L.; Julio, E. Damage assessment on concrete surfaces using multi-spectral image analysis. Constr. Build. Mater. 2013, 40, 971–981. [Google Scholar] [CrossRef]
- Oliveira, H.; Correia, P.L. Supervised strategies for cracks detection in images of road pavement flexible surfaces. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Oliveira, H.; Correia, P. Automatic Crack Pavement Detection Using a Bayesian Stochastic Pattern Recognition System. In Proceedings of the RECPAD2007, Lisbon, Portugal, 31 Ocotber 2007. [Google Scholar]
- Freund, Y.; Schapire, R.; Abe, N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 1612. [Google Scholar]
- Cord, A.; Chambon, S. Automatic Road Defect Detection by Textural Pattern Recognition Based on AdaBoost. Comput. Aided Civ. Infrastruct. Eng. 2012, 27, 244–259. [Google Scholar] [CrossRef]
- Prasanna, P.; Dana, K.; Gucunski, N.; Basily, B.; La, H.; Lim, R.; Parvardeh, H. Automated Crack Detection on Concrete Bridges. IEEE Trans. Autom. Sci. Eng. 2016, 13, 591–599. [Google Scholar] [CrossRef]
- Wagner, C.; Villmann, B.; Slowik, V.; Mechtcherine, V. Water permeability of cracked strain-hardening cement-based composites. Cem. Concr. Compos. 2017, 82, 234–241. [Google Scholar] [CrossRef]
- Wagner, C.; Dollase, A.; Slowik, V. Evaluation of crack patterns in SHCC with respect to water permeability and capillary suction. In Proceedings of the 3rd International Conference on Concrete Repair, Rehabilitation and Retrofitting (ICCRRR), Cape Town, South Africa, 3–5 September 2012; pp. 972–977. [Google Scholar]
- Fic, S.; Szelag, M. Analysis of the development of cluster cracks caused by elevated temperatures in cement paste. Constr. Build. Mater. 2015, 83, 223–229. [Google Scholar] [CrossRef]
- Mobasher, B.; Stang, H.; Shah, S. Microcracking in fiber reinforced-concrete. Cem. Concr. Res. 1990, 20, 665–676. [Google Scholar] [CrossRef]
- Magalhaes, M.; Toledo, R.; Fairbairn, E. Thermal stability of PVA fiber strain hardening cement-based composites. Constr. Build. Mater. 2015, 94, 437–447. [Google Scholar] [CrossRef]
- Szelag, M.; Szewczak, A. Evaluation of Dependencies between Physico-Mechanical Properties and the Thermal Cracks’ Geometry of Cement Pastes Modified with Metakaolinite Using the LSM Method. 3rd World Multidisciplinary Civil Engineering, Architecture, Urban Planning Symposium (WMCAUS 2018). IOP Conf. Ser. Mater. Sci. Eng. 2019, 471. [Google Scholar] [CrossRef]
- Szeląg, M.; Szewczak, A. Dependencies between Cracking Patterns and the Physico-Mechanical Properties of Microsilica Modified Cement Matrix. In Proceedings of IOP Conference Series: Mater. Sci. Eng. 2019, 484, 012015. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH freeman: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; WH freeman: New York, NY, USA, 1977; Volume 706. [Google Scholar]
- Farhidzadeh, A.; Dehghan-Niri, E.; Moustafa, A.; Salamone, S.; Whittaker, A. Damage Assessment of Reinforced Concrete Structures Using Fractal Analysis of Residual Crack Patterns. Exp. Mech. 2013, 53, 1607–1619. [Google Scholar] [CrossRef]
- Wang, K.; Shah, S.; Phuaksuk, P. Plastic shrinkage cracking in concrete materials–Influence of fly ash and fibers. Mater. J. 2001, 98, 458–464. [Google Scholar]
- Bakhshi, M.; Mobasher, B. Experimental observations of early-age drying of Portland cement paste under low-pressure conditions. Cem. Concr. Compos. 2011, 33, 474–484. [Google Scholar] [CrossRef]
- Lepech, M.; Li, V. Water permeability of engineered cementitious composites. Cem. Concr. Compos. 2009, 31, 744–753. [Google Scholar] [CrossRef]
- Aldea, C.; Ghandehari, M.; Shah, S.; Karr, A. Combined effect of cracking and water permeability of concrete. In Proceedings of the 14th Engineering Mechanics Conference, Austin, TX, USA, 21–24 May 2000; pp. 21–24. [Google Scholar]
- Bazant, Z.; Raftshol, W. Effect of cracking in drying and shrinkage specimens. Cem. Concr. Res. 1982, 12, 209–226. [Google Scholar] [CrossRef]
- Bazant, Z.; Sener, S.; Kim, J. Effect of cracking on drying permeability and diffusivity of concrete. Mater. J. 1987, 84, 351–357. [Google Scholar]
- Torrijos, M.; Giaccio, G.; Zerbino, R. Internal cracking and transport properties in damaged concretes. Mater. Struct. 2010, 43, 109–121. [Google Scholar] [CrossRef]
- Lura, P.; Jensen, O.; Weiss, J. Cracking in cement paste induced by autogenous shrinkage. Mater. Struct. 2009, 42, 1089–1099. [Google Scholar] [CrossRef]
- Xuan, D.; Molenaar, A.; Houben, L. Shrinkage cracking of cement treated demolition waste as a road base. Mater. Struct. 2016, 49, 631–640. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Farhidzadeh, A.; Salamone, S. Multifractal analysis of crack patterns in reinforced concrete shear walls. Struct. Health Monit. Int. J. 2016, 15, 81–92. [Google Scholar] [CrossRef]
- Zhuang, N.; Dong, H.; Zhou, Y.; Chen, D. Cracking behavior of reinforced concrete piles externally bonded with carbon fiber reinforced polymer in a marine environment. Constr. Build. Mater. 2018, 190, 1154–1162. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Farhidzadeh, A.; Salamone, S.; Lynch, J.; Wang, K.; Sohn, H. Multifractal analysis of two-dimensional images for damage assessment of reinforced concrete structures. Sens. Smart Struct. Techn. Civil Mech. Aeros. Syst. 2015, 9435. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Athanasiou, A.; Hrynyk, T.; Bayrak, O.; Salamone, S. Fractal and Multifractal Analysis of Crack Patterns in Prestressed Concrete Girders. J. Bridge Eng. 2019, 24. [Google Scholar] [CrossRef]
- Fooladi, A.; Banan, M. Multifractal Analysis of Crack Propagation in Concrete Specimens Considering the Influence of the Aggregates’ Grading. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2016, 40, 97–108. [Google Scholar] [CrossRef]
- Kim, K.; Yun, T.; Park, K. Evaluation of pore structures and cracking in cement paste exposed to elevated temperatures by X-ray computed tomography. Cem. Concr. Res. 2013, 50, 34–40. [Google Scholar] [CrossRef]



| Type of Cracks | Reasons | Occurence Time | Typical Location |
|---|---|---|---|
| plastic settlement | excessive secretion of cement milk—bleeding; rapid initial drying | 10 min–3 h | sections of considerable depth; top of column, trough and coffered panels |
| plastic shrinkage | rapid initial drying; reinforcement at the surface; low speed of drained water discharge | 30 min–6 h | surfaces; slabs |
| early thermal contraction | excessive heat generation; excessive temperature gradients; rapid cooling | 1 day–(2–3 weeks) | thick walls; thick plates |
| prolonged shrinkage during drying | ineffective connections; excessive contraction; inadequate care | several weeks or months | thin panels; walls |
| map-cracking | excessive rubbing; rich mix; inadequate care | 1–7 days | walls; plates |
| corrosion of the reinforcement | insufficient cover; poor concrete quality | over 2 years | columns; beams |
| alkaline reactions in the aggregate | reactive aggregate; cement with high alkali content | over 5 years | moistened elements |
| ankle cracks | aggregates damaged by frost | over 10 years | free ends of plates |
| Digital Image Processing Technique | References | Accuracy Level (Only Where the Authors Have Given It) |
|---|---|---|
| Global thresholding | [54,55,56,84] | ≤90% [54] |
| Locally adaptive thresholding | [55,56,57,58,59,60] | 90–95% [58] |
| Otsu thresholding | [61,62,63,64,73] | ≥95% [63] |
| Edge detection | [54,63,71] | ≤90% [54]; 90–95% [71]; ≥95% [63] |
| Probabilistic approach | [55] | - |
| Median filtering | [55] | - |
| Sobel’s filtering | [62] | - |
| Morphological approach | [57,58,59,77,81] | 90–95% [58]; 90–95% [77] |
| Genetic algorithms | [65,67,68,69] | ≤90% [67] |
| Fuzzy logic based techniques | [70,71,72,73] | 90–95% [71] |
| Artificial neural networks | [71,75,76,77,78,79,80,81] | ≤90% [76,78]; 90–95% [71,77]; ≥95% [75,79,80] |
| Wavelet approach | [76] | ≤90% [76] |
| Dijkstra algorithm | [83,84,85,86] | - |
| The Bayesian classifier | [88,89,90,91,92] | 90–95% [90] |
| The AdaBoost classifier | [94,95] | ≤90% [95] |
| Statistical methods | [89] | - |
| Parameter | References |
|---|---|
| Opening width of the cracks | [9,12,13,14,15,16,96,97,100,101,102,105,106,107,108,109,110,111,112,113,114,115,116] |
| Length and orientation of the cracks | [8,12,13,14,15,16,98,99,107,109,112,113] |
| The crack density | [8,9,13,96,99,100,110,111,112,114] |
| The crack area | [12,13,14,15,16,98,101,102,106,107,109] |
| The fractal dimension | [105,115,116,117,118,119] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, M. Evaluation of Cracking Patterns in Cement Composites—From Basics to Advances: A Review. Materials 2020, 13, 2490. https://doi.org/10.3390/ma13112490
Szeląg M. Evaluation of Cracking Patterns in Cement Composites—From Basics to Advances: A Review. Materials. 2020; 13(11):2490. https://doi.org/10.3390/ma13112490
Chicago/Turabian StyleSzeląg, Maciej. 2020. "Evaluation of Cracking Patterns in Cement Composites—From Basics to Advances: A Review" Materials 13, no. 11: 2490. https://doi.org/10.3390/ma13112490
APA StyleSzeląg, M. (2020). Evaluation of Cracking Patterns in Cement Composites—From Basics to Advances: A Review. Materials, 13(11), 2490. https://doi.org/10.3390/ma13112490





