Study of Carbon Black Types in SBR Rubber: Mechanical and Vibration Damping Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Obtaining the Mixtures and Sample Preparation
2.3. Methods
2.3.1. Curing Characterization
2.3.2. Quasistatic Mechanical Properties
2.3.3. Dynamical Mechanical Properties
2.3.4. The Hysteresis Characteristics
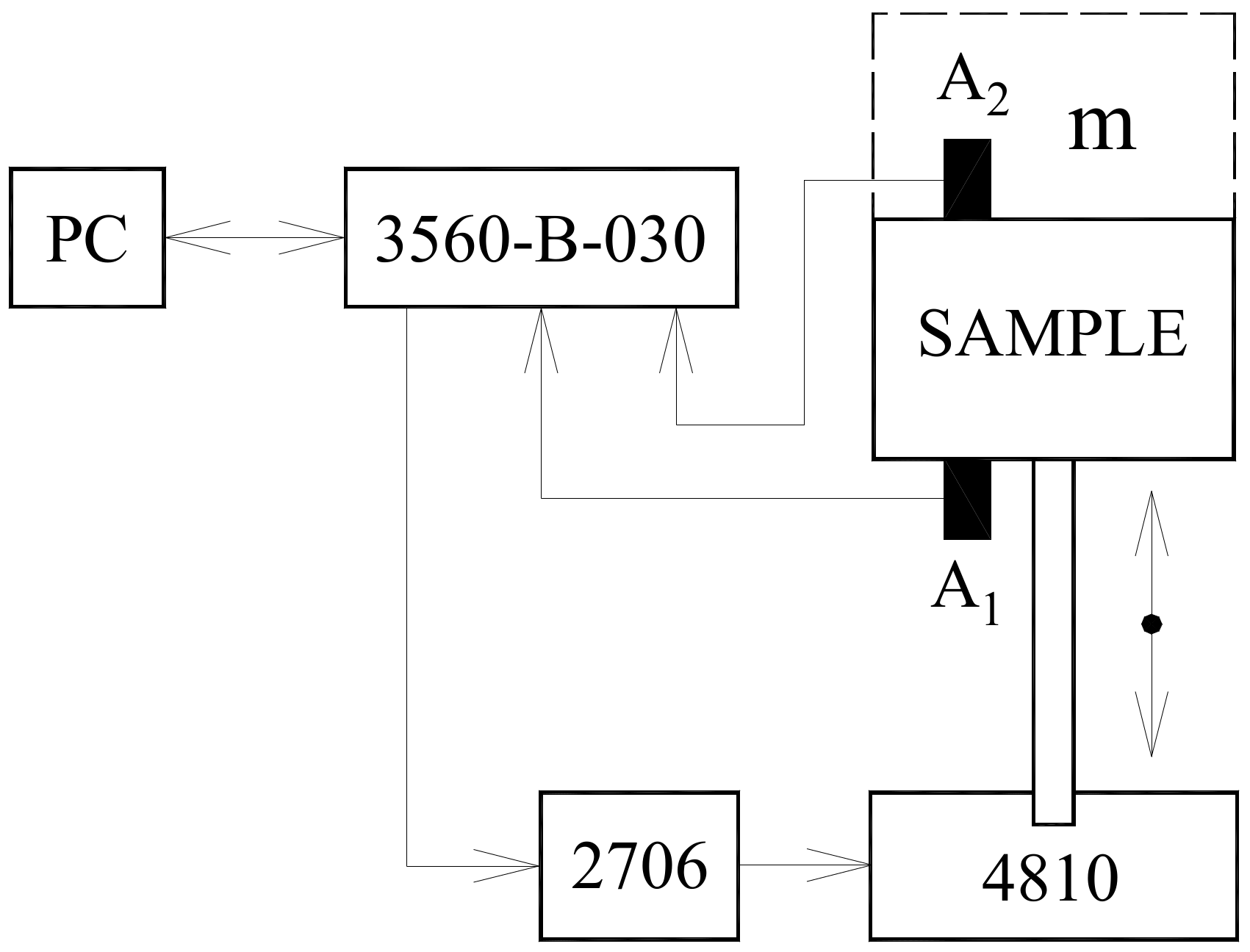
2.3.5. Mechanical Vibration Damping Measurement
3. Results and Discussion
3.1. Curing Characteristics
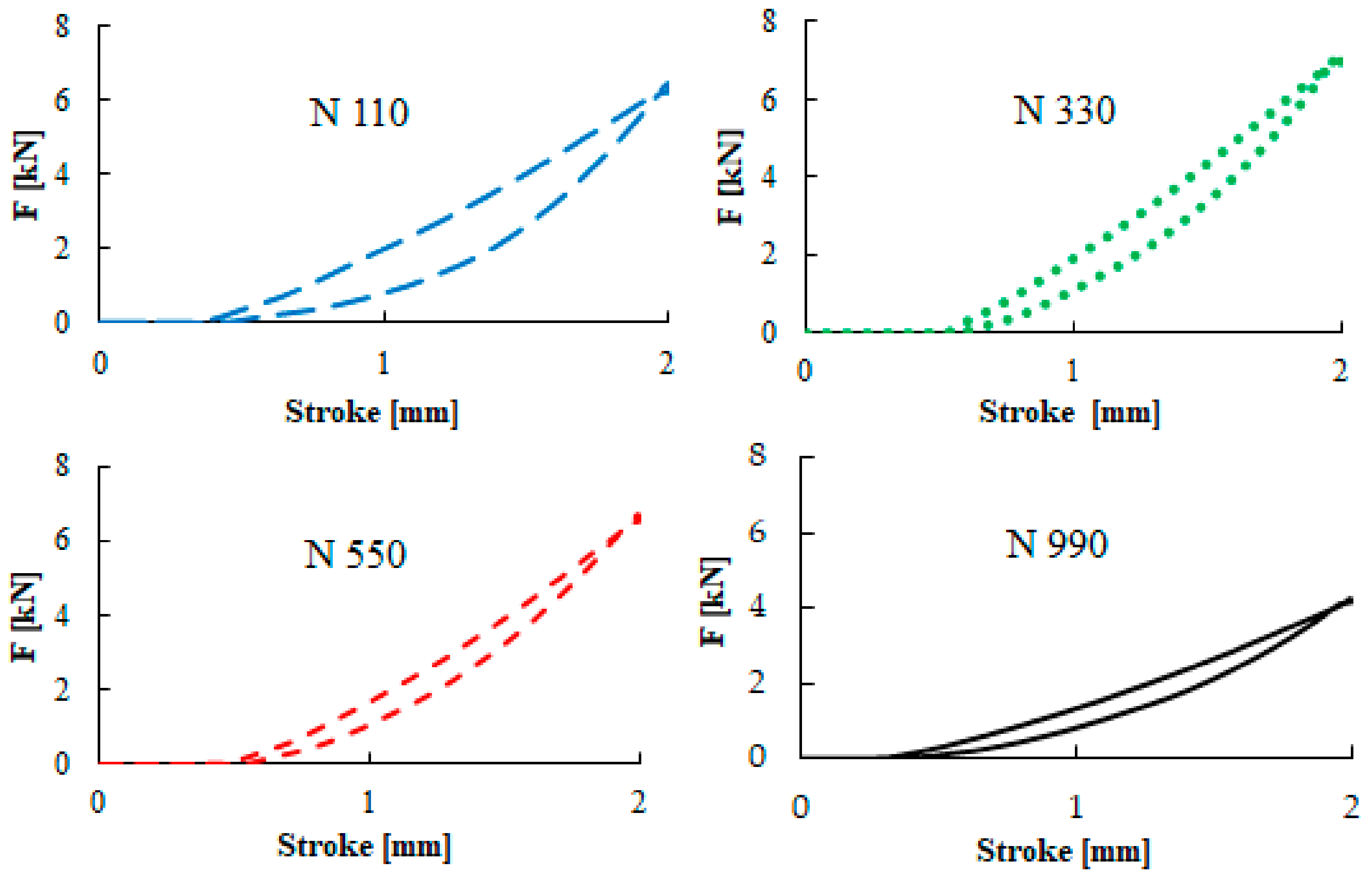
3.2. Quasi-Static Test Results
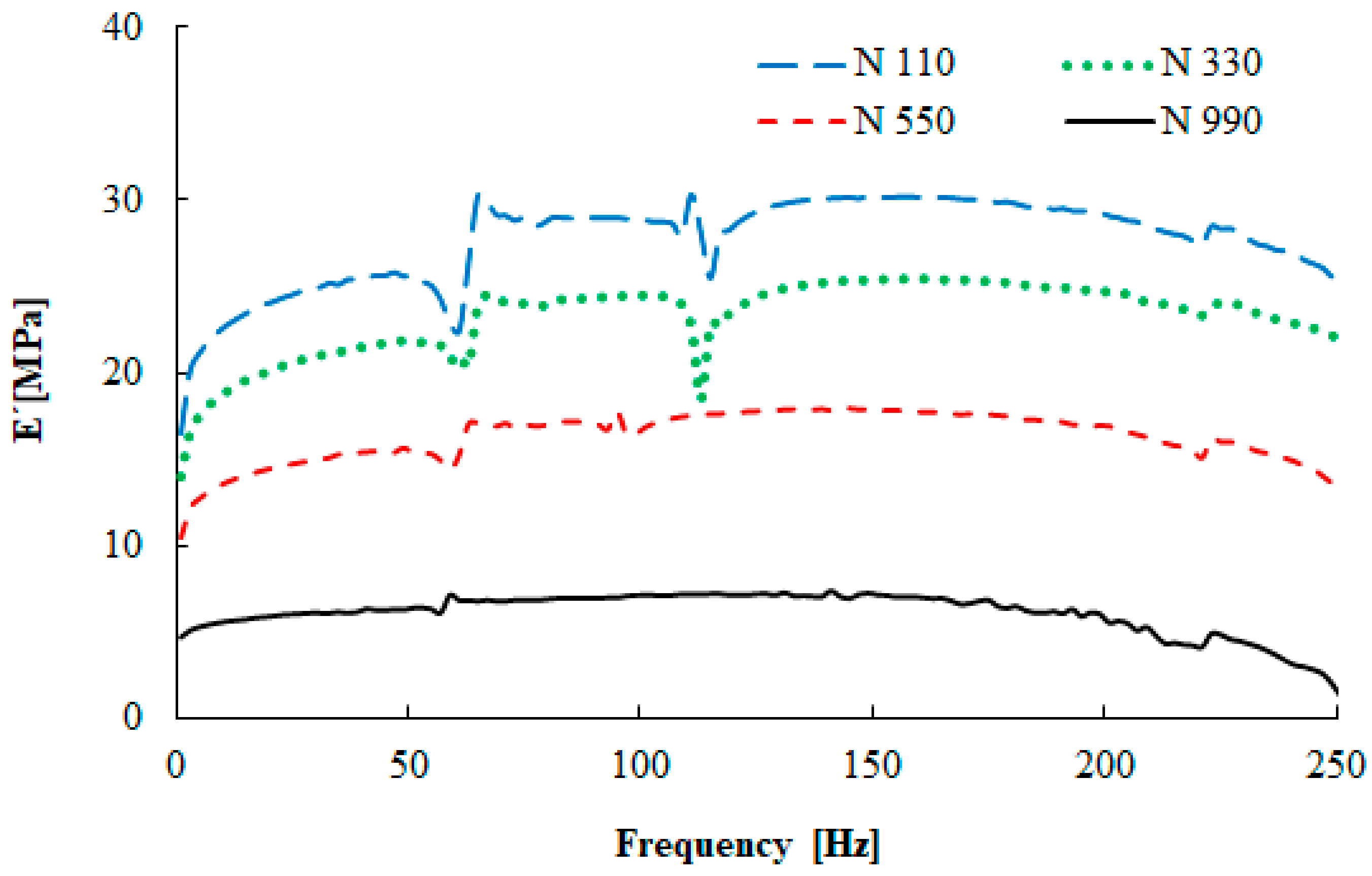
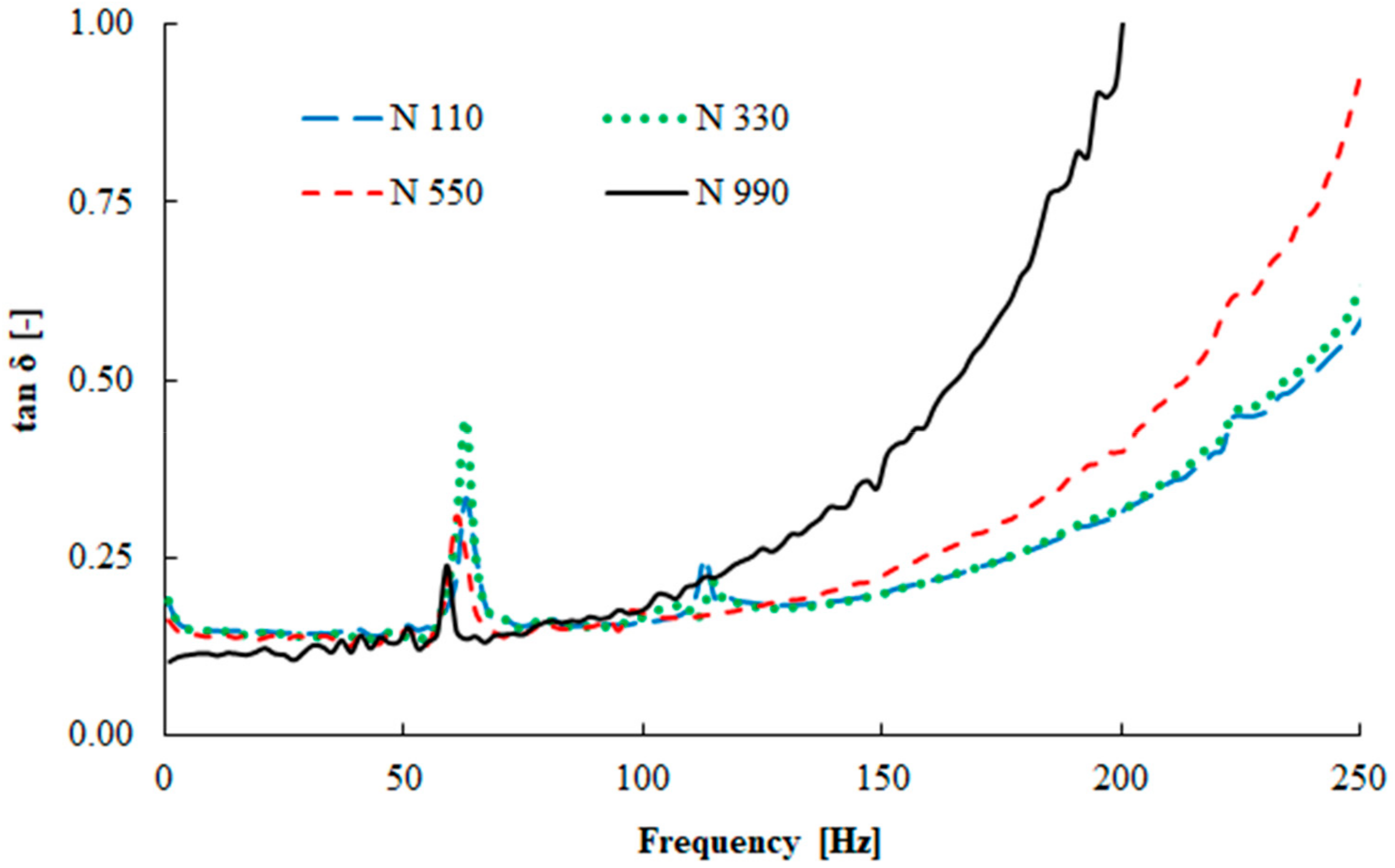
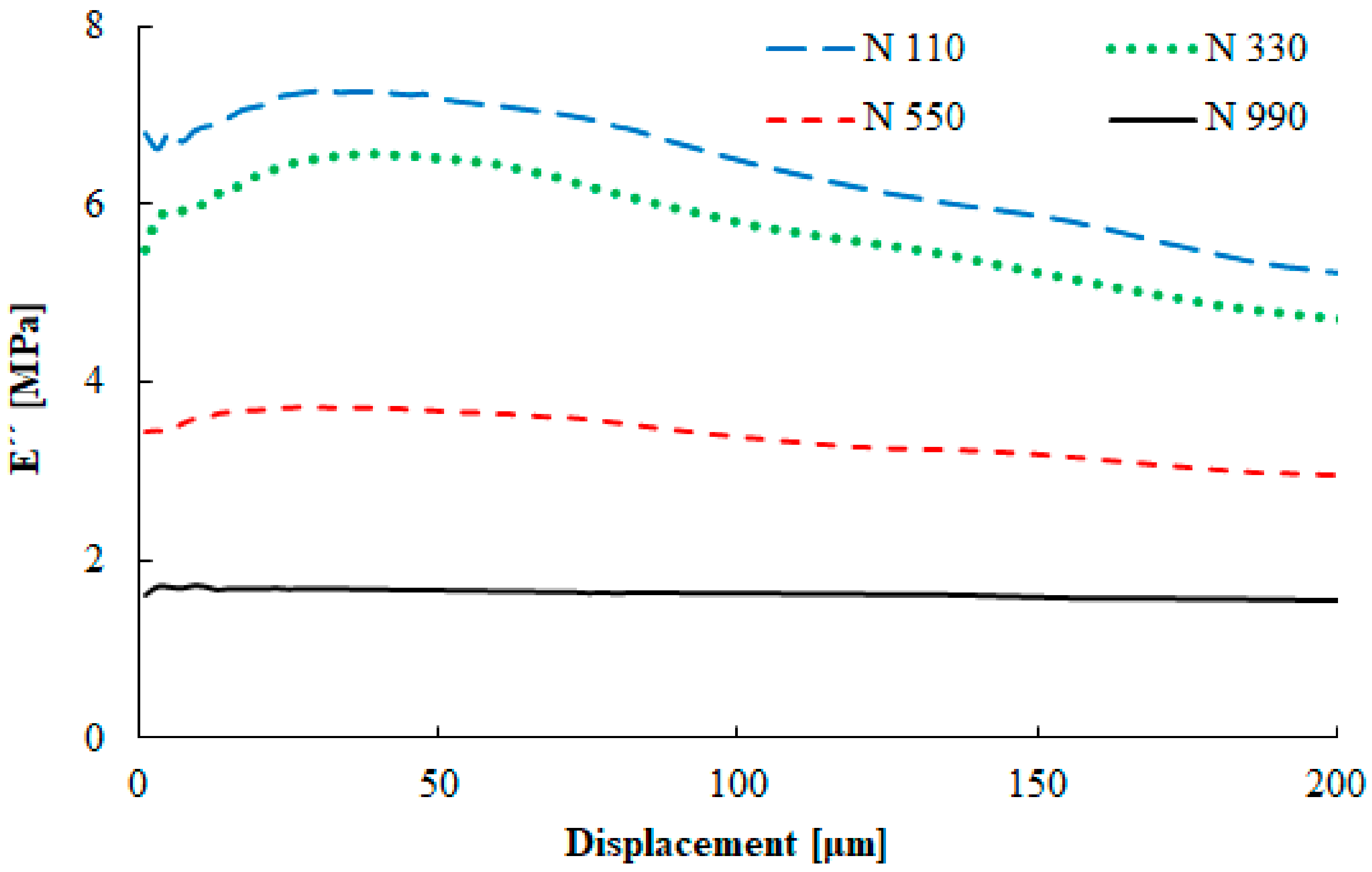
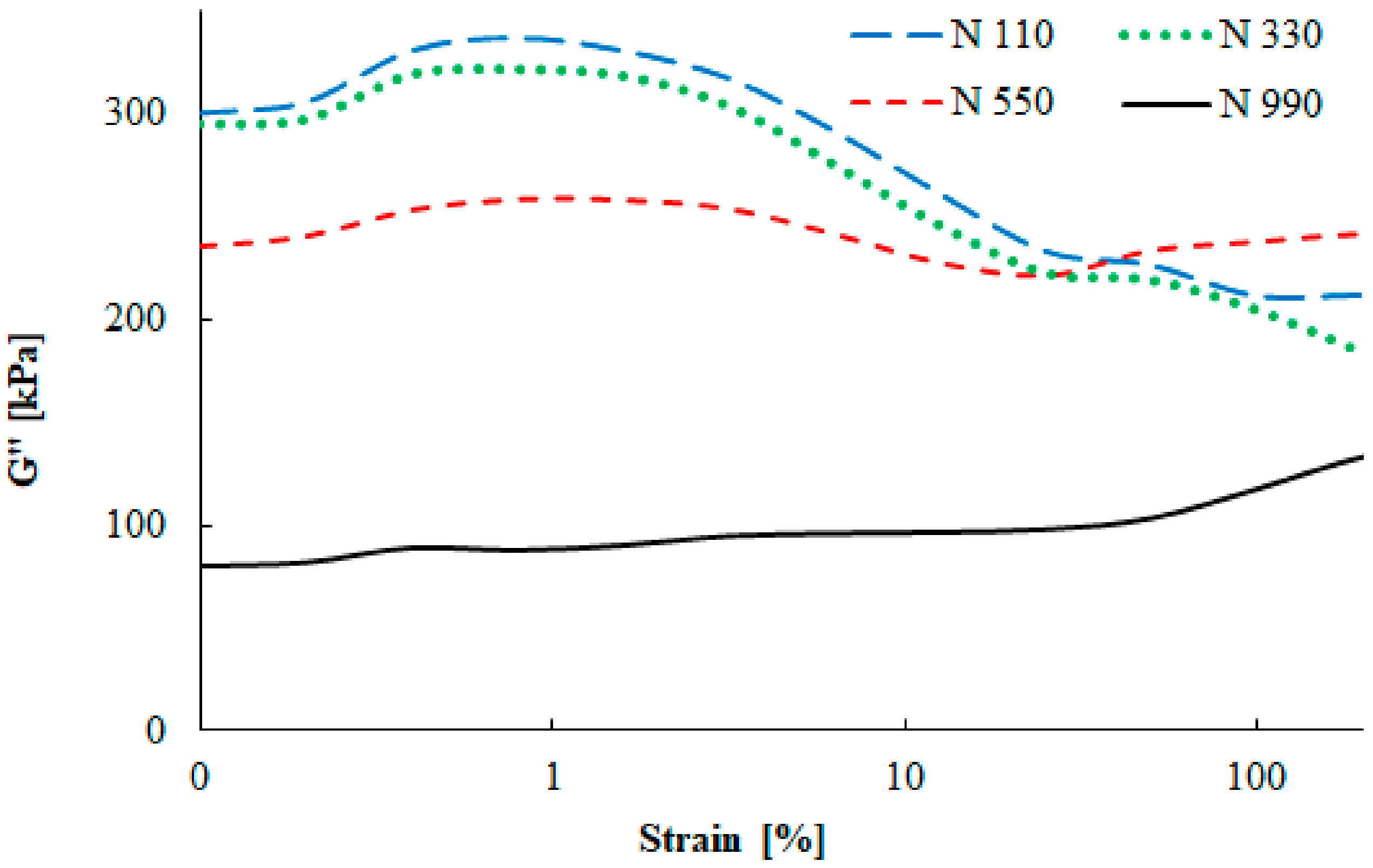
3.3. Dynamical Mechanical Properties
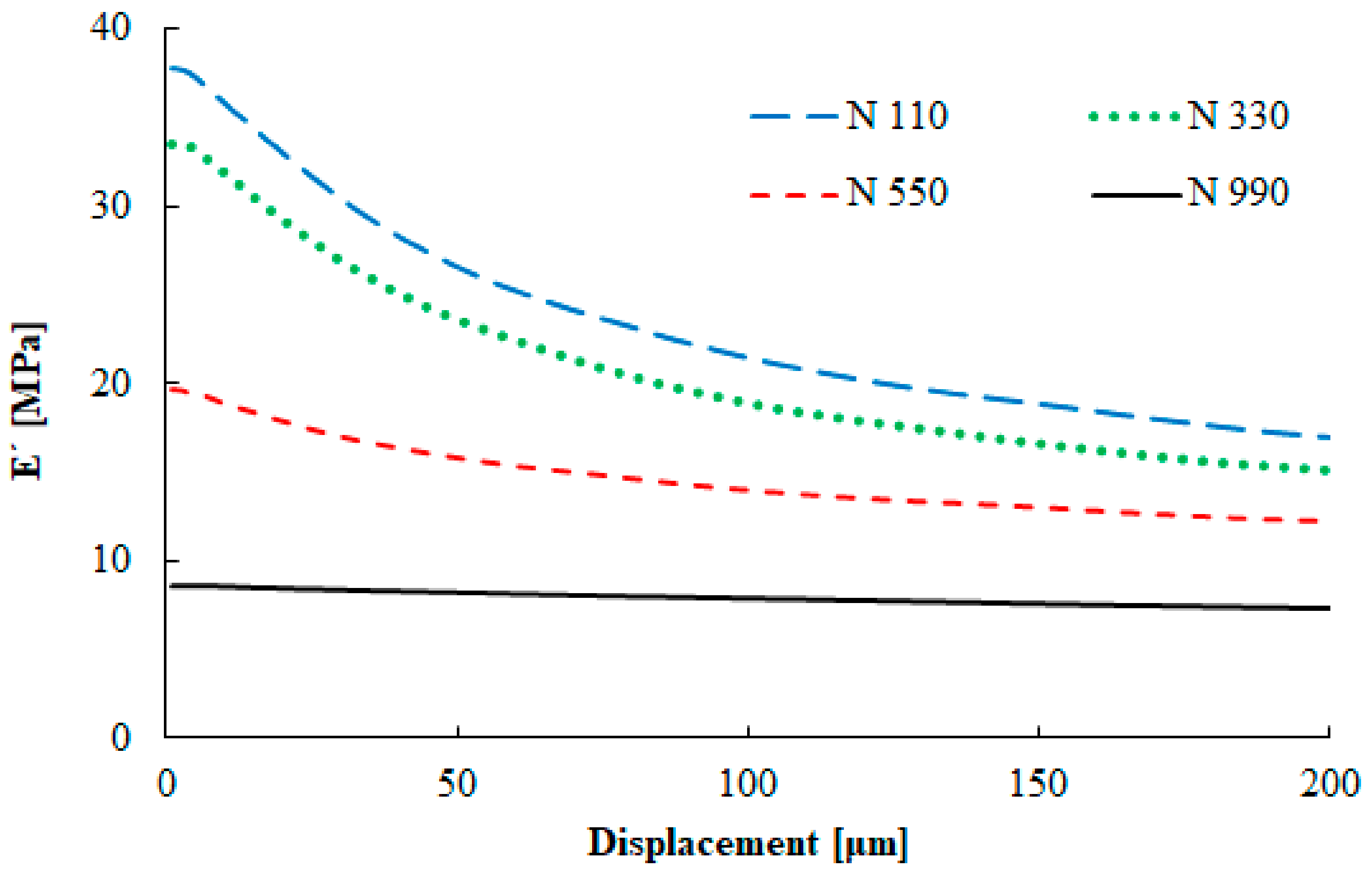
3.4. The Hysteresis Characteristics
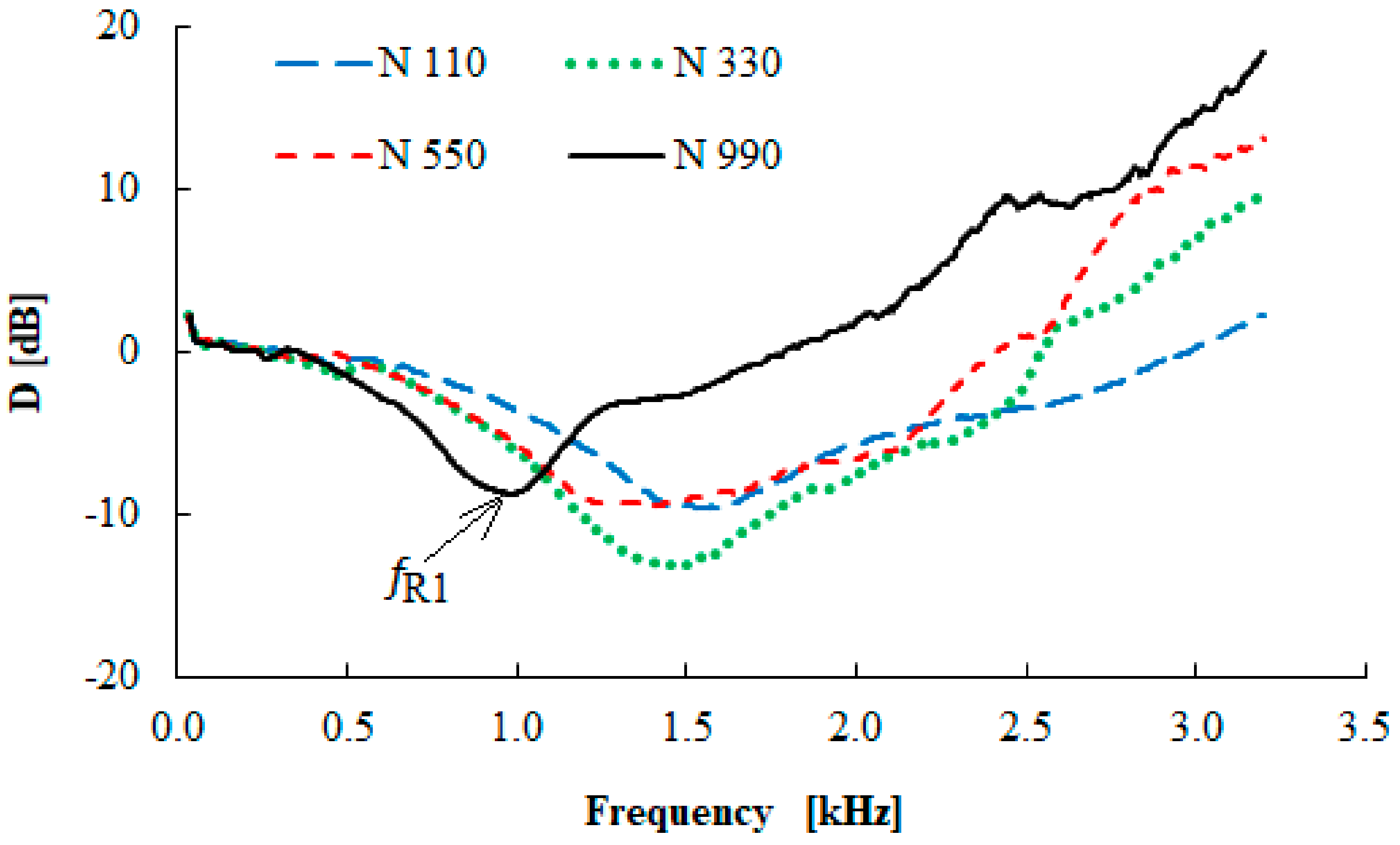
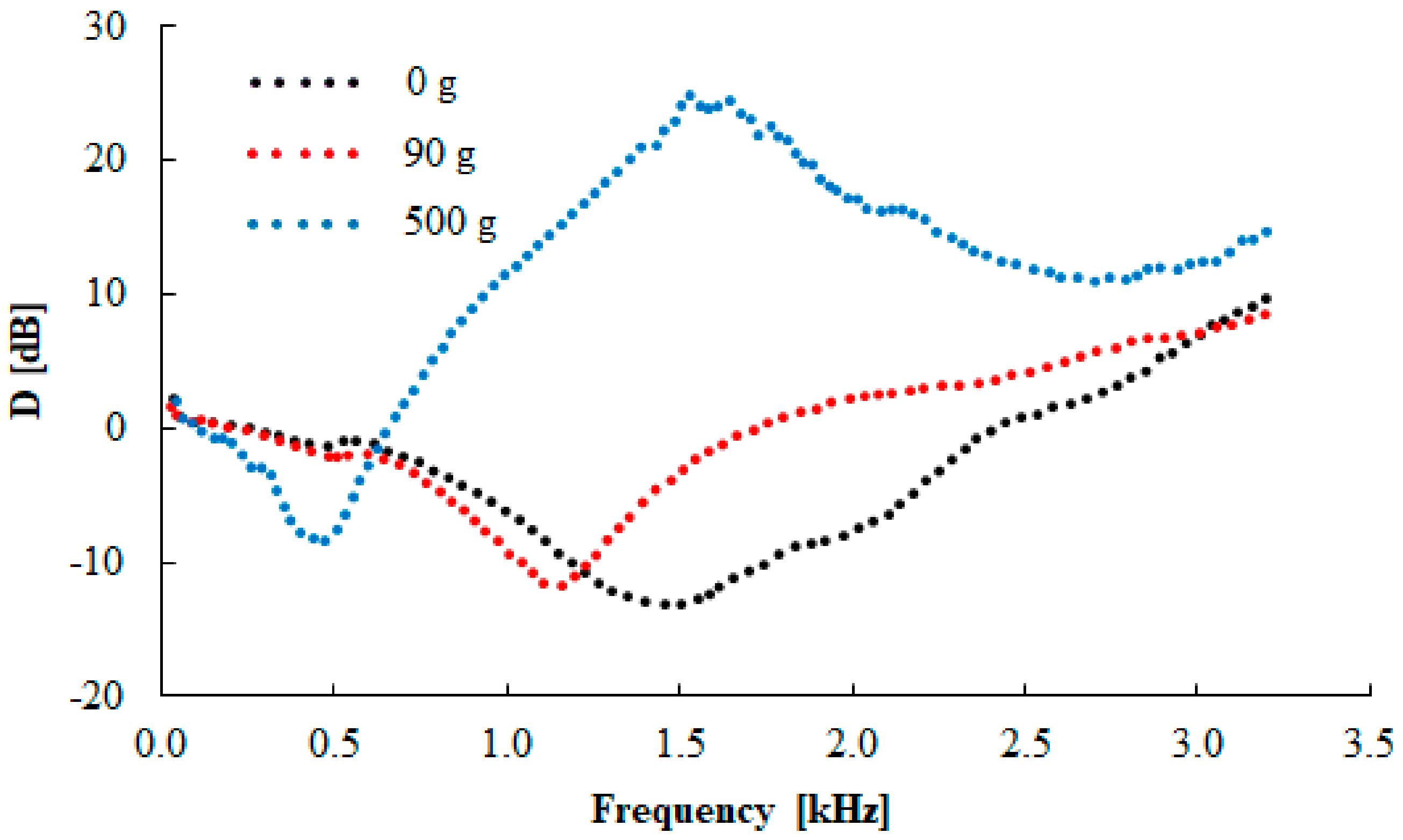
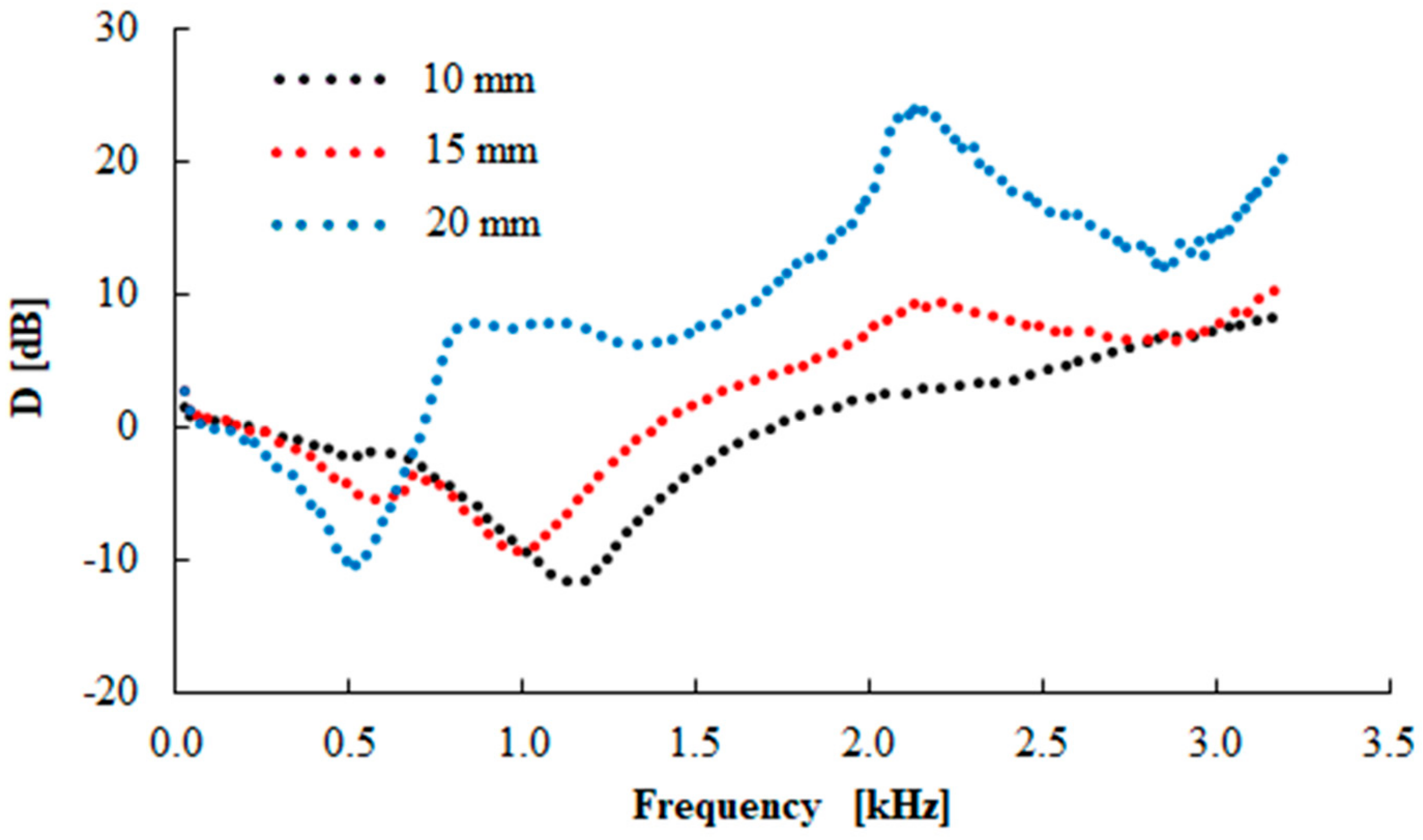
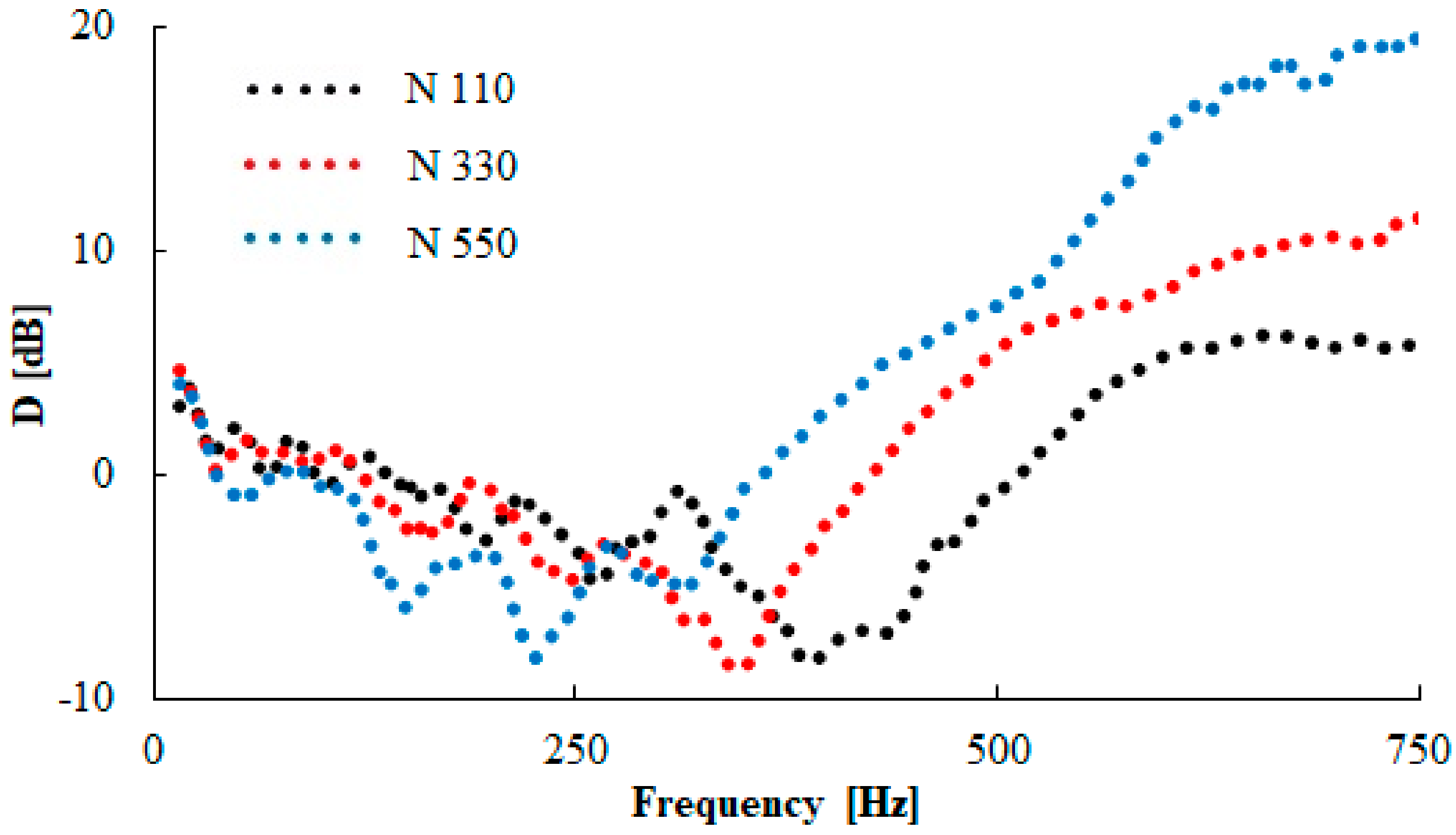
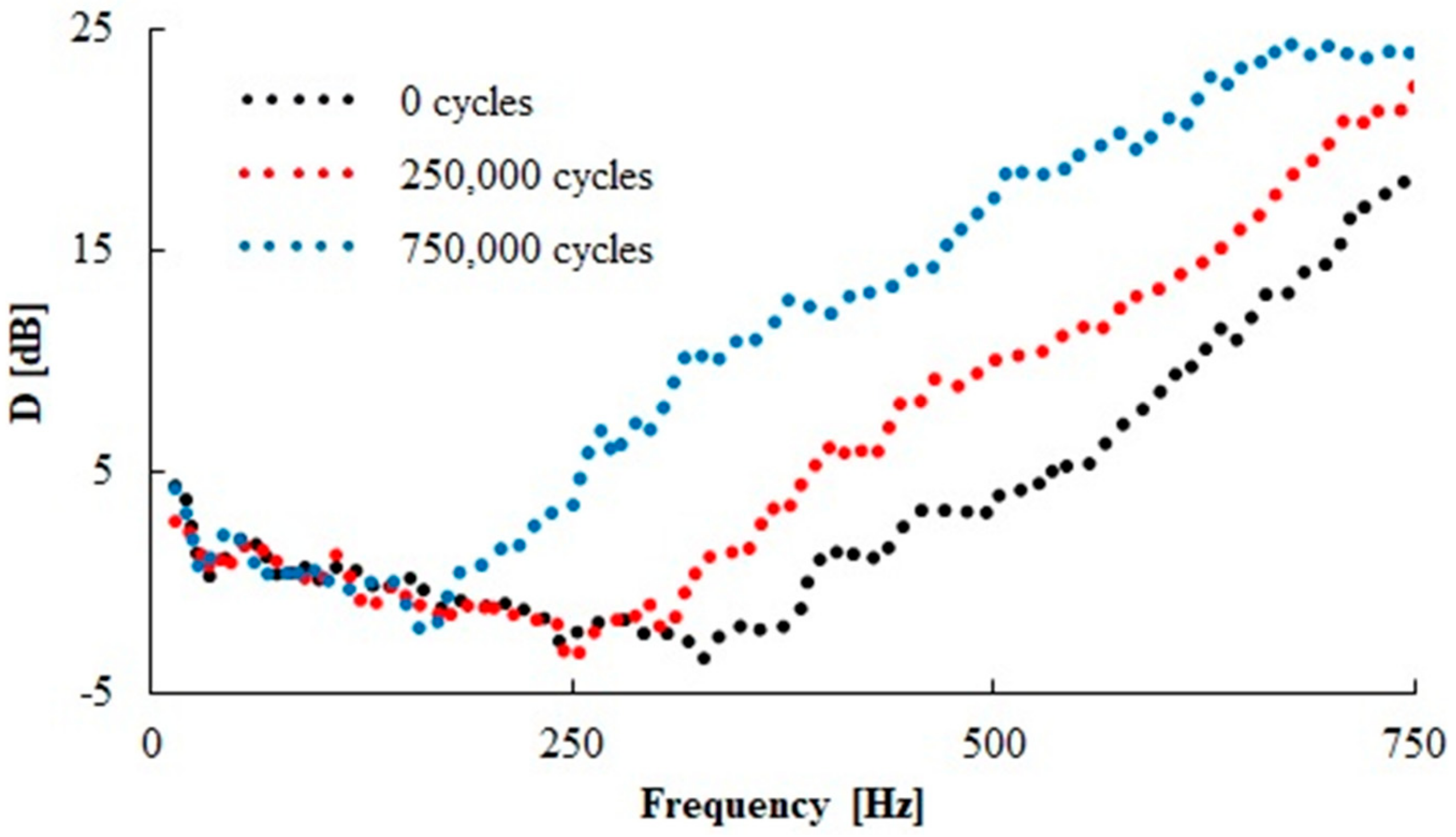
3.5. Vibration Damping Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stephen, N. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef]
- Lapcik, L.; Cetkovsky, V.; Lapcikova, B.; Vasut, S. Materials for noise and vibration attenuation. Chem. Listy 2000, 94, 117–122. [Google Scholar]
- Sakakibara, S. Properties of vibration with fractional derivative damping of order 1/2. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1997, 40, 393–399. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, C.M. Application of viscoelastic damping for passive vibration control in automotive roof using equivalent properties. Int. J. Automot. Technol. 2005, 6, 607–613. [Google Scholar]
- Elias, S. Seismic energy assessment of buildings with tuned vibration absorbers. Shock. Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Qin, C.; Zhao, D.; Bai, X.; Zhang, X.; Zhang, B.; Jin, Z.; Niu, H. Vibration damping properties of gradient polyurethane/vinyl ester resin interpenetrating polymer network. Mater. Chem. Phys. 2006, 97, 517–524. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, B.G.; Shin, D.Y. Vibration and impact noise damping properties of wood/polymer composites. Mater. Sci. Forum 2005, 486, 358–361. [Google Scholar] [CrossRef]
- Goto, A.; Maekawa, Z.; Miyake, K. Analysis of vibration damping properties of hybrid composite with flexible matrix resin. J. Soc. Mater. Sci. Jpn. 1996, 45, 160–165. [Google Scholar] [CrossRef]
- Perez, J.C.L.; Kwok, C.Y.; Senetakis, K. Effect of rubber content on the unstable behaviour of sand–rubber mixtures under static loading: a micro-mechanical study. Géotechnique 2017, 68, 1–14. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y. Enhanced mechanical and thermal properties of SBR composites by introducing graphene oxide nanosheets decorated with silica particles. Compos. Part A Appl. Sci. Manuf. 2017, 102, 236–242. [Google Scholar] [CrossRef]
- Berki, P.; Göbl, R.; Karger-Kocsis, J. Structure and properties of styrene-butadiene rubber (SBR) with pyrolytic and industrial carbon black. Polym. Test. 2017, 61, 404–415. [Google Scholar] [CrossRef]
- Xu, H.; Han, J.; Fang, L.; Shen, F.; Wu, C. Effect of grafted carbon black on properties of vulcanized natural rubber. Polym. Bull. 2007, 58, 951–962. [Google Scholar] [CrossRef]
- Nayak, S.; Chaki, T.K. Effect of hybrid fillers on the nonlinear viscoelasticity of rubber composites and nanocomposites. In Non-Linear Viscoelasticity of Rubber Composites and Nanocomposites; Springer International Publishing: Cham, Switzerland, 2014; pp. 135–160. [Google Scholar]
- Omnès, B.; Thuillier, S.; Pilvin, P.; Grohens, Y.; Gillet, S. Effective properties of carbon black filled natural rubber: Experiments and modeling. Compos. A Appl. Sci. Manuf. 2008, 39, 1141–1149. [Google Scholar] [CrossRef]
- Pan, X.-D.; Kelley, E.D. Enhanced apparent payne effect in a gum vulcanizate at low temperature approaching glass transition. Polym. Eng. Sci. 2003, 43, 1512–1521. [Google Scholar] [CrossRef]
- Mandal, U.K.; Tripathy, D.K.; De, S.K. Effect of carbon-black fillers on dynamic-mechanical properties of ionic elastomer based on carboxylated nitrile rubber. Plast. Rubber Compos. Process. Appl. 1995, 24, 19–25. [Google Scholar]
- Lénárt, J. Contactless vibration measurement using linear CCD sensor. In Proceedings of the 13th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 28–31 May 2012; pp. 426–429. [Google Scholar]
- Cao, Y.; Rong, X.L.; Shao, S.J.; He, K.P. Present situation and prospects of vibration sensors. In Proceedings of the 2012 International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Zhangjiajie, Hunan, China, 5–6 March 2012; pp. 515–518. [Google Scholar]
- Volpe, R.; Ivlev, R. A survey and experimental evaluation of proximity sensors for space robotics. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3466–3473. [Google Scholar]
- Chaurasiya, H. Recent trends of measurement and development of vibration sensors. Int. J. Com. Sci 2012, 9, 1–6. [Google Scholar]
- Botelho, E.C.; Campos, A.N.; de Barros, E.; Pardini, L.C.; Rezende, M.C. Damping behaviour of continuous fiber/metal composite materials by the free vibration method. Compos. B Eng. 2005, 37, 255–263. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2011; Chapter 1. [Google Scholar]
- Lapcik, L.; Vasina, M.; Lapcikova, B.; Valenta, T. Study of bread staling by means of vibro-acoustic, tensile and thermal analysis techniques. J. Food Eng. 2016, 178, 31–38. [Google Scholar] [CrossRef]
- B&K Sound and Vibration Measurenet. Available online: https://www.bksv.com/en/products/transducers/vibration/Vibration-transducers/accelerometers/4393 (accessed on 12 May 2020).
- Litvinov, V.M.; Steeman, P.A.M. EPDM−carbon black interactions and the reinforcement mechanisms, as studied by low-resolution1H NMR. Macromolecules 1999, 32, 8476–8490. [Google Scholar] [CrossRef]
- Heinrich, G.; Vilgis, T.A. Contribution of entanglements to the mechanical properties of carbon black-filled polymer networks. Macromolecules 1993, 26, 1109–1119. [Google Scholar] [CrossRef]
- Li, Z.H. Effects of carbon blacks with various structures on vulcanization and reinforcement of filled ethylene-propylene-diene rubber. Express Polym. Lett. 2008, 2, 695–704. [Google Scholar] [CrossRef]
- Li, Q.; Ma, Y.; Wu, C.; Qian, S. Effect of carbon black nature on vulcanization and mechanical properties of rubber. J. Macromol. Sci. B 2008, 47, 837–846. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Chen, S. Effect of carbon blacks with various structures on electrical properties of filled ethylene-propylene-diene rubber. J. Electrost. 2009, 67, 73–75. [Google Scholar] [CrossRef]
- Edwards, D.C. Polymer-filler interactions in rubber reinforcement. J. Mater. Sci. 1990, 25, 4175–4185. [Google Scholar] [CrossRef]
- Lion, A.; Kardelky, C. The payne effect in finite viscoelasticity. Int. J. Plast. 2004, 20, 1313–1345. [Google Scholar] [CrossRef]
- Markovic, G.; Marinovic-Cincovic, M.; Jovanovic, V.; Samarzija-Jovanovic, S.; Budinski-Simendic, J. Modeling of nonlinear viscoelastic behavior of filled rubbers. In Non-Linear Viscoelasticity of Rubber Composites and Nanocomposites; Springer International Publishing: Cham, Switzerland, 2014; pp. 193–271. [Google Scholar]
- Drozdov, A.; Dorfmann, A. The payne effect for particle-reinforced elastomers. Polym. Eng. Sci. 2002, 42, 591–604. [Google Scholar] [CrossRef]
- Wang, J.; Hamed, G.R.; Umetsu, K.; Roland, C. The payne effect in double network elastomers. Rubber Chem. Technol. 2005, 78, 76–83. [Google Scholar] [CrossRef]
- Bezerra, F.D.O.; Nunes, R.C.R.; Gomes, A.S.; Oliveira, M.G.; Ito, E.N. Payne effect in NBR nanocomposites with organofilic montmorillonite. Polimeros 2013, 23, 223–228. [Google Scholar]
- Fukahori, Y. New progress in the theory and model of carbon black reinforcement of elastomers. J. Appl. Polym. Sci. 2004, 95, 60–67. [Google Scholar] [CrossRef]
- Júnior, J.H.A.; Júnior, H.L.O.; Amico, S.C.; Amado, F.D.R. Study of hybrid intralaminate curaua/glass composites. Mater. Des. 2012, 42, 111–117. [Google Scholar] [CrossRef]
- Rajoria, H.; Jalili, N. Passive vibration damping enhancement using carbon nanotube-epoxy reinforced composites. Compos. Sci. Technol. 2005, 65, 2079–2093. [Google Scholar] [CrossRef]




| Ingredients | Loading [phr] |
|---|---|
| SBR | 100 |
| Carbon black | 50 |
| ZnO | 3 |
| Stearic acid | 1 |
| TBBS | 1 |
| Sulfur | 1.75 |
| Rubber Type | ML [N·m] | MH [N·m] | ΔM [N·m] | ts1 [min] | t90 [min] |
|---|---|---|---|---|---|
| N 110 | 0.27 | 1.71 | 1.44 | 2.6 | 10.5 |
| N 330 | 0.24 | 1.45 | 1.21 | 2.6 | 11.5 |
| N 550 | 0.23 | 1.51 | 1.28 | 3.0 | 12.8 |
| N 990 | 0.12 | 1.07 | 0.95 | 3.3 | 12.6 |
| Rubber Type | Shore A [Sh A] | Stress at Break [MPa] | Strain at Break [%] | 300% Modulus [MPa] | Resilience [%] |
|---|---|---|---|---|---|
| N 110 | 69 ± 1 | 23.0 ± 1.4 | 480 ± 36 | 13.0 ± 1.3 | 38 ± 1 |
| N 330 | 66 ± 1 | 23.9 ± 0.9 | 520 ± 23 | 12.7 ± 1.0 | 39 ± 1 |
| N 550 | 64 ± 1 | 19.8 ± 0.5 | 510 ± 25 | 11.9 ± 0.5 | 44 ± 1 |
| N 990 | 55 ± 1 | 11.9 ± 2.7 | 640 ± 75 | 4.1 ± 0.4 | 51 ± 1 |
| Rubber Type | Thickness [mm] | Inertial Mass [g] | ||
|---|---|---|---|---|
| 0 | 90 | 500 | ||
| N 110 | 10 | 1520 ± 41 | 1146 ± 18 | 430 ± 15 |
| 15 | 1293 ± 29 | 1043 ± 18 | 419 ± 14 | |
| 20 | 1080 ± 15 | 928 ± 17 | 354 ± 12 | |
| N 330 | 10 | 1441 ± 32 | 1138 ± 19 | 412 ± 14 |
| 15 | 1242 ± 22 | 957 ± 16 | 402 ± 13 | |
| 20 | 881 ± 16 | 520 ± 15 | 320 ± 9 | |
| N 550 | 10 | 1404 ± 27 | 900 ± 18 | 379 ± 13 |
| 15 | 977 ± 18 | 737 ± 16 | 288 ± 10 | |
| 20 | 718 ± 16 | 456 ± 12 | 233 ± 8 | |
| N 990 | 10 | 968 ± 20 | 848 ± 16 | 298 ± 10 |
| 15 | 802 ± 19 | 635 ± 15 | 258 ± 9 | |
| 20 | 693 ± 15 | 310 ± 11 | 231 ± 7 | |
| Number of Cycles | Rubber Type | Inertial Mass [g] | ||
|---|---|---|---|---|
| 0 | 90 | 500 | ||
| 0 | N 110 | 1080 ± 15 | 928 ± 17 | 354 ± 12 |
| N 330 | 881 ± 16 | 520 ± 15 | 320 ± 9 | |
| N 550 | 718 ± 16 | 456 ± 12 | 233 ± 8 | |
| 100,000 | N 110 | 1029 ± 17 | 563 ± 14 | 328 ± 11 |
| N 330 | 534 ± 15 | 507 ± 13 | 301 ± 10 | |
| N 550 | 430 ± 13 | 378 ± 11 | 227 ± 9 | |
| 250,000 | N 110 | 482 ± 15 | 430 ± 12 | 245 ± 10 |
| N 330 | 457 ± 12 | 405 ± 11 | 241 ± 9 | |
| N 550 | 381 ± 10 | 356 ± 10 | 192 ± 8 | |
| 500,000 | N 110 | 434 ± 11 | 388 ± 10 | 237 ± 8 |
| N 330 | 399 ± 11 | 371 ± 11 | 231 ± 8 | |
| N 550 | 372 ± 10 | 237 ± 9 | 140 ± 6 | |
| 750,000 | N 110 | 404 ± 12 | 380 ± 11 | 208 ± 8 |
| N 330 | 374 ± 11 | 338 ± 10 | 158 ± 7 | |
| N 550 | 360 ± 11 | 214 ± 8 | 126 ± 5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pöschl, M.; Vašina, M.; Zádrapa, P.; Měřínská, D.; Žaludek, M. Study of Carbon Black Types in SBR Rubber: Mechanical and Vibration Damping Properties. Materials 2020, 13, 2394. https://doi.org/10.3390/ma13102394
Pöschl M, Vašina M, Zádrapa P, Měřínská D, Žaludek M. Study of Carbon Black Types in SBR Rubber: Mechanical and Vibration Damping Properties. Materials. 2020; 13(10):2394. https://doi.org/10.3390/ma13102394
Chicago/Turabian StylePöschl, Marek, Martin Vašina, Petr Zádrapa, Dagmar Měřínská, and Milan Žaludek. 2020. "Study of Carbon Black Types in SBR Rubber: Mechanical and Vibration Damping Properties" Materials 13, no. 10: 2394. https://doi.org/10.3390/ma13102394
APA StylePöschl, M., Vašina, M., Zádrapa, P., Měřínská, D., & Žaludek, M. (2020). Study of Carbon Black Types in SBR Rubber: Mechanical and Vibration Damping Properties. Materials, 13(10), 2394. https://doi.org/10.3390/ma13102394







