Characterization of γ′ Precipitates in Cast Ni-Based Superalloy and Their Behaviour at High-Homologous Temperatures Studied by TEM and in Situ XRD
Abstract
1. Introduction
2. Experimental Procedure
3. Results and Discussion
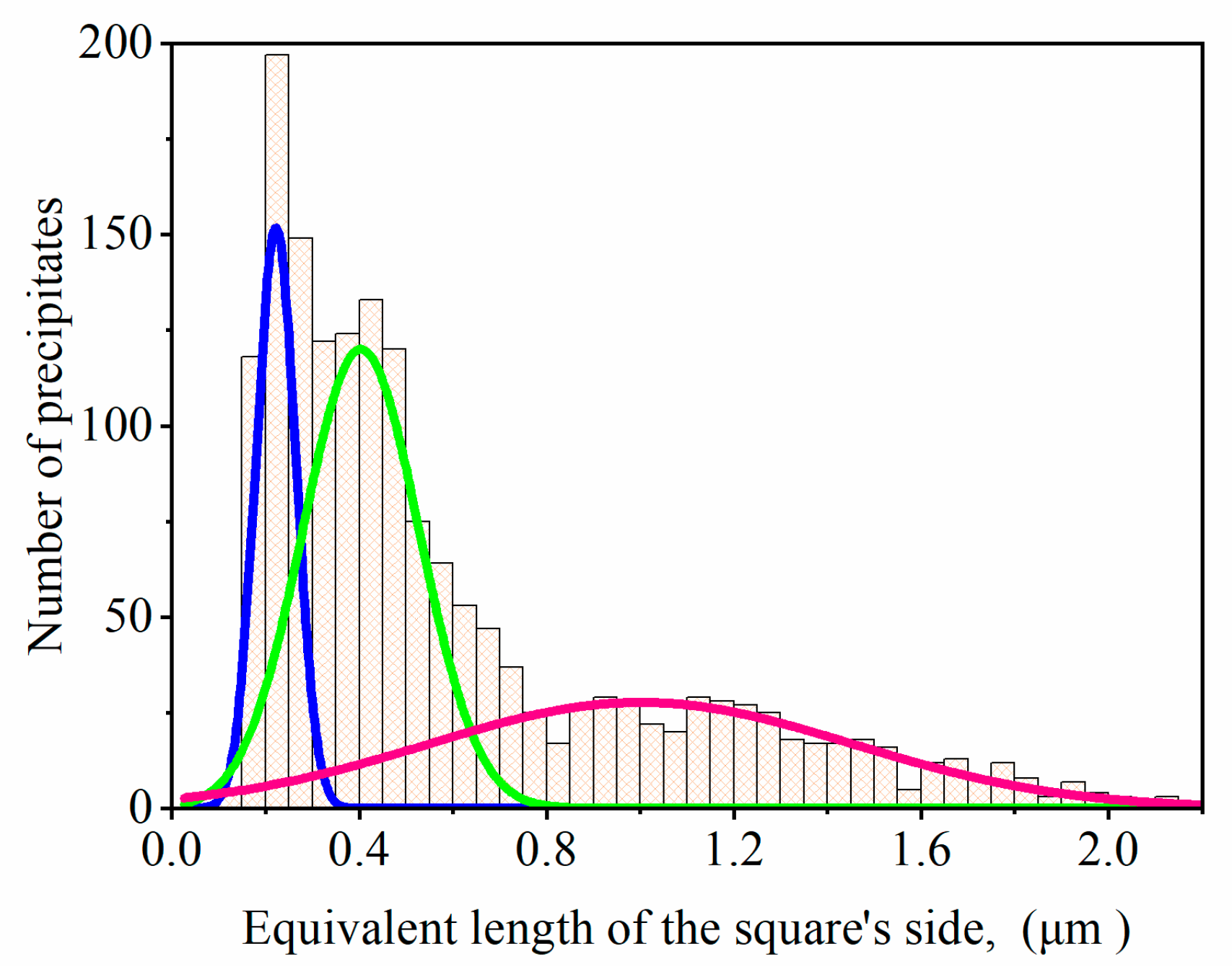
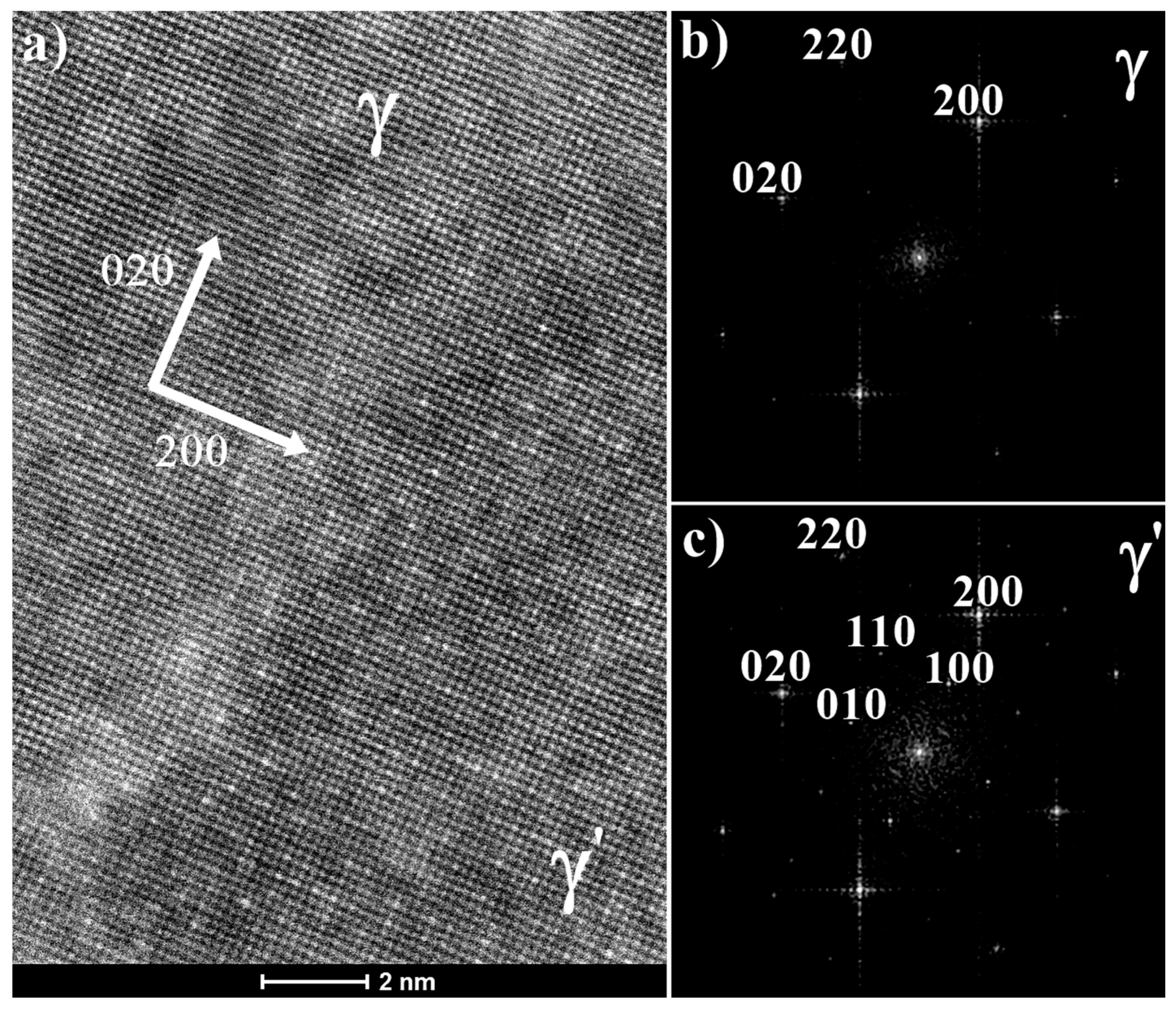
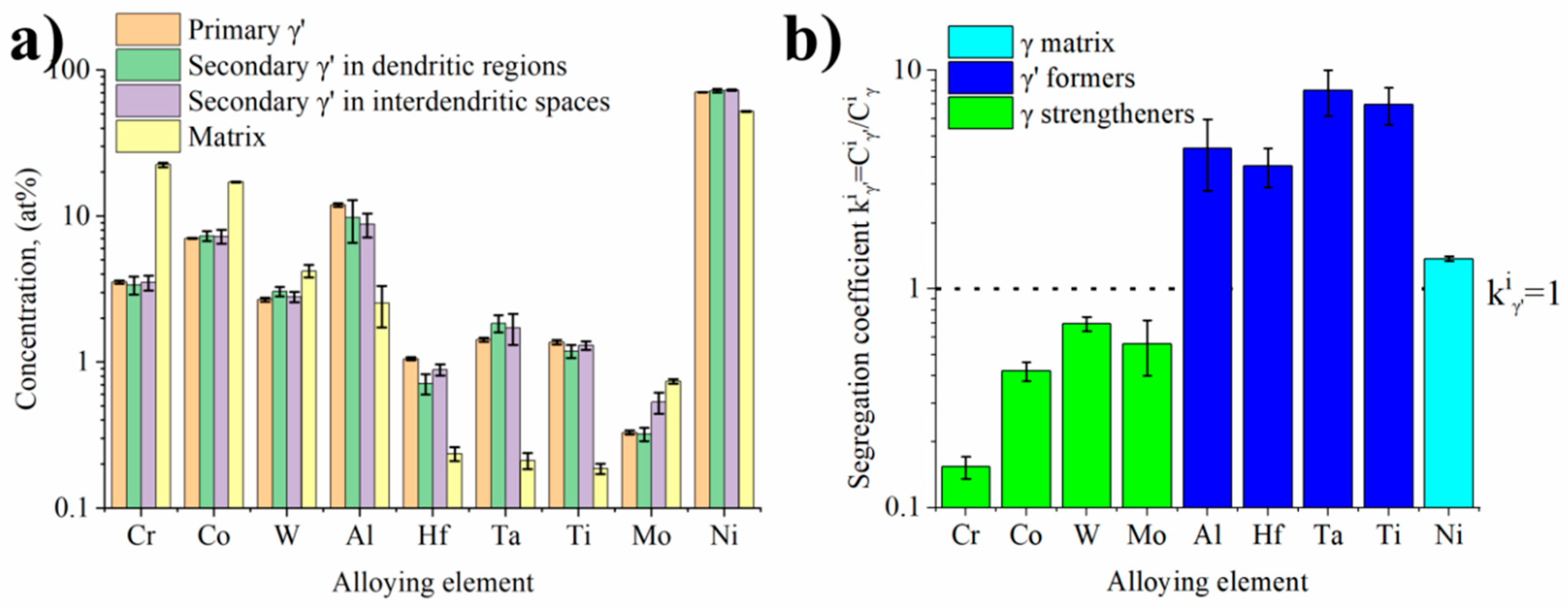
3.1. Characterisation of γ and γ′ Phases Structure in the Initial Condition
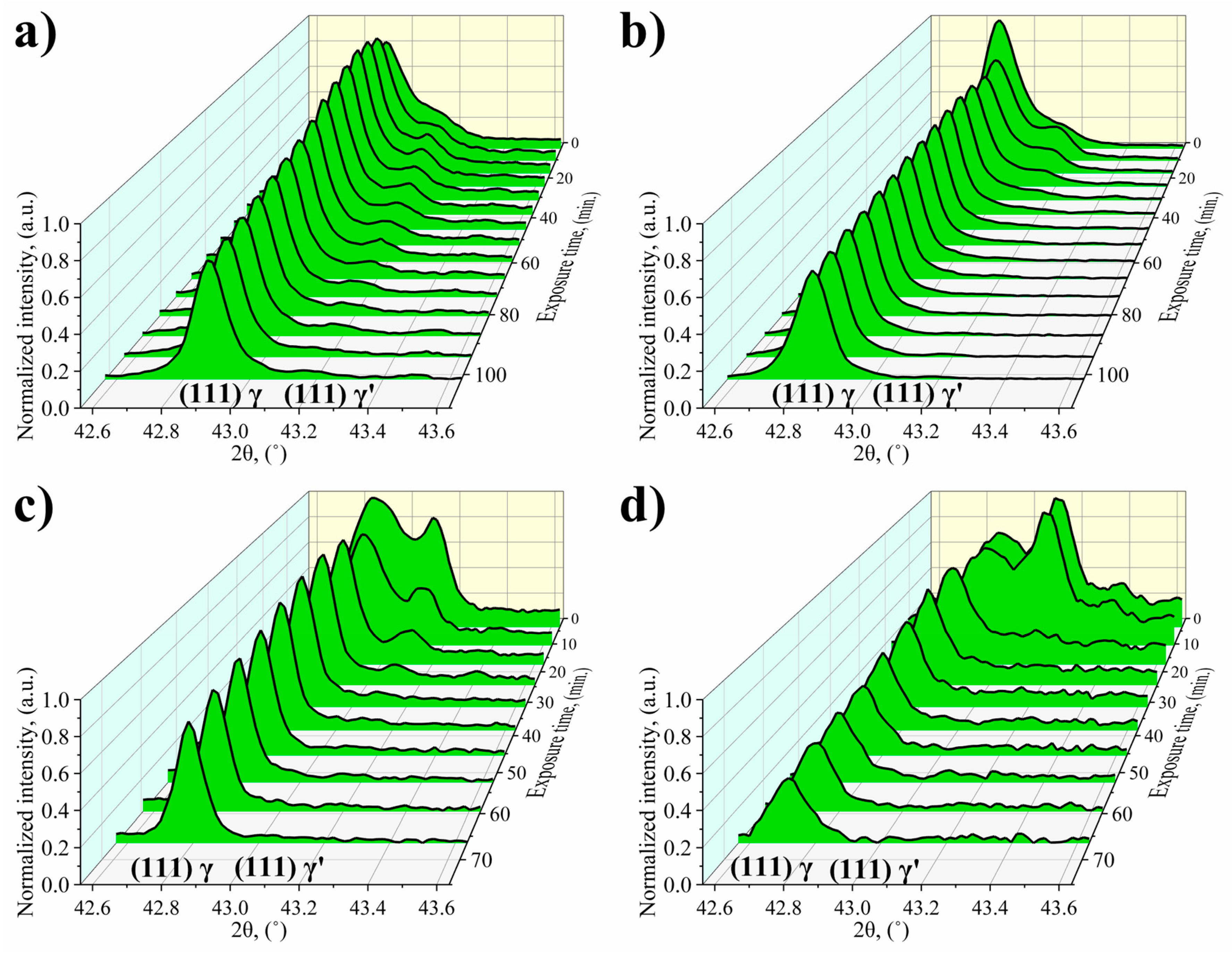
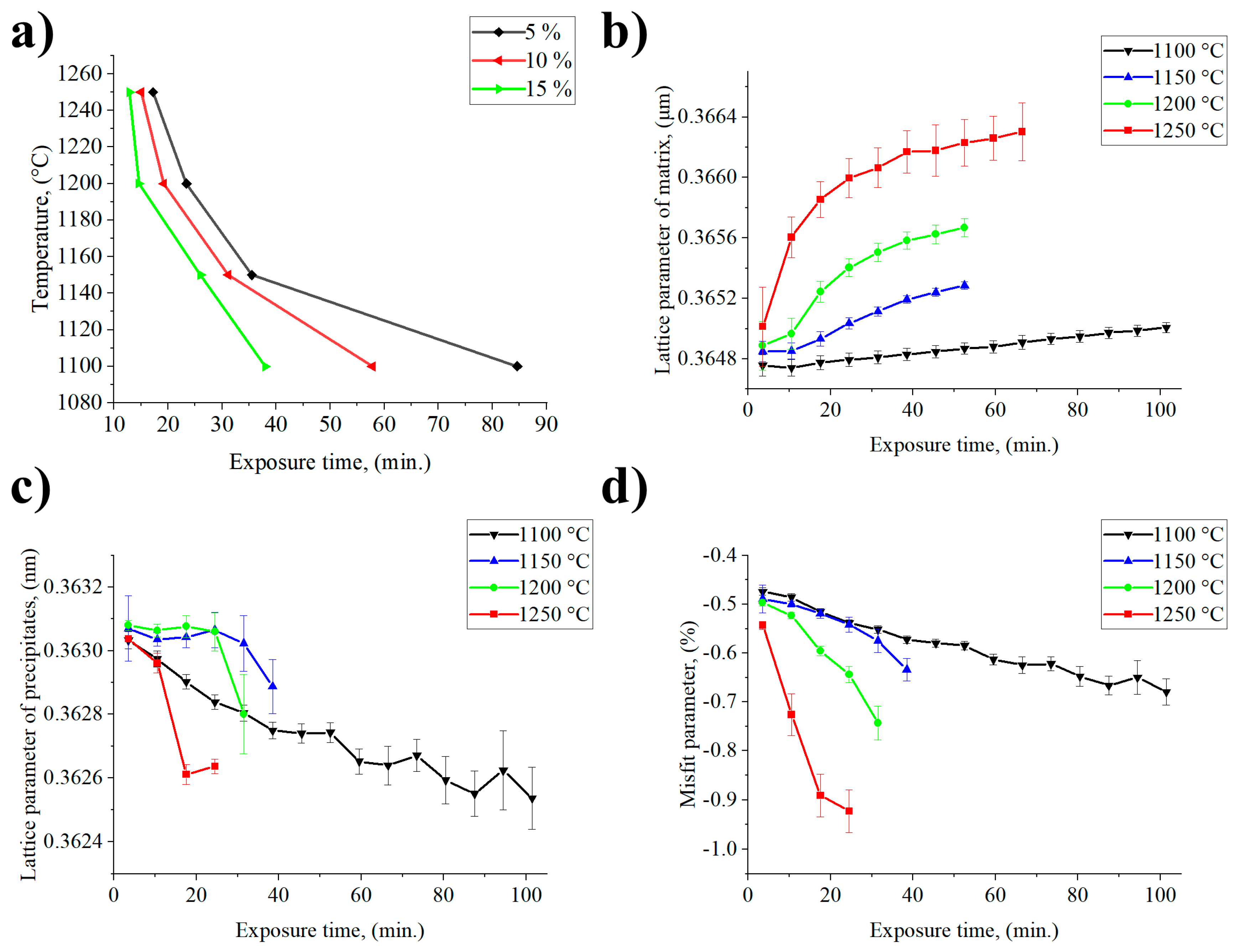
3.2. Dissolution of γ′ Precipitates Studied by in Situ X-Ray Diffractometry
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reed, R.C. The Superalloys Fundaments and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Pollock, T.; Tin, S. Nickel-Based Superalloys for advanced turbine engines: Chemistry, microstructure, and properties. J. Prop. Pow. 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Grudzień, M.; Tuz, L.; Pańcikiewicz, K.; Zielińska-Lipiec, A. Microstructure and properties of a repair weld in a nickel based superalloy gas turbine component. Adv. Mat. Sci. 2017, 17, 55–63. [Google Scholar] [CrossRef]
- Matysiak, H.; Zagorska, M.; Andersson, J.; Balkowiec, A.; Cygan, R.; Rasinski, M.; Pisarek, M.; Andrzejczuk, M.; Kubiak, K.; Kurzydłowski, K.J. Microstructure of Haynes® 282® superalloy after vacuum induction melting and investment casting of thin-walled components. Materials 2013, 6, 5016–5037. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Cygan, R. Analysis of temperature distribution in shell mould during thin-wall superalloy casting and its effect on the resultant microstructure. Arch. Civ. Mech. Eng. 2018, 18, 1441–1450. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Grudzień, M.; Cygan, R.; Zielińska-Lipiec, A. Effect of cobalt aluminate content and pouring temperature on macrostructure, tensile strength and creep rupture of Inconel 713 castings. Arch. Metall. Mater. 2019, 63, 1537–1545. [Google Scholar] [CrossRef]
- Murakumo, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Creep behaviour of Ni-base single-crystal superalloys with various γ′ volume fraction. Acta. Mat. 2004, 52, 3737–3744. [Google Scholar] [CrossRef]
- Long, H.; Mao, S.; Liu, Y.; Zhang, Z.; Han, X. Microstructural and compositional design of Ni-based single crystalline superalloys. J. All. Comp. 2018, 743, 203–220. [Google Scholar] [CrossRef]
- Ru, Y.; Li, S.; Zhou, J.; Pei, Y.; Wang, H.; Gong, S.; Xu, H. Dislocation network with pair-coupling structure in {111} γ/γ′ interface of Ni-based single crystal superalloy. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Liu, C.T.; Cahn, R.W.; Sauthoff, G. Ordered Intermetallics Physical Metallurgy and Mechanical Behaviour; Springer Science & Business Media: Berlin, Germany, 1992. [Google Scholar]
- Bagot, P.J.; Silk, O.B.W.; Douglas, J.O.; Pedrazzini, S.; Crudden, D.J.; Martin, T.L.; Hardy, M.C.; Moody, M.P.; Reed, R.C. An atom probe tomography study of site preference and partitioning in a nickel-based superalloy. Acta. Mat. 2017, 125, 156–165. [Google Scholar] [CrossRef]
- Huang, S.; An, K.; Gao, Y.; Suzuki, A. Determination of γ/γ′ lattice misfit in Ni-based single-crystal superalloys at high temperatures by neutron diffraction. Metall. Mat. Trans. A. 2018, 49, 740–751. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Zhang, G.; Lou, L. Observation of a[100] dislocations in the γ′ phase in a [011]-oriented nickel-base single crystal superalloy during high temperature creep. Metall. Mat. Trans. A. 2019, 50, 4965–4969. [Google Scholar] [CrossRef]
- Reed, R.C.; Cox, D.C.; Rae, C.M.F. Damage accumulation during creep deformation of a single crystal superalloy at 1150 °C. Mat. Sci. Eng. A. 2007, 448, 88–96. [Google Scholar] [CrossRef]
- Collins, D.M.; Crudden, D.J.; Alabort, E.; Connolley, T.; Reed, R.C. Time-resolved synchrotron diffractometry of phase transformations in high strength nickel-based superalloys. Acta Mater. 2015, 94, 244–256. [Google Scholar] [CrossRef]
- Coakley, J.; Reed, R.C.; Warwick, J.; Rahman, K.M.; Dye, D. Lattice strain evolution during creep in single-crystal superalloys. Acta Mater. 2012, 60, 2729–2738. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Grudzień-Rakoczy, M.; Cygan, R. Influence of melt-pouring temperature and composition of primary coating of shell mold on tensile strength and creep resistance of Ni-based superalloy. J. Mat. Eng. Perform. 2019, 28, 3826–3834. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Grudzień-Rakoczy, M.; Cygan, R. The influence of shell mold composition on the as-cast macro- and micro-structure of thin-walled IN713C superalloy casting. J. Mat. Eng. Perform. 2019, 28, 3974–3985. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Cempura, G.; Kruk, A.; Czyrska-Filemonowicz, A.; Zielińska-Lipiec, A. Evolution of γ’ morphology and γ/γ’ lattice parameter misfit in a nickel-based superalloy during non-equilibrium cooling. Int. J. Mater. Res. 2019, 110, 66–69. [Google Scholar] [CrossRef]
- Lahrman, D.F.; Field, R.D.; Darolia, R.; Fraser, H.L. Investigation of techniques for measuring lattice mismatch in a rhenium containing nickel base superalloy. Acta Metall. 1988, 36, 1309–1320. [Google Scholar] [CrossRef]
- Maniar, G.N.; Bridge, J.E. Effect of gamma-gamma prime mismatch, volume fraction gamma prime, and gamma prime morphology on elevated temperature properties of Ni, 20 Cr, 5.5 Mo, Ti, Al alloys. Metall. Trans. 1971, 2, 95–101. [Google Scholar] [CrossRef]
- Grose, D.A.; Ansell, G.S. The influence of coherency strain on the elevated temperature tensile behavior of Ni-15Cr-Al-Ti-Mo alloys. Metall. Trans. A. 1981, 12, 1631–1645. [Google Scholar] [CrossRef]
- Grudzień, M.; Cygan, R.; Pirowski, Z.; Rakoczy, Ł. Microstructural characterization of Inconel 713C superalloy after creep testing. Trans. Found. Res. Inst. 2018, 58, 39–45. [Google Scholar] [CrossRef]
- Matysiak, H.; Zagorska, M.; Balkowiec, A.; Adamczyk-Cieśla, B.; Cygan, R.; Cwajna, J.; Nawrocki, J.; Kurzydłowski, K. The Microstructure Degradation of the IN 713C Nickel-Based Superalloy After the Stress Rupture Tests. J. Mater. Eng. Perform. 2014, 23, 3305–3313. [Google Scholar] [CrossRef]
- Pollock, T.M.; Argon, A.S. Creep resistance of CMSX-3 nickel base superalloy single crystals. Acta Metall. Sin. 1992, 40, 1–30. [Google Scholar] [CrossRef]
- Zla, S.; Dobrovska, J.; Smetana, B.; Zaludova, M.; Vodarek, V.; Konecna, K. Differential Thermal Analysis and Phase Analysis of Nickel Based Superalloy IN738LC. In Proceedings of the Conference Proceedings Metal 2010, Roznov, Czech Republic, 18–20 May 2010. [Google Scholar]
- Strunz, P.; Petrenec, M.; Polak, J.; Gasser, U.; Farkas, G. Formation and Dissolution of γ’ Precipitates in IN792 Superalloy at Elevated Temperatures. Metals 2016, 6, 37. [Google Scholar] [CrossRef]
- Soucail, M.; Bienvenu, Y. Dissolution of the γ′ phase in a nickel base superalloy at equilibrium and under rapid heating. Mat. Sci. Eng. A. 1996, 220, 215–222. [Google Scholar] [CrossRef]
- Sponseller, D.L. Differential thermal analysis of nickel-base superalloys. In Proceedings of the eight International Symposium on Superalloys, Pittsburgh, PA, USA, 22–26 September 1996; TMS: Pittsburgh, PA, USA, 1996; pp. 259–270. [Google Scholar]
- Rakoczy, Ł.; Grudzień, M.; Zielińska-Lipiec, A. Contribution of microstructural constituents on hot cracking of MAR-M247 nickel based superalloy. Arch. Metall. Mat. 2018, 63, 181–189. [Google Scholar] [CrossRef]
- Singh, S.; Andersson, J. Heat-affected zone liquation cracking in welded cast Haynes® 282®. Metals 2020, 10, 29. [Google Scholar] [CrossRef]
- Rakoczy, Ł.; Hanning, F.; Andersson, J.; Grudzień-Rakoczy, M.; Cygan, R. Zielińska-Lipiec, A. Microstructure evolution of the Gleeble-simulated heat-affected zone of Ni-based superalloy. In Proceedings of the 6th International BAPT Conference “Power Transmissions 2019”, Varna, Bulgaria, 19–22 June 2019; MATEC Web of Conferences: Les Ulis, France, 2019; Volume 287, p. 06002. [Google Scholar] [CrossRef]
- David, S.A.; Vitek, J.M.; Babu, S.S.; Boatner, L.A.; Reed, R.W. Welding of nickel base superalloy single crystals. Sci. Tech. Weld. Join. 1997, 2, 79–88. [Google Scholar] [CrossRef]
- Hu, Y.L.; Lin, X.; Song, K.; Jiang, X.Y.; Yang, H.O.; Huang, W.D. Effect of heat input on cracking in laser forming solid formed DZ4125 superalloy. Opt. Las. Tech. 2016, 86, 1–7. [Google Scholar] [CrossRef]
- Xu, J.; Lin, X.; Guo, P.; Hu, Y.; Wen, X.; Xue, L.; Liu, J.; Huang, W. The effect of preheating on microstructure and mechanical properties of laser solid forming IN-738LC alloy. Mat. Sci. Eng. A. 2017, 691, 71–80. [Google Scholar] [CrossRef]
- Clementi, E.; Raimondi, D.L.; Reinhardt, W.P. Atomic screening constants from SCF functions. II. Atoms with 37 to 86 electrons. J. Chem. Phys. 1967, 47, 1300–1307. [Google Scholar] [CrossRef]
- Barba, D.; Pedrazzini, S.; Vilalta-Clemente, A.; Wilkinson, A.J.; Moody, M.P.; Bagot, P.A.J.; Jerusalem, A.; Reed, R.C. On the composition of microtwins in a single crystal nickel-based superalloy. Scr. Mater. 2017, 127, 37–40. [Google Scholar] [CrossRef]
- Smith, T.M.; Esser, B.D.; Good, B.; Hooshmand, M.S.; Viswanathan, G.B.; Rae, C.M.F.; Ghazisaeidi, M.; Mccomb, D.W.; Mills, M.J. Segregation and phase transformations along superlattice intrinsic stacking faults in Ni-based superalloys. Metall. Mat. Trans. A. 2018, 49, 4186–4198. [Google Scholar] [CrossRef]
- Grosdidier, T.; Hazotte, A.; Simon, A. Precipitation and dissolution process in γ/γ′ single crystal nickel-based superalloy. Mat. Sci. Eng. A. 1998, 256, 183–196. [Google Scholar] [CrossRef]
- Royer, A.; Bastie, P.; Veron, M. Temperature dependence of the structural order in the γ′ phase of nickel base superalloy. Scri. Mater. 1999, 40, 955–961. [Google Scholar] [CrossRef]
- Stepanova, N.N.; Sazonova, V.A.; Rodionov, D.P. Influence of solidification conditions on γ′-phase thermal stability in <001> single crystals of Ni-based superalloys. Scri. Mater. 1999, 40, 581–585. [Google Scholar] [CrossRef]



| Element | 1100 °C | 1150 °C | 1200 °C | 1250 °C | ||||
|---|---|---|---|---|---|---|---|---|
| wt.% | at.% | wt.% | at.% | wt.% | at.% | wt.% | at.% | |
| Al | 8.57 | 16.94 | 9.0 | 17.71 | 9.38 | 18.38 | 9.85 | 19.20 |
| Ti | 10.79 | 12.92 | 11.38 | 13.60 | 11.98 | 14.30 | 12.65 | 15.08 |
| Ta | 17.08 | 6.27 | 18.52 | 6.87 | 20.19 | 7.58 | 22.28 | 8.51 |
| Hf | 2.58 | 0.86 | 3.24 | 1.09 | 3.67 | 1.24 | 2.98 | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakoczy, Ł.; Milkovič, O.; Rutkowski, B.; Cygan, R.; Grudzień-Rakoczy, M.; Kromka, F.; Zielińska-Lipiec, A. Characterization of γ′ Precipitates in Cast Ni-Based Superalloy and Their Behaviour at High-Homologous Temperatures Studied by TEM and in Situ XRD. Materials 2020, 13, 2397. https://doi.org/10.3390/ma13102397
Rakoczy Ł, Milkovič O, Rutkowski B, Cygan R, Grudzień-Rakoczy M, Kromka F, Zielińska-Lipiec A. Characterization of γ′ Precipitates in Cast Ni-Based Superalloy and Their Behaviour at High-Homologous Temperatures Studied by TEM and in Situ XRD. Materials. 2020; 13(10):2397. https://doi.org/10.3390/ma13102397
Chicago/Turabian StyleRakoczy, Łukasz, Ondrej Milkovič, Bogdan Rutkowski, Rafał Cygan, Małgorzata Grudzień-Rakoczy, František Kromka, and Anna Zielińska-Lipiec. 2020. "Characterization of γ′ Precipitates in Cast Ni-Based Superalloy and Their Behaviour at High-Homologous Temperatures Studied by TEM and in Situ XRD" Materials 13, no. 10: 2397. https://doi.org/10.3390/ma13102397
APA StyleRakoczy, Ł., Milkovič, O., Rutkowski, B., Cygan, R., Grudzień-Rakoczy, M., Kromka, F., & Zielińska-Lipiec, A. (2020). Characterization of γ′ Precipitates in Cast Ni-Based Superalloy and Their Behaviour at High-Homologous Temperatures Studied by TEM and in Situ XRD. Materials, 13(10), 2397. https://doi.org/10.3390/ma13102397






