Quantum Treatment of Inelastic Interactions for the Modeling of Nanowire Field-Effect Transistors
Abstract
1. Introduction
2. General Theoretical Framework
2.1. Dyson Equation
2.2. Self-Consistent Born Approximation
2.3. Lowest Order Approximation
| Algorithm 1Nth-order LOA calculation. |
| <the order of LOA> for do if then , E (Energy), H (Hamiltonian), and (Contact self-energy) , the superscript r (Retarded), a (Advanced), and ≶ (Lesser/Greater) else for do : interacting self energy calculation and : perturbation term calculation ⇓ applying Langreth Theorem end for end if end for |
2.4. Rescaling Technique
2.5. Matrix Form of the Padé Approximants
2.6. Richardson Extrapolation
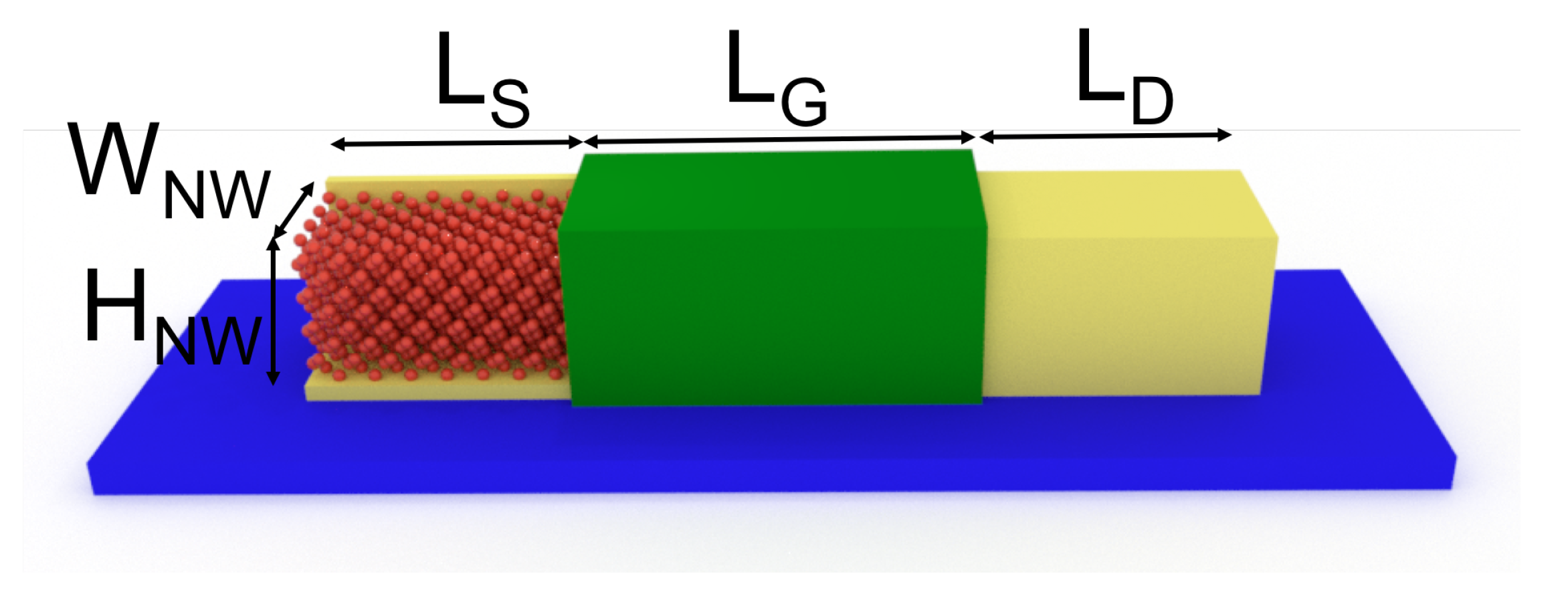
3. Applications to Electron and Phonon Transports in a Nanowire Transistor
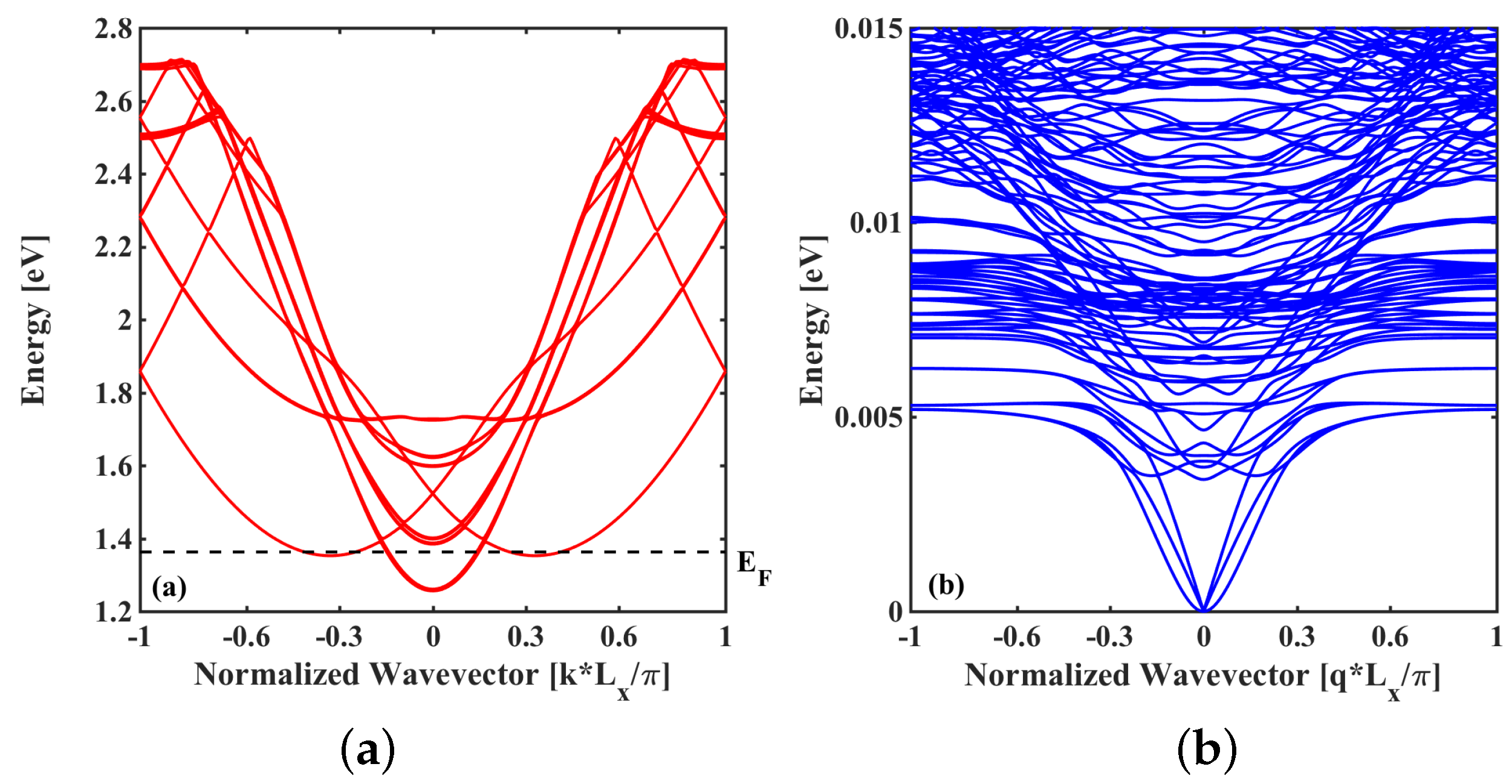
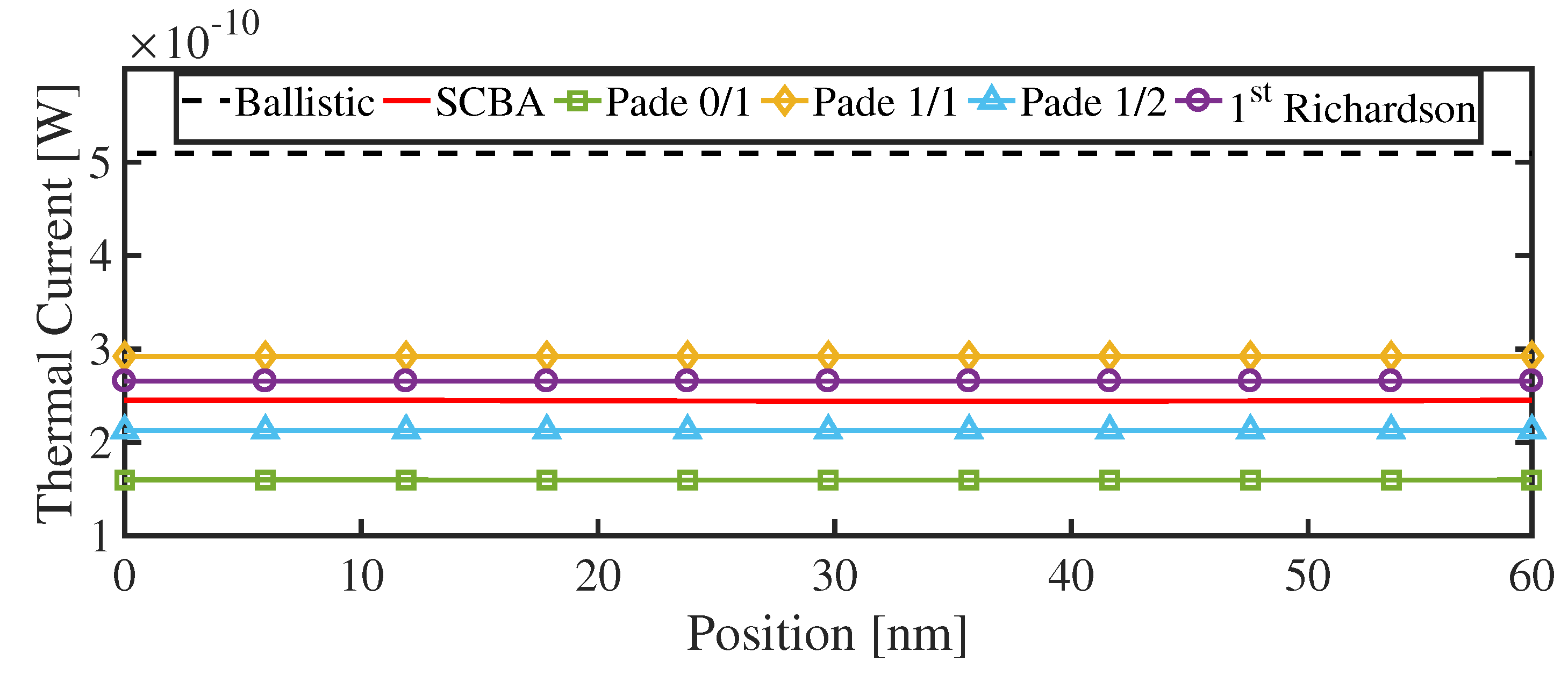
3.1. Electron–Phonon Scattering in a Nanowire Transistor
3.2. Anharmonic Phonon–Phonon Scattering in A Nanowire
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Suk, S.D.; Lee, S.Y.; Kim, S.M.; Yoon, E.J.; Kim, M.S.; Li, M.; Oh, C.W.; Yeo, K.H.; Kim, S.H.; Shin, D.S.; et al. High performance 5nm radius Twin Silicon Nanowire MOSFET (TSNWFET): Fabrication on bulk si wafer, characteristics, and reliability. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5 December 2005; pp. 717–720. [Google Scholar] [CrossRef]
- Law, M.; Greene, L.E.; Johnson, J.C.; Saykally, R.; Yang, P. Nanowire dye-sensitized solar cells. Nat. Mater. 2005, 4, 455–459. [Google Scholar] [CrossRef] [PubMed]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef] [PubMed]
- Mertens, H.; Ritzenthaler, R.; Hikavyy, A.; Kim, M.S.; Tao, Z.; Wostyn, K.; Chew, S.A.; De Keersgieter, A.; Mannaert, G.; Rosseel, E.; et al. Gate-All-Around MOSFETs based on Vertically Stacked Horizontal Si Nanowires in a Replacement Metal Gate Process on Bulk Si Substrates. In Proceedings of the IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar]
- Capogreco, E.; Arimura, H.; Witters, L.; Vohra, A.; Porret, C.; Loo, R.; De Keersgieter, A.; Dupuy, E.; Marinov, D.; Hikavyy, A.; et al. High performance strained Germanium Gate All Around p-channel devices with excellent electrostatic control for sub-Jtlnm LG. In Proceedings of the Symposium on VLSI Technology, Kyoto, Japan, 9–14 June 2019. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotech. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed]
- Franklin, A.D.; Luisier, M.; Han, S.J.; Tulevski, G.; Breslin, C.M.; Gignac, L.; Lundstrom, M.S.; Haensch, W. Sub-10 nm Carbon Nanotube Transistor. Nano Lett. 2012, 12, 758. [Google Scholar] [CrossRef] [PubMed]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotech. 2011, 6, 147. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.; Ganapathi, K.; Salahuddin, S. How Good Can Monolayer MoS2 Transistors Be? Nano Lett. 2011, 11, 3768. [Google Scholar] [CrossRef]
- Szabó, A.; Rhyner, R.; Luisier, M. Ab initio simulation of single- and few-layer MoS2 transistors: Effect of electron-phonon scattering. Phys. Rev. B 2015, 92, 035435. [Google Scholar] [CrossRef]
- Cao, J.; Logoteta, D.; Özkaya, S.; Biel, B.; Cresti, A.; Pala, M.G.; Esseni, D. Operation and Design of van der Waals Tunnel Transistors: A 3-D Quantum Transport Study. IEEE Trans. Electron Devices 2016, 63, 1–7. [Google Scholar] [CrossRef]
- Tatarskiĭ, V.I. The Wigner representation of quantum mechanics. Sov. Phys. Uspekhi 1983, 26, 311–327. [Google Scholar] [CrossRef]
- Jacoboni, C.; Brunetti, R.; Bordone, P.; Bertoni, A. Quantum tansport and its simulation with the wigner-function approach. Int. J. High Speed Electron. Syst. 2001, 11, 387–423. [Google Scholar] [CrossRef]
- Querlioz, D.; Saint-Martin, J.; Bournel, A.; Dollfus, P. Wigner Monte Carlo simulation of phonon-induced electron decoherence in semiconductor nanodevices. Phys. Rev. B 2008, 78, 165306. [Google Scholar] [CrossRef]
- Fischetti, M.V. Theory of electron transport in small semiconductor devices using the Pauli master equation. J. Appl. Phys. 1998, 83, 270–291. [Google Scholar] [CrossRef]
- Fischetti, M.V. Master-equation approach to the study of electronic transport in small semiconductor devices. Phys. Rev. B 1999, 59, 4901. [Google Scholar] [CrossRef]
- Oriols, X. Quantum-Trajectory Approach to Time-Dependent Transport in Mesoscopic Systems with Electron-Electron Interactions. Phys. Rev. Lett. 2007, 98, 066803. [Google Scholar] [CrossRef]
- Marian, D.; Zanghì, N.; Oriols, X. Weak Values from Displacement Currents in Multiterminal Electron Devices. Phys. Rev. Lett. 2016, 116, 110404. [Google Scholar] [CrossRef]
- Baym, G.; Kadanoff, L.P. Conservation Laws and Correlation Functions. Phys. Rev. 1961, 124, 287. [Google Scholar] [CrossRef]
- Baym, G. Self-Consistent Approximations in Many-Body Systems. Phys. Rev. 1962, 127, 1391. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram Technique for Nonequilibrium Processes. Sov. Phys. JETP (Zh. Eksp. Teor. Fiz.) 1965, 20, 1018–1026. [Google Scholar]
- Mahan, G.D. Many-Particle Physics; Plenum: New York, NY, USA, 1990. [Google Scholar]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Vol. 123 of Springer Series in Solid-State Sciences; Springer: Berlin, Germany; New York, NY, USA, 1996. [Google Scholar]
- Ferry, D.K.; Goodnick, S.M. Transport in Nanostructures; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Zhao, X.; Wei, C.M.; Yang, L.; Chou, M.Y. Quantum Confinement and Electronic Properties of Silicon Nanowires. Phys. Rev. Lett. 2004, 92, 236805. [Google Scholar] [CrossRef]
- Pizzi, G.; Gibertini, M.; Dib, E.; Marzari, N.; Iannaccone, G.; Fiori, G. Performance of arsenene and antimonene double-gate MOSFETs from first principles. Nat. Commun. 2016, 7, 12585. [Google Scholar] [CrossRef]
- Moussavou, M.; Cavassilas, N.; Dib, E.; Bescond, M. Influence of uniaxial strain in Si and Ge p-type double-gate metal-oxide-semiconductor field effect transistors. J. Appl. Phys. 2015, 118, 114503. [Google Scholar] [CrossRef]
- Lherbier, A.; Persson, M.P.; Niquet, Y.M.; Triozon, F.; Roche, S. Quantum transport length scales in silicon-based semiconducting nanowires: Surface roughness effects. Phys. Rev. B 2008, 77, 085301. [Google Scholar] [CrossRef]
- Luisier, M.; Klimeck, G. Atomistic full-band simulations of silicon nano-wire transistors: Effects of electron-phonon scattering. Phys. Rev. B 2009, 80, 155430. [Google Scholar] [CrossRef]
- Mera, H.; Lannoo, M.; Li, C.; Cavassilas, N.; Bescond, M. Inelastic scattering in nanoscale devices: One-shot current-conserving lowest-order approximation. Phys. Rev. B 2012, 86, 161404. [Google Scholar] [CrossRef]
- Mera, H.; Lannoo, M.; Cavassilas, N.; Bescond, M. Nanoscale device modeling using a conserving analytic continuation technique. Phys. Rev. B 2013, 88, 075147. [Google Scholar] [CrossRef]
- Lee, Y.; Lannoo, M.; Cavassilas, N.; Luisier, M.; Bescond, M. Efficient quantum modeling of inelastic interactions in nanodevices. Phys. Rev. B 2016, 93, 205411. [Google Scholar] [CrossRef]
- Lee, Y.; Bescond, M.; Cavassilas, N.; Logoteta, D.; Raymond, L.; Lannoo, M.; Luisier, M. Quantum treatment of phonon scattering for modeling of three-dimensional atomistic transport. Phys. Rev. B 2017, 95, 201412. [Google Scholar] [CrossRef]
- Lee, Y.; Bescond, M.; Logoteta, D.; Cavassilas, N.; Lannoo, M.; Luisier, M. Anharmonic phonon-phonon scattering modeling of three-dimensional atomistic transport: An efficient quantum treatment. Phys. Rev. B 2018, 97, 205447. [Google Scholar] [CrossRef]
- Caliceti, E.; Meyer-Hermann, M.; Ribeca, P.; Surzhykov, A.; Jentschura, U.D. From useful algorithms for slowly convergent series to physical predictions based on divergent perturbative expansions. Phys. Rep. 2007, 446, 1–96. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Graves-Morris, P. (Eds.) Pade´ Approximants; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Mera, H.; Pedersen, T.G.; Nikolić, B.K. Hypergeometric resummation of self-consistent sunset diagrams for steady-state electron-boson quantum many-body systems out of equilibrium. Phys. Rev. B 2016, 94, 165429. [Google Scholar] [CrossRef]
- Hardy, G.H. Divergent Series; Chelsea: New York, NY, USA, 1991. [Google Scholar]
- Svizhenko, A.; Anantram, M.P. Role of scattering in nanotransistors. IEEE Trans. Electron Devices 2003, 50, 1459. [Google Scholar] [CrossRef]
- Jin, S.; Park, Y.J.; Min, H.S. A three-dimensional simulation of quantum transport in silicon nanowire transistor in the presence of electron-phonon interactions. J. Appl. Phys. 2006, 99, 123719. [Google Scholar] [CrossRef]
- Carrillo-Nu<i>n</i>˜ez, H.; Bescond, M.; Cavassilas, N.; Dib, E.; Lannoo, M. Influence of electron-phonon interactions in single dopant nanowire transistors. J. Appl. Phys. 2014, 116, 164505. [Google Scholar]
- Luttinger, J.M.; Ward, J.C. Ground-State Energy of a Many-Fermion System. II. Phys. Rev. 1960, 118, 1417. [Google Scholar] [CrossRef]
- Luttinger, J.M. Fermi Surface and Some Simple Equilibrium Properties of a System of Interacting Fermions. Phys. Rev. 1960, 119, 1153. [Google Scholar] [CrossRef]
- Rhyner, R.; Luisier, M. Atomistic modeling of coupled electron-phonon transport in nanowire transistors. Phys. Rev. B 2014, 89, 235311. [Google Scholar] [CrossRef]
- Shanks, D. Nonlinear transformations of divergent and slowly convergent sequences. J. Math. Phys. 1955, 34, 1–42. [Google Scholar] [CrossRef]
- Bescond, M.; Li, C.; Mera, H.; Cavassilas, N.; Lannoo, M. Modeling inelastic pho-non scattering in atomic- and molecular-wire junctions. J. Appl. Phys. 2013, 114, 153712. [Google Scholar] [CrossRef]
- Cavassilas, N.; Bescond, M.; Mera, H.; Lannoo, M. One-shot current conserving quantum transport modeling of phonon scattering in n-type double-gate field-effect-transistors. Appl. Phys. Lett. 2013, 102, 013508. [Google Scholar] [CrossRef]
- Vajta, M. Some remarks on Pade-approximations. In Proceedings of the 3rd TEMPUS INTCOM Symposium on Intelligent Systems in Control and Measurement, Veszprém, Hungary, 9–14 September 2000; p. 53. [Google Scholar]
- Fike, C.T. Computer Evaluation of Mathematical Functions; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1968. [Google Scholar]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Luisier, M. Atomistic modeling of anharmonic phonon-phonon scattering in nanowires. Phys. Rev. B 2012, 86, 245407. [Google Scholar] [CrossRef]
- Luisier, M.; Schenk, A.; Fichtner, W. Atomistic simulation of nanowires in the sp3d5s* tight-binding formalism: From boundary conditions to strain calculations. Phys. Rev. B 2006, 74, 205323. [Google Scholar] [CrossRef]
- Rhyner, R.; Luisier, M. Minimizing Self-Heating and Heat Dissipation in Ultrascaled Nanowire Transistors. Nano Lett. 2016, 16, 1022–1026. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498. [Google Scholar] [CrossRef]
- Boykin, T.B.; Klimeck, G.; Oyafuso, F. Valence band effective-mass expressions in the sp3d5s* empirical tight-binding model applied to a Si and Ge parametrization. Phys. Rev. B 2004, 69, 115201. [Google Scholar] [CrossRef]
- Sui, Z.; Herman, I.P. Effect of strain on phonons in Si, Ge, and Si/Ge heterostructures. Phys. Rev. B 1993, 48, 17938. [Google Scholar] [CrossRef] [PubMed]
- Paul, A.; Luisier, M.; Klimeck, G. Modified valence force field approach for phonon dispersion: From zinc-blende bulk to nanowires. J. Comput. Electron. 2010, 9, 160. [Google Scholar] [CrossRef][Green Version]
- Valin, R.; Aldegunde, M.; Martinez, A.; Barker, J.R. Quantum transport of a nanowire field-effect transistor with complex phonon self-energy. J. Appl. Phys. 2014, 116, 084507. [Google Scholar] [CrossRef]
- Cardona, M.; Ruf, T. Phonon self-energies in semiconductors: Anharmonic and isotopic contributions. Solid State Commun. 2001, 117, 201–212. [Google Scholar] [CrossRef]
- Frey, M.; Esposito, A.; Schenk, A. Simulation of intravalley acoustic phonon scattering in silicon nanowires. In Proceedings of the 38th European Solid-State Device Research Conference (ESSDERC), Edinburgh, UK, 15–19 September 2008; p. 258. [Google Scholar]
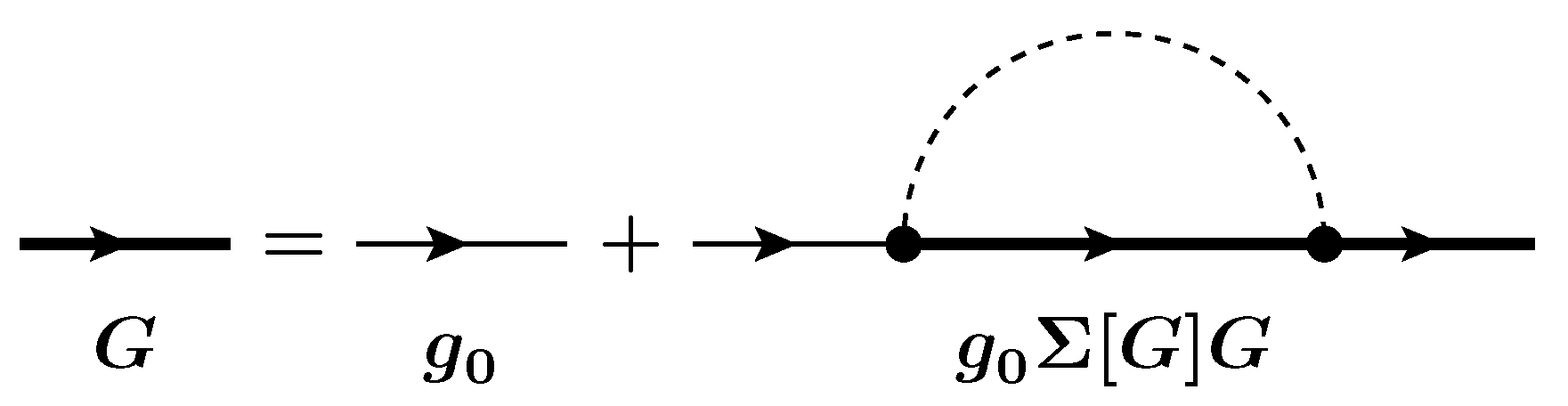



| Ballistic | LOA1 | LOA3 | Padé 0/1 | Padé 1/2 | Richardson | SCBA | |
|---|---|---|---|---|---|---|---|
| Current [A] | 8.9 × 10 | 3.57 × 10 | −2.616 | 5.6 × 10 | 5.9 × 10 | 6.1 × 10 | 6.3 × 10 |
| [%] | 42.1 | 42.0 | 4.2e7 | 10.8 | 6.4 | 2.0 | 0.0 |
| Number of iterations | 0 | 1 | 6 | 1 | 6 | 6 | 35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Logoteta, D.; Cavassilas, N.; Lannoo, M.; Luisier, M.; Bescond, M. Quantum Treatment of Inelastic Interactions for the Modeling of Nanowire Field-Effect Transistors. Materials 2020, 13, 60. https://doi.org/10.3390/ma13010060
Lee Y, Logoteta D, Cavassilas N, Lannoo M, Luisier M, Bescond M. Quantum Treatment of Inelastic Interactions for the Modeling of Nanowire Field-Effect Transistors. Materials. 2020; 13(1):60. https://doi.org/10.3390/ma13010060
Chicago/Turabian StyleLee, Youseung, Demetrio Logoteta, Nicolas Cavassilas, Michel Lannoo, Mathieu Luisier, and Marc Bescond. 2020. "Quantum Treatment of Inelastic Interactions for the Modeling of Nanowire Field-Effect Transistors" Materials 13, no. 1: 60. https://doi.org/10.3390/ma13010060
APA StyleLee, Y., Logoteta, D., Cavassilas, N., Lannoo, M., Luisier, M., & Bescond, M. (2020). Quantum Treatment of Inelastic Interactions for the Modeling of Nanowire Field-Effect Transistors. Materials, 13(1), 60. https://doi.org/10.3390/ma13010060




