New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper
Abstract
1. Introduction
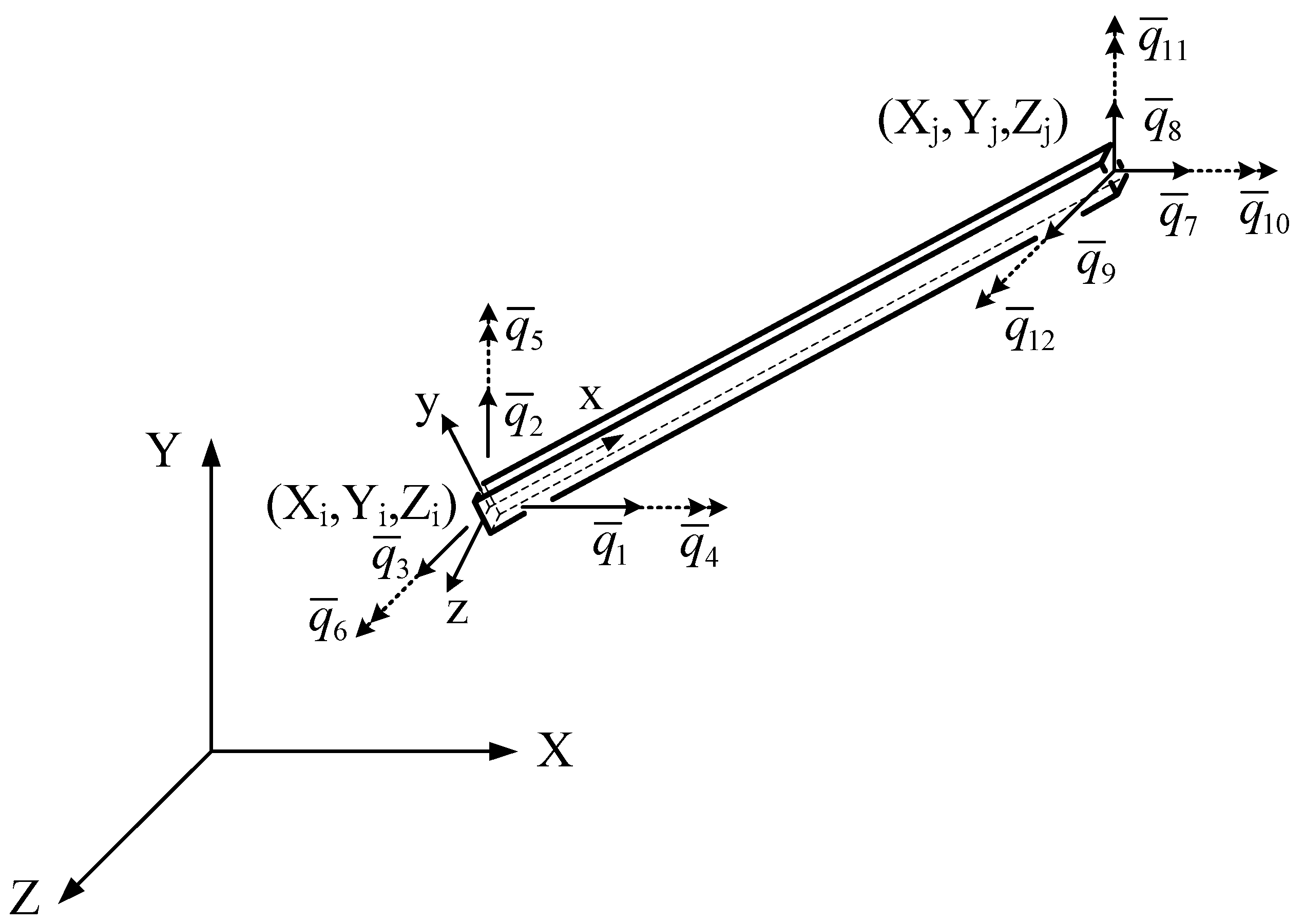
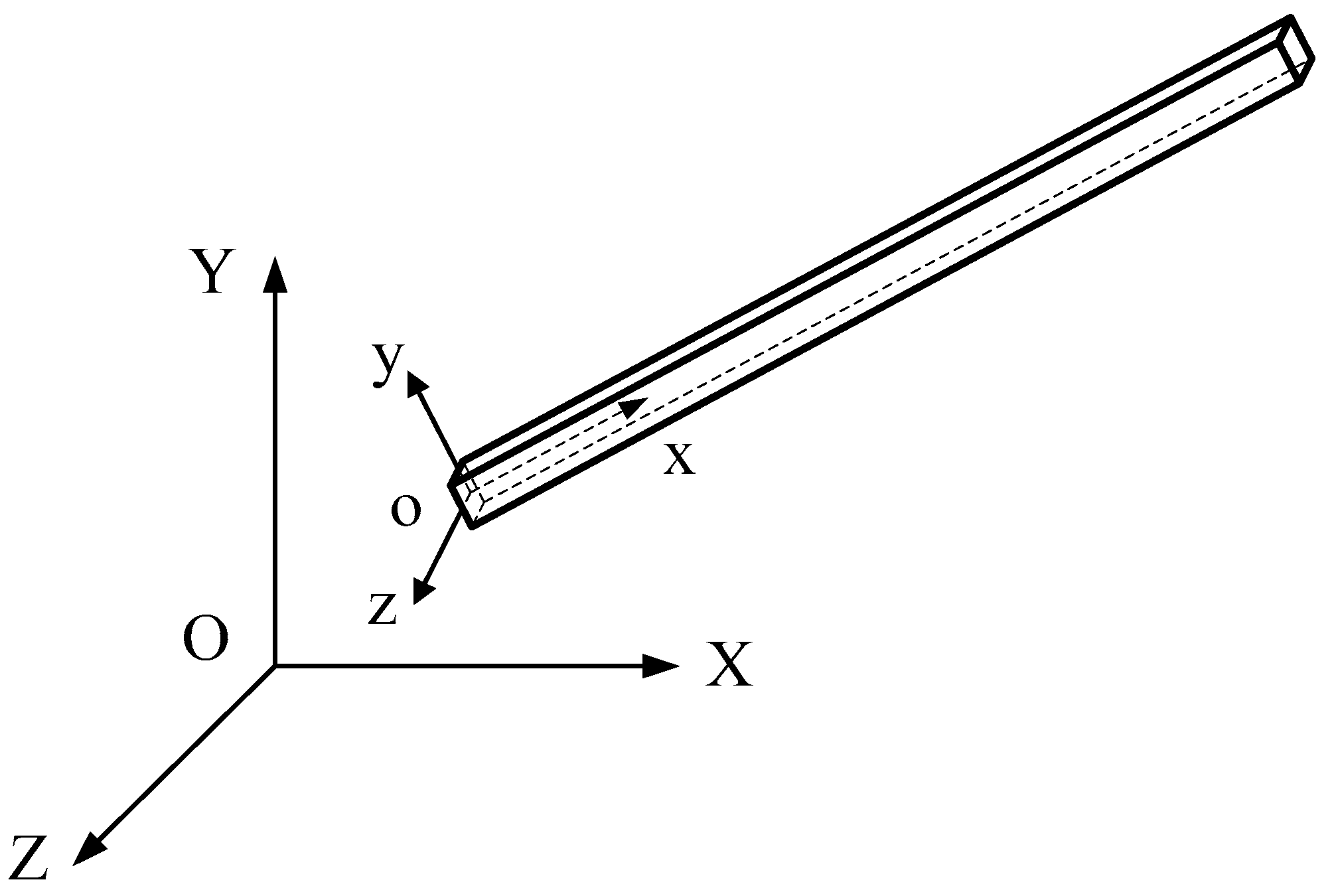
2. Geometry and Theoretical Formulations
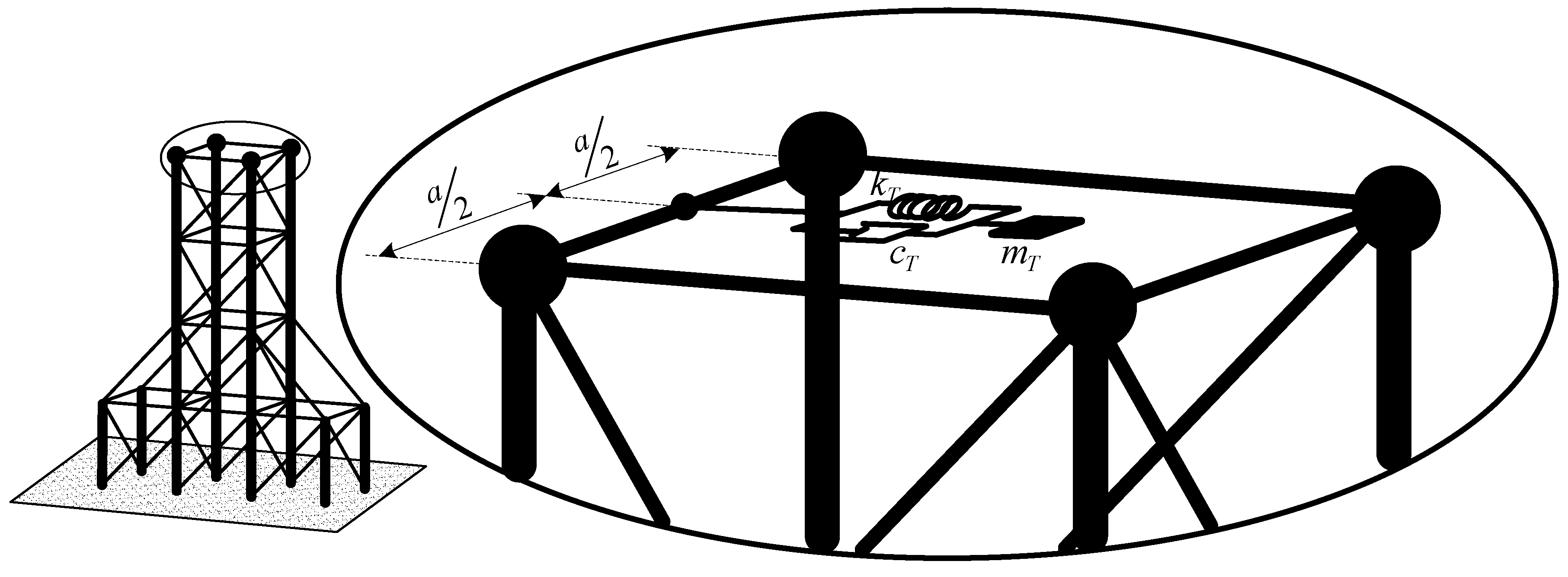
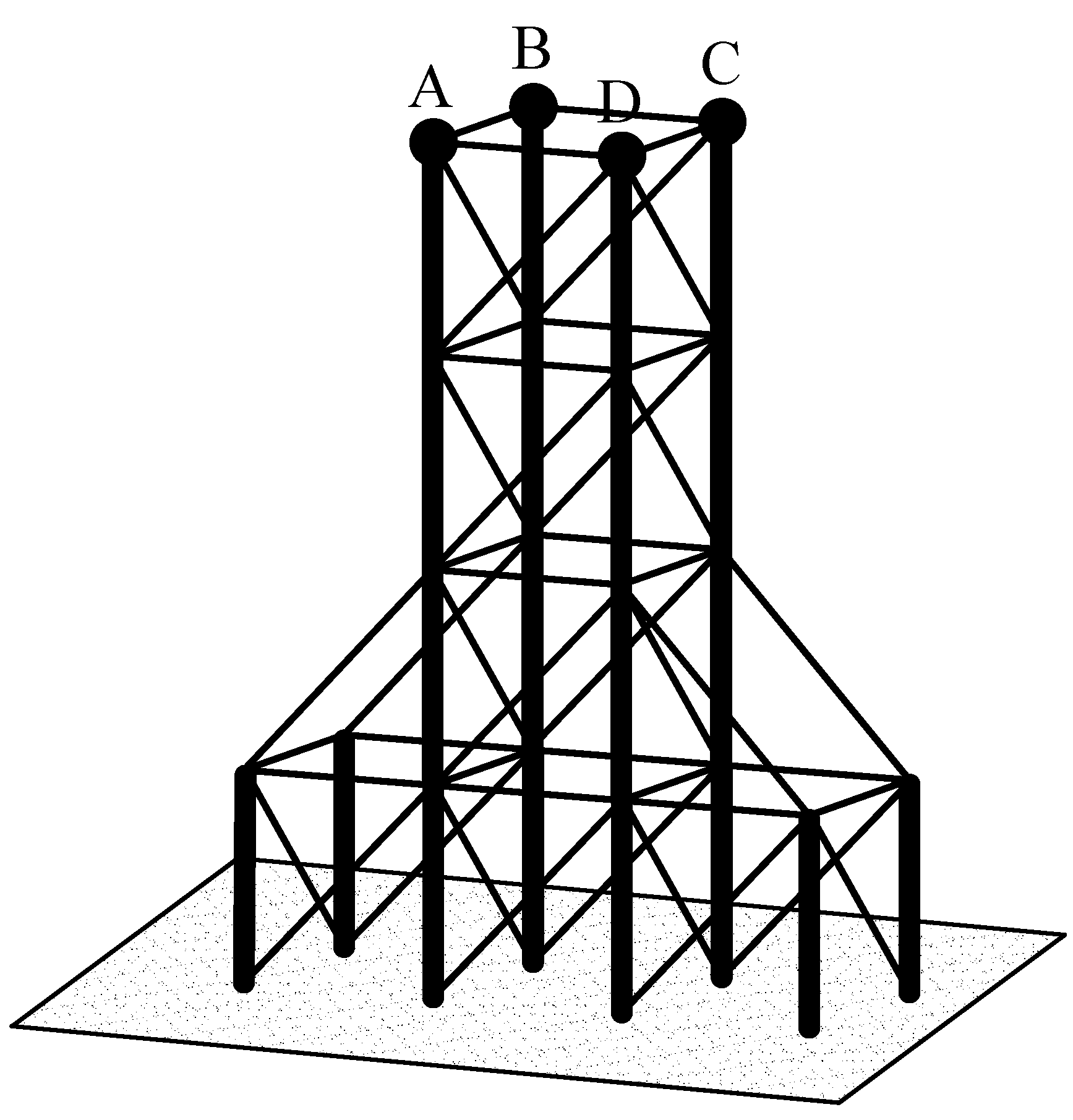
The Space Frame with a TMD
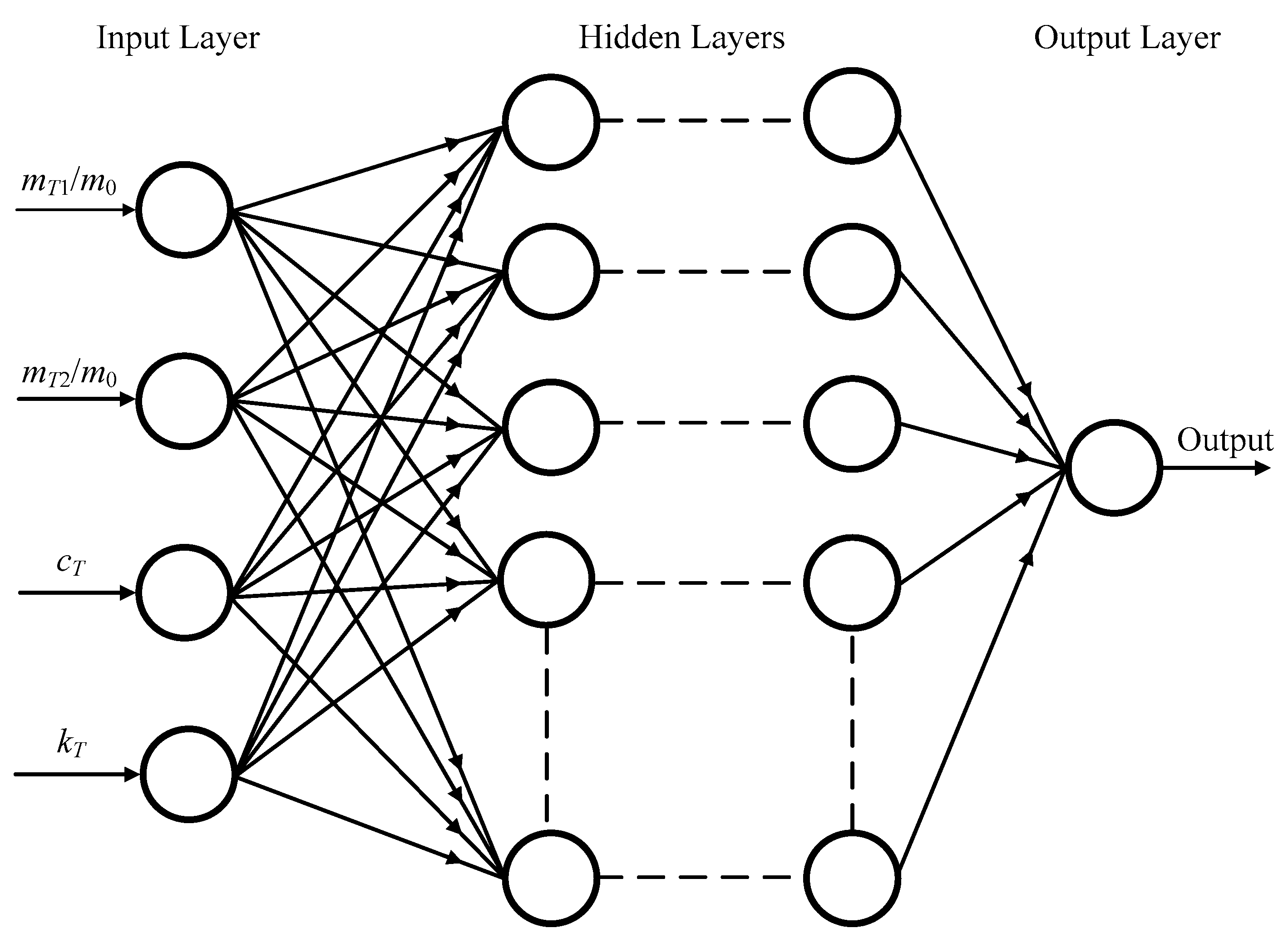
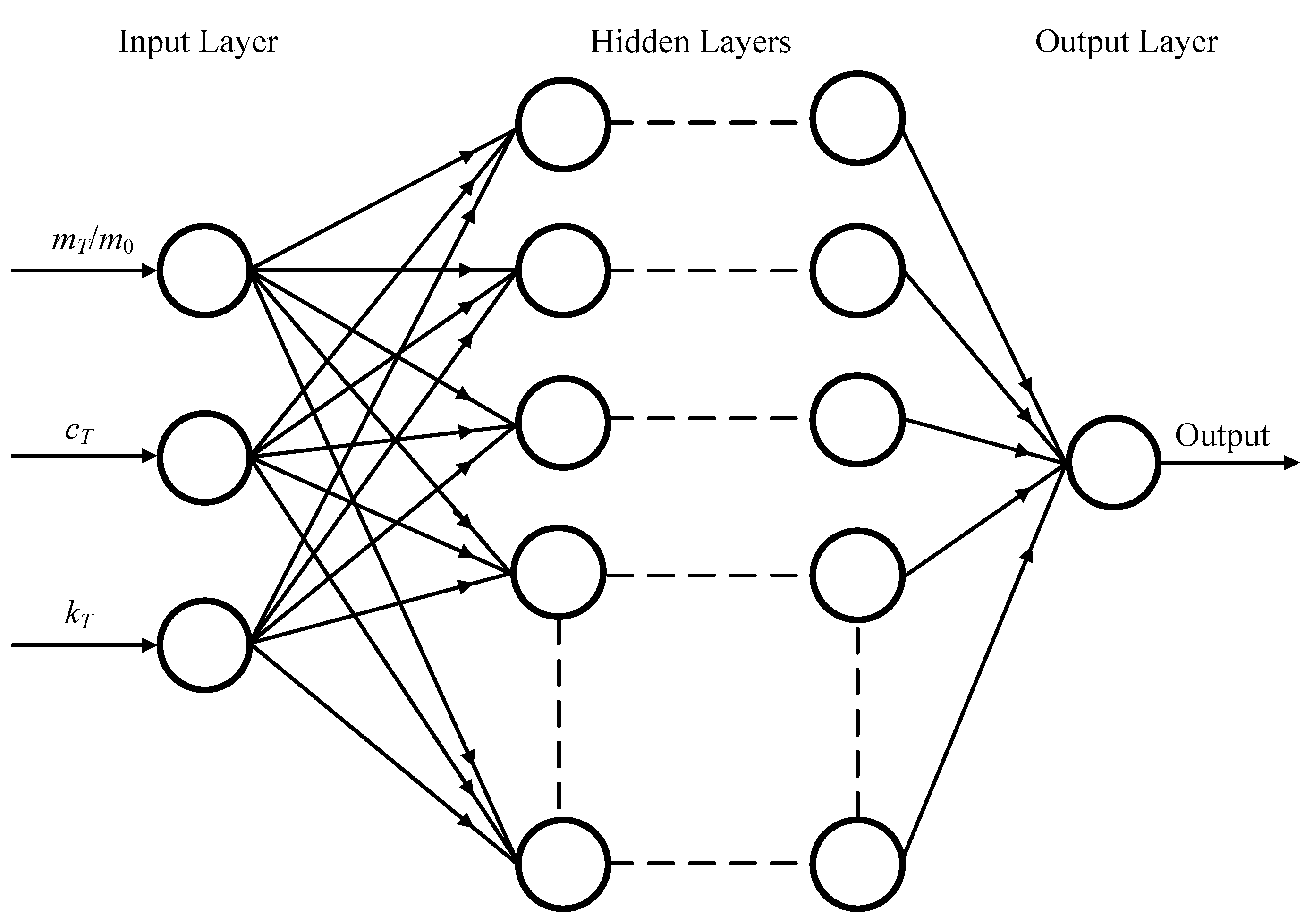
3. Artificial Neural Networks
4. Numerical Results and Discussions
4.1. Numerical Results for Free Vibration Analysis of the Beam and Frame System with a TMD
4.1.1. Accuracy Studies
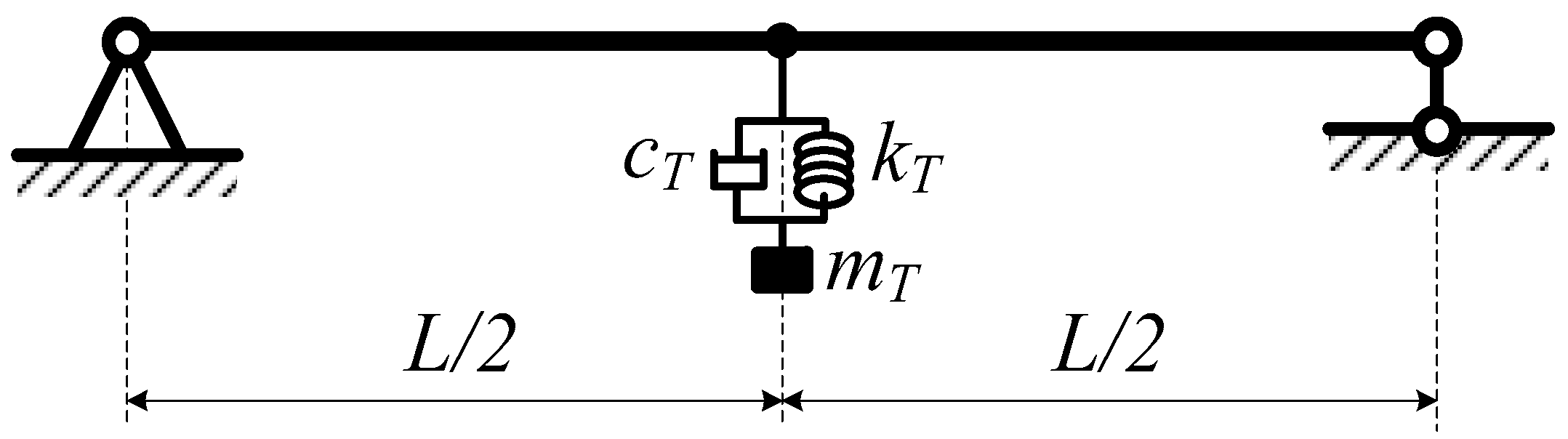
4.1.2. Numerical Results for Free Vibration Analysis of the Plane Beam with a TMD
The Beam with One TMD
The Beam with Three TMDs
4.2. Numerical Results for Free Vibration Analysis of the Space Frame System with a TMD
4.3. Setup of the ANN Model
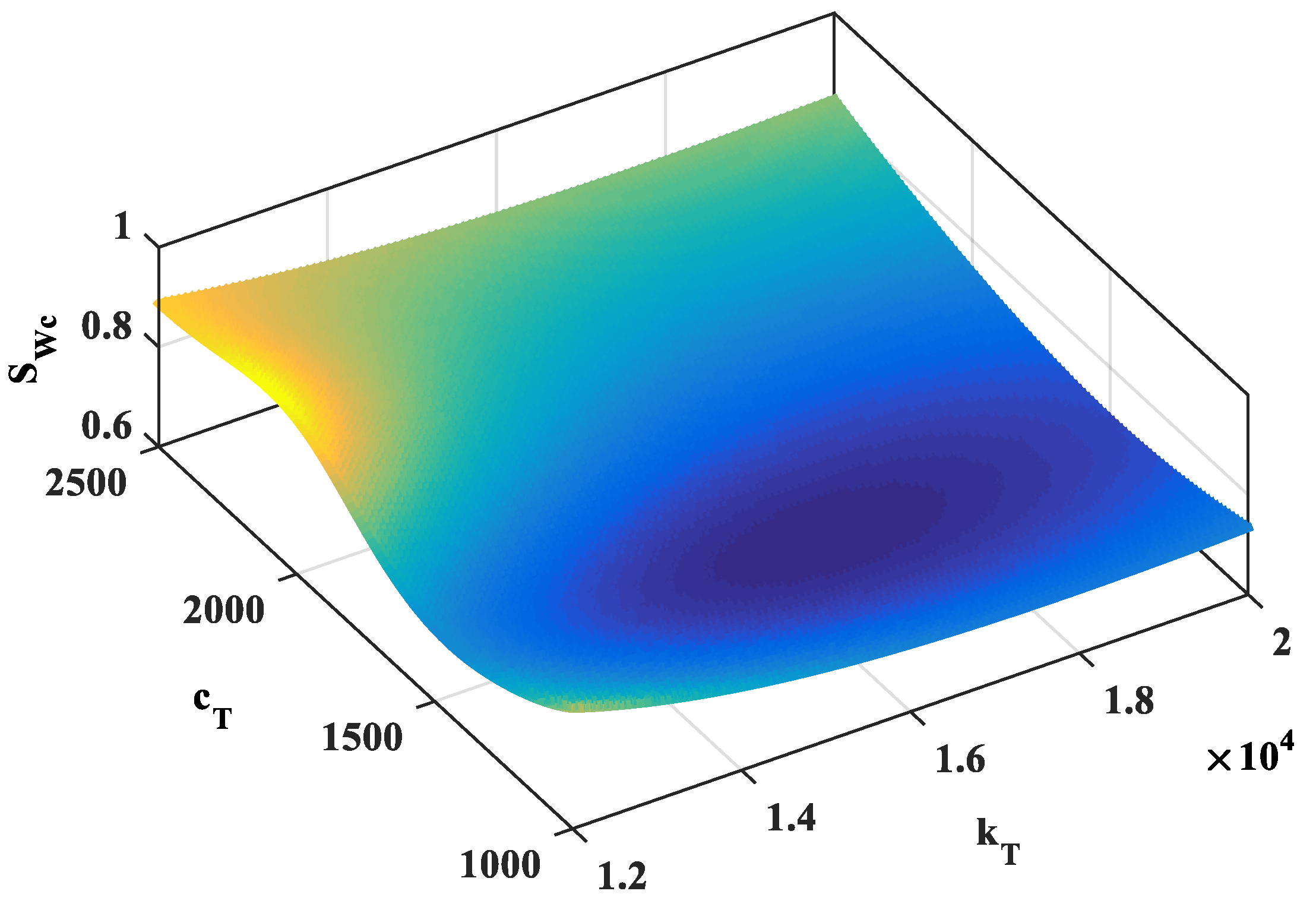
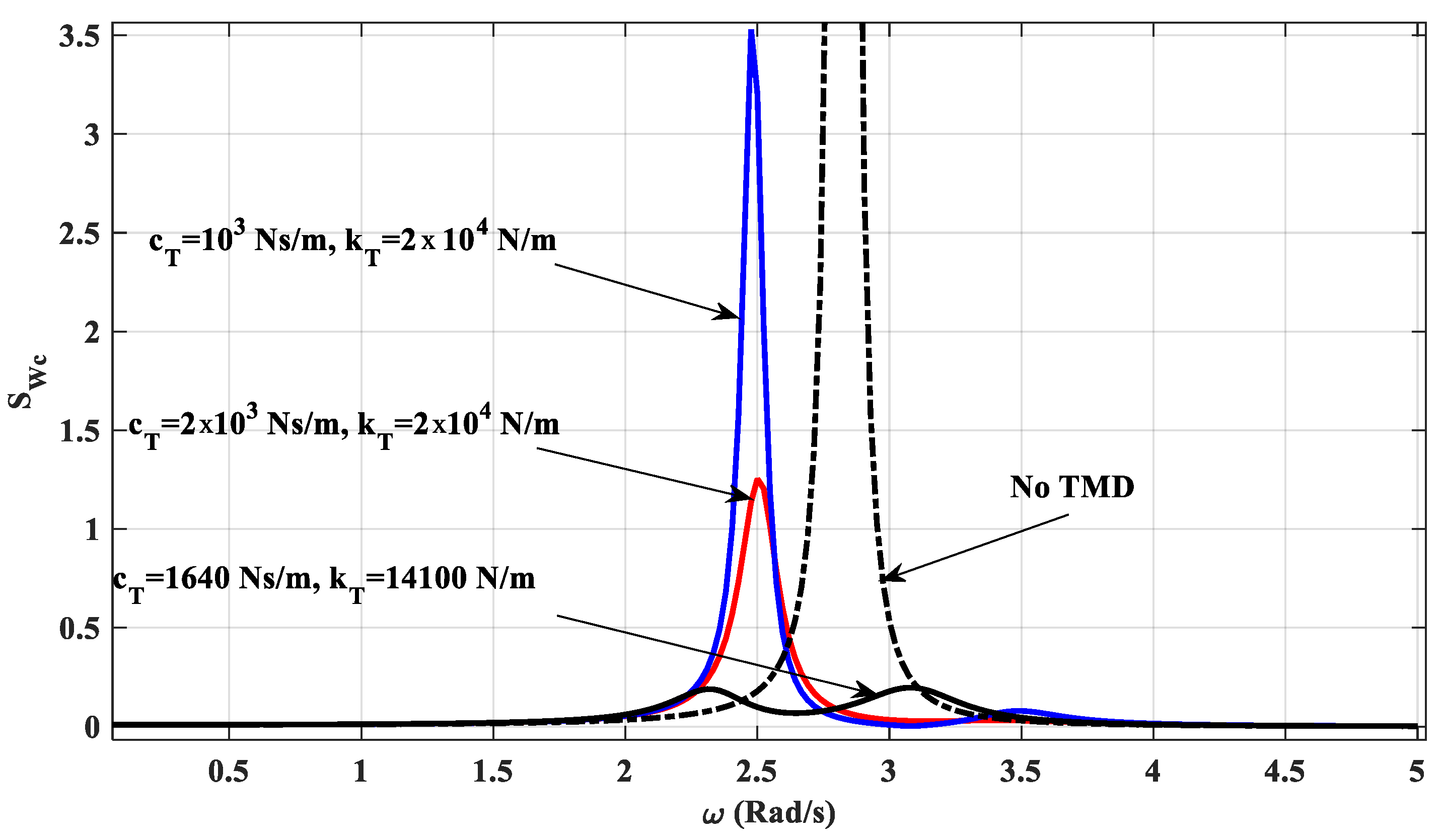
4.4. Numerical Results for Vibration Analysis of Beam with a TMD under Random Loading
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. The Shape Functions
Appendix A.2. The Distributed Mass Matrix Components
Appendix A.3. The Element Matrices
Appendix A.4. The Relationship of the Nodal Displacement Components between the Local Coordinate System and the Global Coordinate System of the Structure
References
- Frahm, H. Device for Damped Vibrations of Bodies. U.S. Patent 989,958, 30 October 1909. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations, 4th ed.; Dover: New York, NY, USA, 1985; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Weisner, K.B. Tuned mass dampers to reduce building wind motion. In ASCE Convention and Exposition, Preprint 3510; American Society of Civil Engineers: New York, NY, USA, 1979. [Google Scholar]
- Lu, Z.; Wang, D.C.; Masri, S.F.; Lu, X.L. An experimental study of vibration control of wind-excited high-rise buildings using particle tuned mass dampers. Smart Struct. Syst. 2016, 18, 93–115. [Google Scholar] [CrossRef]
- Venanzi, I. Robust optimal design of tuned mass dampers for tall buildings with uncertain parameters. Struct. Multidiscipl. Optim. 2015, 51, 239. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Veneziano, D.; John, M.B. Seismic effectiveness of tuned mass dampers. J. Struct. Div. 1981, 107, 1465–1484. [Google Scholar]
- Tuan, A.Y.; Shang, G.Q. Vibration control in a 10-storey building using a tuned mass damper. J. Appl. Sci. Eng. 2014, 17, 141–156. [Google Scholar]
- Domizio, M.N.; Ambrosini, D.; Curadelli, O. Performance of tuned mass damper against structural collapse due to near fault earthquakes. J. Sound 2015, 336, 32–45. [Google Scholar] [CrossRef]
- Krenk, S.; Høgsberg, J. Tuned mass absorbers on damped structures under random load. Probabilistic Eng. Mech. 2008, 23, 408–415. [Google Scholar] [CrossRef]
- Fujino, Y.; Abe, M. Design formulas for tuned mass dampers based on A perturbation technique. Earthq. Eng. Struct. Dyn. 1993, 22, 833–854. [Google Scholar] [CrossRef]
- Gerges, R.R.; Vickery, B.J. Optimum design of pendulum-type tuned mass dampers. Struct. Tall Build. 2005, 14, 353–368. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V. Bi-directional vibration control of offshore wind turbines using a 3D pendulum tuned mass damper. Mech. Syst. N.a. Process. 2018, 105, 338–360. [Google Scholar] [CrossRef]
- Di Matteo, A.; Furtmüller, T.; Adam, C.; Pirrotta, A. Optimal design of tuned liquid column dampers for seismic response control of base-isolated structures. Acta Mech. 2018, 229, 437–454. [Google Scholar] [CrossRef]
- Bigdeli, Y.; Kim, D. Damping effects of the passive control devices on structural vibration control: TMD, TLC and TLCD for varying total masses. J. Civil Eng. 2016, 20, 301–308. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; Roeck, G.D.; Van der Broeck, P. Robust design of a TMD for the vibration serviceability of a footbridge. Eng. Struct. 2016, 123, 408–418. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Sáez, A. Motion-base ddesign of TMD for vibrating footbridges under uncertainty conditions. Smart Struct. Syst. 2018, 21, 727–740. [Google Scholar]
- Tributsch, A.; Adam, C. Evaluation and analytical approximation of Tuned Mass Damper performance in an earthquake environment. Smart Struct. Syst. 2012, 10, 155–179. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Earthquake-resilient design of base isolated buildings with TMD at basement: Application to a case study. Soil Dyn. Earthq. Eng. 2018, 113, 503–521. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1367–1388. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study. Struct. Control Hlth. 2018, 25, e2234. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Along-wind response control of chimneys with distributed multiple tuned mass dampers. Struct. Heal. Monit. 2018, 26, e2275. [Google Scholar] [CrossRef]
- Hashimoto, T.; Fujita, K.; Tsuji, M.; Takewaki, I. Innovative base-isolated building with large mass-ratio TMD at basement for greater earthquake resilience. Futur. Cities 2015, 1, 9. [Google Scholar] [CrossRef]
- What is a Neural Net? Available online: http://www.cormactech.com/neunet/whatis.html (accessed on 2 March 2019).
- Issa, A. Computational control of laser systems for micro-machining. Ph.D. Thesis, Dublin City University, Dublin, Ireland, 2007. [Google Scholar]
- Ye, J.; Yuan, X.C.; Zhou, G. Genetic algorithm for optimization design of diffractive optical elements in laser beam shaping. Proceed. SPIE 2003, 4594, 118–127. [Google Scholar]
- Xie, S.Q. Optimal process planning for a combined punch-and-laser cutting machine using ant colony optimization. Int. J. Prod. 2005, 43, 2195–2216. [Google Scholar]
- Shen, H.; Shi, Y.J.; Yao, Z.Q.; Hu, J. Fuzzy logic model for bending angle in laser forming. Mater. Sci. Technol. 2006, 22, 981–986. [Google Scholar] [CrossRef]
- De Deus, A.M.; Mazumder, J. Two-dimensional thermo-mechanical finite element model for laser cladding. J. Laser Appl. 1996, B174–B183. [Google Scholar] [CrossRef]
- Mohsen, O.S.; Ali, M. The ANN application in FEM modeling of mechanical properties of Al–Si alloy. Appl. Math. Model. 2011, 35, 5707–5713. [Google Scholar]
- Esmailzadeh, M.; Aghaie-Khafri, M. Finite element and artificial neural network analysis of ECAP. Comput. Mater. Sci. 2012, 63, 127–133. [Google Scholar] [CrossRef]
- Miguel, A.; Komal, R.; Konstantinos, D.T.; Tiago, P.R. Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams. Computers 2019, 8, 2. [Google Scholar]
- Yung, H.C.; Yen, H.H. Timoshenko beam with tuned mass dampers and its design curves. J. Sound Vib. 2004, 278, 873–888. [Google Scholar]


| mT/m0 (%) | cT (Ns/m) | kT (N/m) | Beam without TMD | Beam with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 1 | 100 | 2000 | 1.161 | 5.093 | 19.933 | 63.312 | 0.887 | 1.178 | 5.093 | 19.937 |
| 2 | 0.631 | 1.171 | 5.093 | 19.937 | ||||||
| 3 | 0.516 | 1.169 | 5.093 | 19.937 | ||||||
| 4 | 0.447 | 1.169 | 5.093 | 19.937 | ||||||
| 5 | 0.400 | 1.169 | 5.093 | 19.937 | ||||||
| 6 | 0.365 | 1.169 | 5.093 | 19.937 | ||||||
| 7 | 0.338 | 1.168 | 5.093 | 19.937 | ||||||
| 8 | 0.316 | 1.168 | 5.093 | 19.937 | ||||||
| 9 | 0.298 | 1.168 | 5.093 | 19.937 | ||||||
| 10 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| mT/m0 (%) | cT (Ns/m) | kT (N/m) | Beam without TMD | Beam with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 10 | 10 | 2000 | 1.161 | 5.093 | 19.933 | 63.312 | 0.283 | 1.168 | 5.093 | 19.937 |
| 20 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 100 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 150 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 300 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 500 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 700 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 800 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 1000 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| mT/m0 (%) | cT (Ns/m) | kT (N/m) | Beam without TMD | Beam with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 10 | 100 | 100 | 1.161 | 5.093 | 19.933 | 63.312 | 0.063 | 1.161 | 5.093 | 19.935 |
| 500 | 0.142 | 1.162 | 5.093 | 19.936 | ||||||
| 1000 | 0.200 | 1.164 | 5.093 | 19.936 | ||||||
| 1500 | 0.245 | 1.166 | 5.093 | 19.936 | ||||||
| 2000 | 0.283 | 1.168 | 5.093 | 19.937 | ||||||
| 3000 | 0.345 | 1.172 | 5.093 | 19.937 | ||||||
| 5000 | 0.442 | 1.181 | 5.093 | 19.938 | ||||||
| 8000 | 0.552 | 1.197 | 5.093 | 19.940 | ||||||
| 10,000 | 0.611 | 1.209 | 5.093 | 19.941 | ||||||
| mT2/m0 (%) | mT1/m0 (%) | cT1 (Ns/m) | kT1 (N/m) | Beam without TMD | Beam with Three TMDs | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | ||||
| 1 | 4.0 | 102 | 2000 | 1.161 | 5.093 | 19.933 | 63.312 | 0.447 | 0.450 | 0.888 | 1.185 |
| 1 | 3.0 | 0.516 | 0.519 | 0.888 | 1.186 | ||||||
| 1 | 2.0 | 0.631 | 0.638 | 0.888 | 1.187 | ||||||
| 1 | 1.0 | 0.876 | 0.900 | 0.901 | 1.193 | ||||||
| 2 | 4.0 | 0.447 | 0.450 | 0.631 | 1.179 | ||||||
| 2 | 3.0 | 0.512 | 0.519 | 0.631 | 1.179 | ||||||
| 2 | 2.0 | 0.626 | 0.636 | 0.637 | 1.180 | ||||||
| 2 | 1.0 | 0.631 | 0.888 | 0.900 | 1.187 | ||||||
| 3 | 3 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 3 | 2 | 0.516 | 0.632 | 0.636 | 1.179 | ||||||
| 3 | 1 | 0.516 | 0.888 | 0.900 | 1.186 | ||||||
| 4 | 3 | 0.447 | 0.516 | 0.519 | 1.178 | ||||||
| 4 | 2 | 0.447 | 0.631 | 0.636 | 1.179 | ||||||
| 4 | 1 | 0.447 | 0.888 | 0.900 | 1.185 | ||||||
| 5 | 2 | 0.400 | 0.631 | 0.636 | 1.178 | ||||||
| 5 | 1 | 0.400 | 0.888 | 0.900 | 1.185 | ||||||
| mT2/m0 (%) | cT1 (Ns/m) | kT1 (N/m) | Beam without TMD | Beam with Three TMDs | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 3 | 10 | 2000 | 1.161 | 5.093 | 19.933 | 63.312 | 0.512 | 0.519 | 0.520 | 1.178 |
| 20 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 100 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 150 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 300 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 500 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 700 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 800 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 1000 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| mT2/m0 (%) | cT1 (Ns/m) | kT1 (N/m) | Beam without TMD | Beam with Three TMDs | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 3 | 100 | 100 | 1.161 | 5.093 | 19.933 | 63.312 | 0.116 | 0.117 | 0.118 | 1.161 |
| 500 | 0.259 | 0.260 | 0.261 | 1.164 | ||||||
| 1000 | 0.365 | 0.367 | 0.368 | 1.168 | ||||||
| 1500 | 0.445 | 0.450 | 0.451 | 1.173 | ||||||
| 2000 | 0.512 | 0.519 | 0.520 | 1.178 | ||||||
| 3000 | 0.621 | 0.636 | 0.637 | 1.190 | ||||||
| 5000 | 0.780 | 0.821 | 0.822 | 1.224 | ||||||
| 8000 | 0.924 | 1.037 | 1.040 | 1.306 | ||||||
| 10,000 | 0.976 | 1.159 | 1.162 | 1.382 | ||||||
| Method | |||
|---|---|---|---|
| SAP-2000 | 4.437 | 6.375 | 6.784 |
| This work | 4.426 | 6.039 | 6.522 |
| mT/m0 (%) | cT (Ns/m) | kT (N/m) | The Frame System without TMD | The Frame System with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 1 | 103 | 104 | 0.704 | 0.961 | 1.038 | 1.283 | 0.475 | 0.704 | 0.961 | 1.038 |
| 2 | 0.336 | 0.704 | 0.961 | 1.038 | ||||||
| 3 | 0.274 | 0.704 | 0.961 | 1.038 | ||||||
| 4 | 0.237 | 0.704 | 0.961 | 1.038 | ||||||
| 5 | 0.212 | 0.704 | 0.961 | 1.038 | ||||||
| 6 | 0.194 | 0.704 | 0.961 | 1.038 | ||||||
| 7 | 0.179 | 0.704 | 0.961 | 1.038 | ||||||
| 8 | 0.168 | 0.704 | 0.961 | 1.038 | ||||||
| 9 | 0.158 | 0.704 | 0.961 | 1.038 | ||||||
| 10 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| mT/m0 (%) | cT (Ns/m) | kT (N/m) | The Frame System without TMD | The Frame System with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |||
| 10 | 103 | 5000 | 0.704 | 0.961 | 1.038 | 1.283 | 0.106 | 0.704 | 0.961 | 1.038 |
| 7000 | 0.126 | 0.704 | 0.961 | 1.038 | ||||||
| 8000 | 0.134 | 0.704 | 0.961 | 1.038 | ||||||
| 10,000 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 12,000 | 0.164 | 0.704 | 0.961 | 1.038 | ||||||
| 15,000 | 0.184 | 0.704 | 0.961 | 1.038 | ||||||
| 18,000 | 0.201 | 0.704 | 0.961 | 1.038 | ||||||
| 20,000 | 0.212 | 0.704 | 0.961 | 1.038 | ||||||
| 25,000 | 0.237 | 0.704 | 0.961 | 1.038 | ||||||
| mT/m0 (%) | cT (Ns/m) | kT (N/m) | The Frame System without TMD | The Frame System with One TMD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| f1 (Hz) | f2 (Hz) | f1 (Hz) | f2 (Hz) | f1 (Hz) | f2 (Hz) | f1 (Hz) | f2 (Hz) | |||
| 10 | 100 | 104 | 0.704 | 0.961 | 1.038 | 1.283 | 0.150 | 0.704 | 0.961 | 1.038 |
| 500 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 800 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 1000 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 1400 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 1600 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 1800 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 2000 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| 2500 | 0.150 | 0.704 | 0.961 | 1.038 | ||||||
| Order | mT2/m0 (%) | mT1/m0 (%) | cT (Ns/m) | kT (N/m) | Target f1 (Hz) | Predict f1 (Hz) |
|---|---|---|---|---|---|---|
| 1 | 1 | 4.0 | 100 | 2000 | 0.447 | 0.447 |
| 2 | 1 | 3.0 | 100 | 2000 | 0.516 | 0.516 |
| 3 | 1 | 2.0 | 100 | 2000 | 0.631 | 0.631 |
| 4 | 1 | 1.0 | 100 | 2000 | 0.876 | 0.876 |
| 5 | 2 | 4.0 | 100 | 2000 | 0.447 | 0.447 |
| 6 | 2 | 3.0 | 100 | 2000 | 0.512 | 0.512 |
| 7 | 2 | 2.0 | 100 | 2000 | 0.626 | 0.626 |
| 8 | 2 | 1.0 | 100 | 2000 | 0.631 | 0.631 |
| 9 | 3 | 3 | 100 | 2000 | 0.512 | 0.512 |
| 10 | 3 | 2 | 100 | 2000 | 0.516 | 0.516 |
| 11 | 3 | 1 | 100 | 2000 | 0.516 | 0.5199 |
| 12 | 4 | 3 | 100 | 2000 | 0.447 | 0.447 |
| 13 | 4 | 2 | 100 | 2000 | 0.447 | 0.447 |
| 14 | 4 | 1 | 100 | 2000 | 0.447 | 0.447 |
| 15 | 5 | 2 | 100 | 2000 | 0.400 | 0.400 |
| 16 | 5 | 1 | 100 | 2000 | 0.400 | 0.400 |
| 17 | 3 | 3 | 10 | 2000 | 0.512 | 0.512 |
| 18 | 3 | 3 | 20 | 2000 | 0.512 | 0.512 |
| 19 | 3 | 3 | 150 | 2000 | 0.512 | 0.512 |
| 20 | 3 | 3 | 300 | 2000 | 0.512 | 0.512 |
| 21 | 3 | 3 | 500 | 2000 | 0.512 | 0.512 |
| 22 | 3 | 3 | 700 | 2000 | 0.512 | 0.512 |
| 23 | 3 | 3 | 800 | 2000 | 0.512 | 0.5097 |
| 24 | 3 | 3 | 1000 | 2000 | 0.512 | 0.512 |
| 25 | 3 | 3 | 100 | 100 | 0.116 | 0.116 |
| 26 | 3 | 3 | 100 | 500 | 0.259 | 0.259 |
| 27 | 3 | 3 | 100 | 1000 | 0.365 | 0.365 |
| 28 | 3 | 3 | 100 | 1500 | 0.445 | 0.445 |
| 29 | 3 | 3 | 100 | 3000 | 0.621 | 0.6195 |
| 30 | 3 | 3 | 100 | 5000 | 0.780 | 0.790 |
| 31 | 3 | 3 | 100 | 8000 | 0.924 | 0.924 |
| 32 | 3 | 3 | 100 | 10,000 | 0.976 | 0.976 |
| EAverage (%) | 0.0017 | |||||
| Emax (%) | 0.7484 |
| Order | mT/m0 (%) | cT (Ns/m) | kT (N/m) | Target f1 (Hz) | Predict f2 (Hz) |
|---|---|---|---|---|---|
| 1 | 1 | 1000 | 10,000 | 0.475 | 0.475 |
| 2 | 2 | 1000 | 10,000 | 0.336 | 0.336 |
| 3 | 3 | 1000 | 10,000 | 0.274 | 0.2739 |
| 4 | 4 | 1000 | 10,000 | 0.237 | 0.2372 |
| 5 | 5 | 1000 | 10,000 | 0.212 | 0.2121 |
| 6 | 6 | 1000 | 10,000 | 0.194 | 0.1936 |
| 7 | 7 | 1000 | 10,000 | 0.179 | 0.1794 |
| 8 | 8 | 1000 | 10,000 | 0.168 | 0.1678 |
| 9 | 9 | 1000 | 10,000 | 0.158 | 0.158 |
| 10 | 10 | 1000 | 10,000 | 0.150 | 0.150 |
| 11 | 10 | 1000 | 5000 | 0.106 | 0.1061 |
| 12 | 10 | 1000 | 7000 | 0.126 | 0.1256 |
| 13 | 10 | 1000 | 8000 | 0.134 | 0.1343 |
| 14 | 10 | 1000 | 12,000 | 0.164 | 0.1643 |
| 15 | 10 | 1000 | 15,000 | 0.184 | 0.1838 |
| 16 | 10 | 1000 | 18,000 | 0.201 | 0.2013 |
| 17 | 10 | 1000 | 20,000 | 0.212 | 0.2118 |
| 18 | 10 | 1000 | 25,000 | 0.237 | 0.237 |
| 19 | 10 | 100 | 10,000 | 0.150 | 0.150 |
| 20 | 10 | 500 | 10,000 | 0.150 | 0.150 |
| 21 | 10 | 800 | 10,000 | 0.150 | 0.150 |
| 22 | 10 | 1400 | 10,000 | 0.150 | 0.150 |
| 23 | 10 | 1600 | 10,000 | 0.150 | 0.150 |
| 24 | 10 | 1800 | 10,000 | 0.150 | 0.150 |
| 25 | 10 | 2000 | 10,000 | 0.150 | 0.150 |
| 26 | 10 | 2500 | 10,000 | 0.150 | 0.150 |
| EAverage (%) | 0.0073 | ||||
| Emax (%) | 0.3052 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tho, N.C.; Ta, N.T.; Thom, D.V. New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials 2019, 12, 1329. https://doi.org/10.3390/ma12081329
Tho NC, Ta NT, Thom DV. New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials. 2019; 12(8):1329. https://doi.org/10.3390/ma12081329
Chicago/Turabian StyleTho, Nguyen Chi, Nguyen Tri Ta, and Do Van Thom. 2019. "New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper" Materials 12, no. 8: 1329. https://doi.org/10.3390/ma12081329
APA StyleTho, N. C., Ta, N. T., & Thom, D. V. (2019). New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials, 12(8), 1329. https://doi.org/10.3390/ma12081329




