Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis
Abstract
:1. Introduction
2. State of the Art on Retrofitting Techniques for Masonry Structures
2.1. Active and Passive Strengthening
2.2. Some Recent Active Retrofitting Techniques For Masonry Buildings
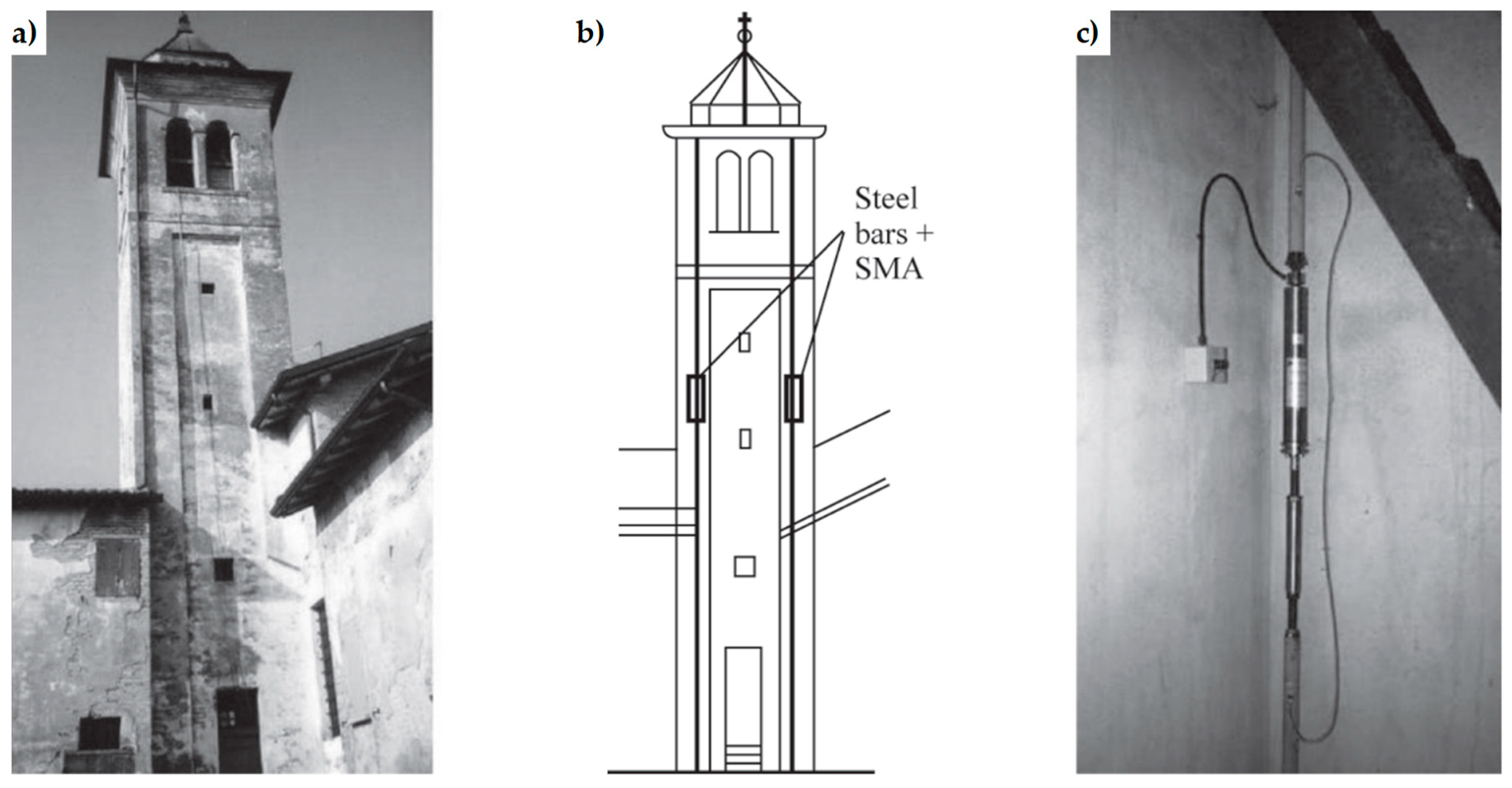
2.2.1. Punctual Retrofitting Techniques
2.2.2. Continuous Retrofitting Techniques
- It is no longer necessary to anchor the ties into the masonry, because the ribbons close on themselves. This eliminates the problem of the excessive concentrations of stresses induced by the anchorages.
- The straps are made of stainless steel. This avoids the typical corrosion problems of tie rods [50], which need of a suitable covering or galvanization zinc plating.
- The cross-section of the straps is very small. This allows a moderate increase in the total weight of the structure, useful to not increase the attraction of seismic forces too much.
- Each strap is a bi-dimensional device. This allows the ribbons to provide in-plane and transversal post-compression at the same time.
- The steel ribbons continue to wrap masonry even after masonry crushing. This is of fundamental importance for safeguarding life, as people do not risk that some part of the structure hits them, due to building collapse.
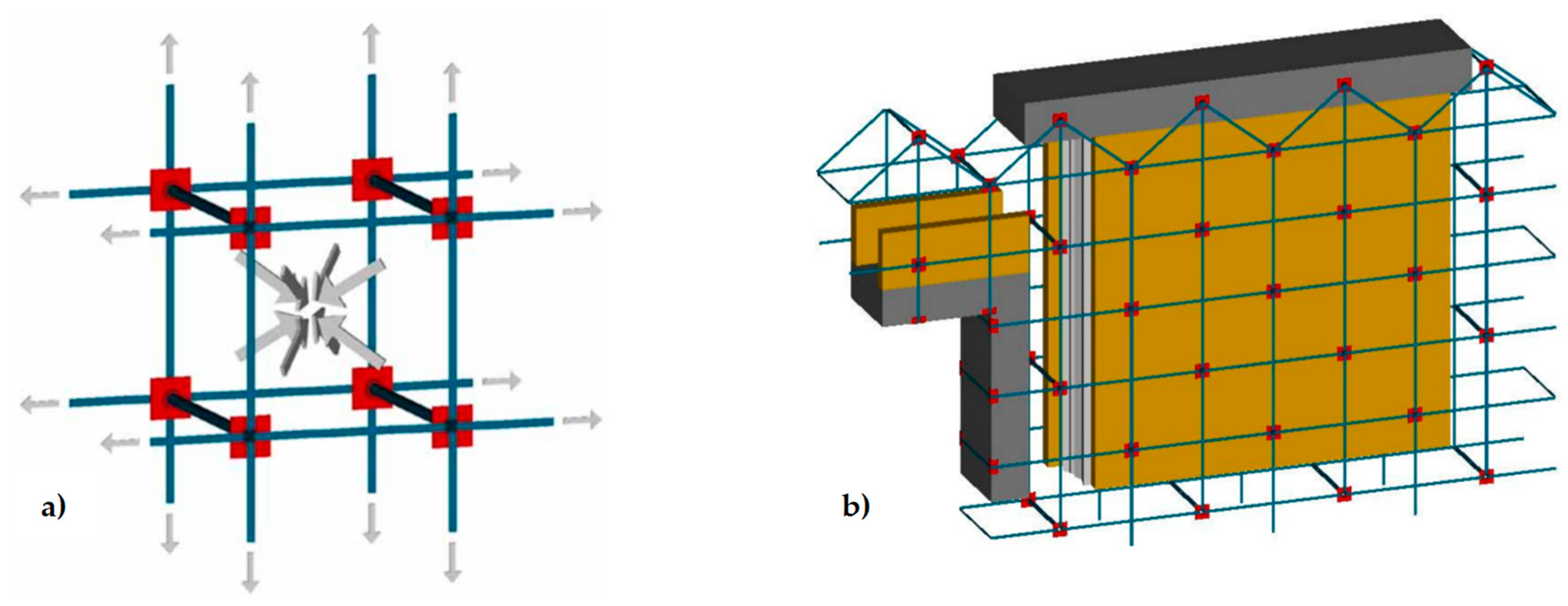
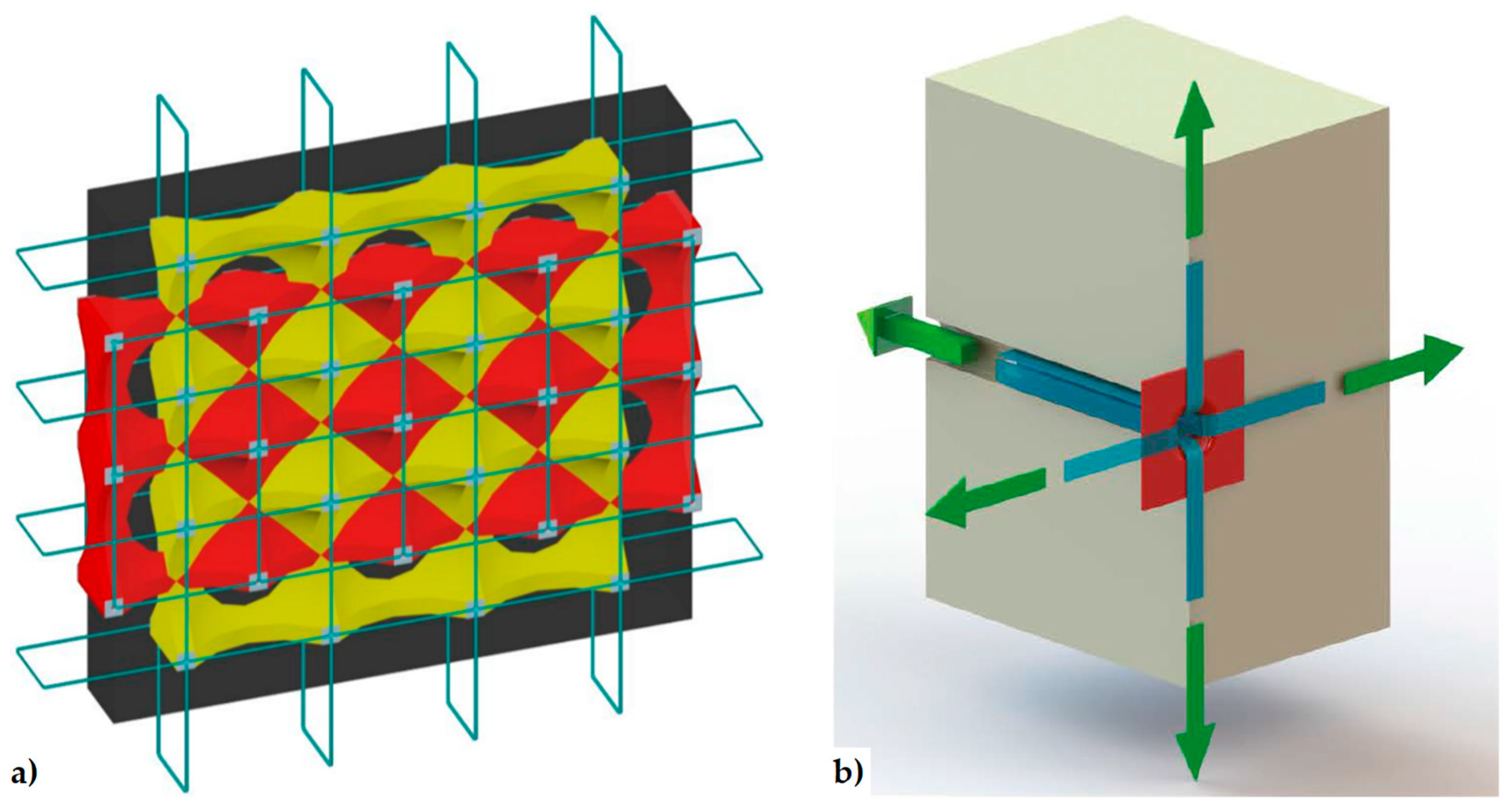
3. An in-Depth Study of the Three-Dimensional Continuous Systems: The Actual Strengthening Mechanisms
3.1. The Φ System
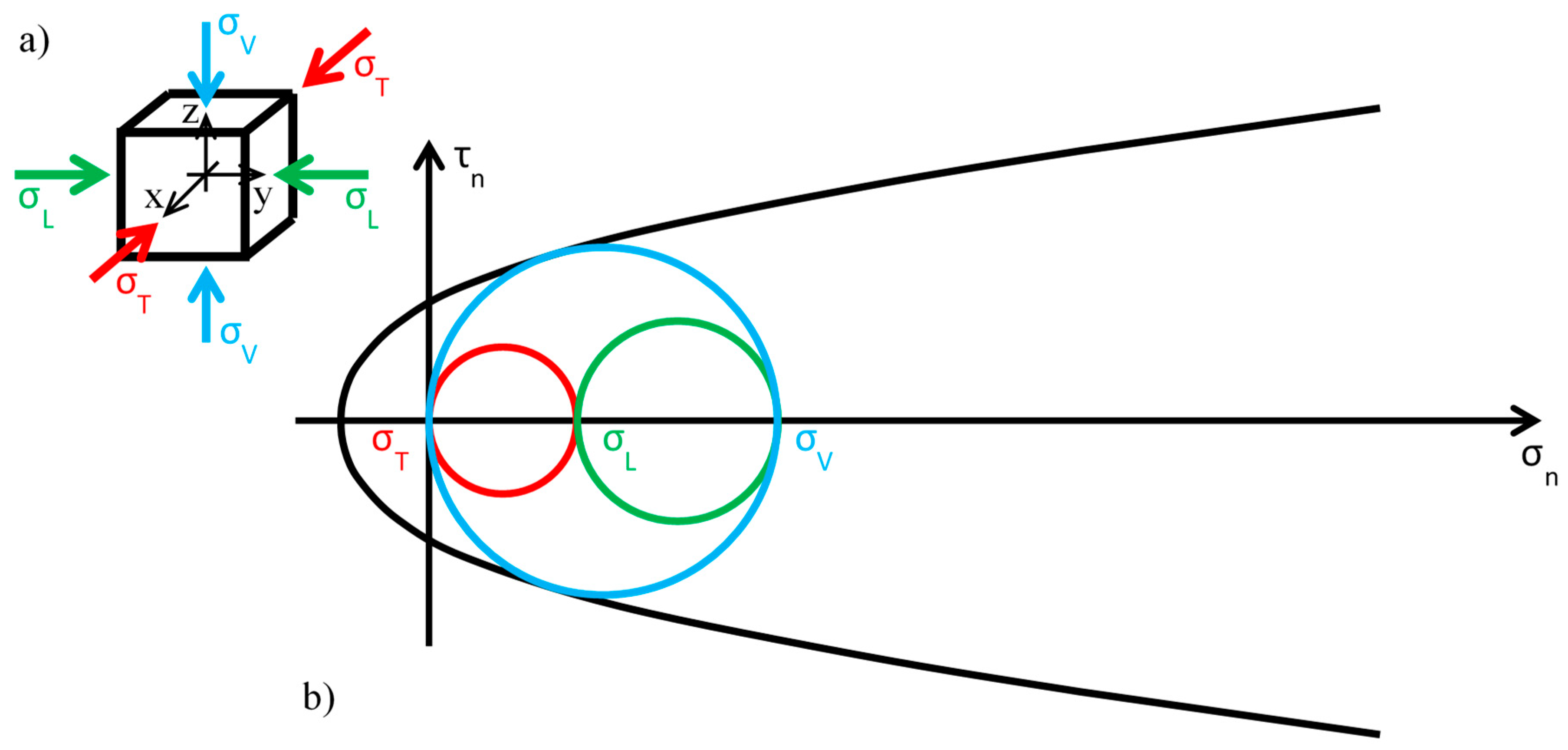
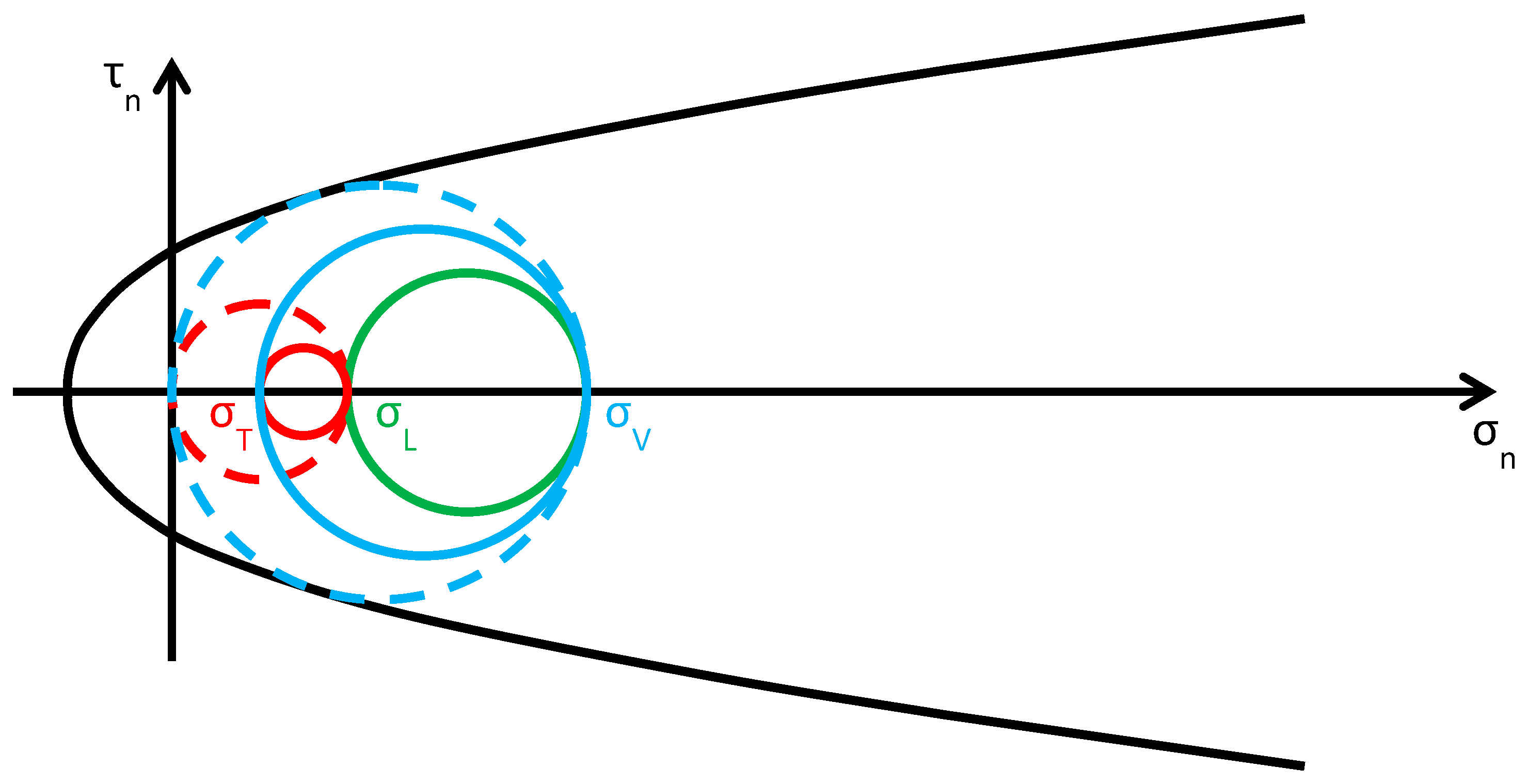
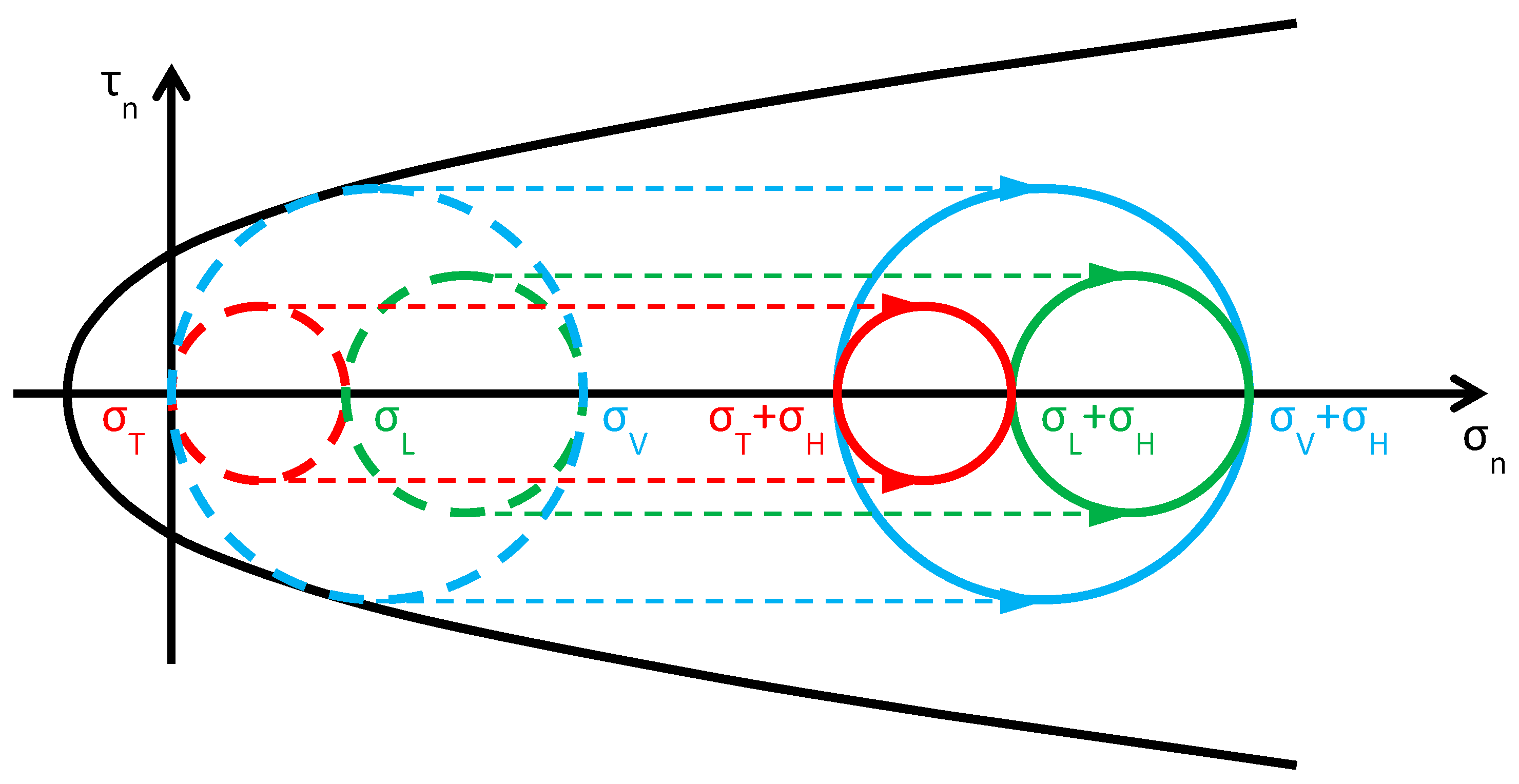
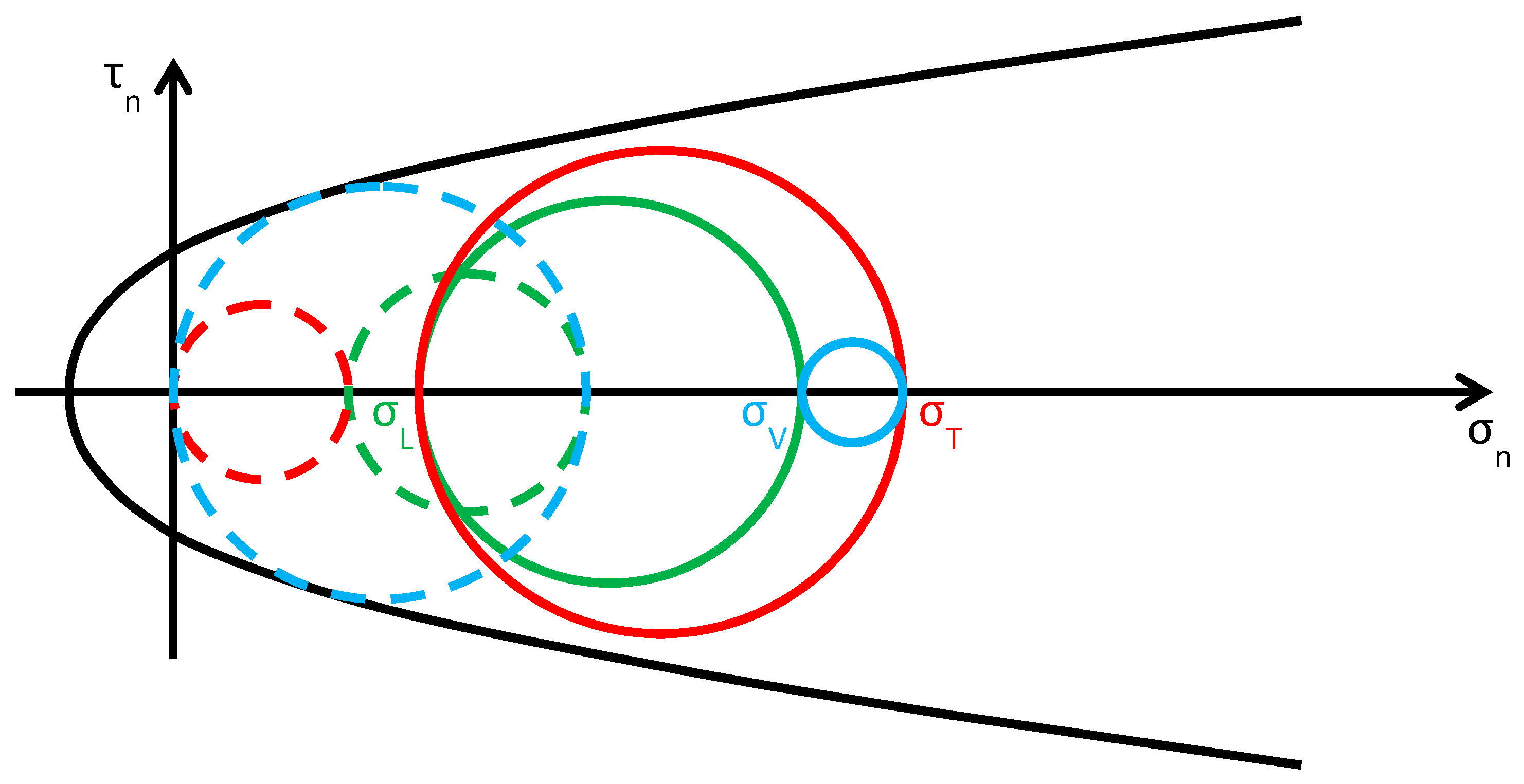
- (Figure 16): the greatest circle is associated with the plane (blue circle). Both the red and blue circles become smaller and move away from the limit surface. This increases the minimum distance between the greatest circle and the limit surface, which provides a measure of the safety factor. Thus, the higher the value of in this interval, the higher the safety factor. In other words, the retrofitting intervention is effective in this field. More precisely, it is all the more effective the higher the out-of-plane post-compression. At the end of the interval, when , the red circle degenerates into a point and the blue circle superimposes onto the green circle.
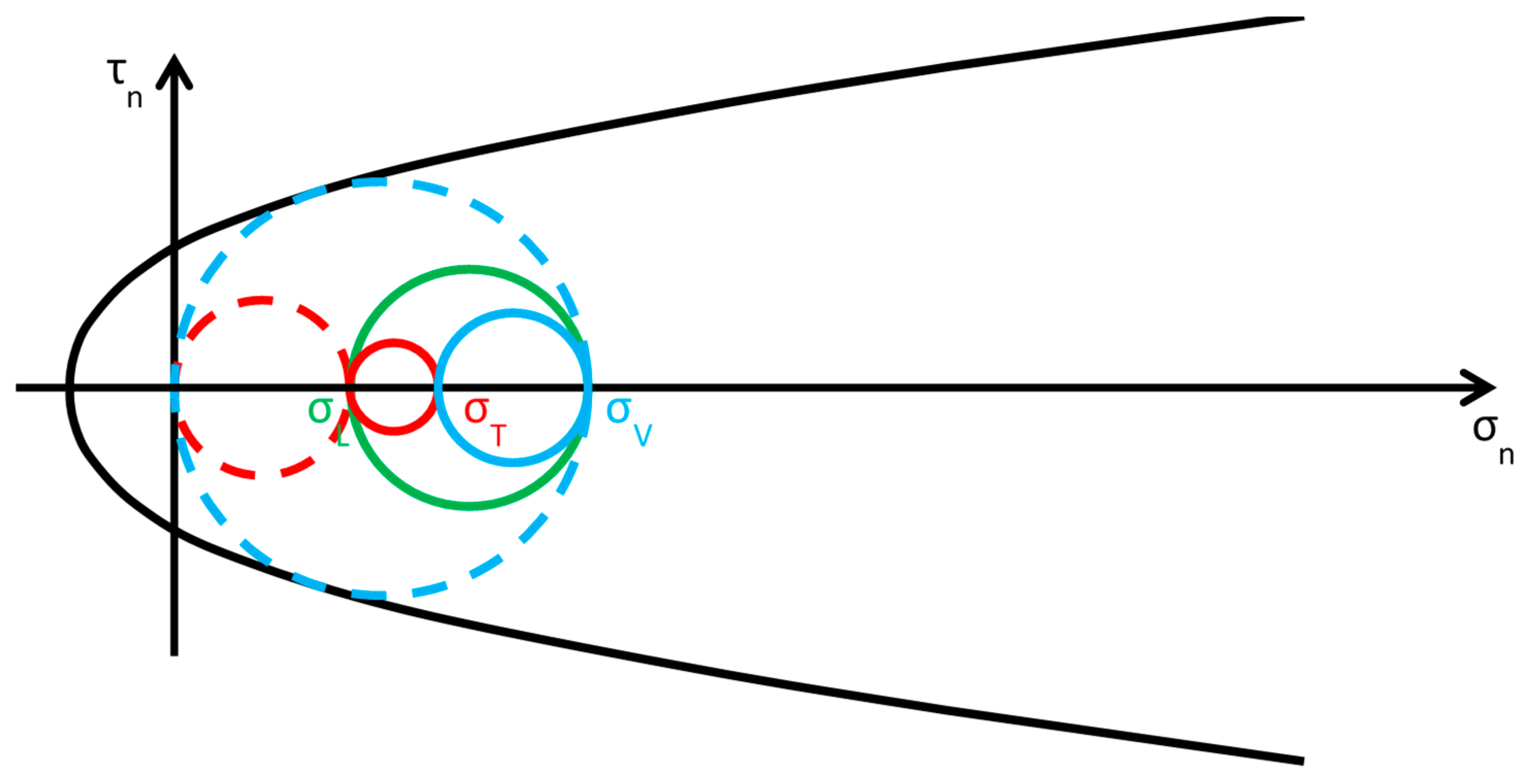
- (Figure 17): the greatest circle is associated with the plane (green circle). When the out-of-plane compression, , increases from the value to the value (in absolute value), the radius of the red circle increases while the radius of the blue circle decreases. It could seem that the safety factor does not change in this interval: since the radius of the greatest (green) circle does not modify, the safety factor does not seem to depend on the value of . In fact, the discussion about the safety factor is a bit more complex. As a matter of fact, retrofitting the masonry wall modifies the overall behavior of the wall, that is, modifies the limit surface, all the more greater as the stress of the threaded bars increases. The new limit surface is a combination of the two limit surfaces of masonry and steel. Thus, it seems reasonable that the new limit surface is wider and flatter than the limit surface in Figure 17. In conclusion, if computed as the minimum distance between the greatest circle and the combined limit surface, the safety factor slightly increases even in this interval. At the end of the interval, when , the red circle superimposes onto the green circle and the blue circle degenerates into a point.
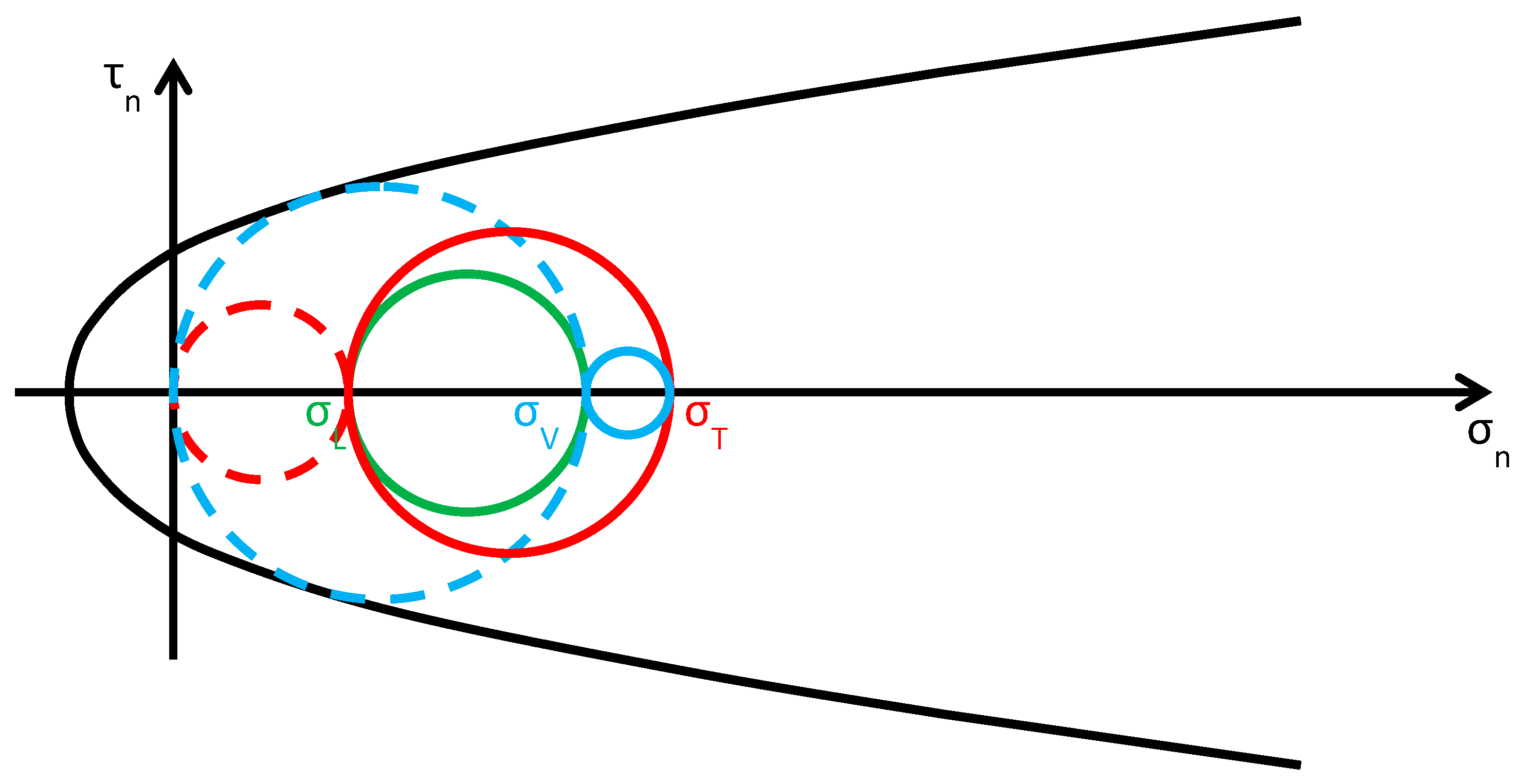
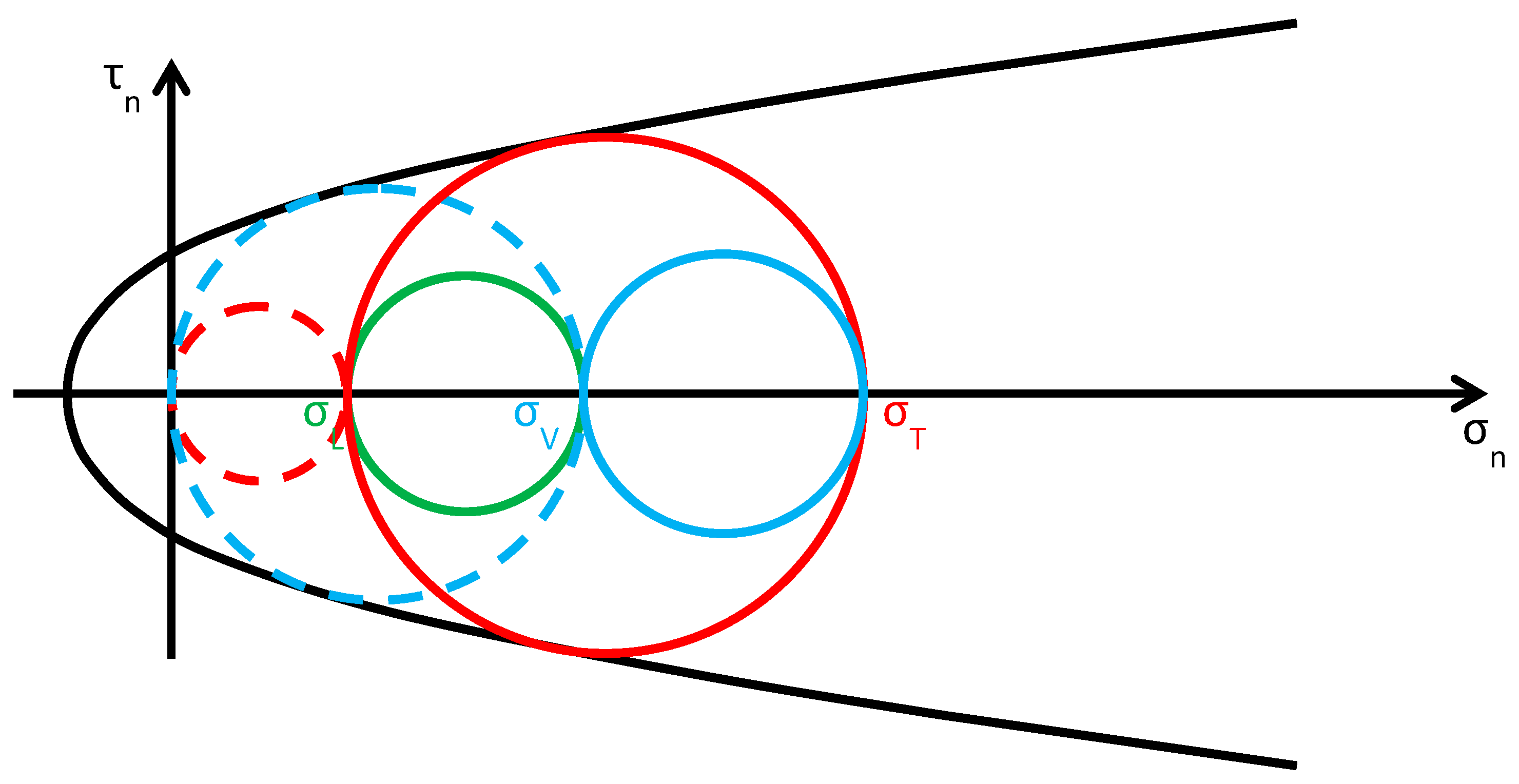
- (Figure 18): the greatest circle is associated with the plane (red circle). Both the red and blue circles become greater. In particular, the red circle grows closer to the limit surface of masonry. This decreases the minimum distance between the greatest circle and the masonry limit surface. The minimum distance between the greatest circle and the combined limit surface also decreases, but slower than the previous one. In conclusion, in the third interval the combined safety factor decreases. Moreover, there are two limit values of : the first limit value of makes the red circle tangent to the masonry limit surface (Figure 19) and the second limit value, , higher than the previous one (in absolute value), makes the red circle tangent to the combined limit surface. The crisis takes place for the second limit value and occurs in a plane parallel to the z axis. Thus, the retrofitting system modifies the crisis mechanism.
3.2. The CAM System
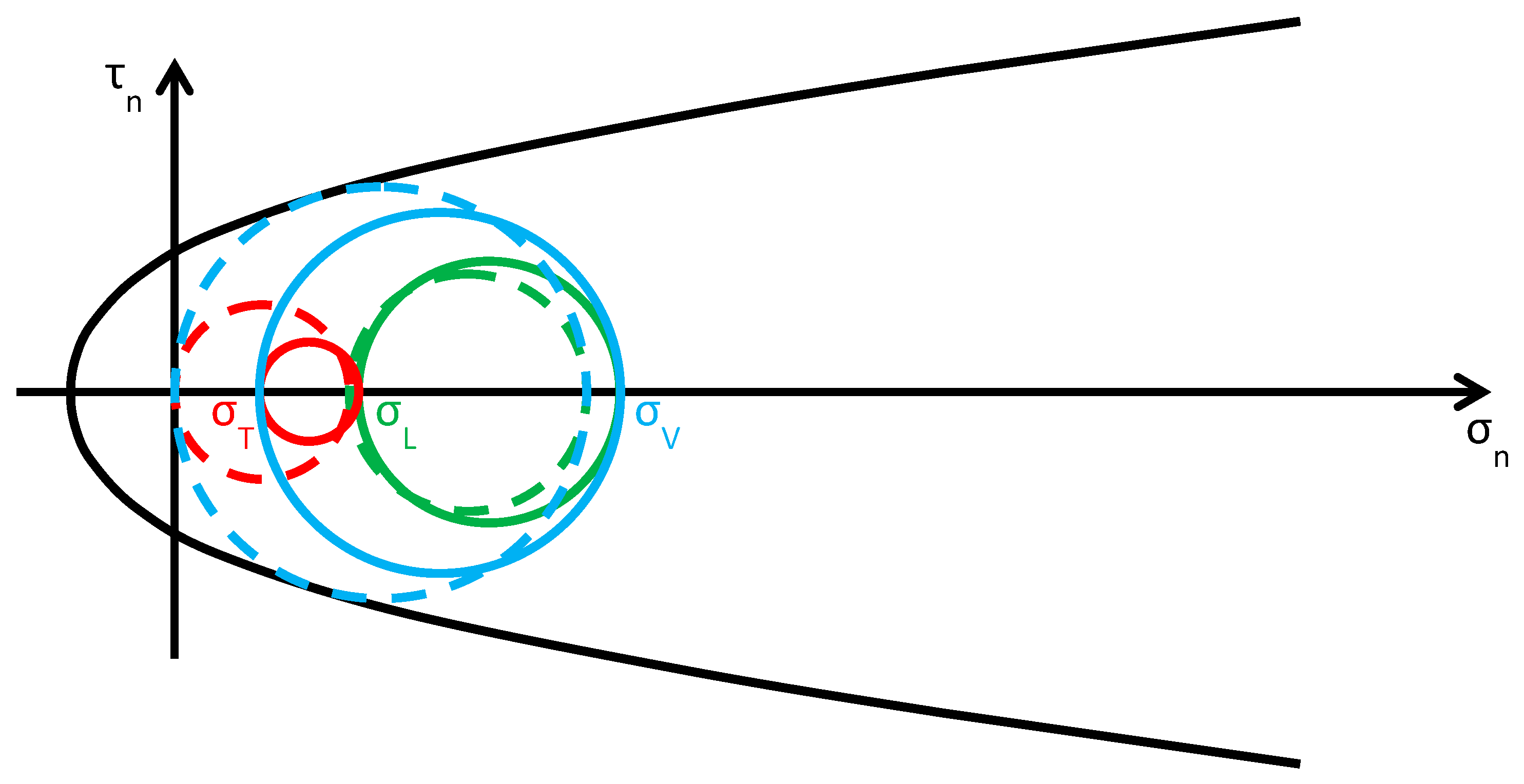
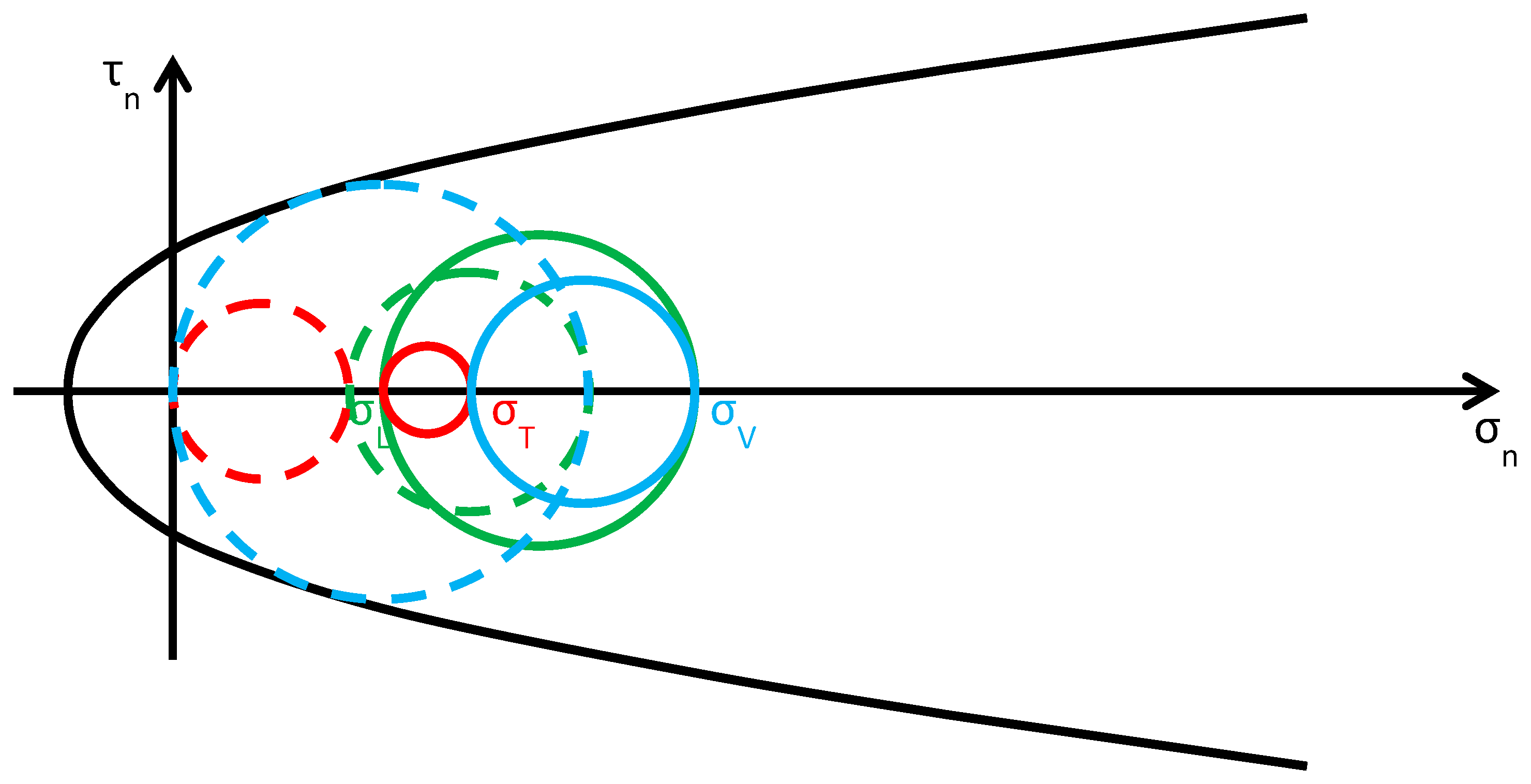
- (Figure 25), where is the modified lateral stress, the greatest circle is associated with the plane (blue circle). As increases (in absolute value), even increases (in absolute value), but , the variation of , is lower than , the variation of , because the constraint degree along the vertical direction is higher than the constraint degree along the transverse direction:Due to Poisson effect, the variation of ultimately causes an increase of , which is lower than the increase of because Poisson’s ratio is lower than 1:Both the red and blue circles become smaller, while the green circle becomes greater. The minimum distance between the largest circle and the limit surface increases, but to a lesser extent than in the case of the Φ system (for each given in the interval). Thus, even for the CAM system, the higher the value of in this interval, the higher the safety factor, but the post-retrofitting safety factor is lower than that achievable with the Φ system for the same . The CAM retrofitting is effective in this interval, all the more as higher is. When , the red circle degenerates into a point and the blue circle superimposes onto the green circle.
- (Figure 26), where and are the modified lateral and vertical stresses, the greatest circle is associated with the plane (green circle). As increases, and increase as for the previous interval:The radii of both the red and green circles increase, while the radius of the blue circle decreases. Moreover, the center of the green circle moves along the positive semi-axis of . Shifting the center and increasing the radius of the green circle have opposite effects on the safety factor: the first increases the safety factor, while the second decreases the safety factor. Depending on which of the two effects prevails over the other, the safety factor can either increase or decrease. Moreover, the minimum distance between the green circle and the limit surface depends on the shape of the combined limit surface, that is, on the number of straps and their stress. In the absence of this information, it is not possible to discriminate whether the safety factor of the CAM system is higher than the safety factor of the Φ system in this interval, or not. When , the red circle superimposes onto the green circle and the blue circle degenerates into a point.
- (Figure 27), where is the modified vertical stress, the greatest circle is associated with the plane (red circle). , , and increase according to the inequalities (5). All the circles become greater, with the red circle that grows closer to the limit surface of masonry (and to the combined limit surface). This decreases the safety factor but, for each given , the safety factor of the CAM system is higher than that achievable with the Φ system. The crisis takes place when the red circle becomes tangent to the combined limit surface and occurs for a value of that is higher than the of the Φ system. Even for the CAM system, the retrofitting modifies the crisis mechanism, since the new sliding plane is parallel to the z axis.
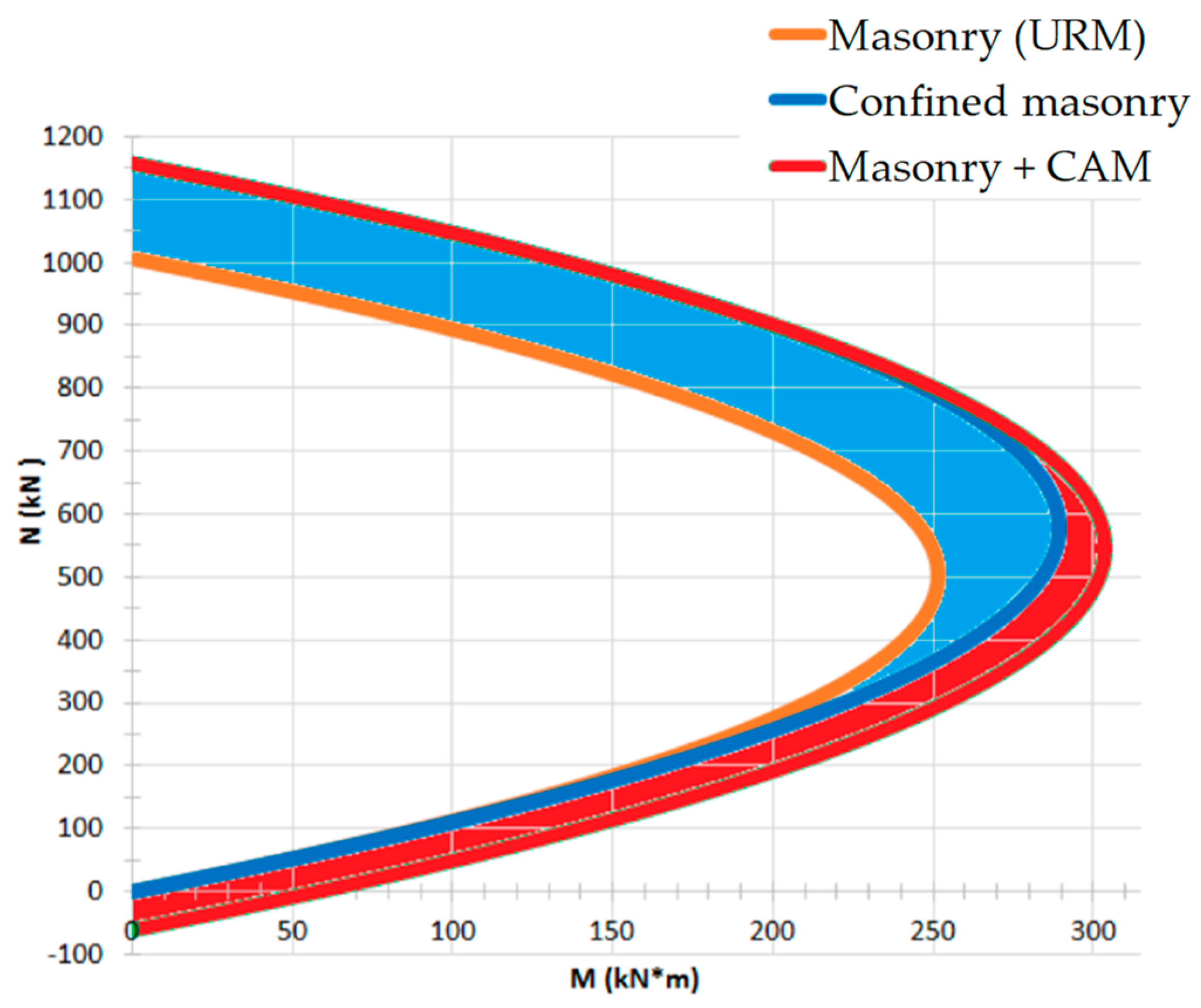
4. A Critical Analysis of the Design Criteria for the CAM System
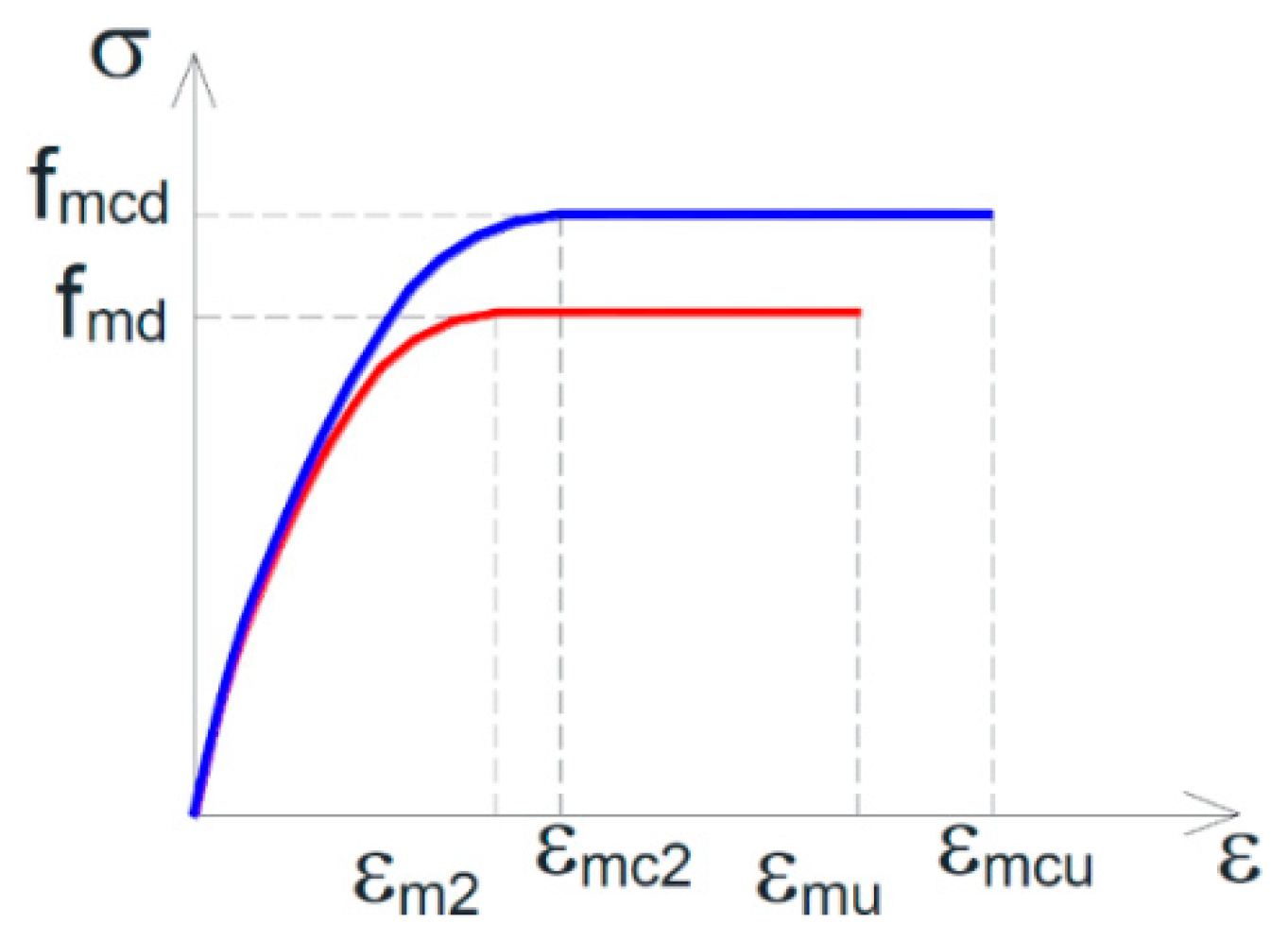
- is the design compressive strength of the unreinforced masonry (URM);
- is a dimensionless coefficient of strength increase, which depends on the mass density, , through the relationship:with expressed in and both coefficients and equal to 1 (in the absence of proven experimental results that justify different assumptions);
- is the effective confinement pressure, that is, the confinement pressure reduced by a coefficient of efficiency, , defined as the ratio between the effectively confined volume of the masonry wall, , and the volume of the masonry wall, :
- , in the absence of proven experimental results, is equal to 0.5.
- The orange plot is the limit domain for unreinforced masonry;
- The blue plot is the limit domain for confined masonry (only horizontal straps);
- The red plot is the limit domain for masonry reinforced by the CAM system (both horizontal and vertical straps).
5. Conclusions
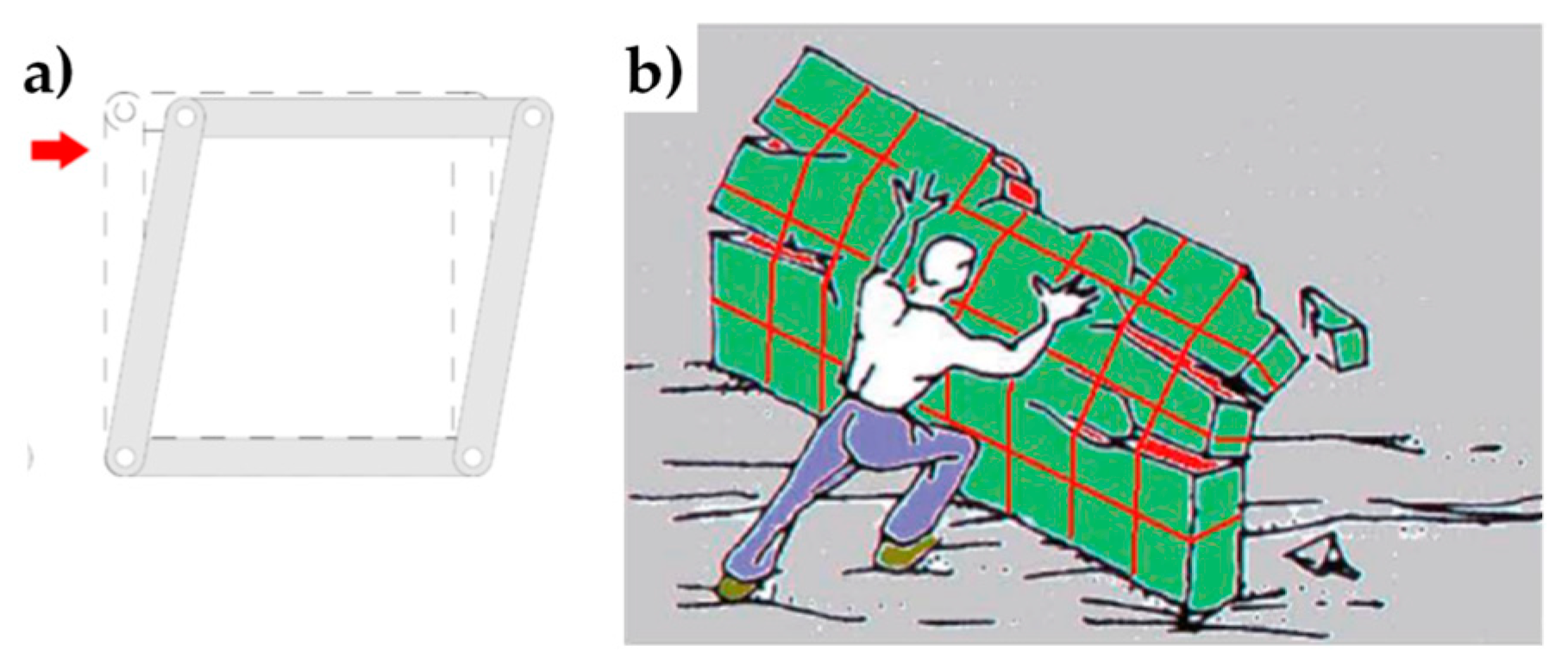
- For masonry units of the lower stories, where the constraint degree is very high—at the limit, infinite—along the in-plane directions, the two continuous retrofitting systems perform almost the same way. In particular, both provide the maximum increase of the safety factor for low values of .
- For masonry units of the upper stories, where the constraint degree is low—but never equal to zero—along the in-plane directions, the effectiveness of the continuous systems depends on the additional transverse stress provided by retrofitting. In particular, for low values of the Φ system is more effective than the CAM system in increasing the safety factor, for intermediate values of the safety factor achieved after retrofitting depends on the single intervention and deserves further deepening and, lastly, for high values of the maximum advantage in terms of safety factor is given by the CAM system.
6. Further Developments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dolce, M.; Nigro, D.; Ponzo, F.C.; Marnetto, R. The CAM System for the Retrofit of Masonry Structures. In Proceedings of the 7th International Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control of Vibrations of Structures, Assisi, Italy, 2–5 October 2001. [Google Scholar]
- Dolce, M.; Ponzo, F.C.; Di Croce, M.; Moroni, C.; Giordano, F.; Nigro, D.; Marnetto, R. Experimental Assessment of the CAM and DIS-CAM Systems for the Seismic Upgrading of Monumental Masonry Buildings. In Proceedings of the PROHITECH 09, 1st International Conference on Protection of Historical Constructions, Rome, Italy, 21–24 June 2009; CRC Press/Balkema: Leiden, The Netherlands, 2009; pp. 1021–1028. [Google Scholar]
- Spina, G.; Ramundo, F.; Mandara, A. Masonry Strengthening by Metal Tie-Bars, a Case Study. In Structural Analysis of Historical Constructions. In Proceedings of the Fourth International Seminar on Structural Analysis of Historical Constructions, Padova, Italy, 10–13 November 2004; Claudio, M., Paulo, B.L., Pere, R., Eds.; A.A. Balkema Publishers: Leiden, The Netherlands; London, UK; New York, NY, USA; Philadelphia, PA, USA; Singapore; Taylor & Francis Group: London, UK, 2005; pp. 1207–1213. [Google Scholar]
- Van Eldere, H.; Ramos, L.F.; Verstrynge, E.; Shetty, N.; Van Balen, K.; Barroso, C.E.; Oliveira, D.V. The Application of Sonic Testing on Double-Leaf Historical Portuguese Masonry to Obtain Morphology and Mechanical Properties. RILEM Bookseries 2019, 18, 661–668. [Google Scholar]
- Sauer, C.; Heine, A.; Riedel, W. Comprehensive Study of Projectile Impact on Lightweight Adobe Masonry. Int. J. Impact Eng. 2019, 125, 56–62. [Google Scholar] [CrossRef]
- Bonacho, J.; Oliveira, C.S. Multi-Hazard Analysis of Earthquake Shaking and Tsunami Impact. IJDRS Int. J. Disaster Risk Reduct. 2018, 31, 275–280. [Google Scholar] [CrossRef]
- Lonetti, P.; Maletta, R. Dynamic Impact Analysis of Masonry Buildings Subjected to Flood Actions. Eng. Struct. 2018, 167, 445–458. [Google Scholar] [CrossRef]
- Pourfalah, S.; Cotsovos, D.M.; Suryanto, B.; Moatamedi, M. Out-of-Plane Behaviour of Masonry Specimens Strengthened with ECC under Impact Loading. Eng. Struct. 2018, 173, 1002–1018. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Impact Behavior of FRP-Strengthened RC Beams without Stirrups. J. Compos. Constr. 2016, 20, 4016011. [Google Scholar] [CrossRef]
- Goswami, A.; Adhikary, S.D. Retrofitting Materials for Enhanced Blast Performance of Structures: Recent advancement and challenges ahead. Constr. Build. Mater. 2019, 204, 224–243. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Shi, Y.; Xu, Q. Experimental Studies on Mitigating Local Damage and Fragments of Unreinforced Masonry Wall under Close-in Explosions. J. Perform. Constr. Facil. 2019, 33, 04019009. [Google Scholar] [CrossRef]
- Michaloudis, G.; Gebbeken, N. Modeling Masonry Walls under Far-Field and Contact Detonations. Int. J. Impact Eng. 2019, 123, 84–97. [Google Scholar] [CrossRef]
- Russo, P.; De Marco, A.; Parisi, F. Failure of Reinforced Concrete and Tuff Stone Masonry Buildings as Consequence of Hydrogen Pipeline Explosions. Int. J. Hydrogen Energy 2019, in press. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Elsanadedy, H.M.; Al-Zaheri, Z.M.; Al-Salloum, Y.A.; Abbas, H. Blast Response of GFRP-Strengthened Infill Masonry Walls. Constr. Build. Mater. 2016, 115, 438–451. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Zhang, D.; Xu, Q.; Li, W. Experimental and Numerical Study on Compressive Performance of Perforated Brick Masonry after Fire Exposure. Fire Mater. 2019, 43, 200–218. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, H.; Li, C.; Xu, Q.; Li, W. Experimental Study on Seismic Performance of Fire-Exposed Perforated Brick Masonry Wall. Constr. Build. Mater. 2018, 180, 77–91. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Karlos, K.; Kefalou, K.; Argyropoulou, E. An Innovative Structural and Energy Retrofitting System for URM Walls using Textile Reinforced Mortars Combined with Thermal Insulation: Mechanical and Fire Behavior. Constr. Build. Mater. 2017, 133, 1–13. [Google Scholar] [CrossRef]
- Martinho, E.; Dionísio, A.; Mendes, M. Simulation of a Portuguese Limestone Masonry Structure Submitted to Fire: 3D Ultrasonic Tomography Approach. Int. J. Conserv. Sci. 2017, 8, 565–580. [Google Scholar]
- Hawileh, R.A.; Naser, M.; Zaidan, W.; Rasheed, H.A. Modeling of Insulated CFRP-Strengthened Reinforced Concrete T-Beam Exposed to Fire. Eng. Struct. 2009, 31, 3072–3079. [Google Scholar] [CrossRef]
- Ataei, S.; Miri, A. Investigating Dynamic Amplification Factor of Railway Masonry Arch Bridges through Dynamic Load Tests. Constr. Build. Mater. 2018, 183, 693–705. [Google Scholar] [CrossRef]
- Belghiat, C.; Messabhia, A.; Plassiard, J.-P.; Guenfoud, M.; Plé, O.; Perrotin, P. Experimental Study of Double-Panel Confined Masonry Walls under Lateral Loading. J. Build. Eng. 2018, 20, 531–543. [Google Scholar] [CrossRef]
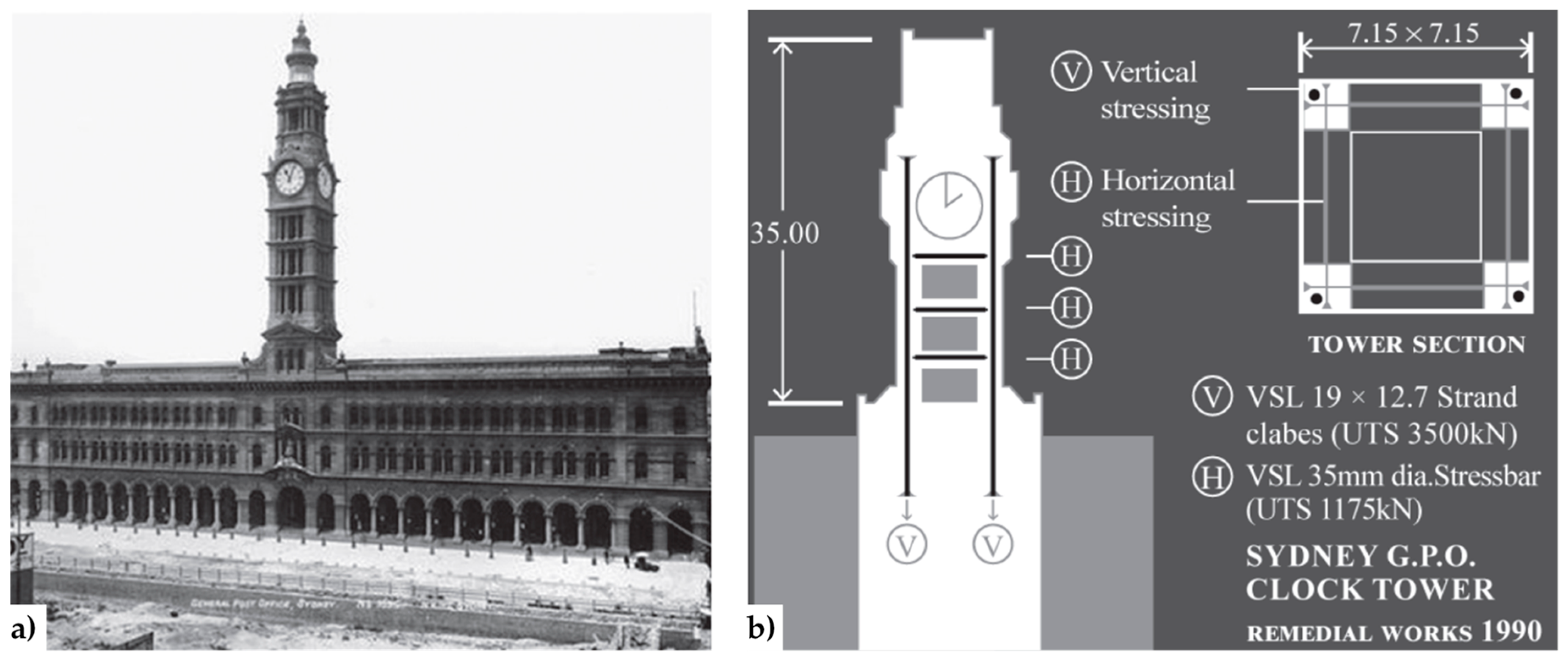
- Preciado, A.; Bartoli, G.; Budelmann, J.H. The use of Prestressing through Time as Seismic Retrofitting of Historical Masonry Constructions: Past, Present and Future Perspective. In CIENCIA ergo-sum; Universidad Autónoma del Estado de México: Toluca, Mexico, 2015; Volume 22, pp. 242–252. [Google Scholar]
- Rota, M.; Penna, A.; Strobbia, C.; Magenes, G. Typological Seismic Risk Maps for Italy. Earthq. Spectra 2011, 27, 907–926. [Google Scholar] [CrossRef]
- Ferretti, E. Shape-Effect in the Effective Laws of Plain and Rubberized Concrete. CMC-Comput. Mater. Contin. 2012, 30, 237–284. [Google Scholar]
- Zuboski, G.R. Stress-Strain Behavior for Actively Confined Concrete Using Shae Memory Alloy Wires. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2013. [Google Scholar]
- Angiuli, R.; Corvaglia, P.; Micelli, F.; Aiello, M.A. SMA-Based Composites for Active Confinement of Masonry Columns. In Proceedings of the International Conference on Shape Memory and Superelastic Technologies (SMST), Honk Hong, China, 6–9 November 2011; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Micelli, F.; Angiuli, R.; Corvaglia, P.; Aiello, M.A. Passive and SMA-Activated Confinement of Circular Masonry Columns with Basalt and Glass Fibers Composites. Compos. Part B-Eng. 2014, 67, 348–362. [Google Scholar] [CrossRef]
- Presidente del Consiglio dei Ministri. Primi Elementi in materia di Criteri Generali per la Classificazione Sismica del Territorio Nazionale e Normative Tecniche per le Costruzioni in Zona Sismica [First Elements on the General Criteria for the Seismic Classification of the National Territory and Technical Regulations for Constructions in the Seismic Area]; Ordinanza n. 3274; Presidenza del Consiglio dei Ministri: Rome, Italy, 2003.
- Ministero delle Infrastrutture e dei Trasporti. Aggiornamento delle Norme Tecniche per le Costruzioni [Updating of the Technical Standards for Constructions]; Decreto; Gazzetta Ufficiale della Repubblica Italiana: Rome, Italy, 2018.
- Tech Notes 44B: Wall Ties for Brick Masonry—Technical Notes on Brick Constructions; The Brick Industry Association: Reston, VA, USA, 2003.
- Curtin, W.G.; Shaw, G.; Beck, J.K.; Howard, J. Design of Post-Tensioned Brickwork; The Brick Development Association: Windsor, UK, 1989. [Google Scholar]
- Ismail, N.; Schultz, A.E.; Ingham, J.M. Out-of-Plane Seismic Performance of Unreinforced Masonry Walls Retrofitted using Post-Tensioning. In Proceedings of the 15th International Brick and Block Masonry Conference, Florianópolis, Santa Caterina, Brazil, 3–6 June 2012; Roman, H.R., Parsekian, G.A., Eds.; Federal University of Santa Catarina: Florianópolis, Brazil, 2012; pp. 1–12. [Google Scholar]
- Al-Manaseer, A.A.; Neis, V.V. Load Tests on Post-Tensioned Masonry Wall Panels. ACI Struct. J. 1987, 84, 467–472. [Google Scholar]
- Ganz, H.R.; Shaw, G. Stressing Masonry’s Future. Civ. Eng. 1997, 67, 42–45. [Google Scholar]
- Rosenboom, O.A.; Kowalsky, M.J. Reversed in-Plane Cyclic Behavior of Post-Tensioned Clay Brick Masonry Walls. J. Struct. Eng.-ASCE 2004, 130, 787–798. [Google Scholar] [CrossRef]
- Bean Popehn, J.R.; Schultz, A.E.; Lu, M.; Stolarski, H.K.; Ojard, N.J. Influence of Transverse Loading on the Stability of Slender Unreinforced Masonry Walls. Eng. Struct. 2008, 30, 2830–2839. [Google Scholar] [CrossRef]
- Sperbeck, S. Seismic Risk Assessment of Masonry Walls and Risk Reduction by means of Prestressing. Ph.D. Thesis, Technical University of Braunschweig, Braunschweig, Germany, University of Florence, Florence, Italy, 2009. [Google Scholar]
- Preciado, A. Seismic Vulnerability Reduction of Historical Masonry Towers by External Prestressing Devices. Ph.D. Thesis, Technical University of Braunschweig, Braunschweig, Germany, University of Florence, Florence, Italy, 2011. [Google Scholar]
- Schultz, A.E.; Scolforo, M.J. An Overview of Prestressed Masonry. Mason. Soc. J. 1991, 10, 6–21. [Google Scholar]
- Ganz, H.R. Post-Tensioning Masonry Around the World. Concr. Int. 2003, 25, 65–69. [Google Scholar]
- Bean Popehn, J.R.; Schultz, A.E.; Drake, C.R. Behavior of Slender, Posttensioned Masonry Walls under Transverse Loading. J. Struct. Eng.-ASCE 2007, 133, 1541–1550. [Google Scholar] [CrossRef]
- Ma, R.; Jiang, L.; He, M.; Fang, C.; Liang, F. Experimental Investigations on Masonry Structures using External Prestressing Techniques for Improving Seismic Performance. Eng. Struct. 2012, 42, 297–307. [Google Scholar] [CrossRef]
- Ganz, H.R. Post-Tensioned Masonry Structures: Properties of Masonry, Design Considerations, Post-Tensioning System for Masonry Structures Applications; VSL Report Series No. 2; VSL International Ltd.: Berne, Switzerland, 1990. [Google Scholar]
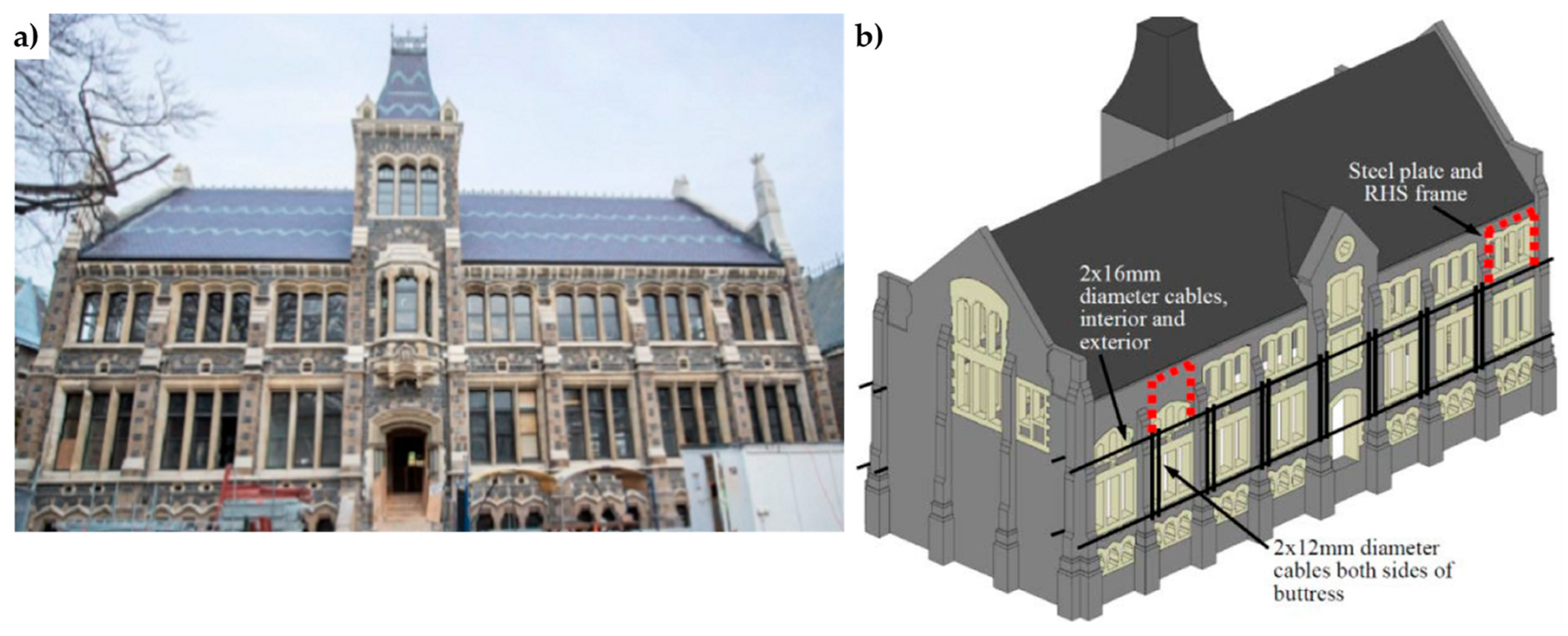
- Dizhur, D.; Bailey, S.; Trowsdale, J.; Griffith, M.; Ingham, J.M. Performance of Posttensioned Seismic Retrofit of two Stone Masonry Buildings during the Canterbury Earthquakes. In Proceedings of the Australian Earthquake Engineering Society 2013 Conference, Hobart, Tasmania, Australia, 15–17 November 2013. [Google Scholar]
- Croci, G.; D’Ayala, D. Recent Developments in the Safety Assessment of the Coliseum. In Proceedings of the Conference on Structural preservation of architectural heritage: Report/IABSE Symposium, Rome, Italy, 13–17 September 1993; International Association for Bridge and Structural Engineering: Zürich, Switzerland, 1993. [Google Scholar]
- Croci, G. The Conservation and Structural Restoration of Architectural Heritage; Advances in Architecture Series; WIT Press: Southampton, UK, 1998. [Google Scholar]
- Darbhanzi, A.; Marefat, M.S.; Khanmohammadi, M. Investigation of in-Plane Seismic Retrofit of Unreinforced Masonry Walls by means of Vertical Steel Ties. Constr. Build. Mater. 2014, 52, 122–129. [Google Scholar] [CrossRef]
- Dolce, M.; Ponzo, F.C.; Goretti, A.; Moroni, C.; Giordano, F.; De Canio, G.; Marnetto, R. 3D Dynamic Tests on 2/3 Scale Masonry Buildings Retrofitted with Different Systems. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Ferretti, E. Effectiveness of Active Confinement Techniques with Steel Ribbons: Masonry Buildings. Eur. J. Eng. Form. Sci. 2018, 2, 17–29. [Google Scholar] [CrossRef]
- Corradi, M.; Di Schino, A.; Borri, A.; Rufini, R. A Review of the use of Stainless Steel for Masonry Repair and Reinforcement. Constr. Build. Mater. 2018, 181, 335–346. [Google Scholar] [CrossRef]
- Spinella, N.; Colajanni, P.; Recupero, A. Experimental in Situ Behaviour of Unreinforced Masonry Elements Retrofitted by pre-Tensioned Stainless Steel Ribbons. Constr. Build. Mater. 2014, 73, 740–753. [Google Scholar] [CrossRef]
- Marnetto, R.; Vari, A.; Marnetto, L.; Leonori, M. Conservare l’Edilizia in Muratura: Il Sistema CAM—Cuciture Attive dei Manufatti [Conserving the Building Heritage in Masonry: The CAM System—Active Confinement of Manufactured Buildings]; Edizioni PREprogetti: Rome, Italy, 2014. [Google Scholar]
- Linee Guida per la Progettazione di Interventi su Strutture in Muratura e Cemento Armato con il Sistema Φ [Guidelines for the Design of Interventions on Masonry Structures and Reinforced Concrete with the Φ System]; SismaS srl: Francavilla al Mare (CH), Italy, 2013.
- Sistema, F.I. Available online: http://www.stefanomarchegiani.com/portfolio/sistema-fi (accessed on 15 November 2018).
- Ferretti, E.; Casadio, E.; Di Leo, A. Masonry Walls under Shear Test: A CM Modeling. CMES-Comp. Model. Eng. 2008, 30, 163–189. [Google Scholar]
- Ferretti, E. A Cell Method Stress Analysis in Thin Floor Tiles Subjected to Temperature Variation. CMES-Comp. Model. Eng. 2013, 36, 293–322. [Google Scholar]
- Ferretti, E. Cell Method Analysis of Crack Propagation in Tensioned Concrete Plates. CMES-Comp. Model. Eng. 2009, 54, 253–281. [Google Scholar]
- Ferretti, E. A Cell Method (CM) Code for Modeling the Pullout Test Step-Wise. CMES-Comp. Model. Eng. 2004, 6, 453–476. [Google Scholar]
- Ferretti, E. Crack-Path Analysis for Brittle and Non-Brittle Cracks: A Cell Method Approach. CMES-Comp. Model. Eng. 2004, 6, 227–244. [Google Scholar]
- Ferretti, E. Modeling of the Pullout Test through the Cell Method. In Proceedings of the International Conference on Restoration, Recycling and Rejuvenation Technology for Engineering and Architecture Application, RRRTEA ’04, Cesena, Italy, 7–11 June 2004; Sih, G.C., Nobile, L., Eds.; Aracne: Cesena, Italy, 2004; pp. 180–192. [Google Scholar]
- Ferretti, E.; Di Leo, A.; Viola, E. Computational Aspects and Numerical Simulations in the Elastic Constants Identification. In Problems in Structural Identification and Diagnostics: General Aspects and Applications; CISM Courses and Lectures No. 471; Davini, C., Viola, E., Eds.; Springer Wien GmbH: Wien, Austria, 2003; pp. 133–147. [Google Scholar]
- Ferretti, E. A Discrete Nonlocal Formulation using Local Constitutive Laws. Int. J. Fract. 2004, 130, L175–L182. [Google Scholar] [CrossRef]
- Ferretti, E. On nonlocality and Locality: Differential and Discrete Formulations. In Proceedings of the ICF11, 11th International Conference on Fracture 2005, Turin, Italy, 20–25 March 2005; Carpinteri, A., Ed.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; pp. 1728–1733. [Google Scholar]
- Marnetto, R.; Vari, A. Linee Guida—Cuciture Attive per la Muratura: Procedura Generale per la Progettazione, Modellazione, Calcolo e Verifica di Edifici in Muratura Rinforzati con il Sistema di Cucitura Attiva CAM [Active Tying for Masonry: General Procedure for the Design, Modeling, Calculation, and Verification of Masonry Buildings Reinforced with the CAM Active Tying System]; EDIL CAM Sistemi S.r.l.: Rome, Italy, October 2015. [Google Scholar]
- Ferretti, E.; Di Leo, A. Cracking and creep role in displacements at constant load: Concrete solids in compression. CMC-Comput. Mater. Con. 2008, 7, 59–79. [Google Scholar]
- Consiglio Nazionale delle Ricerche. Istruzioni per la Progettazione, l’Esecuzione e il Controllo di Interventi di Consolidamento Statico mediante l’utilizzo di Compositi Fibrorinforzati: Materiali, Strutture di C.A. e di C.A.P., Strutture Murarie [Instructions for the Design, Execution and Control of Static Consolidation Interventions through the Use of Fiber-Reinforced Composites: Materials, Structures of Reinforced Concrete and Prestressed Reinforced Concrete, Masonry Structures]; CNR-DT 200 R1/2013: Rome, Italy, 10 October 2013. [Google Scholar]
- Leonori, M.; Vari, A. L’Influenza della Tipologia di Terreno sui Meccanismi Locali di Collasso degli Edifici in Muratura e Miglioramento Sismico con il Sistema CAM® [The Influence of the Type of Land on Local Mechanisms of Collapse of Masonry Buildings and Seismic Improvement with the CAM® System]. In Dynamic Interaction of Soil and Structure (DISS_15), Proceedings of the 4th International Workshop on Archaeology, Cryptoportici, Hypogea, Geology, Geotechnics, Geophysics, Rome, Italy, 12–13 November 2015; Monti, G., Valente, G., Eds.; DISS_Edition c/o DICEAA—L’Aquila University: L’Aquila, Italy, 2015; pp. 1–15. [Google Scholar]
- Ferretti, E. Attaining a Beam-Like Behavior with FRP Strips and CAM Ribbons. Eur. J. Eng. Form. Sci. 2018, 2, 6–16. [Google Scholar] [CrossRef]
- Ferretti, E.; Pascale, G. Combined Strengthening Techniques to Improve the Out-of-Plane Performance of Masonry Walls. Materials 2019. [Google Scholar] [CrossRef]

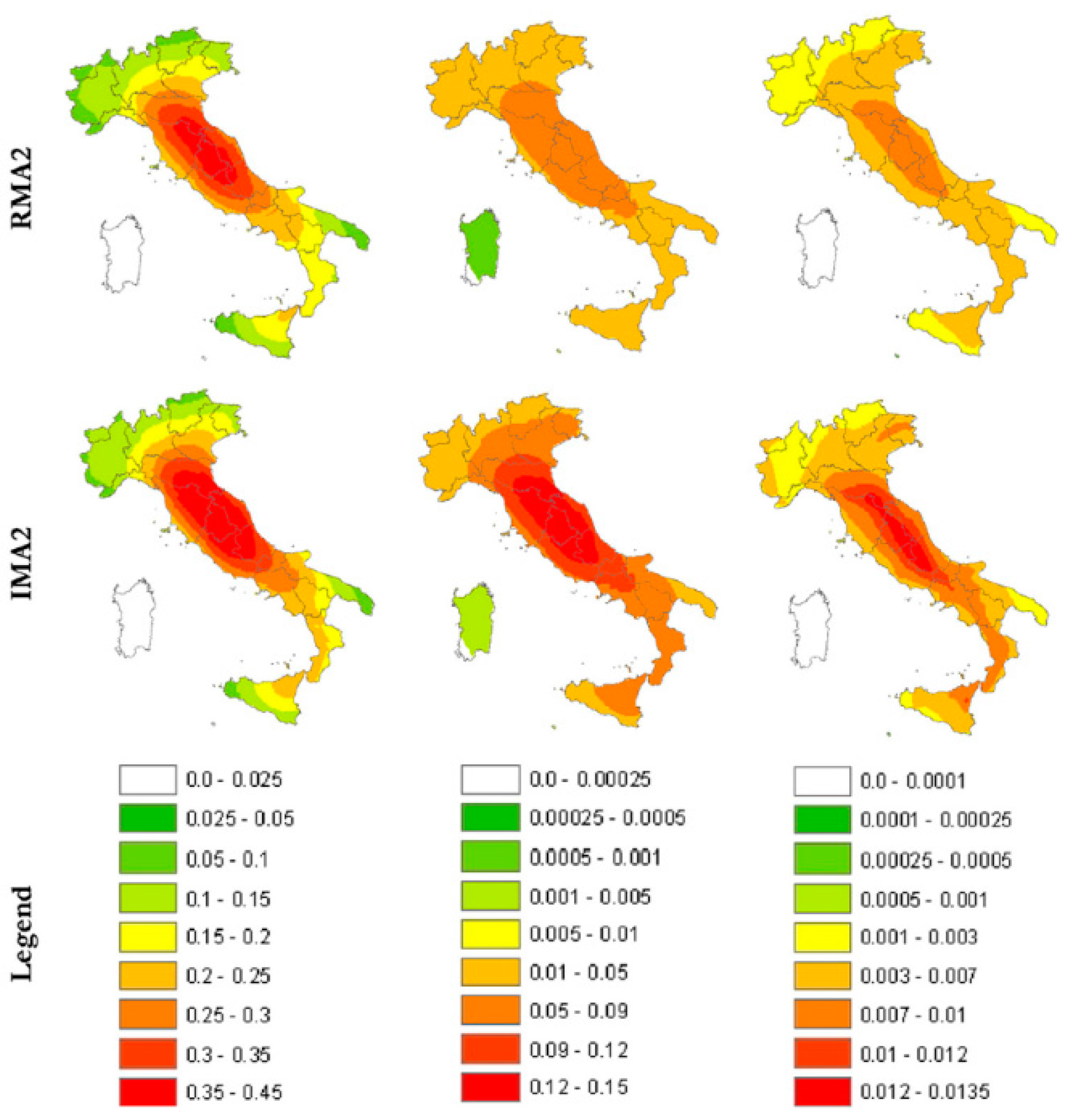
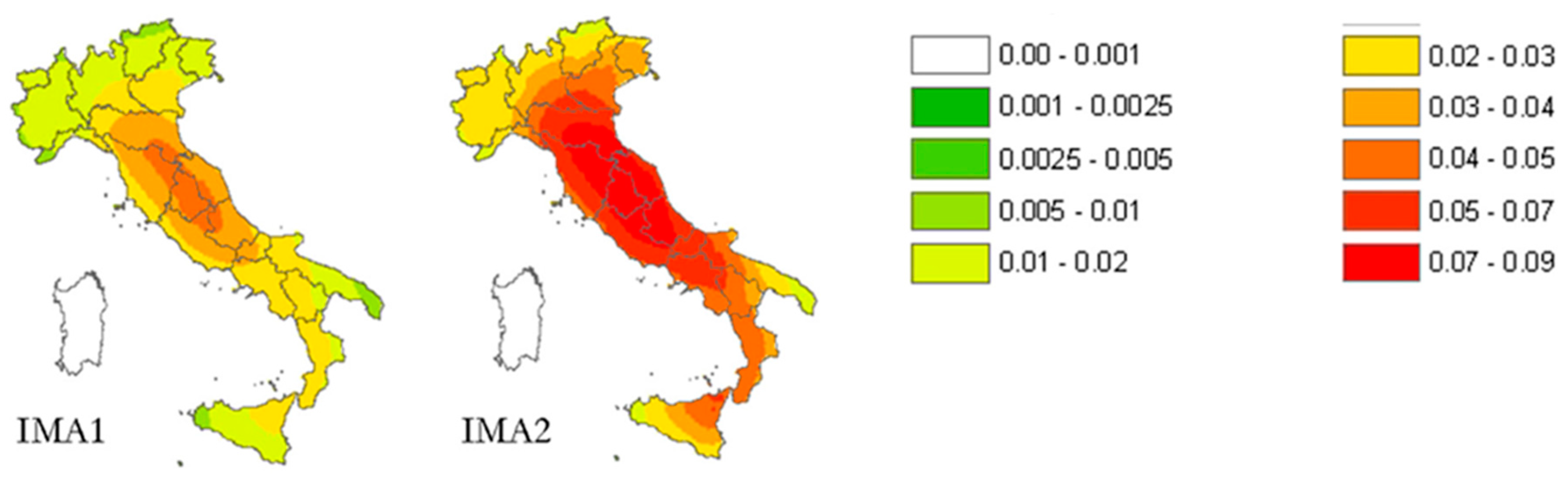









| Label | Damage Level | Description | Masonry Buildings | Reinforced Concrete (RC) Buildings |
|---|---|---|---|---|
| DS0 | No damage | — | ||
| DS1 | Negligible to slight damage | No structural damage, slight nonstructural damage |  |  |
| DS2 | Moderate damage | Slight structural damage, moderate nonstructural damage |  |  |
| DS3 | Substantial to heavy damage | Moderate structural damage, heavy nonstructural damage |  |  |
| DS4 | Very heavy damage | Heavy structural damage, very heavy nonstructural damage |  |  |
| DS5 | Destruction | Very heavy structural damage |  |  |
| Label | Building Class | No. of Stories |
|---|---|---|
| IMA1 | Masonry—irregular layout—flexible floors—with tie rods and/or tie beams | 1–2 |
| IMA2 | Masonry—irregular layout—flexible floors—without tie rods and tie beams | 1–2 |
| RMA2 | Masonry—regular layout—flexible floors—without tie rods and tie beams | 1–2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, E.; Pascale, G. Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis. Materials 2019, 12, 1151. https://doi.org/10.3390/ma12071151
Ferretti E, Pascale G. Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis. Materials. 2019; 12(7):1151. https://doi.org/10.3390/ma12071151
Chicago/Turabian StyleFerretti, Elena, and Giovanni Pascale. 2019. "Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis" Materials 12, no. 7: 1151. https://doi.org/10.3390/ma12071151
APA StyleFerretti, E., & Pascale, G. (2019). Some of the Latest Active Strengthening Techniques for Masonry Buildings: A Critical Analysis. Materials, 12(7), 1151. https://doi.org/10.3390/ma12071151






