ZnCr2O4 Inclusions in ZnO Matrix Investigated by Probe-Corrected STEM-EELS
Abstract
:1. Introduction
2. Experimental Methods
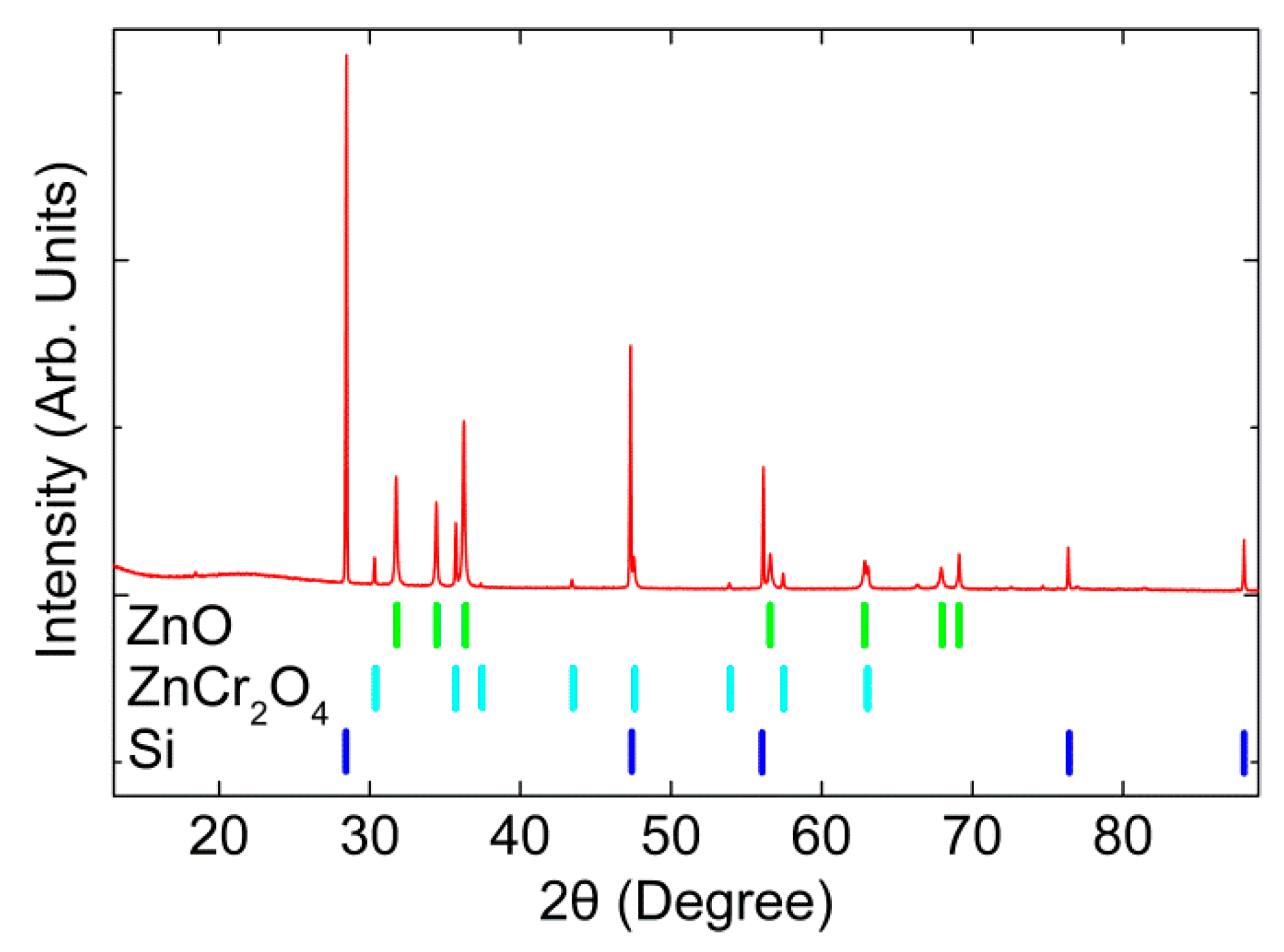
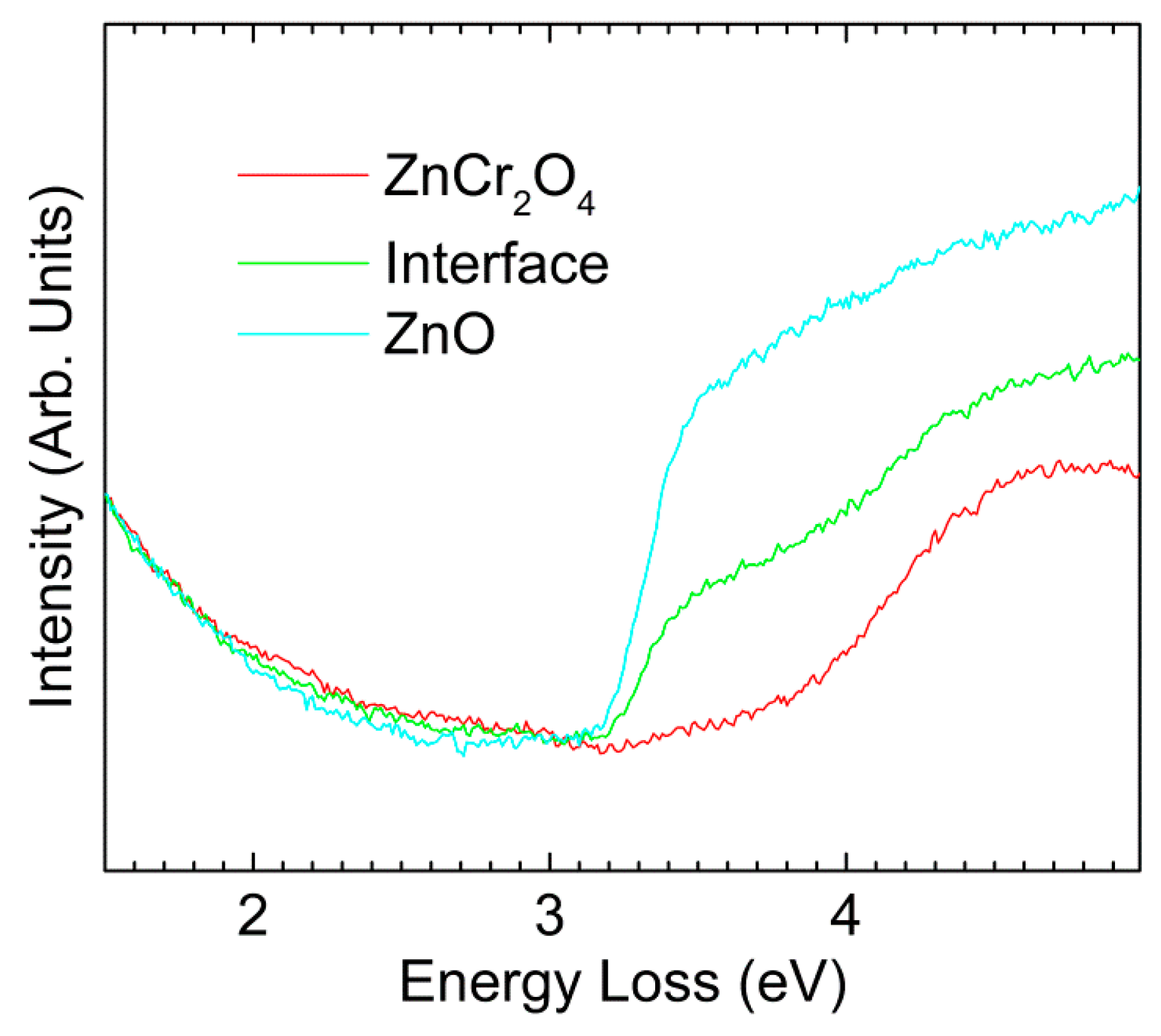
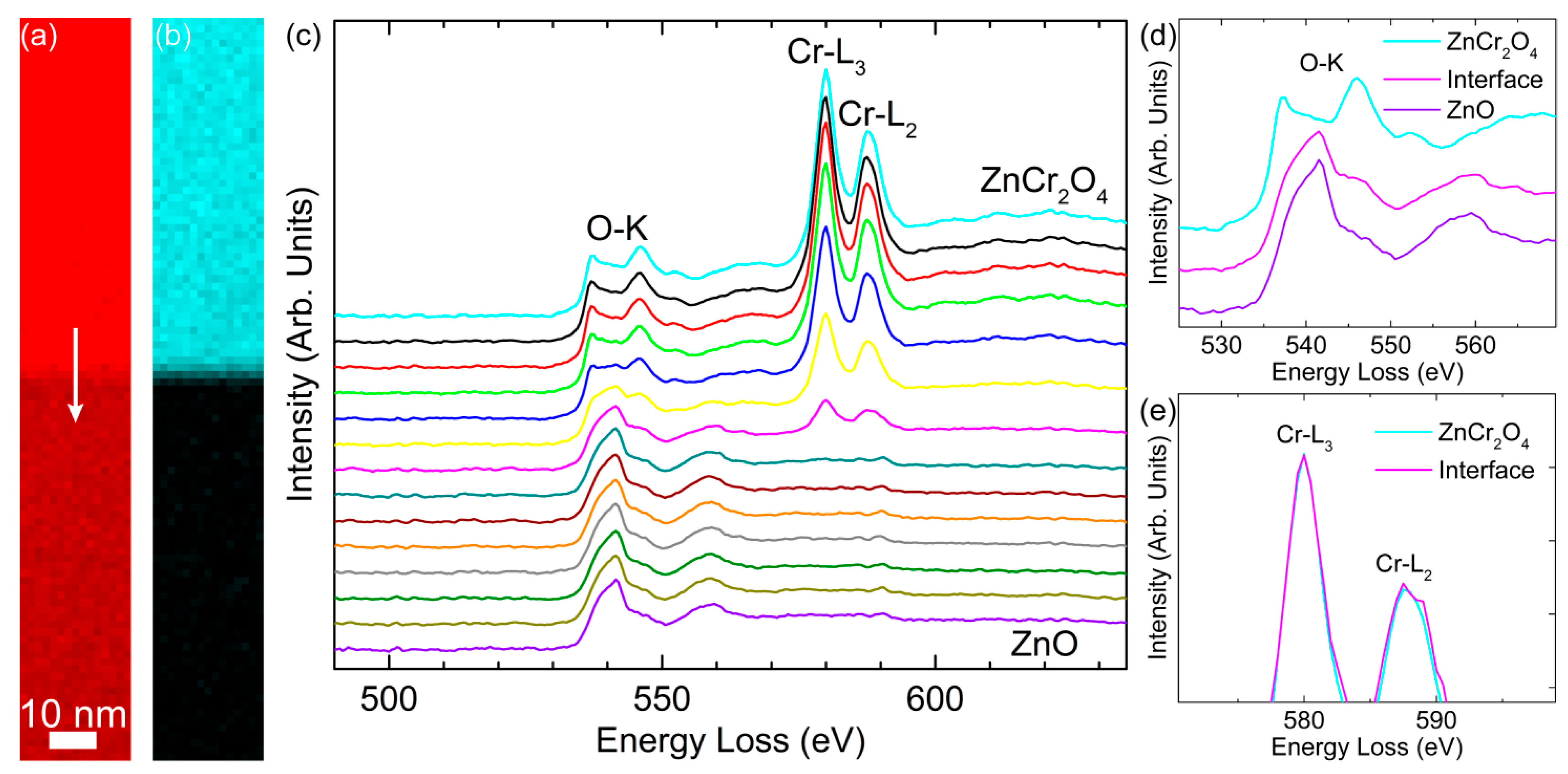
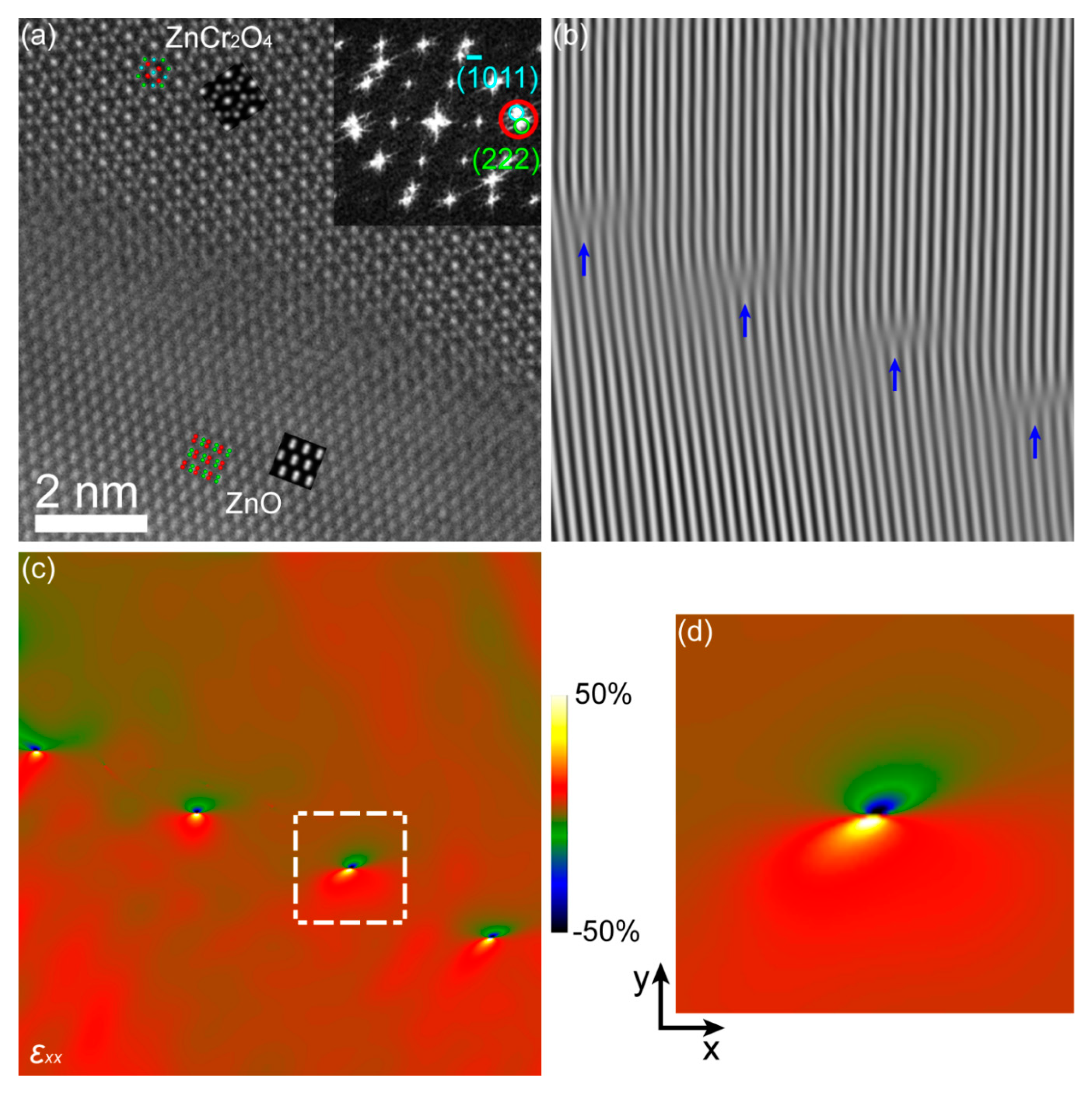
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choudhary, P.; Yadav, A.; Varshney, D. Structural and optical studies of nanocrystalline ZnCr2O4 and CoCr2O4 spinel. AIP Conf. Proc. 2017, 1832, 050051. [Google Scholar] [CrossRef]
- Gene, S.A.; Saion, E.; Shaari, A.H.; Kamarudin, M.A.; Al-Hada, N.M.; Kharazmi, A. Structural, optical, and magnetic characterization of spinel zinc chromite nanocrystallines synthesised by thermal treatment method. J. Nanomater. 2014, 2014, 15. [Google Scholar] [CrossRef]
- Niu, X.; Du, W.; Du, W. Preparation and gas sensing properties of ZnM2O4 (M = Fe, Co, Cr). Sens. Actuators B Chem. 2004, 99, 405–409. [Google Scholar] [CrossRef]
- Bayhan, M.; Hashemi, T.; Brinkman, A.W. Sintering and humidity-sensitive behaviour of the ZnCr2O4–K22CrO4 ceramic system. J. Mater. Sci. 1997, 32, 6619–6623. [Google Scholar] [CrossRef]
- Yokomizo, Y.; Uno, S.; Harata, M.; Hiraki, H.; Yuki, K. Microstructure and humidity-sensitive properties of ZnCr2O4-LiZnVO4 ceramic sensors. Sens. Actuators 1983, 4, 599–606. [Google Scholar] [CrossRef]
- Gabr, R.M.; Girgis, M.M.; El-Awad, A.M. Formation, conductivity and activity of zinc chromite catalyst. Mater. Chem. Phys. 1992, 30, 169–177. [Google Scholar] [CrossRef]
- El-Sharkawy, E.A. Textural, Structural and Catalytic Properties of ZnCr2O4–A12O3 Ternary Solid Catalysts. Adsorpt. Sci. Technol. 1998, 16, 193–216. [Google Scholar] [CrossRef]
- Mousavi, Z.; Soofivand, F.; Esmaeili-Zare, M.; Salavati-Niasari, M.; Bagheri, S. ZnCr2O4 Nanoparticles: Facile Synthesis, Characterization, and Photocatalytic Properties. Sci. Rep. 2016, 6, 20071. [Google Scholar] [CrossRef]
- Rajadurai, S. Synthesis, structural characterization and catalytic study of ZnCrFeO4 spinel. Mater. Chem. Phys. 1987, 16, 459–466. [Google Scholar] [CrossRef]
- Lee, S.H.; Broholm, C.; Ratcliff, W.; Gasparovic, G.; Huang, Q.; Kim, T.H.; Cheong, S.W. Emergent excitations in a geometrically frustrated magnet. Nature 2002, 418, 856. [Google Scholar] [CrossRef]
- Vankudoth, K.; Padmasri, A.H.; Sarkari, R.; Velisoju, V.K.; Gutta, N.; Sathu, N.K.; Rohita, C.N.; Akula, V. The role of Lewis acid-base pair sites in ZnO-ZnCr2O4 catalysts for cyclization via dehydrogenative condensation of crude glycerol and 1,2-propanediamine for the synthesis of 2,6-dimethylpyrazine. New J. Chem. 2017, 41, 9875–9883. [Google Scholar] [CrossRef]
- Thennarasu, G.; Sivasamy, A. Synthesis and characterization of nanolayered ZnO/ZnCr2O4 metal oxide composites and its photocatalytic activity under visible light irradiation. J. Chem. Technol. Biotechnol. 2015, 90, 514–524. [Google Scholar] [CrossRef]
- Liang, Y.C.; Hsia, H.Y.; Cheng, Y.R.; Lee, C.M.; Liu, S.L.; Lin, T.Y.; Chung, C.C. Crystalline quality-dependent gas detection behaviors of zinc oxide-zinc chromite p-n heterostructures. CrystEngComm 2015, 17, 4190–4199. [Google Scholar] [CrossRef]
- Song, H.; Laudenschleger, D.; Carey, J.J.; Ruland, H.; Nolan, M.; Muhler, M. Spinel-Structured ZnCr2O4 with Excess Zn Is the Active ZnO/Cr2O3 Catalyst for High-Temperature Methanol Synthesis. ACS Catal. 2017, 7, 7610–7622. [Google Scholar] [CrossRef]
- Pokhrel, S.; Jeyaraj, B.; Nagaraja, K.S. Humidity-sensing properties of ZnCr2O4–ZnO composites. Mater. Lett. 2003, 57, 3543–3548. [Google Scholar] [CrossRef]
- David, B.; Williams, C.B.C. Transmission Electron Microscopy. In A Textbook for Materials Science; Springer: Berlin, Germany, 2009. [Google Scholar]
- LeBeau, J.M.; Findlay, S.D.; Allen, L.J.; Stemmer, S. Quantitative Atomic Resolution Scanning Transmission Electron Microscopy. Phys. Rev. Lett. 2008, 100, 206101. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.L.; Zhu, Y.L.; Ma, X.L. On the benefit of aberration-corrected HAADF-STEM for strain determination and its application to tailoring ferroelectric domain patterns. Ultramicroscopy 2016, 160, 57–63. [Google Scholar] [CrossRef]
- Zhu, Y.; Ophus, C.; Ciston, J.; Wang, H. Interface lattice displacement measurement to 1pm by geometric phase analysis on aberration-corrected HAADF STEM images. Acta Mater. 2013, 61, 5646–5663. [Google Scholar] [CrossRef]
- Couillard, M.; Radtke, G.; Botton, G.A. Strain fields around dislocation arrays in a Σ9 silicon bicrystal measured by scanning transmission electron microscopy. Philos. Mag. 2013, 93, 1250–1267. [Google Scholar] [CrossRef]
- Cooper, D.; Royer, C.L.; Béché, A.; Rouvière, J.L. Strain mapping for the silicon-on-insulator generation of semiconductor devices by high-angle annular dark field scanning electron transmission microscopy. Appl. Phys. Lett. 2012, 100, 233121. [Google Scholar] [CrossRef]
- Trindade, T.; O’Brien, P.; Pickett, N.L. Nanocrystalline Semiconductors: Synthesis, Properties, and Perspectives. Chem. Mater. 2001, 13, 3843–3858. [Google Scholar] [CrossRef]
- Regulacio, M.D.; Han, M.Y. Composition-Tunable Alloyed Semiconductor Nanocrystals. Acc. Chem. Res. 2010, 43, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Bailey, R.E.; Nie, S. Alloyed Semiconductor Quantum Dots: Tuning the Optical Properties without Changing the Particle Size. J. Am. Chem. Soc. 2003, 125, 7100–7106. [Google Scholar] [CrossRef] [PubMed]
- Brink, H.A.; Barfels, M.M.G.; Burgner, R.P.; Edwards, B.N. A sub-50 meVspectrometer and energy filter for use in combination with 200 kV monochromated (S)TEMs. Ultramicroscopy 2003, 96, 367–384. [Google Scholar] [CrossRef]
- Erni, R.; Browning, N.D. Valence electron energy-loss spectroscopy in monochromated scanning transmission electron microscopy. Ultramicroscopy 2005, 104, 176–192. [Google Scholar] [CrossRef] [PubMed]
- Bosman, M.; Tang, L.J.; Ye, J.D.; Tan, S.T.; Zhang, Y.; Keast, V.J. Nanoscale band gap spectroscopy on ZnO and GaN-based compounds with a monochromated electron microscope. Appl. Phys. Lett. 2009, 95, 101110. [Google Scholar] [CrossRef]
- Zhan, W.; Granerød, C.S.; Venkatachalapathy, V.; Johansen, K.M.H.; Jensen, I.J.T.; Kuznetsov, A.Y.; Prytz, Ø. Nanoscale mapping of optical band gaps using monochromated electron energy loss spectroscopy. Nanotechnology 2017, 28, 105703. [Google Scholar] [CrossRef] [PubMed]
- QSTEM: Quantitative TEM/STEM Simulations. Available online: http://qstem.org/ (accessed on 15 March 2019).
- Egerton, R.F. Limits to the spatial, energy and momentum resolution of electron energy-loss spectroscopy. Ultramicroscopy 2007, 107, 575–586. [Google Scholar] [CrossRef]
- Granerød, C.S.; Zhan, W.; Prytz, Ø. Automated approaches for band gap mapping in STEM-EELS. Ultramicroscopy 2018, 184, 39–45. [Google Scholar] [CrossRef]
- Zhan, W.; Venkatachalapathy, V.; Aarholt, T.; Kuznetsov, A.Y.; Prytz, Ø. Band gap maps beyond the delocalization limit: Correlation between optical band gaps and plasmon energies at the nanoscale. Sci. Rep. 2018, 8, 848. [Google Scholar] [CrossRef]
- Hytch, M.J.; Putaux, J.L.; Penisson, J.M. Measurement of the displacement field of dislocations to 0.03 Å by electron microscopy. Nature 2003, 423, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Hÿtch, M.J.; Putaux, J.L.; Thibault, J. Stress and strain around grain-boundary dislocations measured by high-resolution electron microscopy. Philos. Mag. 2006, 86, 4641–4656. [Google Scholar] [CrossRef]
- Johnson, C.L.; Snoeck, E.; Ezcurdia, M.; Rodriguez-Gonzalez, B.; Pastoriza-Santos, I.; Liz-Marzan, L.M.; Hytch, M.J. Effects of elastic anisotropy on strain distributions in decahedral gold nanoparticles. Nat. Mater. 2008, 7, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Francis, S.; Saravanan, R.; Berchmans, L.J. Phase analysis in Zn1−x Crx O through charge density. Phase Transit. 2013, 86, 620–632. [Google Scholar] [CrossRef]
- Fu, C.F.; Han, L.F.; Liu, C.; Gao, Y.F. Effects of Cr-doping concentration on the structural, optical, and magnetic properties of ZnO thin films. Phys. Status Solidi 2013, 210, 1358–1362. [Google Scholar] [CrossRef]
- Quang, H.T.; Bachmatiuk, A.; Dianat, A.; Ortmann, F.; Zhao, J.; Warner, J.H.; Eckert, J.; Cunniberti, G.; Rümmeli, M.H. In Situ Observations of Free-Standing Graphene-like Mono- and Bilayer ZnO Membranes. ACS Nano 2015, 9, 11408–11413. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Wang, Z.L. Electron energy-loss spectroscopy study of ZnO nanobelts. J. Electron Microsc. 2005, 54, 287–291. [Google Scholar] [CrossRef]
- Wang, N.; Yang, Y.; Yang, G. Great blue-shift of luminescence of ZnO nanoparticle array constructed from ZnO quantum dots. Nanoscale Res. Lett. 2011, 6, 338. [Google Scholar] [CrossRef]
- Eustace, D.A.; McComb, D.W.; Craven, A.J. Probing magnetic order in EELS of chromite spinels using both multiple scattering (FEFF8.2) and DFT (WIEN2k). Micron 2010, 41, 547–553. [Google Scholar] [CrossRef]
- Arévalo-López, Á.M.; Alario-Franco, M.Á. Reliable Method for Determining the Oxidation State in Chromium Oxides. Inorg. Chem. 2009, 48, 11843–11846. [Google Scholar] [CrossRef]
- Daulton, T.L.; Little, B.J. Determination of chromium valence over the range Cr(0)–Cr(VI) by electron energy loss spectroscopy. Ultramicroscopy 2006, 106, 561–573. [Google Scholar] [CrossRef]
- Schmid, H.; Mader, W. Distribution of Fe and In Dopants in Zinc Oxide: Combined EELS and EDS Analysis. Microsc. Anal. 2009, 23, 13–18. [Google Scholar]
- Prytz, Ø.; Taftø, J.; Ahn, C.C.; Fultz, B. Transition metal d-band occupancy in skutterudites studied by electron energy-loss spectroscopy. Phys. Rev. B 2007, 75, 125109. [Google Scholar] [CrossRef]
- Prytz, Ø.; Flage-Larsen, E.; Gu, L.; Sigle, W.; van Aken, P.A.; Taftø, J. The charge-ordered spinel AlV2O4: High energy resolution EELS and computational studies. Phys. Rev. B 2012, 85, 195112. [Google Scholar] [CrossRef]
- Daulton, T.L.; Little, B.J.; Lowe, K.; Jones-Meehan, J. Electron energy loss spectroscopy techniques for the study of microbial chromium(VI) reduction. J. Microbiol. Methods 2002, 50, 39–54. [Google Scholar] [CrossRef]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Clarendon: Oxford, UK, 1995. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, W.; Kosinskiy, A.Y.; Vines, L.; Johansen, K.M.; Carvalho, P.A.; Prytz, Ø. ZnCr2O4 Inclusions in ZnO Matrix Investigated by Probe-Corrected STEM-EELS. Materials 2019, 12, 888. https://doi.org/10.3390/ma12060888
Zhan W, Kosinskiy AY, Vines L, Johansen KM, Carvalho PA, Prytz Ø. ZnCr2O4 Inclusions in ZnO Matrix Investigated by Probe-Corrected STEM-EELS. Materials. 2019; 12(6):888. https://doi.org/10.3390/ma12060888
Chicago/Turabian StyleZhan, Wei, Andrey Yurievich Kosinskiy, Lasse Vines, Klaus Magnus Johansen, Patricia Almeida Carvalho, and Øystein Prytz. 2019. "ZnCr2O4 Inclusions in ZnO Matrix Investigated by Probe-Corrected STEM-EELS" Materials 12, no. 6: 888. https://doi.org/10.3390/ma12060888
APA StyleZhan, W., Kosinskiy, A. Y., Vines, L., Johansen, K. M., Carvalho, P. A., & Prytz, Ø. (2019). ZnCr2O4 Inclusions in ZnO Matrix Investigated by Probe-Corrected STEM-EELS. Materials, 12(6), 888. https://doi.org/10.3390/ma12060888




