Analysis of the Functionally Step-Variable Graded Plate Under In-Plane Compression
Abstract
1. Introduction
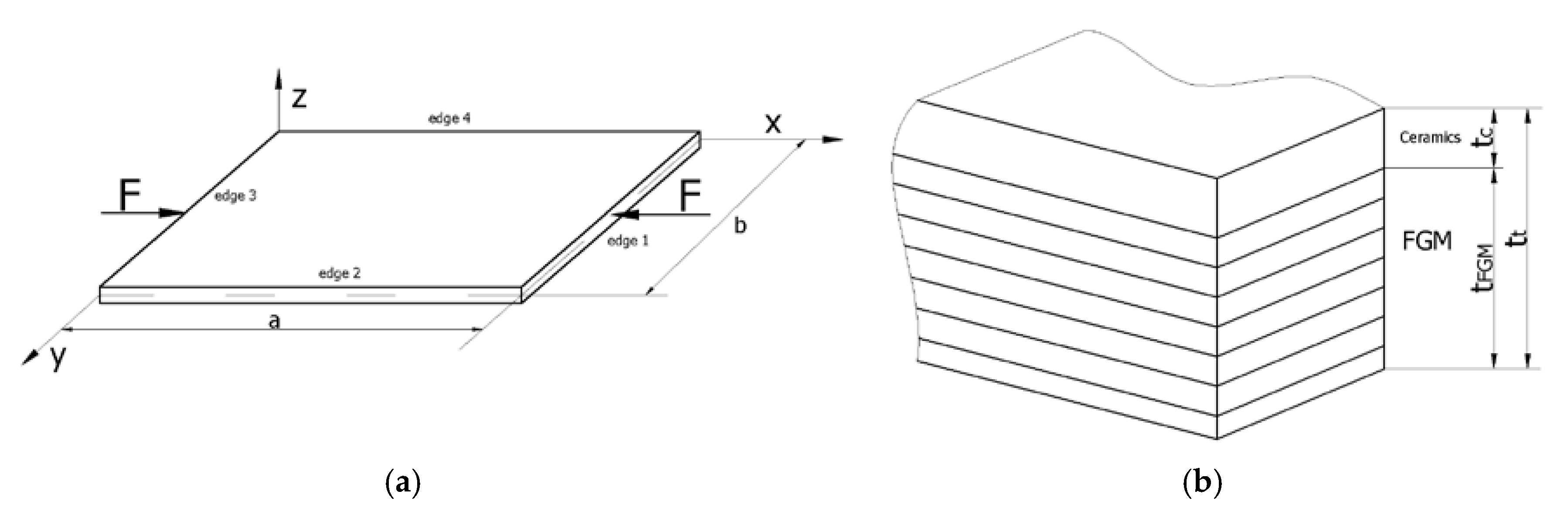
2. Problem Description
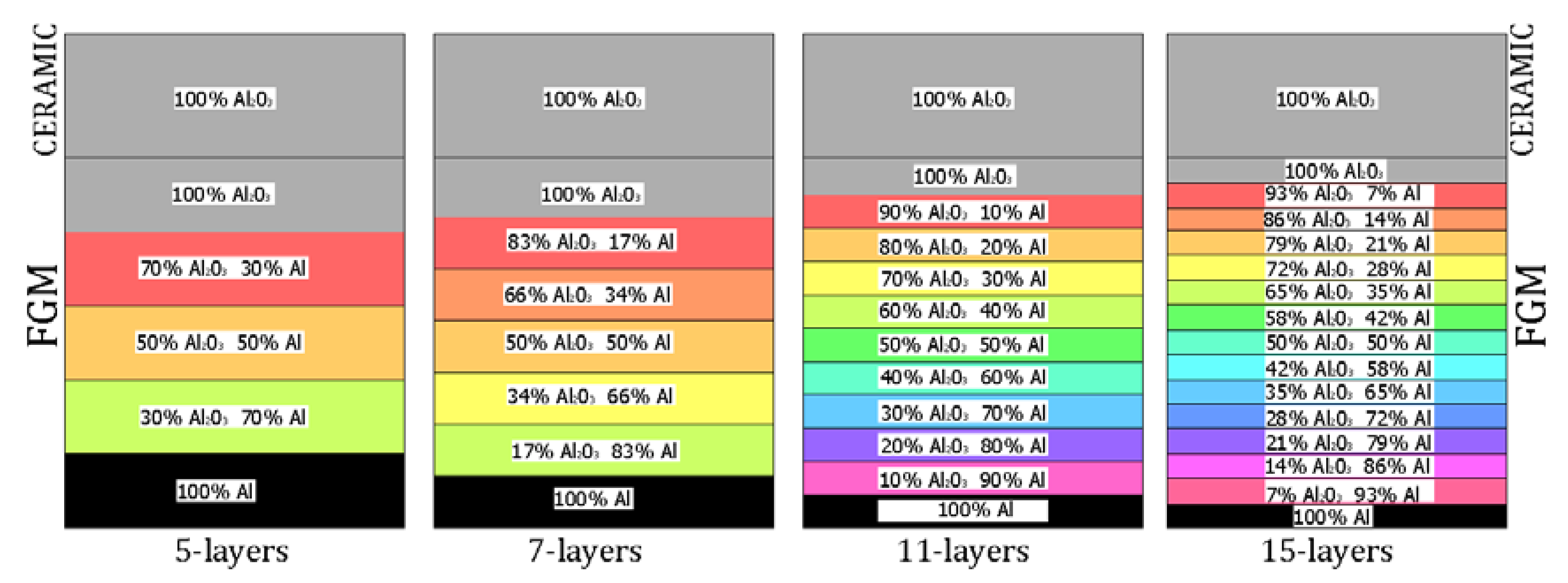
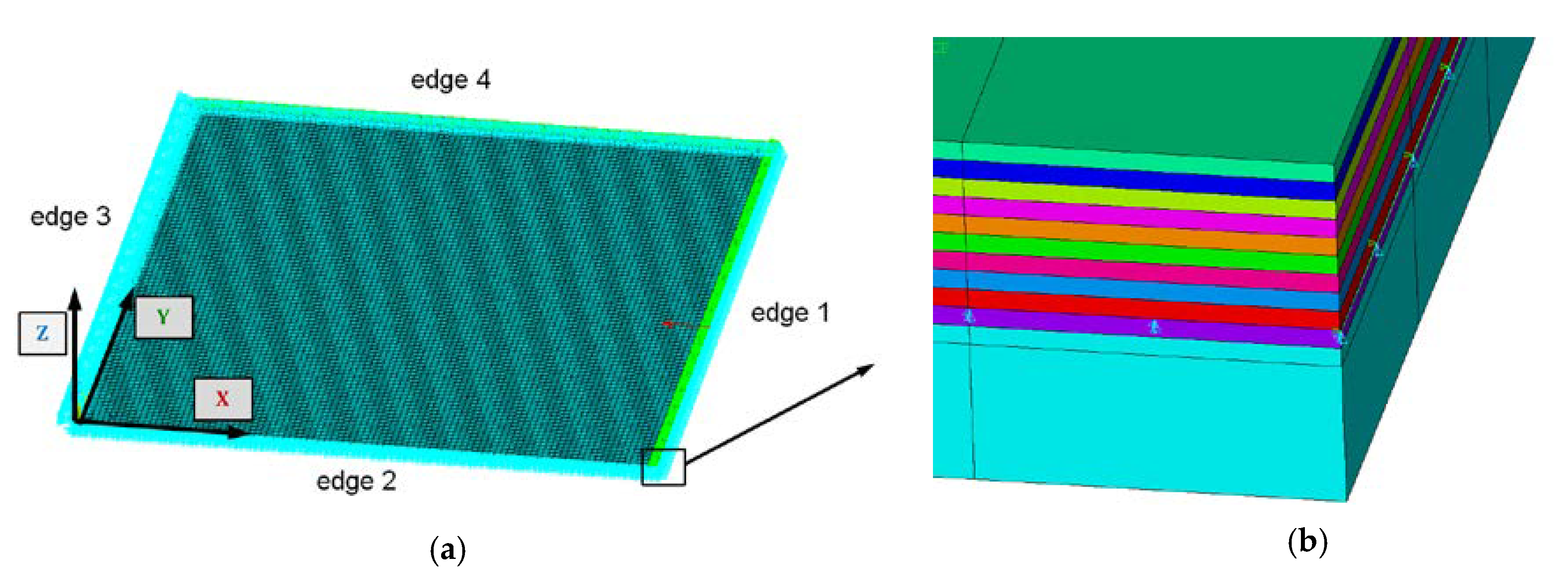
2.1. FE Model
2.2. Koiter’s Asymptotic Approach
3. Results and Discussion
3.1. Buckling Forces
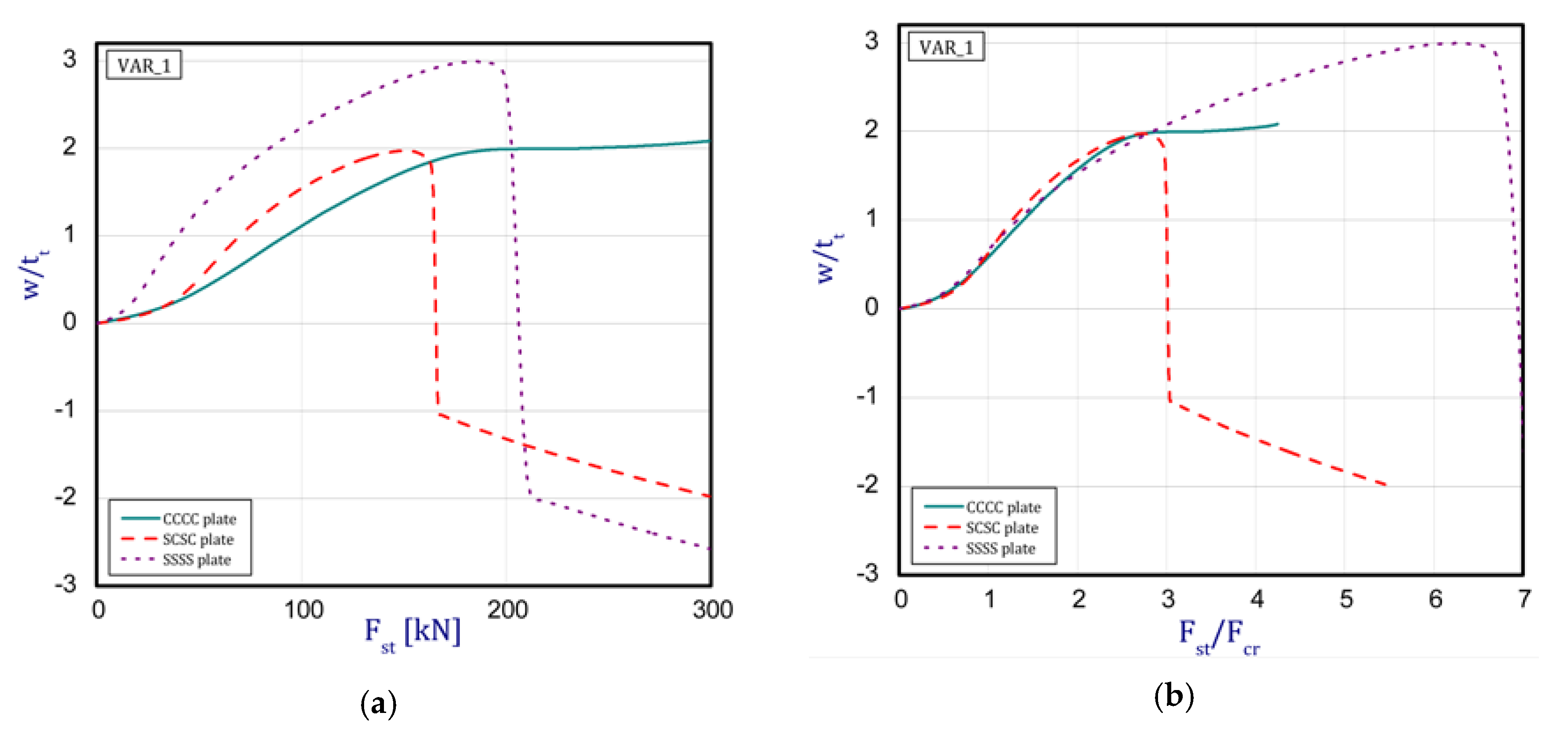
3.2. Post-Buckling Behavior of the Plate
4. Summary
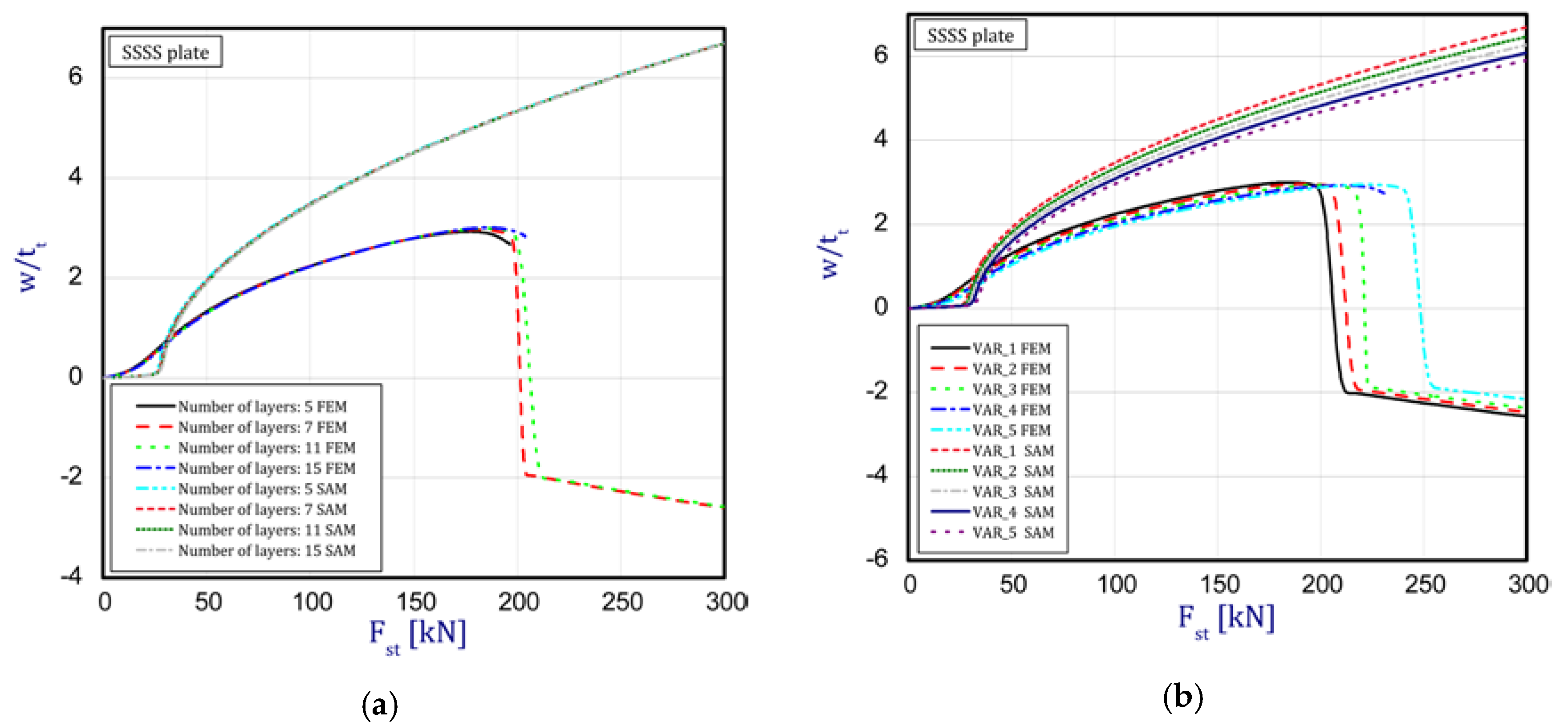
- The gradation of layers in the number of plates from five to 15 revealed a slight influence on the plate stability because the obtained curves in both the methods ran almost identically. It indicates that the overall bending stiffness remains on a comparable level, though a non-symmetrical distribution of normal forces with respect to the neutral axis of the plate exists;
- in a comparison of critical forces based on the two applied methods, a sufficiently good agreement was achieved (a few percent difference, at most). The SAM gave slightly lower values;
- in the cases under consideration, the growth in ceramics thickness (from 0.2 mm to 1 mm) played an insignificant role in post-buckling paths. Indeed, the differences in curves are visible but they differ only slightly from one another;
- a higher discrepancy could be seen by comparing the behavior of the plate obtained using the two methods. Firstly, in the FEM analysis, the plate deflects earlier than in the SAM analysis, but after exceeding the critical load, the SAM indicates a larger deflection. In addition, there is a change in the buckling mode during the plate compression. In contrast to the SAM, the FEM reveals a transformation of the defection function from one half-wave to two or three half-waves;
- when analyzing the curves obtained for three different boundary conditions, a similarity in the plate deflection up to three-fold overloads was noticed if static loads were referred to their critical buckling loads (see Figure 7b).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Koizumi, M.; Niino, M. Overview of FGM Research in Japan. MRS Bull. 1995, 20, 19–21. [Google Scholar] [CrossRef]
- Kayser, W.A.; Ilschner, B. FGM research activities in Europe. MRS Bull. 1995, 20, 22–26. [Google Scholar] [CrossRef]
- Sasaki, M.; Wang, Y.; Hirano, T.; Hirai, T. Design of SiC/C functionally gradient material and its preparation by chemical vapor deposition. J. Ceram. Soc. Jpn. 1989, 97, 539–543. [Google Scholar] [CrossRef][Green Version]
- Rubio, W.M.; Paulino, G.H.; Silva, E.C.N. Analysis, manufacture and characterization of Ni/Cu functionally graded structures. Mater. Des. 2012, 41, 255–265. [Google Scholar] [CrossRef]
- Cai, Y.; Cheng, Y.; Yin, H.; Yin, X.; Tian, Y.; Chen, J.; Wang, N. Preparation and mechanical properties of Ti3SiC2/SiC functionally graded materials. Ceram. Int. 2017, 43, 6648–6658. [Google Scholar] [CrossRef]
- Hangai, Y.; Morita, T.; Utsunomiya, T. Functionally graded aluminium foam consisting of dissimilar aluminium alloys fabricated by sintering and dissolution process. Mater. Sci. Eng. A 2017, 696, 544–551. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.; Wang, Y.; Li, H. Effect of technological parameters on the process performance of pure Al2O3 layer of Ni–Al2O3 FGMs by self-induced EDM. Int. J. Adv. Manuf. Technol. 2017, 90, 3633–3641. [Google Scholar] [CrossRef]
- Shi, G. A new simple third-order shear deformation theory of plates. Int. J. Solids Struct. 2007, 44, 4399–4417. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.S. Nonlinear bending analysis of shear deformable functionally graded plates subjected to thermo-mechanical loads under various boundary conditions. Compos. Part B Eng. 2003, 34, 103–115. [Google Scholar] [CrossRef]
- Samsam Shariat, B.A.; Eslami, M.R. Thermal buckling of imperfect functionally graded plates. Int. J. Solids Struct. 2006, 43, 4082–4096. [Google Scholar] [CrossRef]
- Yin, S.H.; Hale, J.S.; Yu, T.T.; Bui, Q.T.; Bordas, S.P.A. Isogeometric locking-free plate element: A simple first order shear deformation theory for functionally graded plates. Compos. Struct. 2015, 118, 121–138. [Google Scholar] [CrossRef]
- Bhardwaj, G.; Singh, I.V.; Mishra, B.K.; Bui, Q.T. Numerical simulation of functionally graded cracked plates using NURBS based XIGA under different loads and boundary conditions. Compos. Struct. 2015, 126, 347–359. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Mania, R.J. Dynamic response of thin FG plates with a static unsymmetrical stable postbuckling path. Thin Walled Struct. 2015, 86, 10–17. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Mania, J.R. Semi-analytical method versus the FEM for analysis of the local post-buckling. Compos. Struct. 2013, 97, 99–106. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Mania, R.J.; Grudziecki, J. Local nonsymmetric post-buckling equilibrium path in thin FGM plate. Eksploat. Niezawodn. Maint. Reliab. 2015, 17, 135–142. [Google Scholar] [CrossRef]
- Czechowski, L.; Kolakowski, Z. The study of buckling and post-buckling of a step-variable FGM box. Materials 2019, 16, 918. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Teter, A. Static interactive buckling of functionally graded columns with closed cross-sections subjected to axial compression. Compos. Struct. 2015, 123, 257–262. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Teter, A. Load carrying capacity of functionally graded columns with open cross-sections under static compression. Compos. Struct. 2015, 129, 1–7. [Google Scholar] [CrossRef]
- Huang, X.L.; Shen, H.S. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments. Int. J. Solids Struct. 2004, 41, 2403–2427. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Prusty, G.B.; Kelly, D.W. Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int. J. Mech. Sci. 2011, 53, 734–743. [Google Scholar] [CrossRef]
- Czechowski, L.; Kowal-Michalska, K. Static and dynamic buckling of rectangular functionally graded plates subjected to thermal loading. Strength Mater. 2013, 45, 666–673. [Google Scholar] [CrossRef]
- Czechowski, L. Analysis of dynamic response of functionally graded plate due to temperature pulse load. Compos. Struct. 2017, 160, 625–634. [Google Scholar] [CrossRef]
- Bui, T.Q.; Do, T.V.; Ton, L.H.T.; Doan, D.H.; Tanaka, S.; Pham, D.T.; Nguyen-Van, T.-A.; Yu, T.; Hirose, S. On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos. Part B 2016, 92, 218–224. [Google Scholar] [CrossRef]
- Praveen, G.N.; Reddy, J.N. Nonlinear transient thermal elastic analysis of functionally graded ceramic-metal plates. Int. J. Solids Struct. 1998, 35, 4457–4476. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Królak, M. Modal coupled instabilities of thin-walled composite plate and shell structures. Compos. Struct. 2006, 76, 303–313. [Google Scholar] [CrossRef]
- Kumar, R.; Lal, A.; Singh, B.N.; Singh, J. New transverse shear deformation theory for bending analysis of FGM plate under patch load. Compos. Struct. 2019, 208, 91–100. [Google Scholar] [CrossRef]
- Trabelsi, S.; Frikha, A.; Zghal, S.; Dammak, F. Thermal post-buckling analysis of functionally graded material structures using a modified FSDT. Int. J. Mech. Sci. 2018, 144, 74–89. [Google Scholar] [CrossRef]
- Vafakhah, Z.; Navayi Neya, B. An exact three dimensional solution for bending of thick rectangular FGM plate. Compos. Part B 2019, 156, 72–87. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Kim, N.I.; Lee, J. Analysis of thin-walled open-section beams with functionally graded materials. Compos. Struct. 2016, 138, 75–83. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Thang, P.T.; Lee, J. Lateral buckling analysis of thin-walled functionally graded open-section beams. Compos. Struct. 2017, 160, 952–963. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Thang, P.T.; Lee, J. Flexural-torsional stability of thin-walled functionally graded open-section beams. Thin Walled Struct. 2017, 110, 88–96. [Google Scholar] [CrossRef]
- Xu, G.; Huang, H.; Chen, B.; Chen, F. Buckling and postbuckling of elastoplastic FGM plates under inplane loads. Compos. Struct. 2017, 176, 225–233. [Google Scholar] [CrossRef]
- Qin, Z.; Compton, B.G.; Lewis, J.A.; Buehler, M.J. Structural Optimization of 3D-Printed Synthetic Spider Webs for High Strength. Nat. Commun. 2015, 6, 7038. [Google Scholar] [CrossRef]
- Dimas, L.S.; Bratzel, G.H.; Eylon, I.; Buehler, M.J. Tough Composites Inspired by Mineralized Natural Materials: Computation, 3D printing, and Testing. Adv. Funct. Mater. 2013, 23, 4629–4638. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Fang, G.; Leeflanf, S.; Zadpoor, A.A.; Zhou, J. Topological design, permeability and mechanical behavior of additively manufactured functionally graded porous metallic biomaterials. Acta Biomater. 2019, 85, 437–452. [Google Scholar] [CrossRef]
- Studart, A.R. Additive manufacturing of biologically-inspired materials. Chem. Soc. Rev. 2016, 45, 359–376. [Google Scholar] [CrossRef]
- User’s Guide ANSYS® 18.2. Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Users%20Guide.pdf (accessed on 16 November 2019).


| Description of Variant | tt [mm] | tc [mm] | tFGM [mm] |
|---|---|---|---|
| Var_1 | 2 | 0.2 | 1.8 |
| Var_2 | 2 | 0.4 | 1.6 |
| Var_3 | 2 | 0.6 | 1.4 |
| Var_4 | 2 | 0.8 | 1.2 |
| Var_5 | 2 | 1 | 1 |
| Components | Young’s Modulus [GPa] | Poisson’s Ratio [-] |
|---|---|---|
| Al | 70 | 0.33 |
| Al203 | 393 | 0.25 |
| Type of BC | Edge 1 | Edge 2 | Edge 3 | Edge 4 |
|---|---|---|---|---|
| SSSS | uz = 0 ux = moveable applied load Couple degree of freedom for nodes in x-directions | uy,uz = 0 | ux,uz = 0 | uz = 0 uy = moveable Couple degree of freedom for nodes in y-directions |
| SCSC | uz = 0 ux = moveable applied load Couple degree of freedom for nodes in x-directions | uy,uz = 0 rotx = 0 | ux,uz = 0 | uz = 0 uy = moveable rotx = 0 Couple degree of freedom for nodes in y-directions |
| CCCC | uz = 0 ux = moveable roty = 0 applied load Couple degree of freedom for nodes in x-directions | uy,uz = 0 rotx = 0 | ux,uz = 0 roty = 0 | uz = 0 uy = moveable rotx = 0 Couple degree of freedom for nodes in y-directions |
| Number of Layers in the FGM (Var_1) | Type of BC | FEM [N] | SAM [N] |
|---|---|---|---|
| 5 | SSSS | 28,994 | 27,876 |
| 7 | SSSS | 29,179 | 28,776 |
| 11 | SSSS | 29,663 | 29,392 |
| 15 | SSSS | 29,830 | 29,672 |
| 5 | SCSC | 53,491 | 50,888 |
| 7 | SCSC | 53,895 | 52,820 |
| 11 | SCSC | 54,970 | 54,160 |
| 15 | SCSC | 55,339 | 54,772 |
| 5 | CCCC | 68,584 | ------ |
| 7 | CCCC | 69,152 | ------ |
| 11 | CCCC | 70,667 | ------ |
| 15 | CCCC | 71,186 | ------ |
| Variant | Type of BC | FEM [N] | SAM [N] |
|---|---|---|---|
| Var_1 | SSSS | 29,663 | 29,392 |
| Var_2 | SSSS | 30,777 | 30,524 |
| Var_3 | SSSS | 31,910 | 31,716 |
| Var_4 | SSSS | 33,244 | 33,140 |
| Var_5 | SSSS | 34,954 | 34,956 |
| Var_1 | SCSC | 54,970 | 54,160 |
| Var_2 | SCSC | 57,161 | 56,384 |
| Var_3 | SCSC | 59,519 | 58,836 |
| Var_4 | SCSC | 62,374 | 61,840 |
| Var_5 | SCSC | 66,030 | 65,688 |
| Var_1 | CCCC | 70,667 | ------ |
| Var_2 | CCCC | 73,571 | ------ |
| Var_3 | CCCC | 76,776 | ------ |
| Var_4 | CCCC | 80,704 | ------ |
| Var_5 | CCCC | 85,734 | ------ |
| SSSS | SCSC | CCC | |||
|---|---|---|---|---|---|
| Fst = 16.5 kN |  | Fst = 16.5 kN | 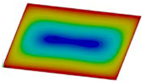 | Fst = 16.5 kN | 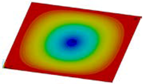 |
| Fst = 88.5 kN | 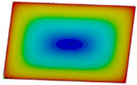 | Fst = 88.5 kN | 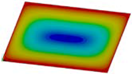 | Fst = 88.5 kN | 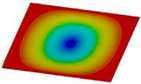 |
| Fst = 154.5 kN | 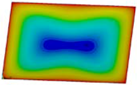 | Fst = 154.5 kN | 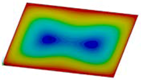 | Fst = 154.5 kN |  |
| Fst = 190.5 kN |  | Fst = 183 kN |  | Fst = 190.5 kN |  |
| Fst = 300 kN |  | Fst = 300 kN |  | Fst = 300 kN |  |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czechowski, L.; Kołakowski, Z. Analysis of the Functionally Step-Variable Graded Plate Under In-Plane Compression. Materials 2019, 12, 4090. https://doi.org/10.3390/ma12244090
Czechowski L, Kołakowski Z. Analysis of the Functionally Step-Variable Graded Plate Under In-Plane Compression. Materials. 2019; 12(24):4090. https://doi.org/10.3390/ma12244090
Chicago/Turabian StyleCzechowski, Leszek, and Zbigniew Kołakowski. 2019. "Analysis of the Functionally Step-Variable Graded Plate Under In-Plane Compression" Materials 12, no. 24: 4090. https://doi.org/10.3390/ma12244090
APA StyleCzechowski, L., & Kołakowski, Z. (2019). Analysis of the Functionally Step-Variable Graded Plate Under In-Plane Compression. Materials, 12(24), 4090. https://doi.org/10.3390/ma12244090





