Effect of Relative Density on Compressive Load Response of Crumpled Aluminium Foil Mesh
Abstract
1. Introduction
2. Methodology
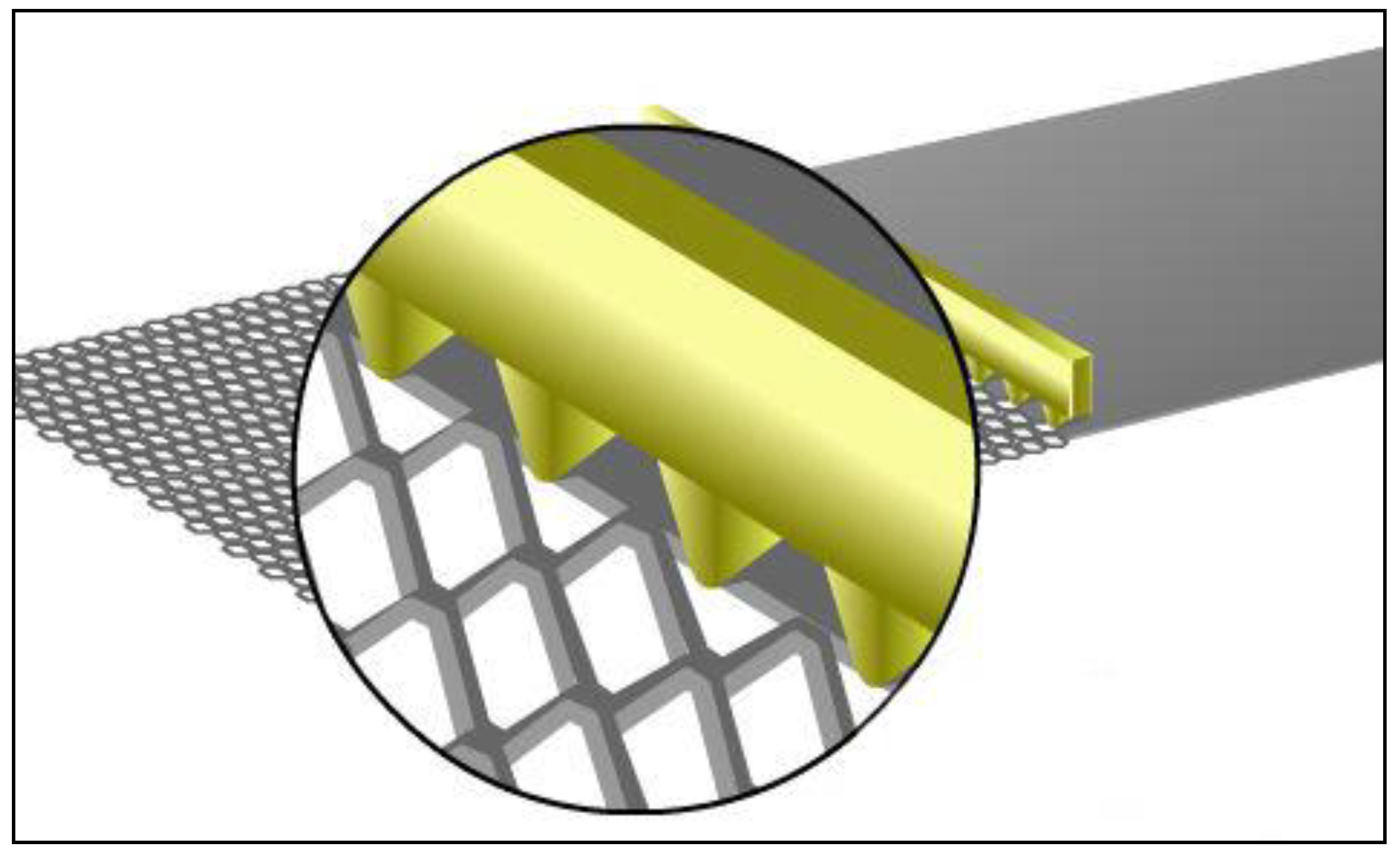
2.1. Materials and Forging of the CAFMs
2.2. Computed Tomography
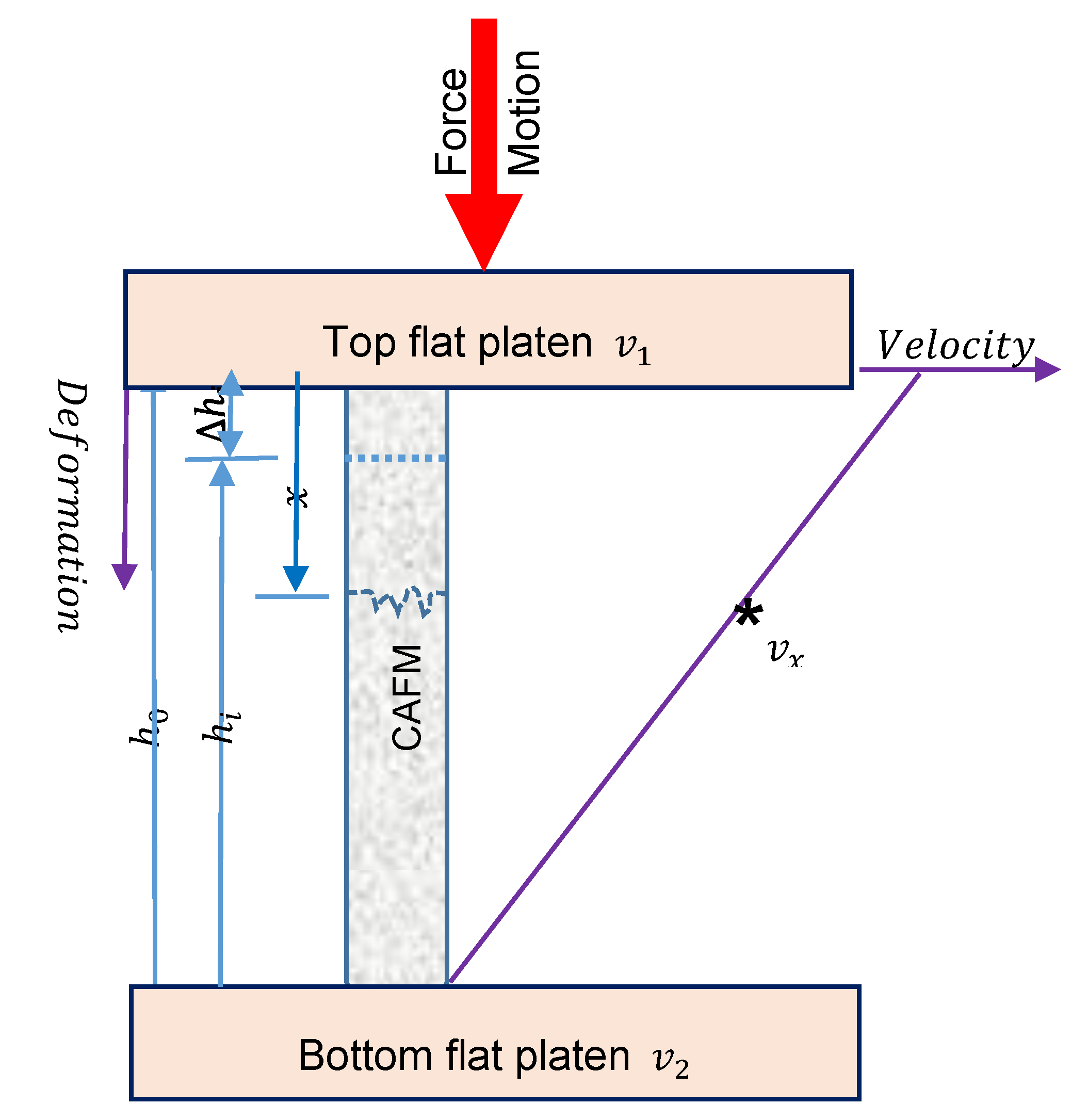
2.3. Uniaxial Compression Loading
Uniaxial Open and Close Die Compression Loading
3. Results and Discussion
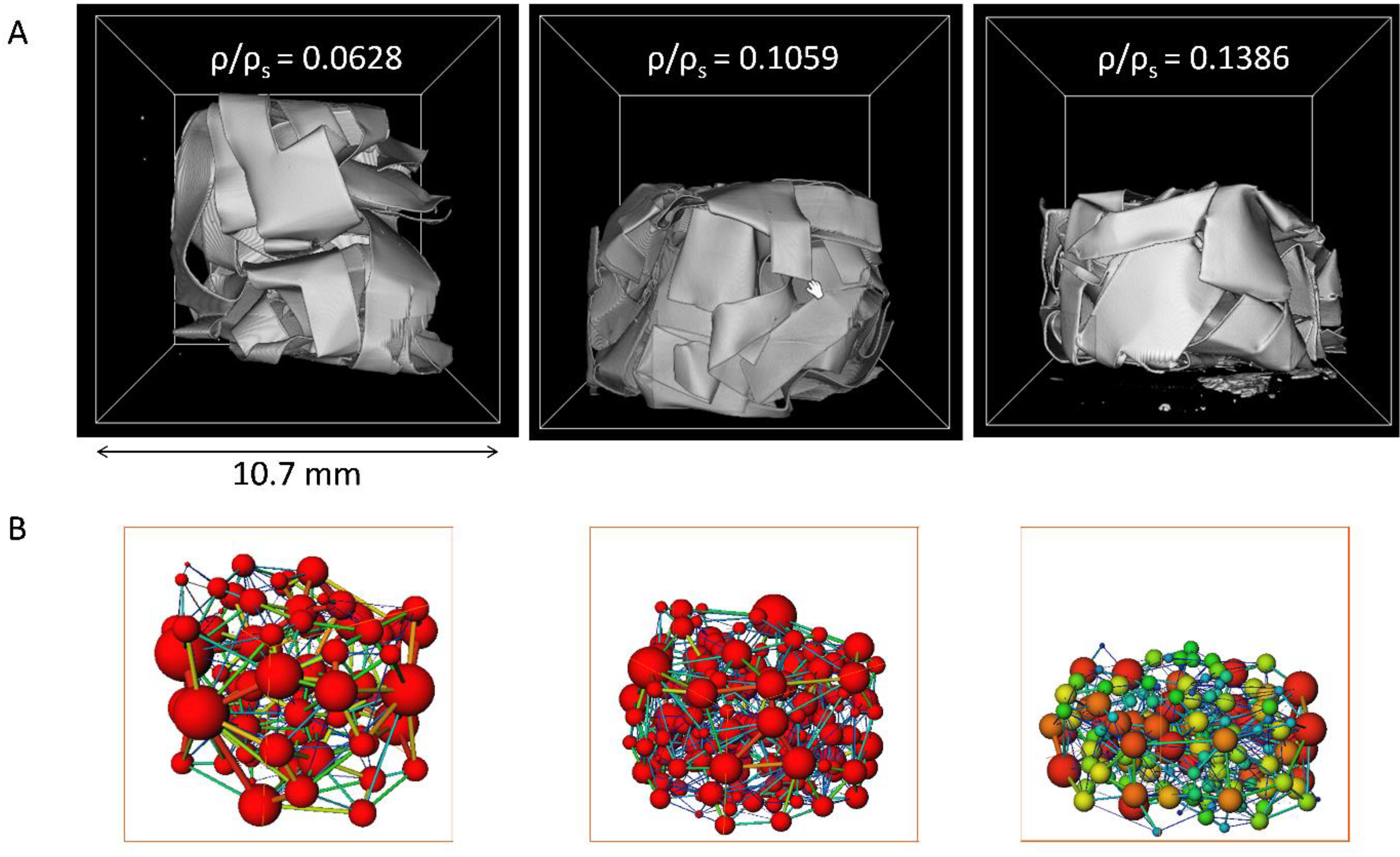
3.1. The X-ray Computed Micro-Tomography
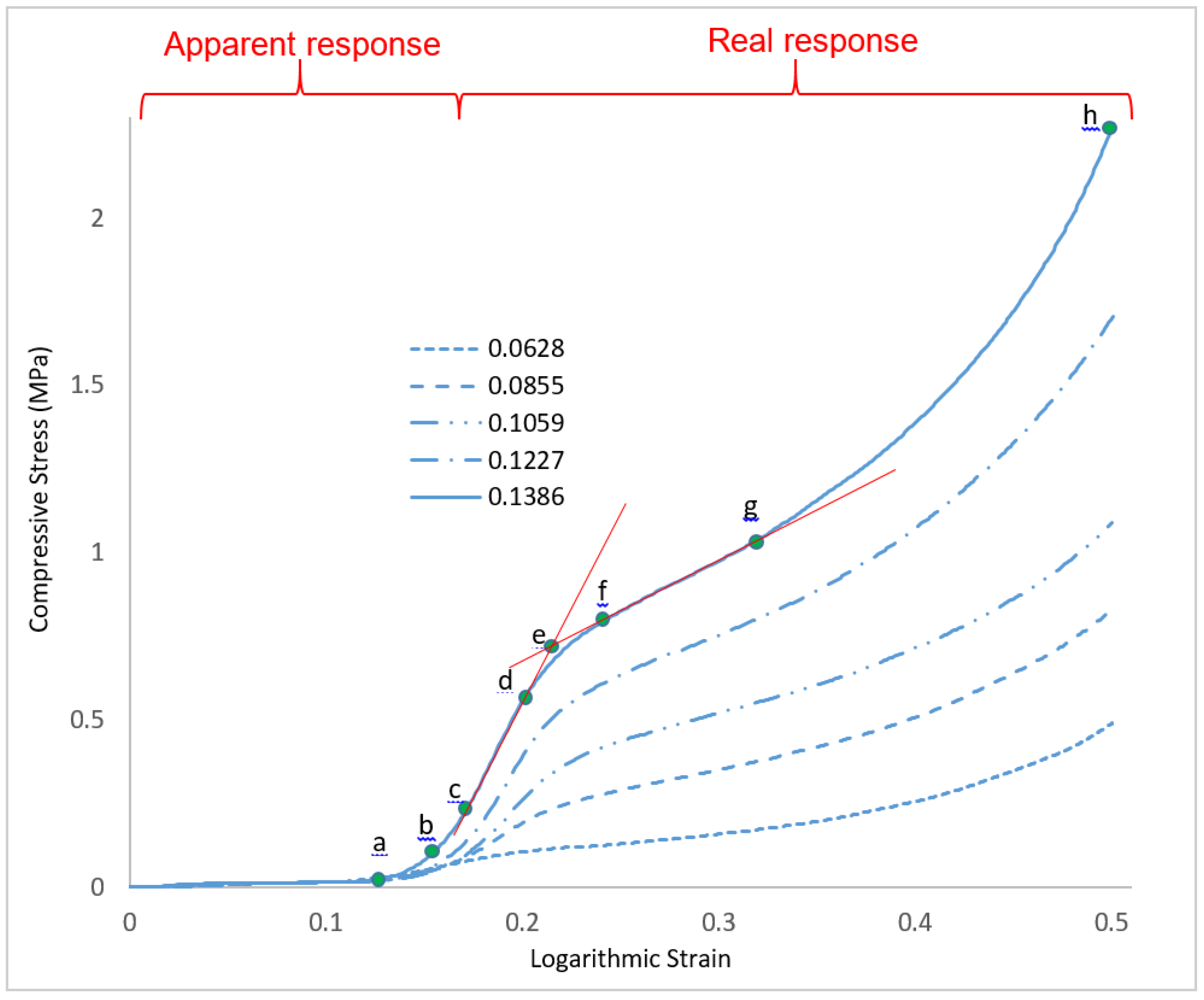
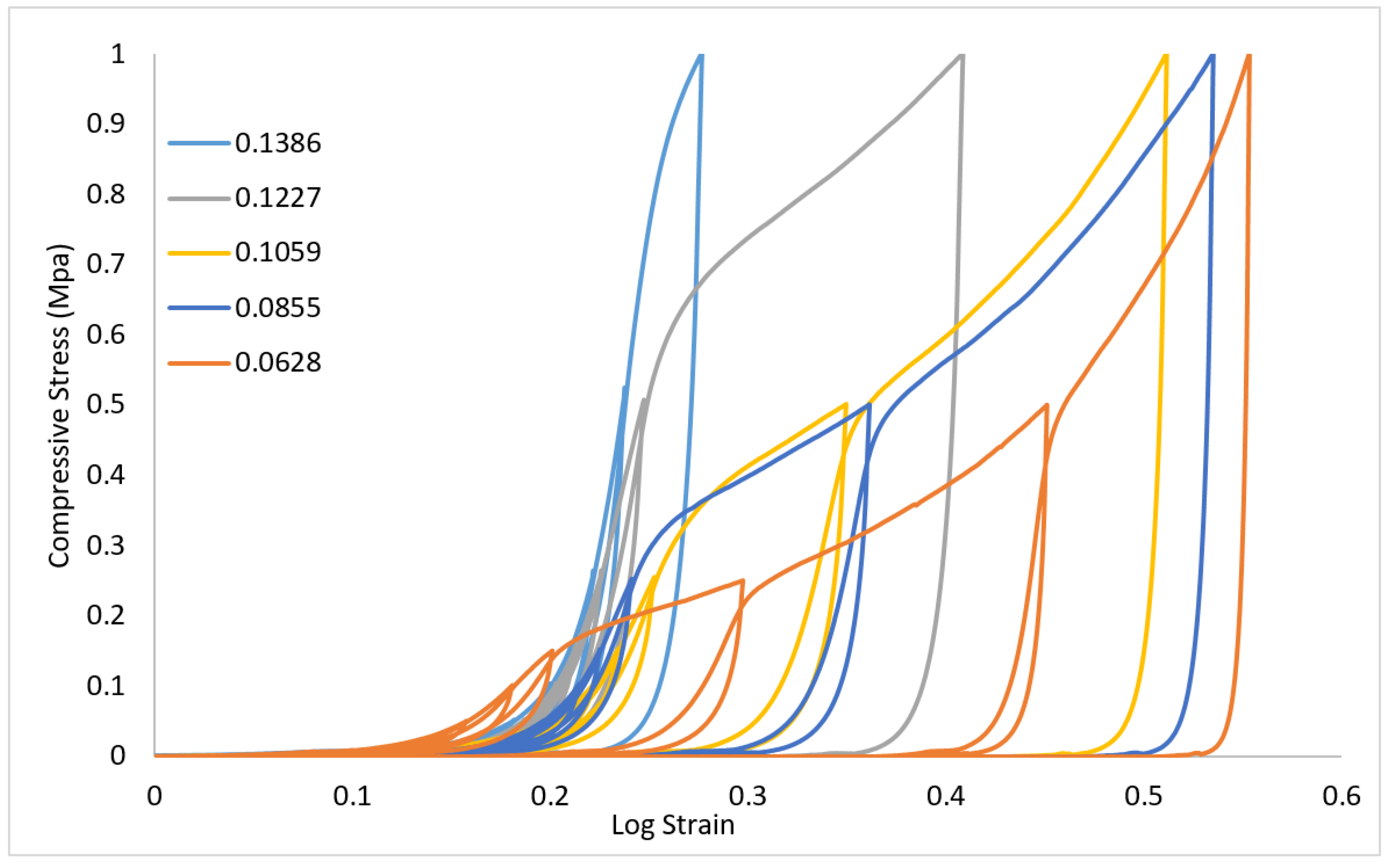
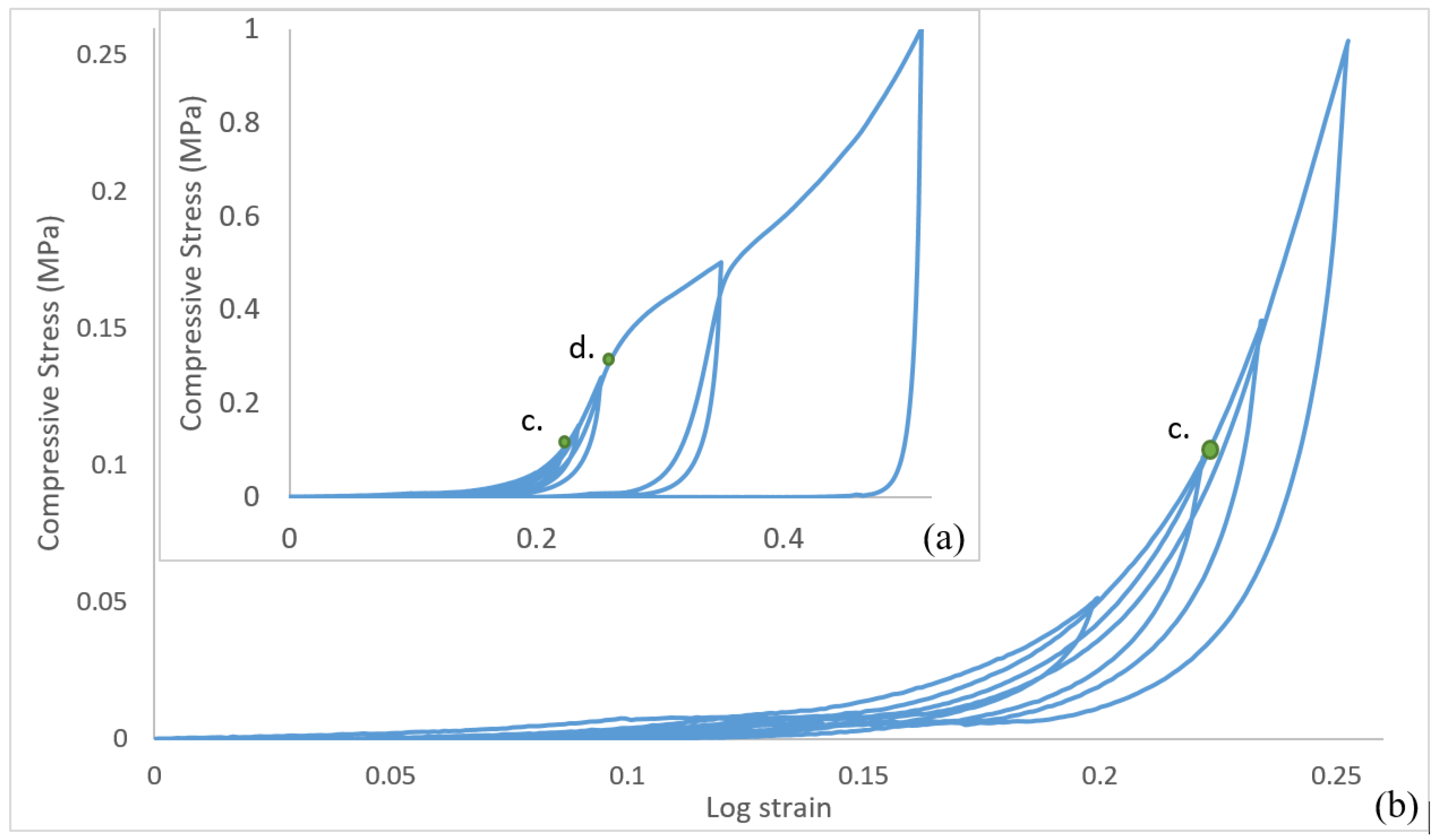
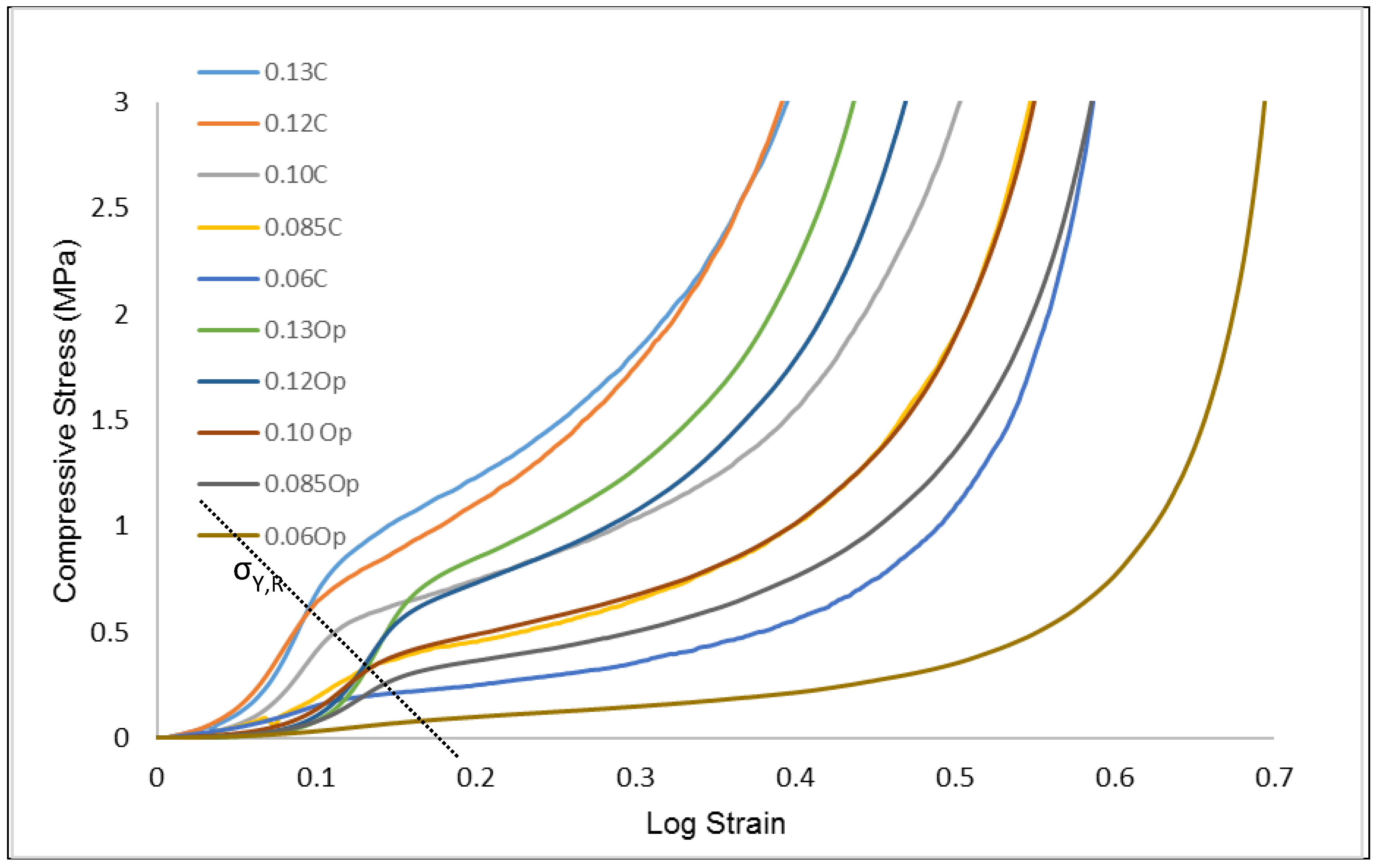
3.2. Effect of Relative Density on CAFMs Compressive Load Response
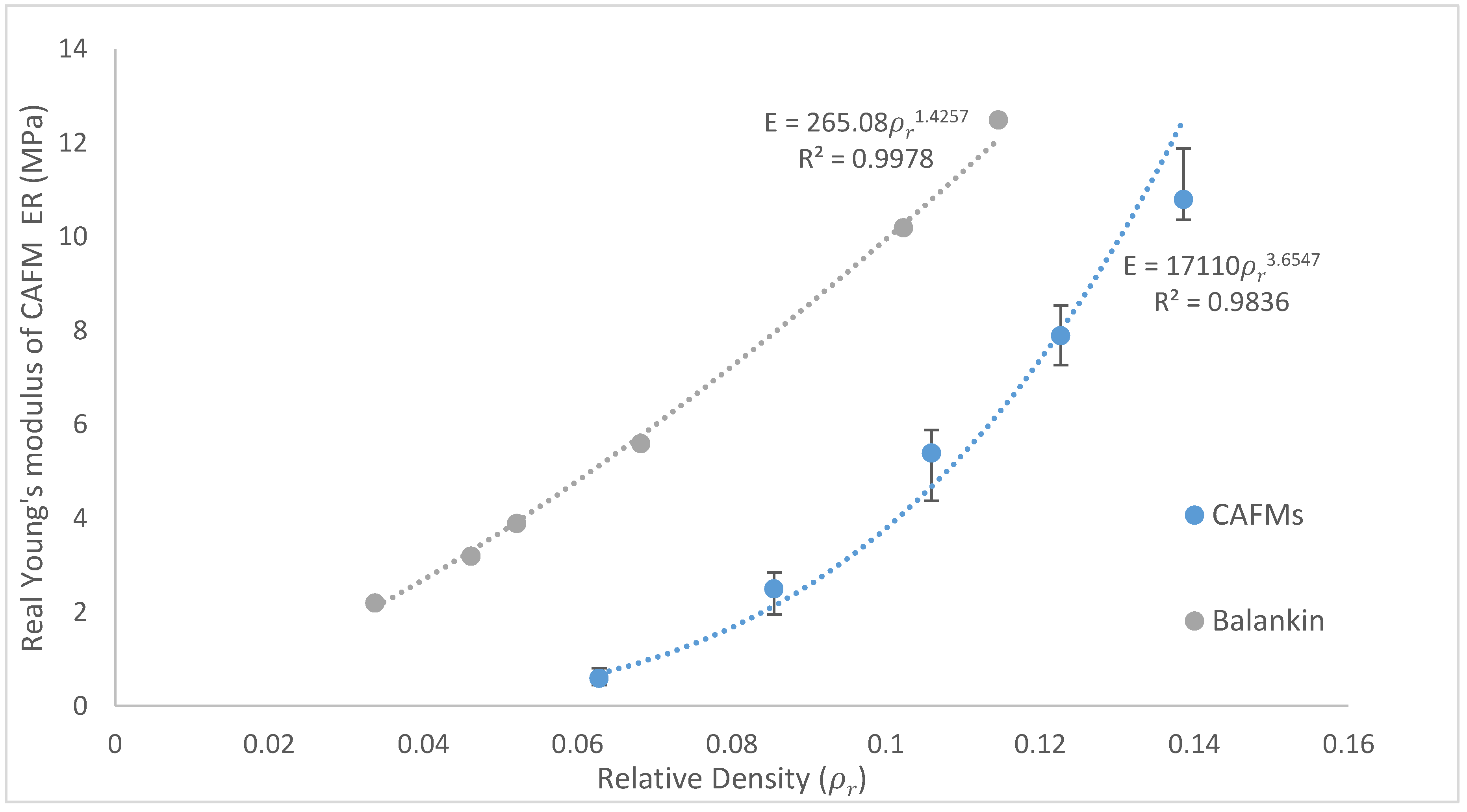
3.3. Effect of Relative Density on the CAFMs Real Young’s Modulus (Stiffness)
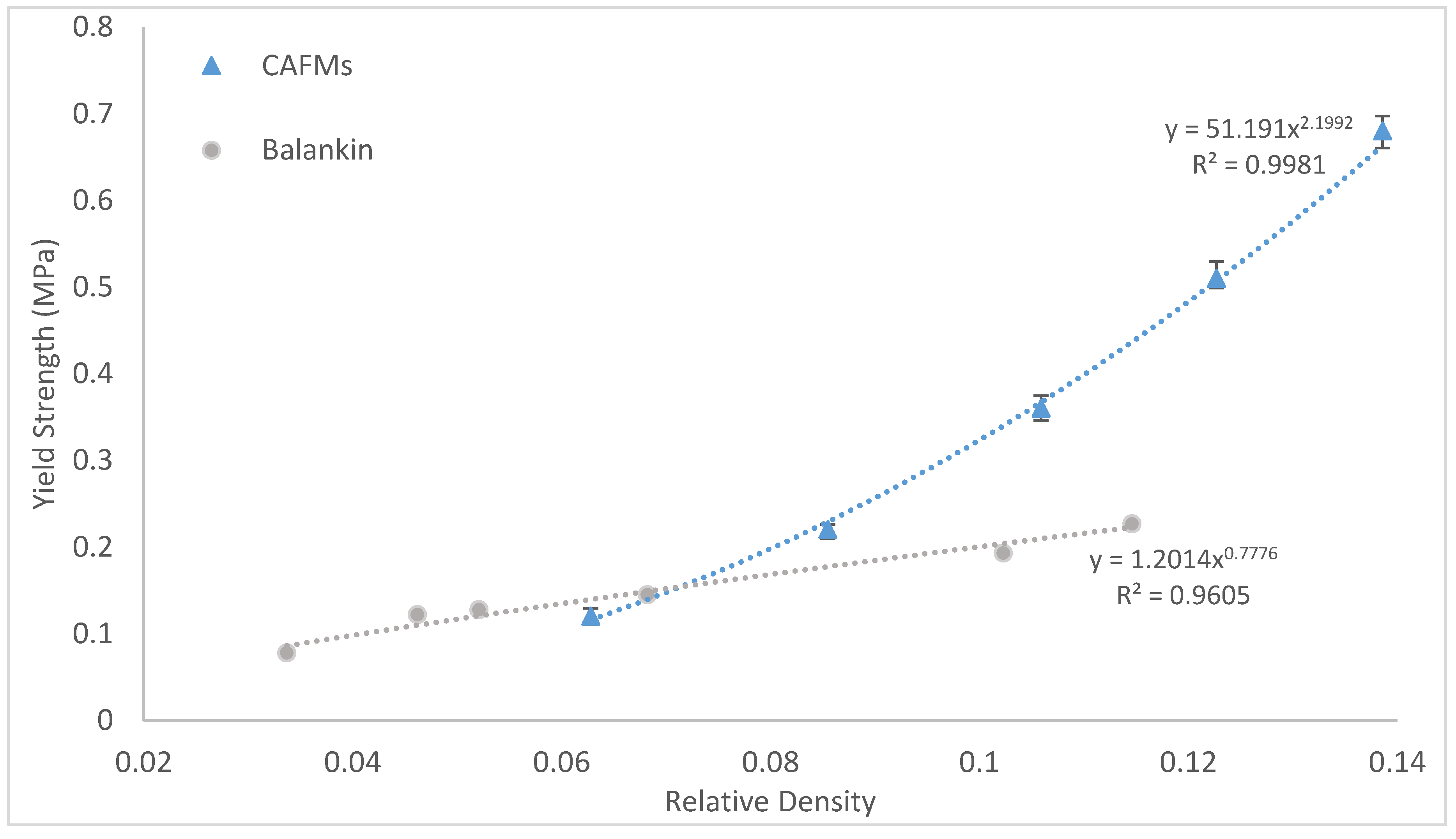
3.4. Effect of Relative Density on the CAFMs Effective Compressive Yield Strength
3.5. Effect of Compression Technique on CAFMs Real Compressive Strength
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Contuzzi, N.; Campanelli, S.L.; Caiazzo, F.; Alfieri, V. Design and Fabrication of Random Metal Foam Structures for Laser Powder Bed Fusion. Materials 2019, 12, 1301. [Google Scholar] [CrossRef] [PubMed]
- Duarte, I.; Peixinho, N.; Andrade-Campos, A.; Valente, R. Special Issue on Cellular Materials. Sci. Technol. Mater. 2018, 30, 1–3. [Google Scholar] [CrossRef]
- Duarte, I.; Ferreira, J.M.F. Composite and Nanocomposite Metal Foams. Materials 2016, 9, 79. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Pergamon Press: Oxford, UK, 1997. [Google Scholar]
- Banhart, J.; Seeliger, H. Aluminium Foam Sandwich Panels: Manufacture, Metallurgy and Applications. Adv. Eng. Mater. 2008, 10. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Banhart, J. Manufacturing routes for metallic foams. JOM 2000, 52, 22–27. [Google Scholar] [CrossRef]
- Lefebvre, L.P.; Banhart, J.; Dunand, D. Porous Metals and Metallic Foams: Current Status and Recent Developments. Adv. Eng. Mater. 2008, 10, 775–787. [Google Scholar] [CrossRef]
- Hill, C.; Eastoe, J. Foams: From nature to industry. Adv. Colloid Interface Sci. 2017, 247, 496–513. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G. Review of current trends in research and applications of sandwich structures. Compos. Part B: Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Bouaziz, O.; Masse, J.P.; Brechet, Y. An analytical description of the mechanical hysteresis of entangled materials during loading-unloading in uniaxial compression. Scr. Mater. 2018, 64, 107–109. [Google Scholar] [CrossRef]
- Barbier, C.; Dendievel, D.; Rodney, D. Numerical study of 3D-compressions of entangled materials. Comput. Mater. Sci. 2009, 45, 593–596. [Google Scholar] [CrossRef]
- Russell, G. Andreas Mortensen, 24—Porous Metals. In Physical Metallurgy, 5th ed.; David, E.L., Kazuhiro, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 2399–2595. ISBN 9780444537706. [Google Scholar] [CrossRef]
- Zhu, B.; Duke, M.; Dumée, L.F.; Merenda, A.; des Ligneris, E.; Kong, L.; Hodgson, P.D.; Gray, S. Short Review on Porous Metal Membranes-Fabrication, Commercial Products, and Applications. Membranes 2018, 8, 83. [Google Scholar] [CrossRef] [PubMed]
- García-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef] [PubMed]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide, 1st ed.; Elsevier: Boston, MA, USA, 2000. [Google Scholar]
- Maine, E.; Ashby, M. Cost Estimation and the Vialibity of Metal Foams. Adv. Eng. Mater. 2000, 2, 205–209. [Google Scholar] [CrossRef]
- Lehmhus, D.; Vesenjak, M.; Schampheleire, S.D.; Fiedler, T. From Stochastic Foam to Designed Structure: Balancing Cost and Performance of Cellular Metals. Materials 2017, 10, 922. [Google Scholar] [CrossRef]
- Bouaziz, O.; Masse, J.; Allain, S.; Orgéas, L.; Latil, P. Compression of crumpled aluminum thin foils and comparison with other cellular materials. Mater. Sci. Eng. A 2013, 570, 1–7. [Google Scholar] [CrossRef]
- Cottrino, S.; Viviès, P.; Fabrègue, D.; Maire, E. Mechanical properties of crumpled aluminum foils. Acta Mater. 2014, 81, 98–110. [Google Scholar] [CrossRef]
- Balankin, A.; Cruz, M.; Caracheo, L.; Huerta, O.; Rivas, C.; Martínez, C.; Ochoa, D.; Ruiz, L.; Gutiérrez, S.; Ortiz, J.; et al. Mechanical properties and relaxation behavior of crumpled aluminum foils. J. Mater. Sci. 2015, 50, 4749–4761. [Google Scholar] [CrossRef]
- Wang, Z.H.; Ma, H.W.; Zhao, L.M.; Yang, G.T. Studies on the dynamic compressive properties of open-cell aluminium alloy foams. Scr. Mater. 2006, 56, 83–87. [Google Scholar] [CrossRef]
- Smith, D.; Graciano, C.; Martínez, G. Recent Patents on Expanded Metal. Recent Pat. Mater. Sci. 2009, 200. [Google Scholar] [CrossRef]
- Smith, D.J.; Graciano, C.A.; Teixeira, P.; Martínez, G.; Pertuz, A. Energy Absorption Characteristics of Coiled Expanded Metal Tubes Under Axial Compression. Lat. Am. J. Solids Struct. 2016, 13, 3145–3160. [Google Scholar] [CrossRef][Green Version]
- Graciano, C.; Martínez, G.; Gutierrez, A. Failure mechanism of expanded metal tubes under axial crushing. Thin-Walled Struct. 2011, 51, 20–24. [Google Scholar] [CrossRef]
- Haghi, M.; Shahsavari, H.; Akbarshahi, H.; Shakeri, M. Bitubular square tubes with different arrangements under quasi-static axial compression loading. Mater. Des. 2013, 51, 1095–1103. [Google Scholar] [CrossRef]
- Nia, A.A.; Chahardoli, S. Mechanical behavior of nested multi-tubular structures under quasi-static axial load. Thin-Walled Struct. 2016, 106, 376–389. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, G.; Li, G.; Luo, Z.; Li, Q. Optimization of foam-filled bitubal structures for crashworthiness criteria. Mater. Des. 2012, 38, 99–109. [Google Scholar] [CrossRef]
- Saeed, S.L.; Martin, M.; Anders, C.O.; Søren, K.K. Experimental and numerical study of flow in expanded metal plate for water electrolysis applications. J. Power Sources 2018, 397, 334–342. [Google Scholar] [CrossRef]
- Ibrahim, G.S.; Yousry, B.S.; Essam, L.E.; Osama, A.K.; Peter, A.A. Flexural characteristics of lightweight ferrocement beams with various types of core materials and mesh reinforcement. Constr. Build. Mater. 2018, 171, 802–816. [Google Scholar] [CrossRef]
- Taghipoor, H.; Nouri, M.D. Axial crushing and transverse bending responses of sandwich structures with lattice core. J. Sandw. Struct. Mater. 2018. [Google Scholar] [CrossRef]
- Wang, A.; Yuan, W.; Huang, S.M.; Tang, Y.; Chen, Y. Structural effects of expanded metal mesh used as a flow field for a passive direct methanol fuel cell. Appl. Energy 2017, 208, 184–194. [Google Scholar] [CrossRef]
- Graciano, C.; Smith, D.; Aparicio, G. An empirical method for the estimation of yield strength on bonds and strands of expanded metal meshes. Rev. Fac. Ing. 2015, 1, 132–142. [Google Scholar]
- Thompson, H.; Skipper, N.T.; Wasse, J.C.; Spencer Howells, W.; Hamilton, M.; Fernandez-Alonso, F. Proton dynamics in lithium-ammonia solutions and expanded metals. J. Chem. Phys. 2006, 124. [Google Scholar] [CrossRef] [PubMed]
- Raj, E.R.; Parameswaran, V.; Daniel, B.S.S. Comparison of quasi-static and dynamic compression behavior of closedcell aluminum foam. Mater. Sci. Eng. A 2009, 526, 11–15. [Google Scholar]
- Linul, E.; Marsavina, L.; Kováčik, J. Collapse mechanisms of metal foam matrix composites under static and dynamic loading conditions. Mater. Sci. Eng. A 2017, 690, 214–224. [Google Scholar] [CrossRef]
- Orbulov, I.N.; Májlinger, K. Description of the compressive response of metal matrix syntactic foams. Mater. Des. 2013, 49, 1–9. [Google Scholar] [CrossRef]
- Liu, H.; Cao, Z.K.; Luo, H.J.; Shi, J.C.; Yao, G.C. Performance of closed-cell aluminum foams subjected to impact loading. Mater. Sci. Eng. A 2013, 570, 27–31. [Google Scholar] [CrossRef]
- Vesenjak, M.; Sulong, M.A.; Krstulović-Opara, L.; Borovinšek, M.; Mathier, V.; Fiedler, T. Dynamic compression of aluminium foam derived from infiltration casting of salt dough. Mech. Mater. 2016, 93, 96–108. [Google Scholar] [CrossRef]
- Montanini, R. Measurement of strain rate sensitivity of aluminium foams for energy dissipation. Int. J. Mech. Sci. 2005, 47, 26–42. [Google Scholar] [CrossRef]
- Doyoyo, M.; Mohr, D. Experimental determination of the mechanical effects of mass density gradient in metallic foams under large multiaxial inelastic deformation. Mech. Mater. 2006, 38, 325–339. [Google Scholar] [CrossRef]
- Linul, E.; Movahedi, N.; Marsavina, L. The temperature and anisotropy effect on compressive behavior of cylindrical closed-cell aluminum-alloy foams. J. Alloys Compd. 2018, 740, 1172–1179. [Google Scholar] [CrossRef]
- Kováik, J.; Jerz, J.; Mináriková, N.; Marsavina, L.; Linul, E. Scaling of Compression Strength in Disordered Solids: Metallic Foams. Frat. Int. Strut. 2016, 10, 55–62. [Google Scholar] [CrossRef]
- Orbulov, I.N.; Ginsztler, J. Compressive characteristics of metal matrix syntactic foams. Compos. Part A: Appl. Sci. Manuf. 2012, 43, 553–561. [Google Scholar] [CrossRef]
- Hsieh, J. Computed Tomography: Principles, Design, Artifacts, and Recent Advances, 3rd ed.; Society of Photo-optical Instrumentation Engineers; SPIE Digital Library: Bellingham, WA, USA, 2015; ISBN 9781628418255. [Google Scholar]
- Saadatfar, M.; Garcia-Morenob, F.; Hutzler, S.; Sheppard, A.P.; Knackstedt, M.A. Imaging of metallic foams using X-ray micro-CT. Colloids Surf. A: Physicochem. Eng. Asp. 2009, 344, 107–112. [Google Scholar] [CrossRef]
- Veyhl, C.; Belova, I.V.; Murch, G.E.; Fiedler, T. Finite element analysis of the mechanical properties of cellular aluminium based on micro-computed tomography. Mater. Sci. Eng. A 2011, 528, 4550–4555. [Google Scholar] [CrossRef]
- Cnudde, V.; Boone, M.N. High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications. Earth-Sci. Rev. 2013, 123, 1–17. [Google Scholar] [CrossRef]
- Fusseis, F.; Xiao, X.; Schrank, C.; De Carlo, F. A brief guide to synchrotron radiation-based microtomography in (structural) geology and rock mechanics. J. Struct. Geol. 2014, 65, 1–16. [Google Scholar] [CrossRef]
- Gonzales, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Proccesing Using MATLAB; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2013; pp. 1–5. ISBN 0130085197. [Google Scholar]






| S/No | Crumpled Aluminium Foil Mesh (CAFM) | Mesh Dimension (mm2) | ho (mm) | ||
|---|---|---|---|---|---|
| 1 | 200 × 200 | 31.57 | 0.0628 | 15.212 | |
| 2 | 22.59 | 0.0855 | 21.758 | ||
| 3 | 17.45 | 0.1059 | 13.958 | ||
| 4 | 15.20 | 0.1227 | 16.786 | ||
| 5 | 14.15 | 0.1386 | 13.908 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hughes, D.; Amalu, E.H.; Pak, T.; Kennedy, R. Effect of Relative Density on Compressive Load Response of Crumpled Aluminium Foil Mesh. Materials 2019, 12, 4018. https://doi.org/10.3390/ma12234018
Hughes D, Amalu EH, Pak T, Kennedy R. Effect of Relative Density on Compressive Load Response of Crumpled Aluminium Foil Mesh. Materials. 2019; 12(23):4018. https://doi.org/10.3390/ma12234018
Chicago/Turabian StyleHughes, David, Emeka H. Amalu, Tannaz Pak, and Ryan Kennedy. 2019. "Effect of Relative Density on Compressive Load Response of Crumpled Aluminium Foil Mesh" Materials 12, no. 23: 4018. https://doi.org/10.3390/ma12234018
APA StyleHughes, D., Amalu, E. H., Pak, T., & Kennedy, R. (2019). Effect of Relative Density on Compressive Load Response of Crumpled Aluminium Foil Mesh. Materials, 12(23), 4018. https://doi.org/10.3390/ma12234018






